The Spin–Orbit Effect on the Electronic Structures, Refractive Indices, and Birefringence of X2PO4I (X = Pb, Sn, Ba and Sr): A First-Principles Investigation
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
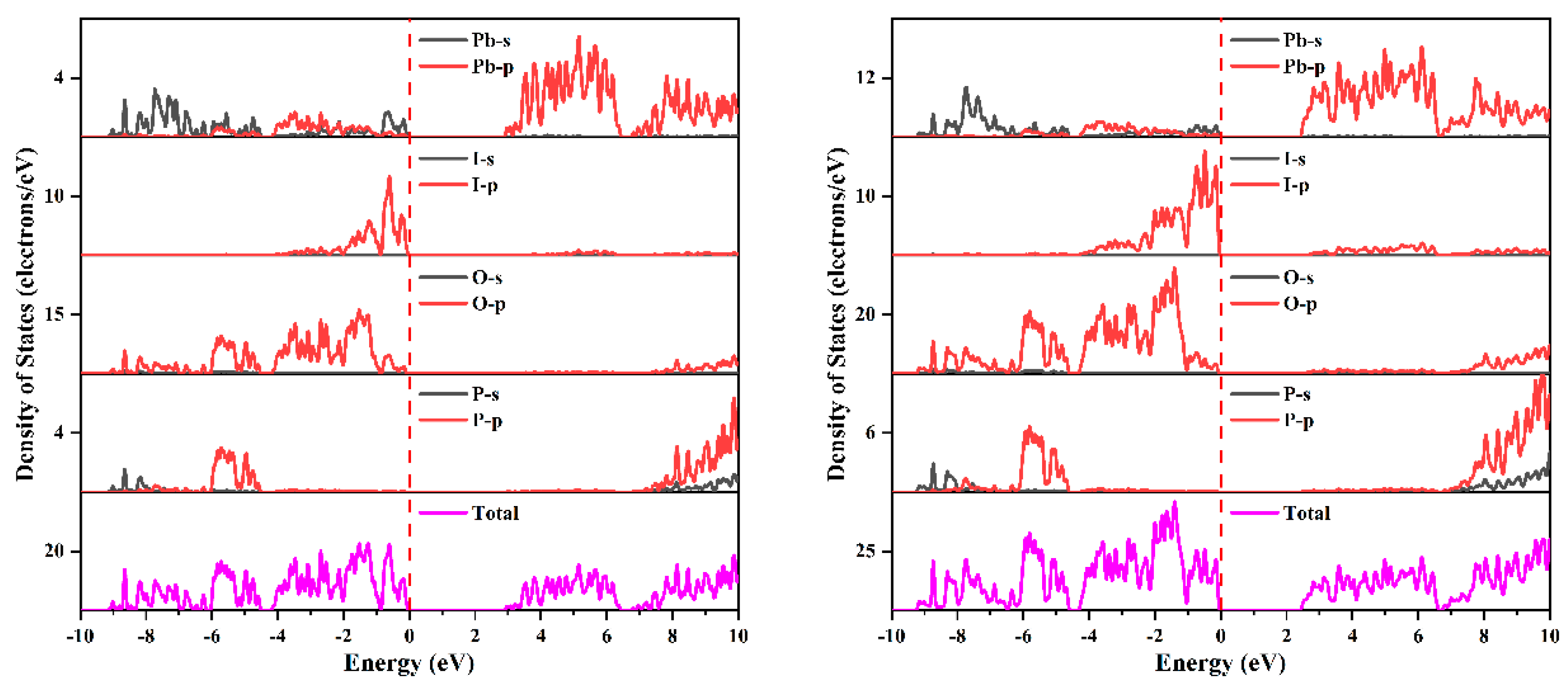
3.1. The Electronic Structures, Refractive Indices, and Birefringence of Pb2PO4I
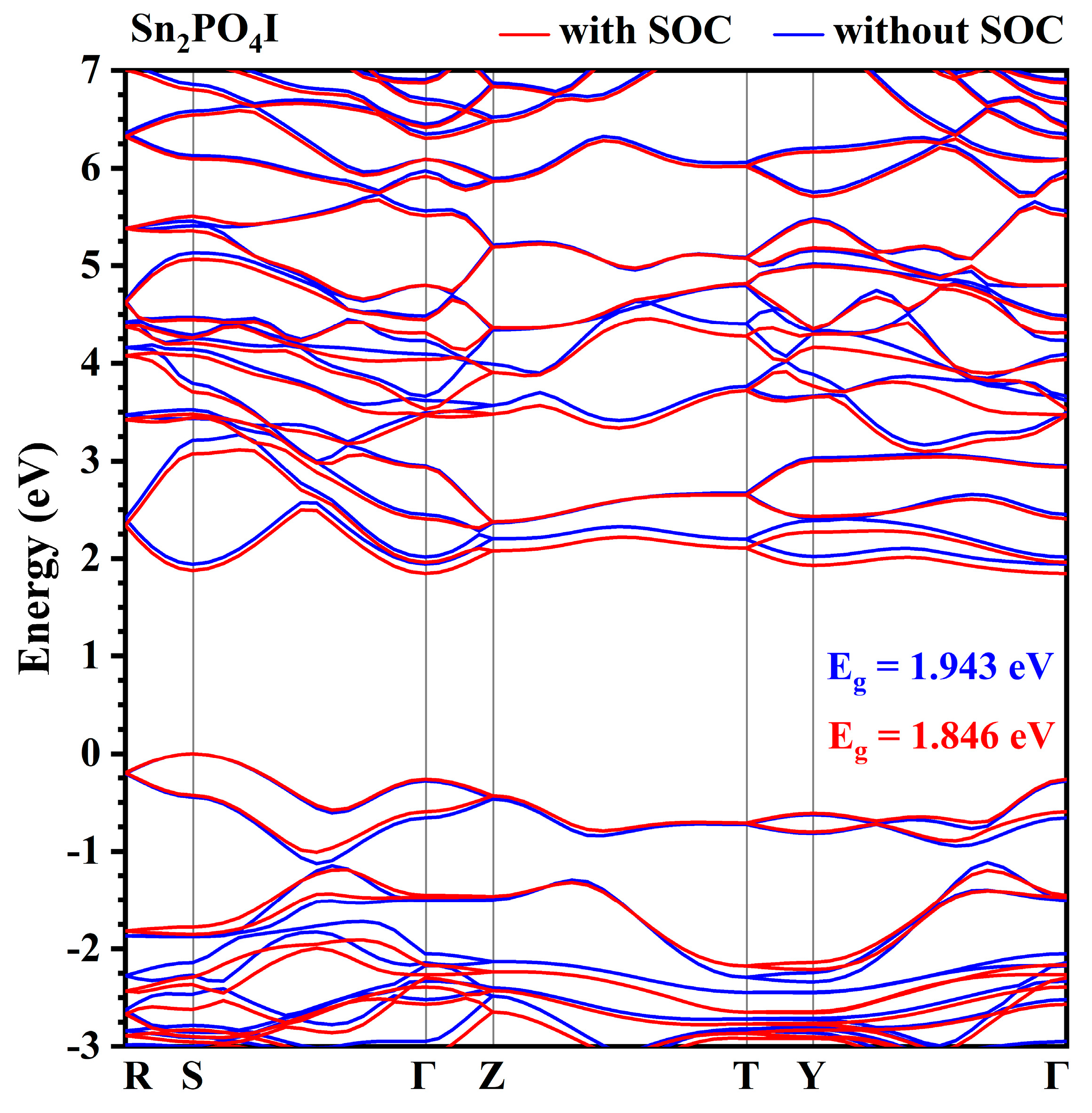
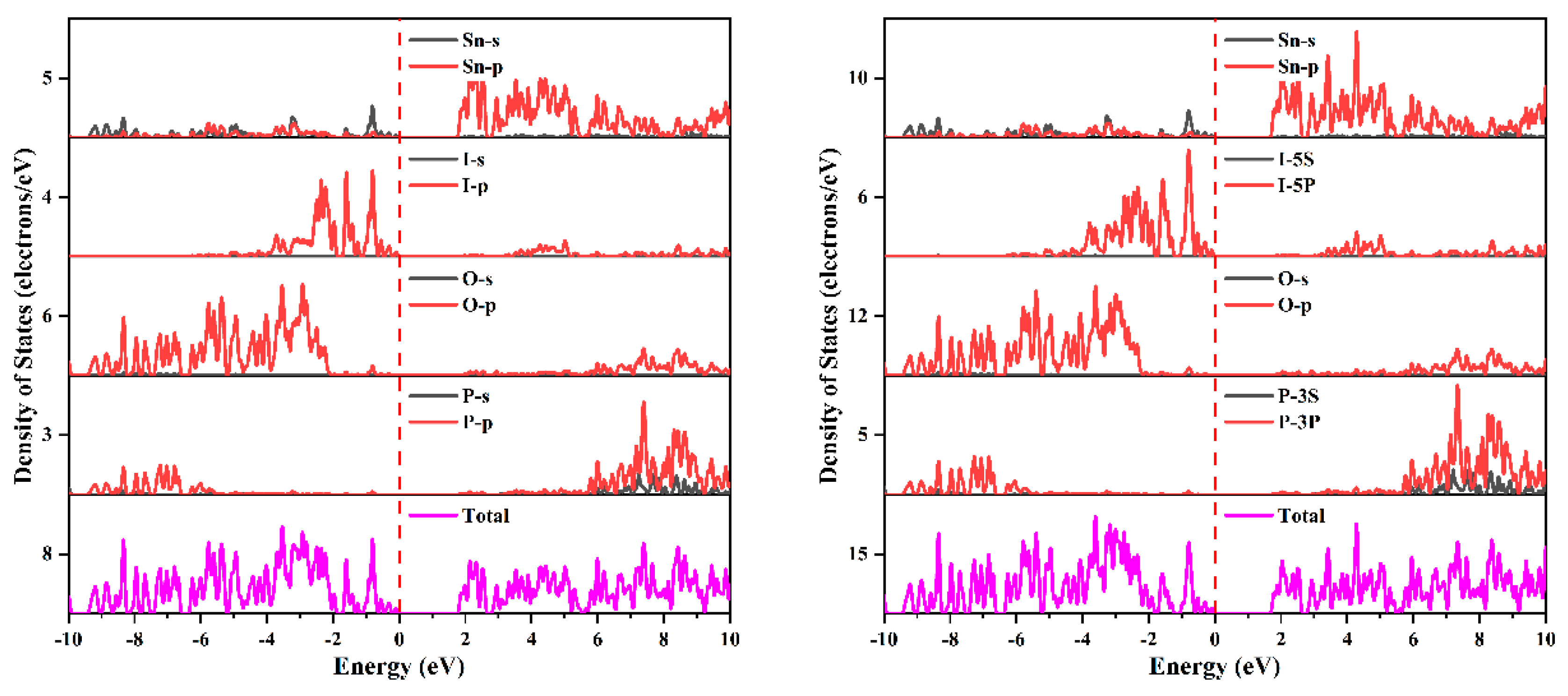
3.2. The Electronic Structures, Refractive Indices, and Birefringence of Sn2PO4I
3.3. The Electronic Structures, Refractive Indices, and Birefringence of X2PO4 (X = Ba, and Sr)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, C.-W.; Yang, Z.-W.; Yan, H.-H.; Li, J.; Yu, H.-X.; Zhang, L.-Y.; Shu, J. Synergistic dual conversion reactions assisting Pb-S electrochemistry for energy storage. Proc. Natl. Acad. Sci. USA 2022, 119, e2118675119. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.; Liu, Y.; Chen, H.-X.; Feng, K.-J.; Jia, K.-X.; Pan, K.-M.; Wang, G.-X.; Huang, T.; Pang, X.-C.; Zhang, Q.-B. Emerging bismuth-based materials: From fundamentals to electrochemical energy storage applications. Energy Storage Mater. 2023, 58, 232–270. [Google Scholar] [CrossRef]
- Little, R.B. Near ambient superconductivity by 15N as needles in the haystack: Lower temperatures and pressures for possible 15N enrichment in LuH2. Eur. J. Appl. Physiol. 2023, 5, 1–4. [Google Scholar] [CrossRef]
- Yue, C.-M.; Christiansson, V.; Werner, P. Correlated electronic structure of Pb10−xCux(PO4)6O. Phys. Rev. B 2023, 108, L201122. [Google Scholar] [CrossRef]
- Zhi, X.; Xie, F.-X.; Zavabeti, A.; Li, G.K.; Harvie, D.J.E.; Kashi, E.; Batterham, R.J.; Liu, J.Z. Fundamentals, applications, and perspectives of liquid metals in catalysis: An overview of molecular simulations. Energy Fuels 2023, 37, 17875–17891. [Google Scholar] [CrossRef]
- Zhan, C.-H.; Bu, L.-Z.; Sun, H.-R.; Huang, X.-W.; Zhu, Z.-P.; Yang, T.; Ma, H.-B.; Li, L.-G.; Wang, Y.-C.; Geng, H.-B.; et al. Medium/high-entropy amalgamated core/shell nanoplate achieves efficient formic acid catalysis for direct formic acid fuel cell. Angew. Chem. Int. Ed. 2022, 62, e202213783. [Google Scholar] [CrossRef] [PubMed]
- Rößner, L.; Patiño Soriano, D.T.; Tiryaki, O.; Burkhardt, U.; Armbrüster, M. Synthesis of isostructural intermetallic Sn–Pb–Bi–Pt platform materials for catalytic investigations. Inorg. Chem. 2023, 62, 4688–4695. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.-J.; Wu, M.-Z.; Peng, J.-B.; Zheng, H.-X. Purification of high-purity tin via vertical zone refining. Separations 2023, 10, 380. [Google Scholar] [CrossRef]
- Zhang, J.-W.; Pang, J.-H.; Chen, H.; Wei, G.; Wei, S.-R.; Wang, K.-Y.; Yan, J. Theoretical study of 2D PbSe/Bi2Se3 heterojunctions as gas sensors for the detection of SO2 and Cl2. Phys. Scr. 2023, 98, 095905. [Google Scholar] [CrossRef]
- Shao, X.; Shi, Y.; Wang, H.-Y.; Sun, X.-F.; Yang, L.; Li, X.; Wang, M.-H. A review on advances in the gas-sensitive properties of perovskite materials. J. Electron. Mater. 2023, 52, 5795–5809. [Google Scholar] [CrossRef]
- Han, S.-J.; Tudi, A.; Zhang, W.-B.; Hou, X.-L.; Yang, Z.-H.; Pan, S.-L. Recent development of SnII, SbIII-based birefringent material: Crystal chemistry and investigation of birefringence. Angew. Chem. Int. Ed. 2023, 62, e202302025. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-F.; Zhang, H.-L.; Jiao, D.-X.; He, C.; Guo, Y.-X.; An, X.-T.; Wei, Q. Pb(OH)I: A lead(II)-based oxyhalide with a large birefringence. Inorg. Chem. Commun. 2023, 154, 110960. [Google Scholar] [CrossRef]
- Bai, Z.-Y.; Ok, K.M. Exceptional optical anisotropy enhancement achieved through dual-ions cosubstitution strategy in novel hybrid bismuth halides. Small 2024, 2311391. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Tu, C.-C.; Yang, Z.-H.; Han, S.-J.; Pan, S.-L. Sn9O4Br9X (X = Cl, Br): Two new Sn(II) oxyhalides exhibiting large birefringence derived from highly distortive polyhedra of lone pair cations. Scr. Mater. 2023, 231, 115437. [Google Scholar] [CrossRef]
- Yang, M.; Liu, W.-L.; Guo, S.-P. Sb5O7I: Exploration of ternary antimony-based oxyhalide as a nonlinear-optical material. Inorg. Chem. 2022, 61, 14517–14522. [Google Scholar] [CrossRef]
- Zhao, C.-Y.; Zhang, B.-B.; Tian, X.-Y.; Zhou, G.-Q.; Xu, J.-J.; Wu, K. Na6Sn3P4S16: Sn(ii)-chelated PS4 groups inspired an ultra-strong SHG response. Inorg. Chem. Front. 2023, 10, 5726–5733. [Google Scholar] [CrossRef]
- Akil, Z.; Boutaleb, H.; Zemouli, M.; Keteb, M.; Amara, K.; Elkeurti, M. Enhancing second harmonic generation response in infrared nonlinear optical material through Pb substitution: A study of Li2PbSiS4 compound. Optik 2023, 294, 171441. [Google Scholar] [CrossRef]
- Ran, M.-Y.; Wang, A.Y.; Wei, W.-B.; Wu, X.-T.; Lin, H.; Zhu, Q.-L. Recent progress in the design of IR nonlinear optical materials by partial chemical substitution: Structural evolution and performance optimization. Coord. Chem. Rev. 2023, 481, 215059. [Google Scholar] [CrossRef]
- Dong, X.-Y.; Jing, Q.; Shi, Y.-J.; Yang, Z.-H.; Pan, S.-L.; Poeppelmeier, K.R.; Young, J.; Rondinelli, J.M. Pb2Ba3(BO3)3Cl: A material with large shg enhancement activated by pb-chelated bo3 groups. J. Am. Chem. Soc. 2015, 137, 9417–9422. [Google Scholar] [CrossRef]
- Abudoureheman, M.; Han, S.-J.; Lei, B.-H.; Yang, Z.-H.; Long, X.; Pan, S.-L. KPb2(PO3)5: A novel nonlinear optical lead polyphosphate with a short deep-UV cutoff edge. J. Mater. Chem. C. 2016, 4, 10630–10637. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.-M.; Zhang, D.; Gao, D.-J.; Bi, J.; Huang, L.; Zou, G.-H. Centrosymmetric RbSnF2NO3 vs. noncentrosymmetric Rb2SbF3(NO3)2. Inorg. Chem. Front. 2021, 8, 3317–3324. [Google Scholar] [CrossRef]
- Deng, Y.-L.; Huang, L.; Dong, X.-H.; Wang, L.; Ok, K.M.; Zeng, H.-M.; Lin, Z.; Zou, G.-H. K2Sb(P2O7)F: Cairo pentagonal layer with bifunctional genes reveal optical performance. Angew. Chem. Int. Ed. 2020, 59, 21151–21156. [Google Scholar] [CrossRef]
- Dong, X.-H.; Huang, L.; Hu, C.-F.; Zeng, H.-M.; Lin, Z.; Wang, X.; Ok, K.M.; Zou, G.-H. CsSbF2SO4: An excellent ultraviolet nonlinear optical sulfate with a KTiOPO4 (KTP)-type Structure. Angew. Chem. Int. Ed. 2019, 58, 6528–6534. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.-L.; Cheng, W.-D.; Zhang, H.; Geng, L.; Lin, C.-S.; He, Z.-Z. A strong second-harmonic generation material Cd4BiO(BO3)3 Originating from 3-chromophore asymmetric structures. J. Am. Chem. Soc. 2010, 132, 1508–1509. [Google Scholar] [CrossRef]
- Mao, F.F.; Hu, C.L.; Xu, X.; Yan, D.; Yang, B.P.; Mao, J.G. Bi(IO3)F2: The first metal iodate fluoride with a very strong second harmonic generation effect. Angew. Chem. Int. Ed. 2017, 56, 2151–2155. [Google Scholar] [CrossRef]
- Guo, J.-Y.; Tudi, A.; Han, S.-J.; Yang, Z.-H.; Pan, S.-L. Sn2B5O9Cl: A material with large birefringence enhancement activated prepared via alkaline-earth-metal substitution by tin. Angew. Chem. Int. Ed. 2019, 58, 17675–17678. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.-Y.; Cheng, S.-C.; Han, S.-J.; Yang, Z.-H.; Pan, S.-L. Sn2B5O9Br as an outstanding bifunctional material with strong second-harmonic generation effect and large birefringence. Adv. Opt. Mater. 2020, 9, 2001734. [Google Scholar] [CrossRef]
- Fouassier, C.; Levasseur, A.; Hagenmuller, P. Les halogénoborates M2B5O9X (M = Ca, Sr, Ba, Eu, Pb; X = Cl, Br). J. Solid State Chem. 1971, 3, 206–208. [Google Scholar] [CrossRef]
- Guo, J.-Y.; Tudi, A.; Han, S.-J.; Yang, Z.-H.; Pan, S.-L. Sn2PO4I: An excellent birefringent material with giant optical anisotropy in non π-conjugated phosphate. Angew. Chem. Int. Ed. 2021, 60, 24901–24904. [Google Scholar] [CrossRef]
- Haberkorn, R.; Bauer, J.; Kickelbick, G. Ba2PO4I, Sr2PO4I, and Pb2PO4I—A new structure type and three of its representatives. z. Anorg. Allg. Chem. 2014, 640, 3153–3158. [Google Scholar] [CrossRef]
- Sławińska, J.; Cerasoli, F.T.; Wang, H.; Postorino, S.; Supka, A.; Curtarolo, S.; Fornari, M.; Nardelli, M.B. Giant spin Hall effect in two-dimensional monochalcogenides. 2D Mater. 2019, 6, 025012. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Narsimha Rao, E.; Vaitheeswaran, G.; Reshak, A.H.; Auluck, S. Role of spin–orbit interaction on the nonlinear optical response of CsPbCO3F using dft. PCCP 2017, 19, 31255–31266. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Ye, L.-T.; Wu, X.-Q.; Kang, L.; Huang, B. Role of large Rashba spin-orbit coupling in second-order nonlinear optical effects of polar BiB3O6. Phys. Rev. B 2022, 106, 195126. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Jia, W.-L.; Fu, J.-Y.; Cao, Z.-Y.; Wang, L.; Chi, X.-B.; Gao, W.-G.; Wang, L.-W. Fast plane wave density functional theory molecular dynamics calculations on multi-GPU machines. J. Comput. Phys. 2013, 251, 102–115. [Google Scholar] [CrossRef]
- Jia, W.-L.; Cao, Z.-Y.; Wang, L.; Fu, J.-Y.; Chi, X.-B.; Gao, W.-G.; Wang, L.-W. The analysis of a plane wave pseudopotential density functional theory code on a GPU machine. Comput. Phys. Commun. 2013, 184, 9–18. [Google Scholar] [CrossRef]
- Perdew, J.P.; Kieron, B.; Matthias, E. Generalized gradient approximation Made Simple. Phys. Rev. Lett. 1997, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Chadi, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1977, 16, 1746–1747. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Inst. Stand. Technol. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Batista, E.R.; Martin, R.L.; Hay, P.J. Density functional investigations of the properties and thermochemistry of UF6 and UF5 using valence-electron and all-electron approaches. J. Chem. Phys. 2004, 121, 2144–2150. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E. Assessment and validation of a screened Coulomb hybrid density functional. J. Chem. Phys. 2004, 120, 7274–7280. [Google Scholar] [CrossRef] [PubMed]
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Ángyán, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef] [PubMed]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Walsh, A.; Payne, D.J.; Egdell, R.G.; Watson, G.W. Stereochemistry of post-transition metal oxides: Revision of the classical lone pair model. Chem. Soc. Rev. 2011, 40, 4455–4463. [Google Scholar] [CrossRef]
- Lin, J.; Lee, M.-H.; Liu, Z.-P.; Chen, C.; Pickard, C.J. Mechanism for linear and nonlinear optical effects in β-BaB2O4 crystals. Phys. Rev. B 1999, 60, 13380–13389. [Google Scholar] [CrossRef]


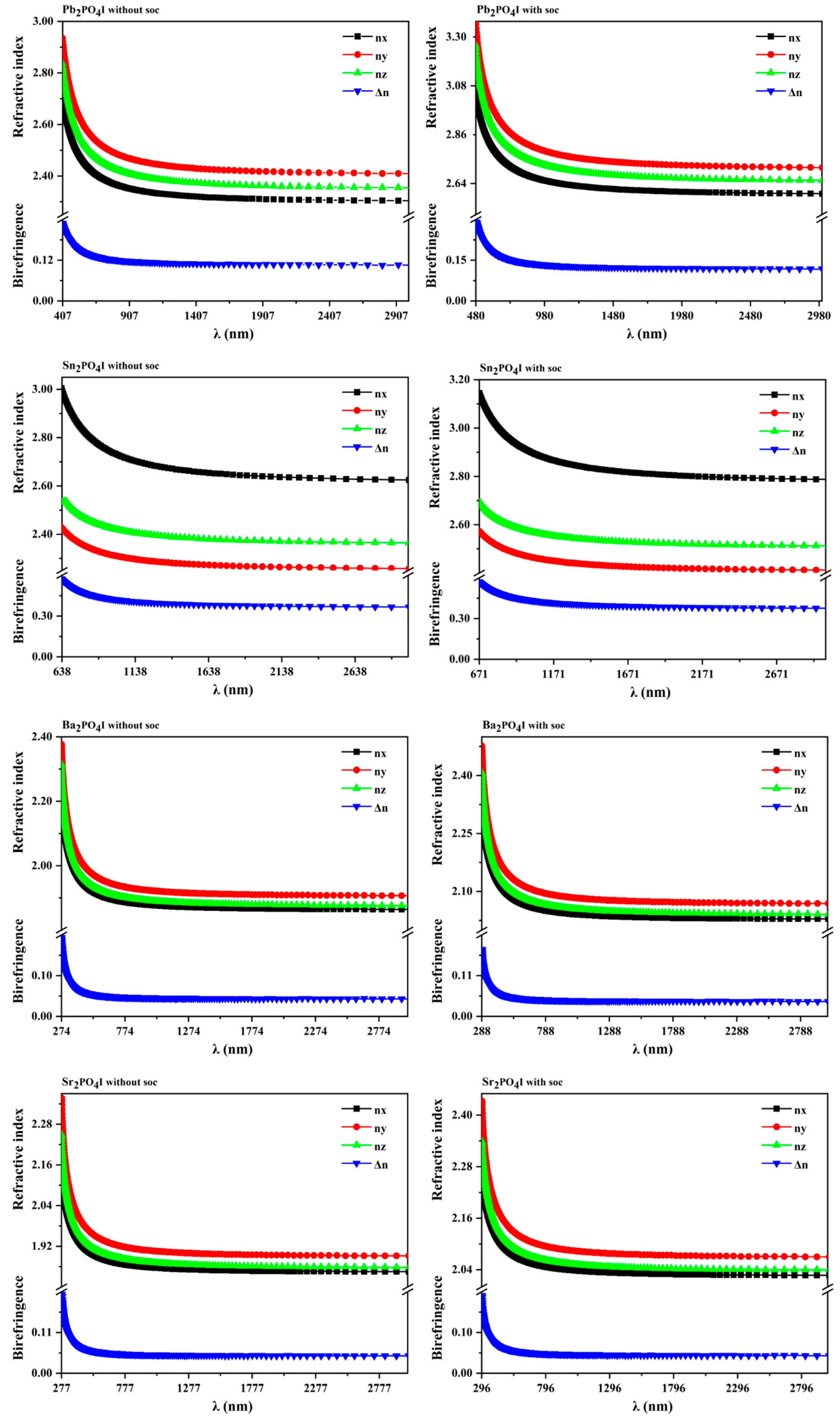

| Compound | nx | ny | nz | Δn | |
|---|---|---|---|---|---|
| Pb2PO4I | Without SOC | 2.393 | 2.337 | 2.450 | 0.113 |
| With SOC | 2.710 | 2.643 | 2.774 | 0.131 | |
| Sn2PO4I | Without SOC | 2.458 | 2.718 | 2.304 | 0.414 |
| With SOC | 2.644 | 2.888 | 2.460 | 0.428 | |
| Ba2PO4I | Without SOC | 1.895 | 1.875 | 1.920 | 0.045 |
| With SOC | 2.059 | 2.040 | 2.082 | 0.042 | |
| Sr2PO4I | Without SOC | 1.876 | 1.855 | 1.904 | 0.049 |
| With SOC | 2.057 | 2.037 | 2.083 | 0.046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, X.; Hu, M.; Jing, Q.; Duan, H.; Chen, H.; Cui, X. The Spin–Orbit Effect on the Electronic Structures, Refractive Indices, and Birefringence of X2PO4I (X = Pb, Sn, Ba and Sr): A First-Principles Investigation. Nanomaterials 2024, 14, 617. https://doi.org/10.3390/nano14070617
Leng X, Hu M, Jing Q, Duan H, Chen H, Cui X. The Spin–Orbit Effect on the Electronic Structures, Refractive Indices, and Birefringence of X2PO4I (X = Pb, Sn, Ba and Sr): A First-Principles Investigation. Nanomaterials. 2024; 14(7):617. https://doi.org/10.3390/nano14070617
Chicago/Turabian StyleLeng, Xudong, Mei Hu, Qun Jing, Haiming Duan, Henglei Chen, and Xiuhua Cui. 2024. "The Spin–Orbit Effect on the Electronic Structures, Refractive Indices, and Birefringence of X2PO4I (X = Pb, Sn, Ba and Sr): A First-Principles Investigation" Nanomaterials 14, no. 7: 617. https://doi.org/10.3390/nano14070617
APA StyleLeng, X., Hu, M., Jing, Q., Duan, H., Chen, H., & Cui, X. (2024). The Spin–Orbit Effect on the Electronic Structures, Refractive Indices, and Birefringence of X2PO4I (X = Pb, Sn, Ba and Sr): A First-Principles Investigation. Nanomaterials, 14(7), 617. https://doi.org/10.3390/nano14070617






