An Analytical Model for Hysteretic Pressure-Sensitive Permeability of Nanoporous Media
Abstract
1. Introduction
2. Materials and Methods
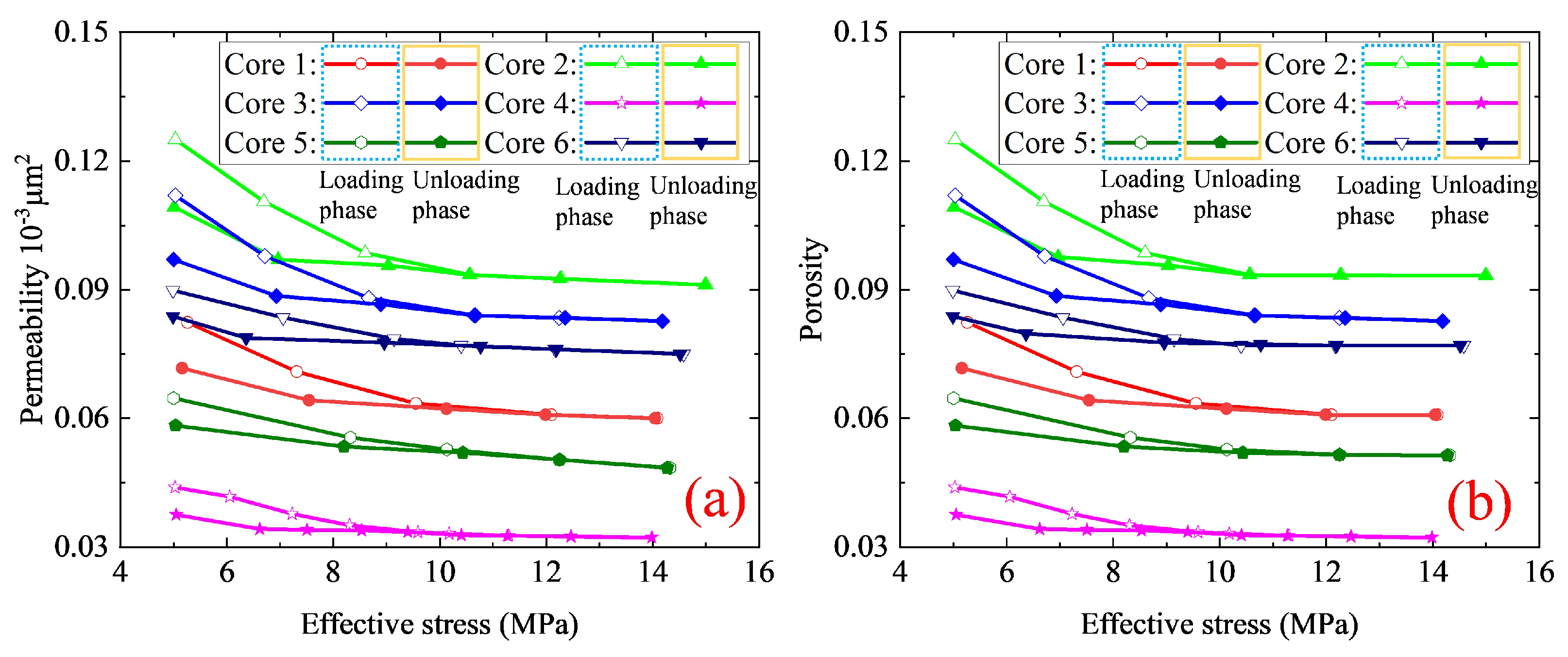
2.1. Experiment Materials and Methods
2.2. Theoretical Model Development
2.2.1. Model Assumptions
- (1)
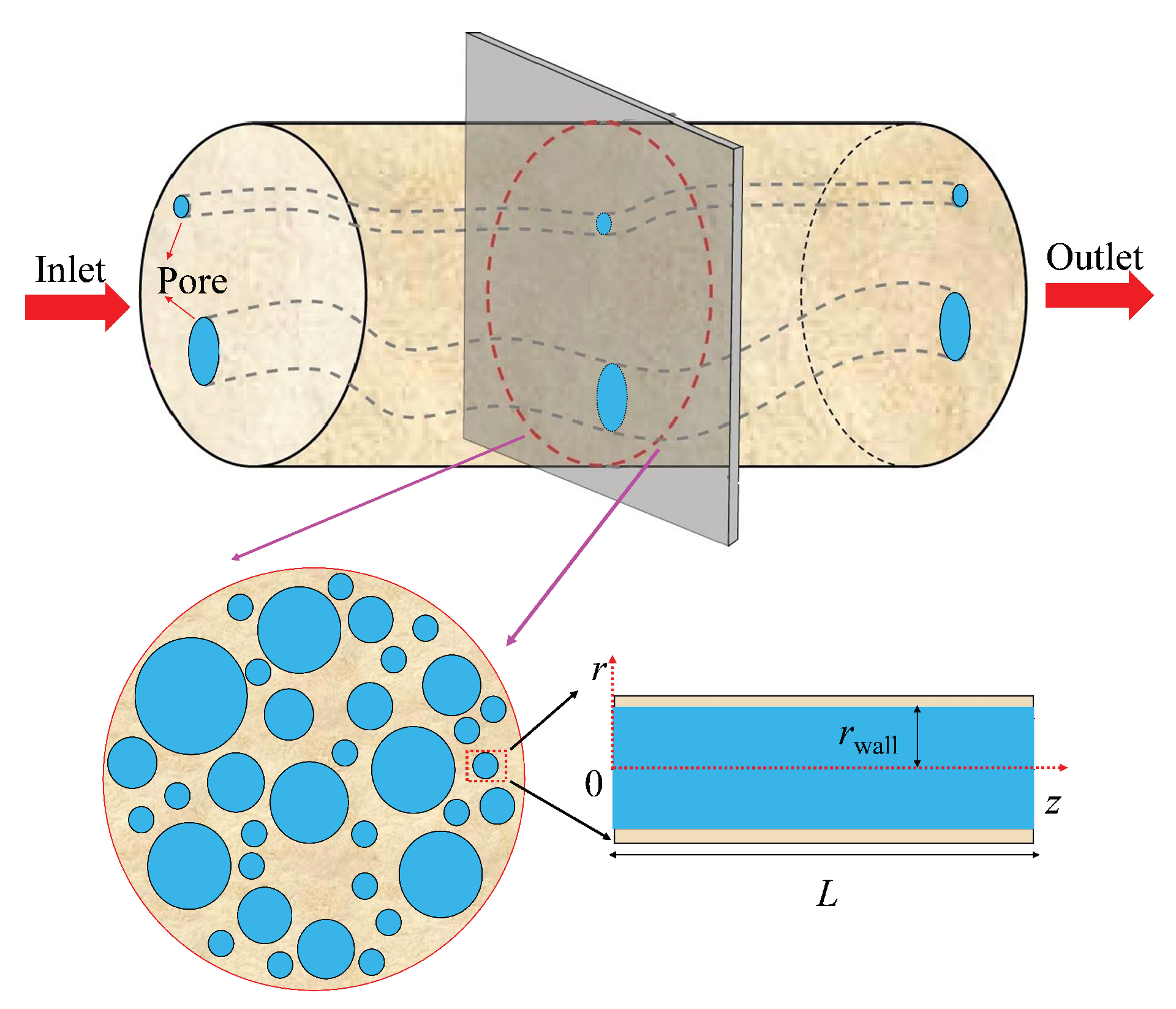
- During fluid flow through nanohybrids, the fluid velocity is assumed to be approximately symmetrically distributed with respect to the tube axis. In addition, as pores in nanohybrids are narrow, due to the gas slippage effect, the fluid velocity at the pore wall is larger than zero.
- (2)
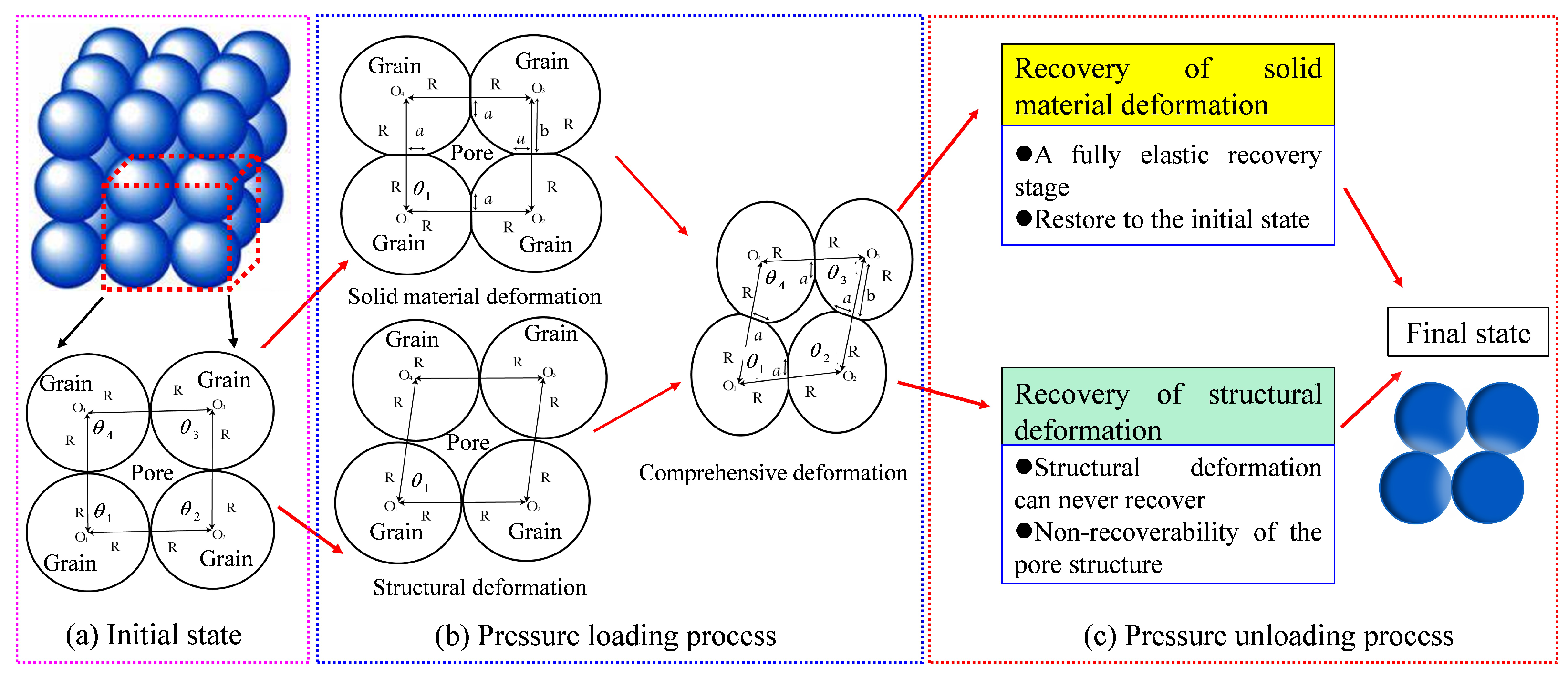
- The effective stress is uniformly distributed in the pore space of the porous materials during pressure loading and unloading processes and act in the same way on all pores in the material. The increased effective stress leads to solid material deformation and structural deformation, as shown in Figure 2b. During the solid material (grains themselves) deformation process, the point contacts between grains transform into surface contacts, determined by the Hertz deformation theory. In other words, solid material deformation is fully elastic deformation. Moreover, during the structural deformation process, particle contact angle changes as the arrangement of grains changes.
- (3)
- When the effective stress decreases (i.e., pressure unloading), the nanoporous media’s solid material deformation will revert to the initial state. This process is a fully elastic recovery stage, as shown in Figure 2c. However, the nanoporous media’s structural deformation can never recover, leading to the non-recoverability of the pore structure.
- (4)
- During the process of effective stress increasing or decreasing, rock mechanical properties (e.g., elastic modulus and Poisson’s ratio) are considered constants. In other words, the variations in the mechanical properties of the nanohybrid are ignored.
- (5)
- The samples are dry nanoporous media and the liquid film on the pore wall is ignored. In addition, as the fluid is nitrogen gas, the adsorption of nitrogen on nanopore’s surface is also ignored. The flow in a circular intergrain nanopore is laminar and in a steady state, and the velocity distribution in the nanopore can be characterized by the modified Navier-Stokes equation [22,62,63,64,65].
2.2.2. Theoretical Models
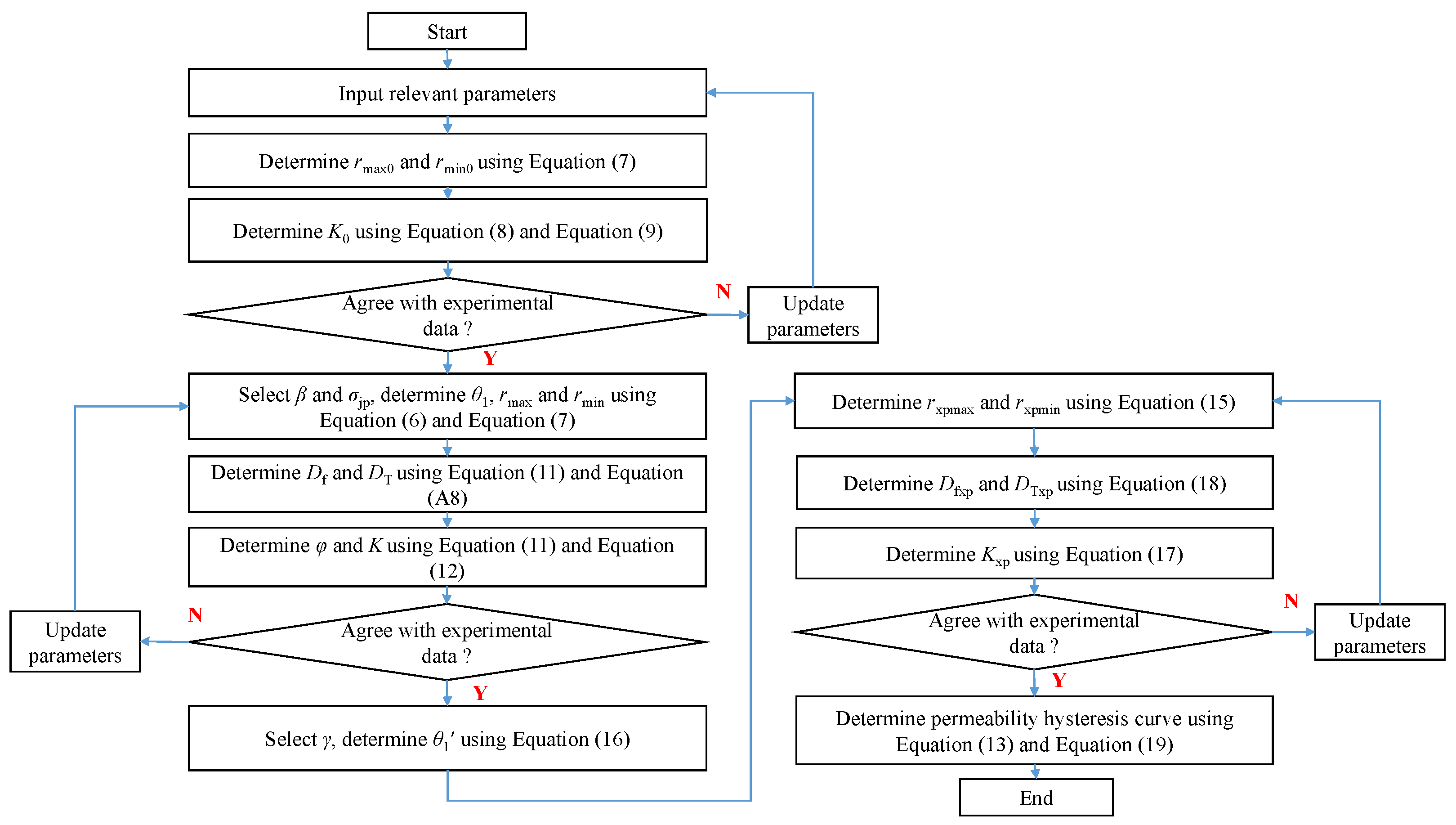
2.2.3. Workflow of Permeability Hysteresis Determination
3. Results
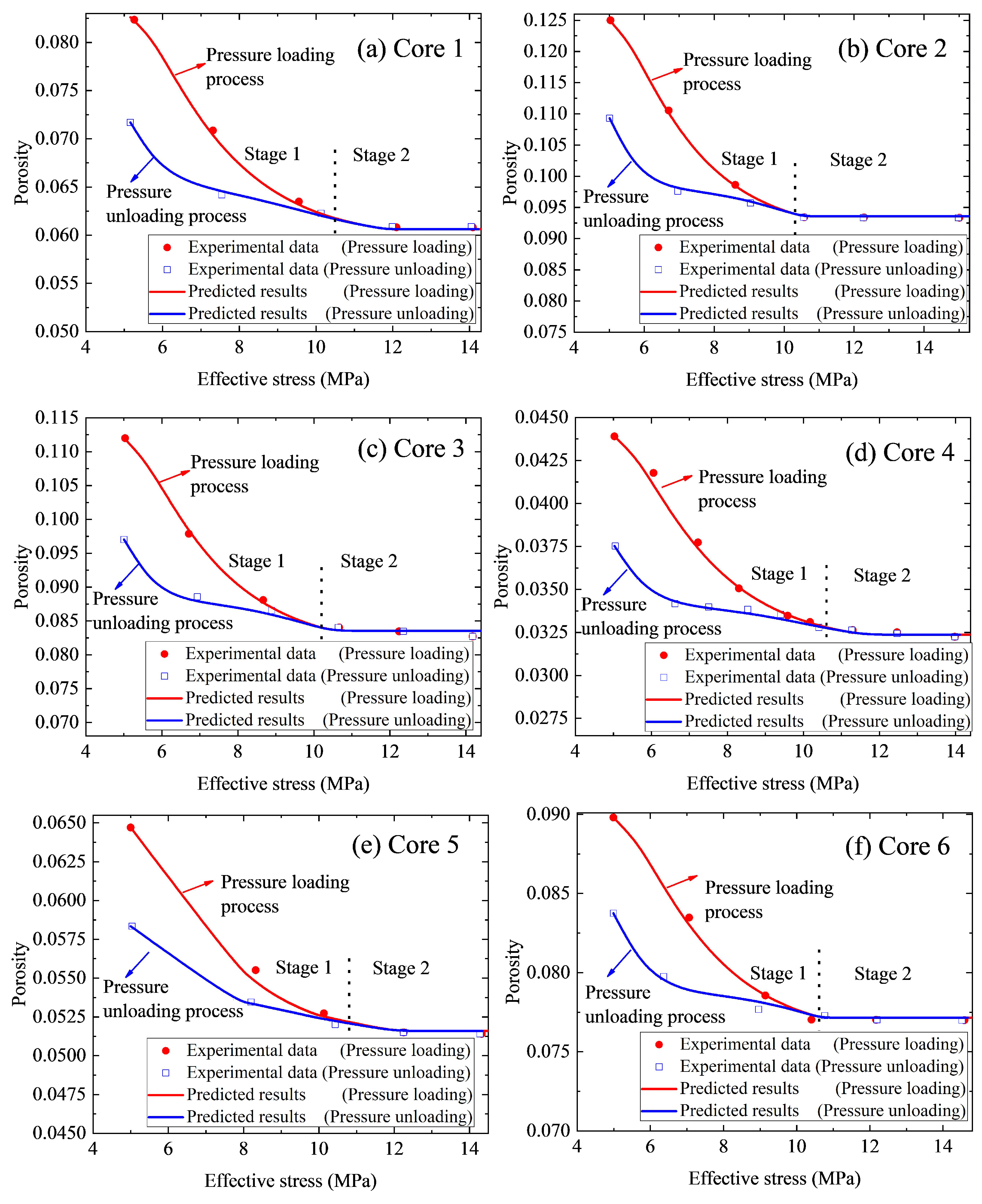
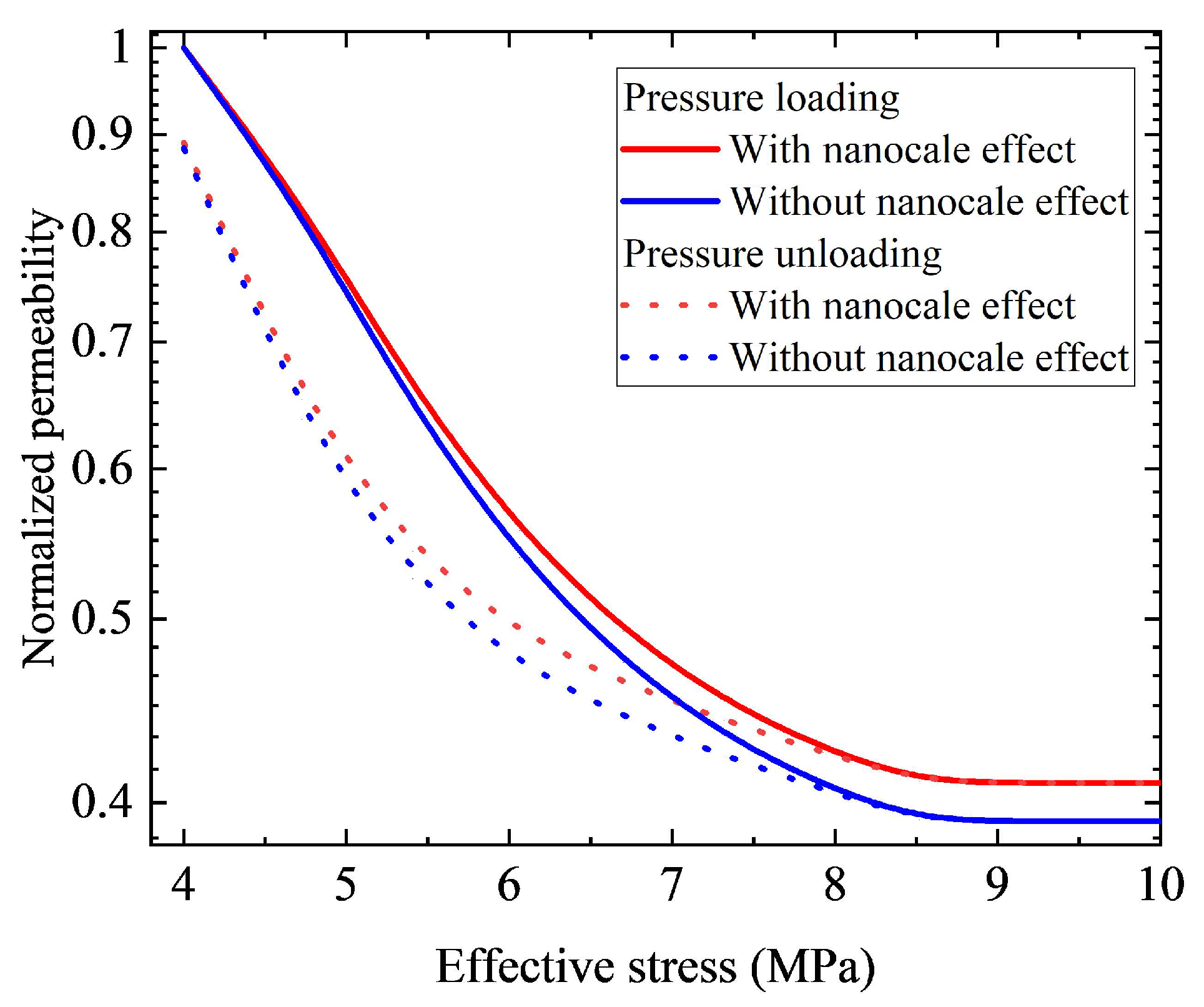
3.1. Validation with Experimental Results
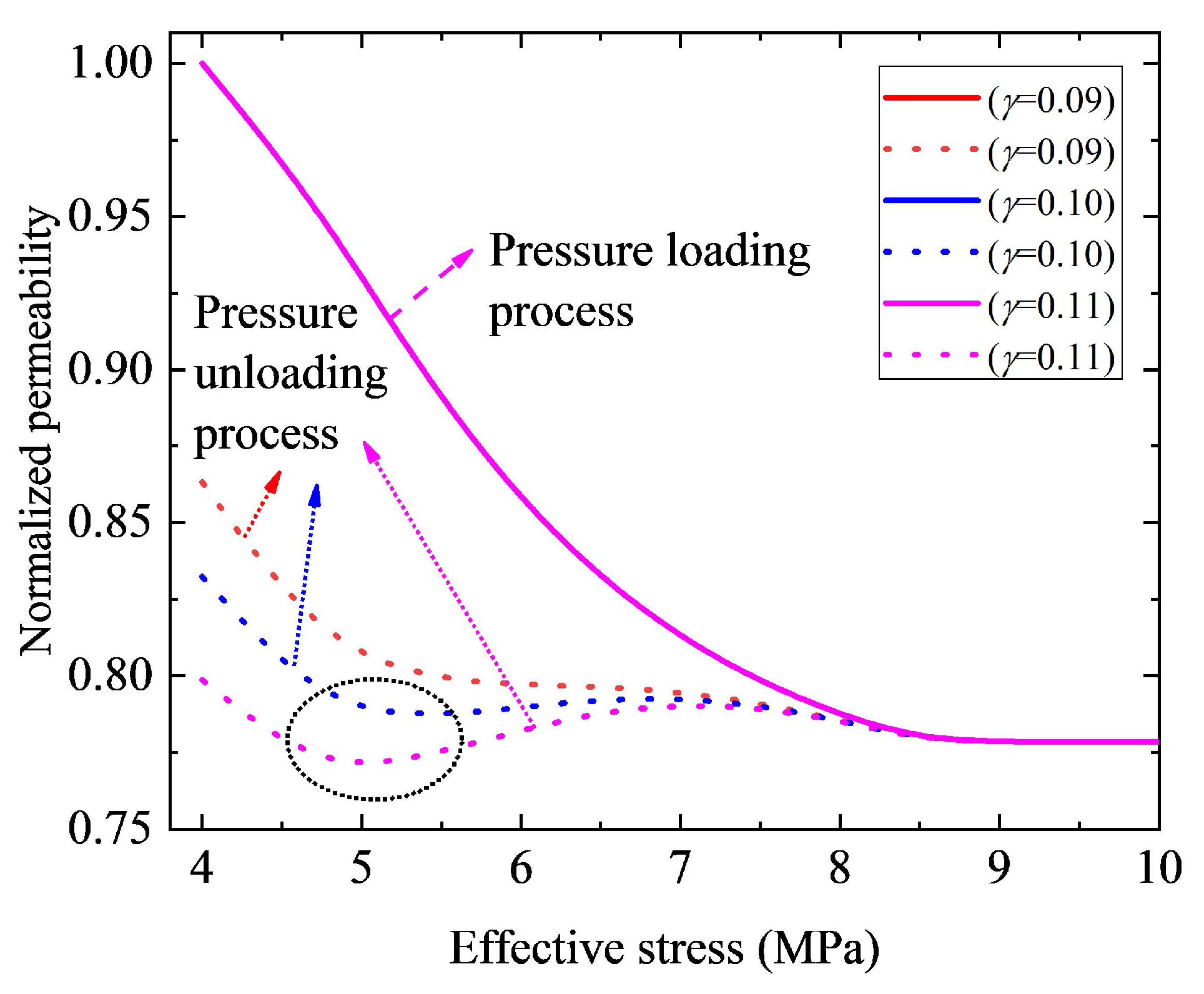
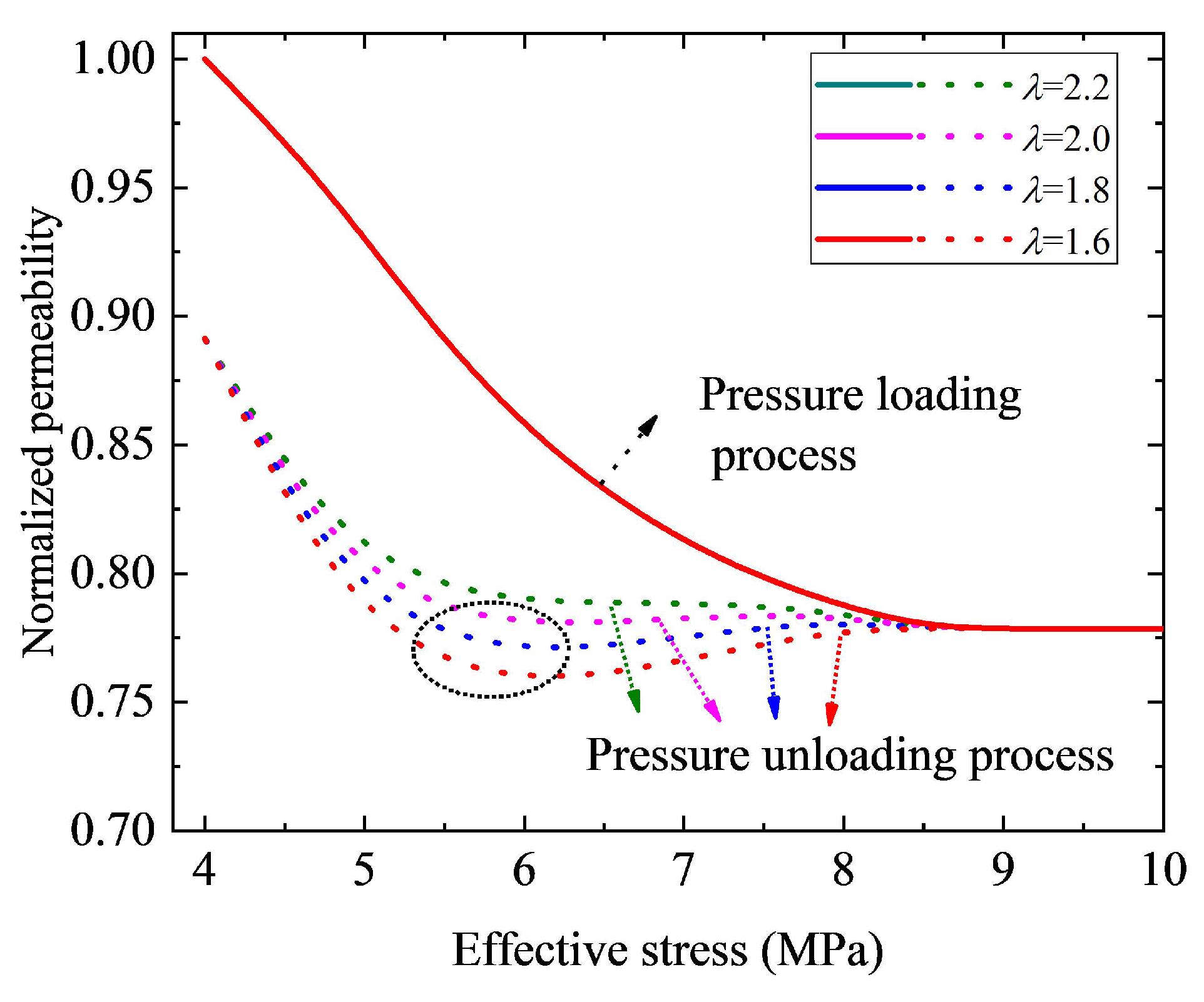
3.2. Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Derivation of Nitrogen Flow in Nanopores
References
- Huang, S.; Yao, Y.; Zhang, S.; Ji, J.; Ma, R. A Fractal Model for Oil Transport in Tight Porous Media. Transp. Porous Media 2018, 121, 725–739. [Google Scholar] [CrossRef]
- Machrafi, H.; Lebon, G. Fluid Flow Through Porous and Nanoporous Media Within the Prisme of Extended Thermodynamics: Emphasis on the Notion of Permeability. Microfluid. Nanofluid. 2018, 22, 65. [Google Scholar] [CrossRef]
- Afagwu, C.; Al-Afnan, S.; Patil, S.; Aljaberi, J.; Mahmoud, M.A.; Li, J. The Impact of Pore Structure and Adsorption Behavior on Kerogen Tortuosity. Fuel 2021, 303, 121261. [Google Scholar] [CrossRef]
- Wang, F.; Zai, Y. Fractal and Multifractal Characteristics of Shale Nanopores. Results Phys. 2021, 25, 104277. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Zhu, Y.; Wang, F.; Wu, H. Multiscale Transport Mechanism of Shale Gas in Micro/Nano-Pores. Int. J. Heat Mass Transf. 2017, 111, 1172–1180. [Google Scholar] [CrossRef]
- Feng, D.; Wu, K.; Wang, X.; Li, J.; Li, X. Modeling the Confined Fluid Flow in Micro-Nanoporous Media Under Geological Temperature and Pressure. Int. J. Heat Mass Transf. 2019, 145, 118758. [Google Scholar] [CrossRef]
- Zhang, J.; Pei, G.; Zhang, L. Molecular Dynamics Simulation of Methane Gas Flow in Nanopores. Petroleum 2019, 5, 252–259. [Google Scholar] [CrossRef]
- Hall, W.A. An Analytical Derivation of the Darcy Equation. Eos Trans. Am. Geophys. Union 1956, 37, 185–188. [Google Scholar] [CrossRef]
- Carlson, F.M. Simulation of Relative Permeability Hysteresis to the Nonwetting Phase. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, October 1981. [Google Scholar] [CrossRef]
- Nield, D.A. The Boundary Correction for the Rayleigh-Darcy Problem: Limitations of the Brinkman Equation. J. Fluid Mech. 1983, 128, 37–46. [Google Scholar] [CrossRef]
- Fand, R.M.; Kim, B.Y.K.; Lam, A.C.C.; Phan, R.T. Resistance to the Flow of Fluids Through Simple and Complex Porous Media Whose Matrices Are Composed of Randomly Packed Spheres. J. Fluids Eng. 1987, 109, 268–273. [Google Scholar] [CrossRef]
- Tweheyo, M.; Talukdar, S.; Torsæter, O. Hysteresis Effects in Capillary Pressure, Relative Permeability and Resistivity Index of North Sea Chalk. In Proceedings of the International Symposium of the Society of Core Analysts, Edinburgh, UK, August 2001; Volume 8, pp. 1–6. [Google Scholar]
- Rust, A.; Cashman, K. Permeability of Vesicular Silicic Magma: Inertial and Hysteresis Effects. Earth Planet. Sci. Lett. 2004, 228, 93–107. [Google Scholar] [CrossRef]
- Lei, G.; Li, W.; Wen, Q. The Convective Heat Transfer of Fractal Porous Media Under Stress Conditions. Int. J. Therm. Sci. 2019, 137, 55–63. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, S.; Li, J.; Zhang, J.; Xue, H.; Chen, C. Permeability Evaluation on Oil-Window Shale Based on Hydraulic Flow Unit: A New Approach. Adv. Geo-Energy Res. 2018, 2, 1–13. [Google Scholar] [CrossRef]
- Lei, G.; Liao, Q.; Patil, S.; Zhao, Y. A New Permeability Model for Argillaceous Porous Media Under Stress Dependence With Clay Swelling. Int. J. Eng. Sci. 2021, 160, 103452. [Google Scholar] [CrossRef]
- Panja, P.; McLennan, J.; Green, S. Impact of Permeability Heterogeneity on Geothermal Battery Energy Storage. Adv. Geo-Energy Res. 2021, 5, 127–138. [Google Scholar] [CrossRef]
- Beliaev, A.Y.; Kozlov, S.M. Darcy Equation for Random Porous Media. Commun. Pure Appl. Math. 1996, 49, 1–34. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman Equation as a Model for Flow in Porous Media. Phys. Fluids 1987, 30, 3329–3341. [Google Scholar] [CrossRef]
- Harder, C.; Paredes, D.; Valentin, F. A Family of Multiscale Hybrid-Mixed Finite Element Methods for the Darcy Equation with Rough Coefficients. J. Comput. Phys. 2013, 245, 107–130. [Google Scholar] [CrossRef]
- Gholami, R.; Shahraki, A.R.; Jamali Paghaleh, M. Prediction of Hydrocarbon Reservoirs Permeability Using Support Vector Machine. Math. Probl. Eng. 2012, 2012, 670723. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Sun, Z.; Feng, D.; Miao, Y.; Li, P.; Zhang, Z. An Analytical Model for Relative Permeability in Water-Wet Nanoporous Media. Chem. Eng. Sci. 2017, 174, 1–12. [Google Scholar] [CrossRef]
- Ioannidis, M.A.; Chatzis, I. A Mixed-Percolation Model of Capillary Hysteresis and Entrapment in Mercury Porosimetry. J. Colloid Interface Sci. 1993, 161, 278–291. [Google Scholar] [CrossRef]
- Farquhar, R.; Smart, B.; Todd, A.; Tompkins, D.; Tweedie, A. Stress Sensitivity of Low-Permeability Sandstones from the Rotliegendes Sandstone. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, October 1993. [Google Scholar] [CrossRef]
- Bustin, R.M. Importance of Fabric and Composition on the Stress Sensitivity of Permeability in Some Coals, Northern Sydney Basin, Australia: Relevance to Coalbed Methane Exploitation. AAPG Bull. 1997, 81, 563428. [Google Scholar] [CrossRef]
- McKee, C.R.; Bumb, A.C.; Koenig, R.A. Stress-Dependent Permeability and Porosity of Coal and Other Geologic Formations. SPE Form. Eval. 1988, 3, 81–91. [Google Scholar] [CrossRef]
- Juanes, R.; Spiteri, E.J.; Orr, F.M., Jr.; Blunt, M.J. Impact of Relative Permeability Hysteresis on Geological CO2 Storage. Water Resour. Res. 2006, 42, 1–13. [Google Scholar] [CrossRef]
- Kadet, V.; Galechyan, A. Percolation Modeling of Relative Permeability Hysteresis. J. Pet. Sci. Eng. 2014, 119, 139–148. [Google Scholar] [CrossRef]
- Wang, X.; Alvarado, V. Analysis of Capillary Pressure and Relative Permeability Hysteresis Under Low-Salinity Waterflooding Conditions. Fuel 2016, 180, 228–243. [Google Scholar] [CrossRef]
- Teklu, T.W.; Li, X.; Zhou, Z.; Cui, Q.; Abass, H. Fracture and Matrix Permeability Hysteresis in Organic Rich Mudrocks. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, August 2016. [Google Scholar] [CrossRef]
- Xiao, W.; Li, T.; Li, M.; Zhao, J.; Zheng, L.; Li, L. Evaluation of the Stress Sensitivity in Tight Reservoirs. Pet. Explor. Dev. 2016, 43, 115–123. [Google Scholar] [CrossRef]
- Geng, Y.; Tang, D.; Xu, H.; Tao, S.; Tang, S.; Ma, L.; Zhu, X. Experimental Study on Permeability Stress Sensitivity of Reconstituted Granular Coal With Different Lithotypes. Fuel 2017, 202, 12–22. [Google Scholar] [CrossRef]
- Cao, N.; Lei, G. Stress Sensitivity of Tight Reservoirs During Pressure Loading and Unloading Process. Pet. Explor. Dev. 2019, 46, 138–144. [Google Scholar] [CrossRef]
- Lei, G.; Liao, Q.; Patil, S.; Zhao, Y. Effect of Clay Content on Permeability Behavior of Argillaceous Porous Media Under Stress Dependence: A Theoretical and Experimental Work. J. Pet. Sci. Eng. 2019, 179, 787–795. [Google Scholar] [CrossRef]
- Civan, F. Effective-Stress Coefficients of Porous Rocks Involving Shocks and Loading/Unloading Hysteresis. SPE J. 2021, 26, 44–67. [Google Scholar] [CrossRef]
- Moos, D.; Vassilellis, G.; Cade, R.; Franquet, J.; Lacazette, A.; Bourtembourg, E.; Daniel, G. Predicting Shale Reservoir Response to Stimulation in the Upper Devonian of West Virginia. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA, October 2011; All Days. [Google Scholar] [CrossRef]
- Chen, T.; Feng, X.T.; Cui, G.; Tan, Y.; Pan, Z. Experimental Study of Permeability Change of Organic-Rich Gas Shales Under High Effective Stress. J. Nat. Gas Sci. Eng. 2019, 64, 1–14. [Google Scholar] [CrossRef]
- Teklu, T.W.; Zhou, Z.; Li, X.; Abass, H. Experimental Investigation on Permeability and Porosity Hysteresis in Low-Permeability Formations. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low Permeability Reservoirs Symposium, Denver, CO, USA, May 2016. [Google Scholar] [CrossRef]
- Teklu, T.W.; Zhou, Z.; Li, X.; Abass, H. Cyclic Permeability and Porosity Hysteresis in Mudrocks—Experimental Study. In Proceedings of the U.S. Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, June 2016. [Google Scholar]
- Colonna, J.; Brissaud, F.; Millet, J. Evolution of Capillarity and Relative Permeability Hysteresis. Soc. Pet. Eng. J. 1972, 12, 28–38. [Google Scholar] [CrossRef]
- Wissler, T.; Simmons, G. The Physical Properties of a Set of Sandstones - Part II. Permanent and Elastic Strains During Hydrostatic Compression to 200 MPa. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 393–406. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, C.; Yin, G.; Wojtanowicz, A.K.; Zhang, D. Permeability and Effective Stress in Dipping Gas Shale Formation with Bedding—Experimental Study. J. Energy Resour. Technol. 2020, 142, 103002. [Google Scholar] [CrossRef]
- Bernabe, Y. The Effective Pressure Law for Permeability During Pore Pressure and Confining Pressure Cycling of Several Crystalline Rocks. J. Geophys. Res. Solid Earth 1987, 92, 649–657. [Google Scholar] [CrossRef]
- Teufel, L.W.; Rhett, D.W.; Farrell, H.E. Effect of Reservoir Depletion and Pore Pressure Drawdown on In Situ Stress and Deformation in the Ekofisk Field, North Sea. In Proceedings of the U.S. Rock Mechanics/Geomechanics Symposium, Norman, OK, USA, July 1991. [Google Scholar]
- Warpinski, N.R.; Teufel, L.W. Determination of the Effective Stress Law for Permeability and Deformation in Low-Permeability Rocks. SPE Form. Eval. 1992, 7, 123–131. [Google Scholar] [CrossRef]
- Ruan, M.; Wang, L. Low-Permeability Oilfield Development and Pressure-Sensitive Effect. Acta Pet. Sin. 2002, 23, 73–76. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Wen, W.; Chi, B.; Sun, Y. Stress Sensitivity and Poroperm Lower Limit of Deliverability in the Low-Permeability Reservoir. Oil Gas Geol. 2003, 24, 162–166. [Google Scholar] [CrossRef]
- Teklu, T.W.; Li, X.; Zhou, Z.; Abass, H. Experimental Investigation on Permeability and Porosity Hysteresis of Tight Formations. SPE J. 2018, 23, 672–690. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, X. Stress Sensitivity Analysis of Changqing Tight Clastic Reservoir. Pet. Explor. Dev. 2001, 28, 85–87. [Google Scholar] [CrossRef]
- Jerauld, G.R.; Salter, S.J. The Effect of Pore-Structure on Hysteresis in Relative Permeability and Capillary Pressure: Pore-Level Modeling. Transp. Porous Media 1990, 5, 103–151. [Google Scholar] [CrossRef]
- Sarkisov, L.; Monson, P.A. Hysteresis in Monte Carlo and Molecular Dynamics Simulations of Adsorption in Porous Materials. Langmuir 2000, 16, 9857–9860. [Google Scholar] [CrossRef]
- Wang, L.; Huang, H.; Lu, X.Y. Scheme for Contact Angle and Its Hysteresis in a Multiphase Lattice Boltzmann Method. Phys. Rev. E 2013, 87, 013301. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman and Co.: San Francisco, CA, USA, 1982; pp. 1–460. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Fractal Sandstone Pores: Implications for Conductivity and Pore Formation. Phys. Rev. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef]
- Yu, B. Analysis of Flow in Fractal Porous Media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Khoshghalb, A.; Pasha, A.; Khalili, N. A Fractal Model for Volume Change Dependency of the Water Retention Curve. Géotechnique 2015, 65, 141–146. [Google Scholar] [CrossRef]
- Lei, G.; Dong, Z.; Li, W.; Wen, Q.; Wang, C. Theoretical Study on Stress Sensitivity of Fractal Porous Media With Irreducible Water. Fractals 2018, 26, 1850004. [Google Scholar] [CrossRef]
- Geng, L.; Li, G.; Zitha, P.; Tian, S.; Sheng, M. A Fractal Permeability Model for Shale Gas Flow Through Heterogeneous Matrix Systems. J. Nat. Gas Sci. Eng. 2016, 35, 593–604. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Liu, J.; Fu, L.Y. Effective Moduli of Rocks Predicted by the Kuster-Toksöz and Mori-Tanaka Models. J. Geophys. Eng. 2021, 18, 539–557. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2008; p. 882. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; pp. 1–452. [Google Scholar] [CrossRef]
- Myers, T.G. Why Are Slip Lengths So Large in Carbon Nanotubes. Microfluid. Nanofluid. 2011, 10, 1141–1145. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, D. Impact of Adsorption on Gas Transport in Nanopores. Sci. Rep. 2016, 6, 23629. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability Effect on Nanoconfined Water Flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358–3363. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Chen, Z.; Wu, K.; Xu, J. Shale Gas Transport in Nanopores With Mobile Water Films and Water Bridge. Pet. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Gangi, A.F. Variation of Whole and Fractured Porous Rock Permeability with Confining Pressure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 249–257. [Google Scholar] [CrossRef]
- Lei, G.; Zhou, X.; Al-Abdrabalnabi, R.; Elsayed, M.; Kamal, M.S. Experimental and Modeling Investigation for the Effect of Effective Stress on Seawater Permeability of Clay-Free Limestones, Dolomites, and Clay-Rich Sandstones. In Proceedings of the IPTC International Petroleum Technology Conference, Riyadh, Saudi Arabia, February 2022. [Google Scholar] [CrossRef]
- Weaver, J.D.; Nguyen, P.D.; Parker, M.A.; van Batenburg, D. Sustaining Fracture Conductivity. In Proceedings of the SPE European Formation Damage Conference and Exhibition, Sheveningen, The Netherland, May 2005. [Google Scholar] [CrossRef]
- Weaver, J.; Parker, M.; van Batenburg, D.; Nguyen, P. Fracture-Related Diagenesis May Impact Conductivity. SPE J. 2007, 12, 272–281. [Google Scholar] [CrossRef]
- Terracina, J.M.; Turner, J.M.; Collins, D.H.; Spillars, S.E. Proppant Selection and Its Effect on the Results of Fracturing Treatments Performed in Shale Formations. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, September 2010. [Google Scholar] [CrossRef]
- Xu, P.; Qiu, S.; Yu, B.; Jiang, Z. Prediction of Relative Permeability in Unsaturated Porous Media with a Fractal Approach. Int. J. Heat Mass Transf. 2013, 64, 829–837. [Google Scholar] [CrossRef]
- Bakhshian, S.; Sahimi, M. Computer Simulation of the Effect of Deformation on the Morphology and Flow Properties of Porous Media. Phys. Rev. E 2016, 94, 042903. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Xiao, F.; Labra, C.; Sun, J.; Yin, X. DEM-LBM Simulation of Stress-Dependent Absolute and Relative Permeabilities in Porous Media. Chem. Eng. Sci. 2021, 239, 116633. [Google Scholar] [CrossRef]
- Cao, W.; Lei, Q.; Cai, W. Stress-Dependent Deformation and Permeability of a Fractured Coal Subject to Excavation-Related Loading Paths. Rock Mech. Rock Eng. 2021, 54, 4299–4320. [Google Scholar] [CrossRef]
- Nie, G.X.; Wang, Y.; Huang, J.P. Shape Effect of Nanochannels on Water Mobility. Front. Phys. 2016, 11, 114702. [Google Scholar] [CrossRef]
- Karniadakis, G.; Beskok, A.; Gad-el Hak, M. Micro Flows: Fundamentals and Simulation. Appl. Mech. Rev. 2002, 55, B76. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A Fractal Permeability Model for Bi-Dispersed Porous Media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]



| No. | Diameter/mm | Length/mm | Initial Porosity/% | Initial Permeability/ | Elastic Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Core-1 | 24.5 | 48.4 | 8.26 | 0.05 | 34.9 | 0.25 |
| Core-2 | 24.8 | 52.6 | 12.5 | 0.15 | ||
| Core-3 | 24.7 | 49.7 | 11.2 | 0.12 | ||
| Core-4 | 25.2 | 43.8 | 4.39 | 0.02 | ||
| Core-5 | 24.9 | 56.2 | 6.47 | 0.04 | ||
| Core-6 | 25.2 | 51 | 8.98 | 0.06 |
| Parameters | Core-1 | Core-2 | Core-3 | Core-4 | Core-5 | Core-6 |
|---|---|---|---|---|---|---|
| /m | 0.38 | 0.52 | 0.49 | 0.36 | 0.4 | 0.39 |
| /10−3m | 3.15 | 4.59 | 4.18 | 2.75 | 2.64 | 3.63 |
| Initial porosity/% | 8.26 | 12.5 | 11.2 | 4.39 | 6.47 | 8.98 |
| Predicted initial permeability/−3 m2 | 0.05 | 0.15 | 0.12 | 0.02 | 0.04 | 0.06 |
| 0.46 | 0.47 | 0.48 | 0.48 | 0.44 | 0.46 | |
| 2.3 | 2.1 | 2.1 | 2.32 | 2.4 | 2.14 | |
| 0.76 | 0.95 | 0.92 | 0.62 | 0.56 | 0.56 | |
| 0.11 | 0.12 | 0.12 | 0.1 | 0.09 | 0.08 | |
| 3.6 | 2.8 | 2.9 | 3.3 | 3.6 | 2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, G.; Liao, Q.; Chen, W.; Lu, C.; Zhou, X. An Analytical Model for Hysteretic Pressure-Sensitive Permeability of Nanoporous Media. Nanomaterials 2022, 12, 4234. https://doi.org/10.3390/nano12234234
Lei G, Liao Q, Chen W, Lu C, Zhou X. An Analytical Model for Hysteretic Pressure-Sensitive Permeability of Nanoporous Media. Nanomaterials. 2022; 12(23):4234. https://doi.org/10.3390/nano12234234
Chicago/Turabian StyleLei, Gang, Qinzhuo Liao, Weiqing Chen, Chunhua Lu, and Xianmin Zhou. 2022. "An Analytical Model for Hysteretic Pressure-Sensitive Permeability of Nanoporous Media" Nanomaterials 12, no. 23: 4234. https://doi.org/10.3390/nano12234234
APA StyleLei, G., Liao, Q., Chen, W., Lu, C., & Zhou, X. (2022). An Analytical Model for Hysteretic Pressure-Sensitive Permeability of Nanoporous Media. Nanomaterials, 12(23), 4234. https://doi.org/10.3390/nano12234234








