1. Introduction
A crucial component of numerous industrial and technological processes is the fluid flow above a stretched surface with mass and heat transfer. Applications include the chilling of sheets, melt-spinning operations, fiber spinning, casting, etc. Additionally, fluids flow is used in geophysics, industrial engineering, petroleum engineering, groundwater hydrology, ceramic engineering, and chemical engineering. The final finishing of products depends upon the amount of heat transfer. Therefore, it is crucial to check the velocity and heat transfer inside a fluid to obtain a basic understanding of these processes.
Crane [
1] gave the concept of boundary layer flow for viscous incompressible fluid over a stretchable surface. Using this concept, researchers have shown their interest in boundary layer flows during the last few decades. Dutta et al. [
2] looked at the heat transfer in the flow by a stretchable surface with uniform heat source. A computational investigation for MHD flow in a rectangular cavity discussed by Hassan et al. [
3]. Exponentially extending surfaces were used by Nadeem and Lee [
4] to characterize the boundary layer flow.
Non-Newtonian nanofluids do not obey the Newton law of viscosity, while Newtonian nanofluids obey this law because they have direct relations between shear stress and shear rate when subjected to applied stress. Such fluid plays an essential part in different industrial applications such as polymer extrusion, cosmetics, coolants, in the food industry and the final finishing of the products. The nanofluids are prepared by suspending nanometer-sized particles in a host fluid, and these fluids have improved heat transfer rates as compared to the host fluid. Similarly, hybrid nanofluids are the mixture of one or more nanoparticles in nanofluids that perform extraordinary heat transmission. Sarada et al. [
5] considered the non-Newtonian fluid flow above the stretching surface with variable thermal conditions. Punith et al. [
6] explored the three-dimensional non-Newtonian magnetic fluid flow over the stretchable surface. Wong and De Leon [
7] described the more detailed applications for nanofluids. Additionally, Punith et al. [
8] explored the non-Newtonian nanofluid flow with chemical reaction and activation energy. Numerical solution for non-Newtonian nanofluid presented by Nadeem et al. [
9]. For the transport of nanofluid through a stretching surface, Ghasemi et al. [
10] used spectrum relaxation approach. Arshad et al. [
11] used the porous stretching surface to examine the fluid considering the chemical reaction.
Rout and Mishra [
12] gave a comparative study for the magnetohydrodynamic nanofluid flow above extending surface and proved that a higher radiation rate increases the heat transfer rate. Reddy et al. [
13] gave the unsteady MHD nanofluid flow above a slandering stretching sheet with a slip effect. The power law index determines whether a fluid is non-Newtonian or Newtonian and with the help of this law, Raju et al. [
14] described a dual solution for 3D magnetohydrodynamic nanofluid flow over a permeable stretching surface. Umavathi et al. [
15] investigated the MHD flow between parallel convectively heated disks for Casson nanofluid. Hussain et al. [
16] explored the time-dependent flow to analyze the heat transmission in cylinder. Naveen et al. [
17] utilized the KKL model to explore the magnetic dipole effect on radiative fluid flow. Ziaei-Rad et al. [
18] elaborated on the dissipation of MHD nanofluid flow with an artificial neural network technique.
Many industrial uses involve different types of heat flow like in plastic industries, molding, blowing, and extrusion of plastic. Similarly, converting industries involve presses, rolls, laminating, and printing. Nuclear power plants involve radiations that play an important role. Zeeshan et al. [
19] explored the magnetic dipole influence on viscous fluid with thermal radiation. Muhammad et al. [
20] used carbon nanotubes for the investigation of MHD flow with heat source/sink and thermal radiation. Jamshed et al. [
21] used the second grade nanofluid to discuss the radiative heat transfer flow. Prasannakumara and Gowda [
22] investigated the heat and mass transfer for radiative heat flux with a uniform magnetic field. Soumya et al. [
23] involved the non-linear radiation and slip conditions to explore the kerosene and water-based hybrid nanoparticles nanofluid in the suction/injection process. Jayaprakash et al. [
24] recently elaborated on the convective heat transfer and activation energy performance in radiative hybrid nanofluid flow. Hussain et al. [
25] explored the hybrid nanofluid flow for single-wall carbon nanotubes and multi-walls carbon nanotubes along the thermal radiation. Ramesh and Gireesha [
26] investigated the dusty fluid flow with radiation above the stretching surface. Hussain et al. [
27] computationally explored the MHD three-dimensional nanofluid flow above the stretchable surface with linear and non-linear radiation.
The thermophoresis phenomenon is defined as the particle’s migration from a higher temperature to a lower temperature. This technique is very useful for the accumulation of particles like the movement of holes of electrical charge in semiconductors. Tsai et al. [
28] presented the thermophoretic decomposition of particles in steady state and unsteady flows. Recently, Arshad et al. [
29] presented the Brownian motion and thermophoresis effect over the non-linear stretchable surface. Hassan et al. [
30] considered the hybrid nanoparticles nanofluid under radiation for heat transportation analysis. Qin et al. [
31] analyzed the thermal and solutal transport of Blasius–Rayleigh–Stokes flow with convective boundary conditions for hybrid nanofluid flow. Madhukesh et al. [
32] presented the influence of thermophoretic particle migration in the flow of a hybrid nanofluid above a thin turning needle. Ullah et al. [
33] explored the unsteady stretchable surface with thermophoresis and Brownian motion effect for Reiner-Philippoff fluid. Sensitivity testing and numerical analysis of the tangent hyperbolic nanofluid flow on a stretching surface is done by Shafiq et al. [
34]. Khan et al. [
35] used the convective boundary conditions to elaborate the heat and mass transfer in 3D flow over a stretchable surface. Arshad et al. [
36] explored the MHD flow over an exponentially stretching surface with thermophoresis and Brownian motion. Pal et al. [
37] investigated the thermophoresis and Brownian motion influence on magneto-convective heat transfer above the stretching surface for viscoelastic fluid.
The temperature gradient is a physical quantity, which describes at which rate and in which direction temperature is being transferred around a particular region. Similarly, the concentration gradient is defined as the mass transfer rate. These types of flow have a crucial impact on various applications. Makinde et al. [
38] presented the boundary layer flow for exponentially stretching surface with heat sink/source and thermal radiation Hamid et al. [
39] investigated the bio-convection flow of magneto-cross nanofluid including microorganisms by using an effective Prandtl number technique. Varun Kumar et al. [
40] explored the Arrhenius activation energy for hybrid nanofluid fluid above a curved stretching surface. Shah et al. [
41] used the Prandtl hybrid nanofluid flow with chemical reactions and motile microorganisms to study the bio-convection effects. Faraz et al. [
42] explored the multi-slip effect on axisymmetric Casson fluid flow with a chemical reaction. Arshad and Hassan [
43] numerically investigated the hybrid nanofluid flow over permeable stretching surface considering magnetic field. Hassan et al. [
44] explored viscous dissipation and heat absorption with chemical reactions and heat source/sink. Krishnamurthy et al. [
45] explored the chemical reaction effects and melting heat transfer for frontier layer slip flow.
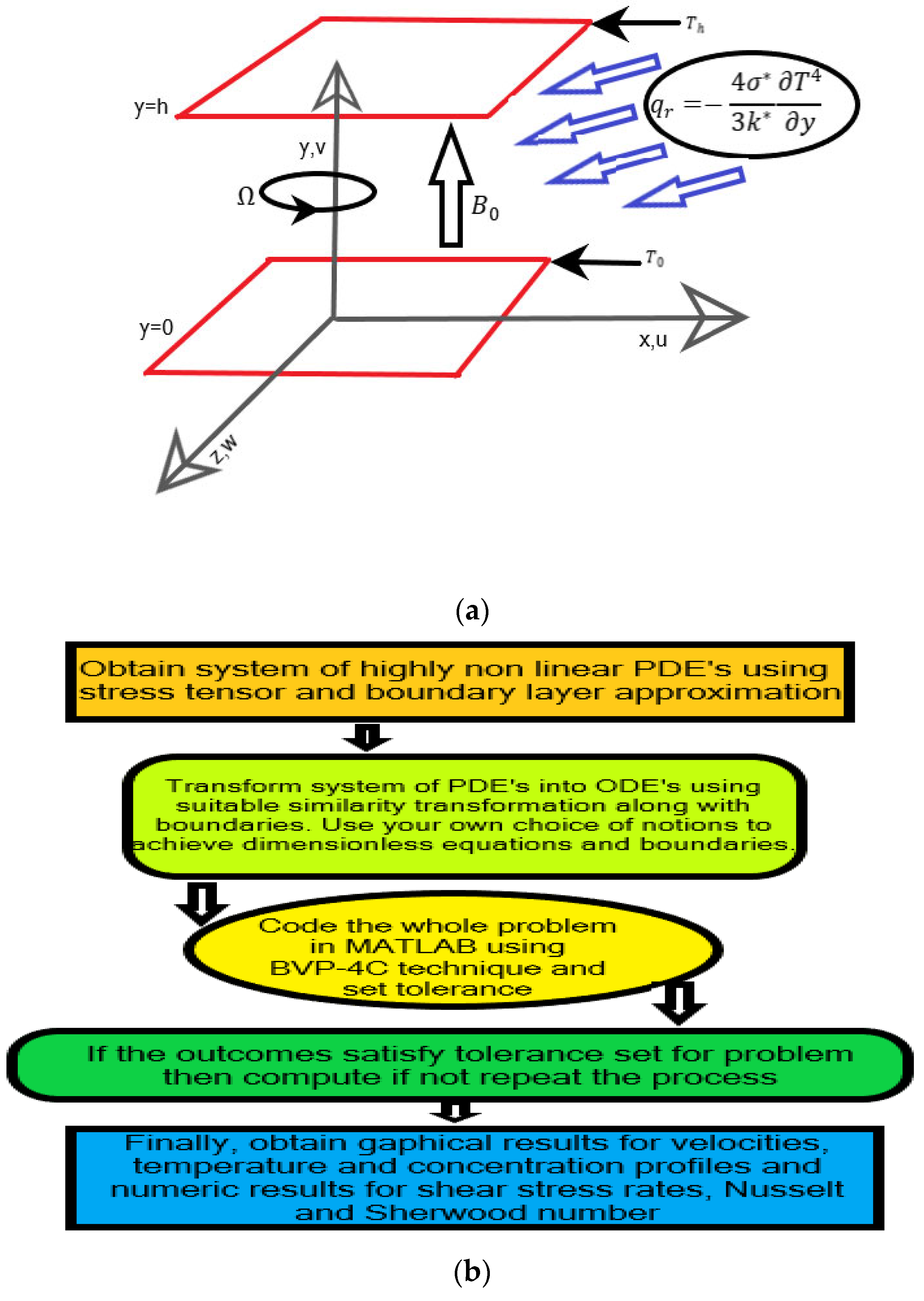
The main objective of this research is to examine the flow of a viscous, incompressible, hybrid nanofluid above a stretchy, rotating, permeable plate with a heat source and chemical reaction under the influence of a magnetic field. The fluid and plates are rotating simultaneously with constant speed about the axis of rotation. The governing equations of momentum, energy and concentration are transformed into ODEs by a similarity transformation and tackled at MATLAB using the boundary value problem technique. The influence of different constraints is discussed in the form of graphs and tables.
2. Problem Formulation
Suppose a rotating three-dimensional, steady, incompressible, and electrically conducting hybrid nanofluid flow between two permeable parallel plates. The cartesian coordinate system is considered to understand the problem as the y-axis is perpendicular to the x-axis and the z-axis is perpendicular to both axes. The lower level is placed at a height and upper-level plate at a height The lower-level plate is being stretched with rate , i.e., proportional to the applied equal and opposite forces maintaining the origin of plates fixed. A uniform magnetic field is applied parallel to y-axis in which fluid is rotating. Two different namely -water and -water hybrid nanofluids are considered for comparison. The heat sink/source, chemical reaction, mixed convection, thermophoresis, and Brownian motion are considered to investigate the effects on different profiles. The governing equations have the following form:
Here,
and
are velocity components in
and
directions, respectively, the parameters
are all defined in the nomenclature section. The missing term
in Equation (4) shows that there is a net cross-flow along the
z-axis The Rosseland thermal radiation approximation relation is defined as
Where
. describes the Stefan–Boltzmann constant, and
presents absorption coefficient. The temperature difference is assumed to be very small, and Taylor’s series expansion of
in terms of
will truncate the temperature to
. Thus, using this truncated form will provide us with the following simplified form:
The corresponding boundary conditions are:
Similarity Transformation:
The following similarity transformation is utilized to convert leading equations into a set of ordinary differential equations.
The differentiation is with respect to
Transformed Governing Equations:
The flow governing equalities of continuity, momentum, energy and concentration takes the following form after employing the similarity transformation. The continuity equation is identically satisfied, and the remaining are:
By removing the pressure gradient term from above mentioned Equations (10) and (11) reduced to
Here,
is a constant. Afterwards, differentiation Equation (13), with respect to
, takes the form:
So, the leading equations of momentum/velocity of the current problem take the following form:
The Roseland approximation in the energy equation for radiative heat flux [
19] is defined as:
Here,
is he Stefan–Boltzman constant and
is the absorption coefficient. Taking into consideration the minimal difference of the temperature, the Taylor series expansion for
in terms of
, can be written as follows:
Energy equality takes the form by utilizing the definition of heat flux
:
Similarly, the following form (dimensionless) takes the concentration Equation (6):
The transformed boundary conditions are:
The is a dimensionless suction/injection parameter.
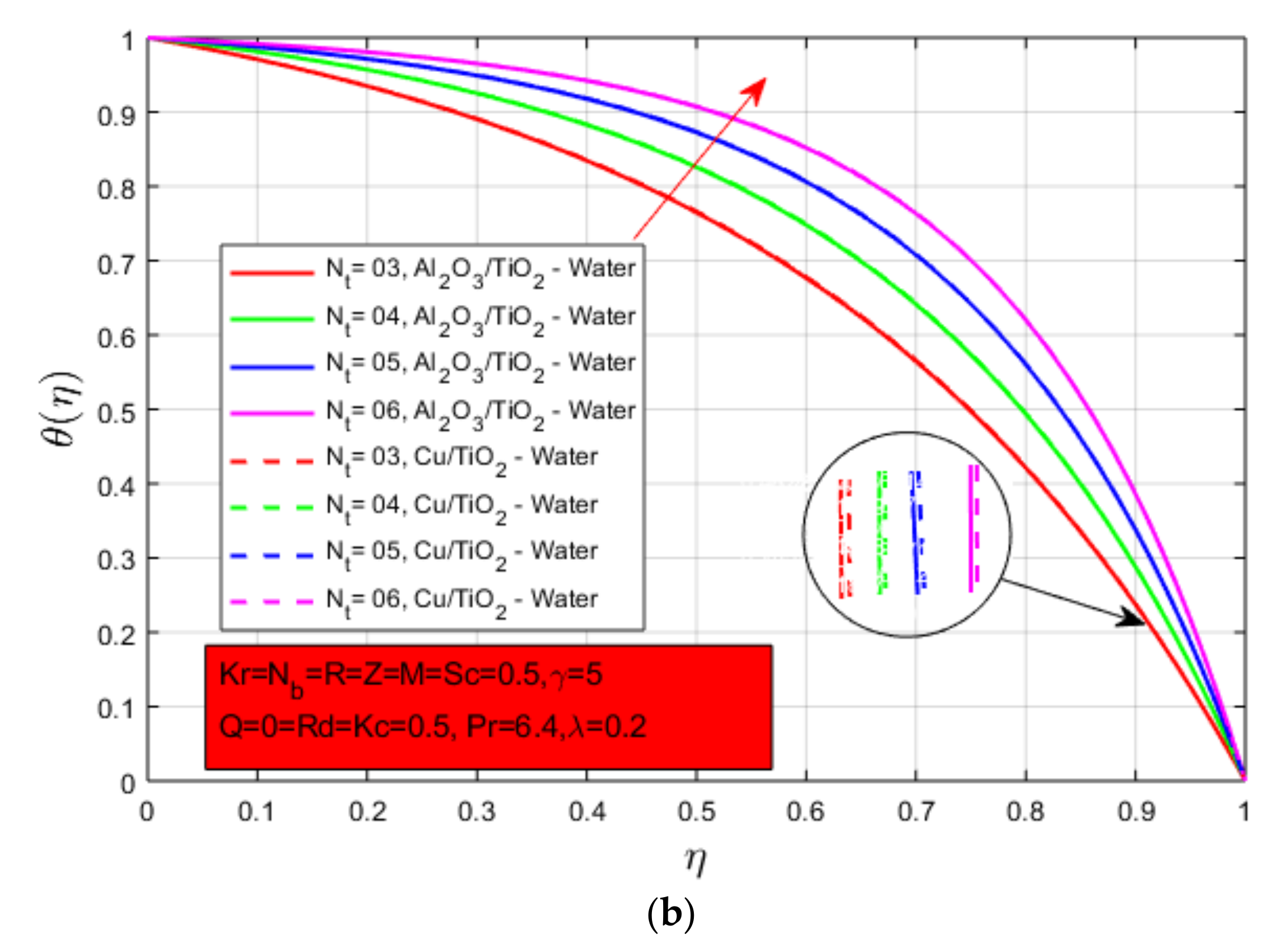
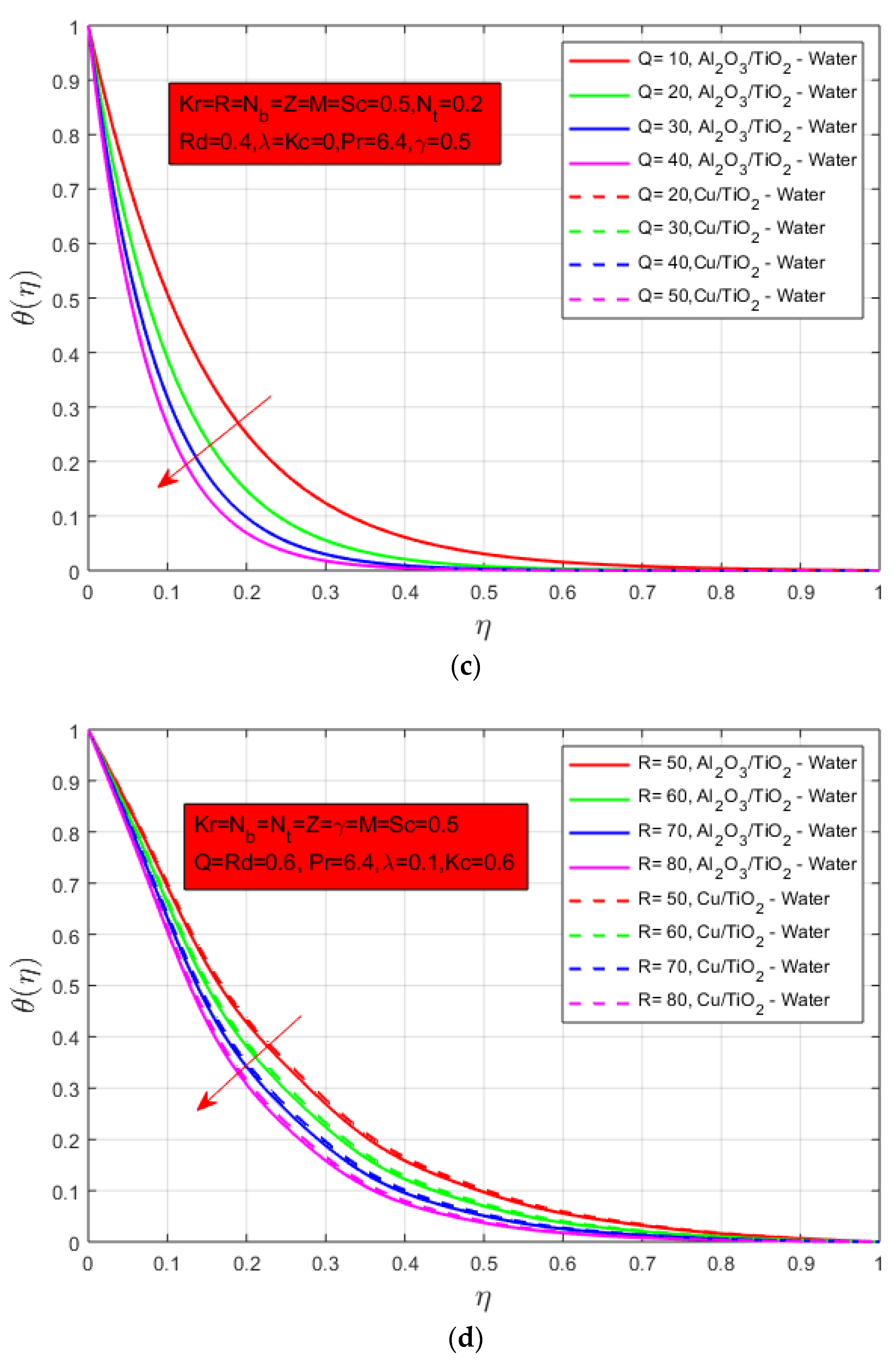
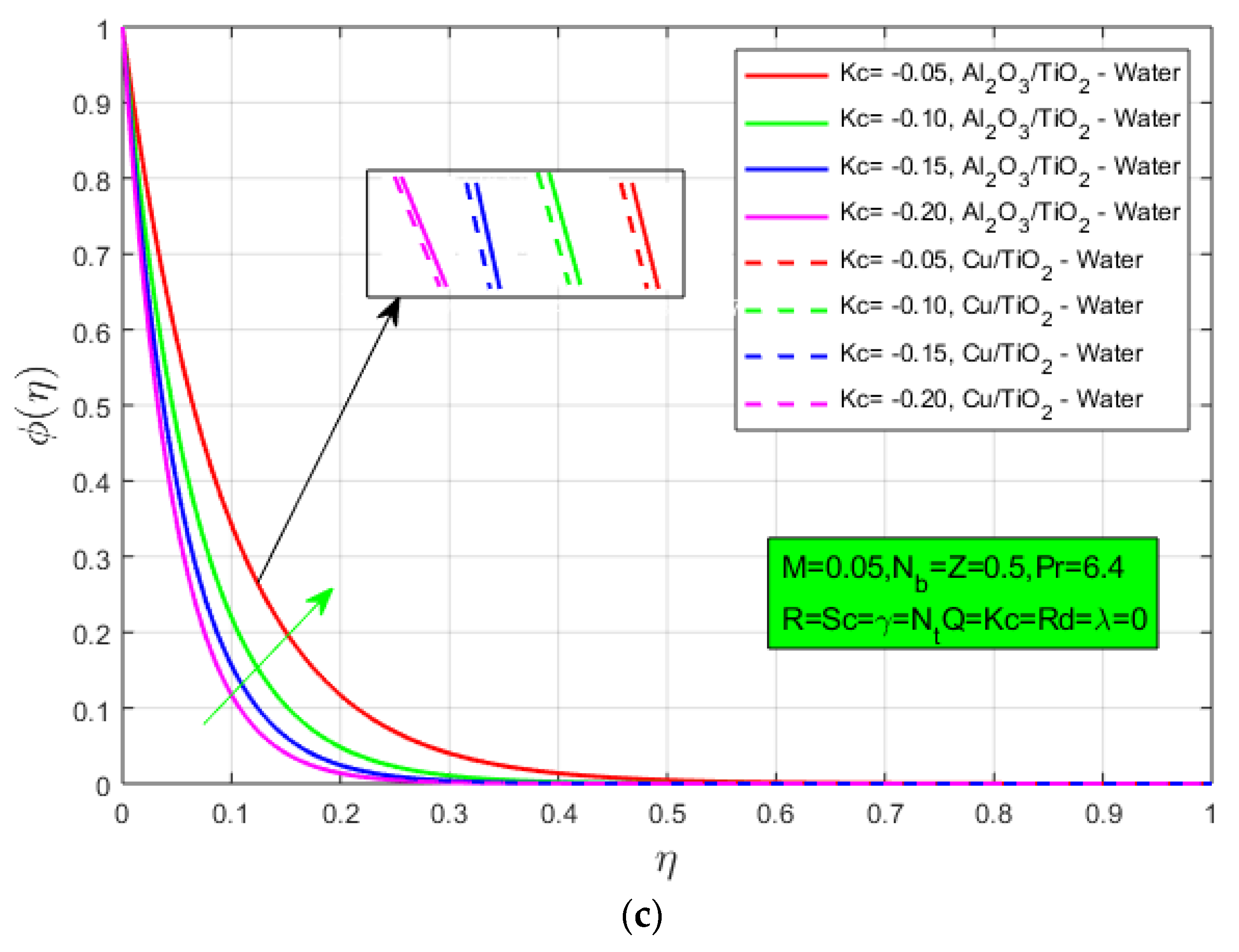
The dimensionless quantities magnetic field, porosity, mixed convection, Prandtl number, Schmidt number, Reynolds number, radiation, Brownian motion, thermophoresis, radiation, heat source/sink, chemical reaction and constants for hybrid nanofluid are defined below as:
Quantities of Physical Interest:
The skin resistance coefficient
along the stretchable wall is the physical quantity of concern in this problem, this one is defined as
Here,
indicates the shear tension or skin friction along the stretched wall, and is defined as
The dimensionless form is:
Here and.
The temperature field can be used to compute the Nusselt number (dimensionless) for the temperature transference constant at the surface:
or
The concentration field can be used to compute the non-dimensional form of the mass transfer coefficient at the sheet in terms of the Sherwood number: