Abstract
As electronic components continue to be miniaturized, the heat flux density continues to increase. Scholars have proposed the use of microchannel heat sinks (MCHS) to dissipate heat from devices with high heat flux density, and have pointed out that the heat dissipation capability of MCHS can be improved in two ways: using nanofluids with high thermal conductivity and optimizing the structure of MCHS. In this paper, the thermophysical parameters and thermo-hydraulic performance of nanofluids in microchannels are reviewed. Improving the heat dissipation of MCHS is analyzed and discussed in terms of both thermal properties and flow properties, respectively.
1. Introduction
With the miniaturization of electronic devices, the integrated density of transistors is increasing. At present, transistors have been developed to the nanometer level. Nano-scale quantum dot thermoelectric transport [1] and molecular-scale thermoelectric devices [2] have been proposed. Single-molecule junction is the most basic research unit. At present, some scholars have studied the thermal power of the single-molecule junctions of some materials (such as metal [3], oligomeric (styrene-acetylene) derivatives [4], carbon nanotubes and graphene [5,6]). The thermoelectric measurement platform using liquid eutectic gallium-indium (EGaln) to obtain large amounts of data was proposed by Park et al. [7]. Heat dissipation and thermoelectric effects in molecular junctions have also received extensive attention [8]. Therefore, it is urgent to find an efficient cooling method for micro devices to reduce energy consumption, improve equipment efficiency and increase service life [9,10].
Most conventional fluids have low thermal conductivity and poor thermal performance, such as water, ethylene glycol (EG) and oil. In 1995, Choi et al. [11] proposed to disperse metal nanoparticles into conventional fluids to make nanofluids and found that the thermal conductivity increased. Therefore, applying nanofluids to micro-nano scale heat dissipation can effectively improve the heat-dissipation effect [12].
Tuckerman and Pease [13] were the first to put forward the concept of microchannel heat sinks (MCHS) in 1981 and designed a water-cooled MCHS for heat transfer at a heat flux density of 790 W/cm2. It was found that the maximum temperature at the bottom was 71 °C higher than the water temperature at the inlet, and MCHS effectively improves the cooling effect. MCHS have the characteristics of small size, compact structure and good heat transfer, which can effectively solve the problem of the high heat flux density of tiny electronic components.
However, with the addition of metal nanoparticles, the viscosity of the nanofluids increases, resulting in a higher pressure drop and weaker flow properties in the microchannel heat sink, affecting the overall performance of the MCHS [14]. In addition, the structure and arrangement of the channels also affect the heat-dissipation effect of the MCHS [15].
Most researchers have reviewed the thermal properties of nanofluids and the effect of microchannel structure on the heat-dissipation effect of MCHS separately. Few researchers have investigated the effect of the combination of both on the flow and heat transfer characteristics of MCHS.
This paper is divided into three main parts. The first part mainly introduces the preparation method, physical properties and methods of passively enhancing heat transfer. The second part presents the state of research on the influence of different microchannel shapes, structures and distributions on the performance of MCHS in recent years. The third part describes the flow and heat transfer characteristics of different nanofluids and fluid flow states in different structures of MCHS. This paper provides a review of improvements in the heat-dissipation capacity of MCHS in terms of fluid properties and MCHS structure, respectively, providing a clearer direction for subsequent research.
2. Nanofluids
This section reviews and summarizes the methods of preparing nanofluids, the measurement methods of stability, the factors influencing physical properties (thermal conductivity, viscosity, surface tension and contact angle), as well as explaining the mechanisms by which nanofluids enhance heat transfer and reviewing methods for enhancing passive heat transfer in nanofluids.
2.1. Preparation
The performance of nanofluids is closely related to the preparation method. Common preparation methods are one-step and two-step methods [16,17,18]. The one-step and two-step methods each have advantages and disadvantages, as shown in Figure 1 and Figure 2. The appropriate method should be chosen for the preparation of nanofluids [19].
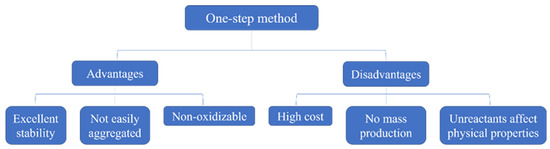
Figure 1.
Advantages and disadvantages of the one-step method.
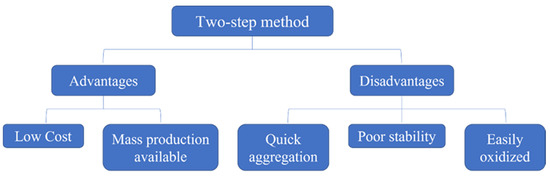
Figure 2.
Advantages and disadvantages of the two-step method.
2.2. Stability
The stability of nanofluids is important for their thermal properties. Factors such as nanofluids preparation method [20], nanoparticle concentration [21], nanoparticle type, surfactant type, surfactant concentration, pH [22], sonication type and time and sonication power can affect the stability of nanofluids [23]. Many approaches are available to assess the stability of nanofluids, including sedimentation observation [24], transmittance method based on ultraviolet spectrophotometer [25], Zeta potential measurements [26], and the 3ω method [27].
2.2.1. Settlement Observation Method
Ali et al. [20] used the settlement observation method to find the dispersed deposition of nanofluids prepared by the two-step method controlling the ultrasonic water-bath temperature below 30 °C and flocculent deposition by the conventional two-step method.
2.2.2. Transmittance Method Based on UV Spectrophotometer
Cacua et al. [25] discovered that nanofluids with a critical micelle concentration of sodium dodecylbenzene sulfonate as the surfactant are more stable, while those without surfactant and those with cetyltrimethylammonium bromide as the surfactant are less stable, using the transmittance method based on a UV spectrophotometer.
2.2.3. Zeta Potential Measurement
Zeta potential measurement is a method for assessing stability based on the DLVO theory [22]. A Zeta-potential greater than ±30 mV is considered stable, and within ±15 mV, it is considered unstable [24]. Parsa et al. [26] used the Zeta-potential method to conclude that nanofluids prepared using the one-step method are significantly higher than those prepared using the two-step method.
Many current studies combine qualitative assessment methods with quantitative methods [28], such as the transmittance method and Zeta-potential measurement method [29], to describe the stability of nanofluids in a more objective and intuitive way [30,31].
2.3. Thermal Conductivity
The thermal conductivity of nanofluids is a significant physical characteristic; the higher the thermal conductivity of the nanofluids, the better the heat-transfer performance. It has been found that the thermal conductivity of nanofluids is related to the type and size of nanoparticles, base fluid, concentration, temperature and pH. Table 1 summarizes the thermal conductivity of common nanofluids. It can be observed that the thermal conductivity improves with the increasing concentration of the nanofluids.

Table 1.
Thermal conductivity of common nanofluids.
Soltani et al. [43] discovered that the thermal conductivity of engine oils decreases with the increasing temperature. However, the higher the temperature, the higher the thermal conductivity of the nanofluids, with the largest increase, by 5.63%, for φ = 0.2% MWCNTs-oil nanofluids from T = 20 °C to T = 60 °C.
Zhang et al. [49] experimentally investigated the effect of pH on the thermal conductivity of TiO2-H2O nanofluids. It was concluded that pH = 6.5 is the isoelectric point and the further the pH is from 6.5, the higher the thermal conductivity; pH = 2 and 10 have the highest thermal conductivity of the nanofluids.
Jeong et al. [50] examined the effect of the shape of nanoparticles on the thermal conductivity of ZnO nanofluids. The thermal properties of the nearly rectangular nanoparticles were more significantly enhanced, with an 18% rise in thermal conductivity.
2.4. Viscosity
The viscosity of nanofluids increases with the addition of nanoparticles. Pumping power and pressure drop are related to the viscosity of the fluid, which is an important physical parameter affecting the flow characteristics [51], and, therefore, the study of nanofluid viscosity is necessary. Existing studies revealed that nanofluids’ viscosity can be affected by temperature, nanoparticle size and shape and concentration, nanofluids preparation methods [52] and pH.
Li et al. [53] prepared and evaluated the viscosity for each mass fraction of ZnO-EG nanofluids at different temperatures. Karimipour et al. [54] analyzed the relationship between temperature and nanofluid viscosity through experiments and numerical simulations. They both conclude that viscosity decreases with increasing temperature.
Agarwal et al. [55] found that the dynamic viscosity of paraffinic alumina nanofluids with different particle sizes (13 nm, 15 nm) decreases with increasing nanoparticles. Figure 3 is the conclusion drawn by Hu et al. [56] using SEM images and DLVO theory. With the change in particle concentration, the change trend of viscosity with particle size can be divided into three trends: decreasing, unchanged and increasing. As the size of the nanoparticles changes, the contact area between the nanoparticles and the base fluid changes, resulting in changes in interfacial resistance and flow layers, which, in turn, affect the viscosity of the nanofluid.
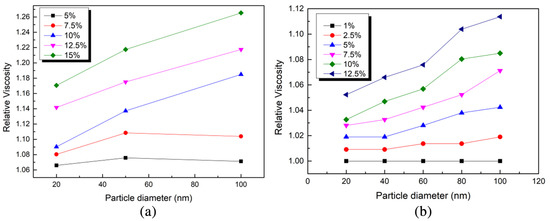
Figure 3.
Effect of nanoparticle size on viscosity [56]: (a) Al2O3; (b) ZnO.
The relationship between volume fraction and viscosity of ZnO-Ag (1:1)-H2O hybrid nanofluids was experimentally investigated by Ruhani et al. [57]. Li et al. [58] and Hu et al. [38] researched the relationship between the viscosity and concentration of CuO-H2O and TiO2-H2O nanofluids, respectively. Both concluded that as the concentration of the nanofluids increases, the viscosity increases.
2.5. Surface Tension and Contact Angle
2.5.1. Surface Tension
The addition of nanoparticles also alters the surface tension of the base fluid, affecting surface-tension-driven convective flow and heat transfer [58]. Kim et al. [59] revealed that incorporating Al2O3 nanoparticles into alcohol-based nanofluids resulted in an average increase in surface tension by 3.4%. Ilyas et al. [60] investigated the effect of concentration and temperature on the surface tension of a graphene nanoplate-based saline nanofluids using the pendant-drop method. Based on previous studies, it can be concluded that surface tension decreases with the addition of nanoparticles, decreases with increasing temperature and that different base fluids also change the surface tension. However, there are some inconsistent results for the effects of concentration and surfactant and further research is needed [61].
2.5.2. Contact Angle
The contact angle is a parameter used to indicate the ability of a liquid to make contact with a surrounding solid surface [62]. The concentration, size and shape of nanoparticles in a nanofluid affect the size of the contact angle and, thus, change the wettability [63]. Huminic et al. [64] experimentally investigated the effect of solid (aluminum, copper and stainless steel) surfaces on the contact angle of nanofluids, using the Wilhelmy plate technique. It can be concluded that the wettability of nanofluids is superior to that of base fluids and that the contact angle of the nanofluids decreases with increasing temperature and concentration.
2.6. Methods of Passively Enhancing Heat Transfer
At present, improving the passive heat transfer of nanofluids has also been widely studied [65,66]. Changing the size [67,68], shape [69] and concentration [70] of the nanofluid can increase the thermal properties of the nanofluid and, thus, improve its thermal performance in the cavity.
In addition, one of the most common methods to enhance the heat-transfer capacity of nanofluids in a cavity is to alter the cavity structure to increase the interference of the nanofluids, disrupt the flow boundary layer and enhance heat transfer [71]. Table 2 lists some of the shape and structure optimizations.

Table 2.
Optimization of cavity shape and structure.
Wang et al. [77] found that adding a magnetic field would lead to the formation of more vortices on the working surface and stronger heat transfer. Table 3 summarizes the influence of external field on the thermal properties of nanofluids.

Table 3.
Simulation of electric and magnetic fields and radiation on the flow properties of nanofluids.
Based on previous studies, it can be concluded that reasonable changes to the cavity structure and the addition of a suitable external force field can lead to an improvement in the thermal properties of nanofluids.
3. Microchannel Heat Sinks (MCHS)
The heat-transfer capacity of MCHS is mainly influenced by the structure and distribution of the microchannels, the thermal capacity of the solid medium and the thermal capacity and flow state of the fluid medium. Microchannels can be optimized by changing the channel shape, and adding ribs and pin-fins to the microchannel and secondary flow channel, etc. [87]. This section summarizes the influence of physical structure on MCHS performance in recent years from four main perspectives: the shape of and variation in the cross-section of the microchannels, the shape of the ribs and cavities, the shape of the pin fins and the form of the distribution of the channels.
3.1. Thermal-Hydraulic Properties of Different Microchannel Shapes in MCHS
Figure 4 lists common channel shapes. Kose et al. [88] concluded that MCHS with rectangular channels (RMCHS) have the best thermal-hydraulic performance; the pump power can be reduced by 17% and 40% compared to trapezoidal and triangular shapes, respectively. Lv et al. [89] and Parlak et al. [90] found that microchannels with high aspect ratios have better heat dissipation and lower pressure drops, and that channel thickness and spacing affect the thermal resistance.

Figure 4.
3D models of different channel cross-section shapes [88]: (a) rectangular channel; (b) triangular channel; (c) trapezoidal channel.
Some researchers have further investigated the effect of rectangular variable section microchannels on the performance of MCHS. The thermal performance of microchannel-width divergence–convergence microchannel heat sinks (DCMCHS) [91] has been studied, as shown in Figure 5. It was obtained that the smaller the inlet-to-center-width ratio of symmetrical DCMCHS, the lower the thermal resistance and the higher the pressure drop. However, the study of microchannel-width-convergence MCHS [92] found that their thermal performance and that of asymmetrical DCMCHS both increase as the ratio of outlet-to-inlet width decreases.
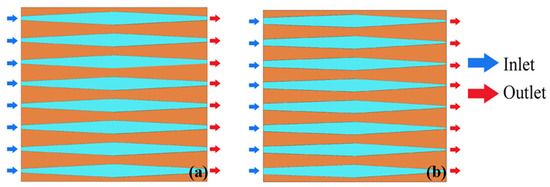
Figure 5.
Microchannels with section width [91]: (a) symmetrical DCMCHCS; (b) asymmetric DCMCHCS.
Hajmohammadi et al. [93] found that channel height divergence can improve the thermal performance of MCHS, as shown in Figure 6. However, the improved performance of the MCHS is achieved by consuming more energy.
Figure 6.
Highly divergent microchannel model [93].
Sajid et al. [94] carried out the waveform optimization of rectangular channels, as shown in Figure 7, and found that the effect of wavelength on the Nu is more significant than the effect of microchannel width. Khan et al. [95] further investigated the effect of base wavy shape on MCHS performance and found that a maximum thermal performance factor of 2.2 can be achieved.

Figure 7.
Wavy microchannel model [94].
3.2. Thermal-Hydraulic Properties of MCHS with Different Rib and Cavity Shapes
Based on the above, it is clear that variable cross sections can affect the performance of MCHS and, therefore, ribbed and cavitated microchannel structures have been proposed. The ribs will cause the flow boundary layer and the thermal boundary layer to be interrupted, which enhances heat transfer. Figure 8a [96] summarizes the common rib shapes and Figure 8b [97] is the truncated rib structure. The fluid in the cavity will form vortices to reduce the pressure drop. Therefore, a structure combining the ribs and cavities is proposed, as shown Figure 8c [98]. Table 4 summarizes the recent studies on the effects of ribs and cavities on MCHS.
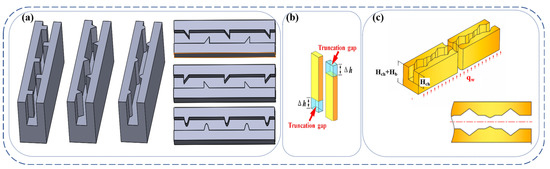
Figure 8.
Models of different shapes of ribs and cavities: (a) shape of ribs [96]; (b) shape of truncated ribs [97]; (c) structure of ribs and cavities [98].

Table 4.
Effect of ribs and cavities on the performance of MCHS.
3.3. Thermal-Hydraulic Properties of MCHS with Different Pin-Fin Shapes
The addition of pin fins in the microchannel can continuously cause the destruction and re-formation of the flow boundary layer, and also enhance the fluid perturbation to fully mix. Pin-fin shapes, sizes and distribution can cause different disturbance and mixing effects. common pin-fin shapes include square, circular, triangular and teardrop [106]. Figure 9 illustrates the different distribution types.

Figure 9.
Distribution types of pin fin in channel [107].
Table 5 lists the effects of pin fins on MCHS. Pin fin, rib and cavity can enhance heat dissipation. Combining them to study the comprehensive effect is also a hot spot of current research.

Table 5.
The effect of pin fins on the thermal and hydrological performance of MCHS.
Based on the above studies, the MCHS with secondary channels was proposed and investigated. Figure 10a,b show the MCHS with secondary channels formed by trapezoidal fins and parallelogram fins, respectively. It was found that the width ratio of secondary to primary flow channels has the greatest impact on the performance of MCHS [115,116]. The comparison of the influence of secondary flow caused by differently shaped pin fins needs further study.
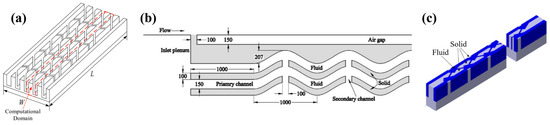
Figure 10.
MCHS with secondary channels: (a) trapezoidal fins [115]; (b) wavy microchannel [117]; (c) microchannel with cavities and ribs [118].
Ma et al. [117] brought a secondary flow structure into the wavy microchannels, as shown in Figure 10b. This structure increases the surface area and creates an evolving thin evaporating liquid film, which are the main reasons for the enhanced heat dissipation, but also a larger pressure drop.
Japar et al. [118] introduced secondary channels into the MCHS with ribs and cavities, as shown in Figure 10c, and found that the thermal boundary layer undergoes a process of interruption, mixing and then re-formation, resulting in the enhanced performance of the MCHS.
3.4. Thermal-Hydraulic Performance of MCHS with Different Distributions
The different distributions of the microchannels will mainly affect the uniformity of the temperature and the flow characteristic. Table 6 shows the influence of microchannel distribution on the thermal-hydraulic performance of the MCHS. It can be observed that the thermal performance of the MCHS is enhanced with increasing contact area between the fluid and the heat surface as well as with increasing fluid disturbance [119].

Table 6.
The influence of microchannel distribution on the thermal-hydraulic performance of the MCHS.
In addition to single-layer microchannel distributions, there are also double-layer distributions. Zhou et al. [125,126] discovered that the maximum temperature and temperature rise of the double-layer MCHS (DL-MCHS) base plate are reduced, and the thermal resistance is decreased. Derakhshanpour et al. [100] found that ribbed DL-MCHS have a 30–60% higher convective heat-transfer coefficient than ribbed SL-MCHS.
Further parametric and structural optimization of the DL-MCHS has been carried out by several researchers. DL-MCHS with a smaller channel width in the upper layer and a larger channel width in the lower layer can reduce the thermal resistance and enhance Nu [127]. As shown in Figure 11, the DL-MCHS with both upper and lower layers having wavy channels have low thermal resistance and induce more Dean vortices, allowing the sufficient mixing of hot and cold fluids for optimal cooling capacity [128].
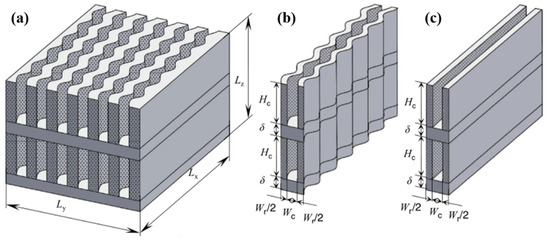
Figure 11.
DL-MCHS structural model [128]: (a) upper layer wavy and lower layer straight; (b) double layer wavy; (c) double layer straight.
4. Thermo-Hydraulic Performance of Nanofluids in MCHS
The heat dissipation capacity of the MCHS is closely related to the thermal properties and flow form of the working fluid. Nanofluids are used as working fluids in MCHS frequently due to their good thermal properties. This section provides a review of the effect of different nanofluids and flow states on the heat dissipation of MCHS. Table 7 summarizes the flow and heat-transfer performance of different MCHS structures using nanofluids in recent years.

Table 7.
Flow and heat-transfer performance of different MCHS structures using nanofluids.
The form of the flow of the fluid is also one of the most important elements affecting the heat-transfer performance of MCHS. Zhang et al. [138] examined the heat-dissipation capability of parallel-flow and counter-flow MCHS through numerical simulations, and found that the thermal performance of counter-flow MCHS is superior to that of parallel-flow MCHS. The thermal performance of parallel-flow and counter-flow DL-MCHS was also studied and it was found that counter flow has better thermal performance [126].
Awad et al. [139] found that the average temperature of jet-impacted MCHS is lower. Xu et al. [140] researched the thermal performance of MCHS driven by the square wave, triangular wave, sawtooth wave and sinusoidal pulsating flows of nanofluids, and the Nu can be increased by 16.5%. Mohammadpour et al. [141] used an algorithm to investigate the effect of dual synthetic jet parameters on the performance of MCHS nanofluids and found that the thermal conductivity could be increased by 53.99% for isotropic driving.
5. Conclusions and Prospects
This paper reviewed the physical properties of nanofluids, the effect of microchannel structures on the thermal performance of MCHS and the effect of different nanofluids and flow states on the thermal dissipation of MCHS, allowing the following conclusions to be drawn:
- (1)
- The thermal conductivity increases with increasing concentration and temperature. The viscosity decreases with increasing temperature and increases with increasing concentration, and the viscosity varies with nanoparticles in relation to the concentration. The surface tension decreases with increasing temperature and the contact angle decreases with increasing temperature and concentration.
- (2)
- Optimization of the cavity structure and the incorporation of external fields can improve passive heat transfer in nanofluids.
- (3)
- Rectangular channels have the best MCHS performance, and variable channel cross-sections can improve heat dissipation. Adding ribs will destroy the boundary layer and increase the pressure drop; cavities will form vortices and reduce the pressure drop; pin fins will cause secondary flow, all three, for the microchannel structure, will increase the the heat dissipation of the MCHS.
- (4)
- The combination of a high thermal-performance nanofluids and an optimized MCHS structure allows for the efficient cooling of the MCHS. A suitable fluid flow state can also improve the cooling performance of MCHS more significantly.
Most of the available findings are that the high thermal-conductivity properties of nanofluids can enhance the heat dissipation from MCHS in different microchannel structures. The effect of properties such as the surface tension and contact angle of nanofluids on MCHS cooling has been little investigated and this should be a key element of future research. It is necessary to explore in depth the coupling effect between each physical property of the nanofluid and the microchannel structure. The rapid miniaturization of electronic devices and the rapid development of molecular electronics are both placing higher demands on micro heat sinks; thus, improving the cooling performance of microchannels is urgent and needs to be looked at by a wide range of academics.
Author Contributions
Investigation and writing—original draft, Y.W.; writing—review and editing, J.Y.; conceptualization, methodology, investigation and writing—review and editing, C.Q.; writing—review and editing, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of Jiangsu Province, China, grant number BK20181359.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Svilans, A.; Leijnse, M.; Linke, H. Experiments on the thermoelectric properties of quantum dots. C. R. Phys. 2016, 17, 1096–1108. [Google Scholar] [CrossRef]
- Park, S.; Kang, H.; Yoon, H.J. Structure–thermopower relationships in molecular thermoelectrics. J. Mater. Chem. A 2019, 7, 14419–14446. [Google Scholar] [CrossRef]
- Reddy, P.; Jang, S.Y.; Segalman, R.A.; Majumdar, A. Thermoelectricity in molecular junctions. Science 2007, 315, 1568–1571. [Google Scholar] [CrossRef] [PubMed]
- Dekkiche, H.; Gemma, A.; Tabatabaei, F.; Batsanov, A.S.; Niehaus, T.; Gotsmann, B.; Bryce, M.R. Electronic conductance and thermopower of single-molecule junctions of oligo (phenyleneethynylene) derivatives. Nanoscale 2020, 12, 18908–18917. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Wang, X.; Lai, X.; Li, G.; Watanable, K.; Taniguchi, T.; Zebarjadi, M.; Andrei, E.Y. High thermoelectricpower factor in graphene/hBN devices. Proc. Natl. Acad. Sci. USA 2016, 113, 14272–14276. [Google Scholar] [CrossRef]
- Paul, A.K.; Ghosh, A.; Chakraborty, S.; Roy, U.; Dutta, R.; Watanable, K.; Taniguchi, T.; Panda, A.; Agarwala, A.; Mukerjee, S.; et al. Interaction-driven giant thermopower in magic-angle twisted bilayer graphene. Nat. Phys. 2022, 18, 691–698. [Google Scholar] [CrossRef]
- Park, S.; Yoon, H.J. New Approach for large-area thermoelectric junctions with a liquid eutectic gallium–indium electrode. Nano Lett. 2018, 18, 7715–7718. [Google Scholar] [CrossRef]
- Cui, L.; Miao, R.; Jiang, C.; Meyhofer, E.; Reddy, P. Perspective: Thermal and thermoelectric transport in molecular junctions. J. Chem. Phys. 2017, 146, 092201. [Google Scholar] [CrossRef]
- He, Z.; Yan, Y.; Zhang, Z. Thermal management and temperature uniformity enhancement of electronic devices by micro heat sinks: A review. Energy 2021, 216, 119223. [Google Scholar] [CrossRef]
- Ramesh, K.N.; Sharma, T.K.; Rao, G.A.P. Latest Advancements in heat transfer enhancement in the micro-channel heat sinks: A review. Arch. Comput. Methods Eng. 2020, 28, 3135–3165. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, Washington, DC, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Qiu, L.; Zhu, N.; Feng, Y.; Michaelides, E.E.; Zyla, G.; Jing, D.; Zhang, X.; Norris, P.M.; Markides, C.N.; Mahian, O. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys. Rep. 2020, 843, 1–81. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Japar, W.M.A.A.; Sidik, N.A.C.; Aid, S.R.; Asako, Y.; Ken, T.L. A comprehensive review on numerical and experimental study of nanofluid performance in microchannel heat sink (MCHS). J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 45, 165–176. [Google Scholar]
- Gao, J.; Hu, Z.; Yang, Q.; Liang, X.; Wu, H. Fluid flow and heat transfer in microchannel heat sinks: Modelling review and recent progress. Therm. Sci. Eng. Prog. 2022, 29, 101203. [Google Scholar] [CrossRef]
- Yang, L.; Ji, W.; Mao, M.; Mao, M.; Huang, J. An updated review on the properties, fabrication and application of hybrid-nanofluids along with their environmental effects. J. Clean. Prod. 2020, 257, 120408. [Google Scholar] [CrossRef]
- Rudyak, V.Y.; Minakov, A.V.; Pryazhnikov, M.I. Preparation, characterization, and viscosity studding the single-walled carbon nanotube nanofluids. J. Mol. Liq. 2021, 329, 115517. [Google Scholar] [CrossRef]
- Yılmaz Aydın, D.; Gürü, M. Nanofluids: Preparation, stability, properties, and thermal performance in terms of thermo-hydraulic, thermodynamics and thermo-economic analysis. J. Therm. Anal. Calorim. 2021, 147, 7631–7664. [Google Scholar] [CrossRef]
- Mondal, S.; Dey, A.; Pal, U. Low temperature wet-chemical synthesis of spherical hydroxyapatite nanoparticles and their in situ cytotoxicity study. Adv. Nano Res. 2016, 4, 295–307. [Google Scholar]
- Ali, N.; Teixeira, J.A.; Addali, A. Aluminium nanofluids stability: A comparison between the conventional two-step fabrication approach and the controlled sonication bath temperature method. J. Nanomater. 2019, 2019, 3930572. [Google Scholar] [CrossRef]
- Qi, C.; Wan, Y.L.; Li, C.Y.; Han, D.T.; Rao, Z.H. Experimental and numerical research on the flow and heat transfer characteristics of TiO2-water nanofluids in a corrugated tube. Int. J. Heat Mass Tranf. 2017, 115, 1072–1084. [Google Scholar]
- Zareei, M.; Yoozbashizadeh, H.; Madaah Hosseini, H.R. Investigating the effects of pH, surfactant and ionic strength on the stability of alumina/water nanofluids using DLVO theory. J. Therm. Anal. Calorim. 2018, 135, 1185–1196. [Google Scholar] [CrossRef]
- Cacua, K.; Buitrago Sierra, R.; Herrera, B.; Pabón, E.; Murshed, S.M.S. Nanofluids’ stability effects on the thermal performance of heat pipes. J. Therm. Anal. Calorim. 2018, 136, 1597–1614. [Google Scholar] [CrossRef]
- Chakraborty, S.; Panigrahi, P.K. Stability of nanofluid: A review. Appl. Therm. Eng. 2020, 174, 115259. [Google Scholar] [CrossRef]
- Cacua, K.; Buitrago Sierra, R.; Pabón, E.; Gallego, A.; Zapata, C.; Herrera, B. Nanofluids stability effect on a thermosyphon thermal performance. Int. J. Therm. Sci. 2020, 153, 106347. [Google Scholar] [CrossRef]
- Masoud Parsa, S.; Yazdani, A.; Aberoumand, H.; Farhadi, Y.; Ansari, A.; Aberoumand, S.; Karimi, N.; Afrand, M.; Cheraghian, G.; Muhammad Ali, H. A critical analysis on the energy and exergy performance of photovoltaic/thermal (PV/T) system: The role of nanofluids stability and synthesizing method. Sustain. Energy Technol. 2022, 51, 101887. [Google Scholar] [CrossRef]
- Said, Z.; Sundar, L.S.; Tiwari, A.K.; Ali, H.M.; Sheikholeslami, M.; Bellos, E.; Babar, H. Recent advances on the fundamental physical phenomena behind stability, dynamic motion, thermophysical properties, heat transport, applications, and challenges of nanofluids. Phys. Rep. 2022, 946, 1–94. [Google Scholar] [CrossRef]
- Sezer, N.; Atieh, M.A.; Koç, M. A comprehensive review on synthesis, stability, thermophysical properties, and characterization of nanofluids. Powder Technol. 2019, 344, 404–431. [Google Scholar] [CrossRef]
- Almanassra, I.W.; Manasrah, A.D.; Al-Mubaiyedh, U.A.; Al-Ansari, T.; Malaibari, Z.O.; Atieh, M.A. An experimental study on stability and thermal conductivity of water/CNTs nanofluids using different surfactants: A comparison study. J. Mol. Liq. 2020, 304, 111025. [Google Scholar] [CrossRef]
- Xian, H.W.; Sidik, N.A.C.; Saidur, R. Impact of different surfactants and ultrasonication time on the stability and thermophysical properties of hybrid nanofluids. Int. Commun. Heat Mass Transf. 2020, 110, 104389. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, S.H.; Lee, J.H.; Jang, S.P. Effect of particle shape on suspension stability and thermal conductivities of water-based bohemite alumina nanofluids. Energy 2015, 90, 1290–1297. [Google Scholar] [CrossRef]
- Aberoumand, S.; Jafarimoghaddam, A. Experimental study on synthesis, stability, thermal conductivity and viscosity of Cu-engine oil nanofluid. J. Taiwan Inst. Chem. Eng. 2017, 71, 315–322. [Google Scholar] [CrossRef]
- Chen, M.; He, Y.; Huang, J.; Zhu, J. Investigation into Au nanofluids for solar photothermal conversion. Int. J. Heat Mass Transf. 2017, 108, 1894–1900. [Google Scholar] [CrossRef]
- Yang, L.; Xu, J.; Du, K.; Zhang, X. Recent developments on viscosity and thermal conductivity of nanofluids. Powder Technol. 2017, 317, 348–369. [Google Scholar] [CrossRef]
- Chen, M.; He, Y.; Zhu, J.; Wen, D. Investigating the collector efficiency of silver nanofluids based direct absorption solar collectors. Appl. Energy 2016, 181, 65–74. [Google Scholar] [CrossRef]
- Arjmandfard, A.; Toghraie, D.; Mehmandoust, B.; Hashemian, M.; Karimipour, A. The study of atomic porosity effect on water/Fe nanofluid flow in a microchannel with a molecular dynamics method. J. Mol. Liq. 2020, 317, 114291. [Google Scholar] [CrossRef]
- Li, Z.; Sarafraz, M.M.; Mazinani, A.; Hayat, T.; Alsulami, H.; Goodarzi, M. Pool boiling heat transfer to CuO-H2O nanofluid on finned surfaces. Int. J. Heat Mass Transf. 2020, 156, 19780. [Google Scholar] [CrossRef]
- Hu, Y.; He, Y.; Wang, S.; Wang, Q.; Inaki Schlaberg, H. Experimental and numerical investigation on natural convection heat transfer of TiO2-Water nanofluids in a square enclosure. J. Heat Transf. 2014, 136, 022502. [Google Scholar] [CrossRef]
- Li, H.; He, Y.; Hu, Y.; Jiang, B.; Huang, Y. Thermophysical and natural convection characteristics of ethylene glycol and water mixture based ZnO nanofluids. Int. J. Heat Mass Transf. 2015, 91, 385–389. [Google Scholar] [CrossRef]
- Wei, H.; Afrand, M.; Kalbasi, R.; Ali, H.M.; Heidarshenas, B.; Rostami, S. The effect of tungsten trioxide nanoparticles on the thermal conductivity of ethylene glycol under different sonication durations: An experimental examination. Powder Technol. 2020, 374, 462–469. [Google Scholar] [CrossRef]
- Soltani, F.; Toghraie, D.; Karimipour, A. Experimental measurements of thermal conductivity of engine oil-based hybrid and mono nanofluids with tungsten oxide (WO3) and MWCNTs inclusions. Powder Technol. 2020, 371, 37–44. [Google Scholar] [CrossRef]
- Choi, T.J.; Park, M.S.; Kim, S.H.; Jang, S.P. Experimental study on the effect of nanoparticle migration on the convective heat transfer coefficient of EG/water-based Al2O3 Nanofluids. Int. J. Heat Mass Transf. 2021, 169, 120903. [Google Scholar] [CrossRef]
- Mei, S.; Qi, C.; Liu, M.; Fan, F.; Liang, L. Effects of paralleled magnetic field on thermo-hydraulic performances of Fe3O4-water nanofluids in a circular tube. Int. J. Heat Mass Transf. 2019, 134, 707–721. [Google Scholar] [CrossRef]
- Harandi, S.S.; Karimipour, A.; Afrand, M.; Akbari, M.; D’Orazio, A. An experimental study on thermal conductivity of F-MWCNTs–Fe3O4/EG hybrid nanofluid: Effects of temperature and concentration. Int. Commun. Heat Mass Transf. 2016, 76, 171–177. [Google Scholar] [CrossRef]
- Pourrajab, R.; Noghrehabadi, A.; Behbahani, M.; Hajidavalloo, E. An efficient enhancement in thermal conductivity of water-based hybrid nanofluid containing MWCNTs-COOH and Ag nanoparticles: Experimental study. J. Therm. Anal. Calorim. 2021, 143, 3331–3343. [Google Scholar] [CrossRef]
- Shahsavar, A.; Talebizadeh Sardari, P.; Toghraie, D. Free convection heat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid nanofluid in a concentric annulus. Int. J. Numer. Method Heat Fluid Flow. 2019, 29, 915–934. [Google Scholar] [CrossRef]
- Shahsavar, A.; Saghafian, M.; Salimpour, M.R.; Shafii, M.B. Experimental investigation on laminar forced convective heat transfer of ferrofluid loaded with carbon nanotubes under constant and alternating magnetic fields. Exp. Therm. Fluid Sci. 2016, 76, 1–11. [Google Scholar] [CrossRef]
- Tu, J.; Fan, F.; Qi, C.; Ding, Z.; Liang, L. Experimental study on the particle fouling properties of magnetic nanofluids in a corrugated tube with built-in twisted turbulator under variable magnetic field. Powder Technol. 2022, 400, 117216. [Google Scholar] [CrossRef]
- Zhang, H.; Qing, S.; Zhai, Y.; Zhang, X.; Zhang, A. The changes induced by pH in TiO2/water nanofluids: Stability, thermophysical properties and thermal performance. Powder Technol. 2021, 377, 748–759. [Google Scholar] [CrossRef]
- Jeong, J.; Li, C.; Kwon, Y.; Lee, J.; Kim, S.H.; Yun, R. Particle shape effect on the viscosity and thermal conductivity of ZnO nanofluids. Int. J. Referig. 2013, 36, 2233–2241. [Google Scholar] [CrossRef]
- Mishra, P.C.; Mukherjee, S.; Nayak, S.K.; Panda, A. A brief review on viscosity of nanofluids. Int. Nano Lett. 2014, 4, 109–120. [Google Scholar] [CrossRef]
- Hamze, S.; Cabaleiro, D.; Estellé, P. Graphene-based nanofluids: A comprehensive review about rheological behavior and dynamic viscosity. J. Mol. Liq. 2021, 325, 115207. [Google Scholar] [CrossRef]
- Li, H.; Wang, L.; He, Y.; Hu, Y.; Zhu, J.; Jiang, B. Experimental investigation of thermal conductivity and viscosity of ethylene glycol based ZnO nanofluids. Appl. Therm. Eng. 2015, 88, 363–368. [Google Scholar] [CrossRef]
- Karimipour, A.; Bagherzadeh, S.A.; Goodarzi, M.; Alnaqi, A.A.; Bahiraei, M.; Safaei, M.R.; Shadloo, M.S. Synthesized CuFe2O4/SiO2 nanocomposites added to water/EG: Evaluation of the thermophysical properties beside sensitivity analysis & EANN. Int. J. Heat Mass Transf. 2018, 127, 1169–1179. [Google Scholar]
- Agarwal, D.K.; Vaidyanathan, A.; Sunil Kumar, S. Synthesis and characterization of kerosene–alumina nanofluids. Appl. Therm. Eng. 2013, 60, 275–284. [Google Scholar] [CrossRef]
- Hu, X.; Yin, D.; Chen, X.; Xiang, G. Experimental investigation and mechanism analysis: Effect of nanoparticle size on viscosity of nanofluids. J. Mol. Liq. 2020, 314, 113604. [Google Scholar] [CrossRef]
- Ruhani, B.; Toghraie, D.; Hekmatifar, M.; Hadian, M. Statistical investigation for developing a new model for rheological behavior of ZnO-Ag (50%–50%)/water hybrid Newtonian nanofluid using experimental data. Physica A 2019, 525, 741–751. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, X. Analysis of flow and heat transfer characteristics of nanofluids surface tension driven convection in a rectangular cavity. Int. J. Mech. Sci. 2019, 153, 154–163. [Google Scholar] [CrossRef]
- Kim, G.; Baek, S.; Choi, W.; Lee, A.; Lee, S.; Jeong, H.; Sung, Y. Stability, surface tension, and thermal conductivity of Al2O3/water nanofluids according to different types of alcohol and their proportion. Case Stud. Therm. Eng. 2021, 28, 101385. [Google Scholar] [CrossRef]
- Ilyas, S.U.; Ridha, S.; Kareem FA, A. Dispersion stability and surface tension of SDS-Stabilized saline nanofluids with graphene nanoplatelets. Colloids Surf. A 2020, 592, 124584. [Google Scholar] [CrossRef]
- Estellé, P.; Cabaleiro, D.; Żyła, G.; Lugo, L.; Murshed, S.S. Current trends in surface tension and wetting behavior of nanofluids. Renew. Sustain. Energy Rev. 2018, 94, 931–944. [Google Scholar] [CrossRef]
- Smaisim, G.F.; Abdulhadi, A.M.; Uktamov, K.F.; Alsultany, F.H.; Izzat, S.E.; Ansari, M.J.; Kzar, H.H.; Al-Gazally, M.E.; Kianfar, E. Nanofluids: Properties and applications. J. Sol-Gel Sci. Technol. 2022, 104, 1–35. [Google Scholar] [CrossRef]
- Çobanoğlu, N.; Karadeniz, Z.H.; Estellé, P.; Martínez-Cuenca, R.; Buschmann, M.H. Prediction of contact angle of nanofluids by single-phase approaches. Energies 2019, 12, 4558. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A.; Dumitrache, F.; Fleaca, C.; Morjan, I. Experimental study on contact angle of water based Si–C nanofluid. J. Mol. Liq. 2021, 332, 115833. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, Y.; Ma, M.; Xuan, Z.; Wang, H. Using molecular dynamics simulations to investigate the effect of the interfacial nanolayer structure on enhancing the viscosity and thermal conductivity of nanofluids. Int. Commun. Heat Mass Transf. 2021, 122, 105181. [Google Scholar] [CrossRef]
- Qi, C.; Li, C.; Zhao, G.; Liu, M.; Han, D. Influence of rotation angle of a triangular tube with a built-in twisted tape on the thermal-exergy efficiency and entropy generation of nanofluids in the heat exchange system. Asia-Pac. J. Chem. Eng. 2020, 15, e2401. [Google Scholar] [CrossRef]
- Qi, C.; Liang, L.; Rao, Z. Study on the flow and heat transfer of liquid metal based nanofluid with different nanoparticle radiuses using two-phase lattice Boltzmann method. Int. J. Heat Mass Transf. 2016, 94, 316–326. [Google Scholar] [CrossRef]
- Qi, C.; Wang, G.; Yang, L.; Wan, Y.; Rao, Z. Two-phase lattice Boltzmann simulation of the effects of base fluid and nanoparticle size on natural convection heat transfer of nanofluid. Int. J. Heat Mass Transf. 2017, 105, 664–672. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Wang, G.; Qi, C.; Tang, J. Natural convection heat transfer characteristics of TiO2–H2O nanofluids in a cavity filled with metal foam. J. Therm. Anal. Calorim. 2020, 141, 15–24. [Google Scholar] [CrossRef]
- Tu, J.; Qi, C.; Li, K.; Tang, Z. Numerical analysis of flow and heat characteristic around micro-ribbed tube in heat exchanger system. Powder Technol. 2022, 395, 562–583. [Google Scholar] [CrossRef]
- Qi, C.; Liu, M.; Wang, G.; Pan, Y.; Liang, L. Experimental research on stabilities, thermophysical properties and heat transfer enhancement of nanofluids in heat exchanger systems. Chin. J. Chem. Eng. 2018, 26, 2420–2430. [Google Scholar] [CrossRef]
- Cimpean, D.S.; Sheremet, M.A.; Pop, I. Mixed convection of hybrid nanofluid in a porous trapezoidal chamber. Int. Commun. Heat Mass Transf. 2020, 116, 104627. [Google Scholar] [CrossRef]
- Qi, C.; Li, C.; Li, K.; Han, D. Natural convection of nanofluids in solar energy collectors based on a two-phase lattice Boltzmann model. J. Therm. Anal. Calorim. 2021, 147, 2417–2438. [Google Scholar] [CrossRef]
- Jamesahar, E.; Sabour, M.; Shahabadi, M.; Mehryan, S.A.M.; Ghalambaz, M. Mixed convection heat transfer by nanofluids in a cavity with two oscillating flexible fins: A fluid–structure interaction approach. Appl. Math. Model. 2020, 82, 72–90. [Google Scholar] [CrossRef]
- Tu, J.; Qi, C.; Tang, Z.; Tian, Z.; Chen, L. Experimental study on the influence of bionic channel structure and nanofluids on power generation characteristics of waste heat utilisation equipment. Appl. Therm. Eng. 2022, 202, 117893. [Google Scholar] [CrossRef]
- Wang, Y.; Qi, C.; Zhao, R.; Wang, C. Study on the mechanism of modified surface and magnetic nanofluids on cooling performance of wireless charging equipment under magnetic field. Appl. Therm. Eng. 2022, 208, 118258. [Google Scholar] [CrossRef]
- Sardari, P.T.; Rahimzadeh, H.; Ahmadi, G.; Giddings, D. Nano-particle deposition in the presence of electric field. J. Aerosol Sci. 2018, 126, 169–179. [Google Scholar] [CrossRef]
- Sivaraj, C.; Sheremet, M.A. MHD natural convection and entropy generation of ferrofluids in a cavity with a non-uniformly heated horizontal plate. Int. J. Mech. Sci. 2018, 149, 326–337. [Google Scholar] [CrossRef]
- Fan, F.; Qi, C.; Tu, J.; Ding, Z. Effects of variable magnetic field on particle fouling properties of magnetic nanofluids in a novel thermal exchanger system. Int. J. Therm. Sci. 2022, 175, 107463. [Google Scholar] [CrossRef]
- Izadi, M.; Sheremet, M.A.; Mehryan, S.A.M. Natural convection of a hybrid nanofluid affected by an inclined periodic magnetic field within a porous medium. Chin. J. Phys. 2020, 65, 447–458. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Dehkordi, R.B.; Abed, H. MHD mixed convection and entropy generation in a lid-driven cavity with rotating cylinders filled by a nanofluid using two phase mixture model. J. Magn. Mater. 2019, 483, 224–248. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Domiri Ganji, D.; Younus Javed, M.; Ellahi, R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Li, Z.; Hussein, A.K.; Younis, O.; Afrand, M.; Feng, S. Natural convection and entropy generation of a nanofluid around a circular baffle inside an inclined square cavity under thermal radiation and magnetic field effects. Int. Commun. Heat Mass Transf. 2020, 116, 104650. [Google Scholar] [CrossRef]
- Afrand, M.; Pordanjani, A.H.; Aghakhani, S.; Oztop, H.F.; Abu-Hamdeh, N. Free convection and entropy generation of a nanofluid in a tilted triangular cavity exposed to a magnetic field with sinusoidal wall temperature distribution considering radiation effects. Int. Commun. Heat Mass Transf. 2020, 112, 104507. [Google Scholar] [CrossRef]
- Izadi, M.; Sheremet, M.A.; Mehryan, S.A.M.; Pop, I.; Öztop, H.F.; Abu-Hamdeh, N. MHD thermogravitational convection and thermal radiation of a micropolar nanoliquid in a porous chamber. Int. Commun. Heat Mass Transf. 2020, 110, 104409. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Gao, J. Influence of geometric parameters on flow and heat transfer performance of micro-channel heat sinks. Appl. Therm. Eng. 2016, 107, 870–879. [Google Scholar] [CrossRef]
- Kose, H.A.; Yildizeli, A.; Cadirci, S. Parametric study and optimization of microchannel heat sinks with various shapes. Appl. Therm. Eng. 2022, 211, 118368. [Google Scholar] [CrossRef]
- Lv, Y.; Xia, G.; Cheng, L.; Ma, D. Experimental investigation into unstable two phase flow phenomena during flow boiling in multi-microchannels. Int. J. Therm. Sci. 2021, 166, 106985. [Google Scholar] [CrossRef]
- Parlak, M.; Özsunar, A.; Koşar, A. High aspect ratio microchannel heat sink optimization under thermally developing flow conditions based on minimum power consumption. Appl. Therm. Eng. 2022, 201, 117700. [Google Scholar] [CrossRef]
- Liu, F.; Jing, D. Hydrothermal performances of symmetric and asymmetric divergent-convergent microchannel heat sinks. Int. Commun. Heat Mass Transf. 2021, 127, 105566. [Google Scholar] [CrossRef]
- Song, J.; Liu, F.; Sui, Y.; Jing, D. Numerical studies on the hydraulic and thermal performances of trapezoidal microchannel heat sink. Int. J. Therm. Sci. 2021, 161, 106755. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Bahrami, M.; Ahmadian-Elmi, M. Thermal performance improvement of microchannel heat sinks by utilizing variable cross-section microchannels filled with porous media. Int. Commun. Heat Mass Transf. 2021, 126, 105360. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M.; Sufyan, A.; Rashid, D.; Zahid, S.U.; Rehman, W.U. Experimental investigation of TiO2–water nanofluid flow and heat transfer inside wavy mini-channel heat sinks. J. Therm. Anal. Calorim. 2019, 137, 1279–1294. [Google Scholar] [CrossRef]
- Khan, M.Z.U.; Younis, M.Y.; Akram, N.; Akbar, B.; Rajput, U.A.; Bhutta, R.A.; Uddin, E.; Jamil, M.A.; García Márquez, F.P.; Zahid, F.B. Investigation of heat transfer in wavy and dual wavy micro-channel heat sink using alumina nanoparticles. Case Stud. Therm. Eng. 2021, 28, 101515. [Google Scholar] [CrossRef]
- Lori, M.S.; Vafai, K. Heat transfer and fluid flow analysis of microchannel heat sinks with periodic vertical porous ribs. Appl. Therm. Eng. 2022, 205, 118059. [Google Scholar] [CrossRef]
- Wang, G.; Chen, T.; Tian, M.; Ding, G. Fluid and heat transfer characteristics of microchannel heat sink with truncated rib on sidewall. Int. J. Heat Mass Tranf. 2020, 148, 119142. [Google Scholar] [CrossRef]
- Yao, P.; Zhai, Y.; Li, Z.; Shen, X.; Wang, H. Thermal performance analysis of multi-objective optimized microchannels with triangular cavity and rib based on field synergy principle. Case Stud. Therm. Eng. 2021, 25, 100963. [Google Scholar]
- Kumar, K.; Kumar, P. Effect of groove depth on hydrothermal characteristics of the rectangular microchannel heat sink. Int. J. Therm. Sci. 2021, 161, 106730. [Google Scholar] [CrossRef]
- Derakhshanpour, K.; Kamali, R.; Eslami, M. Improving performance of single and double-layered microchannel heat sinks by cylindrical ribs: A numerical investigation of geometric parameters. Int. Commun. Heat Mass Transf. 2021, 126, 105440. [Google Scholar] [CrossRef]
- Li, P.; Guo, D.; Huang, X. Heat transfer enhancement in microchannel heat sinks with dual split-cylinder and its intelligent algorithm based fast optimization. Appl. Therm. Eng. 2020, 171, 115060. [Google Scholar] [CrossRef]
- Derakhshanpour, K.; Kamali, R.; Eslami, M. Effect of rib shape and fillet radius on thermal-hydrodynamic performance of microchannel heat sinks: A CFD study. Int. Commun. Heat Mass Transf. 2020, 119, 104928. [Google Scholar] [CrossRef]
- Qi, C.; Sun, L.; Wang, Y.; Wang, C.; Chen, G. Thermo-hydraulic performance of nanofluids in a bionic fractal microchannel heat sink with traveling-wave fins. Korean J. Chem. Eng. 2021, 38, 1592–1607. [Google Scholar] [CrossRef]
- Zhu, Q.; Xia, H.; Chen, J.; Zhang, X.; Chang, K.; Zhang, H.; Wang, H.; Wan, J.; Jin, Y. Fluid flow and heat transfer characteristics of microchannel heat sinks with different groove shapes. Int. J. Therm. Sci. 2021, 161, 106721. [Google Scholar] [CrossRef]
- Huang, P.; Dong, G.; Zhong, X.; Pan, M. Numerical investigation of the fluid flow and heat transfer characteristics of tree-shaped microchannel heat sink with variable cross-section. Chem. Eng. Process. 2020, 147, 107769. [Google Scholar] [CrossRef]
- Bhandari, P.; Prajapati, Y.K. Thermal performance of open microchannel heat sink with variable pin fin height. Int. J. Therm. Sci. 2021, 159, 106609. [Google Scholar] [CrossRef]
- Jia, Y.; Xia, G.; Li, Y.; Ma, D.; Cai, B. Heat transfer and fluid flow characteristics of combined microchannel with cone-shaped micro pin fins. Int. Commun. Heat Mass Transf. 2018, 92, 78–89. [Google Scholar] [CrossRef]
- Polat, M.E.; Ulger, F.; Cadirci, S. Multi-objective optimization and performance assessment of microchannel heat sinks with micro pin-fins. Int. J. Therm. Sci. 2022, 174, 107432. [Google Scholar] [CrossRef]
- Vasilev, M.P.; Abiev, R.S.; Kumar, R. Effect of circular pin-fins geometry and their arrangement on heat transfer performance for laminar flow in microchannel heat sink. Int. J. Therm. Sci. 2021, 170, 107177. [Google Scholar] [CrossRef]
- Ali, A.M.; Angelino, M.; Rona, A. Numerical analysis on the thermal performance of microchannel heat sinks with Al2O3 nanofluid and various fins. Appl. Therm. Eng. 2021, 198, 117458. [Google Scholar] [CrossRef]
- Zeng, L.; Deng, D.; Zhong, N.; Zheng, G. Thermal and flow performance in microchannel heat sink with open-ring pin fins. Int. J. Mech. Sci. 2021, 200, 106445. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, Z.; Lan, Y.; Huang, Z.; Zhang, J. Effects of geometric parameters of circular pin-fins on fluid flow and heat transfer in an interrupted microchannel heat sink. Int. J. Therm. Sci. 2021, 165, 106956. [Google Scholar] [CrossRef]
- Rajalingam, A.; Chakraborty, S. Effect of shape and arrangement of micro-structures in a microchannel heat sink on the thermo-hydraulic performance. Appl. Therm. Eng. 2021, 190, 116755. [Google Scholar]
- Bahiraei, M.; Jamshidmofid, M.; Goodarzi, M. Efficacy of a hybrid nanofluid in a new microchannel heat sink equipped with both secondary channels and ribs. J. Mol. Liq. 2019, 273, 88–98. [Google Scholar] [CrossRef]
- Shi, X.; Li, S.; Mu, Y.; Yin, B. Geometry parameters optimization for a microchannel heat sink with secondary flow channel. Int. Commun. Heat Mass Transf. 2019, 104, 89–100. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, B.; Du, B. Heat transfer optimization based on finned microchannel heat sink. Int. J. Therm. Sci. 2022, 172, 107357. [Google Scholar] [CrossRef]
- Ma, D.D.; Tang, Y.X.; Xia, G.D. Experimental investigation of flow boiling performance in sinusoidal wavy microchannels with secondary channels. Appl. Therm. Eng. 2021, 199, 117502. [Google Scholar] [CrossRef]
- Japar, W.M.A.A.; Sidik, N.A.C.; Mat, S. A comprehensive study on heat transfer enhancement in microchannel heat sink with secondary channel. Int. Commun. Heat Mass Transf. 2018, 99, 62–81. [Google Scholar] [CrossRef]
- Ozguc, S.; Pan, L.; Weibel, J.A. Topology optimization of microchannel heat sinks using a homogenization approach. Int. J. Heat Mass Transf. 2021, 169, 120896. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Thermal performance and second law characteristics of two new microchannel heat sinks operated with hybrid nanofluid containing graphene–silver nanoparticles. Energy Convers. Manag. 2018, 168, 357–370. [Google Scholar] [CrossRef]
- Jia, Y.T.; Xia, G.D.; Zong, L.X.; Ma, D.D.; Tang, Y.X. A comparative study of experimental flow boiling heat transfer and pressure drop characteristics in porous-wall microchannel heat sink. Int. J. Heat Mass Transf. 2018, 127, 818–833. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Efficacy of a novel liquid block working with a nanofluid containing graphene nanoplatelets decorated with silver nanoparticles compared with conventional CPU coolers. Appl. Therm. Eng. 2017, 127, 1233–1245. [Google Scholar] [CrossRef]
- Tang, Z.; Sun, L.; Qi, C.; Wang, Y.; Chen, L. Flow and heat transfer characteristics of a fractal microchannel heat sink with three-dimensional fractal tail. Asia-Pac. J. Chem. Eng. 2022, 17, e2803. [Google Scholar] [CrossRef]
- Gilmore, N.; Timchenko, V.; Menictas, C. Open manifold microchannel heat sink for high heat flux electronic cooling with a reduced pressure drop. Int. J. Heat Mass Transf. 2020, 163, 120395. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, W.; Qiu, Q.; Yu, W.; Chu, X. Investigation of fluid flow and heat transfer characteristics of parallel flow double-layer microchannel heat exchanger. Appl. Therm. Eng. 2018, 137, 616–631. [Google Scholar] [CrossRef]
- Wu, J.M.; Zhao, J.Y.; Tseng, K.J. Parametric study on the performance of double-layered microchannels heat sink. Energy Convers. Manag. 2014, 80, 550–560. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Chen, M.R.; Wu, J.H.; Hung, K.S.; Wang, C.C. Performance improvement of a double-layer microchannel heat sink via novel fin geometry—A numerical study. Energies 2021, 14, 3585. [Google Scholar] [CrossRef]
- Wang, S.L.; Chen, L.Y.; Zhang, B.X.; Yang, Y.R.; Wang, X.D. A new design of double-layered microchannel heat sinks with wavy microchannels and porous-ribs. J. Therm. Anal. Calorim. 2020, 141, 547–558. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, S. Numerical Study on the fluid flow and heat transfer characteristics of Al2O3-water nanofluids in microchannels of different aspect ratio. Micromachines 2021, 12, 868. [Google Scholar] [CrossRef]
- He, W.; Mashayekhi, R.; Toghraie, D.; Akbari, O.A.; Li, Z.; Tlili, I. Hydrothermal performance of nanofluid flow in a sinusoidal double layer microchannel in order to geometric optimization. Int. Commun. Heat Mass Transf. 2020, 117, 104700. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. A comparison of the thermal and hydraulic performances between miniature pin fin heat sink and microchannel heat sink with zigzag flow channel together with using nanofluids. Heat Mass Transf. 2018, 54, 3265–3274. [Google Scholar] [CrossRef]
- Shamsuddin, H.S.; Estellé, P.; Navas, J.; Mohd-Ghazali, N.; Mohamad, M. Effects of surfactant and nanofluid on the performance and optimization of a microchannel heat sink. Int. J. Heat Mass Transf. 2021, 175, 121336. [Google Scholar] [CrossRef]
- Ray, D.R.; Strandberg, R.; Das, D.K. Thermal and fluid dynamic performance comparison of three nanofluids in microchannels using analytical and computational models. Processes 2020, 8, 754. [Google Scholar] [CrossRef]
- Mohamad Noh, N.H.; Fazeli, A.; Che Sidik, N.A. Numerical simulation of nanofluids for cooling efficiency in microchannel heat sink. J. Adv. Res. Fluid Mech. Therm. Sci. 2014, 4, 13–23. [Google Scholar] [CrossRef]
- Shahsavar, A.; Godini, A.; Sardari, P.T.; Toghraie, D.; Salehipour, H. Impact of variable fluid properties on forced convection of Fe3O4/CNT/water hybrid nanofluid in a double-pipe mini-channel heat exchanger. J. Therm. Anal. Calorim. 2019, 137, 1031–1043. [Google Scholar] [CrossRef]
- Al Muallim, B.; Wahid, M.A.; Mohammed, H.A.; Kamil, M.; Habibi, D. Thermal–hydraulic performance in a microchannel heat sink equipped with longitudinal vortex generators (LVGs) and nanofluid. Processes 2020, 8, 231. [Google Scholar] [CrossRef]
- Wang, J.; Yu, K.; Ye, M.; Wang, E.; Wang, W.; Sundén, B. Effects of pin fins and vortex generators on thermal performance in a microchannel with Al2O3 nanofluids. Energy 2022, 239, 122606. [Google Scholar] [CrossRef]
- Zhang, F.; Sundén, B.; Zhang, W.; Xie, G. Constructal parallel-flow and counterflow microchannel heat sinks with bifurcations. Numer. Heat Transf. Part A-Appl. 2015, 68, 1087–1105. [Google Scholar] [CrossRef]
- Awad, M.; Radwan, A.; Abdelrehim, O.; Emam, M.; Shmroukh, A.N.; Ahmed, M. Performance evaluation of concentrator photovoltaic systems integrated with a new jet impingement-microchannel heat sink and heat spreader. Sol. Energy 2020, 199, 852–863. [Google Scholar] [CrossRef]
- Xu, C.; Xu, S.; Wang, Z.; Feng, D. Experimental investigation of flow and heat transfer characteristics of pulsating flows driven by wave signals in a microchannel heat sink. Int. Commun. Heat Mass Transf. 2021, 125, 105343. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Husain, S.; Salehi, F.; Lee, A. Machine learning regression-CFD models for the nanofluid heat transfer of a microchannel heat sink with double synthetic jets. Int. Commun. Heat Mass Transf. 2022, 130, 105808. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).