Efficient Rigorous Coupled-Wave Analysis Simulation of Mueller Matrix Ellipsometry of Three-Dimensional Multilayer Nanostructures
Abstract
1. Introduction
2. RCWA Simulation
2.1. Local s-Matrices
2.1.1. Grating Layer
2.1.2. Homogeneous Layer
2.1.3. Vector-Based Formation
2.2. Global s-Matrix
3. Numerical Demonstration
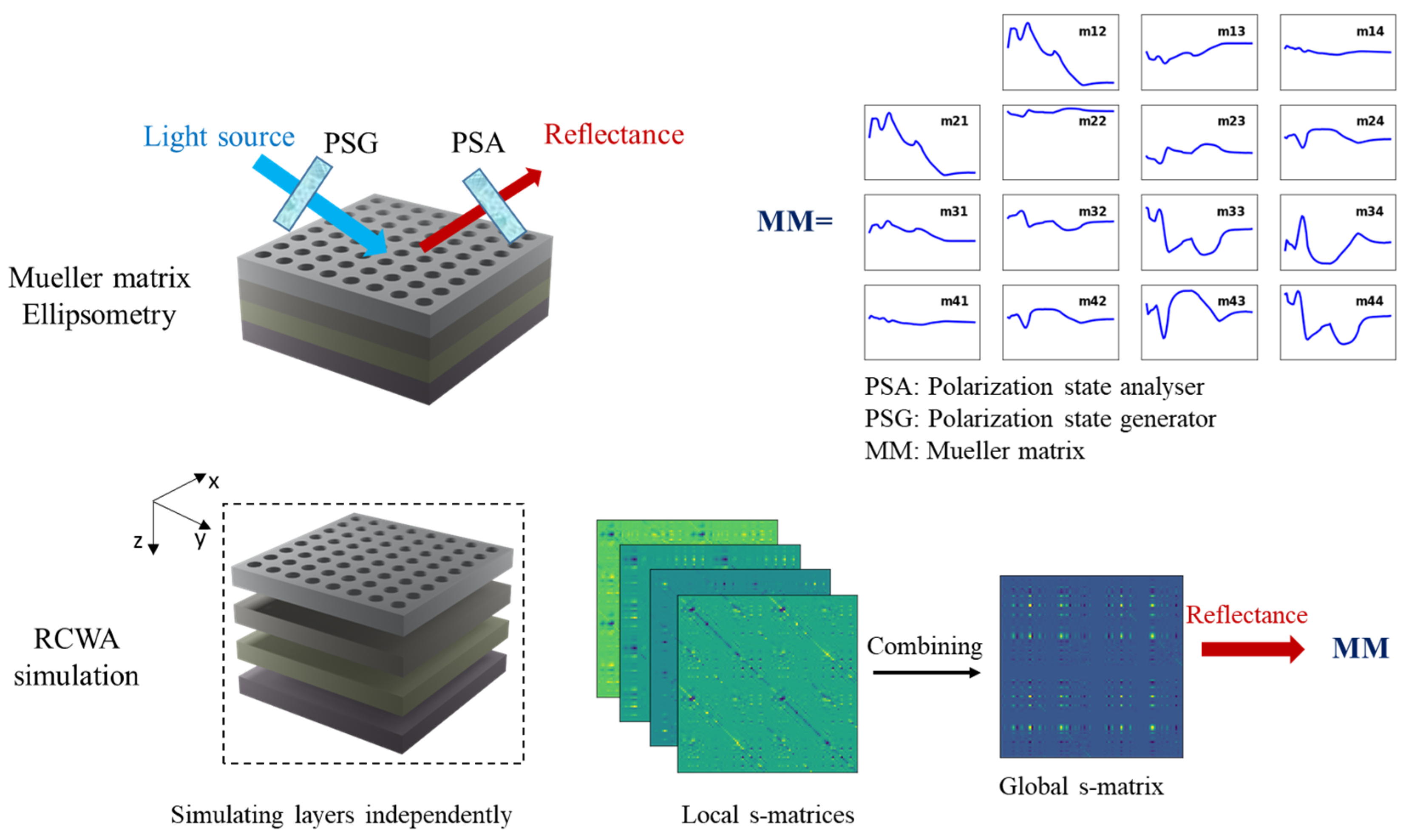
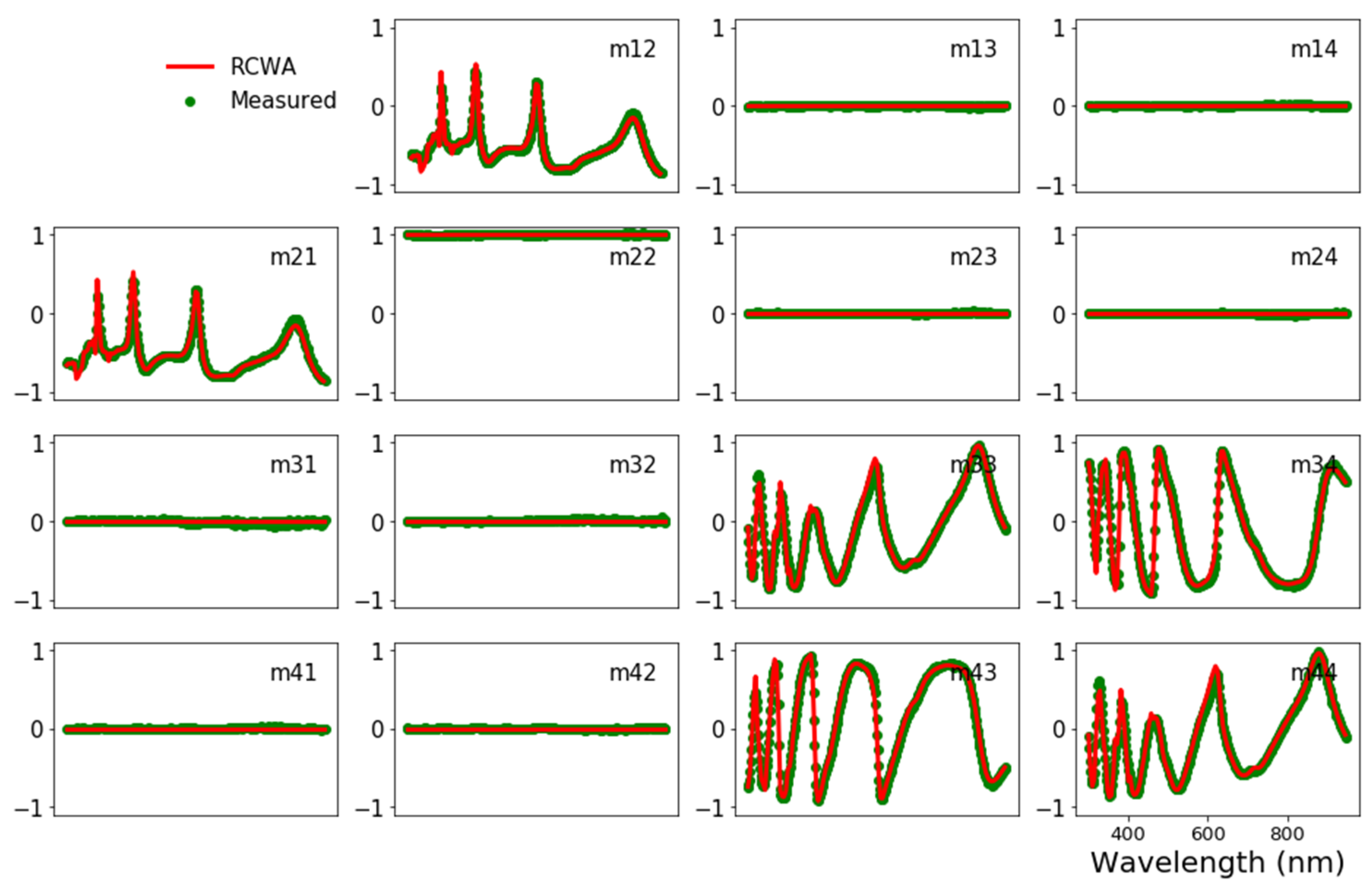
3.1. Case 1: Mueller Matrix Ellipsometry
3.2. Case 2: Full Optical Responses
4. Results and Discussions
4.1. Mueller Matrix Ellipsometry
4.2. Full Optical Responses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Semi-Discretization of Maxwell’s Equations in Fourier Space
Appendix A.2. Wave Vector Component Kx, Ky and Permittivity Distribution ⟦𝛆⟧ in Fourier Space
Appendix A.2.1. Wave Vector Component Kx, Ky
Appendix A.2.2. Permittivity Distribution ⟦𝛆⟧ in Fourier Space
Appendix B. Matrices Used for Calculating Layer s-Matrix
Appendix C. Fast Matrix Computation for Homogeneous Layers
Appendix C.1. Matrix Inverse
Appendix C.2. Matrix Multiplication
Appendix D. Mueller Matrix Ellipsometry
References
- Novikova, T.; De Martino, A.; Ben Hatit, S.; Drévillon, B. Application of Mueller polarimetry in conical diffraction for critical dimension measurements in microelectronics. Appl. Opt. 2006, 45, 3688–3697. [Google Scholar] [CrossRef] [PubMed]
- Banon, J.-P.; Nesse, T.; Ghadyani, Z.; Kildemo, M.; Simonsen, I. Critical dimension metrology of a plasmonic photonic crystal based on Mueller matrix ellipsometry and the reduced Rayleigh equation. Opt. Lett. 2017, 42, 2631–2634. [Google Scholar] [CrossRef] [PubMed]
- Diebold, A.C.; Antonelli, A.; Keller, N. Perspective: Optical measurement of feature dimensions and shapes by scatterometry. APL Mater. 2018, 6, 058201. [Google Scholar] [CrossRef]
- Orji, N.G.; Badaroglu, M.; Barnes, B.M.; Beitia, C.; Bunday, B.D.; Celano, U.; Kline, R.J.; Neisser, M.; Obeng, Y.; Vladar, A. Metrology for the next generation of semiconductor devices. Nat. Electron. 2018, 1, 532. [Google Scholar] [CrossRef] [PubMed]
- Käseberg, T.; Grundmann, J.; Siefke, T.; Klapetek, P.; Valtr, M.; Kroker, S.; Bodermann, B. Mueller Matrix Ellipsometric Approach on the Imaging of Sub-Wavelength Nanostructures. Front. Phys. 2022, 9, 819. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Chen, C.; Sheng, S.; Song, L.; Gu, H.; Jiang, H.; Zhang, C.; Liu, S. Reconstruction of finite deep sub-wavelength nanostructures by Mueller-matrix scattered-field microscopy. Opt. Express 2021, 29, 32158–32168. [Google Scholar] [CrossRef]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; Wiley: Chichester, UK, 2007. [Google Scholar]
- Liu, S.; Chen, X.; Zhang, C. Development of a broadband Mueller matrix ellipsometer as a powerful tool for nanostructure metrology. Thin Solid Film. 2015, 584, 176–185. [Google Scholar] [CrossRef]
- Vahidzadeh, E.; Shankar, K. Artificial Neural Network-Based Prediction of the Optical Properties of Spherical Core–Shell Plasmonic Metastructures. Nanomaterials 2021, 11, 633. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Arbouet, A.; Girard, C.; Muskens, O.L. Deep learning in nano-photonics: Inverse design and beyond. Photonics Res. 2021, 9, B182–B200. [Google Scholar] [CrossRef]
- Fan, C.-Y.; Su, G.-D.J. Time-Effective Simulation Methodology for Broadband Achromatic Metalens Using Deep Neural Networks. Nanomaterials 2021, 11, 1966. [Google Scholar] [CrossRef]
- Robertson, K.W.; Lapierre, R.R.; Krich, J.J. Efficient wave optics modeling of nanowire solar cells using rigorous coupled-wave analysis. Opt. Express 2019, 27, A133–A147. [Google Scholar] [CrossRef]
- Anttu, N.; Mäntynen, H.; Sadi, T.; Matikainen, A.; Turunen, J.; Lipsanen, H. Comparison of absorption simulation in semiconductor nanowire and nanocone arrays with the Fourier modal method, the finite element method, and the finite-difference time-domain method. Nano Express 2020, 1, 030034. [Google Scholar] [CrossRef]
- Colburn, S.; Majumdar, A. Inverse design and flexible parameterization of meta-optics using algorithmic differentiation. Commun. Phys. 2021, 4, 65. [Google Scholar] [CrossRef]
- Han, K.; Chang, C.-H. Numerical Modeling of Sub-Wavelength Anti-Reflective Structures for Solar Module Applications. Nanomaterials 2014, 4, 87–128. [Google Scholar] [CrossRef]
- Roberts, C.M.; Inampudi, S.; Podolskiy, V.A. Diffractive interface theory: Nonlocal susceptibility approach to the optics of metasurfaces. Opt. Express 2015, 23, 2764–2776. [Google Scholar] [CrossRef]
- Edee, K.; Plumey, J.-P.; Granet, G.; Hazart, J. Perturbation method for the Rigorous Coupled Wave Analysis of grating diffraction. Opt. Express 2010, 18, 26274–26284. [Google Scholar] [CrossRef]
- Bischoff, J.; Hehl, K. Perturbation approach applied to modal diffraction methods. J. Opt. Soc. Am. A 2011, 28, 859–867. [Google Scholar] [CrossRef]
- Reitich, F.; Johnson, T.W.; Oh, S.-H.; Meyer, G. A fast and high-order accurate surface perturbation method for nanoplasmonic simulations: Basic concepts, analytic continuation and applications. J. Opt. Soc. Am. A 2013, 30, 2175–2187. [Google Scholar] [CrossRef]
- Mohamad, H.; Essaidi, S.; Blaize, S.; Macias, D.; Benech, P.; Morand, A. Fast Fourier factorization for differential method and RCWA: A powerful tool for the modeling of non-lamellar metallic diffraction gratings. Opt. Quantum Electron. 2021, 52, 127. [Google Scholar] [CrossRef]
- Davids, P.S. Normal vector approach to Fourier modal scattering from planar periodic photonic structures. Photonics Nanostruct.-Fundam. Appl. 2020, 43, 100864. [Google Scholar] [CrossRef]
- Augel, L.; Kawaguchi, Y.; Bechler, S.; Körner, R.; Schulze, J.; Uchida, H.; Fischer, I.A. Integrated collinear refractive index sensor with Ge PIN photodiodes. ACS Photonics 2018, 5, 4586–4593. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, S.; Song, Q.; Liu, Y.; Wu, Y.; Wang, S.; Yu, J.; Han, J.; Tsai, D.-P. All-dielectric metasurface for high-performance structural color. Nat. Commun. 2020, 11, 1864. [Google Scholar] [CrossRef] [PubMed]
- Sannicolo, T.; Chae, W.H.; Mwaura, J.; Bulović, V.; Grossman, J.C. Silver Nanowire Back Electrode Stabilized with Graphene Oxide Encapsulation for Inverted Semitransparent Organic Solar Cells with Longer Lifetime. ACS Appl. Energy Mater. 2021, 4, 1431–1441. [Google Scholar] [CrossRef]
- Senanayake, P.; Hung, C.-H.; Shapiro, J.; Lin, A.; Liang, B.; Williams, B.S.; Huffaker, D.L. Thin 3D Multiplication Regions in Plasmonically Enhanced Nanopillar Avalanche Detectors. Nano Lett. 2011, 11, 5279–5283. [Google Scholar] [CrossRef] [PubMed]
- Rumpf, R.C. Improved formulation of scattering matrices for semi-analytical methods that is consistent with convention. Prog. Electromagn. Res. B 2011, 35, 241–261. [Google Scholar] [CrossRef]
- Li, L. Formulation and comparison of two recursive matrix algorithms for modeling layered diffraction gratings. J. Opt. Soc. Am. A 1996, 13, 1024–1035. [Google Scholar] [CrossRef]
- Liu, V.; Fan, S. S4: A free electromagnetic solver for layered periodic structures. Comput. Phys. Commun. 2012, 183, 2233–2244. [Google Scholar] [CrossRef]
- Fuard, D.; Troscompt, N.; El Kalyoubi, I.; Soulan, S.; Besacier, B. S-Genius, a universal software platform with versatile inverse problem resolution for scatterometry. In Proceedings of the Modeling Aspects in Optical Metrology IV, Munich, Germany, 13–14 May 2013; Volume 8789, p. 878919. [Google Scholar]
- Schlipf, J.; Fischer, I.A. Rigorous coupled-wave analysis of a multi-layered plasmonic integrated refractive index sensor. Opt. Express 2021, 29, 36201. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K.; Grann, E.B.; Pommet, D.A. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Van Der Aa, N.P.; Mattheij, R.M.M. Computing shape parameter sensitivity of the field of one-dimensional surface-relief gratings by using an analytical approach based on RCWA. J. Opt. Soc. Am. A 2007, 24, 2692–2700. [Google Scholar] [CrossRef]
- Anttu, N.; Mäntynen, H.; Sorokina, A.; Turunen, J.; Sadi, T.; Lipsanen, H. Applied electromagnetic optics simulations for nanophotonics. J. Appl. Phys. 2021, 129, 131102. [Google Scholar] [CrossRef]
- Available online: https://www.st.com/content/st_com/en.html.
- Jellison, G.E.; Modine, F.A. Parameterization of the optical functions of amorphous materials in the interband region. Appl. Phys. Lett. 1996, 69, 2137. [Google Scholar] [CrossRef]
- Available online: https://github.com/Hoang-LamPham/ReflectanceRCWA (accessed on 20 August 2022).
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.P.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic Films Can Easily Be Better: Rules and Recipes. ACS Photonics 2015, 2, 326–333. [Google Scholar] [CrossRef]
- Nunley, T.N.; Fernando, N.S.; Samarasingha, N.; Moya, J.M.; Nelson, C.M.; Medina, A.A.; Zollner, S. Optical constants of germanium and thermally grown germanium dioxide from 0.5 to 6.6 eV via a multisample ellipsometry investigation. J. Vac. Sci. Technol. B 2016, 34, 061205. [Google Scholar] [CrossRef]
- Kedenburg, S.; Vieweg, M.; Gissibl, T.; Giessen, H. Linear refractive index and absorption measurements of nonlinear optical liquids in the visible and near-infrared spectral region. Opt. Mater. Express 2012, 2, 1588–1611. [Google Scholar] [CrossRef]





| Parameters | Symbol | Value (eV) |
|---|---|---|
| Oscillator amplitude | 104.27 | |
| Peak energy | 8.22 | |
| Broadening term | 3.38 | |
| Optical band gap | 4.25 | |
| Real part of the dielectric function at infinite energy | 1.64 |
| Simulation | Conventional | Bottom-Up | This Work | Bottom-Up/Conventional | This Work/Conventional |
|---|---|---|---|---|---|
| Total time | 1.91 | 1.51 | 1 | 79% | 52% |
| Grating layers | 0.93 | 0.93 | 0.93 | - | - |
| Homogeneous layers | 0.4 | 0.4 | 0.0026 | - | - |
| Homogeneous layers/Grating layers | 43% | 43% | 0.27% | - | - |
| Global s-matrix | 0.5 | 0.15 | 0.06 | 30% | 12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, H.-L.; Alcaire, T.; Soulan, S.; Le Cunff, D.; Tortai, J.-H. Efficient Rigorous Coupled-Wave Analysis Simulation of Mueller Matrix Ellipsometry of Three-Dimensional Multilayer Nanostructures. Nanomaterials 2022, 12, 3951. https://doi.org/10.3390/nano12223951
Pham H-L, Alcaire T, Soulan S, Le Cunff D, Tortai J-H. Efficient Rigorous Coupled-Wave Analysis Simulation of Mueller Matrix Ellipsometry of Three-Dimensional Multilayer Nanostructures. Nanomaterials. 2022; 12(22):3951. https://doi.org/10.3390/nano12223951
Chicago/Turabian StylePham, Hoang-Lam, Thomas Alcaire, Sebastien Soulan, Delphine Le Cunff, and Jean-Hervé Tortai. 2022. "Efficient Rigorous Coupled-Wave Analysis Simulation of Mueller Matrix Ellipsometry of Three-Dimensional Multilayer Nanostructures" Nanomaterials 12, no. 22: 3951. https://doi.org/10.3390/nano12223951
APA StylePham, H.-L., Alcaire, T., Soulan, S., Le Cunff, D., & Tortai, J.-H. (2022). Efficient Rigorous Coupled-Wave Analysis Simulation of Mueller Matrix Ellipsometry of Three-Dimensional Multilayer Nanostructures. Nanomaterials, 12(22), 3951. https://doi.org/10.3390/nano12223951







