Effective Modulation of Ion Mobility through Solid-State Single-Digit Nanopores
Abstract
1. Introduction
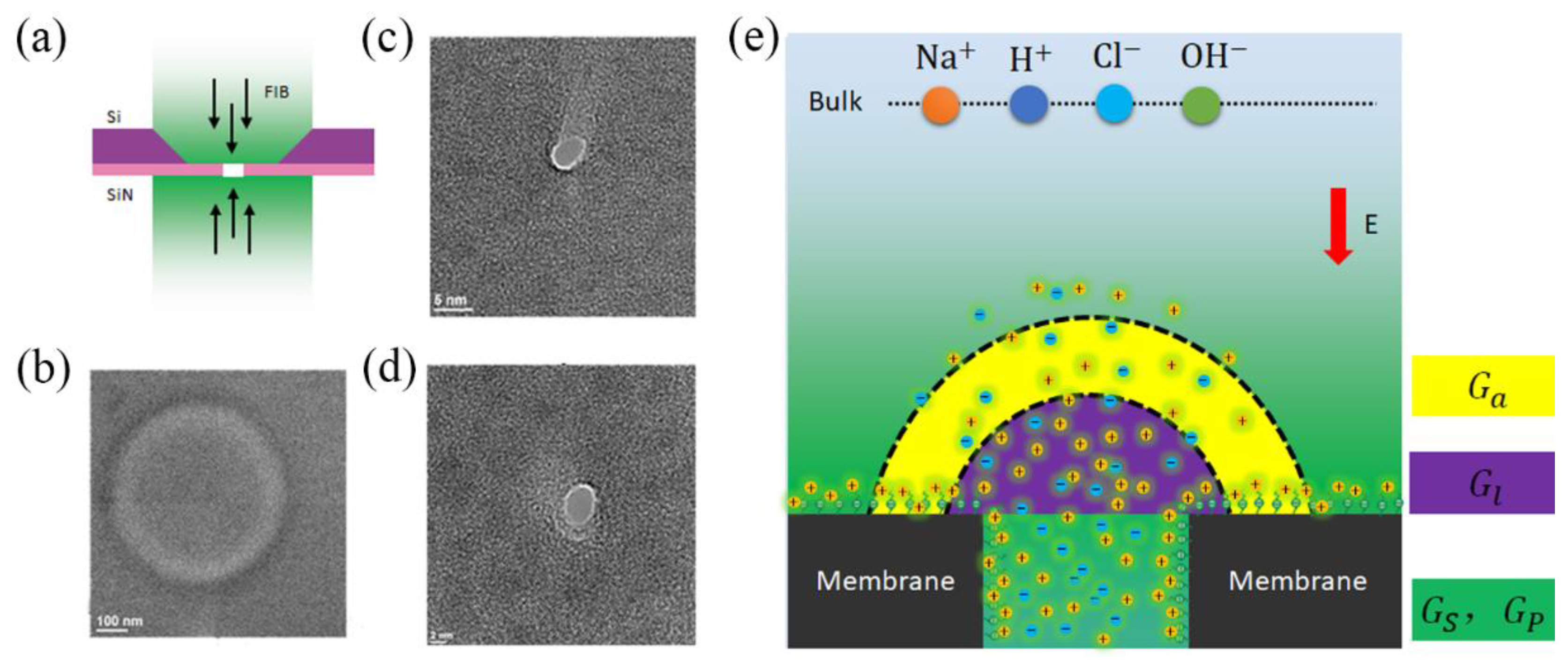
2. Methods
3. Results & Discussion
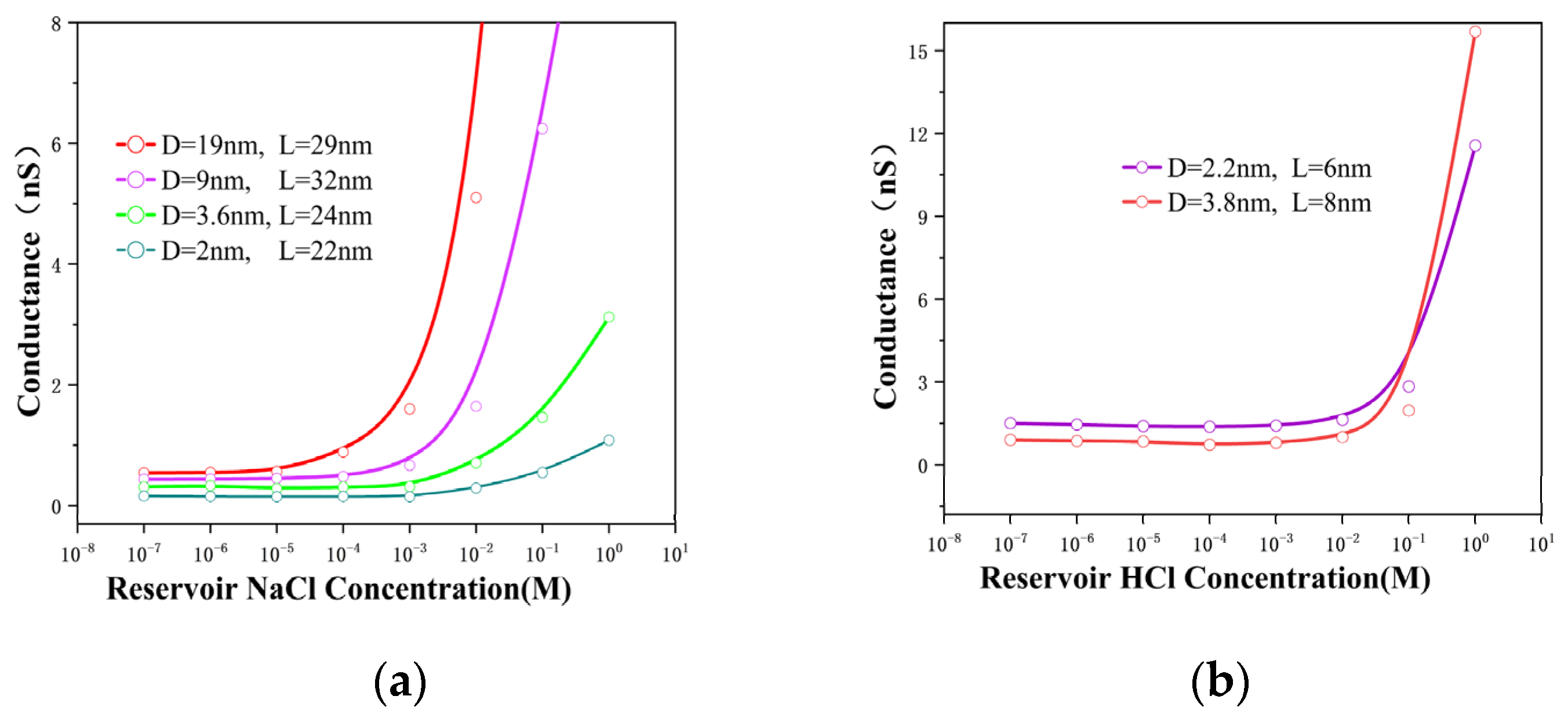
3.1. Ion Conductance with Solid-State Nanopores
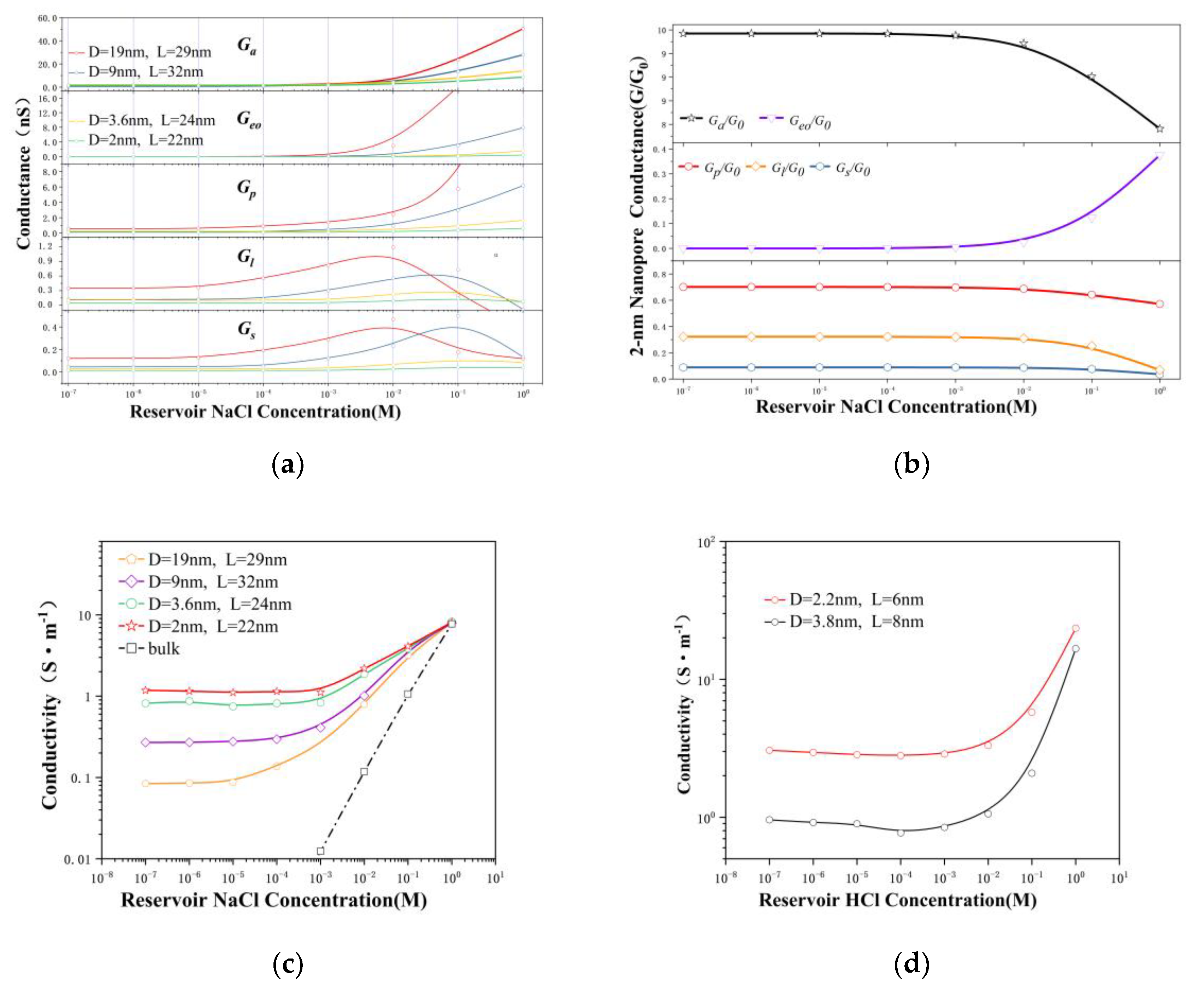
3.2. Theoretical Conductance Model with Electric Potential Leakage
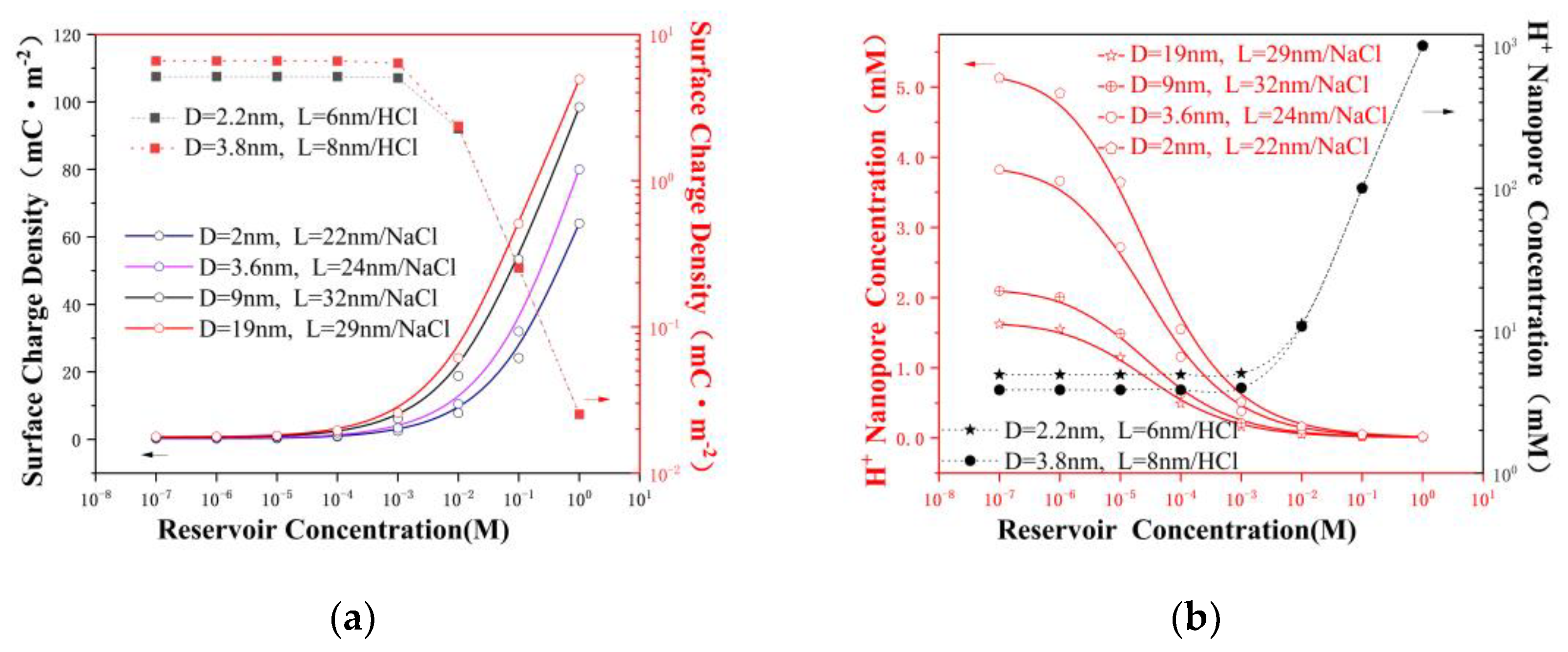
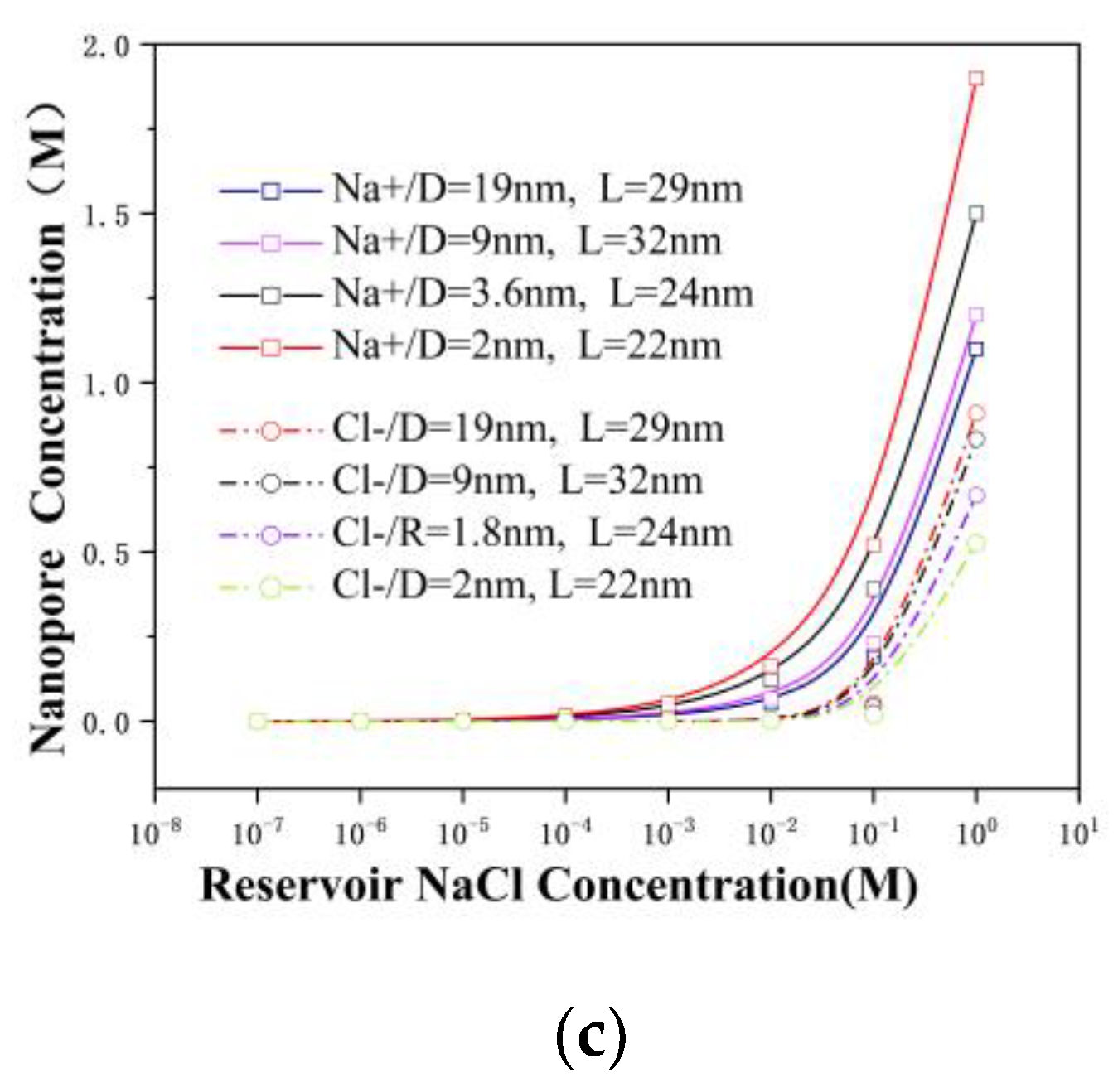
3.3. The Surface Charge and Ensemble-Averaged Concentration inside the Pore
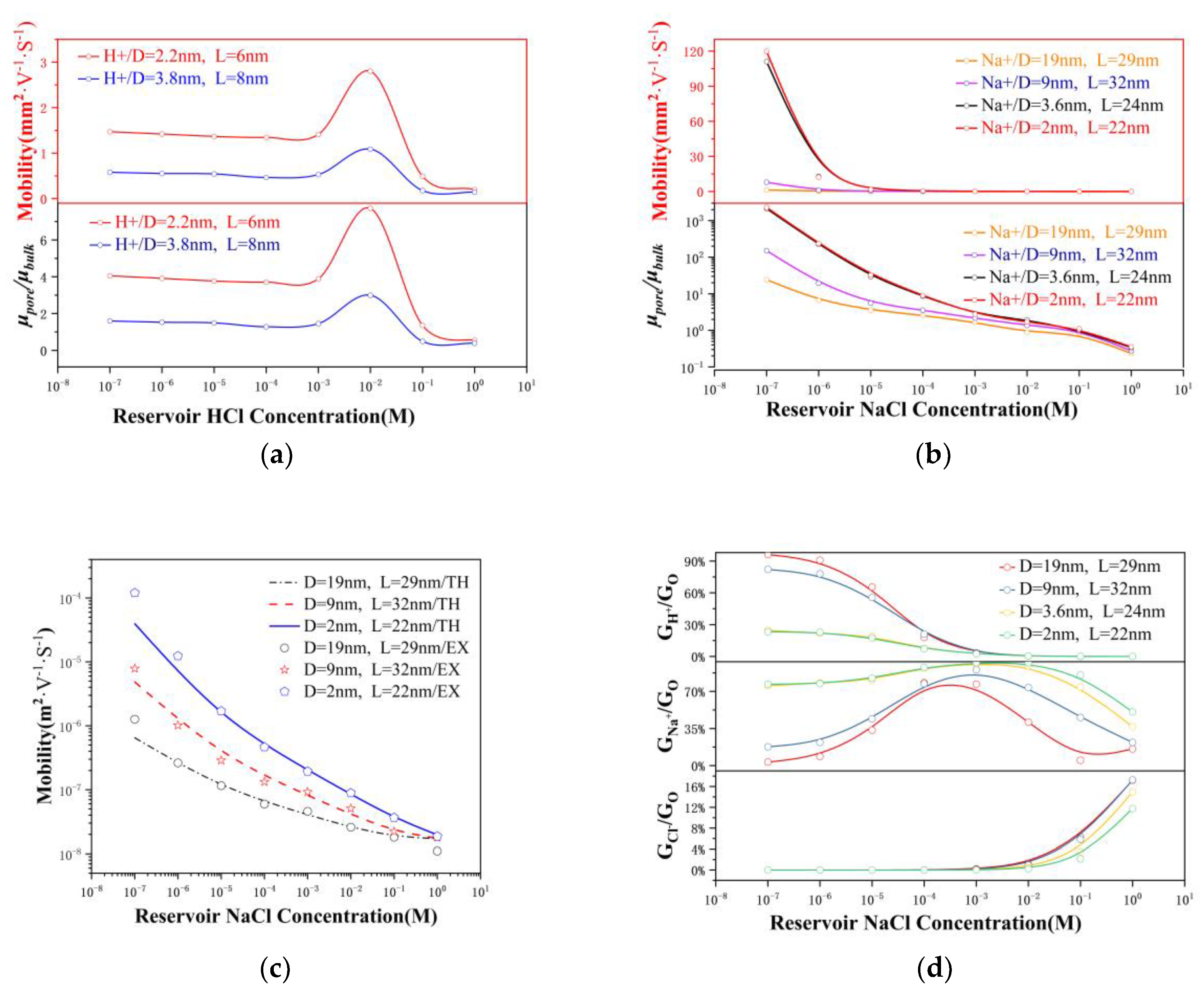
3.4. Ion Mobility
3.5. Ion Selectivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Secchi, E.; Marbach, S.; Nigues, A.; Stein, D.; Siria, A.; Bocquet, L. Massive radius-dependent flow slippage in carbon nanotubes. Nature 2016, 537, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Zhang, Z.; Shi, H.; Zhang, J.; Liang, L.; Wang, Q.; Agren, H.; Tu, Y. Na+ and K+ ion selectivity by size-controlled biomimetic graphene nanopores. Nanoscale 2014, 6, 10666–10672. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Liu, Q.; Kloss, B.; Bruni, R.; Kalathur, R.C.; Guo, Y.; Kloppmann, E.; Rost, B.; Colecraft, H.M.; Hendrickson, W.A. Structure and selectivity in bestrophin ion channels. Science 2014, 346, 355–359. [Google Scholar] [CrossRef]
- Chen, Y.F.; Ni, Z.H.; Wang, G.M.; Xu, D.Y.; Li, D.Y. Electroosmotic flow in nanotubes with high surface charge densities. Nano Lett. 2008, 8, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Wen, Q.; Feng, Y.; Ji, D.; Li, H.; Li, N.; Jiang, L.; Guo, W. On the Origin of Ion Selectivity in Ultrathin Nanopores: Insights for Membrane log cale Osmotic Energy Conversion. Adv. Funct. Mater. 2018, 28, 1804189.1–1804189.8. [Google Scholar] [CrossRef]
- Faucher, S.J.; Aluru, N.R.; Bazant, M.Z.; Blankschtein, D.; Strano, M.S. Critical Knowledge Gaps in Mass Transport through Single-Digit Nanopores: A Review and Perspective. J. Phys. Chem. C 2019, 123, 21309–21326. [Google Scholar] [CrossRef]
- Gupta, A.; Zuk, P.J.; Stone, H.A. Charging Dynamics of Overlapping Double Layers in a Cylindrical Nanopore. Phys. Rev. Lett. 2020, 125, 076001. [Google Scholar] [CrossRef]
- Davoodabadi, A.; Nazari, M.; Huang, D.; Luo, T.; Ghasemi, H. Transport Phenomena in Nano/Molecular Confinements. ACS Nano 2020, 14, 16348–16391. [Google Scholar]
- Sherwood, J.D.; Mao, M.; Ghosal, S. Electroosmosis in a finite cylindrical pore: Simple models of end effects. Langmuir 2014, 30, 9261–9272. [Google Scholar] [CrossRef]
- Levy, A.; Souza, J.P.D.; Bazant, M.Z. Breakdown of electroneutrality in nanopores. J. Colloid Interface Sci. 2020, 579, 162–176. [Google Scholar] [CrossRef]
- Luo, Z.X.; Xing, Y.Z.; Ling, Y.C.; Kleinhammes, A.; Wu, Y. Electroneutrality breakdown and specific ion effects in nanoconfined aqueous electrolytes observed by NMR. Nat. Commun. 2015, 6, 6358. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, L.; Jiang, L. Bioinspired smart asymmetric nanochannel membranes. Chem. Soc. Rev. 2018, 47, 322–356. [Google Scholar] [CrossRef]
- Amy, G.; Ghaffour, N.; Li, Z.; Francis, L.; Linares, R.V.; Missimer, T.; Lattemann, S. Membrane-based seawater desalination: Present and future prospects. Desalination 2017, 401, 16–21. [Google Scholar] [CrossRef]
- Simon, P.; Gogotsi, Y. Materials for electrochemical capacitors. Nat. Mater. 2008, 7, 845–854. [Google Scholar] [CrossRef]
- Salanne, M.; Rotenberg, B.; Naoi, K.; Kaneko, K.; Taberna, P.L.; Grey, C.P.; Dunn, B.; Simon, P. Efficient storage mechanisms for building better supercapacitors. Nat. Energy 2016, 1, 10. [Google Scholar] [CrossRef]
- Duan, C.; Majumdar, A. Anomalous ion transport in 2-nm hydrophilic nanochannels. Nat. Nanotechnol. 2010, 5, 848. [Google Scholar] [CrossRef]
- Gopinadhan, K.; Hu, S.; Esfandiar, A.; Lozada-Hidalgo, M.; Wang, F.C.; Yang, Q.; Tyurnina, A.V.; Keerthi, A.; Radha, B.; Geim, A.K. Complete steric exclusion of ions and proton transport through confined monolayer water. Science 2019, 363, 145–148. [Google Scholar] [CrossRef]
- Guo, W.; Tian, Y.; Jiang, L. Asymmetric Ion Transport through Ion-Channel-Mimetic Solid-State Nanopores. Acc. Chem. Res. 2013, 46, 2834–2846. [Google Scholar] [CrossRef]
- Banerjee, S.; Wilson, J.; Shim, J.; Shankla, M.; Corbin, E.A.; Aksimentiev, A.; Bashir, R. Slowing DNA Transport Using Graphene-DNA Interactions. Adv. Funct. Mater. 2015, 25, 936–946. [Google Scholar] [CrossRef]
- Kondrat, S.; Wu, P.; Qiao, R.; Kornyshev, A.A. Accelerating charging dynamics in subnanometre pores. Nat. Mater. 2014, 13, 387–393. [Google Scholar] [CrossRef]
- Derek, S. Surface-charge-governed ion transport in nanofluidic channels. Phys. Rev. Lett. 2004, 3, 035901. [Google Scholar]
- van der Heyden, F.H.; Stein, D.; Dekker, C. Streaming currents in a single nanofluidic channel. Phys. Rev. Lett. 2005, 95, 116104. [Google Scholar] [CrossRef]
- Kowalczyk, S.W.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Modeling the conductance and DNA blockade of solid-state nanopores. Nanotechnology 2011, 22, 315101. [Google Scholar] [CrossRef]
- Tsutsui, M.; Hongo, S.; He, Y.; Taniguchi, M.; Gemma, N.; Kawai, T. Single-Nanoparticle Detection Using a Low-Aspect-Ratio Pore. ACS Nano 2012, 6, 3499–3505. [Google Scholar] [CrossRef]
- Garaj, S.; Hubbard, W.; Reina, A.; Kong, J.; Branton, D.; Golovchenko, J.A. Graphene as a subnanometre trans-electrode membrane. Nature 2010, 467, 190–193. [Google Scholar] [CrossRef]
- Hyun, C.; Rollings, R.; Li, J.L. Probing Access Resistance of Solid-State Nanopores with a Scanning-Probe Microscope Tip. Small 2012, 8, 385–392. [Google Scholar] [CrossRef]
- Alcaraz, A.; López, M.L.; Queralt-Martín, M.; Aguilella, V.M. Ion Transport in Confined Geometries below the Nanoscale: Access Resistance Dominates Protein Channel Conductance in Diluted Solutions. ACS Nano 2017, 11, 10392–10400. [Google Scholar] [CrossRef]
- Noh, Y.; Aluru, N.R.R. Ion Transport in Electrically Imperfect Nanopores. ACS Nano 2020, 14, 10518–10526. [Google Scholar] [CrossRef]
- Cheng, C.; Jiang, G.; Simon, G.P.; Liu, J.Z.; Li, D. Low-voltage electrostatic modulation of ion diffusion through layered graphene-based nanoporous membranes. Nat. Nanotechnol. 2018, 13, 685–690. [Google Scholar] [CrossRef]
- Chein, R.; Chen, H.; Liao, C. Investigation of ion concentration and electric potential distributions in charged membrane/electrolyte systems. J. Membr. Sci. 2009, 342, 121–130. [Google Scholar] [CrossRef]
- Hu, G.; Mao, M.; Ghosal, S. Ion transport through a graphene nanopore. Nanotechnology 2012, 23, 395501. [Google Scholar] [CrossRef]
- Sahu, S.; Zwolak, M. Maxwell-Hall access resistance in graphene nanopores. Phys. Chem. Chem. Phys. 2018, 20, 4646–4651. [Google Scholar] [CrossRef]
- Sahu, S.; Zwolak, M.P. Access Resistance in Atomically Thin Nanopores. Biophys. J. 2018, 114, 493a. [Google Scholar] [CrossRef]
- Siria, A.; Poncharal, P.; Biance, A.L.; Fulcrand, R.; Blase, X.; Purcell, S.T.; Bocquet, L. Giant osmotic energy conversion measured in a single transmembrane boron nitride nanotube. Nature 2013, 494, 455–458. [Google Scholar] [CrossRef]
- Radha, B.; Esfandiar, A.; Wang, F.C.; Rooney, A.P.; Gopinadhan, K.; Keerthi, A.; Mishchenko, A.; Janardanan, A.; Blake, P.; Fumagalli, L. Molecular transport through capillaries made with atomic-scale precision. Nature 2016, 538, 222–225. [Google Scholar] [CrossRef]
- Luan, B. Numerically testing phenomenological models for conductance of a solid-state nanopore. Nanotechnology 2015, 26, 055502. [Google Scholar] [CrossRef]
- Collinson, M.M. Electrochemistry By Carl H. Hamann (Universitat Oldenburg, Germany), Andrew Hamnett (University of Newcastle, United Kingdom), and Wolf Vielstich (Universitat der Bundes-wehr Munchen, Germany). Wiley-VCH: New York. 1998. xvii + 423 pp. $61.95. ISBN 3-527-29096-6. J. Am. Chem. Soc. 1999, 121, 8413. [Google Scholar]
- Suk, M.E.; Aluru, N.R. Ion transport in sub-5-nm graphene nanopores. J. Chem. Phys. 2014, 140, 084707. [Google Scholar] [CrossRef]
- Lee, C.Y.; Choi, W.; Han, J.-H.; Strano, M.S. Coherence Resonance in a Single-Walled Carbon Nanotube Ion Channel. Science 2010, 329, 1320–1324. [Google Scholar] [CrossRef]
- Yeh, L.-H.; Hughes, C.; Zeng, Z.; Qian, S. Tuning Ion Transport and Selectivity by a Salt Gradient in a Charged Nanopore. Anal. Chem. 2014, 86, 2681–2686. [Google Scholar] [CrossRef]
- Thomas, M.; Corry, B.; Hilder, T.A. What Have We Learnt About the Mechanisms of Rapid Water Transport, Ion Rejection and Selectivity in Nanopores from Molecular Simulation? Small 2014, 10, 1453–1465. [Google Scholar] [CrossRef]
- Tsutsui, M.; He, Y.; Furuhashi, M.; Rahong, S.; Taniguchi, M.; Kawai, T. Transverse electric field dragging of DNA in a nanochannel. Sci. Rep. 2012, 2, 1–7. [Google Scholar] [CrossRef]
- Smeets, R.M.M.; Keyser, U.F.; Krapf, D.; Wu, M.Y.; Dekker, N.H.; Dekker, C. Salt dependence of ion transport and DNA translocation through solid-state nanopores. Nano Lett. 2006, 6, 89–95. [Google Scholar] [CrossRef]
- Hall, J.E. Access resistance of a small circular pore. J. Gen. Physiol. 1975, 66, 531–532. [Google Scholar] [CrossRef]
- Chaudhury, S.; Bhattacharyya, A.; Goswami, A. Electrodriven Ion Transport through Crown Ether-Nafion Composite Membrane: Enhanced Selectivity of Cs+ over Na+ by Ion Gating at the Surface. Ind. Eng. Chem. Res. 2014, 53, 8804–8809. [Google Scholar] [CrossRef]
- Gupta, A.; Shim, S.; Issah, L.; Mckenzie, C.; Stone, H.A. Diffusion of multiple electrolytes cannot be treated independently: Model predictions with experimental validation. Soft Matter 2019, 15, 9965–9973. [Google Scholar] [CrossRef]
- Hashemi Amrei, S.M.H.; Bukosky, S.C.; Rader, S.P.; Ristenpart, W.D.; Miller, G.H. Oscillating Electric Fields in Liquids Create a Long-Range Steady Field. Phys. Rev. Lett. 2018, 121, 185504.1–185504.6. [Google Scholar] [CrossRef]
- Jiang, D.E.; Jin, Z.; Wu, J. Oscillation of Capacitance inside Nanopores. Nano Lett. 2011, 11, 5373–5377. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Bazant, M.Z. Analysis of ionic conductance of carbon nanotubes. Phys. Rev. E 2016, 94, 050601. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, A.; Wang, B.; Xia, G.; Luo, J.; Deng, Z. Effective Modulation of Ion Mobility through Solid-State Single-Digit Nanopores. Nanomaterials 2022, 12, 3946. https://doi.org/10.3390/nano12223946
Ji A, Wang B, Xia G, Luo J, Deng Z. Effective Modulation of Ion Mobility through Solid-State Single-Digit Nanopores. Nanomaterials. 2022; 12(22):3946. https://doi.org/10.3390/nano12223946
Chicago/Turabian StyleJi, Anping, Bo Wang, Guofeng Xia, Jinjie Luo, and Zhenghua Deng. 2022. "Effective Modulation of Ion Mobility through Solid-State Single-Digit Nanopores" Nanomaterials 12, no. 22: 3946. https://doi.org/10.3390/nano12223946
APA StyleJi, A., Wang, B., Xia, G., Luo, J., & Deng, Z. (2022). Effective Modulation of Ion Mobility through Solid-State Single-Digit Nanopores. Nanomaterials, 12(22), 3946. https://doi.org/10.3390/nano12223946




