Resilient Mechanical Metamaterial Based on Cellulose Nanopaper with Kirigami Structure
Abstract
1. Introduction
2. Methods
2.1. Fabrication of Nanopapers from Aqueous CNF Dispersion
2.2. Implementation of Cut Patterns of Kirigami Structure by Laser Processing
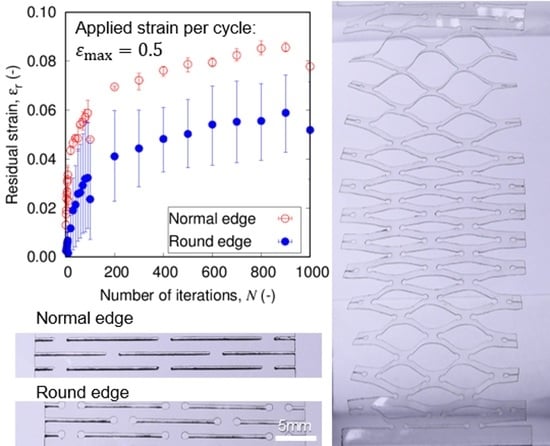
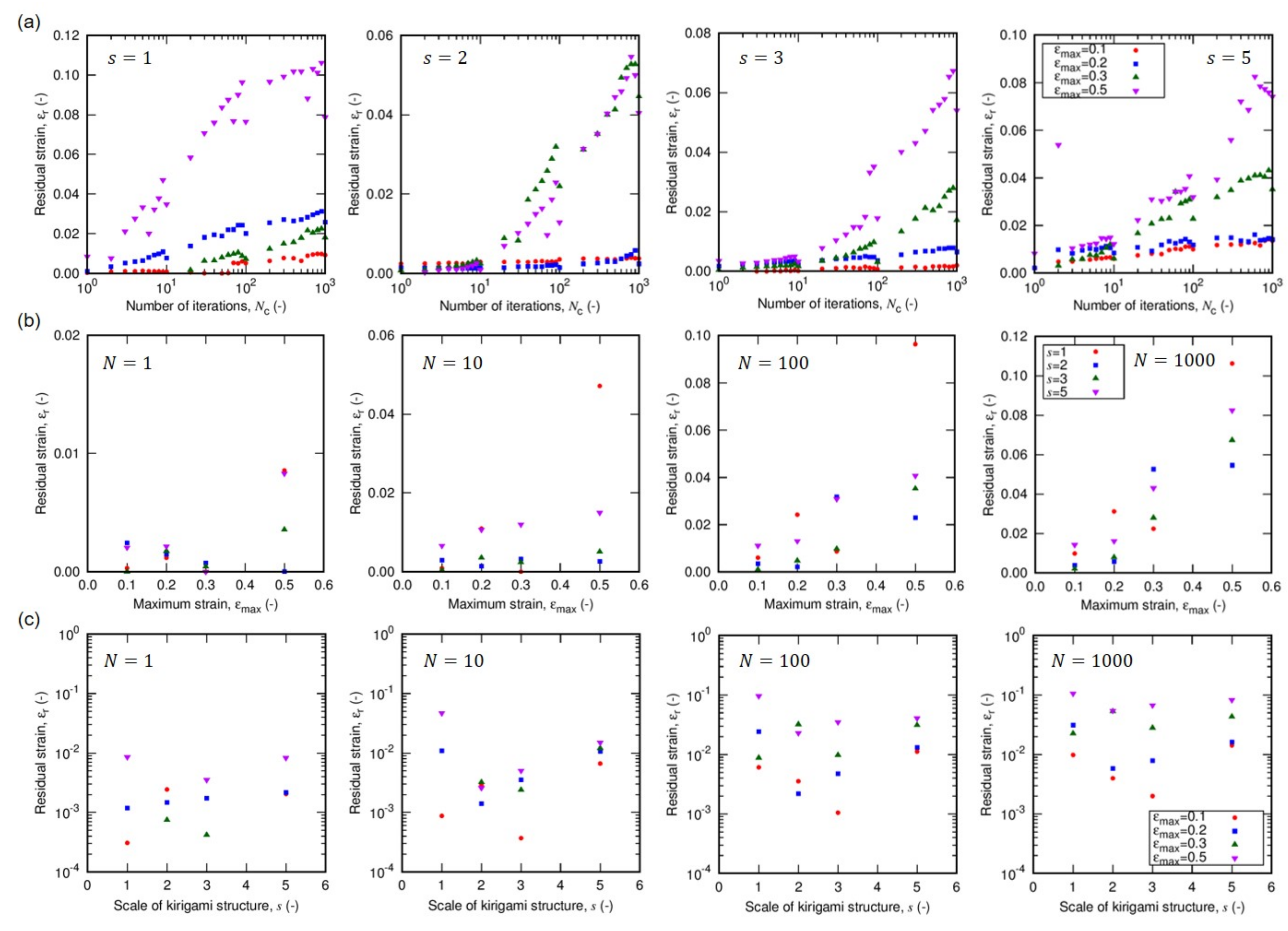
2.3. Evaluation of Resilience by Residual Strain in the Iterative Tensile Test
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, D.; Rogers, J.A. Stretchable electronics: Materials strageties and devices. Adv. Mater. 2008, 20, 4887–4892. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and Mechanics for Stretchable Electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef]
- Nassar, J.M.; Rojas, J.P.; Hussain, A.M.; Hussain, M.M. From stretchable to reconfigurable inorganic electronics. Exreme Mech. Lett. 2017, 9, 245–268. [Google Scholar] [CrossRef]
- Hammock, M.L.; Chortos, A.; Tee, B.C.K.; Tok, J.B.H.; Bao, Z. 25th Anniversary Article: The evolution of electronic skin (E-skin): A brief history, design considerations, and recent progress. Adv. Mater. 2013, 25, 5997–6038. [Google Scholar] [CrossRef]
- Liao, C.; Zhang, M.; Yao, M.Y.; Hua, T.; Li, L.; Yan, F. Flexible organic electronics in biology: Materials and devices. Adv. Mater. 2015, 27, 7493–7527. [Google Scholar] [CrossRef] [PubMed]
- Someya, T.; Bao, Z.; Malliaras, G. The rise of plastic bioelectronics. Nature 2016, 540, 379–385. [Google Scholar] [CrossRef]
- Xiong, C.; Xu, J.; Han, Q.; Qin, C.; Dai, L.; Ni, Y. Construction of flexible cellulose nanofiber fiber@graphene quantum dots hybrid film applied in supercapacitor and sensor. Cellulose 2021, 28, 10359–10372. [Google Scholar] [CrossRef]
- Gonzalez, I.; Alcala, M.; Chinga-Carrasco, G.; Vilaseca, F.; Boufi, S.; Mutje, P. From paper to nanopaper: Evolution of mechanical and physical properties. Cellulose 2014, 212, 2599–2609. [Google Scholar] [CrossRef]
- Barhoum, A.; Samyn, P.; Ohlund, T.; Dufresne, A. Review of recent research on flexible multifunctional nanopapers. Nanoscale 2017, 9, 15181–15205. [Google Scholar] [CrossRef] [PubMed]
- Benitez, A.J.; Walther, A. Cellulose nanofibril nanopapers and bioinspired nanocomposistes: A review to understand the mechanical perperty space. J. Mater. Chem. A 2017, 5, 16003–16024. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, Q.; Liu, J.; Sun, J.; Zhu, Q.; Chen, H. Processing nanocellulose to bulk materials: A review. Cellulose 2019, 26, 7585–7617. [Google Scholar] [CrossRef]
- Nechyporchuk, O.; Belgacem, M.N.; Bras, J. Production of cellulose nanofibers: A review of recent advances. Ind. Crop. Prod. 2016, 93, 2–25. [Google Scholar] [CrossRef]
- Hoeng, F.; Denneulin, A.; Bras, J. Use of nanocellulose in printed electronics: A review. Nanoscale 2016, 8, 13131–13154. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Fang, Z.; Preston, C.; Li, Y.; Hu, L. Transparent paper: Fabrications, properties, and device applications. Energy Environ. Sci. 2014, 7, 269–287. [Google Scholar] [CrossRef]
- Kasuga, T.; Yagyu, H.; Uetani, K.; Koga, H.; Nogi, M. “Return to the Soil” Nanopaper Sensor Device for Hyperdense Sensor Networks. ACS Appl. Mater. Interfaces 2019, 11, 43488–43493. [Google Scholar] [CrossRef] [PubMed]
- Bauer, S.; Kaltenbrunner, M. Built To Disappear. ACS Nano 2014, 8, 5380–5382. [Google Scholar] [CrossRef]
- Tan, M.J.; Owh, C.; Chee, P.L.; Kyaw, A.K.K.; Kai, D.; Loh, X.J. Biodegradable electronics: Cornerstone for sustainable electronics and transient applications. J. Mater. Chem. C 2016, 4, 5531–5558. [Google Scholar] [CrossRef]
- Kenry; Liu, B. Recent Advances in Biodegradable Conducting Polymers and Their Biomedical Applications. Biomacromolecules 2018, 19, 1783–1803. [Google Scholar] [CrossRef] [PubMed]
- Henriksson, M.; Berglund, L.A.; Isaksson, P.; Lindstrom, T.; Nishino, T. Cellulose nanopaper structures of high toughness. Biomacromolecules 2008, 9, 1579–1585. [Google Scholar] [CrossRef]
- Kulachenko, A.; Denoyelle, T.; Galland, S.; Lindstrom, S.B. Elastic properties of cellulose nanopaper. Cellulose 2012, 19, 793–807. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, S.; Jia, Z.; Parvinian, S.; Li, Y.; Vaaland, O.; Hu, L.; Li, T. Anomalous scaling law of strength and toughness of cellulose nanopaper. Proc. Natl. Acad. Sci. USA 2015, 112, 8971–8976. [Google Scholar] [CrossRef]
- Mao, R.; Goutianos, S.; Tu, W.; Meng, N.; Chen, S.; Peijs, T. Modeling the elastic properties of cellulose nanopaper. Mater. Des. 2017, 126, 183–189. [Google Scholar] [CrossRef]
- Qin, X.; Feng, S.; Meng, Z.; Keten, S. Optimizing the mechanical properties of cellulose nanopaper through surface energy and critical length scale considerations. Cellulose 2017, 24, 3289–3299. [Google Scholar] [CrossRef]
- Molnar, G.; Rodney, D.; Martoia, F.; Dumont, P.J.J.; Nishiyama, Y.; Mazeau, K.; Orgeas, L. Cellulose crystals plastify by localized shear. Proc. Natl. Acad. Sci. USA 2018, 115, 7260–7265. [Google Scholar] [CrossRef] [PubMed]
- Ciesielski, P.N.; Wagner, R.; Bharadwaj, V.S.; Killgore, J.; Mittal, A.; Beckham, G.T.; Decker, S.R.; Himmel, M.E.; Crowley, M.F. Nanomechanics of cellulose deformation reveal molecular defects that facilitate natural deconstruction. Proc. Natl. Acad. Sci. USA 2019, 116, 9825–9830. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, T.J. Mechanics of strong and tough cellulose nanopaper. Appl. Mech. Rev. 2019, 71, 040801. [Google Scholar] [CrossRef]
- Mariani, L.M.; Johnson, W.R., III; Considine, J.M.; Turner, K.T. Printing and mechanical characterization of cellulose nanofibril materials. Cellulose 2019, 26, 2639–2651. [Google Scholar] [CrossRef]
- Guan, Q.F.; Yang, H.B.; Han, Z.M.; Zhou, L.C.; Zhu, Y.B.; Ling, Z.C.; Jiang, H.B.; Wang, P.F.; Ma, T.; Wu, H.A.; et al. Lightweight, tough, and sustainable cellulose nanofiber-derived bulk structural materials with low thermal expansion coefficient. Sci. Adv. 2020, 6, eaaz1114. [Google Scholar] [CrossRef] [PubMed]
- Nogi, M.; Komoda, N.; Otsuka, K.; Suganuma, K. Foldable Nanopaper Antennas for Origami Electronics. Nanoscale 2013, 5, 4395–4399. [Google Scholar] [CrossRef]
- Callens, S.J.P.; Zadpoor, A.A. From flat sheets to curved geometries: Origami and kirigami approaches. Mater. Today 2020, 21, 241–264. [Google Scholar] [CrossRef]
- Isobe, M.; Okumura, K. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep. 2016, 6, 24758. [Google Scholar] [CrossRef] [PubMed]
- Lei, X.W.; Nakatani, A.; Doi, Y.; Matsunaga, S. Bifurcation Analysis of Periodic Kirigami Structure with Out-Plane Deformation. J. Soc. Mater. Sci. 2018, 67, 202–207. [Google Scholar] [CrossRef][Green Version]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative Poisson’s Ratio Behavior Induced by an Elastic Instability. Adv. Mater. 2009, 21, 1. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, J.T.B.; Shan, S.; Bertoldi, K. Compaction through buckling in 2D periodic, soft and prous structures: Effect of pore shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef]
- Uetani, K.; Kasuya, K.; Wang, J.; Huang, Y.; Watanabe, R.; Tsuenyasu, S.; Satoh, T.; Koga, H.; Nogi, M. Kirigami-processed cellulose nanofiber films for smart heat dissipation by convection. NPG Asia Mater. 2021, 13, 62. [Google Scholar] [CrossRef]
- Ooi, Y.; Hanasaki, I.; Mizumura, D.; Matsuda, Y. Self-peeling-off in the drying of particulate films mixed with cellulose nanofibers. Micro Nano Lett. 2017, 12, 511–516. [Google Scholar] [CrossRef]
- Koitabashi, T.; Hanasaki, I. Drying path dependence in microrheological characteristics of cellulose nanofiber dispersion revealed by single particle tracking. J. Phys. D Appl. Phys. 2021, 54, 295302. [Google Scholar] [CrossRef]
- Shyu, T.C.; Damasceno, P.F.; Dodd, P.M.; Lamoureux, A.; Xu, L.; Shlian, M.; Shtein, M.; Glotzer, S.C.; Kotov, N.A. A kirigami approach to engineering elasticity in nanocomposites through patterned defects. Nat. Mater. 2015, 14, 785–789. [Google Scholar] [CrossRef]
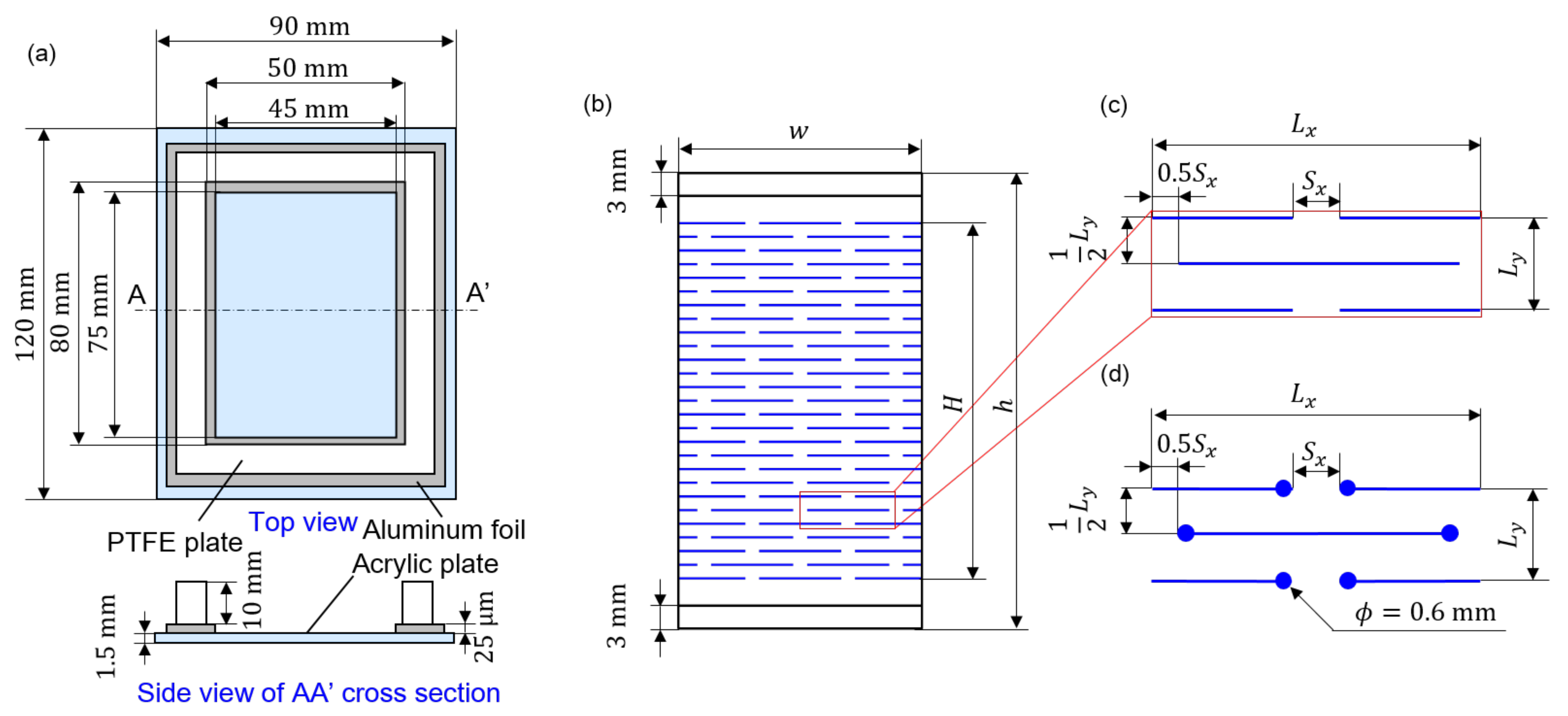



| s (-) | w | h | H | |||
|---|---|---|---|---|---|---|
| 1 | 32.0 | 60.0 | 49.2 | 4.2 | 1.2 | 0.6 |
| 2 | 48.0 | 8.4 | 2.4 | 1.2 | ||
| 3 | 46.8 | 12.6 | 3.6 | 1.8 | ||
| 5 | 48.0 | 21.0 | 6.0 | 3.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujita, T.; Nakagawa, D.; Komiya, K.; Ohira, S.; Hanasaki, I. Resilient Mechanical Metamaterial Based on Cellulose Nanopaper with Kirigami Structure. Nanomaterials 2022, 12, 2431. https://doi.org/10.3390/nano12142431
Fujita T, Nakagawa D, Komiya K, Ohira S, Hanasaki I. Resilient Mechanical Metamaterial Based on Cellulose Nanopaper with Kirigami Structure. Nanomaterials. 2022; 12(14):2431. https://doi.org/10.3390/nano12142431
Chicago/Turabian StyleFujita, Tadaoki, Daisuke Nakagawa, Kazuma Komiya, Shingo Ohira, and Itsuo Hanasaki. 2022. "Resilient Mechanical Metamaterial Based on Cellulose Nanopaper with Kirigami Structure" Nanomaterials 12, no. 14: 2431. https://doi.org/10.3390/nano12142431
APA StyleFujita, T., Nakagawa, D., Komiya, K., Ohira, S., & Hanasaki, I. (2022). Resilient Mechanical Metamaterial Based on Cellulose Nanopaper with Kirigami Structure. Nanomaterials, 12(14), 2431. https://doi.org/10.3390/nano12142431