Bayesian Data Assimilation of Temperature Dependence of Solid–Liquid Interfacial Properties of Nickel
Abstract
:1. Introduction
2. Phase-Field Model
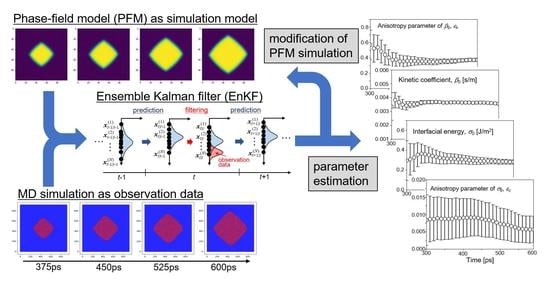
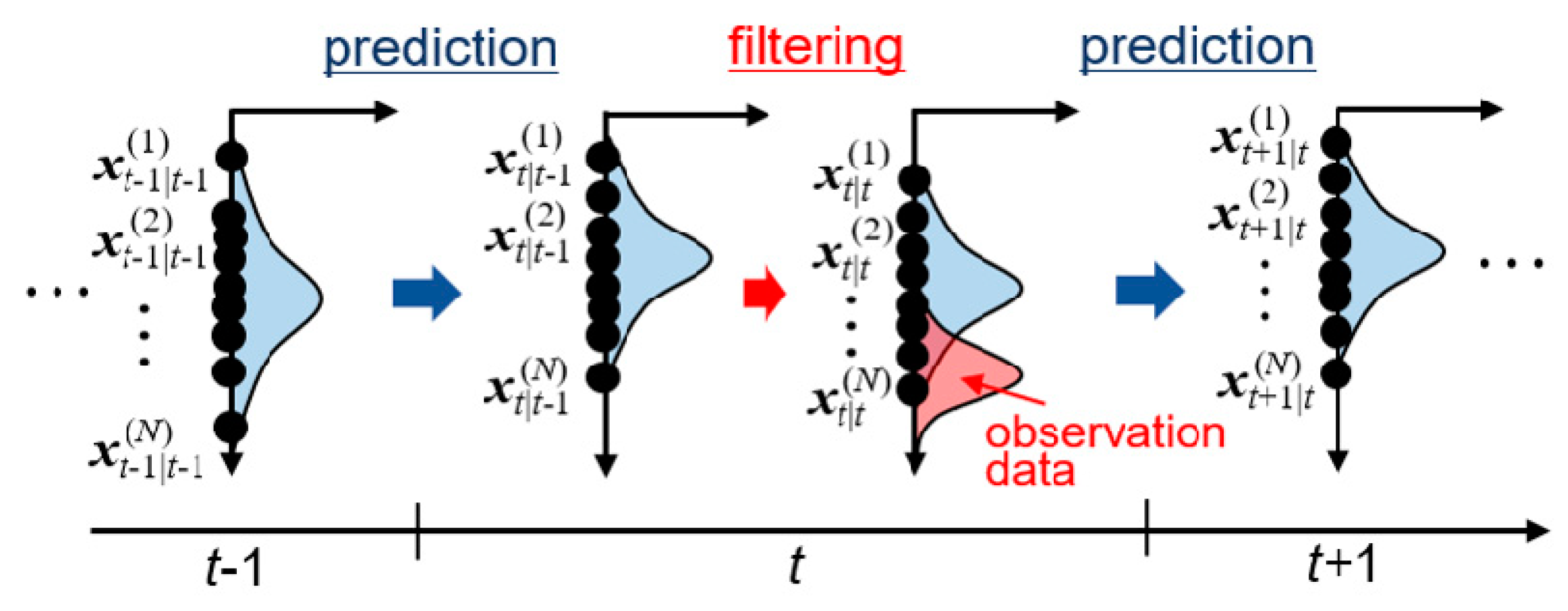
3. Data Assimilation Based on Ensemble Kalman Filter
3.1. State Vector and System Model
3.2. Ensemble Kalman Filter (EnKF)
3.3. Calculation Procedure of Data Assimilation
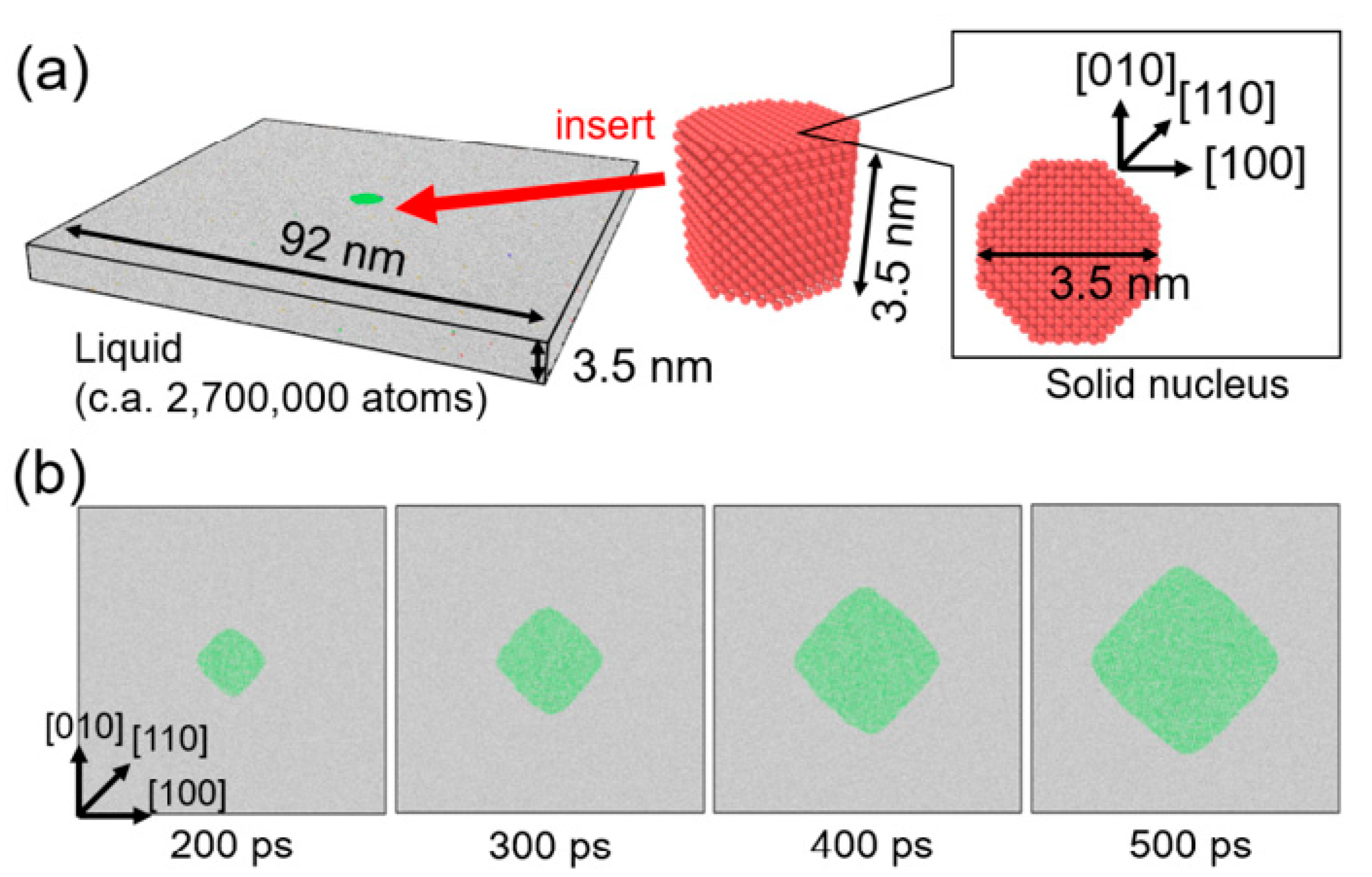
4. Molecular Dynamics Simulation for Observation Data
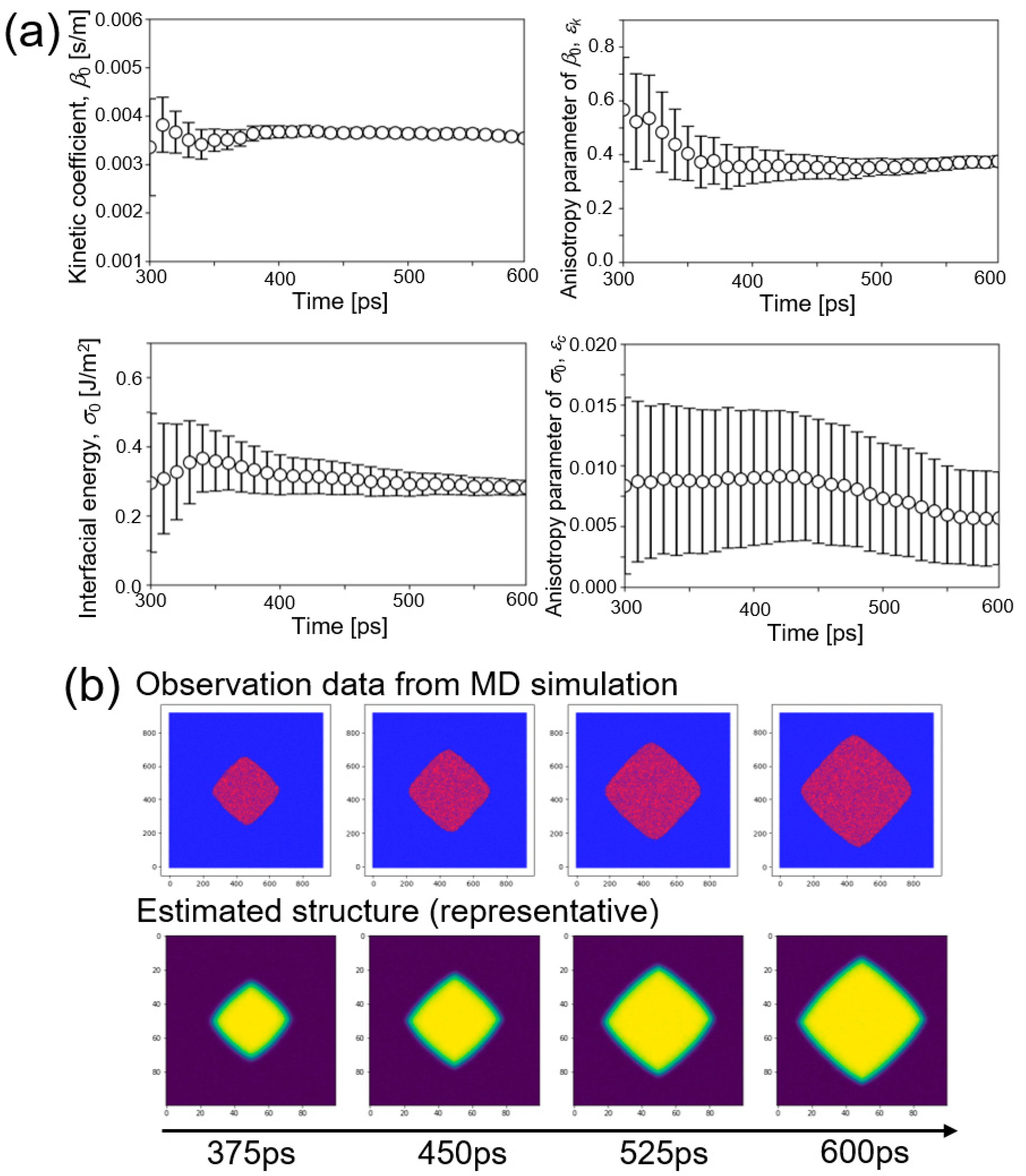
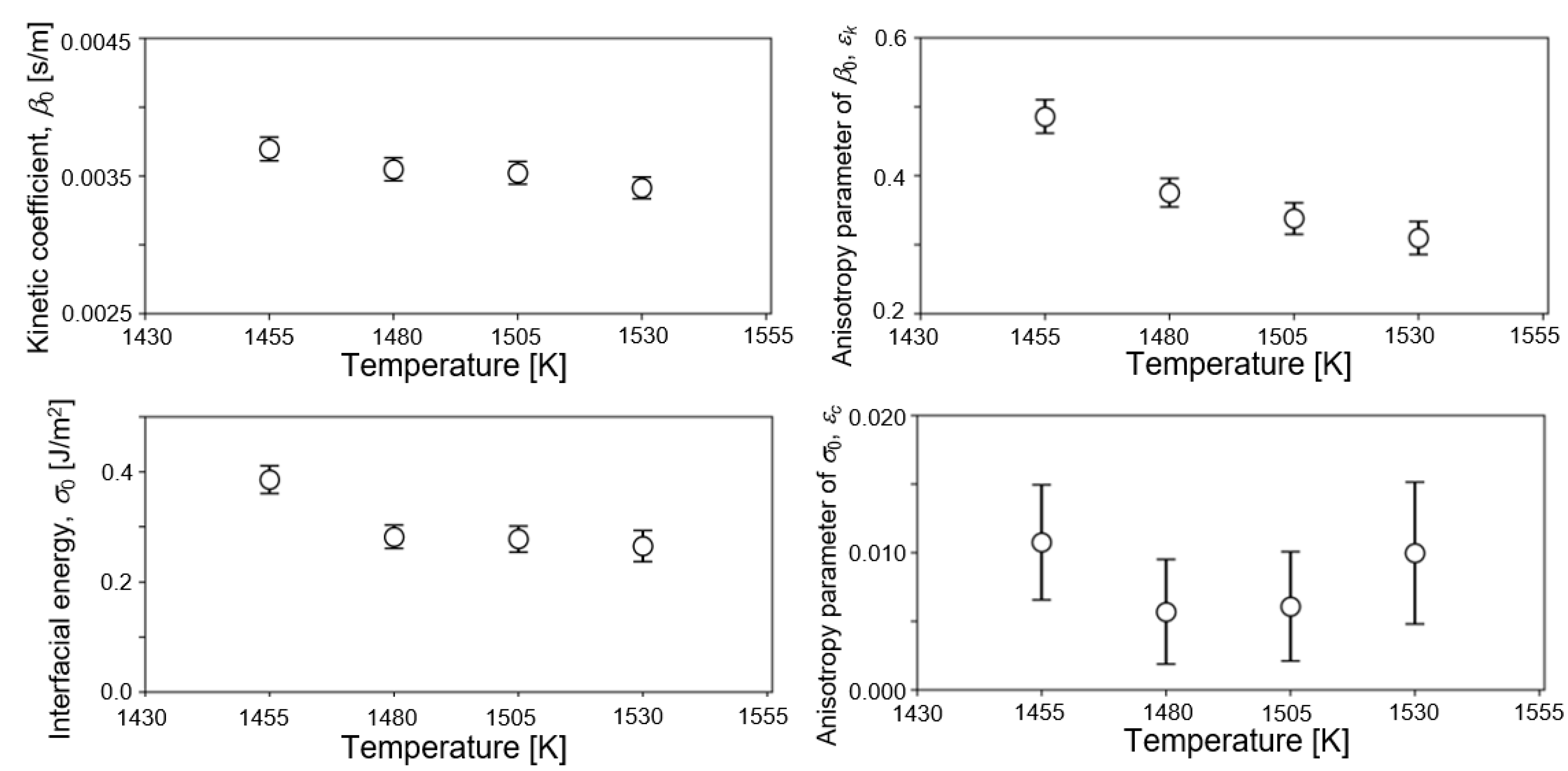
5. Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Expression of Ensemble Kalman Filter
References
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Phys. D 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Asta, M.; Beckermann, C.; Karma, A.; Kurz, W.; Napolitano, R.; Plapp, M.; Purdy, G.; Rappaz, M.; Trivedi, R. Solidification microstructures and solid-state parallels: Recent developments, future directions. Acta Mater. 2009, 57, 941–971. [Google Scholar] [CrossRef] [Green Version]
- Takaki, T. Phase-field modeling and simulations of dendrite growth. ISIJ Int. 2014, 54, 437–444. [Google Scholar] [CrossRef] [Green Version]
- Ohno, M. Quantitative Phase-field Modeling and Simulations of Solidification Microstructures. ISIJ Int. 2020, 60, 2745–2754. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase field simulation of solidification. Annu. Rev. Mater. Res. 2002, 32, 63–94. [Google Scholar] [CrossRef]
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Aoki, T.; Gandin, C.-A. Competitive grain growth during directional solidification of a polycrystalline binary alloy: Three-dimensional large-scale phase-field study. Materialia 2018, 1, 104–113. [Google Scholar] [CrossRef]
- Suwa, Y.; Saito, Y.; Onodera, H. Three-dimensional phase field simulation of the effect of anisotropy in grain-boundary mobility on growth kinetics and morphology of grain structure. Comput. Mater. Sci. 2007, 40, 40–50. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, D.L.; Kim, W.T.; Park, Y.B. Computer simulations of two-dimensional and three-dimensional ideal grain growth. Phys. Rev. E 2006, 74, 61605. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, E.; Takaki, T.; Ohno, M.; Shibuta, Y.; Sakane, S.; Shimokawabe, T.; Aoki, T. Ultra-large-scale phase-field simulation study of ideal grain growth. NPJ Comput. Mater. 2017, 3, 25. [Google Scholar] [CrossRef]
- Takaki, T.; Hisakuni, Y.; Hirouchi, T.; Yamanaka, A.; Tomita, Y. Multi-phase-field simulations for dynamic recrystallization. Comput. Mater. Sci. 2009, 45, 881–888. [Google Scholar] [CrossRef]
- Militzer, M.; Mecozzi, M.; Sietsma, J.; van der Zwaag, S. Three-dimensional phase field modelling of the austenite-to-ferrite transformation. Acta Mater. 2006, 54, 3961–3972. [Google Scholar] [CrossRef]
- Yamanaka, A.; Takaki, T.; Tomita, Y. Elastoplastic phase-field simulation of martensitic transformation with plastic deformation in polycrystal. Int. J. Mech. Sci. 2010, 52, 245–250. [Google Scholar] [CrossRef]
- Turnbull, D. Formation of crystal nuclei in liquid metals. J. Appl. Phys. 1950, 21, 1022–1028. [Google Scholar] [CrossRef]
- Waseda, Y.; Miller, W.A. Calculation of the crystal-melt interfacial free energy from experimental radial distribution function data. Trans. JIM 1978, 19, 546–552. [Google Scholar] [CrossRef] [Green Version]
- Gündüz, M.; Hunt, J.D. The measurement of solid-liquid surface energies in the Al-Cu, Al-Si and Pb-Sn systems. Acta Metall. 1985, 33, 1651–1672. [Google Scholar] [CrossRef]
- Broughton, J.Q.; Gilmer, G.H. Molecular dynamics investigation of the crystal–fluid interface. VI. Excess surface free energies of crystal–liquid systems. J. Chem. Phys. 1986, 84, 5759–5768. [Google Scholar] [CrossRef]
- Hoyt, J.; Asta, M.; Haxhimali, T.; Karma, A.; Napolitano, R.; Trivedi, R.; Laird, B.B.; Morris, J. Crystal–melt interfaces and solidification morphologies in metals and alloys. MRS Bull. 2004, 29, 935–939. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M.; Karma, A. Method for computing the anisotropy of the solid-liquid interfacial free energy. Phys. Rev. Lett. 2001, 86, 5530–5533. [Google Scholar] [CrossRef]
- Morris, J.R.; Song, X. The anisotropic free energy of the Lennard-Jones crystal-melt interface. J. Chem. Phys. 2003, 119, 3920–3925. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, Y.; Shibuta, Y.; Suzuki, T. Molecular dynamics study of thermodynamic and kinetic properties of solid-liquid interface for bcc iron. ISIJ Int. 2010, 50, 1158–1164. [Google Scholar] [CrossRef] [Green Version]
- Shibuta, Y.; Ohno, M.; Takaki, T. Solidification in a Supercomputer: From Crystal Nuclei to Dendrite Assemblages. JOM 2005, 67, 1793–1804. [Google Scholar] [CrossRef] [Green Version]
- Saidi, P.; Freitas, R.; Frolov, T.; Asta, M.; Hoyt, J.J. Free energy of steps at faceted (1 1 1) solid-liquid interfaces in the Si-Al system calculated using capillary fluctuation method. Comput. Mater. Sci. 2017, 134, 184–189. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.; Xu, B.; Kong, L.T.; Li, J.F. Solid-liquid interfacial free energy and its anisotropy in the Cu-Ni binary system investigated by molecular dynamics simulations. J. Alloys Compd. 2017, 708, 1073–1080. [Google Scholar] [CrossRef]
- Ueno, K.; Shibuta, Y. Solid-liquid interfacial energy for Fe-Cr alloy under temperature gradient from molecular dynamics simulation. ISIJ Int. 2020, 60, 2301–2305. [Google Scholar] [CrossRef]
- Ueno, K.; Shibuta, Y. Composition dependence of solid-liquid interfacial energy of Fe-Cr binary alloy from molecular dynamics simulations. Comput. Mater. Sci. 2019, 167, 1–7. [Google Scholar] [CrossRef]
- Kavousi, S.; Novak, B.R.; Baskes, M.I.; Zaeem, M.A.; Moldovan, D. Modified embedded-atom method potential for high-temperature crystal-melt properties of Ti–Ni alloys and its application to phase field simulation of solidification. Model. Simul. Mater. Sci. Eng. 2020, 28, 015006. [Google Scholar] [CrossRef]
- Bai, X.-M.; Li, M. Calculation of solid-liquid interfacial free energy: A classical nucleation theory based approach. J. Chem. Phys. 2006, 124, 124707. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, F.; Song, H.; Mendelev, M.I.; Wang, C.-Z.; Ho, K.-M. Temperature dependence of the solid-liquid interface free energy of Ni and Al from molecular dynamics simulation of nucleation. J. Chem. Phys. 2018, 149, 174501. [Google Scholar] [CrossRef] [Green Version]
- Hoyt, J.J.; Asta, M.; Karma, A. Atomistic and continuum modeling of dendritic solidification. Mater. Sci. Eng. R 2003, 41, 121–163. [Google Scholar] [CrossRef]
- Shibuta, Y.; Ohno, M.; Takaki, T. Advent of cross-scale modeling: High-performance computing of solidification and grain growth. Adv. Theory Simul. 2018, 1, 1800065. [Google Scholar] [CrossRef]
- Spapen, F. A structural model for the solid-liquid interface in monatomic systems. Acta Metall. 1975, 23, 729–743. [Google Scholar] [CrossRef]
- Gránásy, L.; Tegze, M.; Ludwig, A. Solid-liquid interfacial free energy. Mater. Sci. Eng. A 1991, 133, 577–580. [Google Scholar] [CrossRef]
- Spaepen, F. The temperature dependence of the crystal-melt interfacial tension: A simple model. Mater. Sci. Eng. A 1994, 178, 15–18. [Google Scholar] [CrossRef]
- Davidchack, R.L.; Laird, B.B. Direct calculation of the crystal–melt interfacial free energies for continuous potentials: Application to the Lennard-Jones system. J. Chem. Phys. 2003, 118, 7651–7657. [Google Scholar] [CrossRef] [Green Version]
- Laird, B.B.; Davidchack, R.L. Direct calculation of the crystal-melt interfacial free energy via molecular dynamics computer simulation. J. Phys. Chem. B 2005, 109, 17802–17812. [Google Scholar] [CrossRef]
- Jian, Z.; Li, N.; Zhu, M.; Chen, J.; Chang, F.; Jie, W. Temperature dependence of the crystal–melt interfacial energy of metals. Acta Mater. 2012, 60, 3590–3603. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Tipeev, A.O. Crystal nucleation and the solid–liquid interfacial free energy. J. Chem. Phys. 2012, 136, 074510. [Google Scholar] [CrossRef]
- Lippmann, S.; Jung, I.-H.; Paliwal, M.; Rettenmayr, M. Modelling temperature and concentration dependent solid/liquid interfacial energies. Philos. Mag. 2016, 96, 1–14. [Google Scholar]
- Tognato, R. On the temperature dependence of solid-liquid interfacial free energies per unit area. Phase Transit. 1992, 38, 71–76. [Google Scholar] [CrossRef]
- Mondal, K.; Kumar, A.; Gupta, G.; Murty, B.S. Temperature and structure dependency of solid–liquid interfacial energy. Acta Mater. 2009, 57, 3422–3430. [Google Scholar] [CrossRef]
- Wu, D.T.; Gránásy, L.; Spaepen, F. Nucleation and the solid–liquid interfacial free energy. MRS Bull. 2004, 29, 945–950. [Google Scholar] [CrossRef] [Green Version]
- Hoyt, J.J.; Raman, S.M.; Asta, M. Unusual temperature dependence of the solid-liquid interfacial free energy in the Cu-Zr system. Comput. Mater. Sci. 2018, 154, 303–308. [Google Scholar] [CrossRef]
- Wang, L.; Hoyt, J.J.; Wang, N.; Provatas, N.; Sinclair, C.W. Controlling solid-liquid interfacial energy anisotropy through the isotropic liquid. Nat. Commun. 2020, 11, 724. [Google Scholar] [CrossRef]
- Wang, L.; Hoyt, J.J. Layering misalignment and negative temperature dependence of interfacial free energy of B2-liquid interfaces in a glass forming system. Acta Mater. 2021, in press. [Google Scholar] [CrossRef]
- Cheng, B.; Tribello, G.A.; Ceriotti, M. Solid-liquid interfacial free energy out of equilibrium. Phys. Rev. B 2015, 92, 180102(R). [Google Scholar] [CrossRef] [Green Version]
- Ohno, M.; Oka, Y.; Sakane, S.; Shibuta, Y.; Takaki, T. Bayesian inference of solid-liquid interfacial properties out of equilibrium. Phys. Rev. E 2020, 101, 052121. [Google Scholar] [CrossRef]
- Lahoz, W.; Khattatov, B.; Menard, R. Data Assmilation—Making Sense of Observations; Springer: Berlin, Germany, 2010; pp. 13–39. [Google Scholar]
- Ghil, M.; Malanotte-Rizzoli, P. Data assimilation in meteorology and oceanography. Adv. Geophys. 1991, 33, 141–266. [Google Scholar]
- Sasaki, K.; Yamanaka, A.; Ito, S.; Nagao, H. Data assimilation for phase-field models based on the ensemble Kalman filter. Comput. Mater. Sci. 2018, 141, 141–152. [Google Scholar] [CrossRef]
- Yamanaka, A.; Maeda, Y.; Sasaki, K. Ensemble Kalman filter-based data assimilation for three-dimensional multi-phase-field model: Estimation of anisotropic grain boundary properties. Mater. Design 2019, 165, 107577. [Google Scholar] [CrossRef]
- Oka, Y.; Ohno, M. Parameter estimation for heat transfer analysis during casting processes based on ensemble Kalman filter. Int. J. Heat Mass Trans. 2020, 149, 119232. [Google Scholar] [CrossRef]
- Natsume, Y.; Oka, Y.; Ogawa, J.; Ohno, M. Estimation of time-dependent heat transfer coefficient in unidirectional casting using a numerical model coupled with solidification analysis and data assimilation. Int. J. Heat Mass Trans. 2020, 150, 119222. [Google Scholar] [CrossRef]
- Shiraiwa, T.; Enoki, M.; Goto, S.; Hiraide, T. Data Assimilation in the Welding Process for Analysis of Weld Toe Geometry and Heat Source Model. ISIJ Int. 2020, 60, 1301–1311. [Google Scholar] [CrossRef] [Green Version]
- Shiraiwa, T.; Takahashi, H.; Enoki, M. Acoustic emission analysis during fatigue crack propagation by Bayesian statistical modeling. Mater. Sci. Eng. A 2020, 778, 139087. [Google Scholar] [CrossRef]
- Bragard, J.; Karma, A.; Lee, Y.H.; Plapp, M. Linking phase-field and atomistic simulations to model dendritic solidification in highly undercooled melts. Interface Sci. 2002, 10, 121–136. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic. Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean. Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Doucet, A.; Godsill, S.; Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar] [CrossRef]
- Orihara, S.; Shibuta, Y.; Mohri, T. Molecular dynamics simulation of nucleation from undercooled melt of nickel-aluminum alloy and discussion on polymorphism in nucleation. Mater. Trans. 2020, 61, 750–757. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Purja Pun, G.P.; Mishin, Y. Development of an interatomic potential for the Ni-Al system. Philos. Mag. 2009, 89, 3245–3267. [Google Scholar] [CrossRef]
- Mishin, Y. Atomistic modeling of the γ and γ’-phases of the Ni–Al system. Acta Mater. 2004, 52, 1451–1467. [Google Scholar] [CrossRef]
- Sun, D.Y.; Asta, M.; Hoyt, J.J. Crystal-melt interfacial free energies and mobilities in fcc and bcc Fe. Phys. Rev. B 2004, 69, 174103. [Google Scholar] [CrossRef]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Shibuta, Y.; Oguchi, K.; Ohno, M. Million-atom molecular dynamics simulation on spontaneous evolution of anisotropy in solid nucleus during solidification of iron. Scr. Mater. 2014, 86, 20–23. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302–1322. [Google Scholar] [CrossRef]
- Shibuta, Y.; Takamoto, S.; Suzuki, T. A molecular dynamics study of the energy and structure of the symmetric tilt boundary of iron. ISIJ Int. 2008, 48, 1582–1591. [Google Scholar] [CrossRef] [Green Version]
- Shibuta, Y. Estimation of thermodynamic and interfacial parameters of metallic materials by molecular dynamics simulations. Mater. Trans. 2019, 60, 180–188. [Google Scholar] [CrossRef] [Green Version]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2020, 18, 015012. [Google Scholar] [CrossRef]
- Miyoshi, E.; Takaki, T.; Shibuta, Y.; Ohno, M. Bridging molecular dynamics and phase-field methods for grain growth prediction. Comput. Mater. Sci. 2018, 152, 118–124. [Google Scholar] [CrossRef]
- Shibuta, Y.; Sakane, S.; Miyoshi, E.; Takaki, T.; Ohno, M. Micrometer-scale molecular dynamics simulation of microstructure formation linked with multi-phase-field simulation in same space scale. Model. Simul. Mater. Sci. Eng. 2019, 27, 054002. [Google Scholar] [CrossRef]
- Turnbull, D.; Cech, R.E. Microscopic observation of the solidification of small metal droplets. J. Appl. Phys. 1950, 21, 804–810. [Google Scholar] [CrossRef]
- Vinet, B.; Magnusson, L.; Fredriksson, H.; Desre, P.J. Correlations between surface and interface energies with respect to crystal nucleation. J. Colloid Interf. Sci. 2002, 255, 363–374. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Sadigh, B.; Asta, M.; Foiles, S.M. Kinetic phase field parameters for the Cu–Ni system derived from atomistic computations. Acta Mater. 1999, 47, 3181–3187. [Google Scholar] [CrossRef]

| Parameter | Symbol | Value |
|---|---|---|
| Grid size [m] | Δx | 9.0 × 10−10 |
| Interface thickness [m] | W0 | 2.0Δx = 1.8 × 10−9 |
| Latent heat [J/m3] | ΔH | 2.83966 × 109 [60] |
| Constant pressure specific heat [J/(m3K)] | cp | 4.1578 × 106 [60] |
| Temperature [K] | T | 1455, 1480, 1505, 1530 |
| Time step [s] | Δt | 1.0 × 10−14 |
| Parameter | Symbol | Value |
|---|---|---|
| Ensemble number | − | 100 |
| Filtering interval [s] | − | 1.0 × 10−11 |
| Total time [s] | − | 3.0 × 10−10 |
| System noise of ϕ | 1.0 × 10−3 | |
| System noise of β0 | 1.0 × 10−6 | |
| System noise of εk | 1.0 × 10−4 | |
| System noise of σ0 | 1.0 × 10−4 | |
| System noise of εc | 1.0 × 10−5 | |
| Observation noise of ϕ | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagatsuma, Y.; Ohno, M.; Takaki, T.; Shibuta, Y. Bayesian Data Assimilation of Temperature Dependence of Solid–Liquid Interfacial Properties of Nickel. Nanomaterials 2021, 11, 2308. https://doi.org/10.3390/nano11092308
Nagatsuma Y, Ohno M, Takaki T, Shibuta Y. Bayesian Data Assimilation of Temperature Dependence of Solid–Liquid Interfacial Properties of Nickel. Nanomaterials. 2021; 11(9):2308. https://doi.org/10.3390/nano11092308
Chicago/Turabian StyleNagatsuma, Yuhi, Munekazu Ohno, Tomohiro Takaki, and Yasushi Shibuta. 2021. "Bayesian Data Assimilation of Temperature Dependence of Solid–Liquid Interfacial Properties of Nickel" Nanomaterials 11, no. 9: 2308. https://doi.org/10.3390/nano11092308
APA StyleNagatsuma, Y., Ohno, M., Takaki, T., & Shibuta, Y. (2021). Bayesian Data Assimilation of Temperature Dependence of Solid–Liquid Interfacial Properties of Nickel. Nanomaterials, 11(9), 2308. https://doi.org/10.3390/nano11092308