The Role of Grain Boundary Diffusion in the Solute Drag Effect
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
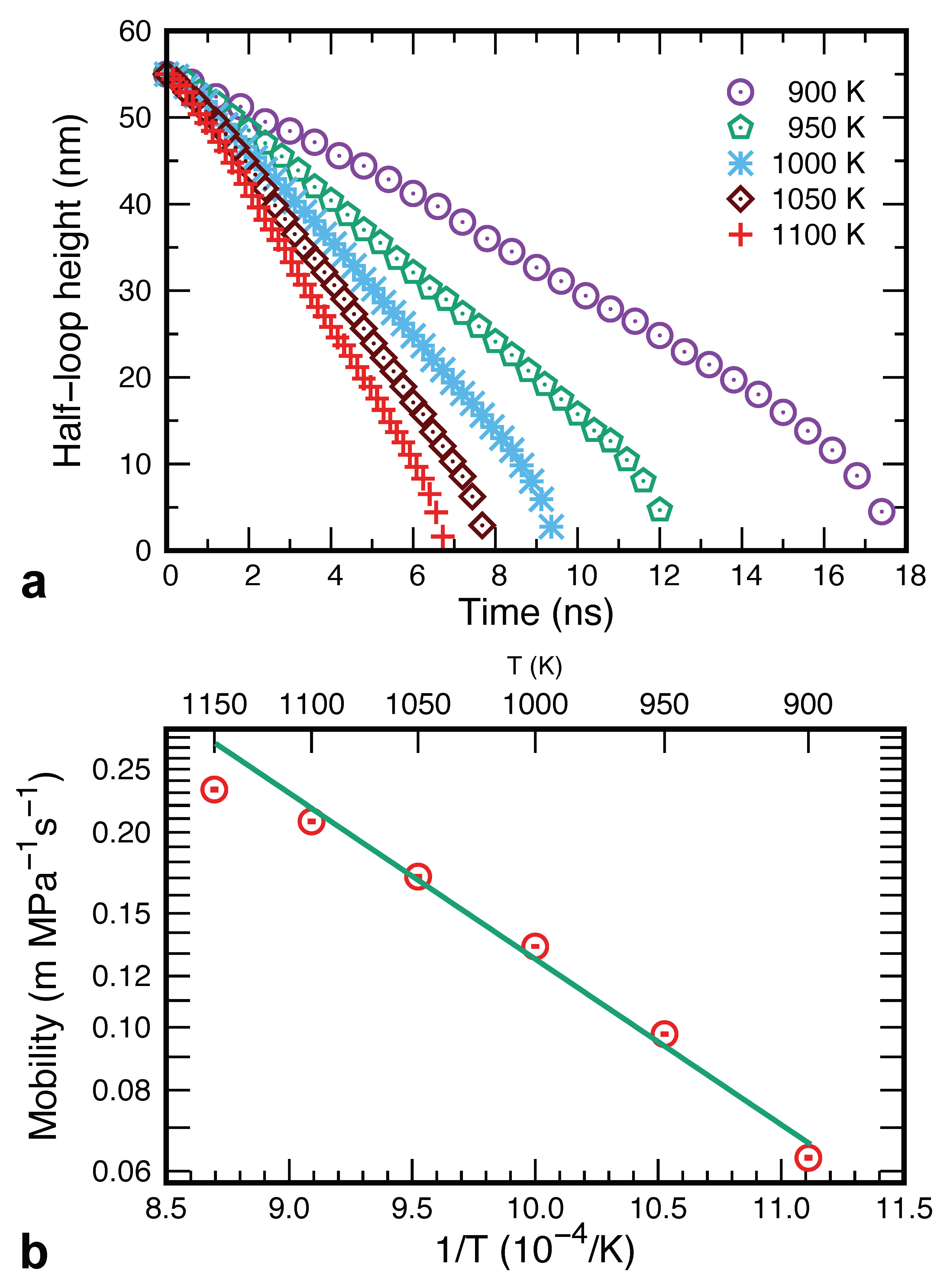
3.1. Grain Migration in Pure Cu
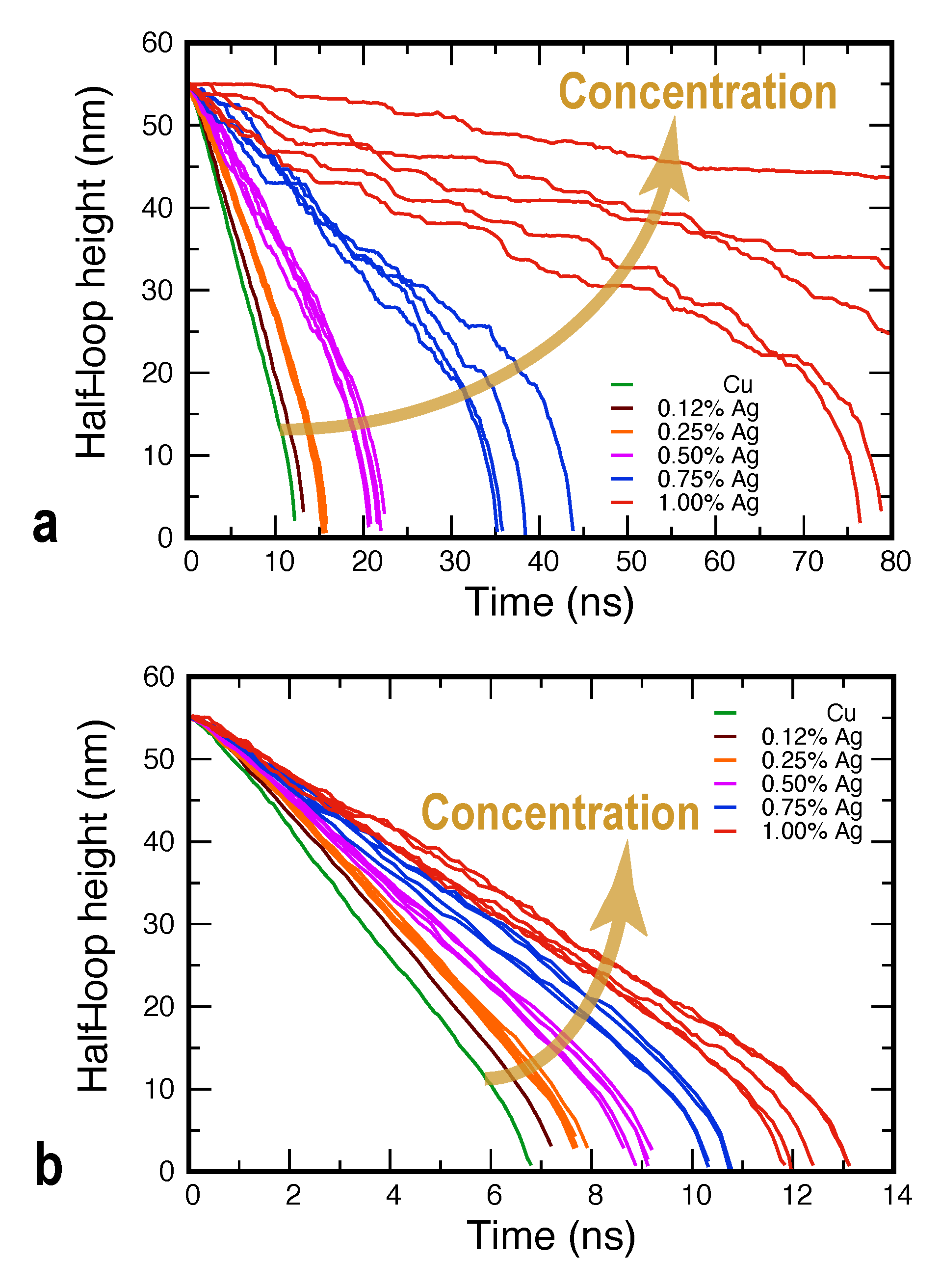
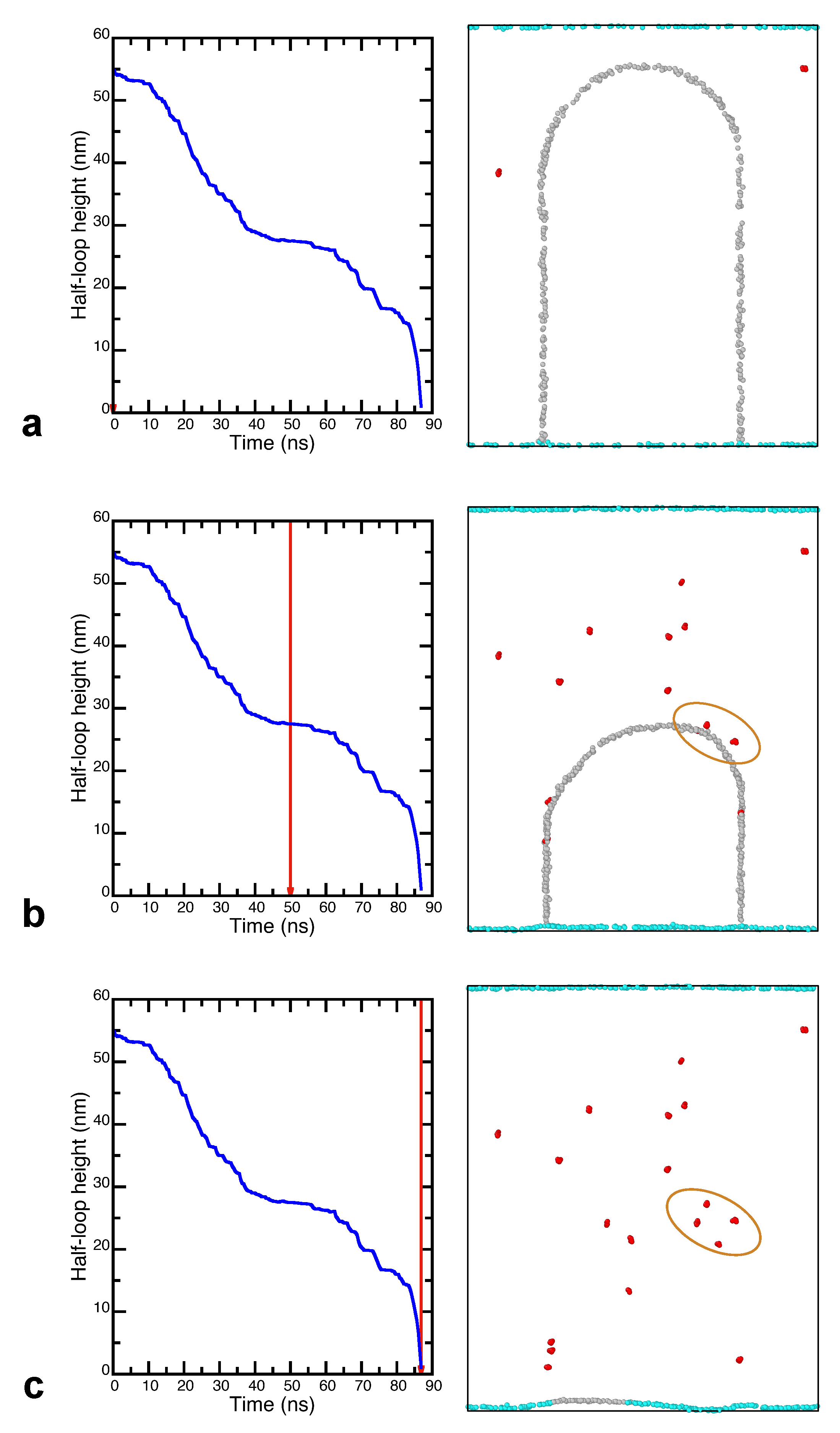
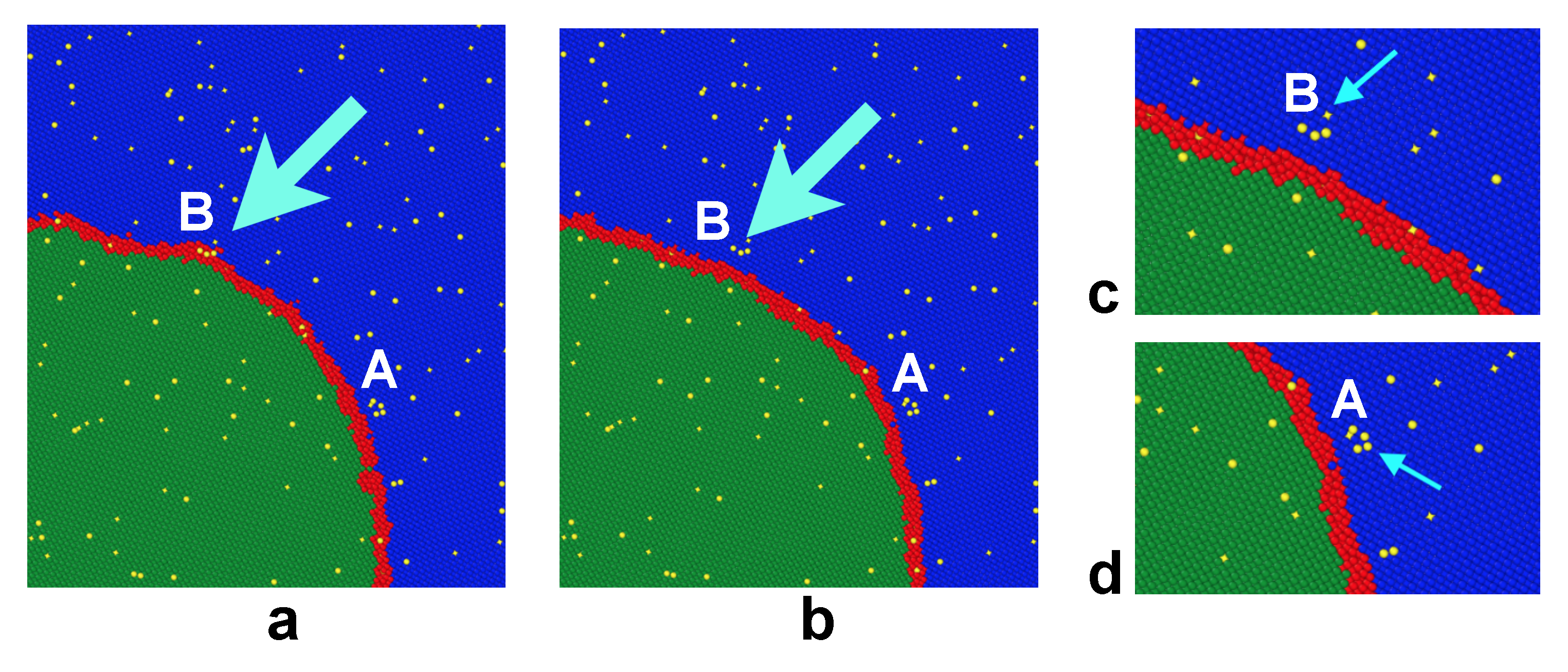
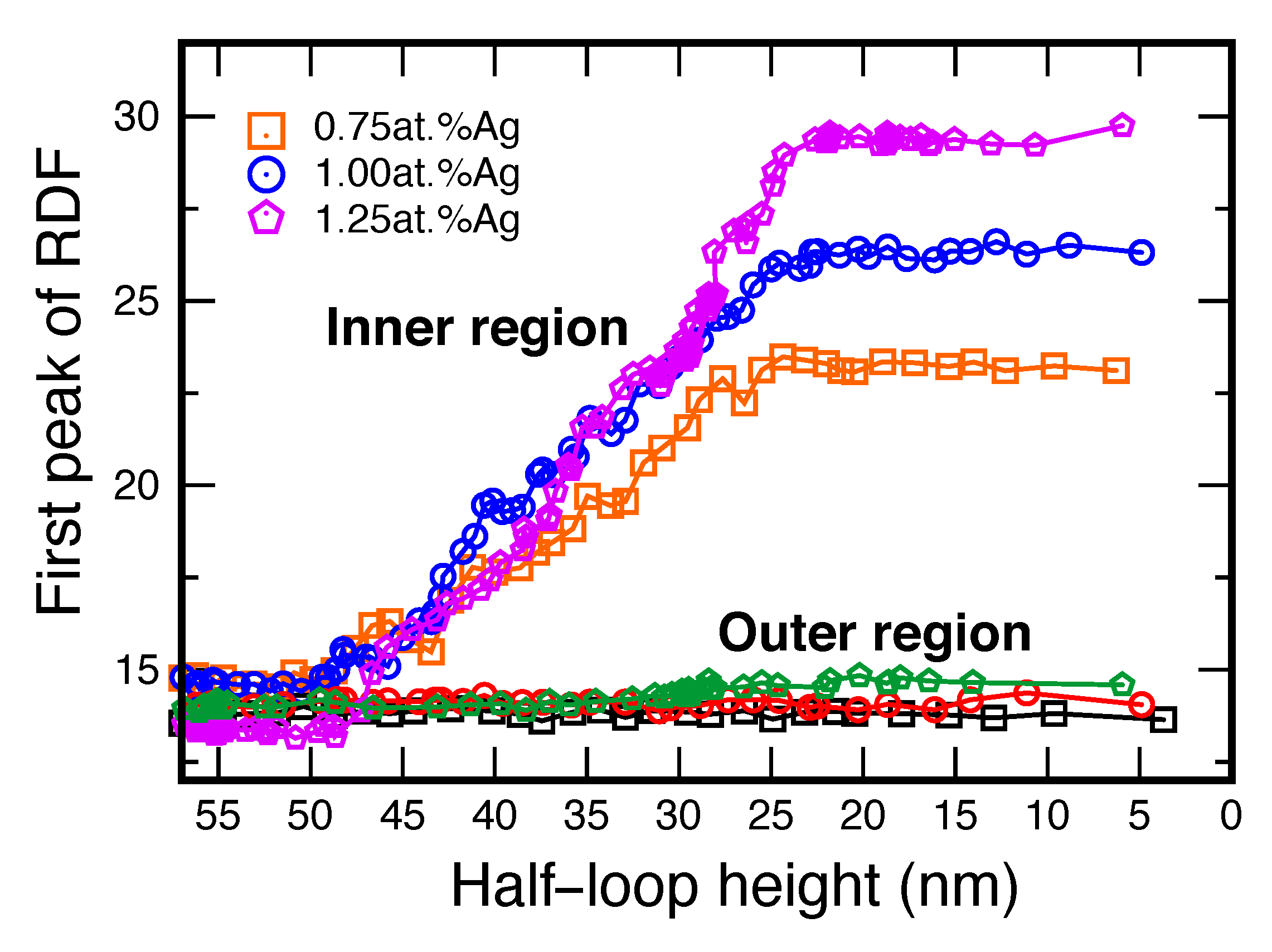
3.2. Grain Boundary Migration in the Random Alloy
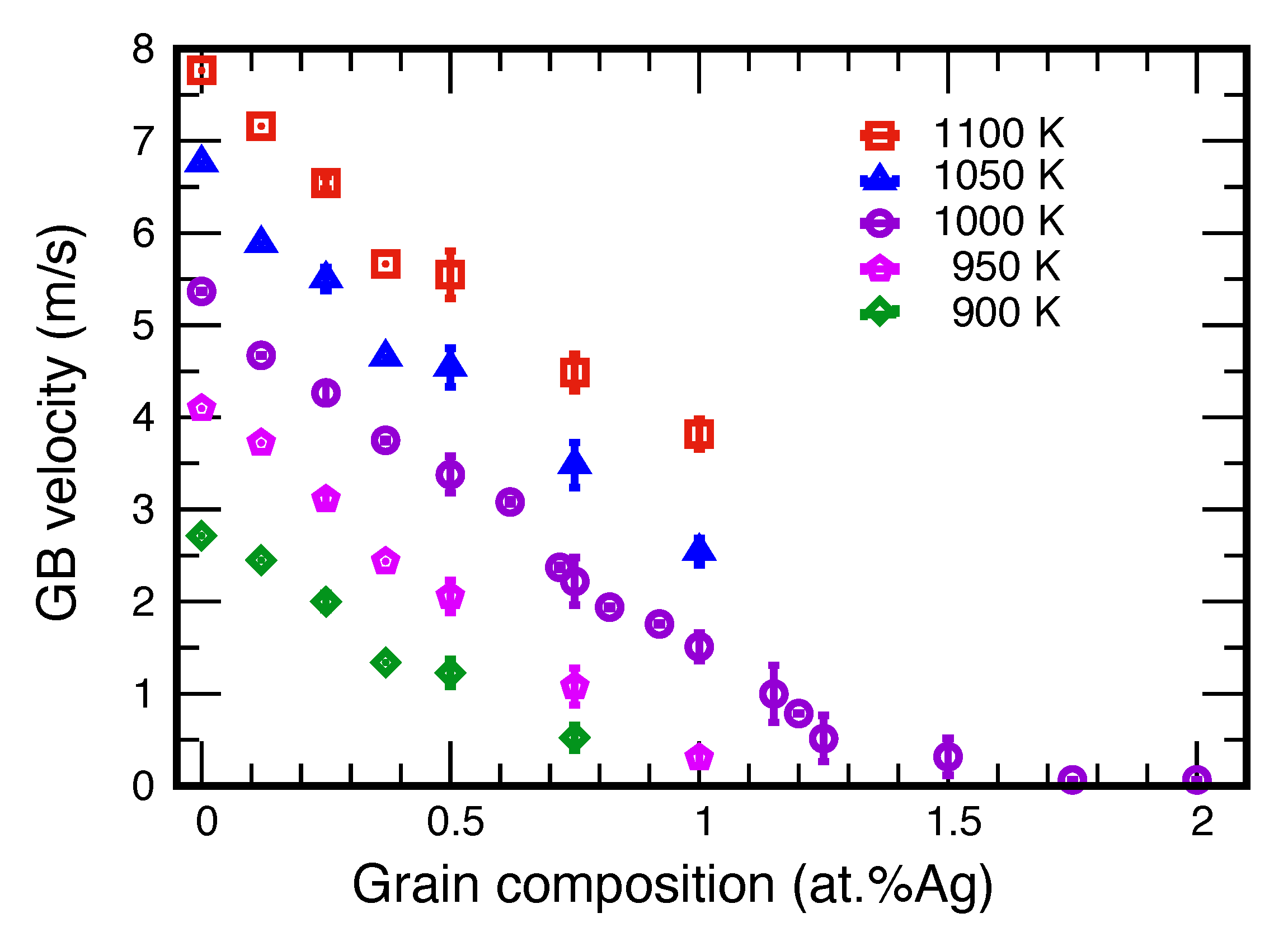
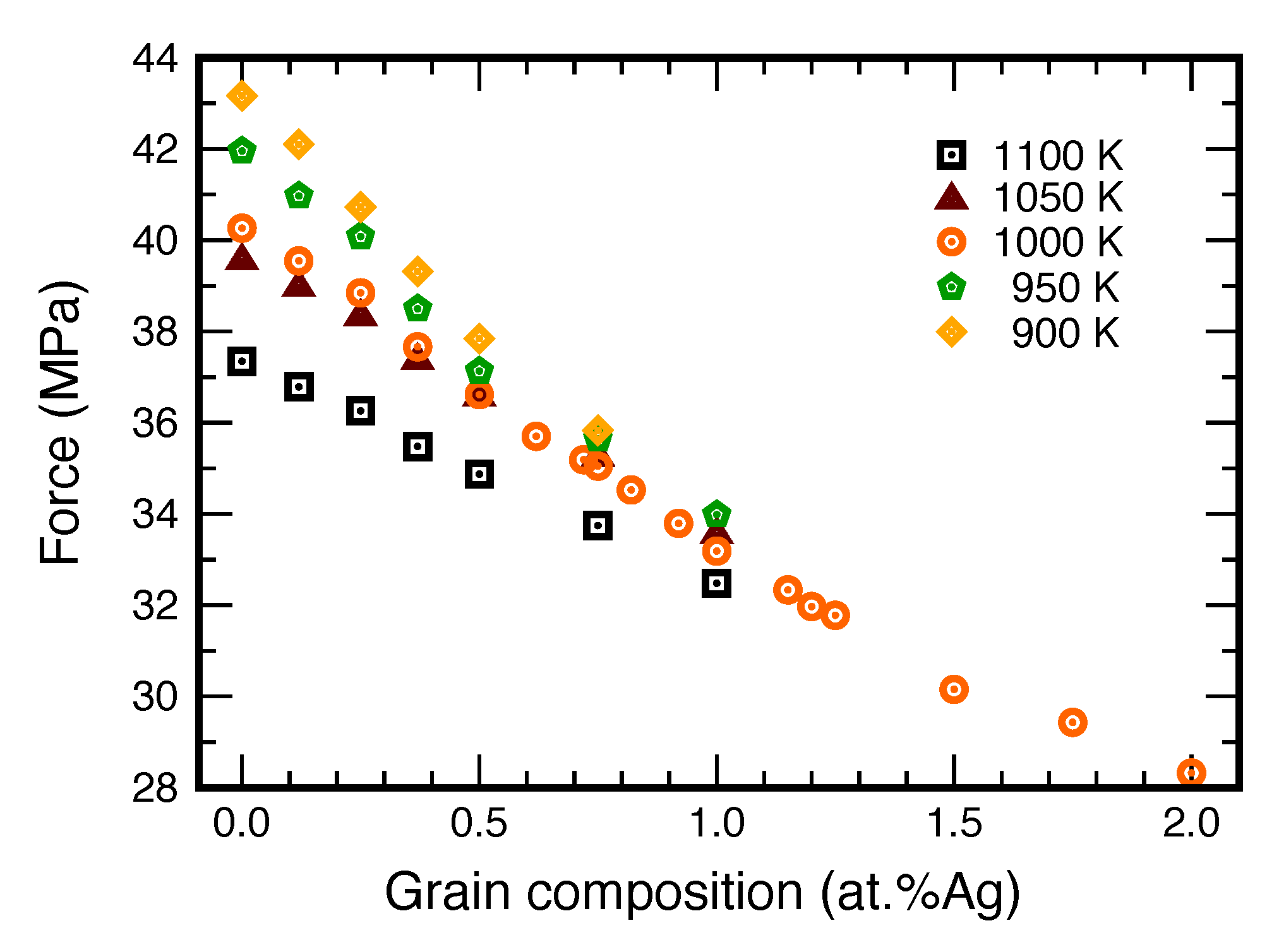
3.3. The Alloying Effect on GB Mobility
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gleiter, H. Nanostructured materials: Basic concepts and microscructure. Acta Mater. 2000, 48, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Materials; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Mishin, Y.; Asta, M.; Li, J. Atomistic modeling of interfaces and their impact on microstructure and properties. Acta Mater. 2010, 58, 1117–1151. [Google Scholar] [CrossRef] [Green Version]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Takeuchi, S. The mechanism of the inverse Hall-Petch relation of nano-crystals. Scr. Mater. 2001, 44, 1483–1487. [Google Scholar] [CrossRef]
- Margulies, L.; Winther, G.; Poulsen, H.F. In situ measurement of grain rotation during deformation of polycrystals. Science 2001, 291, 2392–2394. [Google Scholar] [CrossRef]
- Yue, L.; Zhang, H.; Li, D.Y. A closer look at the local responses of twin and grain boundaries in cu to stress at the nanoscale with possible transition from the P–H to the inverse P–H relation. Acta Mater. 2010, 58, 2677–2684. [Google Scholar] [CrossRef]
- Trautt, Z.T.; Mishin, Y. Grain boundary migration and grain rotation studied by molecular dynamics. Acta Mater. 2012, 60, 2407–2424. [Google Scholar] [CrossRef]
- Wu, Z.X.; Wang, Y.W.; Jhon, M.H.; Srolovitz, D.J. Anatomy of nano-material deformation: Grain boundary sliding, plasticity and cavitation in nanorystalline Ni. Acta Mater. 2013, 61, 5807–5820. [Google Scholar] [CrossRef]
- Li, J.; Soh, A.K. Synergy of grain boundary sliding and shear-coupled migration process in nanocrystalline materials. Acta Mater. 2013, 61, 5449–5457. [Google Scholar] [CrossRef]
- Chen, B.; Lutker, K.; Lei, J.; Yan, J.; Mao, H. Detecting grain rotation at the nanoscale. Proc. Natl. Acad. Sci. USA 2014, 111, 3350–3353. [Google Scholar] [CrossRef] [Green Version]
- Trautt, Z.T.; Mishin, Y. Capillary-driven grain boundary motion and grain rotation in a tricrystal: A molecular dynamics study. Acta Mater. 2014, 65, 19–31. [Google Scholar] [CrossRef]
- Han, X.; Wang, L.; Yue, Y.; Zhang, Z. In situ atomic scale mechanical microscopy discovering the atomistic mechanisms of plasticity in nano-single crystals and grain rotation in polycrystalline metals. Ultramicroscopy 2015, 151, 94–100. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Tamura, N.; Mi, Z.; Lei, J.; Yan, J.; Zhang, L.; Deng, W.; Ke, F.; Yue, B.; Chen, B. Reversal in the size dependence of grain rotation. Phys. Rev. Lett. 2017, 118, 096101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirchheim, R. Reducing grain boundary, dislocation line and vacancy formation energies by solute segregation. I. Theoretical background. Acta Mater. 2007, 55, 5129–5138. [Google Scholar] [CrossRef]
- Kirchheim, R. Reducing grain boundary, dislocation line and vacancy formation energies by solute segregation. II. Experimental evidence and consequences. Acta Mater. 2007, 55, 5139–5148. [Google Scholar] [CrossRef]
- Koch, C.C.; Scattergood, R.O.; Darling, K.A.; Semones, J.E. Stabilization of nanocrystalline grain sizes by solute additions. J. Mater. Sci. 2008, 43, 7264–7272. [Google Scholar] [CrossRef]
- Trelewicz, J.R.; Schuh, C.A. Grain boundary segregation and thermodynamically stable binary nanocrystalline alloys. Phys. Rev. B 2009, 79, 094112. [Google Scholar] [CrossRef]
- Chookajorn, T.; Murdoch, H.A.; Schuh, C.A. Design of stable nano-crystalline alloys. Science 2012, 337, 951–953. [Google Scholar] [CrossRef] [Green Version]
- Saber, M.; Kotan, H.; Koch, C.C.; Scattergood, R.O. Thermodynamic stabilization of nanocrystalline binary alloys. J. Appl. Phys. 2013, 113, 065515. [Google Scholar] [CrossRef]
- Murdoch, H.A.; Schuh, C.A. Stability of binary nanocrystalline alloys against grain growth and phase separation. Acta Mater. 2013, 61, 2121–2132. [Google Scholar] [CrossRef] [Green Version]
- Saber, M.; Kotan, H.; Koch, C.C.; Scattergood, R.O. A predictive model for thermodynamic stability of grain size in nanocrystalline ternary alloys. J. Appl. Phys. 2013, 114, 103510. [Google Scholar] [CrossRef]
- Chookajorn, T.; Schuh, C.A. Thermodynamics of stable nanocrystalline alloys: A Monte Carlo analysis. Phys. Rev. B 2014, 89, 064102. [Google Scholar] [CrossRef]
- Abdeljawad, F.; Foiles, S.M. Stabilization of nanocrystalline alloys via grain boundary segregation: A diffuse interface model. Acta Mater. 2015, 101, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Kalidindi, A.R.; Schuh, C.A. Stability criteria for nanocrystalline alloys. Acta Mater. 2017, 132, 128–137. [Google Scholar] [CrossRef]
- Kalidindi, T.C.A.R.; Schuh, C.A. Nanocrystalline materials at equilibrium: A thermodynamic review. JOM 2015, 67, 2834–2843. [Google Scholar] [CrossRef]
- Kalidindi, A.R.; Schuh, C.A. Phase transitions in stable nanocrystalline alloys. J. Mater. Res. 2017, 32, 1993–2002. [Google Scholar] [CrossRef] [Green Version]
- Abdeljawad, F.; Lu, P.; Argibay, N.; Clark, B.G.; Boyce, B.L.; Foiles, S.M. Grain boundary segregation in immiscible nanocrystalline alloys. Acta Mater. 2017, 126, 528–539. [Google Scholar] [CrossRef] [Green Version]
- Cahn, J.W. The impurity-drag effect in grain boundary motion. Acta Metall. 1962, 10, 789–798. [Google Scholar] [CrossRef]
- Ma, N.; Dregia, S.A.; Wang, Y. Solute segregation transition and drag force on grain boundaries. Acta Mater. 2003, 51, 3687–3700. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Capdevila, C.; Pimentel, G.; De Andres, C.G. Drag effects on grain growth dynamics. Comp. Mater. Sci. 2013, 68, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Nes, E.; Ryum, N.; Hunderi, O. On the Zener drag. Acta Metall. 1985, 33, 11–22. [Google Scholar] [CrossRef]
- Li, W.B.; Easterling, K.E. The influence of particle shape on Zener drag. Acta Metall. Mater. 1990, 38, 1045–1052. [Google Scholar] [CrossRef]
- Manohar, P.A.; Ferry, M.; Chandra, T. Five decades of the Zener equation. ISIJ Int. 1998, 38, 913–924. [Google Scholar] [CrossRef] [Green Version]
- Miodownik, M.; Holm, E.A.; Hassold, G.N. Highly parallel computer simulations of particle pinning: Zener vindicated. Scr. Mater. 2000, 42, 1173–1177. [Google Scholar] [CrossRef]
- Di Prinzio, C.L.; Druetta, E.; Nasello, O.B. More about Zener drag studies with Monte Carlo simulations. Model. Simul. Mater. Sci. Eng. 2013, 21, 025007. [Google Scholar] [CrossRef]
- Koju, R.; Darling, K.; Kecskes, L.J.; Mishin, Y. Zener pinning of grain boundaries and structural stability of immiscible alloys. JOM 2016, 68, 1596–1604. [Google Scholar] [CrossRef]
- Frolov, T.; Darling, K.A.; Kecskes, L.J.; Mishin, Y. Stabilization and strengthening of nanocrystalline copper by alloying with tantalum. Acta Mater. 2012, 60, 2158–2168. [Google Scholar] [CrossRef]
- Darling, K.A.; Roberts, A.J.; Mishin, Y.; Mathaudhu, S.N.; Kecskes, L.J. Grain size stabilization of nanocrystalline copper at high temperatures by alloying with tantalum. J. Alloy. Comp. 2013, 573, 142–150. [Google Scholar] [CrossRef]
- Darling, K.; Tschopp, M.; Guduru, R.; Yin, W.; Wei, Q.; Kecskes, L. Microstructure and mechanical properties of bulk nanostructured Cu–Ta alloys consolidated by equal channel angular extrusion. Acta Mater. 2014, 76, 168–185. [Google Scholar] [CrossRef]
- Purja Pun, G.P.; Darling, K.A.; Kecskes, L.J.; Mishin, Y. Angular-dependent interatomic potential for the Cu–Ta system and its application to structural stability of nano-crystalline alloys. Acta Mater. 2015, 100, 377–391. [Google Scholar] [CrossRef]
- Rojhirunsakool, T.; Darling, K.A.; Tschopp, M.A.; Pun, G.P.P.; Mishin, Y.; Banerjee, R.; Kecskes, L.J. Structure and thermal decomposition of a nanocrystalline mechanically alloyed supersaturated Cu–Ta solid solution. MRS Commun. 2015, 5, 333–339. [Google Scholar] [CrossRef]
- Hornbuckle, B.C.; Rojhirunsakool, T.; Rajagopalan, M.; Alam, T.; Purja Pun, G.P.; Banerjee, R.; Solanki, K.N.; Mishin, Y.; Kecskes, L.J.; Darling, K.A. Effect of Ta solute concentration on the microstructural evolution in immiscible Cu-Ta alloys. JOM 2015, 67, 2802–2809. [Google Scholar] [CrossRef]
- Rajagopalan, M.; Darling, K.; Turnage, S.; Koju, R.; Hornbuckle, B.; Mishin, Y.; Solanki, K. Microstructural evolution in a nanocrystalline Cu-Ta alloy: A combined in-situ TEM and atomistic study. Mater. Des. 2017, 113, 178–185. [Google Scholar] [CrossRef]
- Koju, R.K.; Darling, K.A.; Solanki, K.N.; Mishin, Y. Atomistic modeling of capillary-driven grain boundary motion in Cu-Ta alloys. Acta Mater. 2018, 148, 311–319. [Google Scholar] [CrossRef]
- Darling, K.A.; Srinivasan, S.; Koju, R.K.; Hornbuckle, B.C.; Smeltzer, J.; Mishin, Y.; Solanki, K.N. Stress-driven grain refinement in a microstructurally stable nanocrystalline binary alloy. Scr. Mater. 2021, 191, 185–190. [Google Scholar] [CrossRef]
- Darling, K.A.; Rajagopalan, M.; Komarasamy, M.; Bhatia, M.A.; Hornbuckle, B.C.; Mishra, R.S.; Solanki, K.N. Extreme creep resistance in a microstructurally stable nanocrystalline alloy. Nature 2016, 537, 378–381. [Google Scholar] [CrossRef]
- Lücke, K.; Stüwe, H.P. On the theory of grain boundary motion. In Recovery and Recrystallization of Metals; Himmel, L., Ed.; Interscience Publishers: New York, NY, USA, 1963; pp. 171–210. [Google Scholar]
- Lücke, K.; Stüwe, H.P. On the theory of impurity controlled grain boundary motion. Acta Metall. 1971, 19, 1087–1099. [Google Scholar] [CrossRef]
- Koju, R.; Mishin, Y. Direct atomistic modeling of solute drag by moving grain boundaries. Acta Mater. 2020, 198, 111–120. [Google Scholar] [CrossRef]
- Kaur, I.; Mishin, Y.; Gust, W. Fundamentals of Grain and Interphase Boundary Diffusion; Wiley: Chichester, UK, 1995. [Google Scholar]
- Mishin, Y. An atomistic view of grain boundary diffusion. Defect Diffus. Forum 2015, 363, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Williams, P.L.; Mishin, Y. Thermodynamics of grain boundary premelting in alloys. II. Atomistic simulation. Acta Mater. 2009, 57, 3786–3794. [Google Scholar] [CrossRef]
- Hickman, J.; Mishin, Y. Disjoining potential and grain boundary premelting in binary alloys. Phys. Rev. B 2016, 93, 224108. [Google Scholar] [CrossRef] [Green Version]
- Koju, R.K.; Mishin, Y. Relationship between grain boundary segregation and grain boundary diffusion in Cu-Ag alloys. Phys. Rev. Mater. 2020, 4, 073403. [Google Scholar] [CrossRef]
- Williams, P.L.; Mishin, Y.; Hamilton, J.C. An embedded-atom potential for the Cu-Ag system. Model. Simul. Mater. Sci. Eng. 2006, 14, 817–833. [Google Scholar] [CrossRef]
- Upmanyu, M.; Smith, R.W.; Srolovitz, D.J. Atomistic simulation of curvature driven grain boundary migration. Interface Sci. 1998, 6, 41–58. [Google Scholar] [CrossRef]
- Zhang, H.; Upmanyu, M.; Srolovitz, D.J. Curvature driven grain boundary migration in aluminum: Molecular dynamics simulations. Acta Mater. 2005, 53, 79–86. [Google Scholar] [CrossRef]
- Zepeda-Ruiz, L.A.; Gilmer, G.H.; Sadigh, B.; Caro, A.; Oppelstrup, T.; Hamza, A.V. Atomistic simulations of grain boundary pinning in cufe alloys. Appl. Phys. Lett. 2005, 87, 231904. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Zhang, S.; Wang, X.; Zhao, B.; Dong, X.; Zhang, L. Interaction between coherent second-phase particles and migrating boundaries: Boundary effect and particle reorientation. Scr. Mater. 2016, 116, 100–103. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285–1288. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Yamakov, V. The ParaGrandMC Code Can Be Obtained from the NASA Software Catalog. NASA/CR–2016-219202 (2016). Available online: Https://software.nasa.gov/software/LAR-18773-1 (accessed on 1 February 2016).
- Yamakov, V.; Hochhalter, J.D.; Leser, W.P.; Warner, J.E.; Newman, J.A.; Purja Pun, G.P.; Mishin, Y. Multiscale modeling of sensory properties of Co–Ni–Al shape memory particles embedded in an Al metal matrix. J. Mater. Sci. 2016, 51, 1204–1216. [Google Scholar] [CrossRef]
- Purja Pun, G.P.; Yamakov, V.; Mishin, Y. Interatomic potential for the ternary Ni–Al–Co system and application to atomistic modeling of the B2–L10 martensitic transformation. Model. Simul. Mater. Sci. Eng. 2015, 23, 065006. [Google Scholar] [CrossRef] [Green Version]
- Cahn, J.W.; Mishin, Y.; Suzuki, A. Coupling grain boundary motion to shear deformation. Acta Mater. 2006, 54, 4953–4975. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Cahn, J.W.; Taylor, J.E. A unified approach to motion of grain boundaries, relative tangential translation along grain boundaries, and grain rotation. Acta Mater. 2004, 52, 4887–4998. [Google Scholar] [CrossRef]
- Chen, K.; Han, J.; Pan, X.; Srolovitz, D.J. The grain boundary mobility tensor. Proc. Natl. Acad. Sci. USA 2020, 117, 4533. [Google Scholar] [CrossRef]
- Schönfelder, B.; Gottstein, G.; Schvindlerman, L.S. Comparative study of grain-boundary migration and grain-boundary diffusion of [001] twist-grain boundaries in copper by atomistic simulation. Acta Mater. 2005, 53, 1597–1609. [Google Scholar] [CrossRef]
- Schönfelder, B.; Gottstein, G.; Schvindlerman, L.S. Atomistic simulation of grain boundary migration in copper. Metall. Mater. Trans. A 2006, 37, 1757–1771. [Google Scholar] [CrossRef]
- Zhang, H.; Srolovitz, D.J.; Douglas, J.F.; Warren, J.A. Characterization of atomic motion governing grain boundary migration. Phys. Rev. B 2006, 74, 115404. [Google Scholar] [CrossRef]
- Balluffi, R.W. Vacancy defect mobilities and binding energies obtained from annealing studies. J. Nucl. Mater. 1978, 69–70, 240–263. [Google Scholar] [CrossRef]
- Surholt, T.; Herzig, C. Grain boundary self-diffusion in Cu polycrystals of different purity. Acta Mater. 1997, 45, 3817–3823. [Google Scholar] [CrossRef]
- Mishin, Y.; Herzig, C.; Bernardini, J.; Gust, W. Grain boundary diffusion: Fundamentals to recent developments. Int. Mater. Rev. 1997, 42, 155. [Google Scholar] [CrossRef]
- Mishin, Y.; Herzig, C. Grain boundary diffusion: Recent progress and future research. Mater. Sci. Eng. A 1999, 260, 55–71. [Google Scholar] [CrossRef]
- Frolov, T.; Divinski, S.V.; Asta, M.; Mishin, Y. Effect of interface phase transformations on diffusion and segregation in high-angle grain boundaries. Phys. Rev. Lett. 2013, 110, 255502. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, A.; Mishin, Y. Atomistic modeling of point defects and diffusion in copper grain boundaries. Interface Sci. 2003, 11, 131–148. [Google Scholar] [CrossRef]
- Vanossi, A.; Manini, N.; Urbakh, M.; Zapperi, S.; Tosatti, E. Colloquium: Modeling friction: From nanoscale to mesoscale. Rev. Mod. Phys. 2013, 85, 529–552. [Google Scholar] [CrossRef] [Green Version]
- Frolov, T.; Mishin, Y. Thermodynamics of coherent interfaces under mechanical stresses. I. Theory. Phys. Rev. B 2012, 85, 224106. [Google Scholar] [CrossRef] [Green Version]
- Frolov, T.; Mishin, Y. Thermodynamics of coherent interfaces under mechanical stresses. II. Application to atomistic simulation of grain boundaries. Phys. Rev. B 2012, 85, 224107. [Google Scholar] [CrossRef] [Green Version]
- Foiles, S.M. Temperature dependence of grain boundary free energy and elastic constants. Scr. Mater. 2010, 62, 231–234. [Google Scholar] [CrossRef]
- Frolov, T.; Asta, M.; Mishin, Y. Segregation-induced phase transformations in grain boundaries. Phys. Rev. B 2015, 92, 020103. [Google Scholar] [CrossRef] [Green Version]
- Mishin, Y. Solute drag and dynamic phase transformations in moving grain boundaries. Acta Mater. 2019, 179, 383–395. [Google Scholar] [CrossRef] [Green Version]
- Janssens, K.G.F.; Olmsted, D.; Holm, E.A.; Foiles, S.M.; Plimpton, S.J.; Derlet, P.M. Computing the mobility of grain boundaries. Nat. Mater. 2006, 5, 124–127. [Google Scholar] [CrossRef]
- Race, C.P.; von Pezold, J.; Neugebauer, J. Role of the mesoscale in migration kinetics of flat grain boundaries. Phys. Rev. B 2014, 89, 214110. [Google Scholar] [CrossRef]
- Race, C.P.; Hadian, R.; von Pezold, J.; Grabowski, B.; Neugebauer, J. Mechanisms and kinetics of the migration of grain boundaries containing extended defects. Phys. Rev. B 2015, 92, 174115. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koju, R.K.; Mishin, Y. The Role of Grain Boundary Diffusion in the Solute Drag Effect. Nanomaterials 2021, 11, 2348. https://doi.org/10.3390/nano11092348
Koju RK, Mishin Y. The Role of Grain Boundary Diffusion in the Solute Drag Effect. Nanomaterials. 2021; 11(9):2348. https://doi.org/10.3390/nano11092348
Chicago/Turabian StyleKoju, R. K., and Y. Mishin. 2021. "The Role of Grain Boundary Diffusion in the Solute Drag Effect" Nanomaterials 11, no. 9: 2348. https://doi.org/10.3390/nano11092348
APA StyleKoju, R. K., & Mishin, Y. (2021). The Role of Grain Boundary Diffusion in the Solute Drag Effect. Nanomaterials, 11(9), 2348. https://doi.org/10.3390/nano11092348




