Abstract
Magnetic two-dimensional (2D) van der Waals materials have attracted tremendous attention because of their high potential in spintronics. In particular, the quantum anomalous Hall (QAH) effect in magnetic 2D layers shows a very promising prospect for hosting Majorana zero modes at the topologically protected edge states in proximity to superconductors. However, the QAH effect has not yet been experimentally realized in monolayer systems to date. In this work, we study the electronic structures and topological properties of the 2D ferromagnetic transition-metal dichalcogenides (TMD) monolayer by first-principles calculations with the Heyd–Scuseria–Ernzerhof (HSE) functional. We find that the spin-orbit coupling (SOC) opens a continuous band gap at the magnetic Weyl-like crossing point hosting the quantum anomalous Hall effect with Chern number . Moreover, we demonstrate the topologically protected edge states and intrinsic (spin) Hall conductivity in this magnetic 2D TMD system. Our results indicate that monolayer serves as a stoichiometric quantum anomalous Hall material.
1. Introduction
Topological phase has been one of the main themes in solid-state physics and materials science in the past decade. Especially, topological materials have—in view of their robust topological surface or edge states—shown great promise in spintronics. Since the study of graphene, Haldane shows that the Landau level can be presented in graphene if including an external term [1] such as the spin-orbital coupling (SOC), which is now known as the quantum spin Hall effect or topological insulators [2]. After that, different kinds of topological phase and band inversion induced by various sources have been proposed. The discovery of tuning topological phases, whether through spin-orbital coupling (HgTe quantum well state [3] and [4]), electron–phonon coupling (BiTeI [5]), ion doping ( [6]), and external strain ( [7], HgSe monolayer [8]), has opened new routes to control phases and transport properties.
In particular, the quantum anomalous Hall (QAH) effect, which presents topological properties in time-reversal symmetry breaking systems, has been reported in [9], [10,11], and [12]. Moreover, Majorana fermion mode has been demonstrated experimentally in heterostructures with quantum anomalous Hall materials adjacent to superconductors through proximity effects [13]. However, the QAH effect, the topological phase with magnetism, has not been realized experimentally in monolayer materials by far.
Novel magnetic two-dimensional (2D) materials, another widely studied class of layered materials bounded by van der Waals force, have attracted increasing attention in recent years owing to the great potential for spintronic applications. A number of monolayer magnetic materials, such as [14,15], [16], [17], and [18] have been realized in experiments. Particularly, presents ferromagnetic properties with the Curie temperature [14] above room temperature (RT). has also been shown to exhibit the charge density wave (CDW) phase below 130 K [14,15,19]. The wide temperature range for the ferromagnetic phase from 130 K up to RT achieves a high potential candidate for fulfilling the QAH effect in a single TMD layer. It is, thus, important to study the topological properties and Hall conductivity in monolayer for it can open up a new route to spintronics, QAH, and even the Majorana physics.
In this work, we study the topological properties, Hall conductivity, and spin Hall conductivity in magnetic TMD monolayer via first-principle calculations based on density functional theory (DFT) with the hybrid Heyd–Scuseria–Ernzerhof (HSE) exchange-correlation functional. We show that magnetic monolayer exhibits a continuous band gap opened at the Weyl-like crossing point due to the spin-orbit coupling (SOC), leading to the topological phase with Chern number . We also demonstrate the quantum anomalous Hall (QAH) effect given from the topologically protected edge states. Finally, we present our calculated Hall conductivity and spin Hall conductivity for future experiments to examine such transport properties in monolayer .
2. Method
The first-principles calculations of monolayer are performed using the full-potential projected augmented wave method as implemented in the Vienna Ab-initio Simulation Package (VASP) [20,21] based on the density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) type [22] generalized-gradient-approximation (GGA) functional. The Heyd–Scuseria–Ernzerhof (HSE06) [23] hybrid exchange-correlation functional is adopted to correct the band gap problem. The () grids with the energy cut-off of 400 eV are used in PBE (HSE) simulations. Atomic positions are optimized with the residual force less than 0.02 eV/Å. The Wannier wave-functions and tight-binding Hamiltonian are constructed from V and Se orbitals based on the DFT results using the vasp2wannier90 interface [24]. The band structures and edge states of ribbon are calculated using the semi-infinite Green function simulations with the Sancho–Rubio method [25].
To carry out the Wilson loop [26,27] and Hall conductivity, we start with the Berry phase [28] by
Here, is the wave-function of the mth band at point. Then, the Berry curvature of the mth band, , is calculated via the Stokes’ theorem
The intrinsic Hall conductivity of energy E and temperature T is just the integral over Brillouin zone (BZ) [29], that is
Here is the Fermi–Dirac distribution. The grids are used for Hall conductivity calculations in this work.
3. Result and Discussion
Figure 1a,b show the lattice structure of monolayer. Similar to other transition metal dichalcogenides in the phase, the transition metal atom, vanadium (V), locates at the center plane sandwiched between two chalcogen anions, selenium (Se). By adopting the experimental lattice constant 3.36 Å [14,30], the optimized V–Se bond length is 2.49 Å with the corresponding interlayer distance being 1.56 Å.
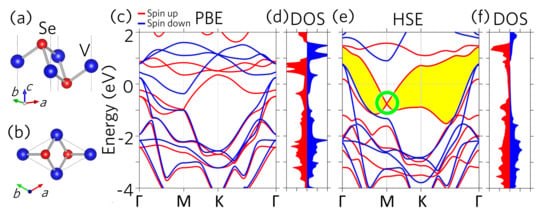
Figure 1.
(a) Side-view and (b) top-view of the monolayer lattice structure. (c) Band structures given from PBE simulations. The red (blue) lines indicate the spin up (down) bands. (d) Density of states (DOS) from PBE. The red (blue) region presents the spin up (down) contributions. (e) Band structures and (f) DOS obtained using HSE functional. The green circle indicates the Weyl point (WP).
Figure 1c,d illustrate the band structures and density of states (DOS) given from the PBE calculations, respectively. The electronic bands near the Fermi level (above eV) are mainly contributed from V orbitals. Owing to the broken time-reversal symmetry, the spin up (red) and spin down (blue) bands are relatively shifted due to the Zeeman effect in the V orbitals. The exchange splitting around the Fermi level is roughly 1 eV, leading to the magnetic moment of 0.71 per V ion. As for the Se orbitals, which contributes mainly below eV, the band splitting between the spin up and spin down channels are thus much weaker due to the trivial Zeeman effect therein.
The exchange-correlation potential and band gap are usually underestimated in DFT simulations [31], including the local-density approximation (LDA) and PBE functional. Although LDA (PBE) underestimates band gaps due to the self-interaction problem, the Hartree–Fock approach, on the other hand, overestimates band gaps because no correlation is considered. Therefore, the Heyd–Scuseria–Ernzerhof (HSE06) [23] hybrid exchange-correlation functional is usually adopted to correct the band gap problem by adding a portion of Hartree–Fock exact exchange functional to PBE (LDA). The HSE hybrid functional has been widely used in 2D material simulations [32,33,34,35] for obtaining correct results in comparison with experimental observations. Consequently, we also perform HSE calculations to avoid possible band gap problems in this work as discussed below.
Figure 1e,f show the HSE band structures and DOS, respectively. As expected, the band gaps are significantly enhanced by the HSE functional, especially around the Fermi level. In particular, there opens up a continuous band gap, as shown in the yellow region (Figure 1e). Accordingly, the DOS peaks of V orbitals are pushed away from the Fermi level, resulting in the enhanced magnetic moment of 1.1 per V ion. A remarkable emerging feature is the band crossing at the M point by two spin up single bands at the energy of eV as highlighted by the green circle in Figure 1c. Some of the previous works have named such crossings in 2D systems as Weyl points [36,37,38], even though the Weyl point was originally defined in three-dimensional materials [39]. In this work, following previous works, we hereafter call this band crossing as the Weyl point. Our analysis as discussed below also shows band inversions around the Weyl point, implying that a topological phase occur in this TMD monolayer, similar to the two bands crossing at K points in graphene [2] and Xene monolayer [40].
To study the topological phase of monolayer , we include the spin–orbit coupling (SOC) in the self-consistent-field calculations using the HSE functional. As shown in Figure 2a, the SOC opens up an energy gap at the Weyl point, forming a complete continuous band gap (the yellow region) through out the Brillouin Zone (BZ). Consequently, the topological behavior can be well defined below this continuous band gap by performing the Wilson loop calculations. The Wilson loop [26,27] (also known as Wannier charge center, WCC [27]) simulations for Chern number are shown in Figure 2b. Different from the topological index, which can only be 0 or 1, the Chern number of QAH effect can be any non-negative integer , such as 0, 1, 2, and 3, etc. As can be seen in Figure 2b, the Berry phase winds for two times when going through the first Brillouin zone, indicating that the Chern number is two (). On the contrary, the Wilson loop simulations using PBE functional with SOC result in the Chern number as shown in Supporting Materials. This indicates that the PBE functional, which underestimate the band gap, gives a topologically trivial normal magnetic metal ground state for monolayer . Further, the two sharp slopes in the Wilson loop simulations based on HSE results as highlighted by the red arrows in Figure 2b indicates that the Berry curvatures originate from the and M points. Our Wilson loop simulations evidence that the monolayer is a QAH material with the topological invariant , that is, two topologically protected edge states can be found at the layer boundary.
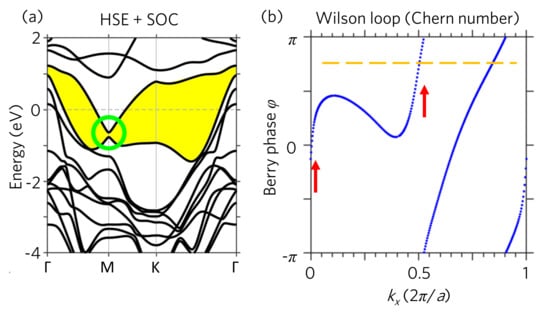
Figure 2.
(a) HSE+SOC band structure of monolayer . The yellow region presents the continuous band gap and the green circle indicates the SOC band gap. (b) Wilson loop of monolayer with HSE functional and SOC. The red arrows highlight the sharp slope in the Wilson loop. The two crossings through the reference line (the orange dashed line) indicate that the Chern number is two ().
To show the topological edge states on the (010) boundary of the ribbon, we perform the semi-infinite Green function calculations. Figure 3a illustrates the relation between the 2D and 1D BZ of monolayer and (010) ribbon, respectively. The M point in the 2D BZ projects to the point of the (010) 1D BZ. The and M points project to the point of the (010) 1D BZ. The band structure of the 2D monolayer is depicted in Figure 3b. The green circle in Figure 3b highlight the SOC band gap at the M point corresponding to that shown in Figure 2a. In comparison with the band structure of the 1D (010) ribbon shown in Figure 3c, one can clearly identify four edge states. Among them, two edge states indicated by red arrows (1) and (2) connecting the conduction and valence bands are topologically non-trivial. Whereas the other two edge states indicated by yellow arrows (3) and (4) are topologically trivial. The edge state (3), which is coincident with the 2D bulk band edge as compared with Figure 3b, can be identified as the edge resonance state. Although the edge state (4) connecting the conduction band at to the conduction band at is thus a topologically trivial edge state. Our Green-function simulations present two topological edge states in good consistency with our Wilson loop simulations discussed in the last paragraph.
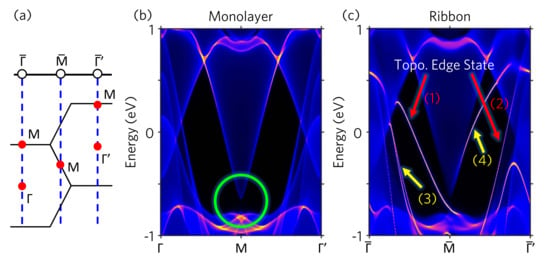
Figure 3.
(a) 2D and 1D Brillouin zone of monolayer and ribbon at the (010) edge, respectively. The blue dash lines indicate the relation between the high symmetry points in the 2D and 1D BZ. (b) Band structure of monolayer from the semi-infinite Green functions method. (c) Band structure of ribbon from the semi-infinite Green functions method. In comparison with (b), four edge states (bright yellow curves) can be identified. Two of them are topological edge states as indicated by the red arrows (1) and (2). The other two edge states are topologically trivial as indicated by yellow arrows (3) and (4).
To detect the edge states of two-dimensional materials is a great challenge in experiments. However, the Hall conductivity and spin Hall conductivity measurements serve as a much more viable approach for evidencing the edge states. The intrinsic Hall conductivity can be obtained from the Hall conductivity of spin up and down channels via
Here the () is the intrinsic Hall conductivity of the spin up (down) channel, which can be calculated through the Berry curvature calculations as described in the Section 2. In addition, the intrinsic spin Hall conductivity is defined by
In this work, we focus on the ferromagnetic phase of monolayer , i.e., below the Curie temperature [14] while above the CDW phase transition at [14]. Therefore, we consider an intermediate temperature for the Fermi-Dirac distributions in Equation (3).
The calculated intrinsic Hall conductivity of monolayer from PBE is presented in Figure 4a. The Hall conductivity of both the spin up and down channels are nearly zero, indicating the topological trivial phase given from PBE. This is consistent with the zero Chern number discussed in our previous Wilson loop calculation using PBE. As the HSE hybrid exchange-correlation potentials are taken into consideration, significant Hall conductivity emerges in the spin up channel owing to the topological non-trivial Chern number of , as shown in Figure 4b. The Hall conductivity curve shows a peak value of 1.25 (or ) at the band crossing energy, as indicated by green arrow in Figure 4b. It is worth noting that this value is not equal to two because the band splitting in happens within a continuous energy gap rather than within a full band gap. The Hall conductivity integral (Equation (3)) over the energy instead of over band numbers thus does not yield a corresponding integer number. As the energy increases, the Hall conductivity decreases, leaving a smaller value of 0.67 (or ) at the Fermi level. On the other hand, the Hall conductivity of the spin down channel, which is topologically trivial, remains zero (Figure 4c). Based on the HSE results, we conclude the following relation for the Hall conductivity of :

Figure 4.
The intrinsic Hall conductivity from DFT simulations with temperature . (a) The Hall conductivity of spin up and down electrons from PBE simulations. The left (right) axis show the Hall conductivity in the unit (). (b,c) The Hall conductivity of spin up and down electrons from HSE simulations. The green arrow highlights the peak enhanced by the band crossing point.
This relation presents a clear route to experimentally examine the topological properties of the 2D TMD material in the phase.
A large number of recent studies have demonstrated various classes of topological phases with magnetism both experimentally [9,10,11,12,41,42] and theoretically [43,44,45,46,47,48,49]. However, 2D monolayer materials with quantum anomalous Hall effect have not been shown by experiments to date. On the other hand, there have been several DFT simulations for and [50,51], but the topological phase has not been report yet. The Hall conductivity study on monolayer [52] shows that , implying that is topologically trivial. Our results thus provide a timely interesting results for the topological phases in 2D TMD materials with magnetism, and thus invite future theoretical and experimental studies toward this direction.
4. Conclusions
In summary, we propose that monolayer is a quantum anomalous Hall (QAH) semimetal with the same Hall conductivity and spin Hall conductivity, i.e., the same charge Hall current and spin Hall current. The HSE hybrid exchange-correlation functional demonstrate a topological phase with Chern number in monolayer, resulting in a 2D QAH semimetal. We present 2 topological edge states for the ribbon, intrinsic Hall conductivity , and intrinsic spin Hall conductivity . We confirm that this intrinsic spin Hall conductivity is robust against the temperature variation for it appears in a wide range of several eV near the Fermi level (see Figure 4b). This indicates that is a good candidate for experimentally realizing 2D QAH at room temperature and, thus, is highly applicable in spintronics device based on topological and Hall properties [53,54,55]. Previous study has discovered the external-magnetic-field dependent conductivity, which implies anomalous Hall conductivity [15]. This is consistent with our finding, and thus could be a new kind of stoichiometric quantum anomalous Hall material. The intrinsic quantum anomalous hall effect has been reported in twisted bilayer graphene experiment with very low [56]. Our study demonstrates that the anomalous Hall conductivity and spin anomalous Hall conductivity can be observed in with , which opens up a new route to room-temperature spintronics. Moreover, our study can also be extended to other two-dimensional magnetic materials, such as , , and .
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/nano11081998/s1. Figure S1: The band structures and the Wilson loop simulations of monolayer 1T-VSe2 with PBE exchange-correlation potential and spin-orbital coupling. (a) The band structure. The yellow region indicates continuous band gap. (b) The Wilson loop result, without crossing along the reference line (the orange dashed line), shown the Chern number C = 0 in PBE simulations; Figure S2: The Hall conductivity of monolayer 1T-VSe2 with different temperatures, from HSE result. (a) (b) Spin up and down channel with T = 150 K. (c) (d) Spin up and down channel with T = 300 K.
Author Contributions
Conceptualization, A.H., C.-H.C. (Ching-Hao Chang), H.-T.J.; methodology and first-principles calculations, A.H., C.-H.C. (Chin-Hsuan Chen); writing, A.H., H.-T.J.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is available on reasonable request from the corresponding author.
Acknowledgments
This work was supported by the Ministry of Science and Technology, Taiwan. J.H.T. also thanks support from NCHC, CINC-NTU, AS-iMATE-109-13, and CQT-NTHU-MOE, Taiwan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haldane, F.D.M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015–2018. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [Green Version]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.L.; Analytis, J.G.; Chu, J.H.; Liu, Z.K.; Mo, S.K.; Qi, X.L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z.; et al. Experimental Realization of a Three-Dimensional Topological Insulator, Bi2Te3. Science 2009, 325, 178–181. [Google Scholar] [CrossRef] [Green Version]
- Brousseau-Couture, V.; Antonius, G.; Côté, M. Temperature dependence of the topological phase transition of BiTeI from first principles. Phys. Rev. Res. 2020, 2, 023185. [Google Scholar] [CrossRef]
- Chang, T.R.; Xu, S.Y.; Chang, G.; Lee, C.C.; Huang, S.M.; Wang, B.; Bian, G.; Zheng, H.; Sanchez, D.S.; Belopolski, I.; et al. Prediction of an arc-tunable Weyl Fermion metallic state in MoxW1-xTe2. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Li, Y.Y.; Rajput, S.; Gilks, D.; Lari, L.; Galindo, P.L.; Weinert, M.; Lazarov, V.K.; Li, L. Tuning Dirac states by strain in the topological insulator Bi2Se3. Nat. Phys. 2014, 10, 294–299. [Google Scholar] [CrossRef]
- Li, S.S.; Ji, W.X.; Zhang, C.W.; Li, P.; Wang, P.J. Robust room-temperature inversion-asymmetry topological transitions in functionalized HgSe monolayer. J. Mater. Chem. C 2016, 4, 2243–2251. [Google Scholar] [CrossRef]
- Chang, C.Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Yu, Y.; Shi, M.Z.; Guo, Z.; Xu, Z.; Wang, J.; Chen, X.H.; Zhang, Y. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895–900. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, Y.; Du, S.; Wang, Z.; Gu, B.L.; Zhang, S.C.; He, K.; Duan, W.; Xu, Y. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 2019, 5, eaaw5685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, J.X.; Ma, W.; Cochran, T.A.; Xu, X.; Zhang, S.S.; Tien, H.J.; Shumiya, N.; Cheng, G.; Jiang, K.; Lian, B.; et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 2020, 583, 533–536. [Google Scholar] [CrossRef] [PubMed]
- He, Q.L.; Pan, L.; Stern, A.L.; Burks, E.C.; Che, X.; Yin, G.; Wang, J.; Lian, B.; Zhou, Q.; Choi, E.S.; et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 2017, 357, 294–299. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Li, J.; Herng, T.S.; Wang, Z.; Zhao, X.; Chi, X.; Fu, W.; Abdelwahab, I.; Zhou, J.; Dan, J.; et al. Chemically Exfoliated VSe2 Monolayers with Room-Temperature Ferromagnetism. Adv. Mater. 2019, 31, 1903779. [Google Scholar] [CrossRef]
- Bonilla, M.; Kolekar, S.; Ma, Y.; Diaz, H.C.; Kalappattil, V.; Das, R.; Eggers, T.; Gutierrez, H.R.; Phan, M.H.; Batzill, M. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 2018, 13, 289–293. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef] [Green Version]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Yu, Y.; Song, Y.; Zhang, J.; Wang, N.Z.; Sun, Z.; Yi, Y.; Wu, Y.Z.; Wu, S.; Zhu, J.; et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 2018, 563, 94–99. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Howard, S.T.; Maghirang, A.B.; Nguyen Cong, K.; Villaos, R.A.B.; Feng, L.Y.; Cai, K.; Ganguli, S.C.; Swiech, W.; Morosan, E.; et al. Correlating structural, electronic, and magnetic properties of epitaxial VSe2 thin films. Phys. Rev. B 2020, 102, 115149. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Franchini, C.; Kováčik, R.; Marsman, M.; Murthy, S.S.; He, J.; Ederer, C.; Kresse, G. Maximally localized Wannier functions in LaMnO3 within PBE + U, hybrid functionals and partially self-consistent GW: An efficient route to construct ab initio tight-binding parameters for eg perovskites. J. Phys. Condens. Matter 2012, 24, 235602. [Google Scholar] [CrossRef] [Green Version]
- Sancho, M.P.L.; Sancho, J.M.L.; Rubio, J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F Met. Phys. 1985, 15, 851–858. [Google Scholar] [CrossRef]
- Yu, R.; Qi, X.L.; Bernevig, A.; Fang, Z.; Dai, X. Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection. Phys. Rev. B 2011, 84, 075119. [Google Scholar] [CrossRef] [Green Version]
- Soluyanov, A.A.; Vanderbilt, D. Wannier representation of Z2 topological insulators. Phys. Rev. B 2011, 83, 035108. [Google Scholar] [CrossRef] [Green Version]
- Vanderbilt, D. Berry Phases and Curvatures. In Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators; Cambridge University Press: Cambridge, UK, 2018; pp. 75–96. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef] [Green Version]
- Feroze, A.; Na, H.R.; Park, Y.C.; Jun, J.H.; Jung, M.H.; Lee, J.H.; Kim, J.H.; Seong, M.J.; Hong, S.; Chun, S.H.; et al. In-Depth Structural Characterization of 1T-VSe2 Single Crystals Grown by Chemical Vapor Transport. Cryst. Growth Des. 2020, 20, 2860–2865. [Google Scholar] [CrossRef]
- Perdew, J.P.; Levy, M. Physical Content of the Exact Kohn-Sham Orbital Energies: Band Gaps and Derivative Discontinuities. Phys. Rev. Lett. 1983, 51, 1884–1887. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S.Y.; Shen, H.; MacNeill, D.; Fatemi, V.; Chang, T.R.; Mier Valdivia, A.M.; Wu, S.; Du, Z.; Hsu, C.H.; et al. Observation of the nonlinear Hall effect under time-reversal-symmetric conditions. Nature 2019, 565, 337–342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, S.Y.; Ma, Q.; Shen, H.; Fatemi, V.; Wu, S.; Chang, T.R.; Chang, G.; Valdivia, A.M.M.; Chan, C.K.; Gibson, Q.D.; et al. Electrically switchable Berry curvature dipole in the monolayer topological insulator WTe2. Nat. Phys. 2018, 14, 900–906. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Xu, K.; Yao, Q.; Jannat, A.; Ren, G.; Field, M.R.; Wen, X.; Zhou, C.; Zavabeti, A.; Ou, J.Z. Hexagonal metal oxide monolayers derived from the metal–gas interface. Nat. Mater. 2021, 20, 1073–1078. [Google Scholar] [CrossRef]
- Zhu, Z.; Cai, X.; Yi, S.; Chen, J.; Dai, Y.; Niu, C.; Guo, Z.; Xie, M.; Liu, F.; Cho, J.H.; et al. Multivalency-Driven Formation of Te-Based Monolayer Materials: A Combined First-Principles and Experimental study. Phys. Rev. Lett. 2017, 119, 106101. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Lin, Z.; Zhao, J.Q.; Lou, J.; Chen, Y. Two-dimensional Tunable Dirac/Weyl Semimetal in Non-Abelian Gauge Field. Sci. Rep. 2019, 9, 18516. [Google Scholar] [CrossRef] [PubMed]
- You, J.Y.; Chen, C.; Zhang, Z.; Sheng, X.L.; Yang, S.A.; Su, G. Two-dimensional Weyl half-semimetal and tunable quantum anomalous Hall effect. Phys. Rev. B 2019, 100, 064408. [Google Scholar] [CrossRef] [Green Version]
- Jia, T.; Meng, W.; Zhang, H.; Liu, C.; Dai, X.; Zhang, X.; Liu, G. Weyl Fermions in VI3 Monolayer. Front. Chem. 2020, 8, 722. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Chang, G.; Belopolski, I.; Bian, G.; Xu, S.Y.; Yin, J.X. Weyl, Dirac and high-fold chiral fermions in topological quantum matter. Nat. Rev. Mater. 2021. [Google Scholar] [CrossRef]
- Balendhran, S.; Walia, S.; Nili, H.; Sriram, S.; Bhaskaran, M. Elemental Analogues of Graphene: Silicene, Germanene, Stanene, and Phosphorene. Small 2015, 11, 640–652. [Google Scholar] [CrossRef]
- Grauer, S.; Fijalkowski, K.M.; Schreyeck, S.; Winnerlein, M.; Brunner, K.; Thomale, R.; Gould, C.; Molenkamp, L.W. Scaling of the Quantum Anomalous Hall Effect as an Indicator of Axion Electrodynamics. Phys. Rev. Lett. 2017, 118, 246801. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Jiang, J.; Shin, J.H.; Wang, W.; Wang, F.; Zhao, Y.F.; Liu, C.; Wu, W.; Chan, M.H.W.; Samarth, N.; et al. Realization of the Axion Insulator State in Quantum Anomalous Hall Sandwich Heterostructures. Phys. Rev. Lett. 2018, 120, 056801. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Liang, Q.F.; Weng, H.; Chen, Y.B.; Yao, S.H.; Chen, Y.F.; Dong, J.; Guo, G.Y. Predicted Quantum Topological Hall Effect and Noncoplanar Antiferromagnetism in K0.5RhO2. Phys. Rev. Lett. 2016, 116, 256601. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Quantum Anomalous Hall Effect in Hg1-yMnyTe Quantum Wells. Phys. Rev. Lett. 2008, 101, 146802. [Google Scholar] [CrossRef] [Green Version]
- Si, L.; Janson, O.; Li, G.; Zhong, Z.; Liao, Z.; Koster, G.; Held, K. Quantum Anomalous Hall State in Ferromagnetic SrRuO3 (111) Bilayers. Phys. Rev. Lett. 2017, 119, 026402. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.C.; Shan, G.; Yan, B. Prediction of Near-Room-Temperature Quantum Anomalous Hall Effect on Honeycomb Materials. Phys. Rev. Lett. 2014, 113, 256401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, C.; Zhou, J.; Wu, H.; Deng, K.; Jena, P.; Kan, E. Quantum anomalous Hall effect in ferromagnetic transition metal halides. Phys. Rev. B 2017, 95, 045113. [Google Scholar] [CrossRef] [Green Version]
- Pushkarev, G.V.; Mazurenko, V.G.; Mazurenko, V.V.; Boukhvalov, D.W. Structural phase transitions in VSe2: Energetics, electronic structure and magnetism. Phys. Chem. Chem. Phys. 2019, 21, 22647–22653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esters, M.; Hennig, R.G.; Johnson, D.C. Dynamic instabilities in strongly correlated VSe2 monolayers and bilayers. Phys. Rev. B 2017, 96, 235147. [Google Scholar] [CrossRef] [Green Version]
- Fuh, H.R.; Chang, C.R.; Wang, Y.K.; Evans, R.F.L.; Chantrell, R.W.; Jeng, H.T. Newtype single-layer magnetic semiconductor in transition-metal dichalcogenides VX2 (X=S, Se and Te). Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Tu, K.; Chen, Z. Versatile Electronic Properties of VSe2 Bulk, Few-Layers, Monolayer, Nanoribbons, and Nanotubes: A Computational Exploration. J. Phys. Chem. C 2014, 118, 21264–21274. [Google Scholar] [CrossRef]
- Fuh, H.R.; Yan, B.; Wu, S.C.; Felser, C.; Chang, C.R. Metal-insulator transition and the anomalous Hall effect in the layered magnetic materials VS2 and VSe2. New J. Phys. 2016, 18, 113038. [Google Scholar] [CrossRef]
- Qi, X.L.; Hughes, T.L.; Zhang, S.C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 2008, 78, 195424. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.L.; Li, R.; Zang, J.; Zhang, S.C. Inducing a Magnetic Monopole with Topological Surface States. Science 2009, 323, 1184–1187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.X.; Zhang, S.C.; Qi, X.L. The Quantum Anomalous Hall Effect: Theory and Experiment. Annu. Rev. Condens. Matter Phys. 2016, 7, 301–321. [Google Scholar] [CrossRef]
- Serlin, M.; Tschirhart, C.L.; Polshyn, H.; Zhang, Y.; Zhu, J.; Watanabe, K.; Taniguchi, T.; Balents, L.; Young, A.F. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 2020, 367, 900–903. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).