Nonlocal Analysis of the Flexural–Torsional Stability for FG Tapered Thin-Walled Beam-Columns
Abstract
1. Introduction
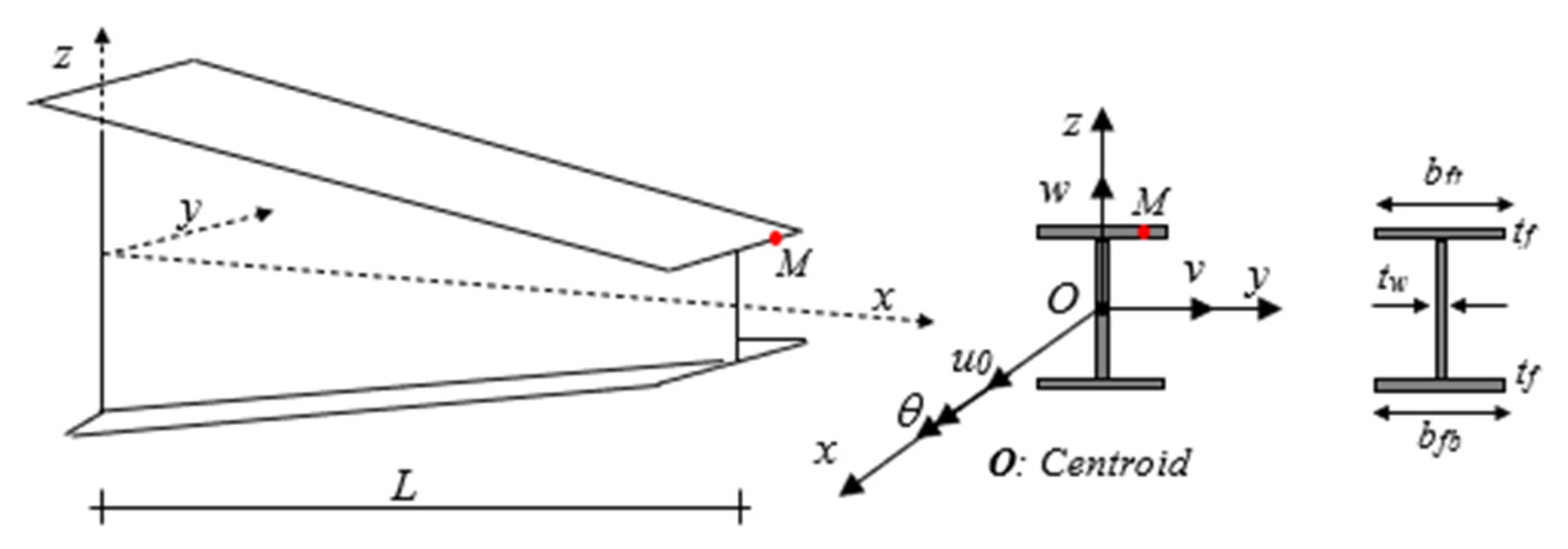
2. Problem Definition
2.1. Kinematics
2.2. Constitutive Relations
2.3. Equilibrium Equations
3. Numerical Solution Method
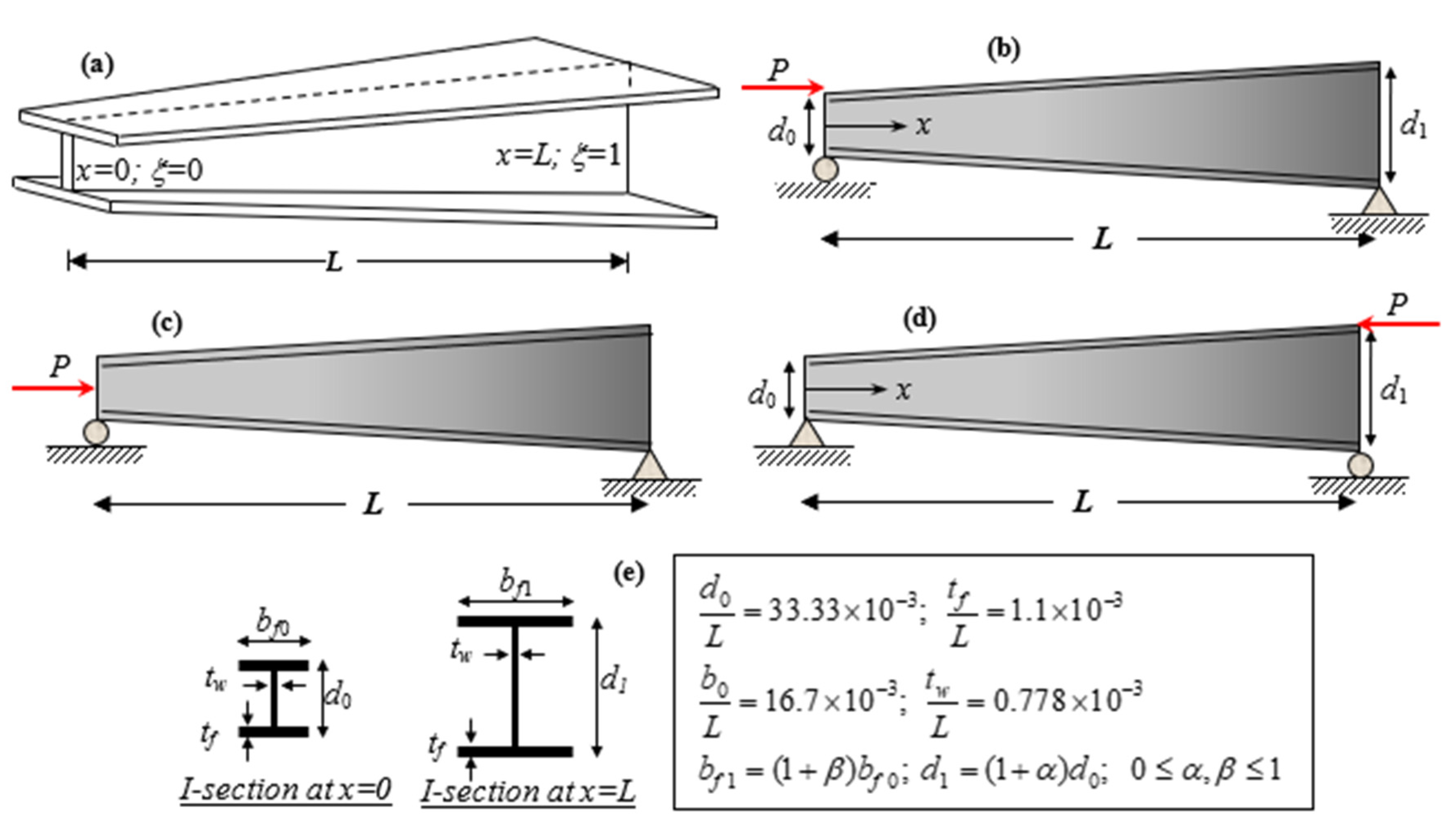
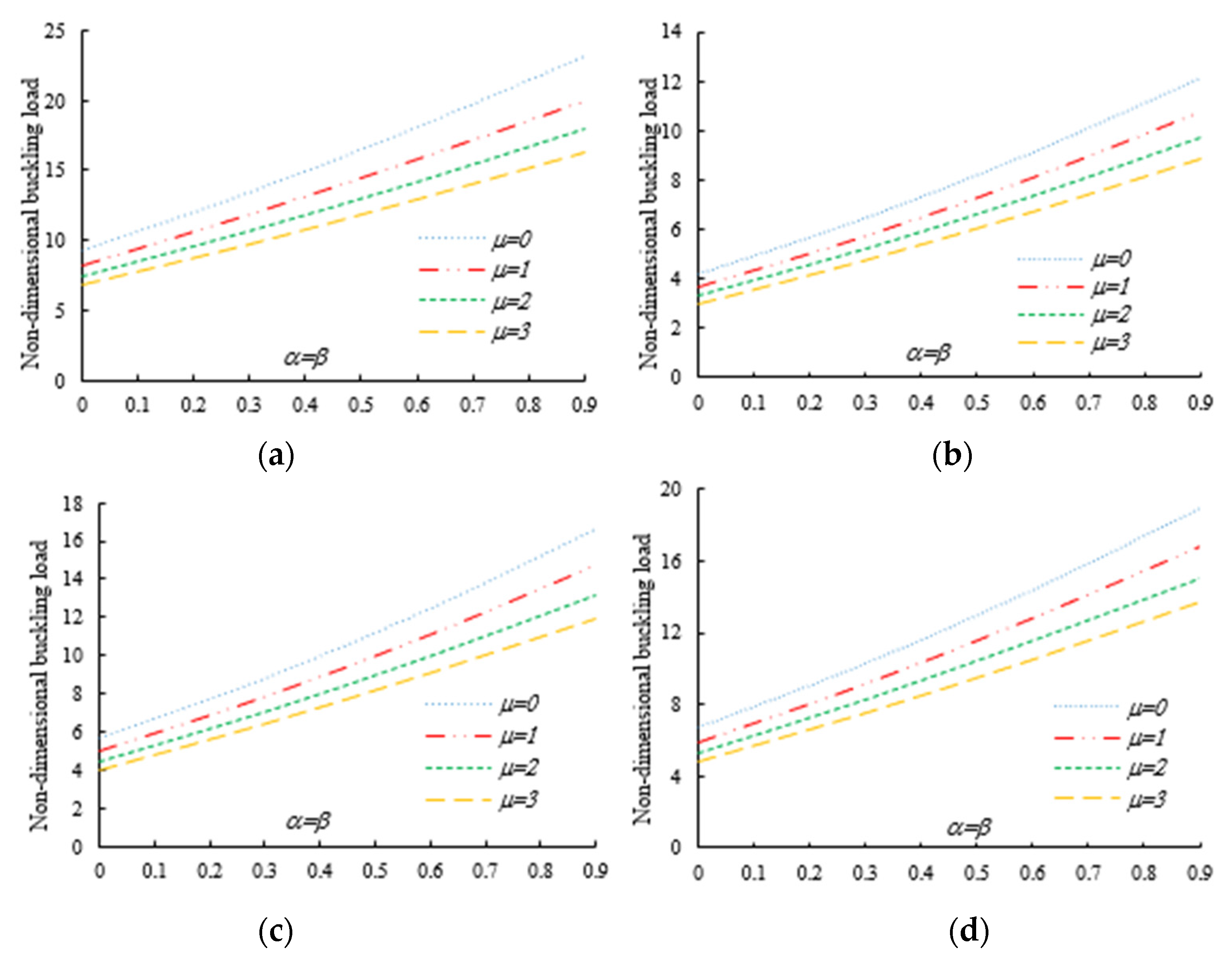
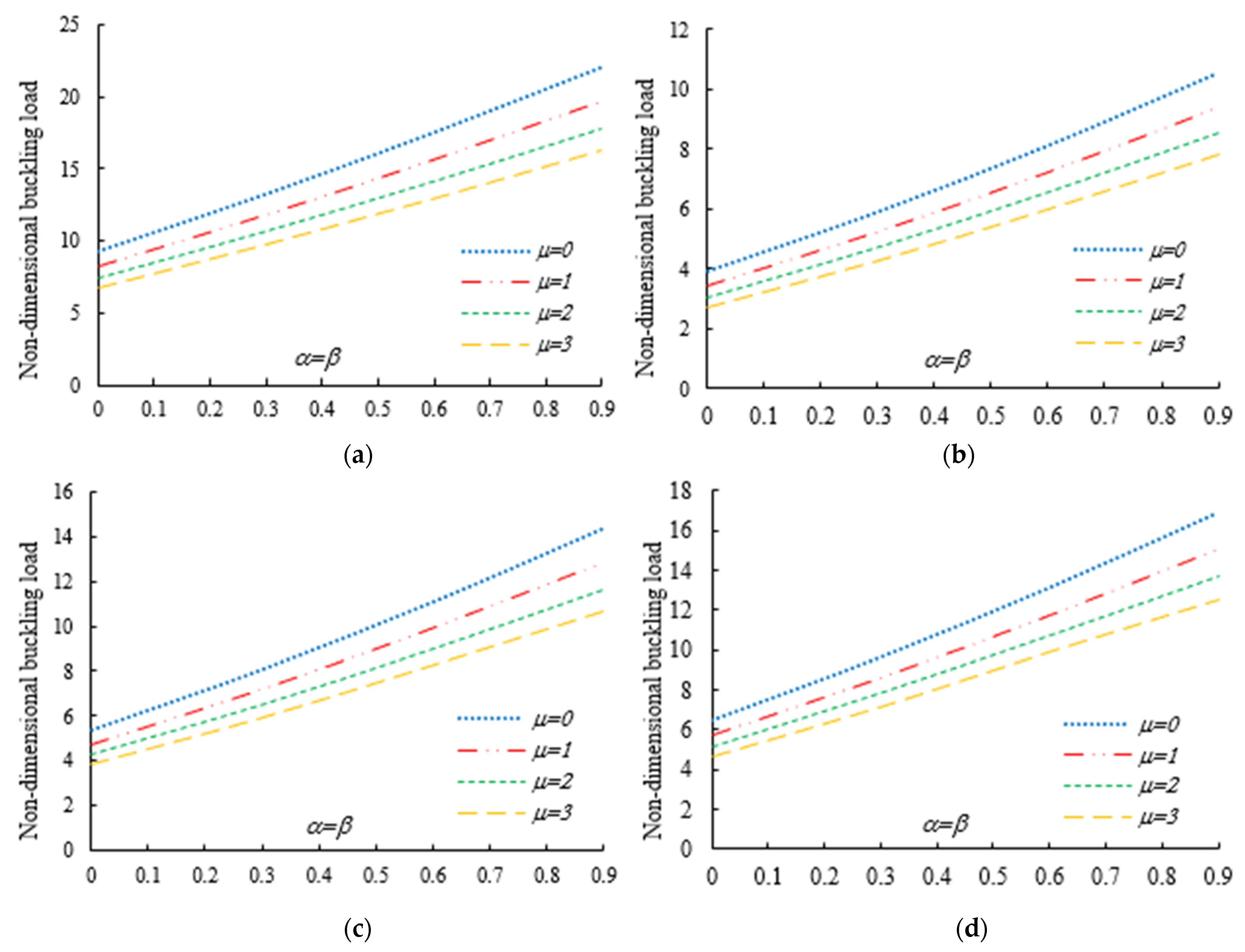
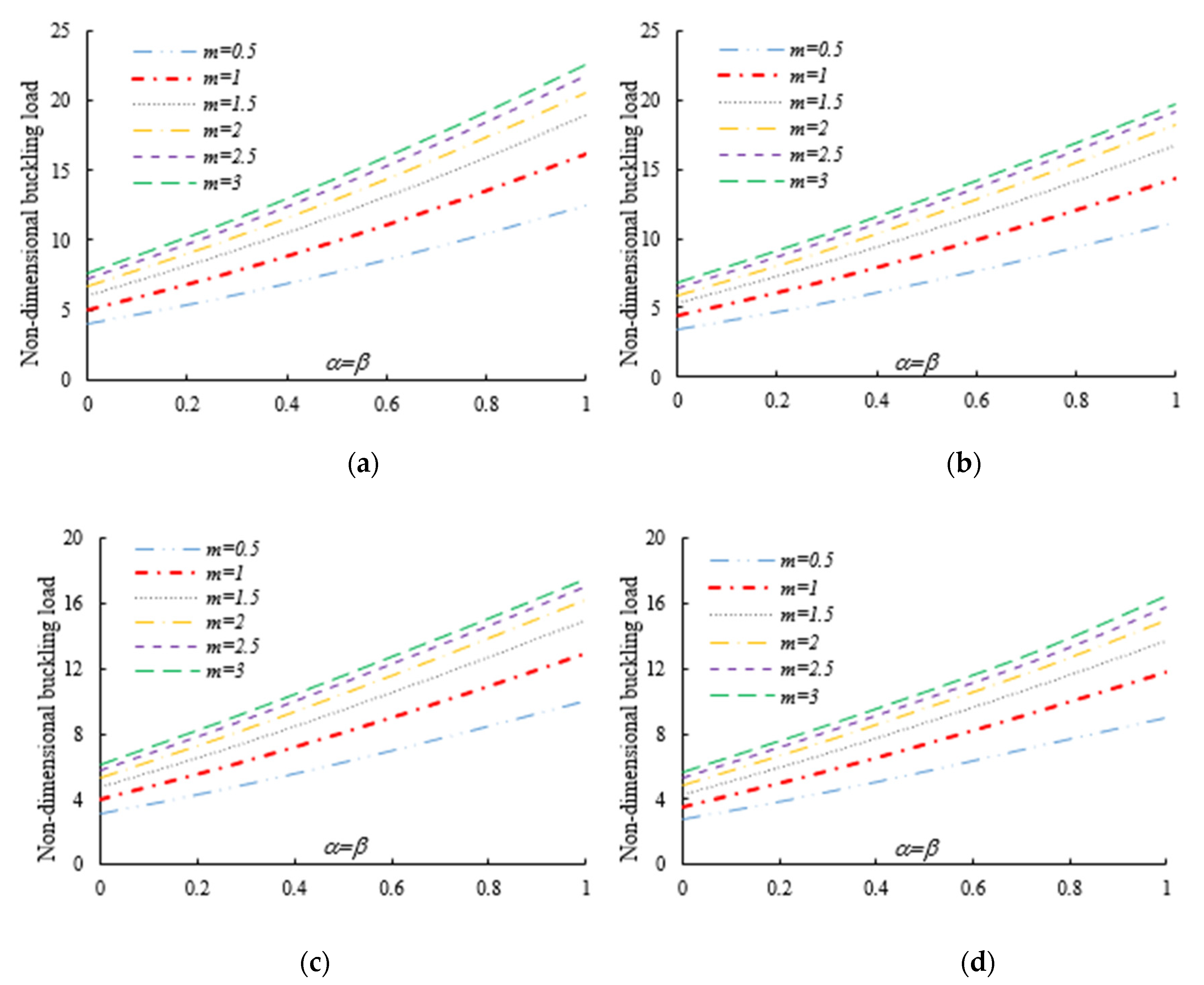
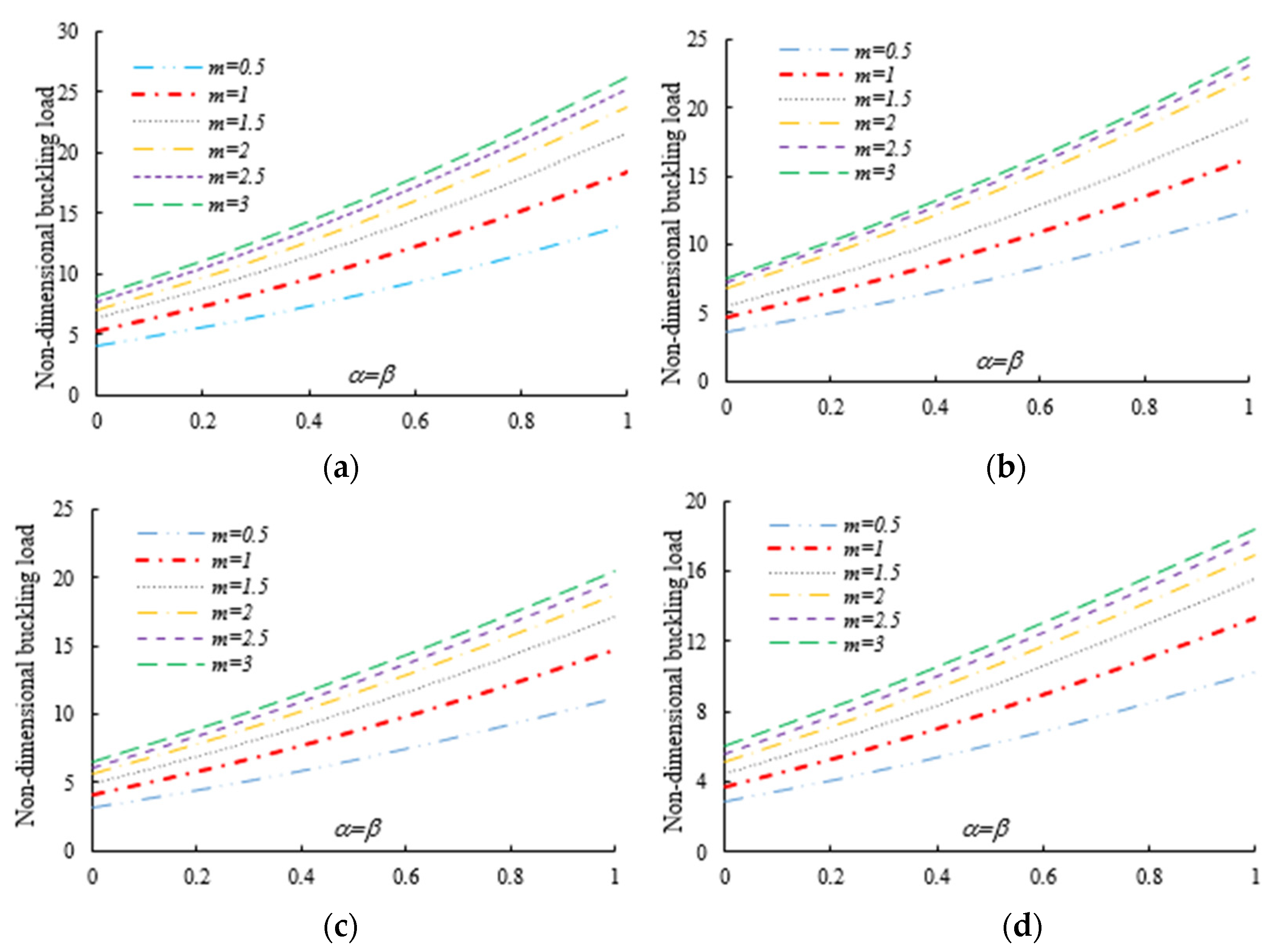
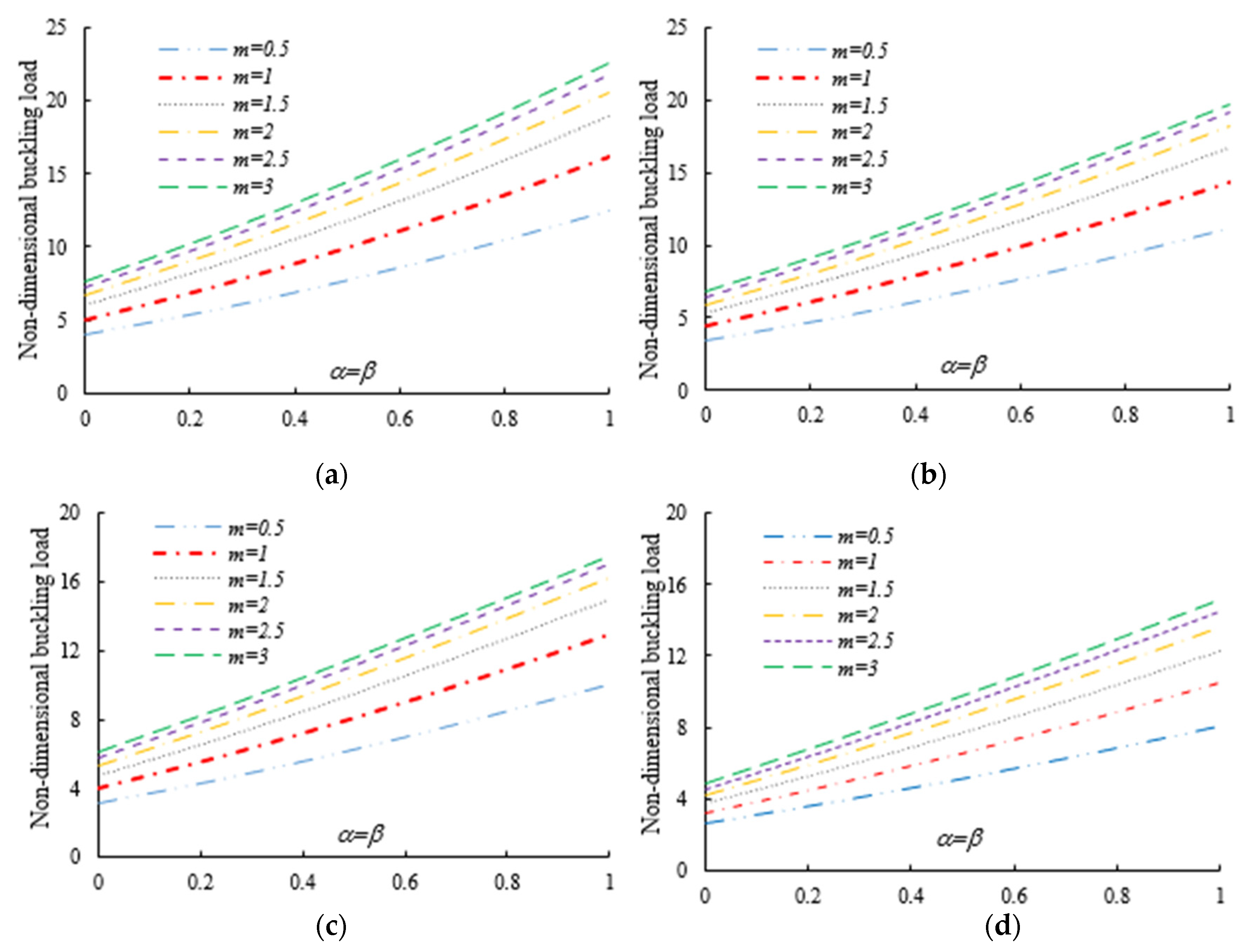
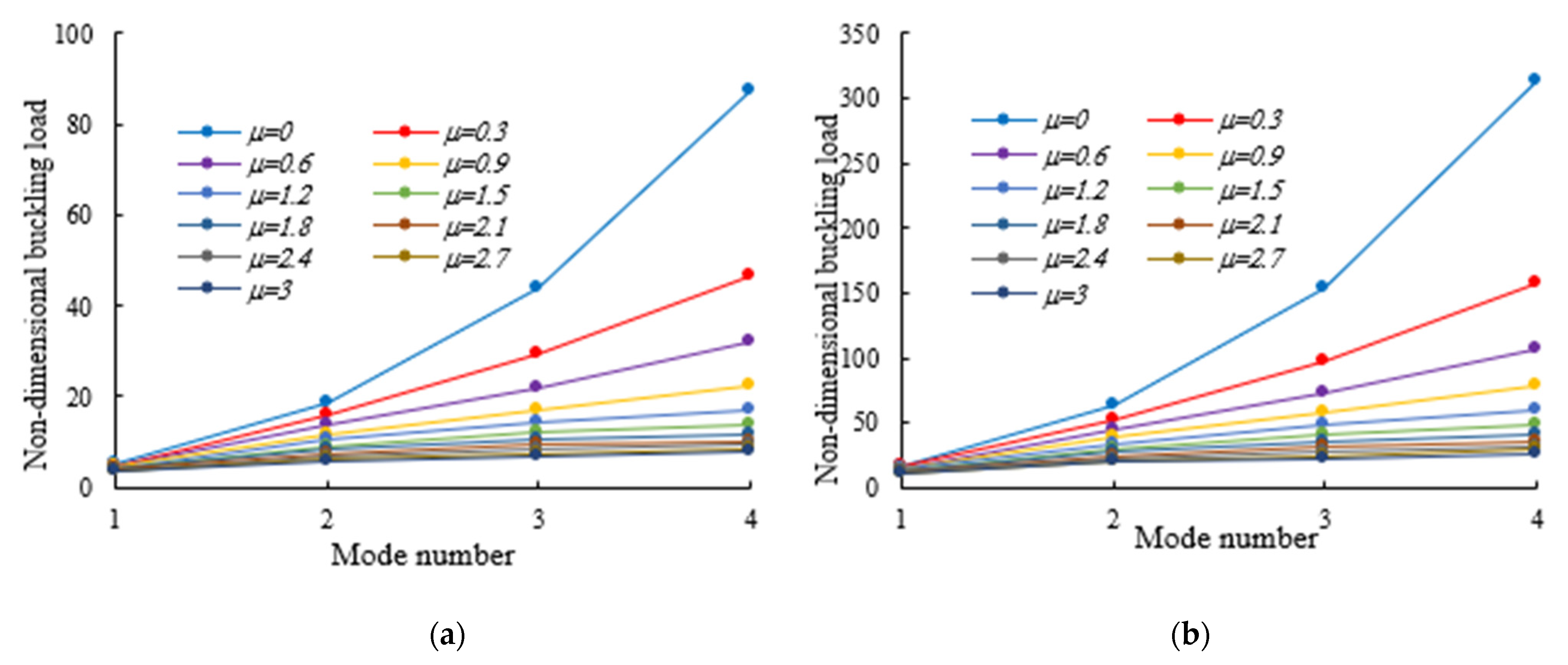
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, F.; Chong, A.; Lam, D.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Weissmüller, J.; Larche, F. A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A 1998, 78, 1093–1109. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Trahair, N.S. Elastic behaviour of tapered monosymmetric I-beams. J. Struct. Div. 1975, 101, 1661–1678. [Google Scholar] [CrossRef]
- Wekezer, J.W. Elastic torsion of thin walled bars of variable cross sections. Comput. Struct. 1984, 19, 401–407. [Google Scholar] [CrossRef]
- Wekezer, J.W. Instability of thin-walled bars. J. Eng. Mech. ASCE 1985, 111, 923–935. [Google Scholar] [CrossRef]
- Yang, Y.; Yau, J. Stability of Beams with Tapered I-Sections. J. Eng. Mech. 1987, 113, 1337–1357. [Google Scholar] [CrossRef]
- Bradford, M.A.; Cuk, P.E. Elastic Buckling of Tapered Monosymmetric I-Beams. J. Struct. Eng. 1988, 114, 977–996. [Google Scholar] [CrossRef]
- Baker, G. Lateral buckling of nonprismatic cantilevers using weighted residuals. J. Eng. Mech. 1993, 119, 1899–1919. [Google Scholar] [CrossRef]
- Rajasekaran, S. Equations for Tapered Thin-Walled Beams of Generic Open Section. J. Eng. Mech. 1994, 120, 1607–1629. [Google Scholar] [CrossRef]
- Rajasekaran, S. Instability of Tapered Thin?Walled Beams of Generic Section. J. Eng. Mech. 1994, 120, 1630–1640. [Google Scholar] [CrossRef]
- Gupta, P.; Wang, S.T.; Blandford, G.E. Lateral-Torsional Buckling of Nonprismatic I-Beams. J. Struct. Eng. 1996, 122, 748–755. [Google Scholar] [CrossRef]
- Ronagh, H.; Bradford, M.; Attard, M. Nonlinear analysis of thin-walled members of variable cross-section. Part I: Theory. Comput. Struct. 2000, 77, 285–299. [Google Scholar] [CrossRef]
- Chen, C.-N. Dynamic Equilibrium Equations of Non-Prismatic Beams Defined on an Arbitrarily Selected Co-Òrdinate System. J. Sound Vib. 2000, 230, 241–260. [Google Scholar] [CrossRef]
- Kim, S.-B.; Kim, M.-Y. Improved formulation for spatial stability and free vibration of thin-walled tapered beams and space frames. Eng. Struct. 2000, 22, 446–458. [Google Scholar] [CrossRef]
- Li, G.-Q.; Li, J.-J. A tapered Timoshenko–Euler beam element for analysis of steel portal frames. J. Constr. Steel Res. 2002, 58, 1531–1544. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Elishakoff, I.; Guédé, Z. Analytical Polynomial Solutions for Vibrating Axially Graded Beams. Mech. Adv. Mater. Struct. 2004, 11, 517–533. [Google Scholar] [CrossRef]
- Andrade, A.; Camotim, D. Lateral–Torsional Buckling of Singly Symmetric Tapered Beams: Theory and Applications. J. Eng. Mech. 2005, 131, 586–597. [Google Scholar] [CrossRef]
- Andrade, A.; Camotim, D.; Dinis, P.B. Lateral-torsional buckling of singly symmetric web-tapered thin-walled I-beams: 1D model vs. shell FEA. Comput. Struct. 2007, 85, 1343–1359. [Google Scholar] [CrossRef]
- Andrade, A.; Camotim, D.; e Costa, P.P. On the evaluation of elastic critical moments in doubly and singly symmetric I-section cantilevers. J. Constr. Steel Res. 2007, 63, 894–908. [Google Scholar] [CrossRef]
- Mohri, F.; Azrar, L.; Potier-Ferry, M. Lateral post-buckling analysis of thin-walled open section beams. Thin-Walled Struct. 2002, 40, 1013–1036. [Google Scholar] [CrossRef]
- Mohri, F.; Damil, N.; Potier-Ferry, M.; Mohri, F.; Damil, N.; Potier-Ferry, M. Buckling and lateral buckling interaction in thin-walled beam-column elements with mono-symmetric cross sections. Appl. Math. Model. 2013, 37, 3526–3540. [Google Scholar] [CrossRef]
- Samanta, A.; Kumar, A. Distortional buckling in monosymmetric I-beams. Thin-Walled Struct. 2006, 44, 51–56. [Google Scholar] [CrossRef]
- Reddy, J. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Challamel, N.; Andrade, A.; Camotim, D. An Analytical Study on The Lateral-Torsional Buckling of Linearly Tapered Cantilever Strip Beams. Int. J. Struct. Stab. Dyn. 2007, 7, 441–456. [Google Scholar] [CrossRef]
- Wang, C.M.; Zhang, Y.Y.; He, X.Q. Vibration of Non-local Timoshenko Beams. Nanotechnology 2007, 18, 105401. [Google Scholar] [CrossRef]
- Pradhan, S.; Sarkar, A. Analyses of tapered fgm beams with nonlocal theory. Struct. Eng. Mech. 2009, 32, 811–833. [Google Scholar] [CrossRef]
- Aydogdu, M. A general nonlocal beam theory: Its application to nanobeam bending, buckling and vibration. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 41, 1651–1655. [Google Scholar] [CrossRef]
- Civalek, Ö.; Akgöz, B. Free vibration analysis of microtubules as cytoskeleton components: Nonlocal Euler-Bernoulli beam modeling. Sci. Iran. Trans. B Mech. Eng. 2010, 17, 367–375. [Google Scholar]
- Danesh, M.; Farajpour, A.; Mohammadi, M. Axial vibration analysis of a tapered nanorod based on nonlocal elasticity theory and differential quadrature method. Mech. Res. Commun. 2012, 39, 23–27. [Google Scholar] [CrossRef]
- Şimşek, M.; Yurtcu, H. Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos. Struct. 2013, 97, 378–386. [Google Scholar] [CrossRef]
- McCann, F.; Gardner, L.; Wadee, M.A. Design of steel beams with discrete lateral restraints. J. Constr. Steel Res. 2013, 80, 82–90. [Google Scholar] [CrossRef]
- Eltaher, M.; Alshorbagy, A.; Mahmoud, F. Determination of neutral axis position and its effect on natural frequencies of functionally graded macro/nanobeams. Compos. Struct. 2013, 99, 193–201. [Google Scholar] [CrossRef]
- Eltaher, M.; Emam, S.A.; Mahmoud, F. Static and stability analysis of nonlocal functionally graded nanobeams. Compos. Struct. 2013, 96, 82–88. [Google Scholar] [CrossRef]
- Shahba, A.; Attarnejad, R.; Hajilar, S. A Mechanical-Based Solution for Axially Functionally Graded Tapered Euler-Bernoulli Beams. Mech. Adv. Mater. Struct. 2013, 20, 696–707. [Google Scholar] [CrossRef]
- Benyamina, A.B.; Meftah, S.A.; Mohri, F.; Daya, E.M. Analytical solutions attempt for lateral torsional buckling of doubly symmetric web-tapered I-beams. Eng. Struct. 2013, 56, 1207–1219. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Moon, J.; Le, V.N.; Lee, H.-E. Lateral–torsional buckling of I-girders with discrete torsional bracings. J. Constr. Steel Res. 2010, 66, 170–177. [Google Scholar] [CrossRef]
- Attard, M.; Kim, M.-Y. Lateral buckling of beams with shear deformations—A hyperelastic formulation. Int. J. Solids Struct. 2010, 47, 2825–2840. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C.M. Exact lateral–torsional buckling solutions for cantilevered beams subjected to intermediate and end transverse point loads. Thin-Walled Struct. 2010, 48, 71–76. [Google Scholar] [CrossRef]
- Ke, L.-L.; Wang, Y.-S. Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos. Struct. 2011, 93, 342–350. [Google Scholar] [CrossRef]
- De Borbón, F.; Mirasso, A.; Ambrosini, D. A beam element for coupled torsional-flexural vibration of doubly unsymmetrical thin walled beams axially loaded. Comput. Struct. 2011, 89, 1406–1416. [Google Scholar] [CrossRef]
- Serna, M.A.; Ibáñez, J.R.; López, A. Elastic flexural buckling of non-uniform members: Closed-form expression and equivalent load approach. J. Constr. Steel Res. 2011, 67, 1078–1085. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Free vibration analysis of axially functionally graded tapered Bernoulli–Euler microbeams based on the modified couple stress theory. Compos. Struct. 2013, 98, 314–322. [Google Scholar] [CrossRef]
- Lezgy-Nazargah, M.; Vidal, P.; Polit, O. An efficient finite element model for static and dynamic analyses of functionally graded piezoelectric beams. Compos. Struct. 2013, 104, 71–84. [Google Scholar] [CrossRef]
- Trahair, N. Bending and buckling of tapered steel beam structures. Eng. Struct. 2014, 59, 229–237. [Google Scholar] [CrossRef]
- Ke, L.-L.; Wang, Y.-S. Free vibration of size-dependent magneto-electro-elastic nanobeams based on the nonlocal theory. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 63, 52–61. [Google Scholar] [CrossRef]
- Rahmani, O.; Pedram, O. Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory. Int. J. Eng. Sci. 2014, 77, 55–70. [Google Scholar] [CrossRef]
- Liu, C.; Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Buckling and post-buckling of size-dependent piezoelectric Timoshenko nanobeams subject to thermo-electro-mechanical loadings. Int. J. Struct. Stab. Dyn. 2014, 14. [Google Scholar] [CrossRef]
- Nami, M.R.; Janghorban, M.; Damadam, M. Thermal buckling analysis of functionally graded rectangular nanoplates based on nonlocal third-order shear deformation theory. Aerosp. Sci. Technol. 2015, 41, 7–15. [Google Scholar] [CrossRef]
- Mohri, F.; Meftah, S.A.; Damil, N. A large torsion beam finite element model for tapered thin-walled open cross sections beams. Eng. Struct. 2015, 99, 132–148. [Google Scholar] [CrossRef]
- Kus, J. Lateral-torsional buckling steel beams with simultaneously tapered flanges and web. Steel Compos. Struct. 2015, 19, 897–916. [Google Scholar] [CrossRef]
- Pandeya, A.; Singhb, J. A variational principle approach for vibration of non-uniform nanocantilever using nonlocal elasticity theory. Proced. Mater. Sci. 2015, 10, 497–506. [Google Scholar] [CrossRef][Green Version]
- Shafiei, N.; Kazemi, M.; Safi, M.; Ghadiri, M. Nonlinear vibration of axially functionally graded non-uniform nanobeams. Int. J. Eng. Sci. 2016, 106, 77–94. [Google Scholar] [CrossRef]
- Zhang, Y.; He, B.; Yao, L.-K.; Long, J. Buckling analysis of thin-walled members via semi-analytical finite strip transfer matrix method. Adv. Mech. Eng. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Zhang, W.-F.; Liu, Y.-C.; Hou, G.-L.; Chen, K.-S.; Ji, J.; Deng, Y.; Deng, S.-L. Lateral-torsional buckling analysis of cantilever beam with tip lateral elastic brace under uniform and concentrated load. Int. J. Steel Struct. 2016, 16, 1161–1173. [Google Scholar] [CrossRef]
- Kiani, K. Free dynamic analysis of functionally graded tapered nanorods via a newly developed nonlocal surface energy-based integro-differential model. Compos. Struct. 2016, 139, 151–166. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Mohandes, M.; Moradi, M. Size dependent effect on the buckling and vibration analysis of double-bonded nanocomposite piezoelectric plate reinforced by boron nitride nanotube based on modified couple stress theory. J. Vib. Control 2016, 22, 1790–1807. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Employing sinusoidal shear deformation plate theory for transient analysis of three layers sandwich nanoplate integrated with piezo-magnetic face-sheets. Smart Mater. Struct. 2016, 25, 115040. [Google Scholar] [CrossRef]
- Bourihane, O.; Ed-Dinari, A.; Braikat, B.; Jamal, M.; Mohri, F.; Damil, N. Stability analysis of thin-walled beams with open section subject to arbitrary loads. Thin-Walled Struct. 2016, 105, 156–171. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Salari, E. Thermo-mechanical vibration analysis of nonlocal temperature-dependent FG nanobeams with various boundary conditions. Compos. Part B Eng. 2015, 78, 272–290. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A Nonlocal Higher-Order Shear Deformation Beam Theory for Vibration Analysis of Size-Dependent Functionally Graded Nanobeams. Arab. J. Sci. Eng. 2016, 41, 1679–1690. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Vibration analysis of nonlocal beams made of functionally graded material in thermal environment. Eur. Phys. J. Plus 2016, 131. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Shaghaghi, G.R.; Boreiry, M. A Semi-Analytical Evaluation of Surface and Nonlocal Effects on Buckling and Vibrational Characteristics of Nanotubes with Various Boundary Conditions. Int. J. Struct. Stab. Dyn. 2016, 16. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Buckling analysis of nonlocal third-order shear deformable functionally graded piezoelectric nanobeams embedded in elastic medium. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 937–952. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams. Compos. Struct. 2017, 159, 174–182. [Google Scholar] [CrossRef]
- Maalawi, K.Y. Dynamic optimization of functionally graded thin-walled box beams. Int. J. Struct. Stab. Dyn. 2017, 17, 1750109. [Google Scholar] [CrossRef]
- Lezgy-Nazargah, M. A generalized layered global-local beam theory for elasto-plastic analysis of thin-walled members. Thin-Walled Struct. 2017, 115, 48–57. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Thang, P.T.; Lee, J. Flexural-torsional stability of thin-walled functionally graded open-section beams. Thin-Walled Struct. 2017, 110, 88–96. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Thang, P.T.; Lee, J. Lateral buckling analysis of thin-walled functionally graded open-section beams. Compos. Struct. 2017, 160, 952–963. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Hu, Y.; Ding, Z.; Deng, W. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos. Struct. 2017, 165, 250–265. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Hashemi, S.H. Dynamic transverse vibration characteristics of nonuniform nonlocal strain gradient beams using the generalized differential quadrature method. Eur. Phys. J. Plus 2017, 132, 500. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Khaniki, H.B. Dynamic Behavior of Multi-Layered Viscoelastic Nanobeam System Embedded in a Viscoelastic Medium with a Moving Nanoparticle. J. Mech. 2017, 33, 559–575. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Hosseini-Hashemi, S. Buckling analysis of tapered nanobeams using nonlocal strain gradient theory and a generalized differential quadrature method. Mater. Res. Express 2017, 4, 065003. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Khaniki, H.B. Bending, buckling and vibration of small-scale tapered beams. Int. J. Eng. Sci. 2017, 120, 172–188. [Google Scholar] [CrossRef]
- Khaniki, H.B. On vibrations of nanobeam systems. Int. J. Eng. Sci. 2018, 124, 85–103. [Google Scholar] [CrossRef]
- Khaniki, H.B. Vibration analysis of rotating nanobeam systems using Eringen’s two-phase local/nonlocal model. Physica E 2018, 99, 310–319. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Khaniki, H.B. Finite element static and dynamic analysis of axially functionally graded nonuniform small-scale beams based on nonlocal strain gradient theory. Mech. Adv. Mater. Struct. 2018, 26, 1245–1259. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Rajasekaran, S. Mechanical analysis of non-uniform bi-directional functionally graded intelligent micro-beams using modified couple stress theory. Mater. Res. Express 2018, 5, 055703. [Google Scholar] [CrossRef]
- Koutoati, K.; Mohri, F.; Daya, E.M. Finite element approach of axial bending coupling on static and vibration behaviors of functionally graded material sandwich beams. Mech. Adv. Mater. Struct. 2021, 28, 1537–1553. [Google Scholar] [CrossRef]
- Glabisz, W.; Jarczewska, K.; Hołubowski, R. Stability of Timoshenko beams with frequency and initial stress dependent nonlocal parameters. Arch. Civ. Mech. Eng. 2019, 19, 1116–1126. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Civalek, Ö. Application of Chebyshev–Ritz method for static stability and vibration analysis of nonlocal microstructure-dependent nanostructures. Eng. Comput. 2020, 36, 953–964. [Google Scholar] [CrossRef]
- Jrad, W.; Mohri, F.; Robin, G.; Daya, E.M.; Al-Hajjar, J. Analytical and finite element solutions of free and forced vibration of unrestrained and braced thin-walled beams. J. Vib. Control. 2019, 26, 255–276. [Google Scholar] [CrossRef]
- Arefi, M.; Civalek, O. Static analysis of functionally graded composite shells on elastic foundations with nonlocal elasticity theory. Arch. Civ. Mech. Eng. 2020, 20, 1–17. [Google Scholar] [CrossRef]
- Osmani, A.; Meftah, S.A. Lateral buckling of tapered thin walled bi-symmetric beams under combined axial and bending loads with shear deformations allowed. Eng. Struct. 2018, 165, 76–87. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Sun, L. Calculation of Critical Lateral-Torsional Buckling Loads of Beams Subjected to Arbitrarily Transverse Loads. Int. J. Struct. Stab. Dyn. 2019, 19. [Google Scholar] [CrossRef]
- Achref, H.; Foudil, M.; Cherif, B. Higher buckling and lateral buckling strength of unrestrained and braced thin-walled beams: Analytical, numerical and design approach applications. J. Constr. Steel Res. 2019, 155, 1–19. [Google Scholar] [CrossRef]
- Asgarian, B.; Soltani, M.; Mohri, F.; Asgarian, B.; Soltani, M.; Mohri, F. Lateral-torsional buckling of tapered thin-walled beams with arbitrary cross-sections. Thin-Walled Struct. 2013, 62, 96–108. [Google Scholar] [CrossRef]
- Soltani, M.; Gharebaghi, S.A.; Mohri, F. Lateral stability analysis of steel tapered thin-walled beams under various boundary conditions. Numer. Methods Civ. Eng. 2018, 3, 13–25. [Google Scholar] [CrossRef]
- Soltani, M.; Asgarian, B.; Mohri, F. Improved finite element formulation for lateral stability analysis of axially functionally graded non-prismatic I-beams. Int. J. Struct. Stab. Dyn. 2019, 19, 1950108. [Google Scholar] [CrossRef]
- Lal, A.; Markad, K. Thermo-Mechanical Post Buckling Analysis of Multiwall Carbon Nanotube-Reinforced Composite Laminated Beam under Elastic Foundation. Curved Layer. Struct. 2019, 6, 212–228. [Google Scholar] [CrossRef]
- Pavlović, I.R.; Pavlović, R.; Janevski, G.; Despenić, N.; Pajković, V. Dynamic Behavior of Two Elastically Connected Nanobeams Under a White Noise Process. Facta Univ. Ser. Mech. Eng. 2020, 18, 219–227. [Google Scholar] [CrossRef]
- Soltani, M.; Atoufi, F.; Mohri, F.; Dimitri, R.; Tornabene, F. Nonlocal elasticity theory for lateral stability analysis of tapered thin-walled nanobeams with axially varying materials. Thin-Walled Struct. 2021, 159, 107268. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Thin-Walled Elastic Beams, Moscow, 1959 (French Translation, Pièces Longues en Voiles Minces); Eyrolles: Paris, France, 1962. [Google Scholar]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential Quadrature Method in Computational Mechanics: A Review. Appl. Mech. Rev. 1996, 49, 1–28. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science and Business Media LLC: Berlin, Germany, 2000. [Google Scholar]
- Zong, Z.; Zhang, Y. Advanced Differential Quadrature Methods. Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Tornabene, F.; Dimitri, R.; Viola, E. Transient dynamic response of generally-shaped arches based on a GDQ-time-stepping method. Int. J. Mech. Sci. 2016, 114, 277–314. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative numerical methods based on SFEM and IGA for computing stress concentrations in isotropic plates with discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S. 3D capability of refined GDQ models for the bending analysis of composite and sandwich plates, spherical and doubly-curved shells. Thin-Walled Struct. 2018, 129, 94–124. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Viscoti, M.; Dimitri, R.; Tornabene, F. 1D-Hierarchical Ritz and 2D-GDQ Formulations for the free vibration analysis of circular/elliptical cylindrical shells and beam structures. Compos. Struct. 2021, 258, 113338. [Google Scholar] [CrossRef]
- ANSYS, Version 5.4; Swanson Analysis System, Inc.: Canonsburg, PA, USA, 2007.

| Axial Load Position | α = β | DQM | ANSYS [104] | ||||
|---|---|---|---|---|---|---|---|
| Number of Points along x-Direction | |||||||
| n = 5 | n = 10 | n = 15 | n = 20 | n = 30 | |||
| Centroid | 0 | 9.824 | 9.870 | 9.870 | 9.870 | 9.870 | 9.866 |
| 0.2 | 12.970 | 13.006 | 13.006 | 13.006 | 13.006 | 12.997 | |
| 0.4 | 16.550 | 16.494 | 16.494 | 16.494 | 16.494 | 16.466 | |
| 0.6 | 20.647 | 20.326 | 20.326 | 20.326 | 20.326 | 20.276 | |
| 0.8 | 25.426 | 24.497 | 24.497 | 24.497 | 24.497 | 24.414 | |
| 1.0 | 31.184 | 29.004 | 29.003 | 29.003 | 29.003 | 27.605 | |
| TF of left end section | 0 | 9.213 | 9.248 | 9.248 | 9.248 | 9.248 | 9.274 |
| 0.2 | 11.974 | 11.964 | 11.964 | 11.964 | 11.964 | 12.000 | |
| 0.4 | 15.050 | 14.895 | 14.895 | 14.895 | 14.895 | 14.907 | |
| 0.6 | 18.570 | 18.029 | 18.029 | 18.029 | 18.029 | 18.050 | |
| 0.8 | 22.915 | 21.358 | 21.357 | 21.357 | 21.357 | 21.399 | |
| 1.0 | 29.257 | 24.877 | 24.876 | 24.876 | 24.876 | 24.956 | |
| TF of right end section | 0 | 9.213 | 9.248 | 9.248 | 9.248 | 9.248 | 9.274 |
| 0.2 | 11.805 | 11.862 | 11.862 | 11.862 | 11.862 | 11.922 | |
| 0.4 | 14.557 | 14.610 | 14.610 | 14.610 | 14.610 | 14.690 | |
| 0.6 | 17.524 | 17.469 | 17.469 | 17.469 | 17.469 | 17.638 | |
| 0.8 | 20.912 | 20.429 | 20.429 | 20.429 | 20.429 | 20.737 | |
| 1.0 | 25.283 | 23.488 | 23.489 | 23.489 | 23.489 | 23.992 | |
| μ (nm2) | α = β | Axial Load on the TF at | Axial Load on the Centroid | Axial Load on the TF at | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous | m = 0.8 | m = 1.6 | m = 2.4 | Homogeneous | m = 0.8 | m = 1.6 | m = 2.4 | Homogeneous | m = 0.8 | m = 1.6 | m = 2.4 | ||
| 0 | 0.0 | 9.248 | 4.602 | 6.165 | 7.151 | 9.870 | 4.816 | 6.489 | 7.571 | 9.248 | 4.383 | 5.863 | 6.843 |
| 0.3 | 13.416 | 7.140 | 9.516 | 10.879 | 14.711 | 7.641 | 10.272 | 11.833 | 13.232 | 6.596 | 8.804 | 10.165 | |
| 0.6 | 18.070 | 10.143 | 13.401 | 15.154 | 20.338 | 11.104 | 14.836 | 16.929 | 17.506 | 9.086 | 12.071 | 13.839 | |
| 0.9 | 23.186 | 13.578 | 17.787 | 19.927 | 26.738 | 15.194 | 20.169 | 22.823 | 22.029 | 11.827 | 15.648 | 17.827 | |
| 2.0 | 0.0 | 7.453 | 3.595 | 4.836 | 5.684 | 7.936 | 3.756 | 5.088 | 6.028 | 7.453 | 3.389 | 4.714 | 5.705 |
| 0.3 | 10.646 | 5.744 | 7.658 | 8.754 | 11.750 | 6.102 | 8.204 | 9.471 | 10.679 | 5.180 | 6.899 | 8.010 | |
| 0.6 | 14.010 | 8.171 | 10.752 | 12.080 | 15.996 | 8.922 | 11.902 | 13.547 | 14.110 | 7.261 | 9.655 | 11.113 | |
| 0.9 | 17.488 | 10.850 | 14.071 | 15.572 | 20.591 | 12.178 | 16.080 | 18.061 | 17.713 | 9.558 | 12.662 | 14.450 | |
| μ (nm2) | α | m = 0.6 | m = 1.2 | m = 1.8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | ||
| 0 | 0.0 | 4.057 | 5.488 | 7.943 | 10.725 | 5.483 | 7.413 | 10.693 | 14.373 | 6.462 | 8.685 | 12.418 | 16.559 |
| 0.2 | 4.065 | 5.503 | 7.973 | 10.778 | 5.496 | 7.435 | 10.739 | 14.454 | 6.479 | 8.713 | 12.475 | 16.658 | |
| 0.5 | 4.077 | 5.524 | 8.015 | 10.852 | 5.514 | 7.467 | 10.802 | 14.565 | 6.502 | 8.754 | 12.554 | 16.793 | |
| 0.8 | 4.089 | 5.543 | 8.053 | 10.919 | 5.531 | 7.496 | 10.859 | 14.664 | 6.524 | 8.790 | 12.625 | 16.914 | |
| 1.0 | 0.0 | 3.588 | 4.886 | 7.089 | 9.543 | 4.842 | 6.598 | 9.539 | 12.765 | 5.715 | 7.735 | 11.062 | 14.650 |
| 0.2 | 3.595 | 4.899 | 7.115 | 9.590 | 4.852 | 6.617 | 9.578 | 12.835 | 5.729 | 7.760 | 11.111 | 14.736 | |
| 0.5 | 3.605 | 4.916 | 7.151 | 9.654 | 4.868 | 6.643 | 9.632 | 12.932 | 5.748 | 7.793 | 11.179 | 14.854 | |
| 0.8 | 3.614 | 4.933 | 7.184 | 9.713 | 4.881 | 6.668 | 9.682 | 13.020 | 5.765 | 7.824 | 11.242 | 14.962 | |
| 3.0 | 0.0 | 2.899 | 4.008 | 5.853 | 7.848 | 3.886 | 5.405 | 7.871 | 10.461 | 4.586 | 6.346 | 9.109 | 11.916 |
| 0.2 | 2.904 | 4.017 | 5.873 | 7.885 | 3.893 | 5.418 | 7.901 | 10.516 | 4.594 | 6.363 | 9.147 | 11.985 | |
| 0.5 | 2.911 | 4.030 | 5.901 | 7.936 | 3.902 | 5.437 | 7.943 | 10.594 | 4.605 | 6.387 | 9.200 | 12.083 | |
| 0.8 | 2.917 | 4.042 | 5.927 | 7.985 | 3.910 | 5.454 | 7.982 | 10.667 | 4.615 | 6.409 | 9.250 | 12.173 | |
| μ (nm2) | α | m = 0.6 | m = 1.2 | m = 1.8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | ||
| 0 | 0.0 | 4.243 | 5.837 | 8.689 | 12.096 | 5.756 | 7.928 | 11.796 | 16.392 | 6.815 | 9.345 | 13.814 | 19.077 |
| 0.2 | 4.244 | 5.838 | 8.690 | 12.097 | 5.757 | 7.929 | 11.797 | 16.392 | 6.816 | 9.346 | 13.815 | 19.078 | |
| 0.5 | 4.245 | 5.839 | 8.691 | 12.098 | 5.759 | 7.930 | 11.798 | 16.394 | 6.817 | 9.348 | 13.817 | 19.079 | |
| 0.8 | 4.246 | 5.840 | 8.692 | 12.099 | 5.760 | 7.931 | 11.800 | 16.395 | 6.819 | 9.349 | 13.818 | 19.081 | |
| 1.0 | 0.0 | 3.736 | 5.177 | 7.741 | 10.775 | 5.054 | 7.023 | 10.504 | 14.589 | 5.989 | 8.287 | 12.299 | 16.949 |
| 0.2 | 3.736 | 5.178 | 7.742 | 10.776 | 5.055 | 7.024 | 10.505 | 14.589 | 5.990 | 8.288 | 12.300 | 16.950 | |
| 0.5 | 3.737 | 5.179 | 7.743 | 10.777 | 5.056 | 7.026 | 10.506 | 14.590 | 5.992 | 8.289 | 12.302 | 16.951 | |
| 0.8 | 3.738 | 5.180 | 7.744 | 10.777 | 5.058 | 7.027 | 10.507 | 14.592 | 5.993 | 8.291 | 12.303 | 16.953 | |
| 3.0 | 0.0 | 2.990 | 4.210 | 6.353 | 8.840 | 4.000 | 5.688 | 8.610 | 11.945 | 4.725 | 6.716 | 10.077 | 13.823 |
| 0.2 | 2.990 | 4.210 | 6.353 | 8.840 | 4.001 | 5.689 | 8.611 | 11.946 | 4.726 | 6.717 | 10.078 | 13.823 | |
| 0.5 | 2.991 | 4.211 | 6.354 | 8.841 | 4.002 | 5.690 | 8.612 | 11.947 | 4.727 | 6.718 | 10.079 | 13.824 | |
| 0.8 | 2.992 | 4.212 | 6.355 | 8.842 | 4.003 | 5.691 | 8.613 | 11.948 | 4.729 | 6.719 | 10.080 | 13.826 | |
| μ (nm2) | α | m = 0.6 | m = 1.2 | m = 1.8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | β = 0 | β = 0.2 | β = 0.5 | β = 0.8 | ||
| 0 | 0.0 | 3.881 | 5.299 | 7.808 | 10.770 | 5.218 | 7.133 | 10.513 | 14.484 | 6.160 | 8.392 | 12.304 | 16.869 |
| 0.2 | 3.785 | 5.158 | 7.585 | 10.447 | 5.080 | 6.934 | 10.200 | 14.037 | 5.995 | 8.156 | 11.939 | 16.352 | |
| 0.5 | 3.648 | 4.961 | 7.277 | 10.005 | 4.889 | 6.658 | 9.775 | 13.434 | 5.766 | 7.830 | 11.441 | 15.652 | |
| 0.8 | 3.526 | 4.785 | 7.005 | 9.621 | 4.719 | 6.416 | 9.404 | 12.912 | 5.564 | 7.544 | 11.007 | 15.046 | |
| 1.0 | 0.0 | 3.378 | 4.661 | 6.928 | 9.595 | 4.509 | 6.250 | 9.312 | 12.894 | 5.320 | 7.358 | 10.909 | 15.020 |
| 0.2 | 3.288 | 4.531 | 6.726 | 9.308 | 4.382 | 6.066 | 9.030 | 12.498 | 5.168 | 7.141 | 10.581 | 14.566 | |
| 0.5 | 3.164 | 4.352 | 6.450 | 8.917 | 4.209 | 5.819 | 8.650 | 11.965 | 4.963 | 6.849 | 10.138 | 13.953 | |
| 0.8 | 3.054 | 4.195 | 6.209 | 8.577 | 4.060 | 5.605 | 8.323 | 11.507 | 4.787 | 6.598 | 9.756 | 13.423 | |
| 3.0 | 0.0 | 2.659 | 3.748 | 5.668 | 7.908 | 3.465 | 4.968 | 7.585 | 10.607 | 4.038 | 5.832 | 8.891 | 12.354 |
| 0.2 | 2.584 | 3.640 | 5.501 | 7.678 | 3.365 | 4.818 | 7.354 | 10.292 | 3.924 | 5.656 | 8.624 | 12.000 | |
| 0.5 | 2.484 | 3.494 | 5.276 | 7.364 | 3.235 | 4.621 | 7.047 | 9.868 | 3.779 | 5.429 | 8.270 | 11.519 | |
| 0.8 | 2.400 | 3.370 | 5.082 | 7.093 | 3.128 | 4.457 | 6.787 | 9.505 | 3.658 | 5.239 | 7.968 | 11.103 | |
| α | μ = 0 | μ = 0.5 | μ = 1.0 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β = 0 | β = 0.25 | β = 0.5 | β = 0.75 | β = 1.0 | β = 0 | β = 0.25 | β = 0.5 | β = 0.75 | β = 1.0 | β = 0 | β = 0.25 | β = 0.5 | β = 0.75 | β = 1.0 | ||
| m = 1 | 0.0 | 26.399 | 31.400 | 36.266 | 41.068 | 45.851 | 23.116 | 28.587 | 33.610 | 38.395 | 43.059 | 19.151 | 25.731 | 31.080 | 35.936 | 40.536 |
| 0.25 | 23.264 | 28.179 | 33.116 | 38.108 | 43.174 | 20.578 | 25.743 | 30.737 | 35.666 | 40.588 | 17.772 | 23.395 | 28.526 | 33.445 | 38.266 | |
| 0.5 | 21.048 | 25.814 | 30.706 | 35.739 | 40.919 | 18.770 | 23.667 | 28.555 | 33.493 | 38.514 | 16.526 | 21.651 | 26.582 | 31.464 | 36.362 | |
| 0.75 | 19.410 | 24.025 | 28.831 | 33.836 | 39.040 | 17.424 | 22.099 | 26.863 | 31.755 | 36.793 | 15.526 | 20.319 | 25.074 | 29.885 | 34.787 | |
| 1.0 | 18.155 | 22.633 | 27.343 | 32.291 | 37.476 | 16.386 | 20.881 | 25.526 | 30.351 | 35.365 | 14.726 | 19.276 | 23.882 | 28.610 | 33.484 | |
| m = 2 | 0.0 | 32.917 | 39.157 | 45.200 | 51.149 | 57.068 | 28.810 | 35.822 | 42.067 | 47.952 | 53.660 | 22.425 | 32.135 | 39.040 | 45.017 | 50.590 |
| 0.25 | 29.212 | 35.391 | 41.552 | 47.747 | 54.009 | 25.880 | 32.480 | 38.722 | 44.811 | 50.846 | 21.761 | 29.544 | 36.068 | 42.145 | 48.015 | |
| 0.5 | 26.565 | 32.587 | 38.713 | 44.971 | 51.374 | 23.745 | 30.005 | 36.136 | 42.258 | 48.427 | 20.660 | 27.504 | 33.757 | 39.811 | 45.799 | |
| 0.75 | 24.596 | 30.445 | 36.477 | 42.709 | 49.145 | 22.138 | 28.118 | 34.109 | 40.187 | 46.387 | 19.612 | 25.915 | 31.943 | 37.923 | 43.935 | |
| 1.0 | 23.080 | 28.767 | 34.688 | 40.853 | 47.264 | 20.890 | 26.642 | 32.492 | 38.494 | 44.671 | 18.718 | 24.658 | 30.496 | 36.382 | 42.371 | |
| m = 3 | 0.0 | 36.991 | 43.765 | 50.277 | 56.664 | 63.005 | 32.637 | 40.321 | 46.990 | 53.227 | 59.259 | 24.922 | 36.356 | 43.842 | 50.097 | 55.888 |
| 0.25 | 32.952 | 39.692 | 46.349 | 53.002 | 59.699 | 29.420 | 36.657 | 43.364 | 49.843 | 56.229 | 24.530 | 33.542 | 40.580 | 46.993 | 53.131 | |
| 0.5 | 30.034 | 36.619 | 43.249 | 49.973 | 56.819 | 27.038 | 33.908 | 40.519 | 47.052 | 53.592 | 23.509 | 31.257 | 38.008 | 44.432 | 50.724 | |
| 0.75 | 27.845 | 34.249 | 40.783 | 47.482 | 54.361 | 25.229 | 31.794 | 38.266 | 44.764 | 51.346 | 22.406 | 29.456 | 35.971 | 42.336 | 48.675 | |
| 1.0 | 26.151 | 32.379 | 38.794 | 45.421 | 52.272 | 23.816 | 30.130 | 36.454 | 42.879 | 49.441 | 21.420 | 28.021 | 34.335 | 40.613 | 46.942 | |
| Homogeneous | 0.0 | 55.172 | 61.392 | 67.658 | 73.998 | 80.419 | 52.003 | 57.786 | 63.516 | 69.265 | 75.059 | 49.179 | 54.536 | 59.728 | 64.886 | 70.053 |
| 0.25 | 49.161 | 55.583 | 62.099 | 68.739 | 75.511 | 46.296 | 52.418 | 58.496 | 64.612 | 70.798 | 43.724 | 49.607 | 55.278 | 60.896 | 66.524 | |
| 0.5 | 44.446 | 50.894 | 57.492 | 64.265 | 71.217 | 41.822 | 48.036 | 54.265 | 60.575 | 66.994 | 39.462 | 45.506 | 51.410 | 57.301 | 63.234 | |
| 0.75 | 40.765 | 47.145 | 53.724 | 60.521 | 67.539 | 38.353 | 44.530 | 50.784 | 57.168 | 63.700 | 36.189 | 42.219 | 48.196 | 54.216 | 60.321 | |
| 1.0 | 37.852 | 44.126 | 50.635 | 57.395 | 64.408 | 35.627 | 41.713 | 47.927 | 54.311 | 60.880 | 33.635 | 39.582 | 45.549 | 51.611 | 57.798 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soltani, M.; Atoufi, F.; Mohri, F.; Dimitri, R.; Tornabene, F. Nonlocal Analysis of the Flexural–Torsional Stability for FG Tapered Thin-Walled Beam-Columns. Nanomaterials 2021, 11, 1936. https://doi.org/10.3390/nano11081936
Soltani M, Atoufi F, Mohri F, Dimitri R, Tornabene F. Nonlocal Analysis of the Flexural–Torsional Stability for FG Tapered Thin-Walled Beam-Columns. Nanomaterials. 2021; 11(8):1936. https://doi.org/10.3390/nano11081936
Chicago/Turabian StyleSoltani, Masoumeh, Farzaneh Atoufi, Foudil Mohri, Rossana Dimitri, and Francesco Tornabene. 2021. "Nonlocal Analysis of the Flexural–Torsional Stability for FG Tapered Thin-Walled Beam-Columns" Nanomaterials 11, no. 8: 1936. https://doi.org/10.3390/nano11081936
APA StyleSoltani, M., Atoufi, F., Mohri, F., Dimitri, R., & Tornabene, F. (2021). Nonlocal Analysis of the Flexural–Torsional Stability for FG Tapered Thin-Walled Beam-Columns. Nanomaterials, 11(8), 1936. https://doi.org/10.3390/nano11081936








