Quantum Confined Stark Effect on the Linear and Nonlinear Optical Properties of SiGe/Si Semi Oblate and Prolate Quantum Dots Grown in Si Wetting Layer
Abstract
1. Introduction
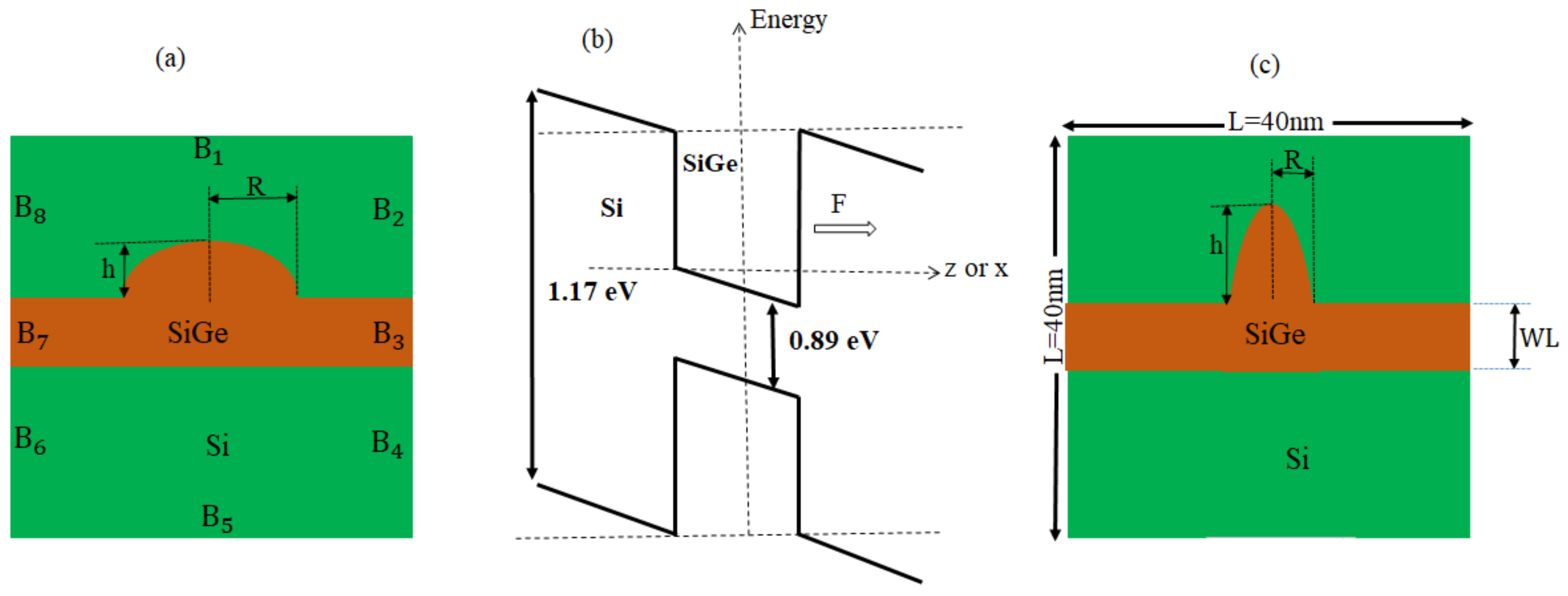
2. Theory and Model
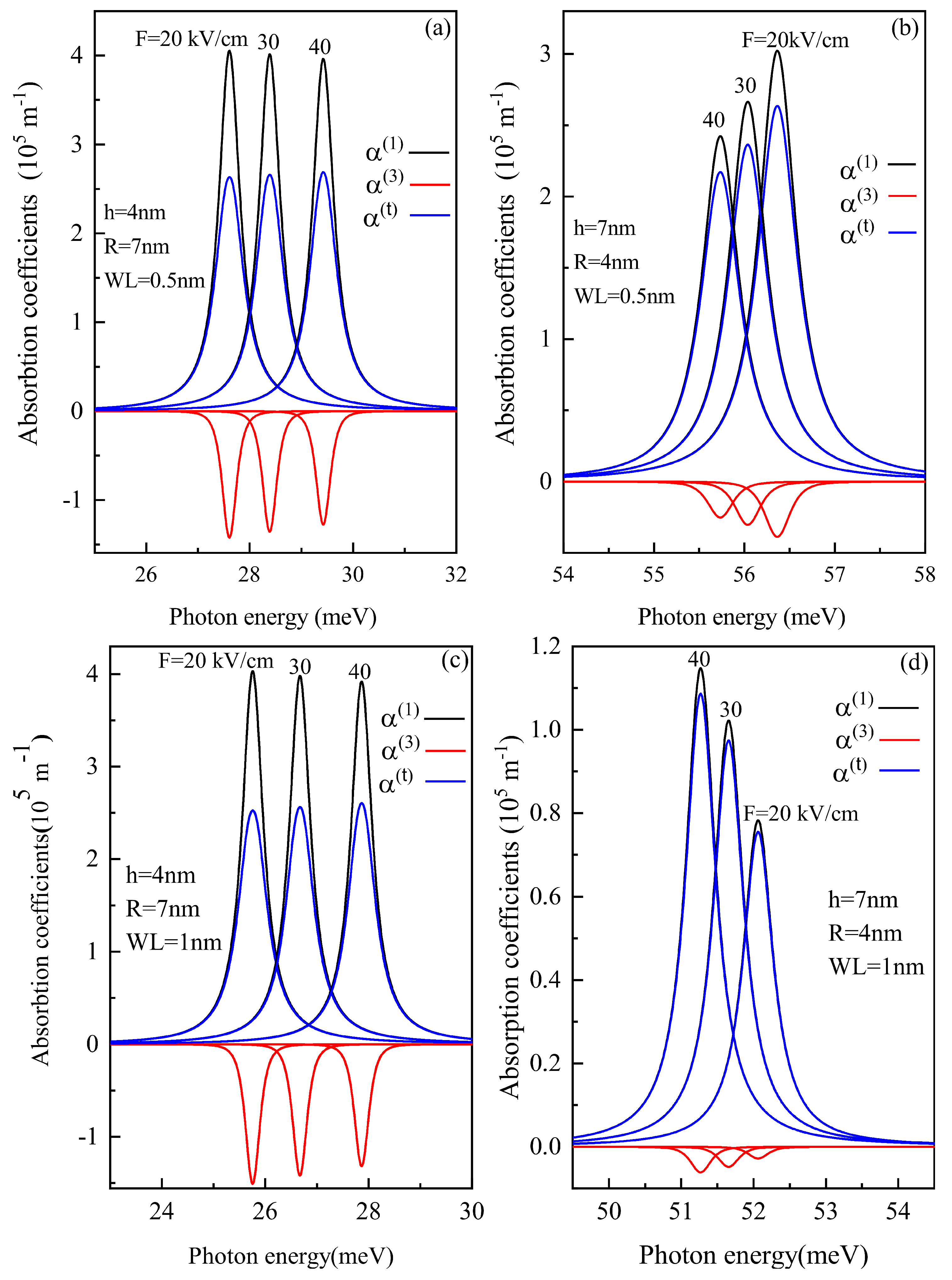
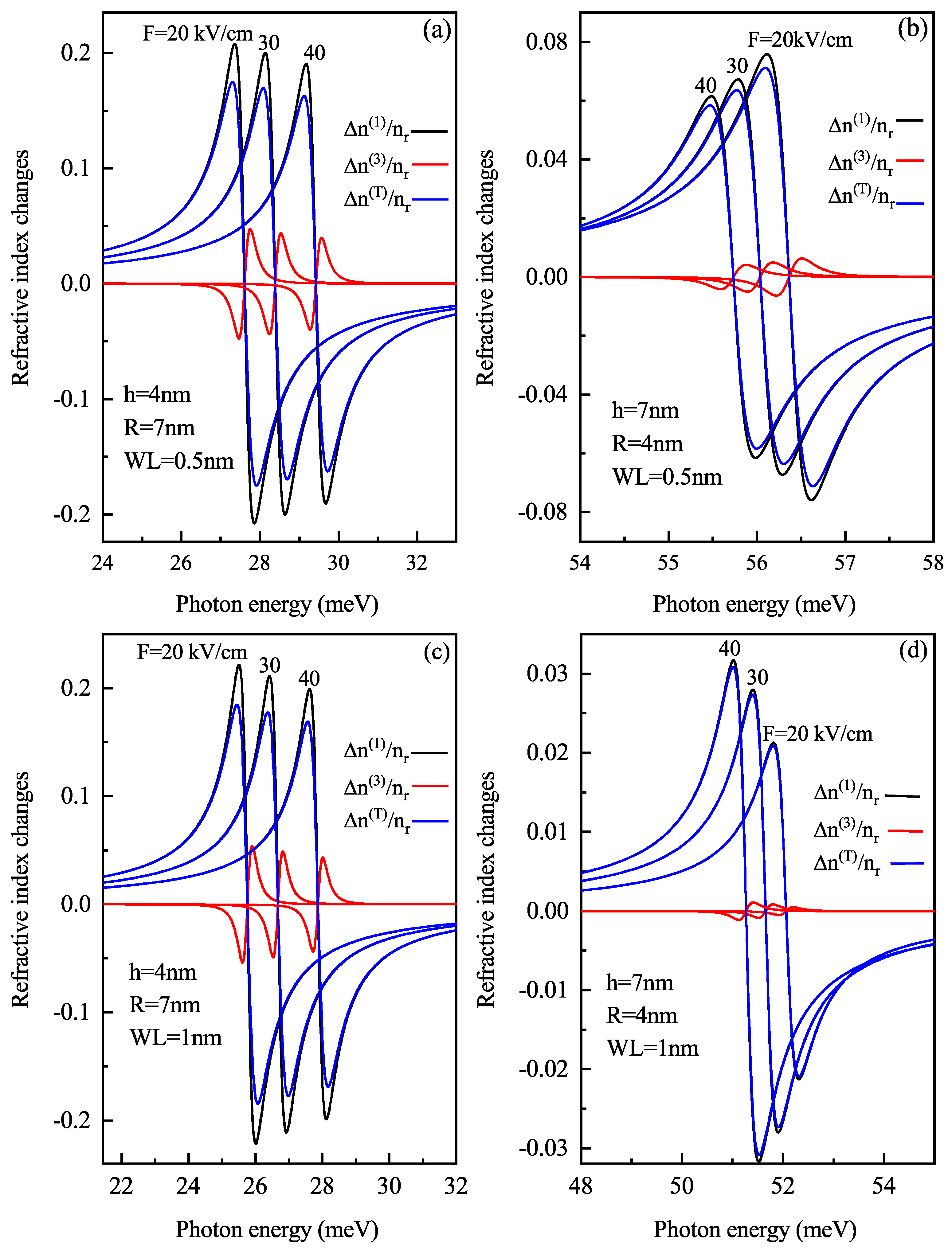
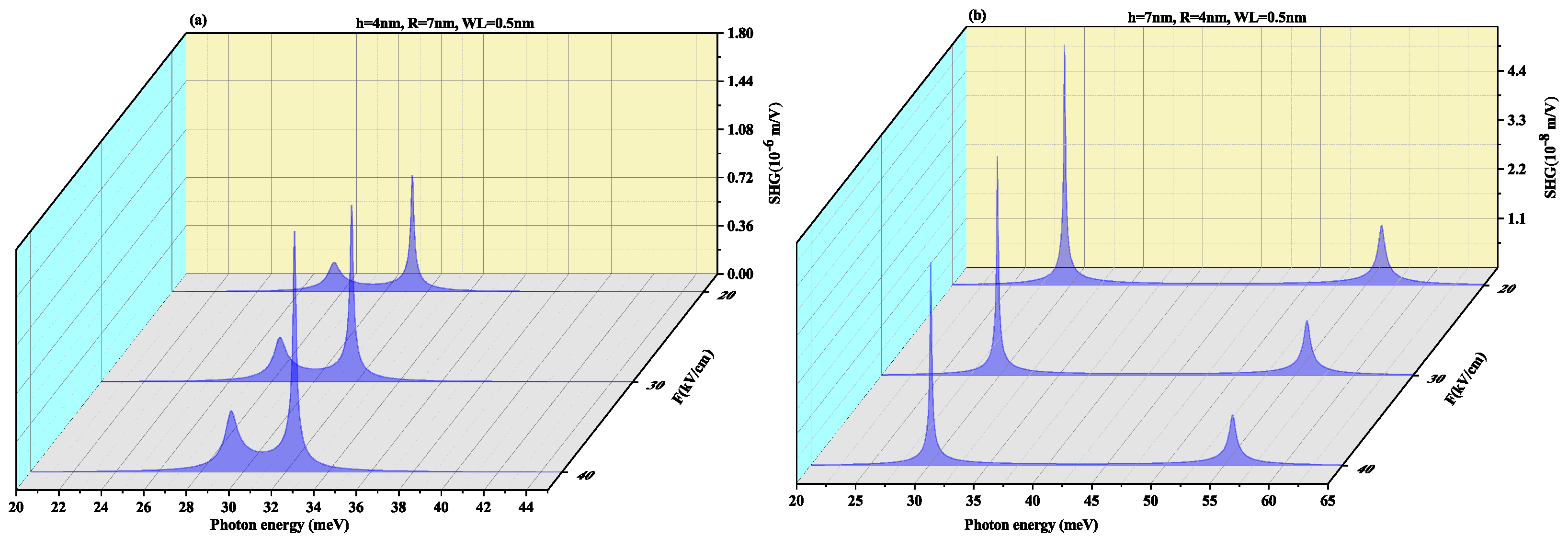
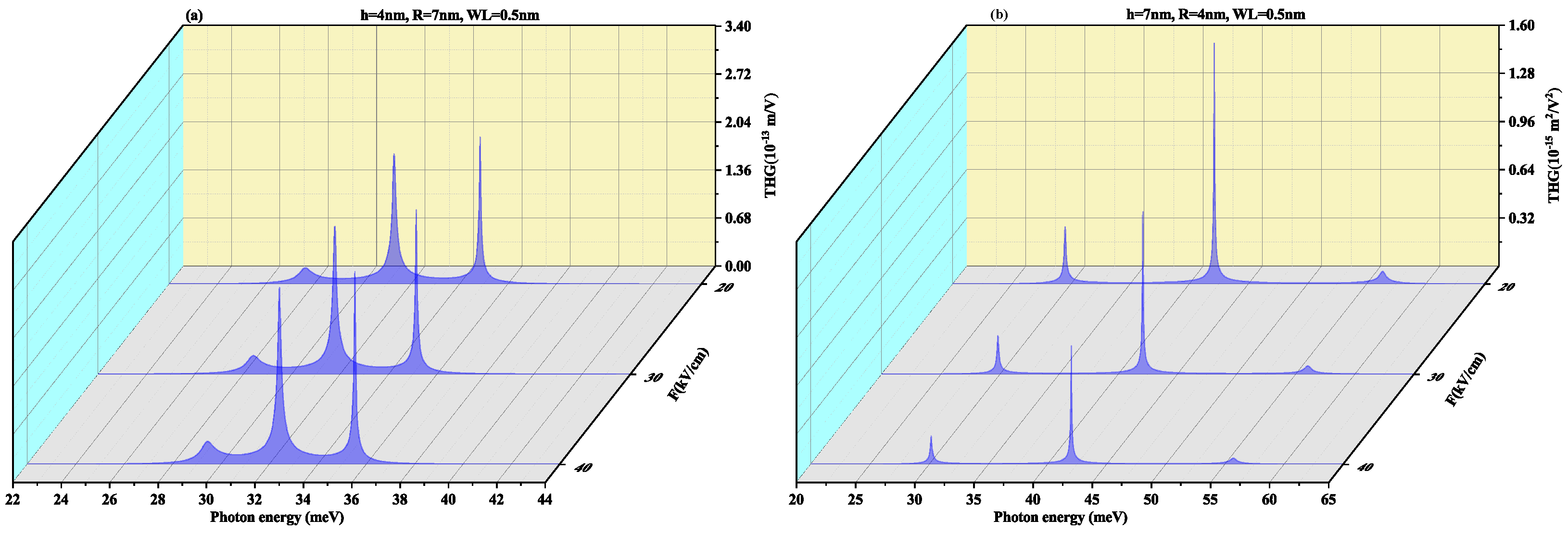
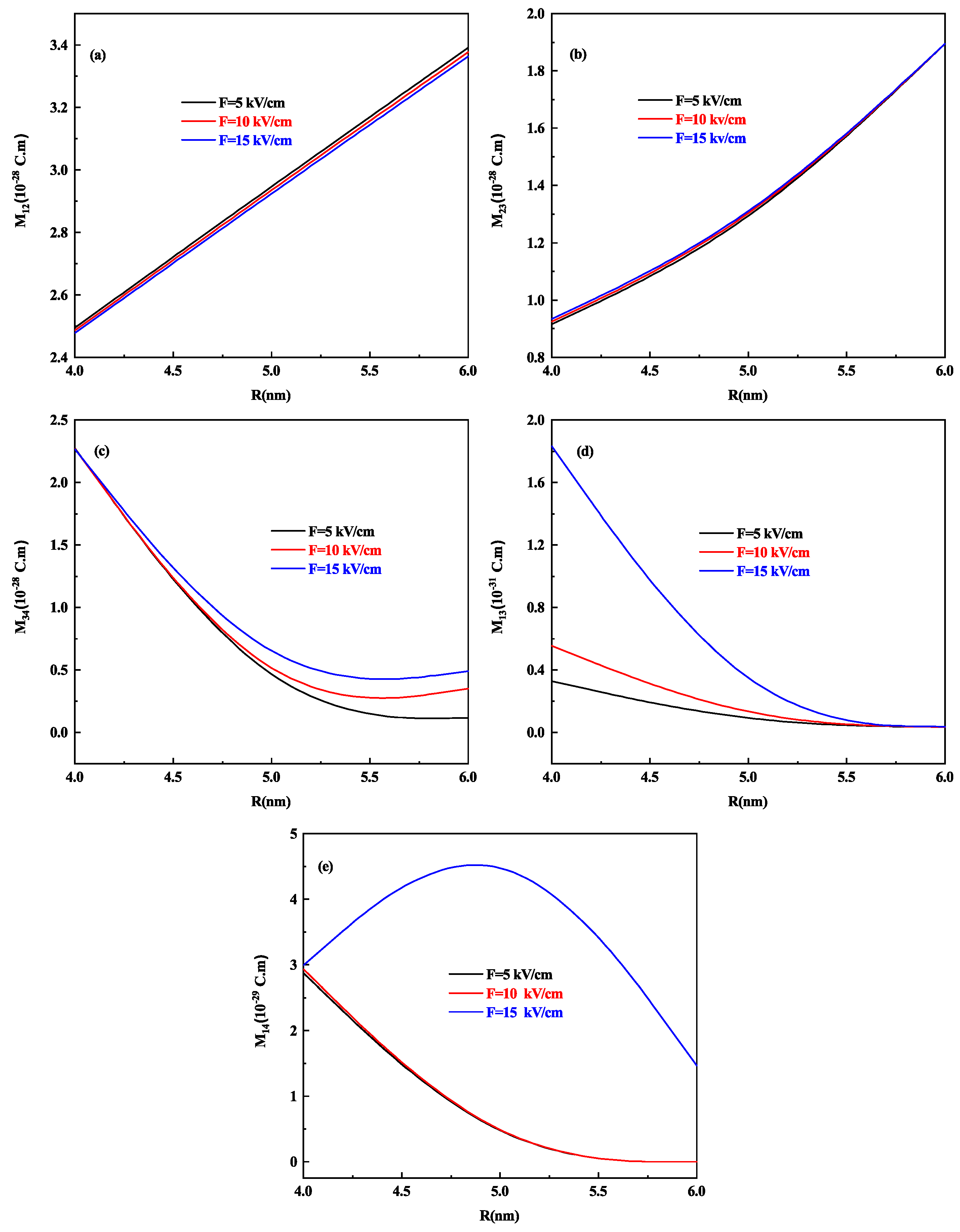
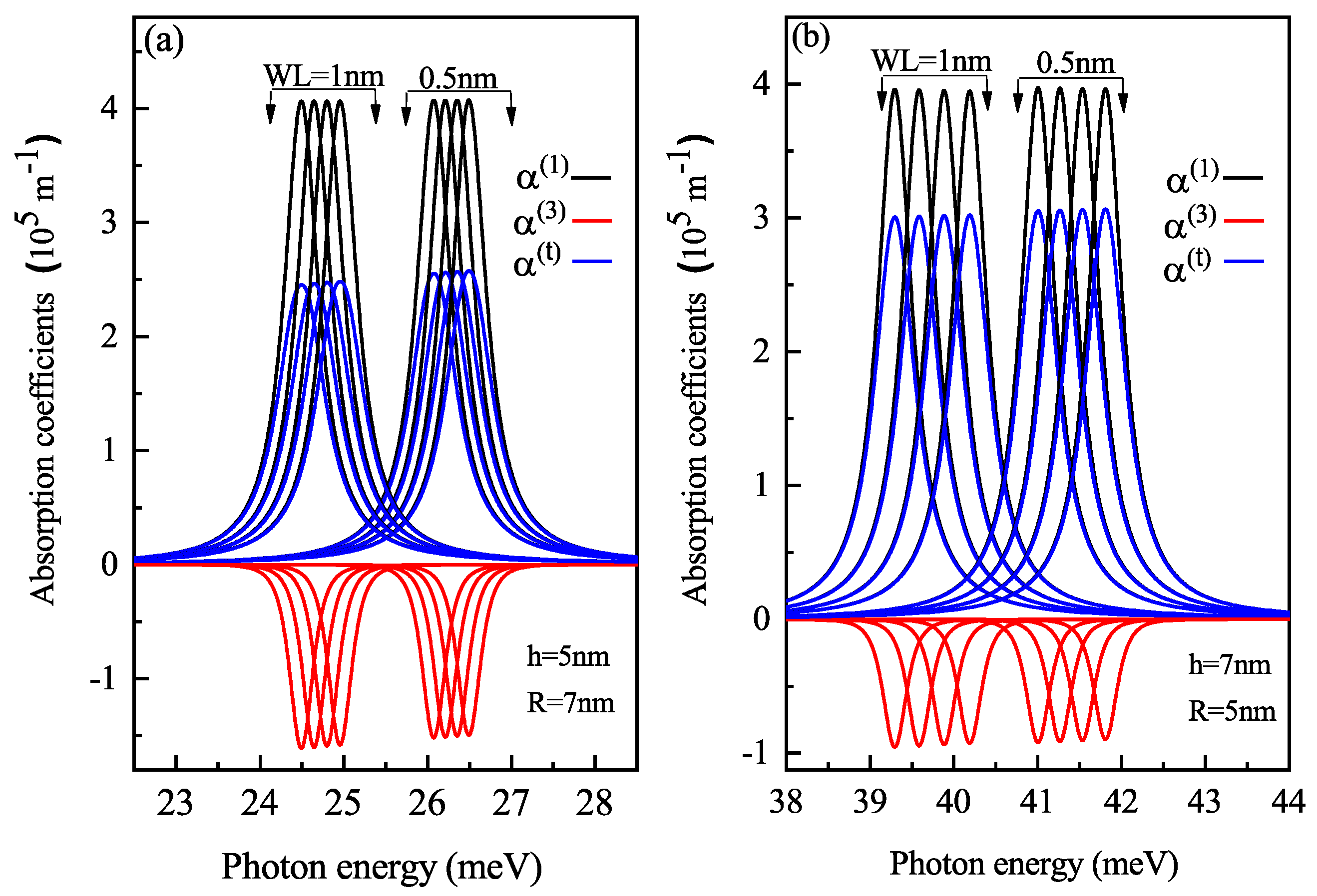
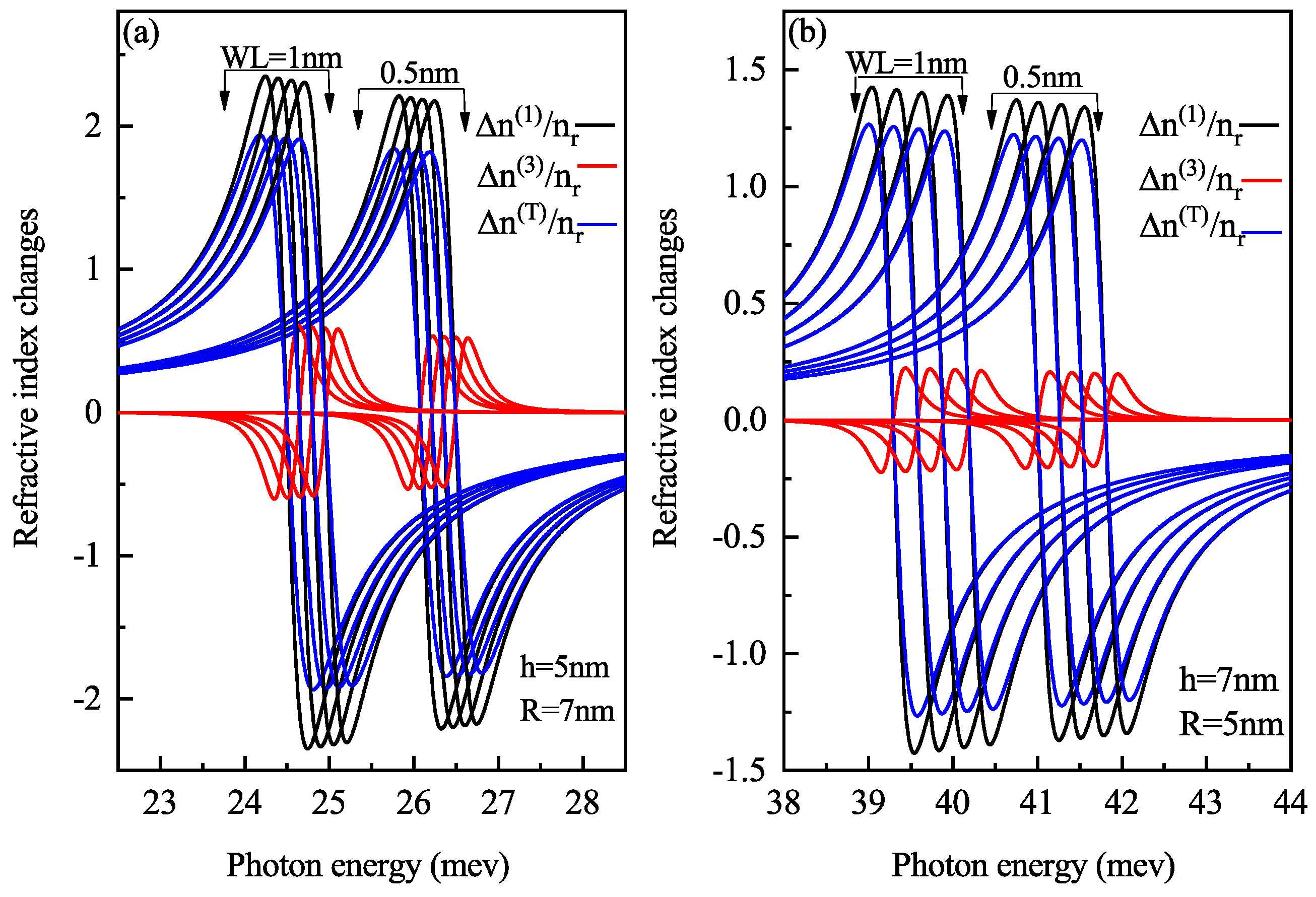
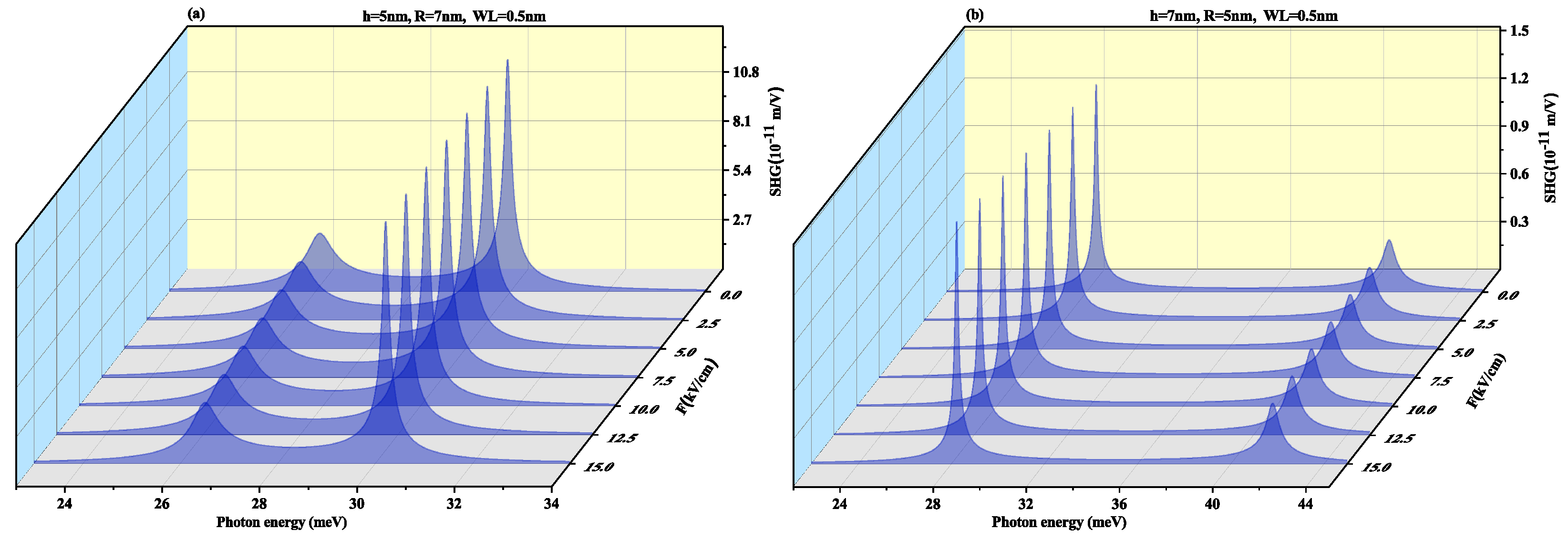
3. Results and Discussion
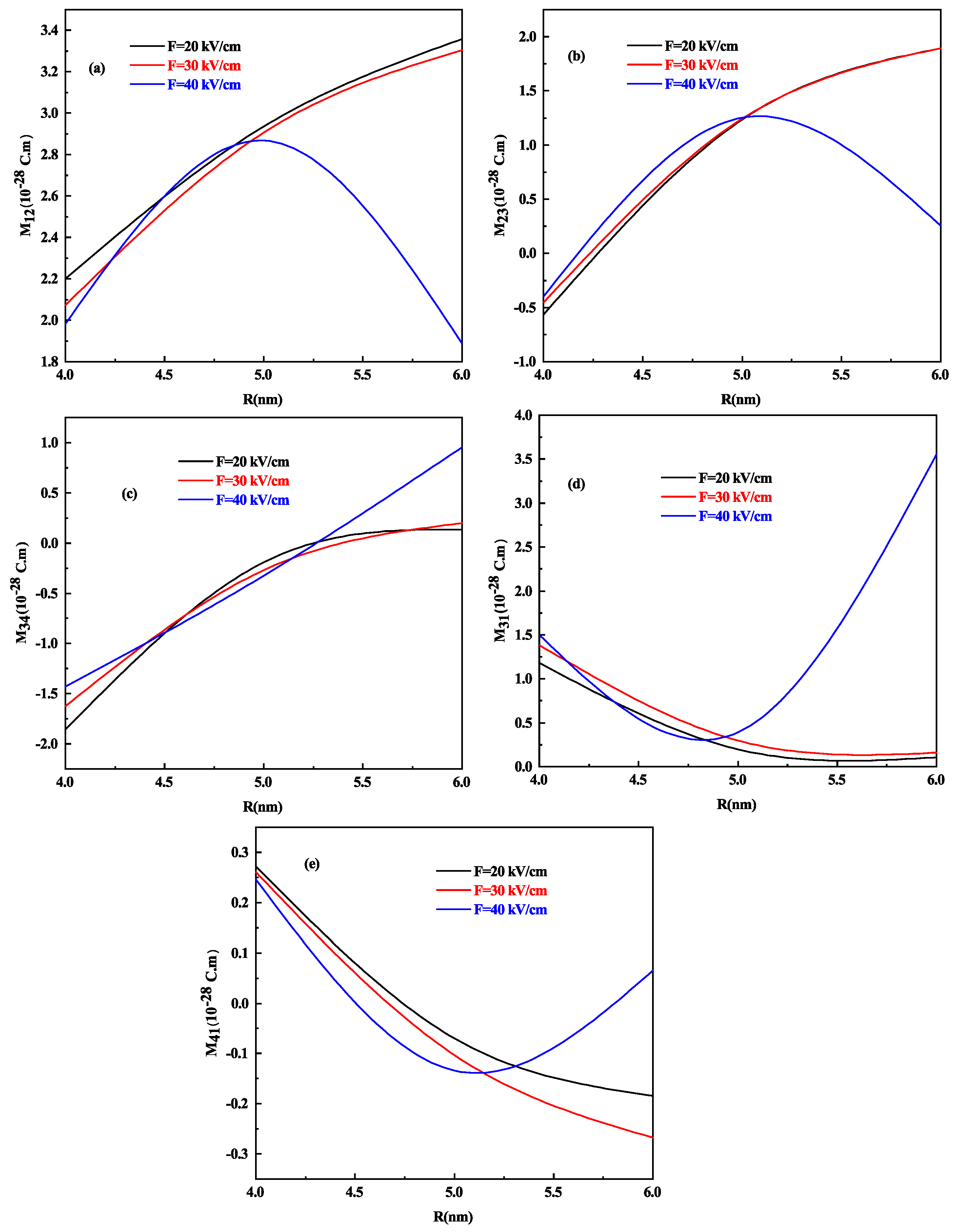
3.1. With Lateral Electric Field (In x-Direction)
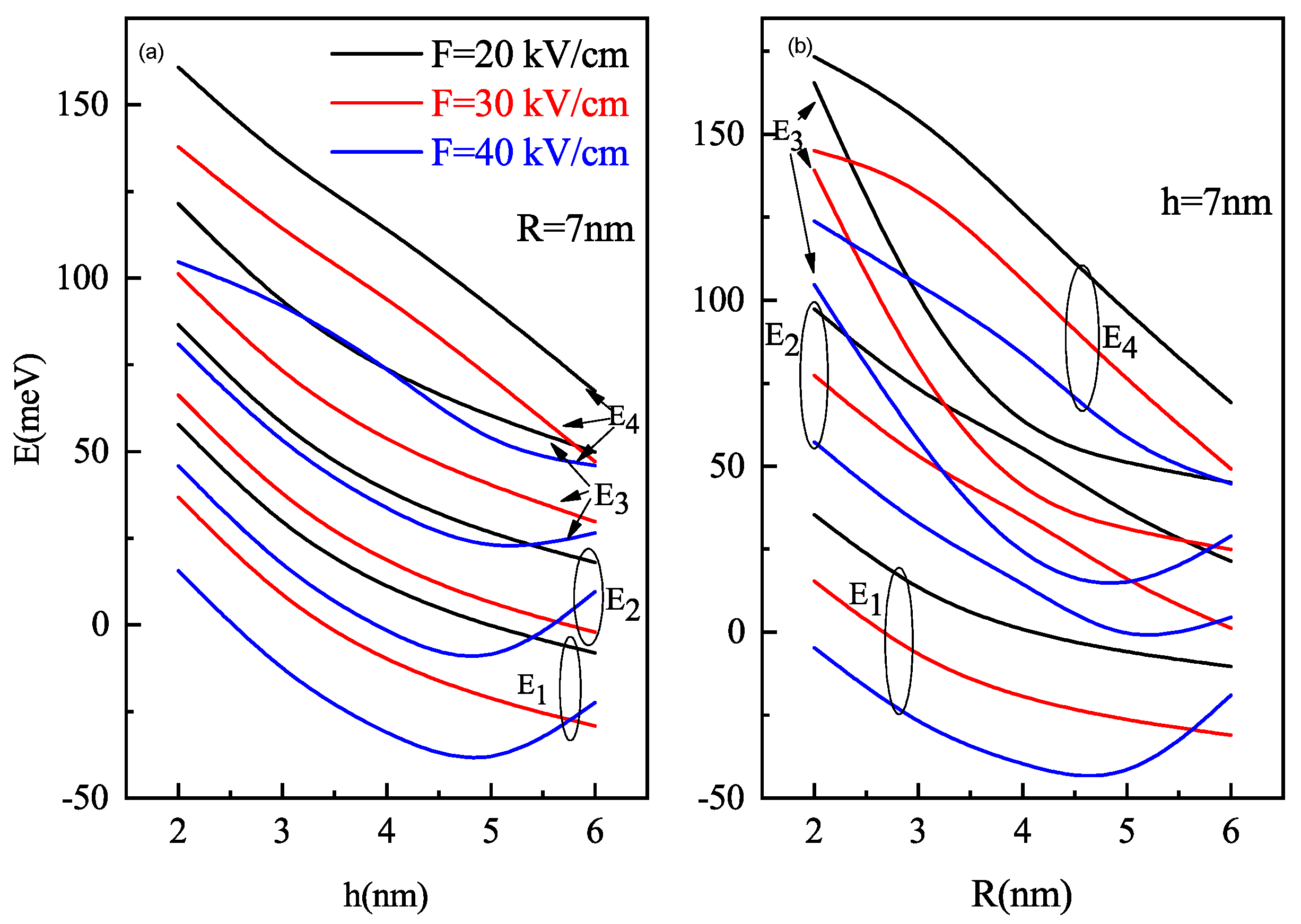
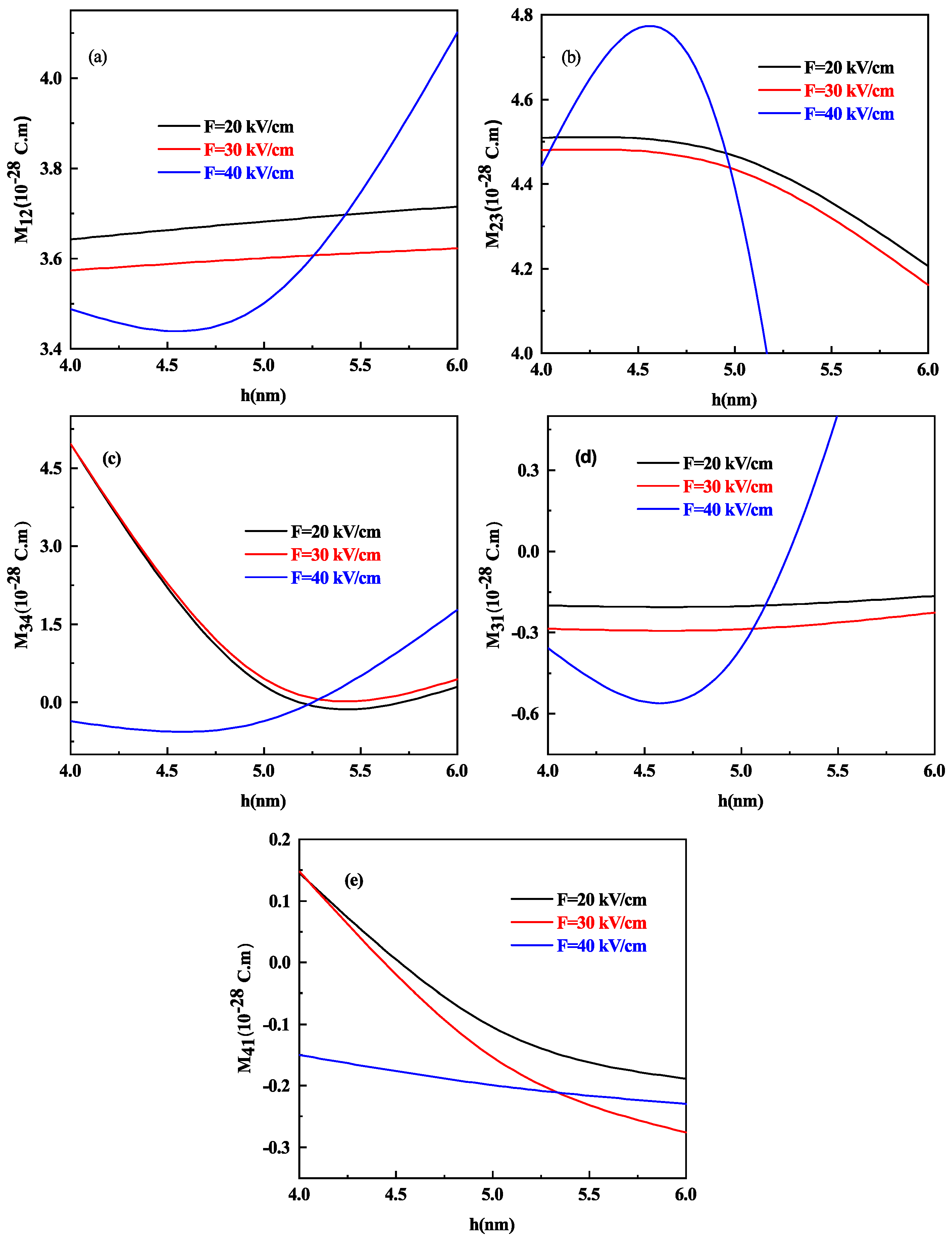
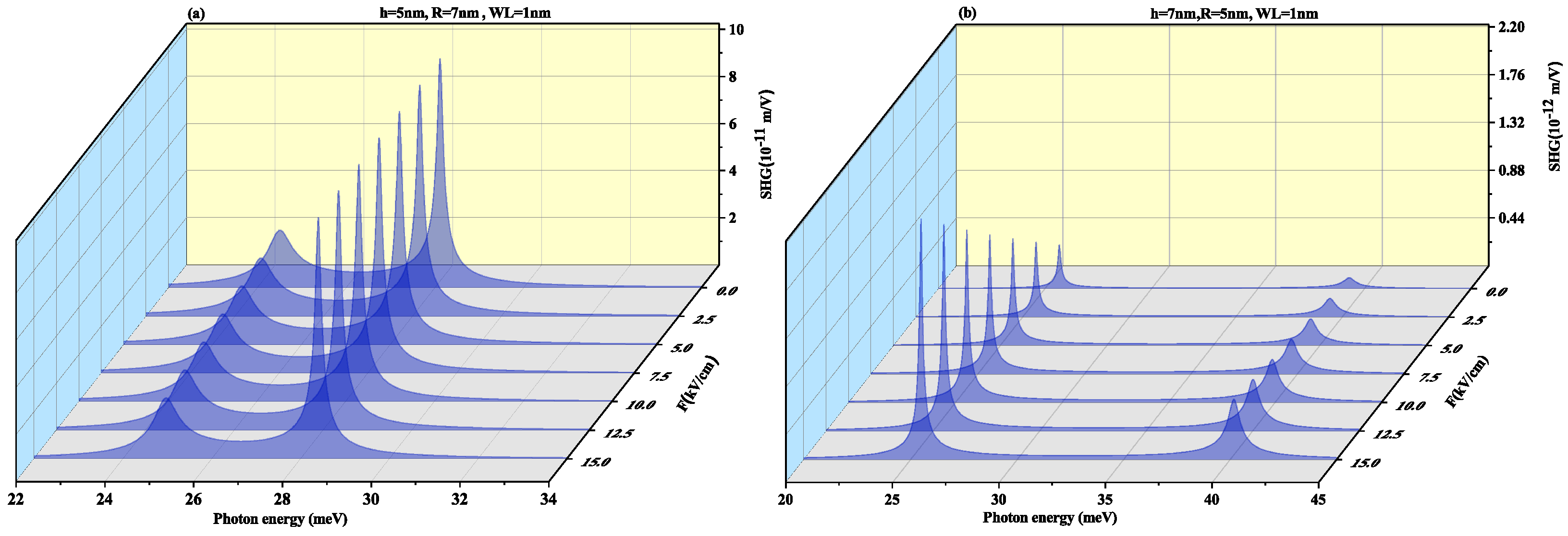
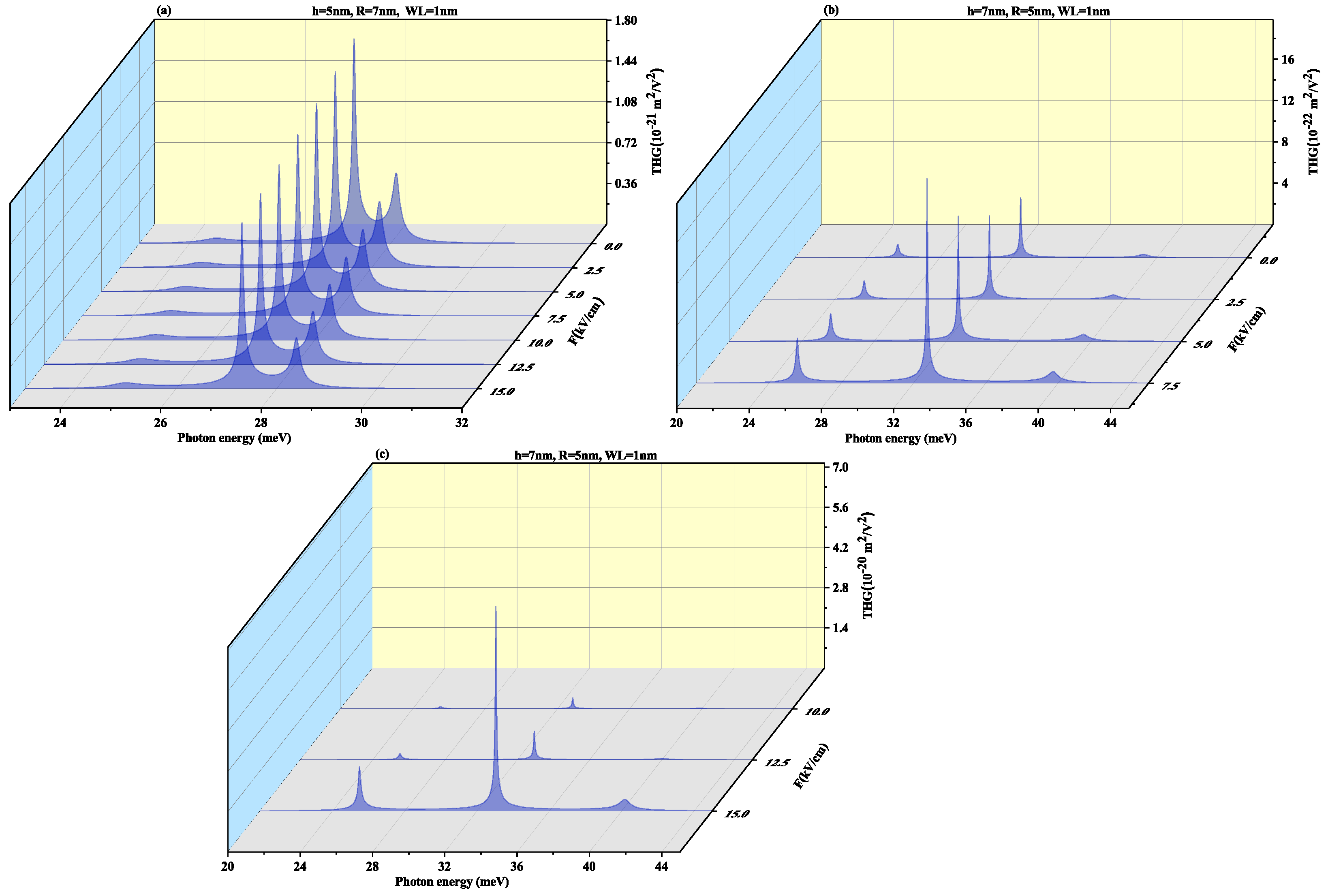
3.2. With Electric Field (In z-Direction) Perpendicular to Wl
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, W.; Coleman, J.J. Semiconductor Quantum Dots. Curr. Opin. Solid State Mater. Sci. 2016, 20, 352. [Google Scholar] [CrossRef]
- Krishan, B.; Garg, M.R. A literature Review on Quantum Dots. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2015, 4, 7857. [Google Scholar]
- Chakraborty, T. Nanoscopic quantum rings: A new perspective. In Advance in Solid State Physics; Kramer, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 43, pp. 79–94. [Google Scholar]
- Vinasco, J.A.; Radu, A.; Kasapoglu, E.S.; Restrepo, R.L.; Morales, A.L.; Feddi, E.; Mora-Ramos, M.E.; Duque, C.A. Effects of geometry on the electronic properties of semiconductor elliptical quantum rings. Sci. Rep. 2018, 8, 1. [Google Scholar] [CrossRef] [PubMed]
- Meyer, B.K.; Sann, J.; Lautenschlger, S.; Wagner, M.R.; Hoffmann, A. Ionized and neutral donor-bound excitons in ZnO. Phys. Rev. B 2007, 76, 184120. [Google Scholar] [CrossRef]
- Zeng, Z.; Garoufalis, C.S.; Baskoutas, S.; Bester, G. Electronic and optical properties of ZnO quantum dots under hydrostatic pressure. Phys. Rev. B 2013, 87, 125302. [Google Scholar] [CrossRef]
- Boxberg, F.; Tulkki, J. Quantum Dots: Phenomenology, Photonic and Electronic Properties, Modeling and Technology. In Handbook of Nanotechnology: Nanometer Structure Theory, Modeling, and Simulation; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Vahdani, M.R.K.; Rezaei, G. Intersubband optical absorption coefficients and refractive index changes in a parabolic cylinder quantum dot. Phys. Lett. A 2010, 374, 637. [Google Scholar] [CrossRef]
- Cantele, G.; Ninno, D.; Iadonisi, G. Shape effects on the one-and two-electron ground state in ellipsoidal quantum dots. Phys. Rev. B 2001, 64, 125325. [Google Scholar] [CrossRef]
- Nayak, D.K.; Woo, J.C.S.; Park, J.S.; Wang, K.; MacWilliams, K.P.; MACWIL-LIAMS, K. Enhancement-mode quantum-well Ge/sub x/Si/sub 1-x/PMOS. IEEE Electron Device Lett. 1991, EDL-12, 154. [Google Scholar] [CrossRef]
- Lee, H.; Leventis, H.C.; Moon, S.J.; Chen, P.; Ito, S.; Haque, S.A.; Torres, T.; Nesch, F.; Geiger, T.; Zakeeruddin, S.M.; et al. PbS and CdS quantum dot-sensitized solid-state solar cells:Old concepts, new results. Adv. Funct. Mater. 2009, 19, 2735. [Google Scholar] [CrossRef]
- Lew Yan Voon, L.C.; Willatzen, M. Confined states in lens-shaped quantum dots. J. Phys. Condens. Matter. 2002, 14, 13667. [Google Scholar] [CrossRef]
- Lbl, M.C.; Scholz, S.; Sllner, I.; Ritzmann, J.; Denneulin, T.; Kovcs, A.; Kardynal, B.E.; Wieck, A.D.; Ludwig, A.; Warburton, R.J. Excitons in InGaAs quantum dots without electron wetting layer states. Commun. Phys. 2019, 2, 1. [Google Scholar] [CrossRef]
- Heyn, C.; Radu, A.; Vinasco, J.A.; Laroze, D.; Restrepo, R.L.; Tulupenko, V.; Hieu, N.N.; Phuc, H.V.; Mora-Ramos, M.E.; Ojeda, J.H.; et al. Exciton states in conical quantum dots under applied electric and magnetic fields. Opt. Laser Technol. 2021, 139, 106953. [Google Scholar] [CrossRef]
- Sabaeian, M.; Riyahi, M. Truncated pyramidal-shaped InAs/GaAs quantum dots in the presence of a vertical magnetic field: An investigation of THz wave emission and absorption. Physica E 2017, 89, 105. [Google Scholar] [CrossRef]
- Sabaeian, M.; Nasab, A.K. Size-dependent intersubband optical properties of dome-shaped InAs/GaAs quantum dots with wetting layer. Appl. Opt. 2012, 51, 4176. [Google Scholar] [CrossRef] [PubMed]
- Oukerroum, A.; Feddi, E.; Bosch Bailach, J.; Martinez-Pastor, J.; Dujardin, F.; Assaid, E. On the anomalous Stark effect in a thin disc-shaped quantum dot. J. Phys. Condens. Matter. 2010, 22, 375301. [Google Scholar] [CrossRef]
- Warburton, R.J.; Schulhauser, C.; Haft, D.; Scheflein, C.; Karrai, K.; Garcia, J.M.; Schoenfeld, W.; Petroff, P.M. Giant permanent dipole moments of excitons in semiconductor nanostructures. Phys. Rev. B 2002, 65, 113303. [Google Scholar] [CrossRef]
- Cantele, G.; Ninno, D.; Iadonisi, G. Calculation of the infrared optical transitions in semiconductor ellipsoidal quantum dots. Nano Lett. 2001, 1, 121. [Google Scholar] [CrossRef]
- Kria, M.; Varsha; Farkous, M.; Prasad, V.; Dujardin, F.; Perez, L.M.; Laroze, D.; Feddi, E. Wetting layer and size effects on the nonlinear optical properties of semi oblate and prolate Si0.7Ge0.3/Si quantum dots. Curr. Appl. Phys. 2021, 25, 1–11. [Google Scholar] [CrossRef]
- Van den Broek, M.; Peeters, F.M. Confined states in two-dimensional flat elliptic quantum dots and elliptic quantum wires. Phys. E Low-Dimens. Syst. Nanostruct. 2001, 11, 345. [Google Scholar] [CrossRef]
- Cantele, G.; Piacente, G.; Ninno, D.; Iadonisi, G. Optical anisotropy of ellipsoidal quantum dots. Phys. Rev. B 2002, 66, 113308. [Google Scholar] [CrossRef]
- Even, J.; Loualiche, S. New analytical calculations of the resonance modes in lens-shaped cavities: Applications to the calculations of the energy levels and electronic wavefunctions in quantum dots. J. Phys. A. Math. Gen. 2003, 36, 11677. [Google Scholar] [CrossRef]
- Assaid, M.; Aydi, M.; Feddi, M.; Dujardin, F. Exact analytical solutions for shallow impurity states in symmetrical paraboloidal and hemiparaboloidal quantum dots. Cent. Eur. J. Phys. 2008, 6, 97. [Google Scholar] [CrossRef]
- Aderras, L.; Feddi, E.; Bah, A.; Dujardin, F.; Duque, C.A. On the electronic states in lens-shaped quantum dots. Phys. Status Solidi Basic Res. 2017, 254, 1700144. [Google Scholar] [CrossRef]
- Aderras, L.; Bah, A.; Feddi, E.; Dujardin, F.; Duque, C.A. Stark-shift of impurity fundamental state in a lens shaped quantum dot. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 89, 119. [Google Scholar] [CrossRef]
- Rezaei, G.; Mousazadeh, Z.; Vaseghi, B. Nonlinear optical properties of a two-dimensional elliptic quantum dot. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 1477. [Google Scholar] [CrossRef]
- Dvoyan, K.G.; Hayrapetyan, D.B.; Kazaryan, E.M.; Tshantshapanyan, A.A. Electron states and light absorption in strongly oblate and strongly prolate ellipsoidal quantum dots in presence of electrical and magnetic fields. Nanoscale Res. Lett. 2007, 2, 601. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Shi, L.; Yan, Z. Effects of electric field and shape on the ground state energy of an exciton bound to an ionized donor impurity in ellipsoidal quantum dots. J. Appl. Phys. 2013, 114, 194301. [Google Scholar]
- Dujardin, F.; Feddi, E.; Assaid, E. Excitonic binding energy in prolate and oblate spheroidal quantum dots. Superlattices Microstruct. 2018, 114, 296. [Google Scholar] [CrossRef]
- Temkin, H.; Bean, J.C.; Antreasyan, A.; Leibenguth, R. GexSi1−x strained-layer heterostructure bipolar transistors. Appl. Phys. Lett. 1988, 52, 1089. [Google Scholar] [CrossRef]
- Luryi, S.; Kastalsky, A.; Bean, J.C. New infrared detector on a silicon chip. IEEE Trans. Electron Devices 1984, ED-31, 1135. [Google Scholar] [CrossRef]
- Park, J.S.; Karunasiri, R.P.G.; Wang, K.L. Observation of large Stark shift in GexSi1−x/Si multiple quantum wells. J. Vac. Sci. Technol. B 1990, 8, 217. [Google Scholar] [CrossRef]
- Rhee, S.S.; Park, J.S.; Karunasiri, R.P.G.; Ye, Q.; Wang, K.L. Resonant tunneling through a Si/GexSi1−x/Si heterostructure on a GeSi buffer layer. Appl. Phys. Lett. 1988, 53, 204. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, Z.; Yao, W.; Liu, Y.; Ye, H. Linear and nonlinear optical properties of strained GaN/AlN quantum dots: Effects of impurities, radii of QDs, and the incident optical intensity. Superlattices Microstruct. 2010, 48, 434. [Google Scholar] [CrossRef]
- Lu, L.; Xie, W.; Shu, Z. Combined effects of hydrostatic pressure and temperature on nonlinear properties of an exciton in a spherical quantum dot under the applied electric field. Phys. B Condens. Matter 2011, 406, 3735. [Google Scholar] [CrossRef]
- Li, B.; Guo, K.X.; Liu, Z.L.; Zheng, Y.B. Nonlinear optical rectification in parabolic quantum dots in the presence of electric and magnetic fields. Phys. Lett. A 2008, 372, 1337. [Google Scholar] [CrossRef]
- Deng, H.X.; Li, S.S.; Li, J. Quantum confinement effects and electronic properties of SnO2 quantum wires and dots. J. Phys. Chem. C 2010, 114, 4841. [Google Scholar] [CrossRef]
- Duque, C.M.; Mora-Ramos, M.E.; Duque, C.A. Properties of the second and third harmonics generation in a quantum disc with inverse square potential. A modeling for nonlinear optical responses of a quantum ring. J. Lumin. 2013, 138, 53. [Google Scholar] [CrossRef]
- Talbi, A.; Haouari, E.; Feddi, E.; Dujardin, F.; Addou, M.; Duque, C.A. Interplay between normal and abnormal stark shift according to the quantum dot spherical core/shell size ratio. Philos. Mag. Lett. 2018, 98, 252. [Google Scholar] [CrossRef]
- Ruddock, I.S. Nonlinear optical second harmonic generation. Eur. J. Phys. 1994, 15, 53. [Google Scholar] [CrossRef]
- Dvoyan, K.G.; Kazaryan, E.M. Impurity states in a weakly prolate (oblate) ellipsoidal microcrystal placed in a magnetic field. Phys. Stat. Sol. 2001, 228, 695. [Google Scholar] [CrossRef]
- Shahzadeh, M.; Sabaeian, M. Numerical analysis of optical properties of oblate semi-spheroid-shaped quantum dots coupled to wetting layer. J. Opt. Soc. Am. B 2015, 32, 1097. [Google Scholar] [CrossRef]
- Armstrong, G.A.; Maiti, C.K. Technology Computer Aided Design for Si, SiGe and GaAs Integrated Circuits; IET: London, UK, 2007; Volume 2. [Google Scholar]
- Rezaei, G.; Vaseghi, B.; Ebrahimi, J. External electric field effects on the electronic and hydrogenic impurity states in ellipsoidal and semi-ellipsoidal quantum dots. Superlattices Microst. 2013, 49, 591–598. [Google Scholar] [CrossRef]
- Baira, M.; Aljaghwani, M.; Salem, B.; Madhar, N.A.; Ilahi, B. Investigation of GeSn/Ge quantum dots’ optical transitions for integrated optics on Si substrate. Results Phys. 2019, 12, 1732. [Google Scholar] [CrossRef]
- Baira, M.; Salem, B.; Madhar, N.A.; Ilahi, B. Intersubband Optical Nonlinearity of GeSn Quantum Dots under Vertical Electric Field. Micromachine 2019, 10, 243. [Google Scholar] [CrossRef]
- Nobandegani, S.G.; Karimi, M.J. Effects of hydrogenic impurity and external fields on the optical absorption in a ring-shaped elliptical quantum dot. Opt. Mater. 2018, 82, 75. [Google Scholar] [CrossRef]
- Kasper, E.; Paul, D.J. Silicon quantum integrated circuits: Silicon-germanium heterostructure devices: Basics and realisations. Nanosci. Technol. 2005, xii, 360. [Google Scholar]
- Naffouti, M.; David, T.; Benkouider, A.; Favre, L.; Cabie, M.; Ronda, A.; Berbezier, I.; Abbarchi, M. Fabrication of core–shell nanostructures via silicon on insulator dewetting and germanium condensation: Towards a strain tuning method for SiGe-based heterostructures in a three-dimensional geometry. Nanotechnology 2016, 27, 305602. [Google Scholar] [CrossRef]
- David, T.; Liu, K.; Ronda, A.; Favre, L.; Abbarchi, M.; Gailhanou, M.; Gentile, P.; Buttard, D.; Calvo, V.; Amato, M.; et al. Tailoring strain and morphology of core–shell SiGe nanowires by low-temperature ge condensation. Nano Lett. 2017, 17, 7299. [Google Scholar] [CrossRef]
- Toliopoulos, D.; Khoury, M.; Bouabdellaoui, M.; Granchi, N.; Claude, J.-B.; Benali, A.; Berbezier, I.; Hannani, D.A.; Ronda, J.; Wenger, M.; et al. Fabrication of spectrally sharp Si-based dielectric resonators: Combining etaloning with Mie resonances. Opt. Express 2020, 28, 37734. [Google Scholar] [CrossRef] [PubMed]
- Poborchii, V.; Bouabdellaoui, M.; Uchida, N.; Ronda, A.; Berbezier, I.; David, T.; Ruiz, C.M.; Zazoui, M.; Sena, R.P.; Abbarchi, M. Raman microscopy and infrared optical properties of SiGe Mie resonators formed on SiO2 via Ge condensation and solid state dewetting. Nanotechnology 2020, 31, 195602. [Google Scholar] [CrossRef]
- Carletti, L.; Ma, P.; Luther-Davies, B.; Hudson, D.; Monat, C.; Madden, S.; Moss, D.J.; Brun, M.; Ortiz, S.; Nicoletti, S.; et al. Nonlinear optical properties of SiGe waveguides in the mid-infrared. CLEO Opt. Soc. Am. 2014, SW3M.7. [Google Scholar] [CrossRef]
- Duque, C.A.; Akimov, V.; Demediuk, R.; Belykh, V.; Tiutiunnyk, A.; Morales, A.L.; Restrepo, R.L.; Mora-Ramos, M.E.; Fomina, O.; Tulupenko, V. Intersubband linear and nonlinear optical response of the delta-doped SiGe quantum well. Superlattices Microstruct. 2015, 87, 125. [Google Scholar] [CrossRef]
- Lacava, C.; Ettabib, M.A.; Petropoulos, P. Nonlinear silicon photonic signal processing devices for future optical networks. Appl. Sci. 2017, 7, 103. [Google Scholar] [CrossRef]
- Lange, C.; Köster, N.S.; Chatterjee, S.; Sigg, H.; Chrastina, D.; Isella, G.; von Känel, H.; Kunert, B.; Stolz, W. Comparison of ultrafast carrier thermalization in GaxIn1−x As and Ge quantum wells. Phys. Rev. B 2010, 81, 045320. [Google Scholar] [CrossRef]
- Soref, R.A. Electro-optical and nonlinear optical coefficients of ordered group IV semiconductor alloys. J. Appl. Phys. 1992, 72, 626. [Google Scholar] [CrossRef]
- Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe; John Wiley Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Vahdani, M.R.K.; Rezaei, G. Linear and nonlinear optical properties of a hydrogenic donor in lens-shaped quantum dots. Phys. Lett. A 2009, 373, 3079. [Google Scholar] [CrossRef]
- Varsha; Silotia, P.; Prasad, V. Study of optical properties of Wannier-Mott exciton in spherical quantum dot in Kratzer potential. AIP Conf. Proc. 2020, 2220, 020154. [Google Scholar]
- Kria, M.; El-Yadri, M.; Aghoutane, N.; Peŕez, L.M.; Laroze, D.; Feddi, E. Forecasting and analysis of nonlinear optical responses by tuning the thickness of a doped hollow cylindrical quantum dot. Chin. J. Phys. 2020, 66, 444. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 2nd ed.; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Hanamura, E.; Kawabe, Y.; Yamanaka, A. Quantum Nonlinear Optics; Springer Press: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Nautiyal, V.V.; Silotia, P. Second harmonic generation in a disk shaped quantum dot in the presence of spin-orbit interaction. Phys. Lett. A 2018, 382, 2061. [Google Scholar] [CrossRef]
- El Aouami, A.; Bikerouin, M.; Feddi, K.; Aghoutane, N.; El-Yadri, M.; Feddi, E.; Dujardin, F.; Radu, A.; Restrepo, R.L.; Vinasco, J.A.; et al. Linear and nonlinear optical properties of a single dopant in GaN conical quantum dot with spherical cap. Philos. Mag. 2020, 100, 2503. [Google Scholar] [CrossRef]
- Sasso, G.; Rinaldi, N.; Matz, G.; Jungemann, C. Accurate mobility and energy relaxation time models for SiGe HBTs numerical simulation. In Proceedings of the 2009 International Conference on Simulation of Semiconductor Processes and Devices, San Diego, CA, USA, 9–11 September 2009; pp. 1–4. [Google Scholar]
- COMSOL Multiphysics Software Version 5.2. Available online: www.comsol.com (accessed on 6 June 2021).
- Yu, Y.; Shang, X.-J.; Li, M.-F.; Zha, G.-W.; Xu, J.-X.; Wang, L.-J.; Wang, G.-W.; Ni, H.-Q.; Dou, X.; Sun, B. Single InAs quantum dot coupled to different “environments” in one wafer for quantum photonics. Appl. Phys. Lett. 2013, 102, 201103. [Google Scholar] [CrossRef]
- Li, B.; Guo, K.X.; Zhang, C.J.; Zheng, Y.B. The second-harmonic generation in parabolic quantum dots in the presence of electric and magnetic fields. Phys. Lett. A 2007, 367, 493. [Google Scholar] [CrossRef]
- Karabulut, I.; Baskoutas, S. Second and third harmonic generation susceptibilities of spherical quantum dots: Effects of impurities, electric field and size. J. Compt. Theo. Nano. 2009, 6, 153. [Google Scholar] [CrossRef]
- Kirak, M.; Altinok, Y. The electric field effects on the third-harmonic generation in spherical quantum dots with parabolic confinement. Eurp. Phys. J. B 2012, 85, 344. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varsha; Kria, M.; Hamdaoui, J.E.; Pérez, L.M.; Prasad, V.; El-Yadri, M.; Laroze, D.; Feddi, E.M. Quantum Confined Stark Effect on the Linear and Nonlinear Optical Properties of SiGe/Si Semi Oblate and Prolate Quantum Dots Grown in Si Wetting Layer. Nanomaterials 2021, 11, 1513. https://doi.org/10.3390/nano11061513
Varsha, Kria M, Hamdaoui JE, Pérez LM, Prasad V, El-Yadri M, Laroze D, Feddi EM. Quantum Confined Stark Effect on the Linear and Nonlinear Optical Properties of SiGe/Si Semi Oblate and Prolate Quantum Dots Grown in Si Wetting Layer. Nanomaterials. 2021; 11(6):1513. https://doi.org/10.3390/nano11061513
Chicago/Turabian StyleVarsha, Mohamed Kria, Jawad El Hamdaoui, Laura M. Pérez, Vinod Prasad, Mohamed El-Yadri, David Laroze, and El Mustapha Feddi. 2021. "Quantum Confined Stark Effect on the Linear and Nonlinear Optical Properties of SiGe/Si Semi Oblate and Prolate Quantum Dots Grown in Si Wetting Layer" Nanomaterials 11, no. 6: 1513. https://doi.org/10.3390/nano11061513
APA StyleVarsha, Kria, M., Hamdaoui, J. E., Pérez, L. M., Prasad, V., El-Yadri, M., Laroze, D., & Feddi, E. M. (2021). Quantum Confined Stark Effect on the Linear and Nonlinear Optical Properties of SiGe/Si Semi Oblate and Prolate Quantum Dots Grown in Si Wetting Layer. Nanomaterials, 11(6), 1513. https://doi.org/10.3390/nano11061513





