Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble
Abstract
1. Introduction
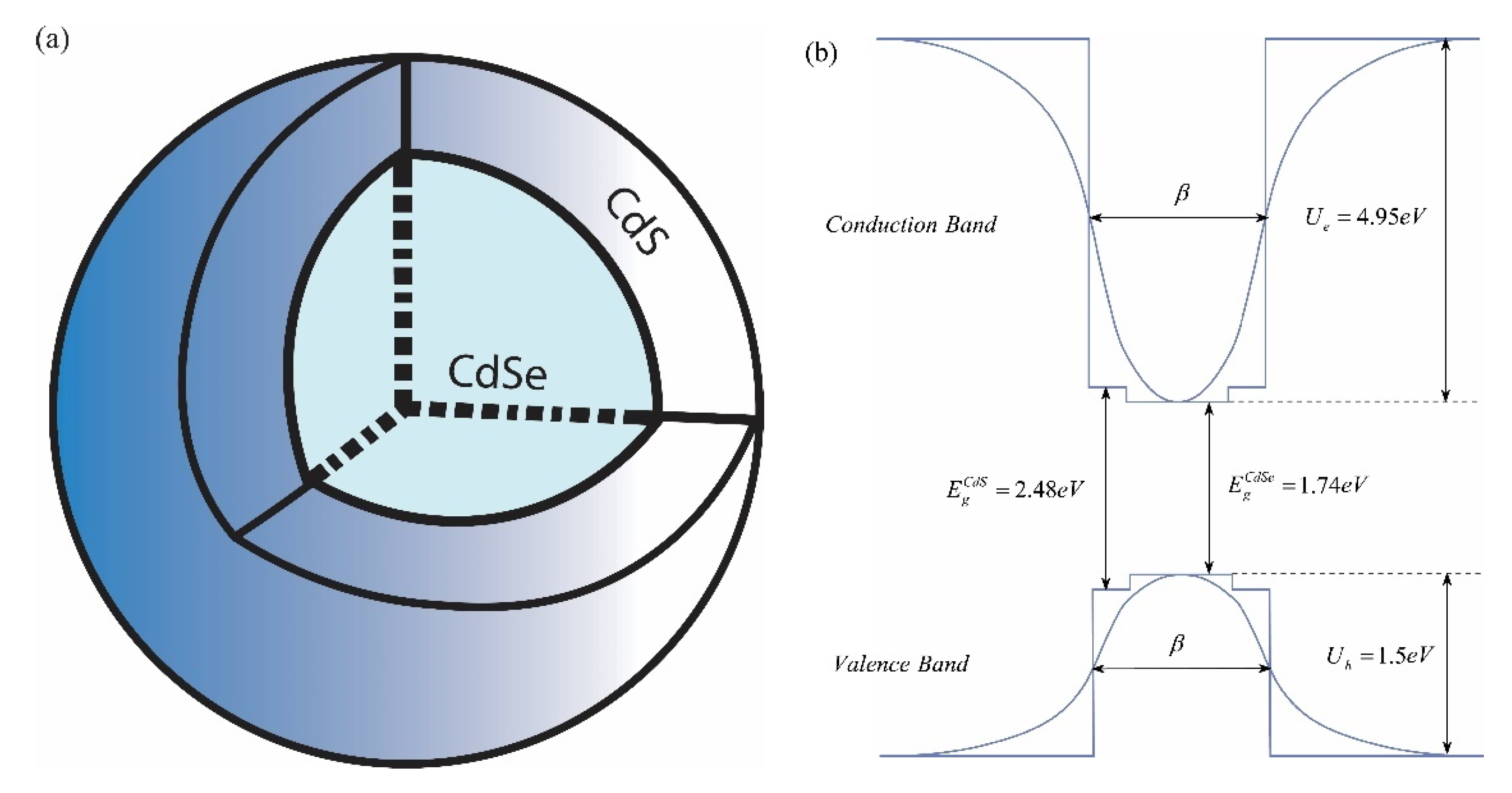
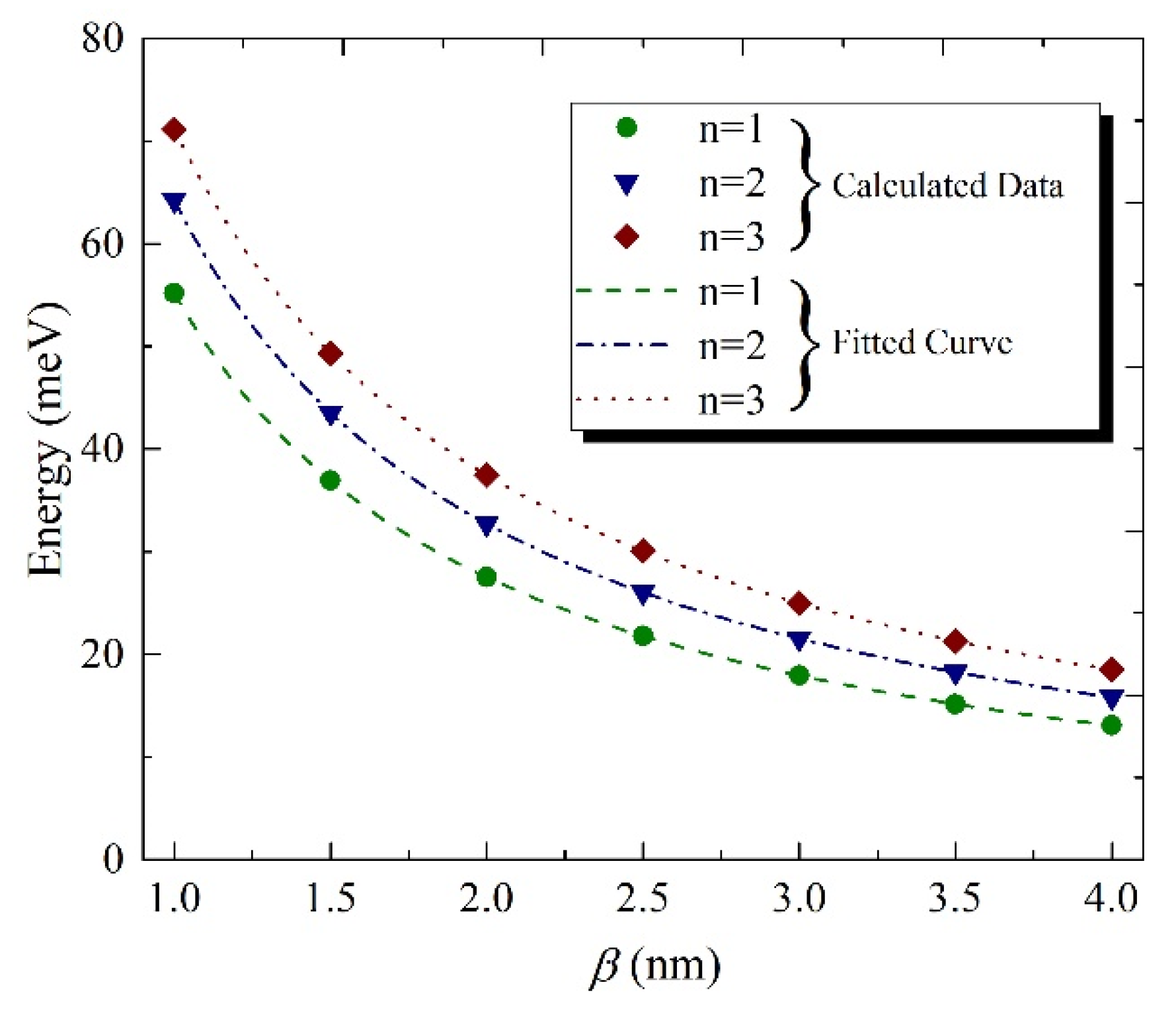
2. Exciton States
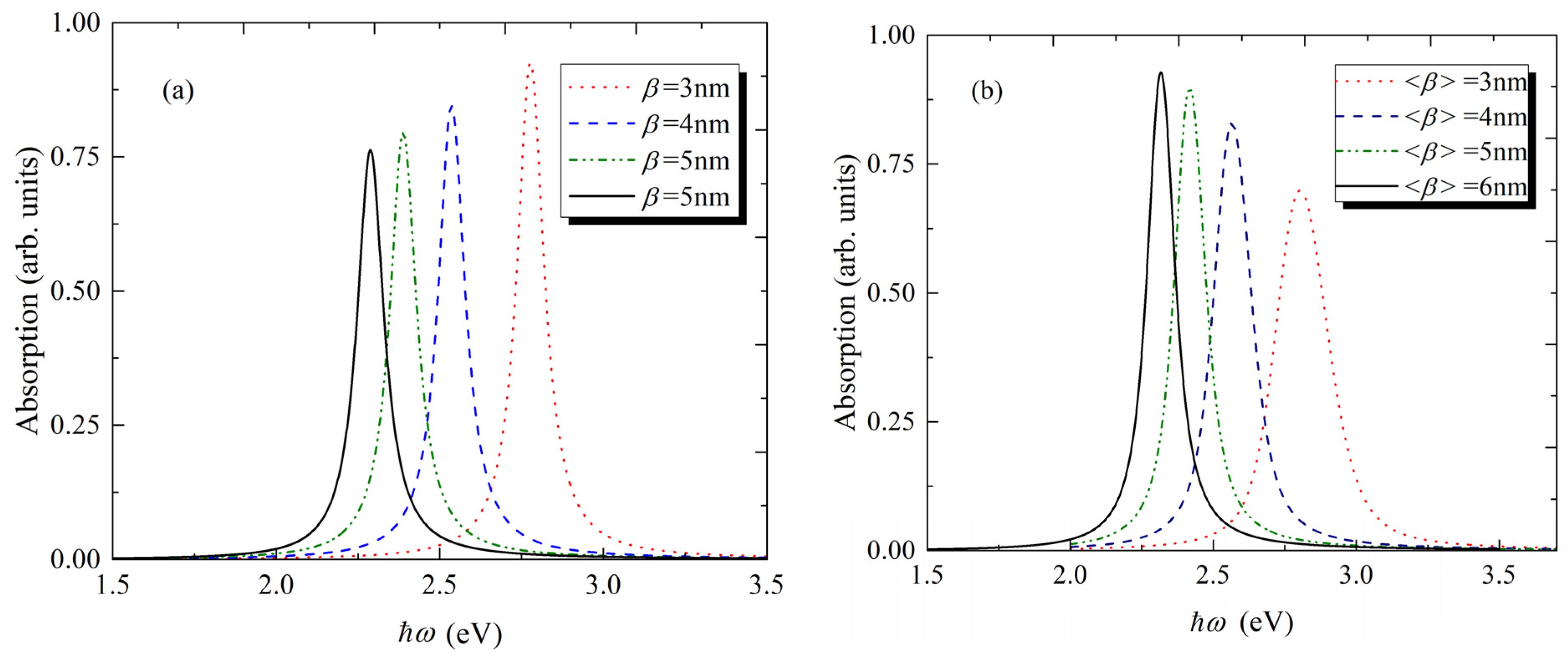
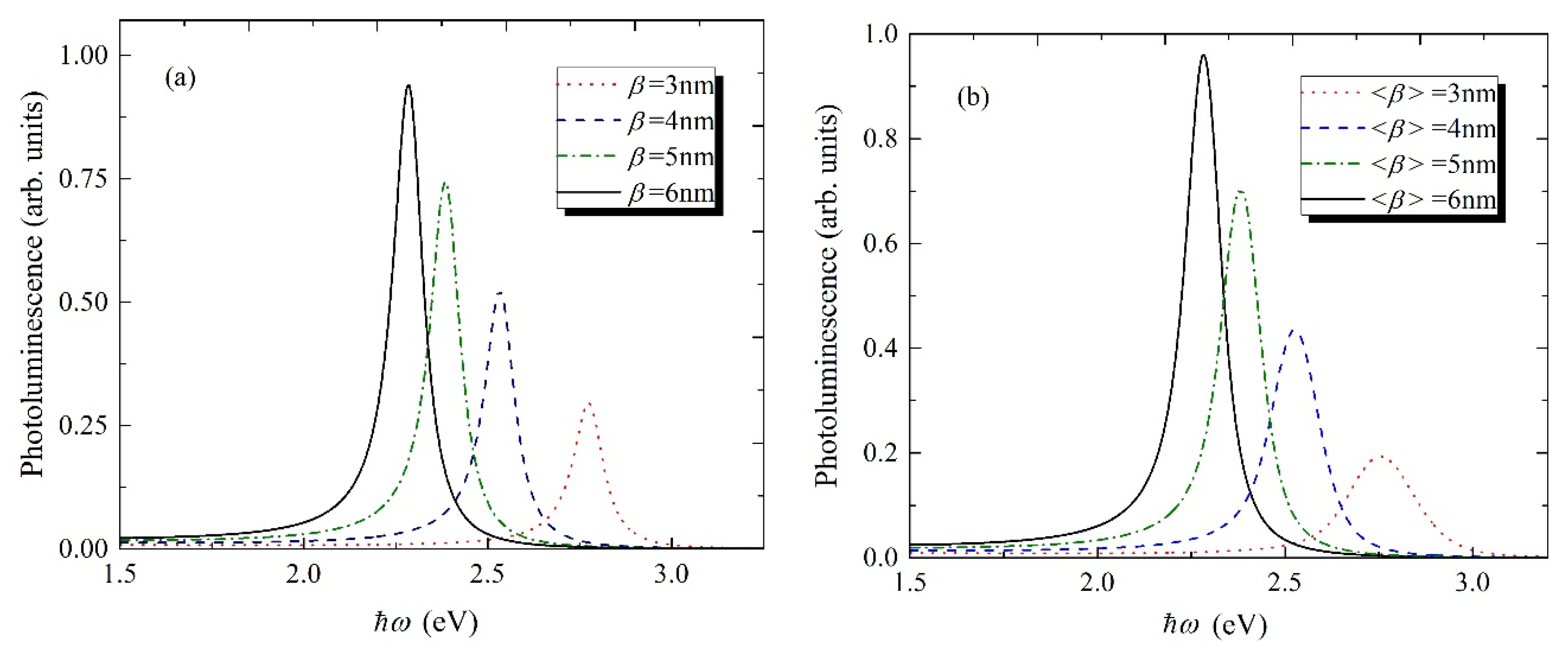
3. Optical Properties
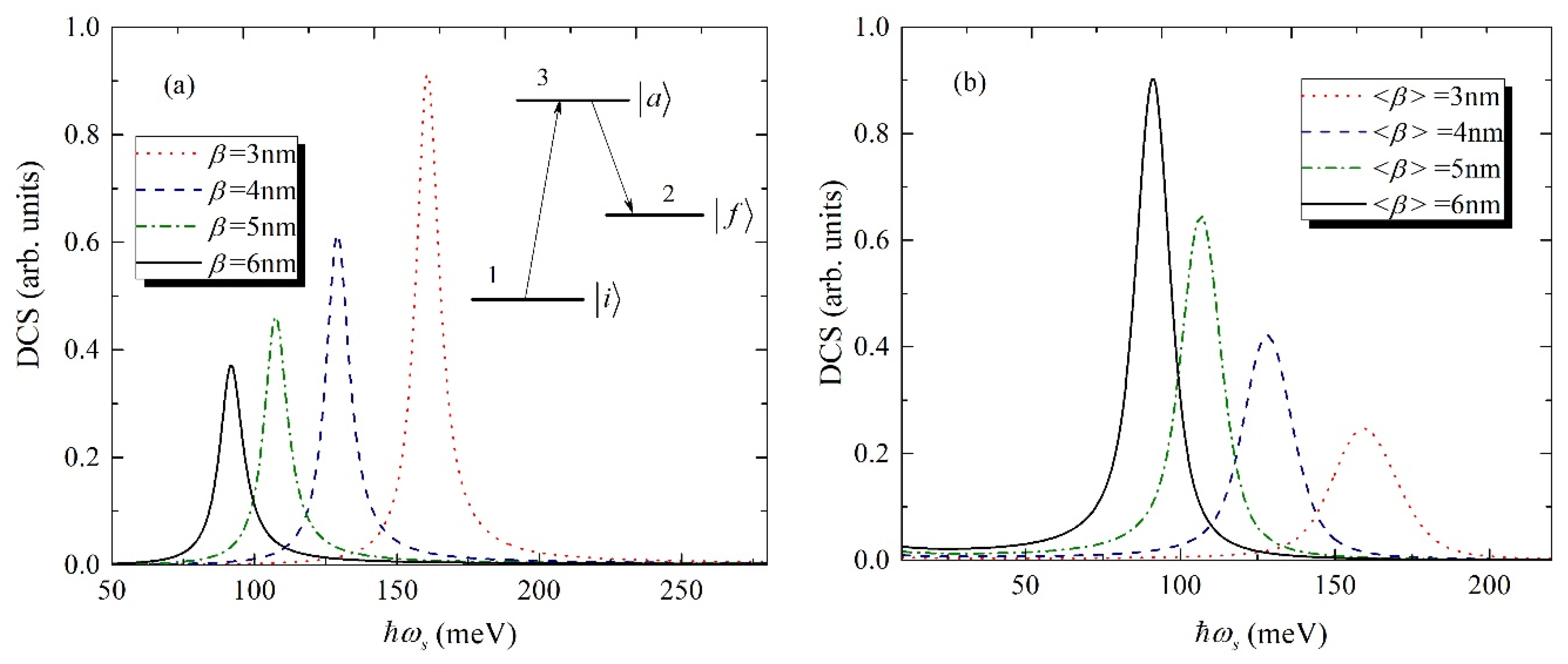
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kagan, C.R.; Lifshitz, E.; Sargent, E.H.; Talapin, D.V. Building devices from colloidal quantum dots. Science 2016, 353, 885. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Guo, X.; Luo, Y.; Li, Q.; Zhu, R.; Pang, H. Core-shell materials for advanced batteries. Chem. Eng. J. 2019, 355, 208–237. [Google Scholar] [CrossRef]
- Clifford, J.P.; Konstantatos, G.; Johnston, K.W.; Hoogland, S.; Levina, L.; Sargent, E.H. Fast, sensitive and spectrally tuneable colloidal-quantum-dot photodetectors. Nat. Nanotechnol. 2008, 4, 40–44. [Google Scholar] [CrossRef] [PubMed]
- Konstantatos, G.; Howard, I.S.; Fischer, A.; Hoogland, S.; Clifford, J.P.; Klem, E.J.D.; Levina, L.; Sargent, E.H. Ultrasensitive solution-cast quantum dot photodetectors. Nat. Cell Biol. 2006, 442, 180–183. [Google Scholar] [CrossRef] [PubMed]
- Chen, O.; Zhao, J.; Chauhan, V.P.; Cui, J.; Wong, C.; Harris, D.K.; Wei, H.; Han, H.-S.; Fukumura, D.; Jain, R.K.; et al. Compact high-quality CdSe–CdS core–shell nanocrystals with narrow emission linewidths and suppressed blinking. Nat. Mater. 2013, 12, 445–451. [Google Scholar] [CrossRef] [PubMed]
- Vasudevan, D.; Gaddam, R.R.; Trinchi, A.; Cole, I. Core–shell quantum dots: Properties and applications. J. Alloys Compd. 2015, 636, 395–404. [Google Scholar] [CrossRef]
- Selopal, G.S.; Zhao, H.; Wang, Z.M.; Rosei, F. Core/shell quantum dots solar cells. Adv. Funct. Mater. 2020, 30, 1908762. [Google Scholar] [CrossRef]
- Yuan, X.; Zheng, J.; Zeng, R.; Jing, P.; Ji, W.; Zhao, J.; Yang, W.; Li, H. Thermal stability of Mn2+ion luminescence in Mn-doped core–shell quantum dots. Nanoscale 2014, 6, 300–307. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Garoufalis, C.S.; Terzis, A.F.; Baskoutas, S. Linear and nonlinear optical properties of ZnO/ZnS and ZnS/ZnO core shell quantum dots: Effects of shell thickness, impurity, and dielectric environment. J. Appl. Phys. 2013, 114, 023510. [Google Scholar] [CrossRef]
- Zeiri, N.; Naifar, A.; Nasrallah, S.A.-B.; Said, M. Third nonlinear optical susceptibility of CdS/ZnS core-shell spherical quantum dots for optoelectronic devices. Optik 2019, 176, 162–167. [Google Scholar] [CrossRef]
- Loitsch, B.; Winnerl, J.; Grimaldi, G.; Wierzbowski, J.; Rudolph, D.; Morkotter, S.; Finley, J.J. Crystal phase quantum dots in the ultrathin core of GaAs–AlGaAs core–shell nanowires. Nano Lett. 2015, 15, 7544–7551. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Petrosyan, L.S.; Sarkisyan, H.A. Core/shell/shell spherical quantum dot with Kratzer confining potential: Impurity states and electrostatic multipoles. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 66, 7–12. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, Y.; Li, L.; Liu, H.; Ren, C.; Liu, X.; Tian, G. Hierarchical ZnO nanorod/ZnFe2O4 nanosheet core/shell nanoarray decorated with PbS quantum dots for efficient photoelectrochemical water splitting. J. Alloys Compd. 2020, 828, 154449. [Google Scholar] [CrossRef]
- Kayaci, F.; Vempati, S.; Ozgit-Akgun, C.; Donmez, I.; Biyikli, N.; Uyar, T. Transformation of polymer-ZnO core–shell nano-fibers into ZnO hollow nanofibers: Intrinsic defect reorganization in ZnO and its influence on the photocatalysis. Appl. Catal. B Environ. 2015, 176, 646–653. [Google Scholar] [CrossRef]
- Wang, M.; Peng, Z.; Qian, J.; Li, H.; Zhao, Z.; Fu, X. Highly efficient solar-driven photocatalytic degradation on environmental pollutants over a novel C fibers MoSe2 nanoplates core-shell composite. J. Hazard. Mater. 2018, 347, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Gong, K.; Kelley, D.F.; Kelley, A.M. Electron–Phonon Coupling in CdSe/CdS Core/Shell Quantum Dots. ACS Nano 2015, 9, 8131–8141. [Google Scholar] [CrossRef]
- Kong, D.; Jia, Y.; Ren, Y.; Xie, Z.; Wu, K.; Lian, T. Shell-thickness-dependent biexciton lifetime in type I and quasi-type II CdSe@ CdS core/shell quantum dots. J. Phys. Chem. C 2018, 122, 14091–14098. [Google Scholar] [CrossRef]
- Gong, K.; Kelley, D.F. A predictive model of shell morphology in CdSe/CdS core/shell quantum dots. J. Chem. Phys. 2014, 141, 194704. [Google Scholar] [CrossRef]
- Greytak, A.B.; Allen, P.M.; Liu, W.; Zhao, J.; Young, E.R.; Popović, Z.; Walker, B.J.; Nocera, D.G.; Bawendi, M.G. Alternating layer addition approach to CdSe/CdS core/shell quantum dots with near-unity quantum yield and high on-time fractions. Chem. Sci. 2012, 3, 2028–2034. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Qin, H.; Zhou, J.; Peng, X. Oxygen Stabilizes Photoluminescence of CdSe/CdS Core/Shell Quantum Dots via Deionization. J. Am. Chem. Soc. 2020, 142, 4254–4264. [Google Scholar] [CrossRef]
- Peng, X.; Schlamp, M.C.; Kadavanich, A.V.; Alivisatos, A.P. Epitaxial Growth of Highly Luminescent CdSe/CdS Core/Shell Nanocrystals with Photostability and Electronic Accessibility. J. Am. Chem. Soc. 1997, 119, 7019–7029. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, L.-W. Electronic Structures of the CdSe/CdS Core−Shell Nanorods. ACS Nano 2010, 4, 91–98. [Google Scholar] [CrossRef] [PubMed]
- Tan, R.; Yuan, Y.; Nagaoka, Y.; Eggert, D.; Wang, X.; Thota, S.; Chen, O. Monodisperse hexagonal pyramidal and bipyramidal wurtzite CdSe-CdS core–shell nanocrystals. Chem. Mater. 2017, 29, 4097–4108. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Xie, W. Raman scattering of an exciton in a quantum dot. Phys. B Condens. Matter 2013, 413, 96–99. [Google Scholar] [CrossRef]
- Guo, X.; Liu, C. Exciton-mediated Raman scattering in CdS quantum dot. Phys. E Low Dimens. Syst. Nanostruct. 2017, 93, 271–274. [Google Scholar] [CrossRef]
- Badlyan, N.M.; Biermann, A.; Aubert, T.; Hens, Z.; Maultzsch, J. Thermal expansion of colloidal CdSe/CdS core/shell quantum dots. Phys. Rev. B 2019, 99, 195425. [Google Scholar] [CrossRef]
- Xie, W. Raman scattering of a donor impurity in a quantum ring. Chem. Phys. 2012, 405, 22–25. [Google Scholar] [CrossRef]
- Lu, L.; Xu, X.-L.; Liang, W.-T.; Lu, H.-F. Raman analysis of CdSe/CdS core–shell quantum dots with different CdS shell thickness. J. Phys. Condens. Matter 2007, 19, 406221. [Google Scholar] [CrossRef]
- Martynenko, I.V.; Baimuratov, A.S.; Osipova, V.A.; Kuznetsova, V.A.; Purcell-Milton, F.; Rukhlenko, I.D.; Baranov, A.V. Ex-citation energy dependence of the photoluminescence quantum yield of core/shell CdSe/CdS quantum dots and correlation with circular dichroism. Chem. Mater. 2018, 30, 465–471. [Google Scholar] [CrossRef]
- Stroyuk, O.; Raevskaya, A.; Gaponik, N.; Selyshchev, O.; Dzhagan, V.; Schulze, S.; Zahn, D.R. Origin of the broadband pho-toluminescence of pristine and Cu+/Ag+-doped ultrasmall CdS and CdSe/CdS quantum dots. J. Phys. Chem. C 2018, 122, 10267–10277. [Google Scholar] [CrossRef]
- Dunlap, M.K.; Ryan, D.P.; Goodwin, P.M.; Werner, J.H.; Majumder, S.; Hollingsworth, J.A.; Gelfand, M.P.; Van Orden, A. Super-resolution photoluminescence lifetime and intensity mapping of interacting CdSe/CdS quantum dots. Appl. Phys. Lett. 2020, 116, 021103. [Google Scholar] [CrossRef]
- Purcell-Milton, F.; Visheratina, A.K.; Kuznetsova, V.A.; Ryan, A.; Orlova, A.O.; Gun’Ko, Y.K. Impact of Shell Thickness on Photoluminescence and Optical Activity in Chiral CdSe/CdS Core/Shell Quantum Dots. ACS Nano 2017, 11, 9207–9214. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.-L.; Yang, R.-X.; Yan, W.-G.; Chen, C.-M.; Liu, S.-Y.; Zhao, S.-J.; Ge, W.-Q.; Liu, Z.-F.; Jia, G.-Z. Surface Plasmon-Enhanced Luminescence of CdSe/CdS Quantum Dots Film Based on Au Nanoshell Arrays. Materials 2019, 12, 362. [Google Scholar] [CrossRef] [PubMed]
- Poerschke, R.; Madelung, O. Semiconductors: Other than Group IV Elements and 2I-V Compounds; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Parang, Z.; Keshavarz, A.; Zamani, N. Optimization of optical absorption coefficient in double modified Pöschl–Teller quantum wells. J. Comput. Electron. 2014, 13, 1020–1025. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Tevosyan, H.K. Optical properties of spherical quantum dot with modified Pöschl–Teller potential. Superlattices Microstruct. 2013, 64, 204–212. [Google Scholar] [CrossRef]
- Karimi, M.; Rezaei, G. Effects of external electric and magnetic fields on the linear and nonlinear intersubband optical properties of finite semi-parabolic quantum dots. Phys. B Condens. Matter 2011, 406, 4423–4428. [Google Scholar] [CrossRef]
- Efros, A.L.; Efros, A.L. Interband absorption of light in a semiconductor sphere. Semiconductors 1982, 16, 772–775. [Google Scholar]
- Ramaniah, L.M.; Nair, S.V. Optical absorption in semiconductor quantum dots: A tight-binding approach. Phys. Rev. B 1993, 47, 7132–7139. [Google Scholar] [CrossRef]
- Van Roosbroeck, W.; Shockley, W. Photon-Radiative Recombination of Electrons and Holes in Germanium. Phys. Rev. 1954, 94, 1558–1560. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Pal, B.; Bansal, B. On conversion of luminescence into absorption and the van Roosbroeck-Shockley relation. Appl. Phys. Lett. 2012, 100, 222103. [Google Scholar] [CrossRef]
- Chamberlain, M.P.; Trallero-Giner, C.; Cardona, M. Theory of one-phonon Raman scattering in semiconductor microcrys-tallites. Phys. Rev. B 1995, 51, 1680. [Google Scholar] [CrossRef] [PubMed]
- Trallero-Giner, C.; Debernardi, A.; Cardona, M.; Menendez-Proupin, E.; Ekimov, A.I. Optical vibrons in CdSe dots and dis-persion relation of the bulk material. Phys. Rev. B 1998, 57, 4664. [Google Scholar] [CrossRef]
- Trallero-Giner, C.; Cardona, M. Vibrational Resonant Raman Scattering in Spherical Quantum Dots: Exciton Effects. Phys. Status Solidi B 1997, 199, 81–94. [Google Scholar] [CrossRef]
- Gellen, T.A.; Lem, J.; Turner, D.B. Probing Homogeneous Line Broadening in CdSe Nanocrystals Using Multidimensional Electronic Spectroscopy. Nano Lett. 2017, 17, 2809–2815. [Google Scholar] [CrossRef] [PubMed]
- Fonoberov, V.A.; Balandin, A.A. Origin of ultraviolet photoluminescence in ZnO quantum dots: Confined excitons versus surface-bound impurity exciton complexes. Appl. Phys. Lett. 2004, 85, 5971–5973. [Google Scholar] [CrossRef]
- Gerdova, I.; Haché, A. Third-order non-linear spectroscopy of CdSe and CdSe/ZnS core shell quantum dots. Opt. Commun. 2005, 246, 205–212. [Google Scholar] [CrossRef]
| 1 (i) | −1.816 | 60.339 | −3.338 |
| 2 (f) | −1.809 | 71.940 | −5.873 |
| 3 (a) | −1.886 | 84.390 | −11.360 |
| , ps | 367 | 487 | 610 | 736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mantashian, G.A.; Mantashyan, P.A.; Sarkisyan, H.A.; Kazaryan, E.M.; Bester, G.; Baskoutas, S.; Hayrapetyan, D.B. Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble. Nanomaterials 2021, 11, 1274. https://doi.org/10.3390/nano11051274
Mantashian GA, Mantashyan PA, Sarkisyan HA, Kazaryan EM, Bester G, Baskoutas S, Hayrapetyan DB. Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble. Nanomaterials. 2021; 11(5):1274. https://doi.org/10.3390/nano11051274
Chicago/Turabian StyleMantashian, Grigor A., Paytsar A. Mantashyan, Hayk A. Sarkisyan, Eduard M. Kazaryan, Gabriel Bester, Sotirios Baskoutas, and David B. Hayrapetyan. 2021. "Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble" Nanomaterials 11, no. 5: 1274. https://doi.org/10.3390/nano11051274
APA StyleMantashian, G. A., Mantashyan, P. A., Sarkisyan, H. A., Kazaryan, E. M., Bester, G., Baskoutas, S., & Hayrapetyan, D. B. (2021). Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble. Nanomaterials, 11(5), 1274. https://doi.org/10.3390/nano11051274








