Micron-Scale Anomalous Hall Sensors Based on FexPt1−x Thin Films with a Large Hall Angle and near the Spin-Reorientation Transition
Abstract
1. Introduction
2. Materials and Methods
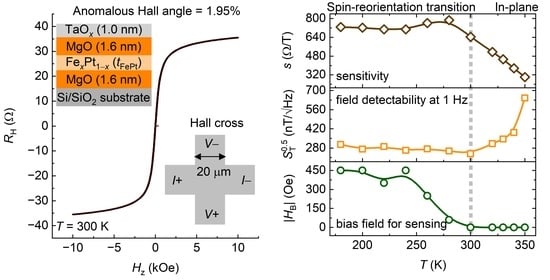
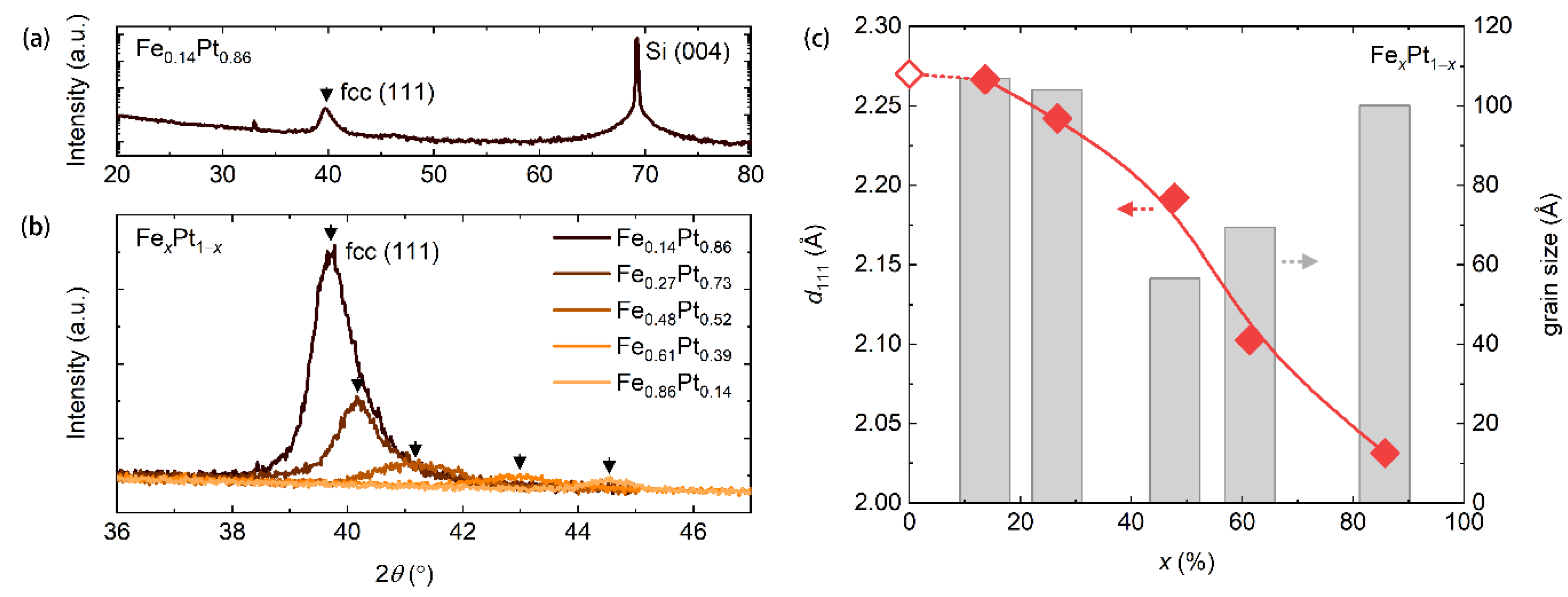
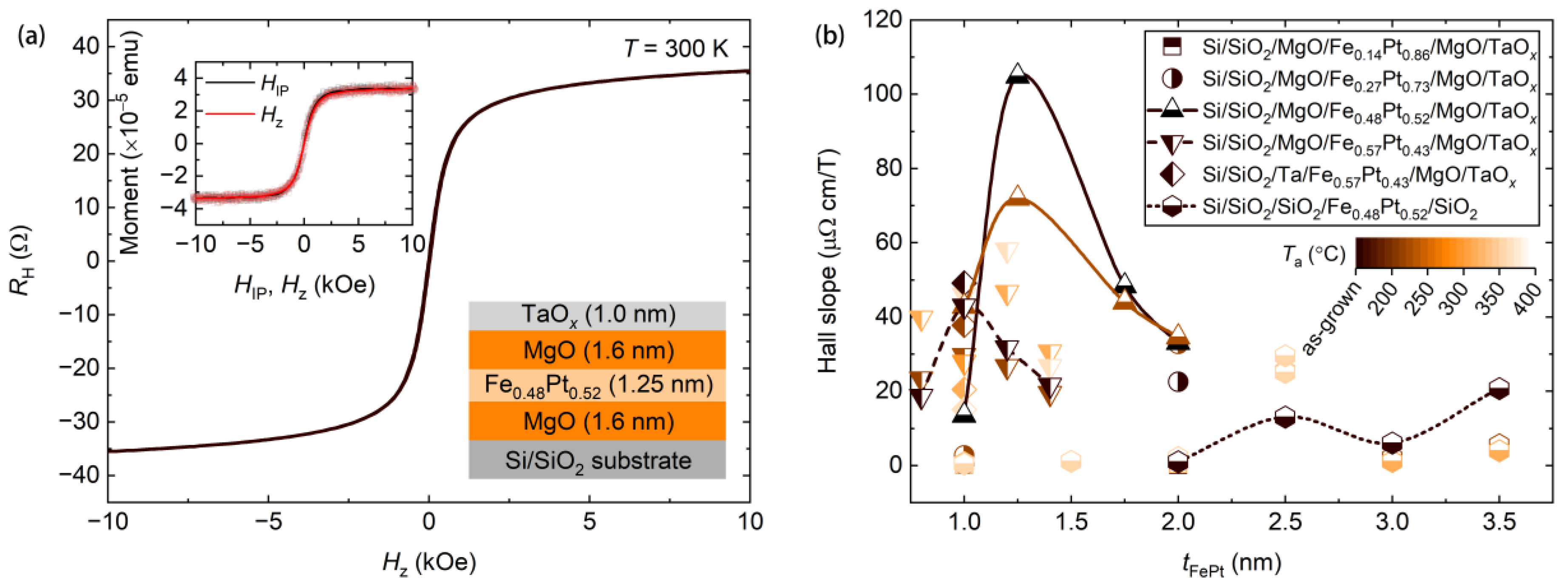
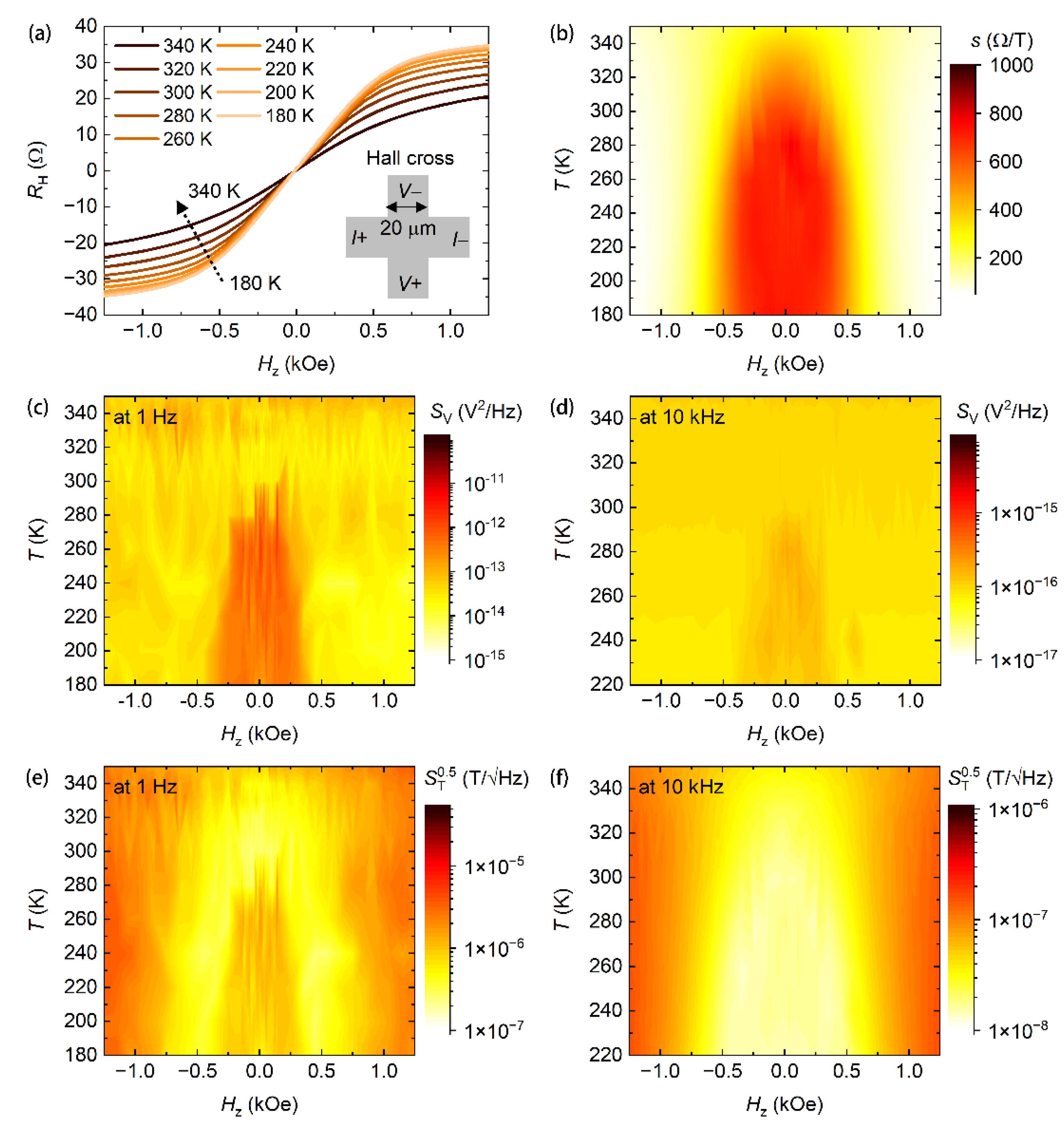
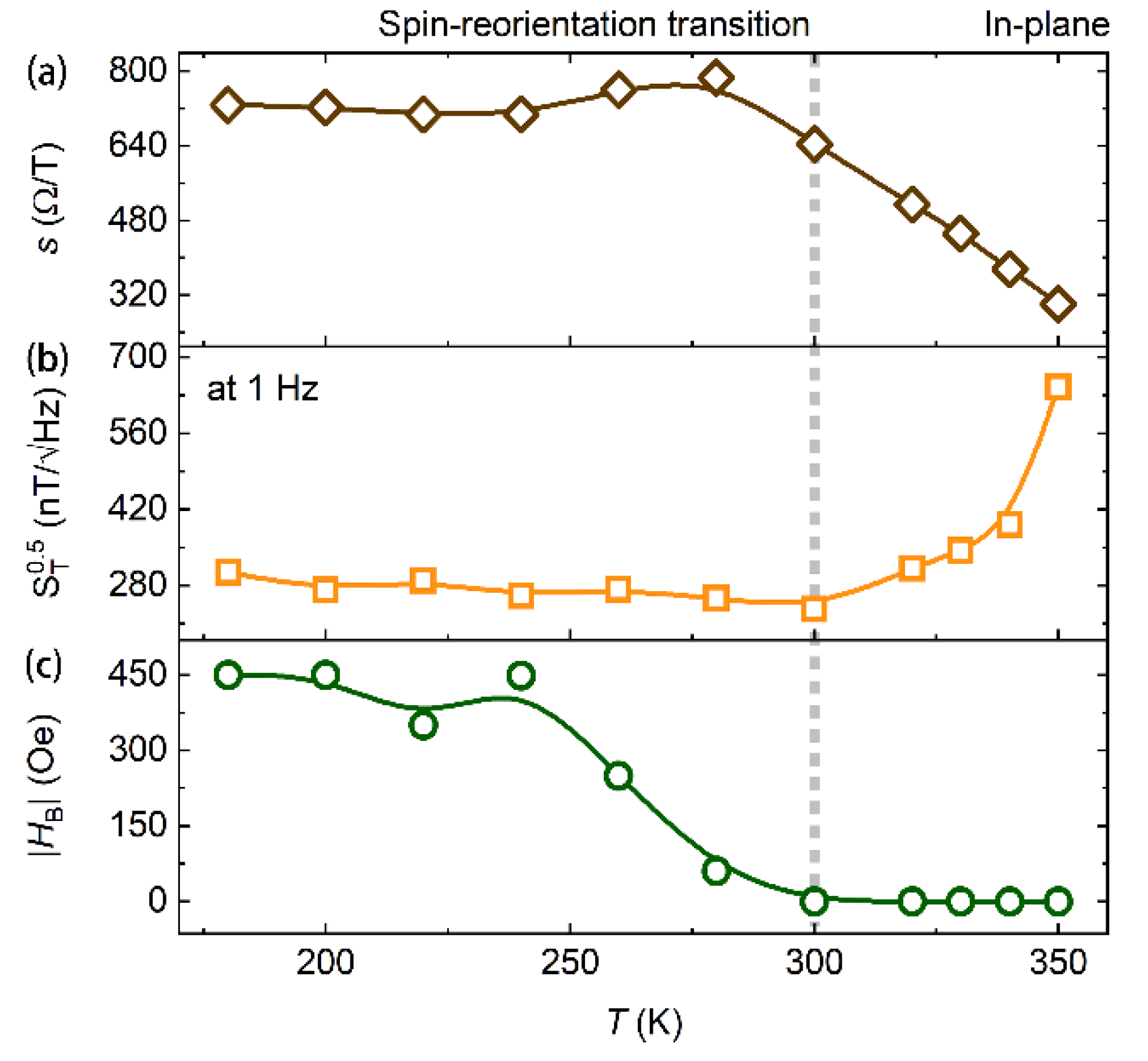
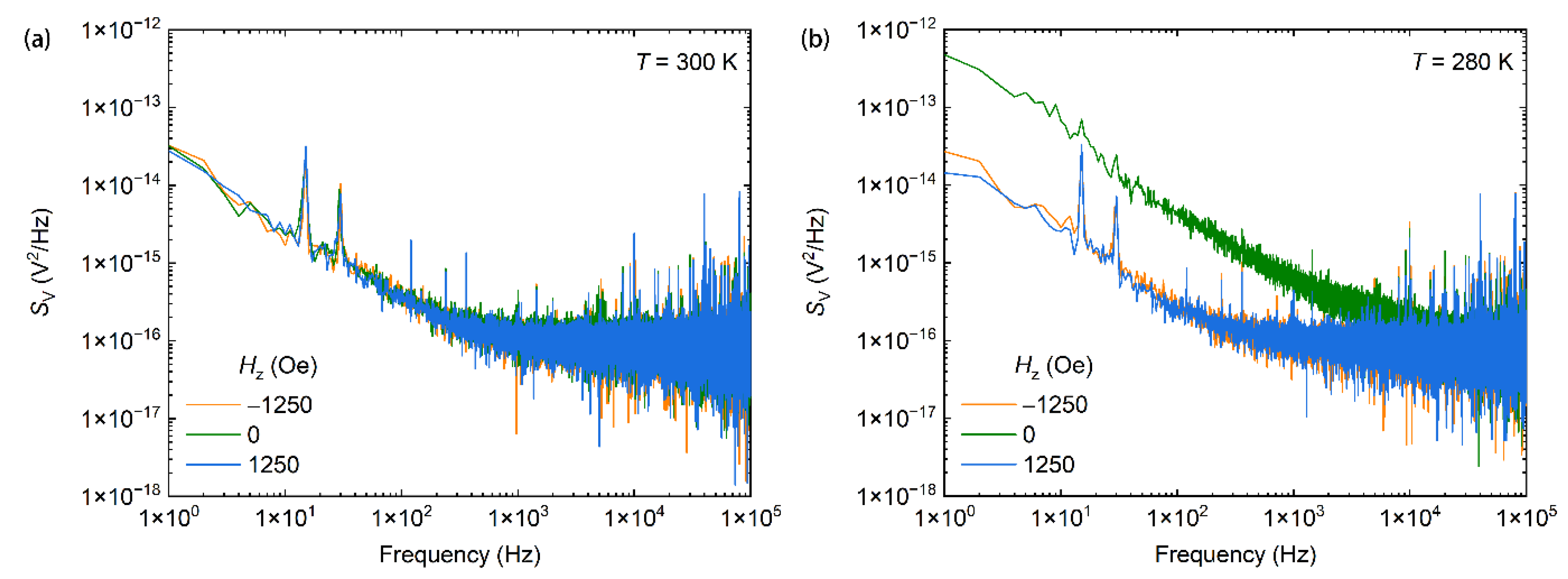
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.; Cai, J.; Pan, H.; Sun, L. Ultrasensitive anomalous Hall effect in SiO2/Fe-Pt/SiO2 sandwich structure films. Appl. Phys. Lett. 2012, 100, 022404. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Y.; Xiao, G. Anomalous Hall Sensors with High Sensitivity and Stability Based on Interlayer Exchange-Coupled Magnetic Thin Films. Phys. Rev. Appl. 2020, 13, 064009. [Google Scholar] [CrossRef]
- Yang, G.; Li, Y.; Chen, X.; Zhang, J.; Yu, G. Ultrasensitive Anomalous Hall Effect in Ta/CoFe/Oxide/Ta Multilayers. Adv. Condens. Matter Phys. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Hao, Q.; Xiao, G. Low-Frequency Noise of Magnetic Sensors Based on the Anomalous Hall Effect in Fe–Pt Alloys. Sensors 2019, 19, 3537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, K.; Xiao, G. Noise characterization of ultrasensitive anomalous Hall effect sensors based on Co40Fe40B20 thin films with compensated in-plane and perpendicular magnetic anisotropies. Appl. Phys. Lett. 2020, 116, 212404. [Google Scholar] [CrossRef]
- Zhu, T.; Chen, P.; Zhang, Q.H.; Yu, R.C.; Liu, B.G. Giant linear anomalous Hall effect in the perpendicular CoFeB thin films. Appl. Phys. Lett. 2014, 104, 202404. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; Macdonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Valadeiro, J.P.; Amaral, J.; Leitao, D.C.; Ferreira, R.; Cardoso, S.F.; Freitas, P.J.P. Strategies for pTesla Field Detection Using Magnetoresistive Sensors with a Soft Pinned Sensing Layer. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Paz, E.; Serrano-Guisan, S.; Ferreira, R.; Freitas, P.P. Room temperature direct detection of low frequency magnetic fields in the 100 pT/Hz0.5 range using large arrays of magnetic tunnel junctions. J. Appl. Phys. 2014, 115, 17E501. [Google Scholar] [CrossRef]
- Guerrero, R.; Pannetier-Lecoeur, M.; Fermon, C.; Cardoso, S.; Ferreira, R.; De Freitas, S.C. Low frequency noise in arrays of magnetic tunnel junctions connected in series and parallel. J. Appl. Phys. 2009, 105, 113922. [Google Scholar] [CrossRef]
- Zhang, Y.; He, G.; Zhang, X.; Xiao, G. Magnetotransport and electronic noise in superparamagnetic magnetic tunnel junctions. Appl. Phys. Lett. 2019, 115, 022402. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J.M. Hall Effect in Ferromagnetics. Phys. Rev. 1954, 95, 1154–1160. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Fang, Z.; Nagaosa, N.; Takahashi, K.S.; Asamitsu, A.; Mathieu, R.; Ogasawara, T.; Yamada, H.; Kawasaki, M.; Tokura, Y.; Terakura, K. The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space. Science 2003, 302, 92–95. [Google Scholar] [CrossRef]
- Suzuki, T.; Chisnell, R.; Devarakonda, A.; Liu, Y.-T.; Feng, W.; Xiao, D.; Lynn, R.C.J.W.; Checkelsky, T.S.A.D.Y.-T.L.J.G. Large anomalous Hall effect in a half-Heusler antiferromagnet. Nat. Phys. 2016, 12, 1119–1123. [Google Scholar] [CrossRef]
- Liu, E.; Sun, Y.; Kumar, N.; Muechler, L.; Sun, A.; Jiao, L.; Yang, S.-Y.; Liu, D.; Liang, A.; Xu, Q.; et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 2018, 14, 1125–1131. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef]
- Tokura, Y.; Yasuda, K.; Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 2019, 1, 126–143. [Google Scholar] [CrossRef]
- Miyasato, T.; Abe, N.; Fujii, T.; Asamitsu, A.; Onoda, S.; Onose, Y.; Nagaosa, N.; Tokura, Y. Crossover Behavior of the Anomalous Hall Effect and Anomalous Nernst Effect in Itinerant Ferromagnets. Phys. Rev. Lett. 2007, 99, 086602. [Google Scholar] [CrossRef] [PubMed]
- Onoda, S.; Sugimoto, N.; Nagaosa, N. Quantum transport theory of anomalous electric, thermoelectric, and thermal Hall effects in ferromagnets. Phys. Rev. B 2008, 77, 165103. [Google Scholar] [CrossRef]
- Smit, J. The spontaneous hall effect in ferromagnetics II. Physica 1958, 24, 39–51. [Google Scholar] [CrossRef]
- Berger, L. Side-Jump Mechanism for the Hall Effect of Ferromagnets. Phys. Rev. B 1970, 2, 4559–4566. [Google Scholar] [CrossRef]
- Shiomi, Y.; Onose, Y.; Tokura, Y. Extrinsic anomalous Hall effect in charge and heat transport in pure iron, Fe0.997Si0.003, and Fe0.97Co0. Phys. Rev. B 2009, 79, 100404. [Google Scholar] [CrossRef]
- Hou, D.; Su, G.; Tian, Y.; Jin, X.; Yang, S.A.; Niu, Q. Multivariable Scaling for the Anomalous Hall Effect. Phys. Rev. Lett. 2015, 114, 217203. [Google Scholar] [CrossRef]
- Hao, Q.; Chen, W.; Wang, S.; Xiao, G. Anomalous Hall effect and magnetic properties of FexPt100−x alloys with strong spin-orbit interaction. J. Appl. Phys. 2017, 122, 033901. [Google Scholar] [CrossRef]
- Miao, G.X.; Xiao, G. Giant Hall resistance in Pt-based ferromagnetic alloys. Appl. Phys. Lett. 2004, 85, 73. [Google Scholar] [CrossRef]
- Canedy, C.; Gong, G.; Wang, J.; Xiao, G. Large magnetic Hall effect in ferromagnetic FexPt100−x thin films. J. Appl. Phys. 1996, 79, 6126–6128. [Google Scholar] [CrossRef][Green Version]
- Liu, X.; Bauer, M.; Bertagnolli, H.; Roduner, E.; Van Slageren, J.; Phillipp, F. Structure and Magnetization of Small Monodisperse Platinum Clusters. Phys. Rev. Lett. 2006, 97, 253401. [Google Scholar] [CrossRef]
- Dieny, B.; Chshiev, M. Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev. Mod. Phys. 2017, 89, 025008. [Google Scholar] [CrossRef]
- Yang, H.; Chshiev, M.; Dieny, B.; Lee, J.; Manchon, A.; Shin, K. First-principles investigation of the very large perpendicular magnetic anisotropy at Fe| MgO and Co| MgO interfaces. Phys. Rev. B 2011, 84, 054401. [Google Scholar] [CrossRef]
- Hao, Q.; Xiao, G. Giant spin Hall effect and magnetotransport in a Ta/CoFeB/MgO layered structure: A temperature dependence study. Phys. Rev. B 2015, 91, 224413. [Google Scholar] [CrossRef]
- Wang, K.; Qian, L.; Chen, W.; Ying, S.-C.; Xiao, G.; Wu, X. Spin torque effect on topological defects and transitions of magnetic domain phases in Ta/CoFeB/MgO. Phys. Rev. B 2019, 99, 184410. [Google Scholar] [CrossRef]
- Wang, K.; Qian, L.; Ying, S.-C.; Xiao, G. Spin-orbit torque switching of chiral magnetization across a synthetic antiferromagnet. Commun. Phys. 2021, 4, 1–7. [Google Scholar] [CrossRef]
- Hooge, F.; Hoppenbrouwers, A. 1/⨍ noise in continuous thin gold films. Physica 1969, 45, 386–392. [Google Scholar] [CrossRef]
- Hooge, F.N. 1/ƒ noise is no surface effect. Phys. Lett. A 1969, 29, 139–140. [Google Scholar] [CrossRef]
- Hooge, F. Discussion of recent experiments on 1/ƒ noise. Physica 1972, 60, 130–144. [Google Scholar] [CrossRef]
- Mazumdar, D.; Liu, X.; Schrag, B.D.; Carter, M.; Shen, W.; Xiao, G. Low frequency noise in highly sensitive magnetic tunnel junctions with (001) MgO tunnel barrier. Appl. Phys. Lett. 2007, 91, 033507. [Google Scholar] [CrossRef]
- Mazumdar, D.; Shen, W.; Liu, X.; Schrag, B.D.; Carter, M.; Xiao, G. Field sensing characteristics of magnetic tunnel junctions with (001) MgO tunnel barrier. J. Appl. Phys. 2008, 103, 113911. [Google Scholar] [CrossRef]
- He, G.; Zhang, Y.; Qian, L.; Xiao, G.; Zhang, Q.; Santamarina, J.C.; Patzek, T.W.; Zhang, X. PicoTesla magnetic tunneling junction sensors integrated with double staged magnetic flux concentrators. Appl. Phys. Lett. 2018, 113, 242401. [Google Scholar] [CrossRef]
- Sampietro, M.; Fasoli, L.G.; Ferrari, G. Spectrum analyzer with noise reduction by cross-correlation technique on two channels. Rev. Sci. Instrum. 1999, 70, 2520–2525. [Google Scholar] [CrossRef]
- Davey, W.P. Precision Measurements of the Lattice Constants of Twelve Common Metals. Phys. Rev. 1925, 25, 753–761. [Google Scholar] [CrossRef]
- Seki, I.; Nagata, K. Lattice Constant of Iron and Austenite Including Its Supersaturation Phase of Carbon. ISIJ Int. 2005, 45, 1789–1794. [Google Scholar] [CrossRef]
- Srivastava, T.; Lim, W.; Joumard, I.; Auffret, S.; Baraduc, C.; Béa, H. Mapping different skyrmion phases in double wedges of Ta/FeCoB/TaOx trilayers. Phys. Rev. B 2019, 100, 220401. [Google Scholar] [CrossRef]
- Alzate, J.G.; Khalili Amiri, P.; Yu, G.; Upadhyaya, P.; Katine, J.A.; Langer, J.; Ocker, B.; Krivorotov, I.N.; Wang, K.L. Temperature dependence of the voltage-controlled perpendicular anisotropy in nanoscale MgO| CoFeB| Ta magnetic tunnel junctions. Appl. Phys. Lett. 2014, 104, 112410. [Google Scholar] [CrossRef]
- Sato, H.; Chureemart, P.; Matsukura, F.; Chantrell, R.W.; Ohno, H.; Evans, R.F.L. Temperature-dependent properties of CoFeB/MgO thin films: Experiments versus simulations. Phys. Rev. B 2018, 98, 214428. [Google Scholar] [CrossRef]
- Chen, W.; Xiao, G.; Zhang, Q.; Zhang, X. Temperature study of the giant spin Hall effect in the bulk limit of β− W. Phys. Rev. B 2018, 98, 134411. [Google Scholar] [CrossRef]
- Haddab, Y.; Mosser, V.; Lysowec, M.; Suski, J.; Demeus, L.; Renaux, C.; Adriensen, S.; Flandre, D. Low-noise SOI Hall devices. SPIEs First Int. Symp. Fluct. Noise 2003, 5115, 196–203. [Google Scholar] [CrossRef]
- Behet, M.; Bekaert, J.; De Boeck, J.; Borghs, G. InAs/Al0.2Ga0.8Sb quantum well Hall effect sensors. Sens. Actuators A Phys. 2000, 81, 13–17. [Google Scholar] [CrossRef]
- Jankowski, J.; El-Ahmar, S.; Oszwaldowski, M. Hall Sensors for Extreme Temperatures. Sensors 2011, 11, 876–885. [Google Scholar] [CrossRef]
- He, G.; Zhang, Y.; Xiao, G. Nonhysteretic Vortex Magnetic Tunnel Junction Sensor with High Dynamic Reserve. Phys. Rev. Appl. 2020, 14, 034051. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Zhang, Y.; Zhou, S.; Xiao, G. Micron-Scale Anomalous Hall Sensors Based on FexPt1−x Thin Films with a Large Hall Angle and near the Spin-Reorientation Transition. Nanomaterials 2021, 11, 854. https://doi.org/10.3390/nano11040854
Wang K, Zhang Y, Zhou S, Xiao G. Micron-Scale Anomalous Hall Sensors Based on FexPt1−x Thin Films with a Large Hall Angle and near the Spin-Reorientation Transition. Nanomaterials. 2021; 11(4):854. https://doi.org/10.3390/nano11040854
Chicago/Turabian StyleWang, Kang, Yiou Zhang, Shiyu Zhou, and Gang Xiao. 2021. "Micron-Scale Anomalous Hall Sensors Based on FexPt1−x Thin Films with a Large Hall Angle and near the Spin-Reorientation Transition" Nanomaterials 11, no. 4: 854. https://doi.org/10.3390/nano11040854
APA StyleWang, K., Zhang, Y., Zhou, S., & Xiao, G. (2021). Micron-Scale Anomalous Hall Sensors Based on FexPt1−x Thin Films with a Large Hall Angle and near the Spin-Reorientation Transition. Nanomaterials, 11(4), 854. https://doi.org/10.3390/nano11040854