Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links
Abstract
1. Introduction
2. Current State of the Art
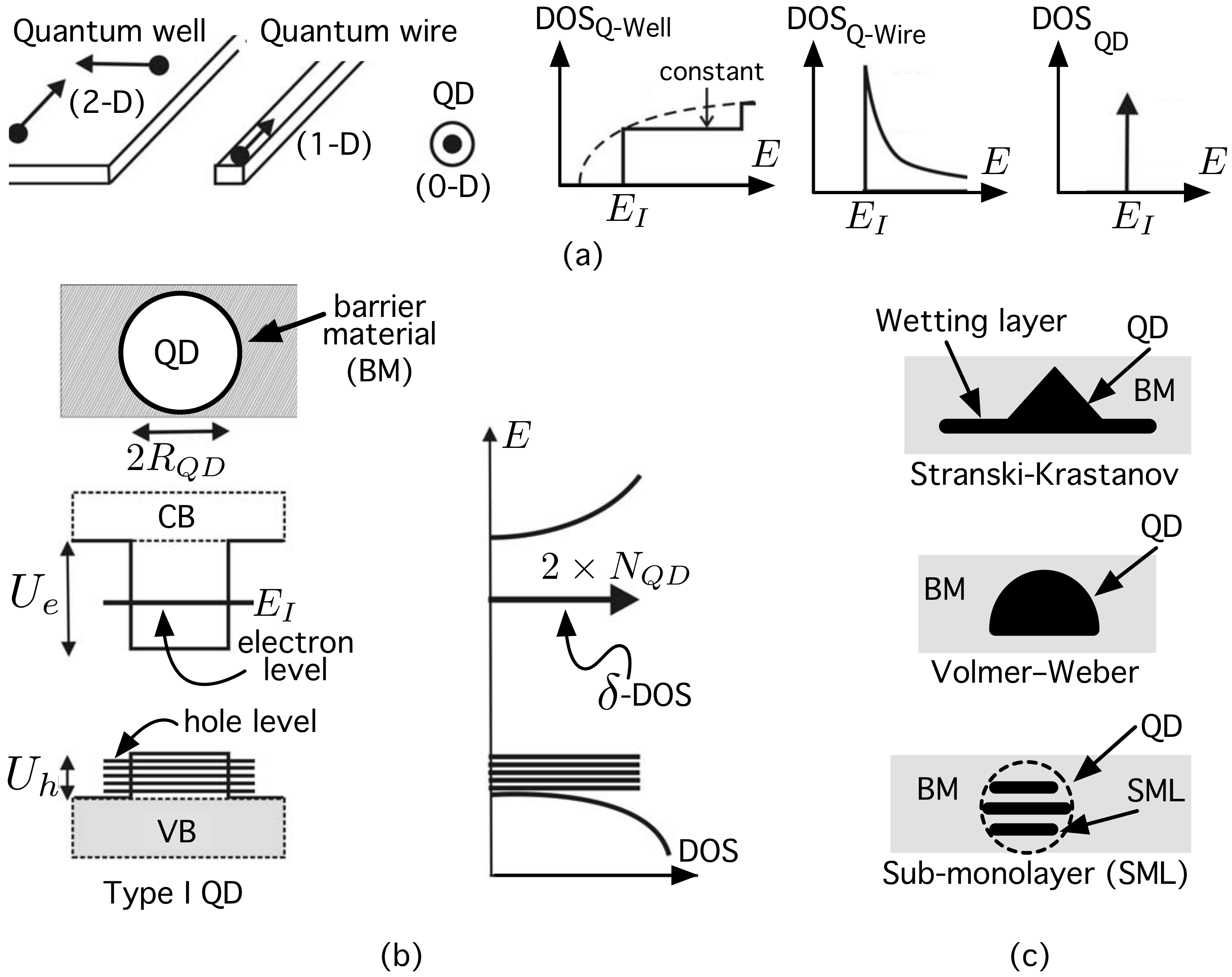
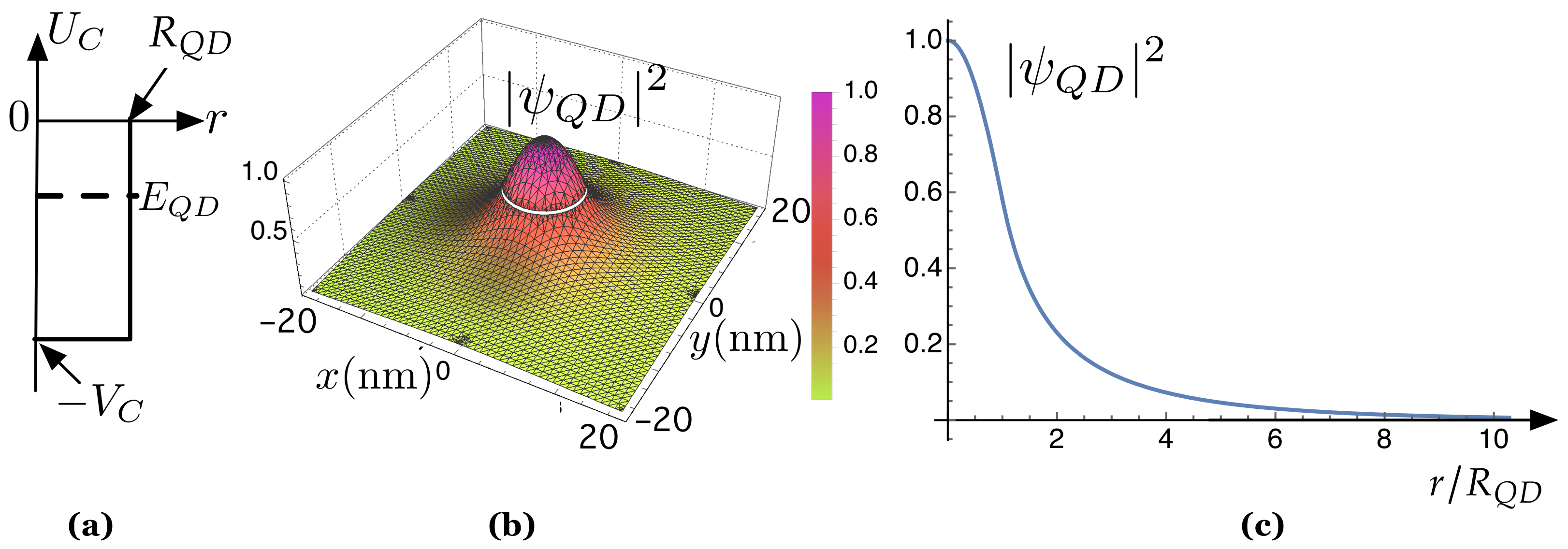
3. The QD System
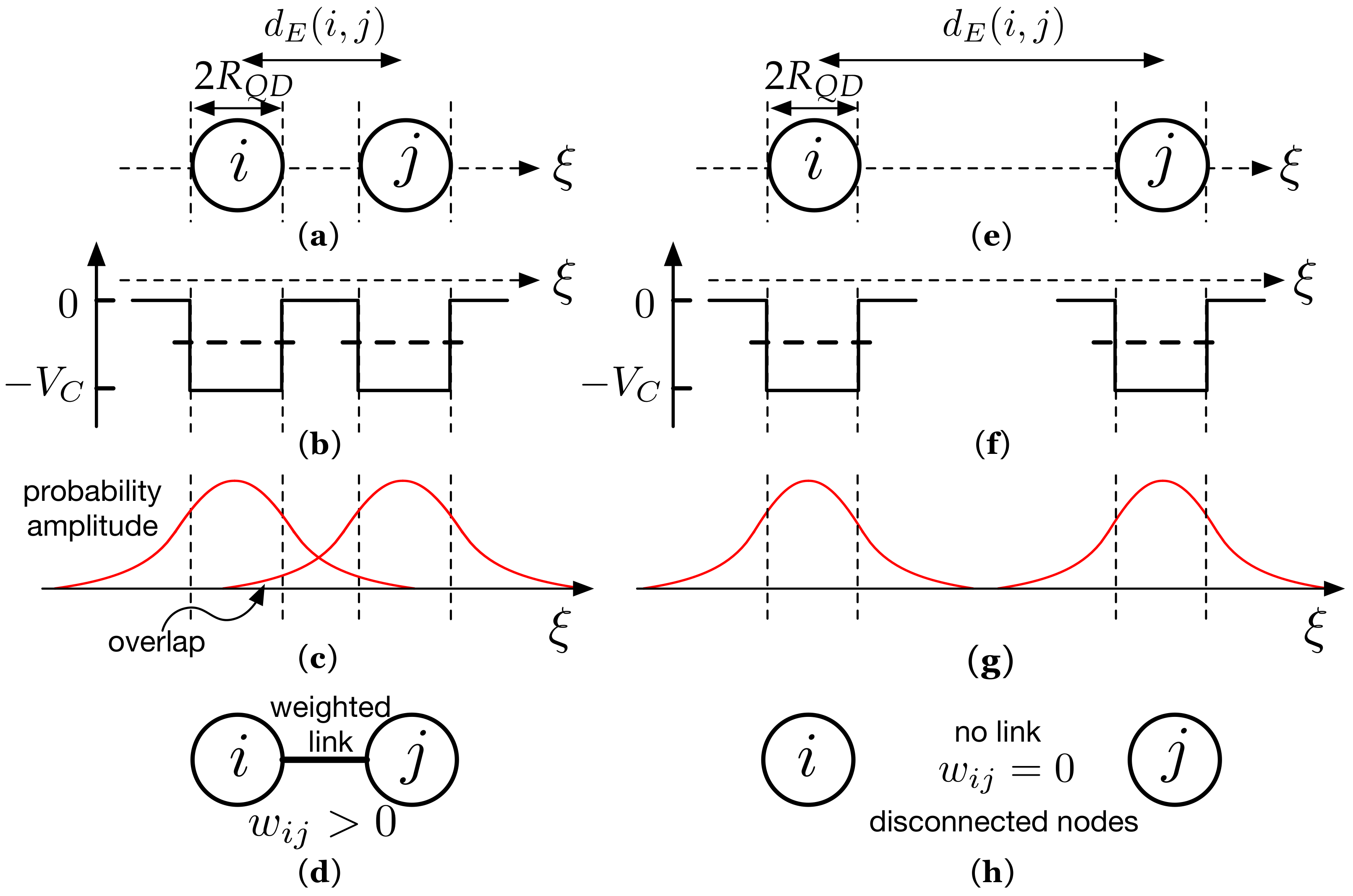
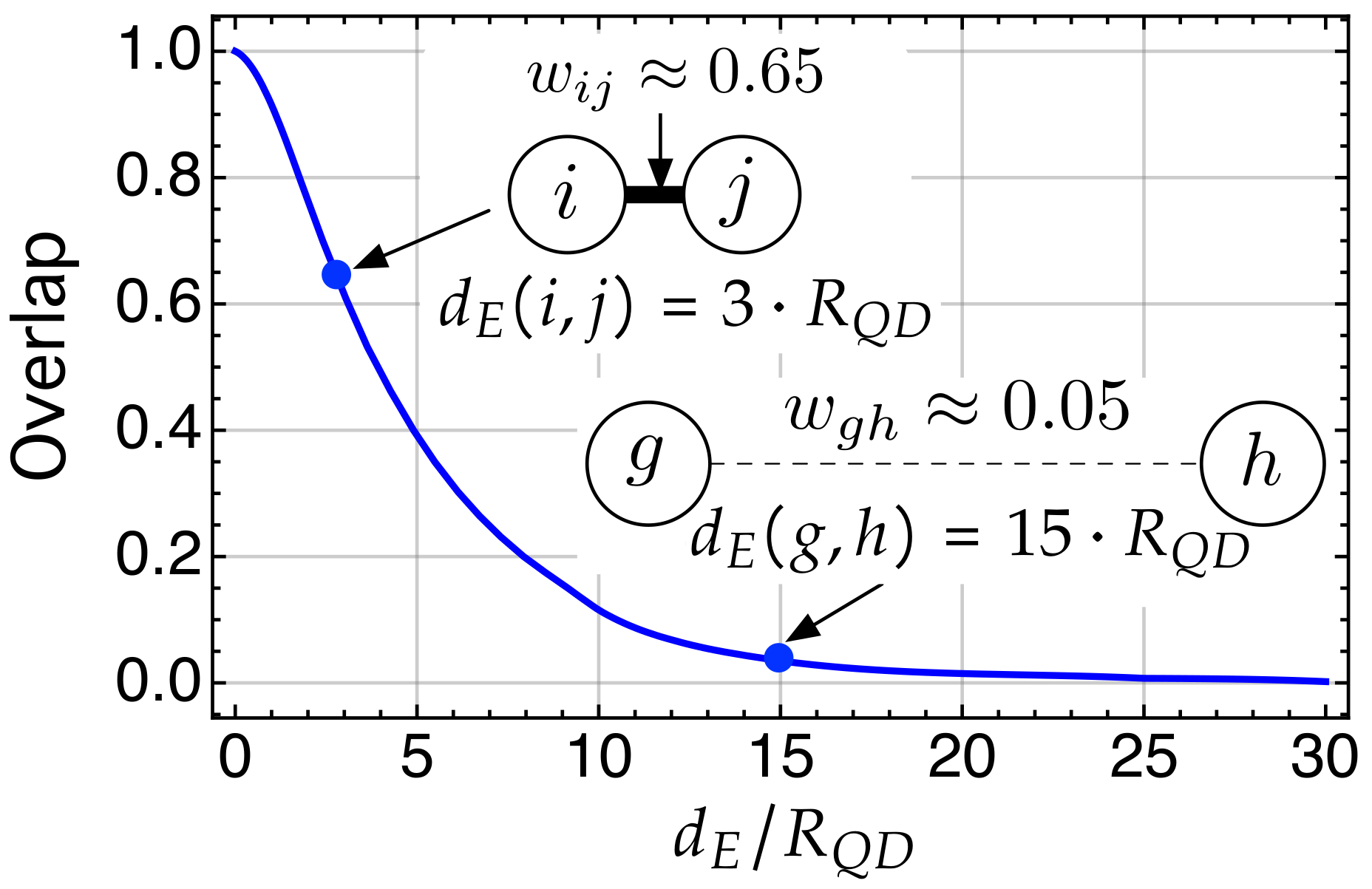
4. Modeling the QD System as a Spatial Network: The Proposed Model
5. Experimental Work: Simulations
5.1. Network Parameters
- The degree distribution of a network captures the probability that a randomly chosen node exhibits “degree” k (= number of links). and its mean value (mean degree) are very useful since it quantifies to what extent nodes are heterogeneous with respect to their connectivity. In fact, many real-world networks exhibit broad, heterogeneous degree distributions. In a degree-heterogeneous network, the probability to find a node with decreases slower than exponentially, leading to the existence of a non-negligible number of nodes with very high degrees. A key feature of such degree distributions is the so-called scale-free behavior [32], characterized by a degree distribution . This means that most of the nodes have very few links, while only a few nodes have a large percentage of all links. These most connected nodes are called “hubs”.
- The clustering or transitivity [32] quantify the probability that two neighbors of a given node i are connected. This concept is clear in social networks: the fact that usually “the friend of a friend is a friend” leads to high clustering coefficient. The “clustering coefficient” is a local property capturing “the density” of triangles in the graph, that is, two nodes that both are connected to a third node are also directly connected to each other. A node i in the network has links that connects it to other nodes. The clustering coefficient of node i is defined as the ratio between the number of links that actually exist between these nodes and the maximum possible number of links, that is, . The clustering coefficient of the whole network is:
- The average shortest path length, ℓ, quantifies the extent to which a node is accessible from any other [32]. The average path length of a network is the average value of distances between any pair of nodes in the network:where is the distance between node i and node j. The length of the shortest path between two nodes i and j in a network is the minimum number of links for going from node i to j. Its average is computed over all possible pairs of nodes. When ℓ is small when compared to the “network size” (number of nodes, N), the small-world property arises. Intuitively, this means that any pair of nodes are relatively “close”. Mathematically, this means that the average shortest path scales logarithmically with the network size [32]: .
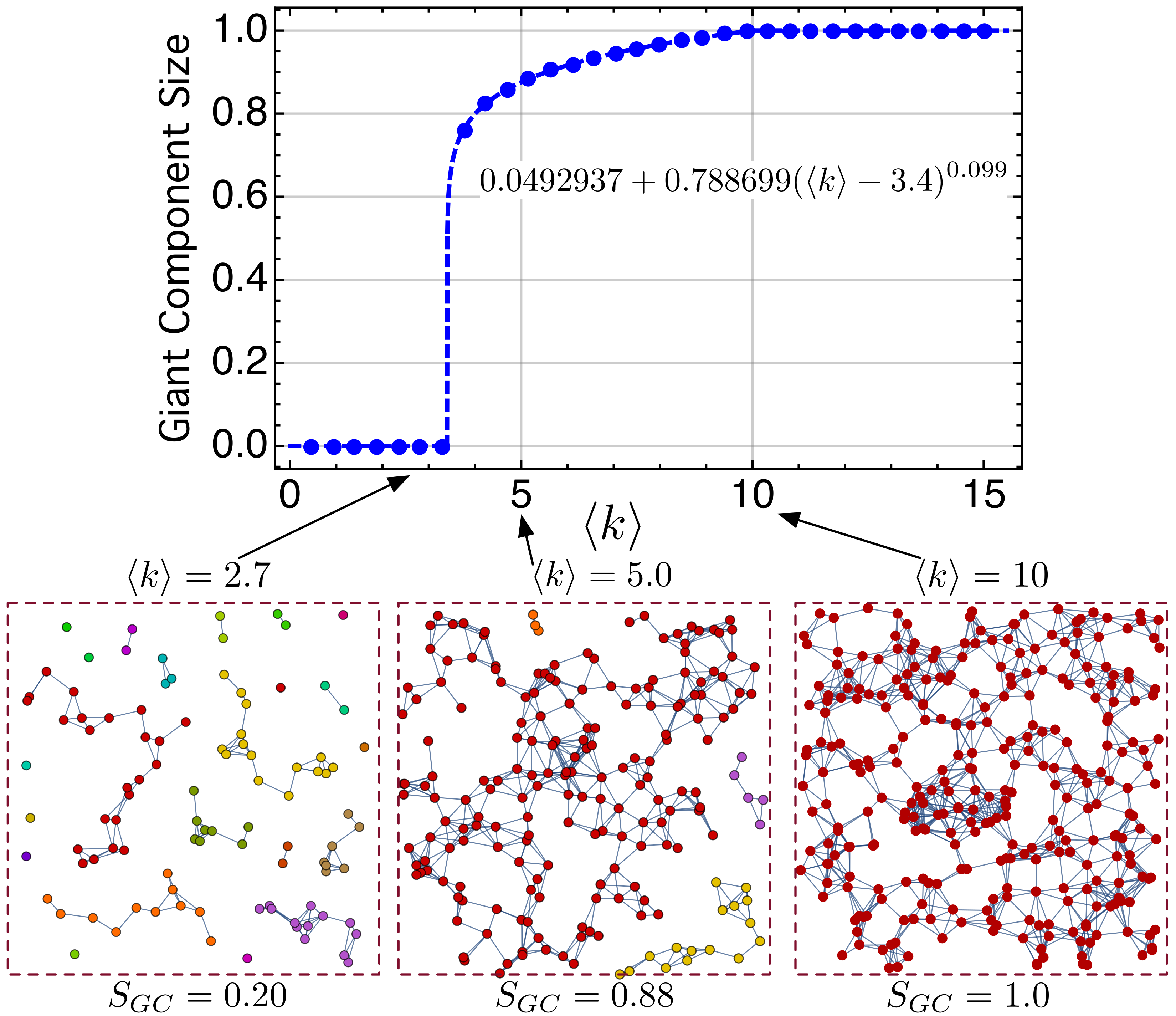
5.2. The Network Has a Percolation Transition as the Dot Density Increases
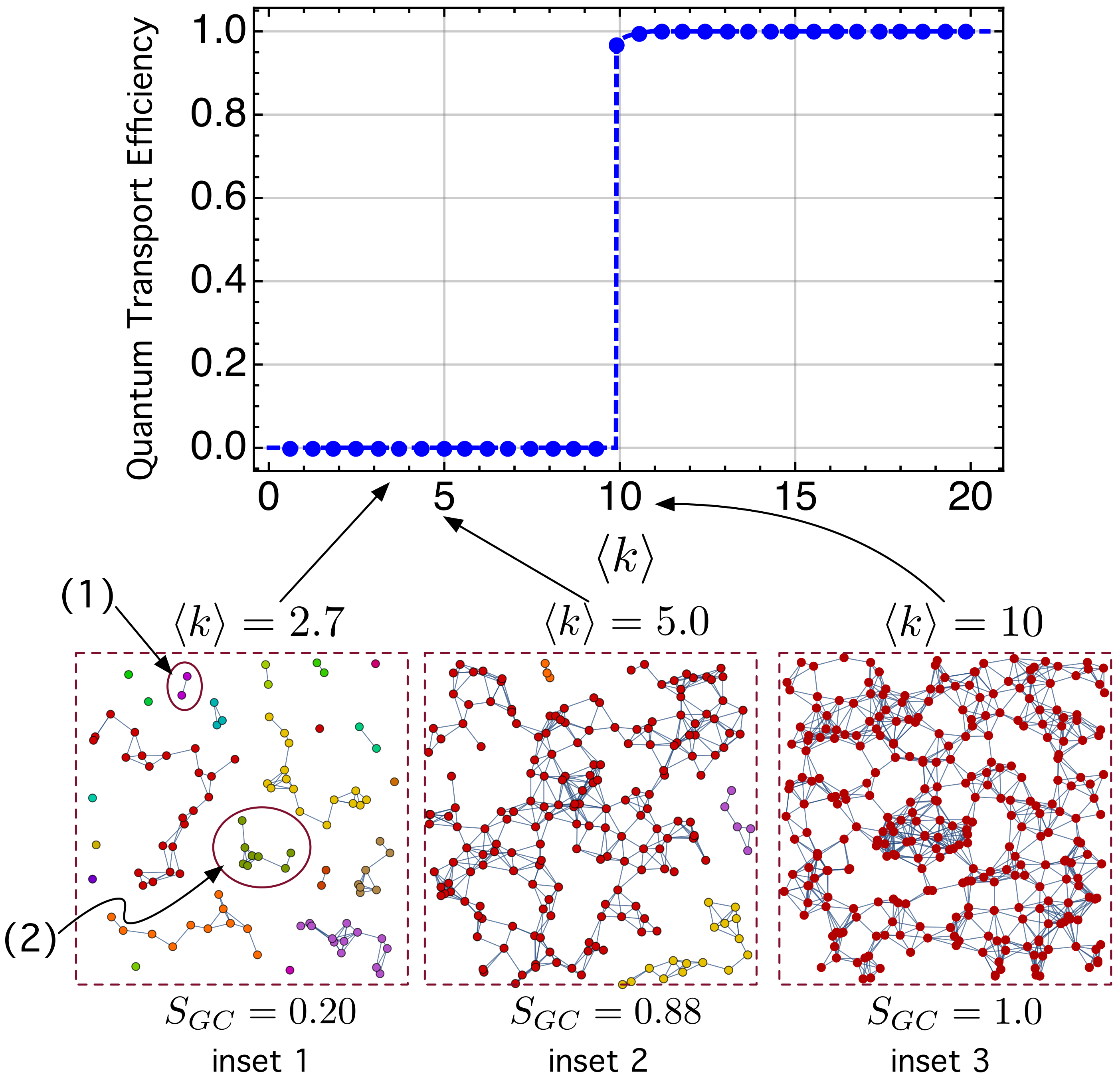
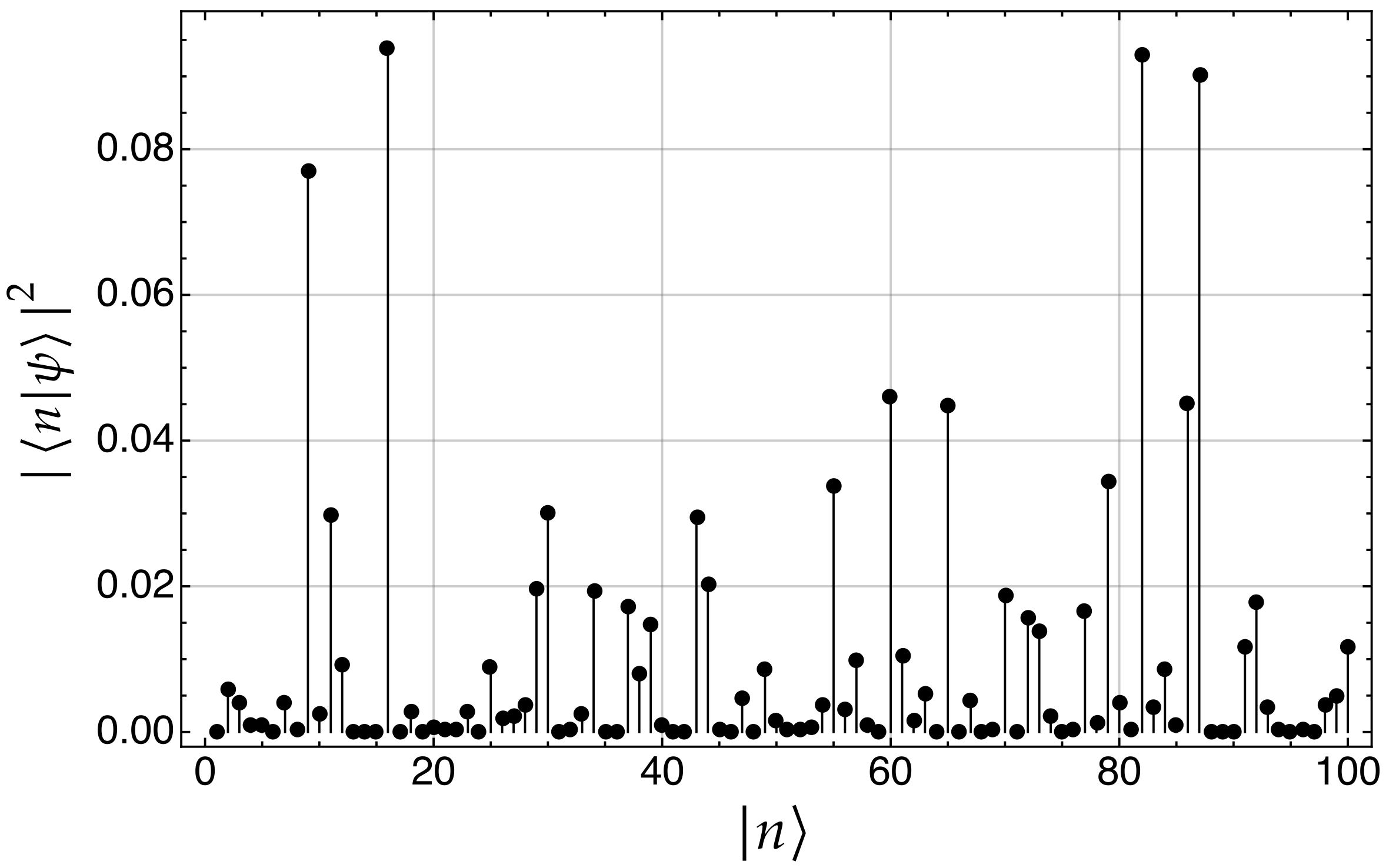
5.3. Studying the Emergence of Electron Transport
6. Potential Applications, Strengths, and Weaknesses of the Proposed Method
6.1. Prospective Applications
6.1.1. Intermediate Band Materials
6.1.2. Light-Harvesting Materials
6.2. Strengths and Weaknesses
7. Summary and Conclusions
- The spatial network generated by the proposed model prohibits the existence of shortcuts between distant nodes because of the impossibility of the electron tunneling between two very distant QDs. This leads, as expected, to high clustering coefficient and makes it impossible for the network to be small-world.
- The proposed network is also able to capture the inner properties of the QD system: it predicts the system quantum state, its time evolution, and the emergence of quantum transport (QT) as the mean node degree increases (or, equivalently, when the QD increases). In fact, QT efficiency exhibits an abrupt change, from electron localization (no QT) to delocalization (QT emerges), which has also been observed in [60], although with a different approach.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 0D | Zero-dimensional |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| CN | Complex Networks |
| CTQW | Continuous-Time Quantum Walks |
| GC | Giant Component |
| IB | Intermediate Band |
| IBSC | Intermediate Band Solar Cell |
| QCP | Quantum Confinement Potential |
| QD | Quantum Dot |
| QD-IBSC | Quantum Dot Intermediate Band Solar Cell |
| QM | Quantum Mechanics |
| QT | Quantum Transport |
| RGG | Random Geometric Graph |
| RN | Random Network |
| SAQDs | Self-Assembled Quantum Dots |
| SML-QDs | Sub-monolayer Quantum Dots |
| SN | Spatial Network |
| SK | Stranski–Krastanow |
| SW | Small-world |
| VW | Volmer–Weber |
| WL | Wetting layer |
Appendix A
| Adjacency matrix of a graph . | |
| Element of the adjacency matrix | |
| Average return probability | |
| Mean clustering coefficient of a network. | |
| Node degree matrix: diag . It is the diagonal matrix formed from the nodes degrees. | |
| Euclidean distance between any pair of nodes i and j in a network. | |
| Distance between two nodes i and j. It is the length of the shortest path (geodesic path) between them, that is, the minimum number of links when going from one node to the other. | |
| Euclidean distance limit beyond which there is no link formation. | |
| Discrete electron energy in a quantum dot (QD). | |
| Quantum transport efficiency. | |
| Graph , where is the set of nodes (card), is the set of links, and is weighted adjacency matrix that emerges from our method to link formation. | |
| Hamiltonian operator corresponding to the total energy of a quantum system. | |
| Hamiltonian in matrix form. | |
| h | Planck constant. |
| ℏ | Reduced Planck constant. |
| Ket vector in the Hilbert space . It corresponds to the electron wave function in nanostructure (≡ site ≡ node ≡ ket) i. | |
| Bra vector in the dual space corresponding to the ket | |
| Average node degree. | |
| Degree of a node i. It is the number of links connecting i to any other node. | |
| ℓ | Average path length of a network. It is the mean value of distances between any pair of nodes in the network. |
| Set of links (edges) of a network (graph). | |
| Laplacian matrix of a graph . | |
| Normalized Laplacian matrix, . | |
| m | Electron mass. |
| M | Size of a graph . It is the number of links in the set . |
| N | Order of a graph . It is the number of nodes in set , that is, the cardinality of set : . |
| Set of nodes (or vertices) of a graph. | |
| Laplace operator. | |
| Probability for an electron to evolve between kets and in the time interval t. | |
| Probability density function giving the probability that a randomly selected node has k links. | |
| Ket or vector state in Dirac notation corresponding to the wave function . | |
| Radius of the quantum dot. | |
| Electron wavefunction in a quantum dot. | |
| normalized size of the giant component (GC) with respect to the total number of nodes N. | |
| Sum of the probability amplitudes on ket , . | |
| Potential energy operator. | |
| Depth of confinement potential. | |
| Confining, spherical (depending only on the radial co-ordinate r), finite, and “square” potential energy. | |
| Time evolution operator generated by the normalized Laplacian matrix . | |
| Weight of the link between node i and j. We define it as the overlap integral between the electron wave functions in kets i and j or the probability amplitude . | |
| weighted adjacency matrix whose elements are quantum probability amplitudes. |
References
- Cotta, M.A. Quantum Dots and Their Applications: What Lies Ahead? ACS Appl. Nano Mater. 2020, 3, 4920–4924. [Google Scholar] [CrossRef]
- Harrison, P.; Valavanis, A. Quantum Wells, Wires and Dots: Theoretical and Computational Physics of Semiconductor Nanostructures; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Sengupta, S.; Chakrabarti, S. Structural, Optical and Spectral Behaviour of InAs-based Quantum Dot Heterostructures: Applications for High-performance Infrared Photodetectors; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Nowozin, T. Self-Organized Quantum Dots for Memories: Electronic Properties and Carrier Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cipriano, L.A.; Di Liberto, G.; Tosoni, S.; Pacchioni, G. Quantum confinement in group III–V semiconductor 2D nanostructures. Nanoscale 2020, 12, 17494–17501. [Google Scholar] [CrossRef]
- Bimberg, D.; Grundmann, M.; Ledentsov, N.N. Quantum Dot Heterostructures; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Wang, Z.M. Self-Assembled Quantum Dots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 1. [Google Scholar]
- Kim, J.S.; Shin, J.C.; Kim, J.O.; Noh, S.K.; Lee, S.J.; Krishna, S. Photoluminescence study of InAs/InGaAs sub-monolayer quantum dot infrared photodetectors with various numbers of multiple stack layers. J. Lumin. 2019, 207, 512–519. [Google Scholar]
- Leon, R.; Lobo, C.; Chin, T.; Woodall, J.; Fafard, S.; Ruvimov, S.; Liliental-Weber, Z.; Stevens Kalceff, M. Self-forming InAs/GaP quantum dots by direct island growth. Appl. Phys. Lett. 1998, 72, 1356–1358. [Google Scholar] [CrossRef]
- Germann, T.; Strittmatter, A.; Pohl, J.; Pohl, U.; Bimberg, D.; Rautiainen, J.; Guina, M.; Okhotnikov, O. High-power semiconductor disk laser based on In As/Ga As submonolayer quantum dots. Appl. Phys. Lett. 2008, 92, 101123. [Google Scholar] [CrossRef]
- Xu, Z.; Birkedal, D.; Hvam, J.M.; Zhao, Z.; Liu, Y.; Yang, K.; Kanjilal, A.; Sadowski, J. Structure and optical anisotropy of vertically correlated submonolayer InAs/GaAs quantum dots. Appl. Phys. Lett. 2003, 82, 3859–3861. [Google Scholar] [CrossRef]
- Kiyama, H.; Korsch, A.; Nagai, N.; Kanai, Y.; Matsumoto, K.; Hirakawa, K.; Oiwa, A. Single-electron charge sensing in self-assembled quantum dots. Sci. Rep. 2018, 8, 1–6. [Google Scholar] [CrossRef]
- Gao, W.; Fallahi, P.; Togan, E.; Miguel-Sánchez, J.; Imamoglu, A. Observation of entanglement between a quantum dot spin and a single photon. Nature 2012, 491, 426–430. [Google Scholar] [CrossRef]
- De Greve, K.; Yu, L.; McMahon, P.L.; Pelc, J.S.; Natarajan, C.M.; Kim, N.Y.; Abe, E.; Maier, S.; Schneider, C.; Kamp, M.; et al. Quantum-dot spin–photon entanglement via frequency downconversion to telecom wavelength. Nature 2012, 491, 421–425. [Google Scholar] [CrossRef]
- Michler, P.; Kiraz, A.; Becher, C.; Schoenfeld, W.; Petroff, P.; Zhang, L.; Hu, E.; Imamoglu, A. A quantum dot single-photon turnstile device. Science 2000, 290, 2282–2285. [Google Scholar] [CrossRef]
- Press, D.; Ladd, T.D.; Zhang, B.; Yamamoto, Y. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature 2008, 456, 218–221. [Google Scholar] [CrossRef] [PubMed]
- Deacon, R.S.; Oiwa, A.; Sailer, J.; Baba, S.; Kanai, Y.; Shibata, K.; Hirakawa, K.; Tarucha, S. Cooper pair splitting in parallel quantum dot Josephson junctions. Nat. Commun. 2015, 6, 1–7. [Google Scholar]
- Hamaya, K.; Masubuchi, S.; Kawamura, M.; Machida, T.; Jung, M.; Shibata, K.; Hirakawa, K.; Taniyama, T.; Ishida, S.; Arakawa, Y. Spin transport through a single self-assembled InAs quantum dot with ferromagnetic leads. Appl. Phys. Lett. 2007, 90, 053108. [Google Scholar] [CrossRef]
- Kanai, Y.; Deacon, R.; Takahashi, S.; Oiwa, A.; Yoshida, K.; Shibata, K.; Hirakawa, K.; Tokura, Y.; Tarucha, S. Electrically tuned spin–orbit interaction in an InAs self-assembled quantum dot. Nat. Nanotechnol. 2011, 6, 511–516. [Google Scholar] [CrossRef]
- Takahashi, S.; Deacon, R.; Oiwa, A.; Shibata, K.; Hirakawa, K.; Tarucha, S. Electrically tunable three-dimensional g-factor anisotropy in single InAs self-assembled quantum dots. Phys. Rev. B 2013, 87, 161302. [Google Scholar] [CrossRef]
- Kanai, Y.; Deacon, R.; Oiwa, A.; Yoshida, K.; Shibata, K.; Hirakawa, K.; Tarucha, S. Electrical control of Kondo effect and superconducting transport in a side-gated InAs quantum dot Josephson junction. Phys. Rev. B 2010, 82, 054512. [Google Scholar] [CrossRef]
- Qi, H.; Wang, S.; Jiang, X.; Fang, Y.; Wang, A.; Shen, H.; Du, Z. Research progress and challenges of blue light-emitting diodes based on II–VI semiconductor quantum dots. J. Mater. Chem. C 2020, 8, 10160–10173. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, Y.; Chen, J.; Wang, J.; Zhou, Y.; Han, S.T. Semiconductor quantum dots for memories and neuromorphic computing systems. Chem. Rev. 2020, 120, 3941–4006. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Shi, J.; Li, M.; Wang, Y.; Zhang, Q.; Liu, X. Perovskite quantum dot lasers. InfoMat 2020, 2, 170–183. [Google Scholar] [CrossRef]
- Geiregat, P.; Van Thourhout, D.; Hens, Z. A bright future for colloidal quantum dot lasers. NPG Asia Mater. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Norman, J.C.; Jung, D.; Zhang, Z.; Wan, Y.; Liu, S.; Shang, C.; Herrick, R.W.; Chow, W.W.; Gossard, A.C.; Bowers, J.E. A review of high-performance quantum dot lasers on silicon. IEEE J. Quantum Electron. 2019, 55, 1–11. [Google Scholar] [CrossRef]
- Bimberg, D.; Kirstaedter, N.; Ledentsov, N.; Alferov, Z.I.; Kop’Ev, P.; Ustinov, V. InGaAs-GaAs quantum-dot lasers. IEEE J. Sel. Top. Quantum Electron. 1997, 3, 196–205. [Google Scholar] [CrossRef]
- Vichi, S.; Bietti, S.; Khalili, A.; Costanzo, M.; Cappelluti, F.; Esposito, L.; Somaschini, C.; Fedorov, A.; Tsukamoto, S.; Rauter, P.; et al. Droplet epitaxy quantum dot based infrared photodetectors. Nanotechnology 2020, 31, 245203. [Google Scholar] [CrossRef]
- Ren, A.; Yuan, L.; Xu, H.; Wu, J.; Wang, Z. Recent progress of III–V quantum dot infrared photodetectors on silicon. J. Mater. Chem. C 2019, 7, 14441–14453. [Google Scholar] [CrossRef]
- Sogabe, T.; Shen, Q.; Yamaguchi, K. Recent progress on quantum dot solar cells: A review. J. Photonics Energy 2016, 6, 040901. [Google Scholar] [CrossRef]
- Grundmann, M.; Stier, O.; Bimberg, D. InAs/GaAs pyramidal quantum dots: Strain distribution, optical phonons, and electronic structure. Phys. Rev. B 1995, 52, 11969. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Cuadra, L.; Salcedo-Sanz, S.; Del Ser, J.; Jiménez-Fernández, S.; Geem, Z.W. A critical review of robustness in power grids using complex networks concepts. Energies 2015, 8, 9211–9265. [Google Scholar] [CrossRef]
- Cuadra, L.; Pino, M.D.; Nieto-Borge, J.C.; Salcedo-Sanz, S. Optimizing the structure of distribution smart grids with renewable generation against abnormal conditions: A complex networks approach with evolutionary algorithms. Energies 2017, 10, 1097. [Google Scholar] [CrossRef]
- Doyle, J.C.; Alderson, D.L.; Li, L.; Low, S.; Roughan, M.; Shalunov, S.; Tanaka, R.; Willinger, W. The “robust yet fragile” nature of the Internet. Proc. Natl. Acad. Sci. USA 2005, 102, 14497–14502. [Google Scholar] [CrossRef]
- Chimal-Eguía, J.C.; Castillo-Montiel, E.; Paez-Hernández, R.T. Properties of the vascular networks in malignant tumors. Entropy 2020, 22, 166. [Google Scholar] [CrossRef]
- Braun, P.; Gingras, A.C. History of protein–protein interactions: From egg-white to complex networks. Proteomics 2012, 12, 1478–1498. [Google Scholar] [CrossRef]
- Guimera, R.; Amaral, L.A.N. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Montoya, J.M.; Solé, R.V. Small world patterns in food webs. J. Theor. Biol. 2002, 214, 405–412. [Google Scholar] [CrossRef]
- Pond, T.; Magsarjav, S.; South, T.; Mitchell, L.; Bagrow, J.P. Complex contagion features without social reinforcement in a model of social information flow. Entropy 2020, 22, 265. [Google Scholar] [CrossRef]
- Iannelli, F.; Koher, A.; Brockmann, D.; Hövel, P.; Sokolov, I.M. Effective distances for epidemics spreading on complex networks. Phys. Rev. E 2017, 95, 012313. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Yang, Z.; Liu, X.; Zhang, Y.; Wei, Z. Modeling the propagation of mobile malware on complex networks. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 249–264. [Google Scholar] [CrossRef]
- Ding, L.; Liu, S.Y.; Yang, Q.; Xu, X.K. Uncovering the Dependence of Cascading Failures on Network Topology by Constructing Null Models. Entropy 2019, 21, 1119. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 026103. [Google Scholar] [CrossRef]
- Fu, X.; Li, W. Cascading failures of wireless sensor networks. In Proceedings of the 11th IEEE International Conference on Networking, Sensing and Control, Miami, FL, USA, 7–9 April 2014; pp. 631–636. [Google Scholar]
- Cui, L.; Kumara, S.; Albert, R. Complex networks: An engineering view. Circuits Syst. Mag. IEEE 2010, 10, 10–25. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 2004, 69, 045104. [Google Scholar] [CrossRef]
- Kinney, R.; Crucitti, P.; Albert, R.; Latora, V. Modeling cascading failures in the North American power grid. Eur. Phys. J. Condens. Matter Complex Syst. 2005, 46, 101–107. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Bashan, A.; Berezin, Y.; Buldyrev, S.V.; Havlin, S. The extreme vulnerability of interdependent spatially embedded networks. Nat. Phys. 2013, 9, 667–672. [Google Scholar]
- Barthelemy, M. Morphogenesis of spatial networks; Springer: New York, NY, USA, 2018. [Google Scholar]
- Zhao, J.; Li, D.; Sanhedrai, H.; Cohen, R.; Havlin, S. Spatio-temporal propagation of cascading overload failures in spatially embedded networks. Nat. Commun. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Penrose, M. Random Geometric Graphs; Oxford University Press: Cambridge, UK, 2003; Volume 5. [Google Scholar]
- Kenniche, H.; Ravelomananana, V. Random Geometric Graphs as model of wireless sensor networks. In Proceedings of the 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; Volume 4, pp. 103–107. [Google Scholar]
- Nemeth, G.; Vattay, G. Giant clusters in random ad hoc networks. Phys. Rev. E 2003, 67, 036110. [Google Scholar] [CrossRef]
- Gong, L.; Tong, P. von Neumann entropy and localization-delocalization transition of electron states in quantum small-world networks. Phys. Rev. E 2006, 74, 056103. [Google Scholar] [CrossRef]
- Umeyama, T.; Igarashi, K.; Sasada, D.; Tamai, Y.; Ishida, K.; Koganezawa, T.; Ohtani, S.; Tanaka, K.; Ohkita, H.; Imahori, H. Efficient light-harvesting, energy migration, and charge transfer by nanographene-based nonfullerene small-molecule acceptors exhibiting unusually long excited-state lifetime in the film state. Chem. Sci. 2020, 11, 3250–3257. [Google Scholar] [CrossRef]
- Biamonte, J.; Faccin, M.; De Domenico, M. Complex networks from classical to quantum. Commun. Phys. 2019, 2, 1–10. [Google Scholar] [CrossRef]
- Sánchez-Burillo, E.; Duch, J.; Gómez-Gardenes, J.; Zueco, D. Quantum navigation and ranking in complex networks. Sci. Rep. 2012, 2, 605. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Susskind, L.; Friedman, A. Quantum Mechanics: The Theoretical Minimum; Penguin Books: London, UK, 2015. [Google Scholar]
- Ritter, S.; Nölleke, C.; Hahn, C.; Reiserer, A.; Neuzner, A.; Uphoff, M.; Mücke, M.; Figueroa, E.; Bochmann, J.; Rempe, G. An elementary quantum network of single atoms in optical cavities. Nature 2012, 484, 195. [Google Scholar] [CrossRef]
- Mülken, O.; Dolgushev, M.; Galiceanu, M. Complex quantum networks: From universal breakdown to optimal transport. Phys. Rev. E 2016, 93, 022304. [Google Scholar] [CrossRef]
- Faccin, M.; Migdał, P.; Johnson, T.H.; Bergholm, V.; Biamonte, J.D. Community detection in quantum complex networks. Phys. Rev. X 2014, 4, 041012. [Google Scholar] [CrossRef]
- Mohseni, M.; Rebentrost, P.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 11B603. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Efficiency of quantum and classical transport on graphs. Phys. Rev. E 2006, 73, 066117. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Darázs, Z.; Kiss, T. Pólya number of the continuous-time quantum walks. Phys. Rev. A 2010, 81, 062319. [Google Scholar] [CrossRef]
- Mülken, O.; Volta, A.; Blumen, A. Asymmetries in symmetric quantum walks on two-dimensional networks. Phys. Rev. A 2005, 72, 042334. [Google Scholar] [CrossRef]
- Agliari, E.; Blumen, A.; Mülken, O. Dynamics of continuous-time quantum walks in restricted geometries. J. Phys. Math. Theor. 2008, 41, 445301. [Google Scholar] [CrossRef]
- Mülken, O.; Bierbaum, V.; Blumen, A. Coherent exciton transport in dendrimers and continuous-time quantum walks. J. Chem. Phys. 2006, 124, 124905. [Google Scholar] [CrossRef]
- Agliari, E.; Blumen, A.; Muelken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 2010, 82, 012305. [Google Scholar] [CrossRef]
- Blumen, A.; Bierbaum, V.; Mülken, O. Coherent dynamics on hierarchical systems. Phys. Stat. Mech. Its Appl. 2006, 371, 10–15. [Google Scholar] [CrossRef][Green Version]
- Mülken, O.; Blumen, A. Slow transport by continuous time quantum walks. Phys. Rev. E 2005, 71, 016101. [Google Scholar] [CrossRef]
- Xu, X.P.; Li, W.; Liu, F. Coherent transport on Apollonian networks and continuous-time quantum walks. Phys. Rev. E 2008, 78, 052103. [Google Scholar] [CrossRef]
- Xu, X.; Liu, F. Coherent exciton transport on scale-free networks. New J. Phys. 2008, 10, 123012. [Google Scholar] [CrossRef]
- Mülken, O.; Pernice, V.; Blumen, A. Quantum transport on small-world networks: A continuous-time quantum walk approach. Phys. Rev. E 2007, 76, 051125. [Google Scholar] [CrossRef]
- Salimi, S. Continuous-time quantum walks on star graphs. Ann. Phys. 2009, 324, 1185–1193. [Google Scholar] [CrossRef]
- Anishchenko, A.; Blumen, A.; Mülken, O. Enhancing the spreading of quantum walks on star graphs by additional bonds. Quantum Inf. Process. 2012, 11, 1273–1286. [Google Scholar] [CrossRef]
- Kulvelis, N.; Dolgushev, M.; Mülken, O. Universality at breakdown of quantum transport on complex networks. Phys. Rev. Lett. 2015, 115, 120602. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small-world” networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Caldarelli, G.; Vespignani, A. Large Scale Structure and Dynamics of Complex Networks: From Information Technology to Finance and Natural Science; World Scientific: Singapore, 2007; Volume 2. [Google Scholar]
- Newman, M.E.; Watts, D.J. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Martinez-Mendoza, A.; Alcazar-López, A.; Méndez-Bermúdez, J. Scattering and transport properties of tight-binding random networks. Phys. Rev. E 2013, 88, 012126. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mandl, F. Quantum Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Galindo, A.; Pascual, P. Quantum Mechanics I; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ballentine, L.E. Quantum Mechanics: A Modern Development; World Scientific Publishing Company: Singapore, 2014. [Google Scholar]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F.; Dui, B. Quantum Mechanics; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915. [Google Scholar] [CrossRef]
- Faccin, M.; Johnson, T.; Biamonte, J.; Kais, S.; Migdał, P. Degree distribution in quantum walks on complex networks. Phys. Rev. X 2013, 3, 041007. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. From Continuous-Time Random Walks to Continuous-Time Quantum Walks: Disordered Networks. In Nonlinear Phenomena in Complex Systems: From Nano to Macro Scale; Springer: Berlin/Heidelberg, Germany, 2014; pp. 189–197. [Google Scholar]
- Darázs, Z.; Anishchenko, A.; Kiss, T.; Blumen, A.; Mülken, O. Transport properties of continuous-time quantum walks on Sierpinski fractals. Phys. Rev. E 2014, 90, 032113. [Google Scholar] [CrossRef]
- Anishchenko, A.; Blumen, A.; Muelken, O. Geometrical aspects of quantum walks on random two-dimensional structures. Phys. Rev. E 2013, 88, 062126. [Google Scholar] [CrossRef]
- Ray, R.K. Solving Quantum Random Walker Using Steepest Entropy Ascent Ansatz: A Pathway Towards Typicality. arXiv 2019, arXiv:1907.04548. [Google Scholar]
- Gualtieri, V.; Benedetti, C.; Paris, M.G. Quantum-classical dynamical distance and quantumness of quantum walks. Phys. Rev. A 2020, 102, 012201. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Spacetime structures of continuous-time quantum walks. Phys. Rev. E 2005, 71, 036128. [Google Scholar] [CrossRef]
- Stevanovic, D. Applications of graph spectra in quantum physics. In Selected Topics in Applications of Graph Spectra; Mathematical Institute of the Serbian Academy of Sciences and Arts: Belgrade, Serbia, 2011; pp. 85–111. [Google Scholar]
- Lee, D.; Kahng, B.; Cho, Y.; Goh, K.I.; Lee, D.S. Recent advances of percolation theory in complex networks. J. Korean Phys. Soc. 2018, 73, 152–164. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; Stanley, C. Understanding intermediate-band solar cells. Nat. Photonics 2012, 6, 146–152. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A. Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett. 1997, 78, 5014. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Luque, A.; Linares, P.; Antolín, E.; Ramiro, I.; Farmer, C.; Hernández, E.; Tobías, I.; Stanley, C.; Martí, A. Understanding the operation of quantum dot intermediate band solar cells. J. Appl. Phys. 2012, 111, 044502. [Google Scholar] [CrossRef]
- López, E.; Datas, A.; Ramiro, I.; Linares, P.; Antolín, E.; Artacho, I.; Martí, A.; Luque, A.; Shoji, Y.; Sogabe, T.; et al. Demonstration of the operation principles of intermediate band solar cells at room temperature. Sol. Energy Mater. Sol. Cells 2016, 149, 15–18. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; López, N.; Antolín, E.; Cánovas, E.; Stanley, C.; Farmer, C.; Caballero, L.; Cuadra, L.; Balenzategui, J. Experimental analysis of the quasi-Fermi level split in quantum dot intermediate-band solar cells. Appl. Phys. Lett. 2005, 87, 083505. [Google Scholar] [CrossRef]
- Martí, A.; Antolín, E.; Stanley, C.; Farmer, C.; López, N.; Díaz, P.; Cánovas, E.; Linares, P.; Luque, A. Production of photocurrent due to intermediate-to-conduction-band transitions: A demonstration of a key operating principle of the intermediate-band solar cell. Phys. Rev. Lett. 2006, 97, 247701. [Google Scholar] [CrossRef]
- Datas, A.; López, E.; Ramiro, I.; Antolín, E.; Martí, A.; Luque, A.; Tamaki, R.; Shoji, Y.; Sogabe, T.; Okada, Y. Intermediate band solar cell with extreme broadband spectrum quantum efficiency. Phys. Rev. Lett. 2015, 114, 157701. [Google Scholar] [CrossRef]
- Wełna, M.; Żelazna, K.; Létoublon, A.; Cornet, C.; Kudrawiec, R. Stability of the intermediate band energy position upon temperature changes in GaNP and GaNPAs. Sol. Energy Mater. Sol. Cells 2019, 196, 131–137. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, W.; Xue, Y.; Ning, H.; Liang, X.; Zhou, W.; Guo, J.; Huang, D. Intermediate band insertion by group-IIIA elements alloying in a low cost solar cell absorber CuYSe2: A first-principles study. Phys. Lett. A 2019, 383, 1972–1976. [Google Scholar] [CrossRef]
- Ramiro, I.; Martí, A.; Antolín, E.; Luque, A. Review of experimental results related to the operation of intermediate band solar cells. IEEE J. Photovoltaics 2014, 4, 736–748. [Google Scholar] [CrossRef]
- Martí, A.; Luque, A. Fundamentals of intermediate band solar cells. In Next, Generation of Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 209–228. [Google Scholar]
- Marrón, D.F. Thin-Film Technology in Intermediate Band Solar Cells. In Next, Generation of Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 277–307. [Google Scholar]
- Foxon, C.T.; Novikov, S.V.; Campion, R.P. InGaN Technology for IBSC Applications. In Next, Generation of Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 309–319. [Google Scholar]
- Olea, J.; Pastor, D.; Luque, M.T.; Mártil, I.; Díaz, G.G. Ion implant technology for intermediate band solar cells. In Next, Generation of Photovoltaics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 321–346. [Google Scholar]
- Antolín, E.; Martí, A.; Olea, J.; Pastor, D.; González-Díaz, G.; Mártil, I.; Luque, A. Lifetime recovery in ultrahighly titanium-doped silicon for the implementation of an intermediate band material. Appl. Phys. Lett. 2009, 94, 042115. [Google Scholar] [CrossRef]
- Persans, P.D.; Berry, N.E.; Recht, D.; Hutchinson, D.; Peterson, H.; Clark, J.; Charnvanichborikarn, S.; Williams, J.S.; DiFranzo, A.; Aziz, M.J.; et al. Photocarrier lifetime and transport in silicon supersaturated with sulfur. Appl. Phys. Lett. 2012, 101, 111105. [Google Scholar] [CrossRef][Green Version]
- Luque, A.; Martí, A.; Antolín, E.; Tablero, C. Intermediate bands versus levels in non-radiative recombination. Phys. Condens. Matter 2006, 382, 320–327. [Google Scholar] [CrossRef]
- Mott, N. Metal-insulator transition. Rev. Mod. Phys. 1968, 40, 677. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Scholes, G.D.; Fleming, G.R.; Olaya-Castro, A.; Van Grondelle, R. Lessons from nature about solar light harvesting. Nat. Chem. 2011, 3, 763–774. [Google Scholar] [CrossRef]
- Kundu, S.; Patra, A. Nanoscale strategies for light harvesting. Chem. Rev. 2017, 117, 712–757. [Google Scholar] [CrossRef]
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 2010, 6, 462–467. [Google Scholar] [CrossRef]
- Nalbach, P.; Thorwart, M. Enhanced quantum efficiency of light-harvesting in a biomolecular quantum “steam engine”. Proc. Natl. Acad. Sci. USA 2013, 110, 2693–2694. [Google Scholar] [CrossRef]
- Jiang, Y.; McNeill, J. Light-harvesting and amplified energy transfer in conjugated polymer nanoparticles. Chem. Rev. 2017, 117, 838–859. [Google Scholar] [CrossRef]
- Yang, P.Y.; Cao, J. Steady-state analysis of light-harvesting energy transfer driven by incoherent light: From dimers to networks. J. Phys. Chem. Lett. 2020, 11, 7204–7211. [Google Scholar] [CrossRef]

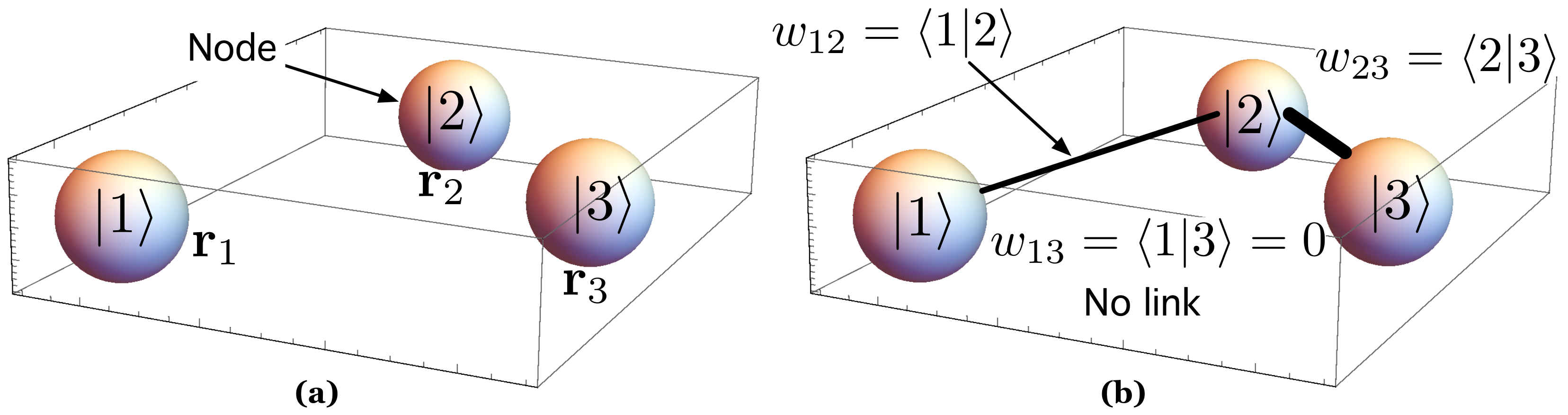
| 0.000172176 | 0.00582029 | 0.00387988 | 0.00106017 | 0.000970012 |
| 0.0000719148 | 0.00413783 | 0.000454207 | 0.0768675 | 0.00242522 |
| 0.0298138 | 0.00921407 | 0.0000565646 | 0.000102786 | 0.0000761972 |
| 0.0938865 | 0.00010824 | 0.0027705 | 0.0000545876 | 0.000735455 |
| 0.000247052 | 0.000190905 | 0.00274959 | 0.0000908889 | 0.00886395 |
| 0.00197876 | 0.00202883 | 0.003812 | 0.0197223 | 0.0300932 |
| 0.000148517 | 0.000360844 | 0.00247567 | 0.0193588 | 0.0000203756 |
| 0.0000281 | 0.0172012 | 0.00814919 | 0.0147341 | 0.00103512 |
| 0.000150275 | 0.0000862307 | 0.0294795 | 0.0203633 | 0.00025177 |
| 0.0000518012 | 0.00469129 | 0.0000315912 | 0.00847614 | 0.00144027 |
| 0.000285581 | 0.000261477 | 0.000582733 | 0.00371945 | 0.0336232 |
| 0.0032206 | 0.00980407 | 0.000807111 | 0.000121867 | 0.0459497 |
| 0.0105552 | 0.00168941 | 0.00534086 | 0.000115002 | 0.0447992 |
| 0.0001218 | 0.00431284 | 0.000201637 | 0.0188286 | |
| 0.000133976 | 0.0156714 | 0.0137177 | 0.0022036 | 0.000168711 |
| 0.000250133 | 0.0166772 | 0.00114926 | 0.0344186 | 0.00393284 |
| 0.000493777 | 0.0928017 | 0.00341317 | 0.00876622 | 0.000893781 |
| 0.0451846 | 0.0901622 | 0.0000291204 | 0.0000476467 | 0.0000574528 |
| 0.0117769 | 0.0178166 | 0.0034605 | 0.000244178 | 0.000142244 |
| 0.00037752 | 0.000129045 | 0.00373535 | 0.00499453 | 0.0118115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuadra, L.; Nieto-Borge, J.C. Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links. Nanomaterials 2021, 11, 375. https://doi.org/10.3390/nano11020375
Cuadra L, Nieto-Borge JC. Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links. Nanomaterials. 2021; 11(2):375. https://doi.org/10.3390/nano11020375
Chicago/Turabian StyleCuadra, Lucas, and José Carlos Nieto-Borge. 2021. "Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links" Nanomaterials 11, no. 2: 375. https://doi.org/10.3390/nano11020375
APA StyleCuadra, L., & Nieto-Borge, J. C. (2021). Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links. Nanomaterials, 11(2), 375. https://doi.org/10.3390/nano11020375







