Micromagnetic Simulations of Fe and Ni Nanodot Arrays Surrounded by Magnetic or Non-Magnetic Matrices
Abstract
1. Introduction
2. Materials and Methods
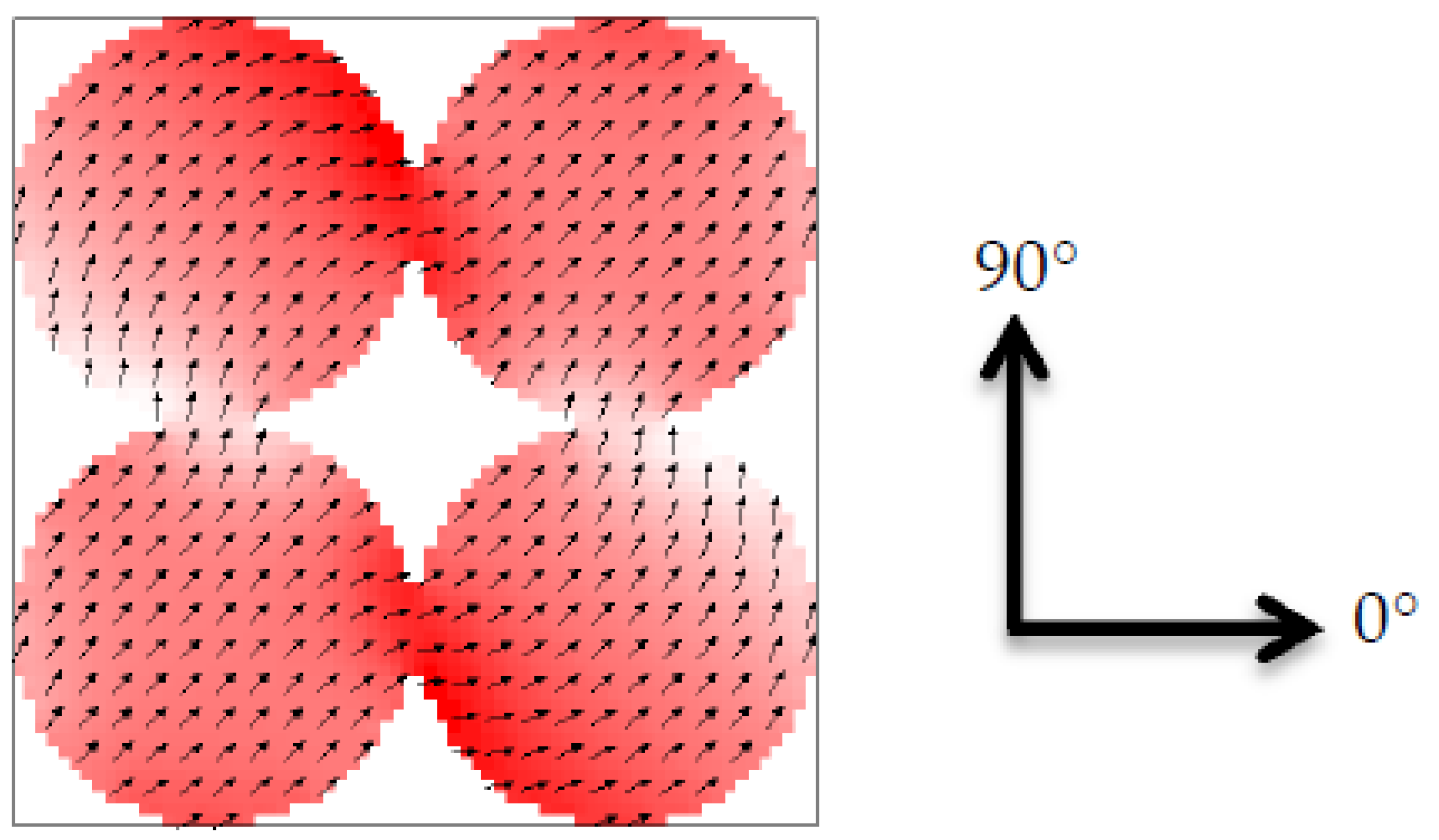
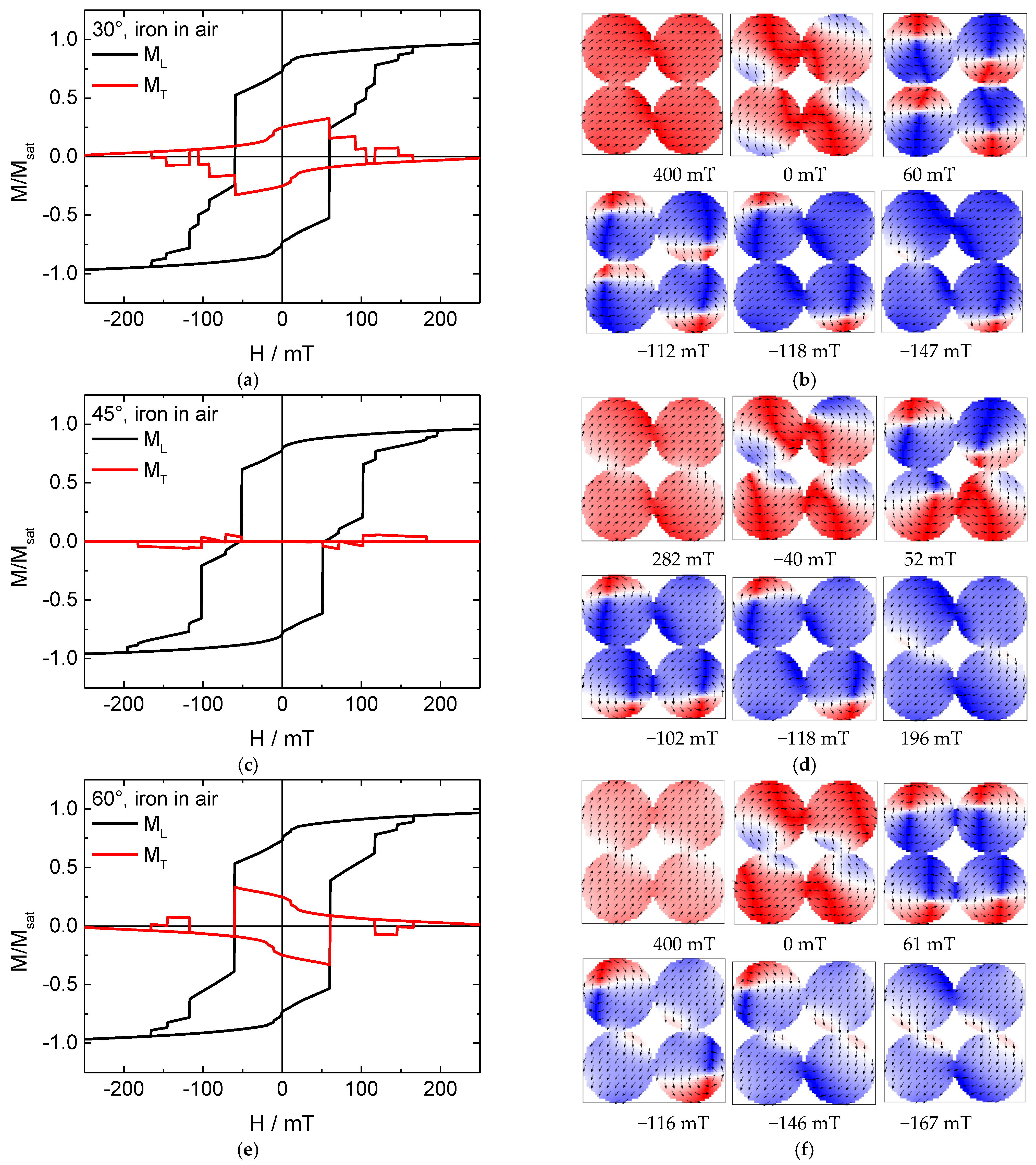
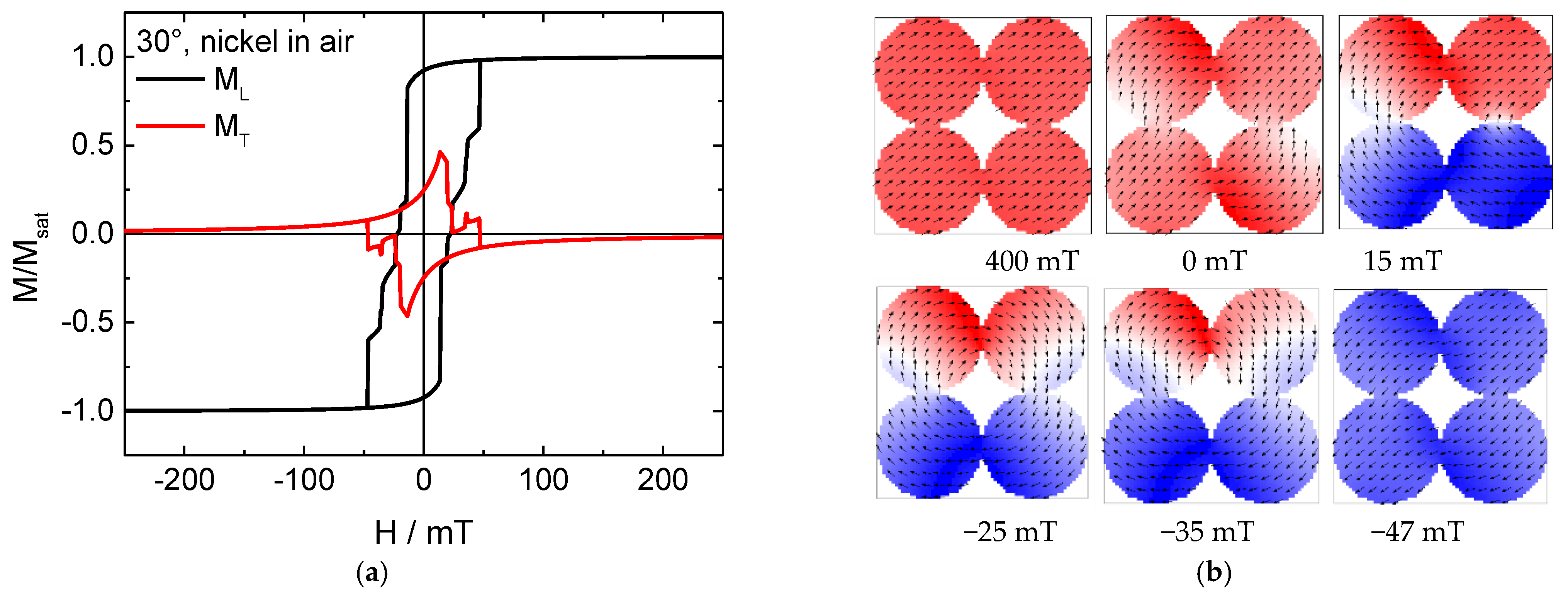
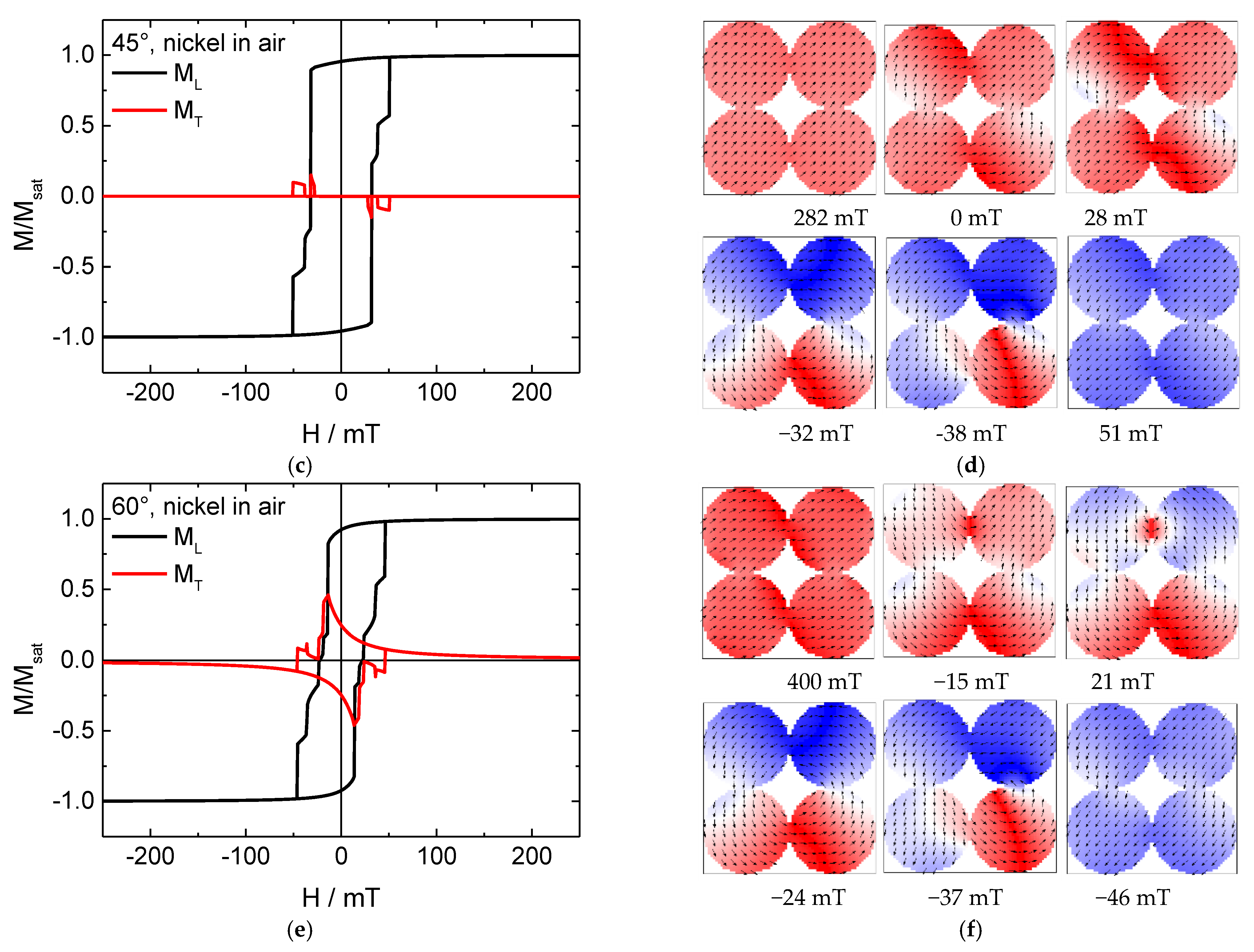
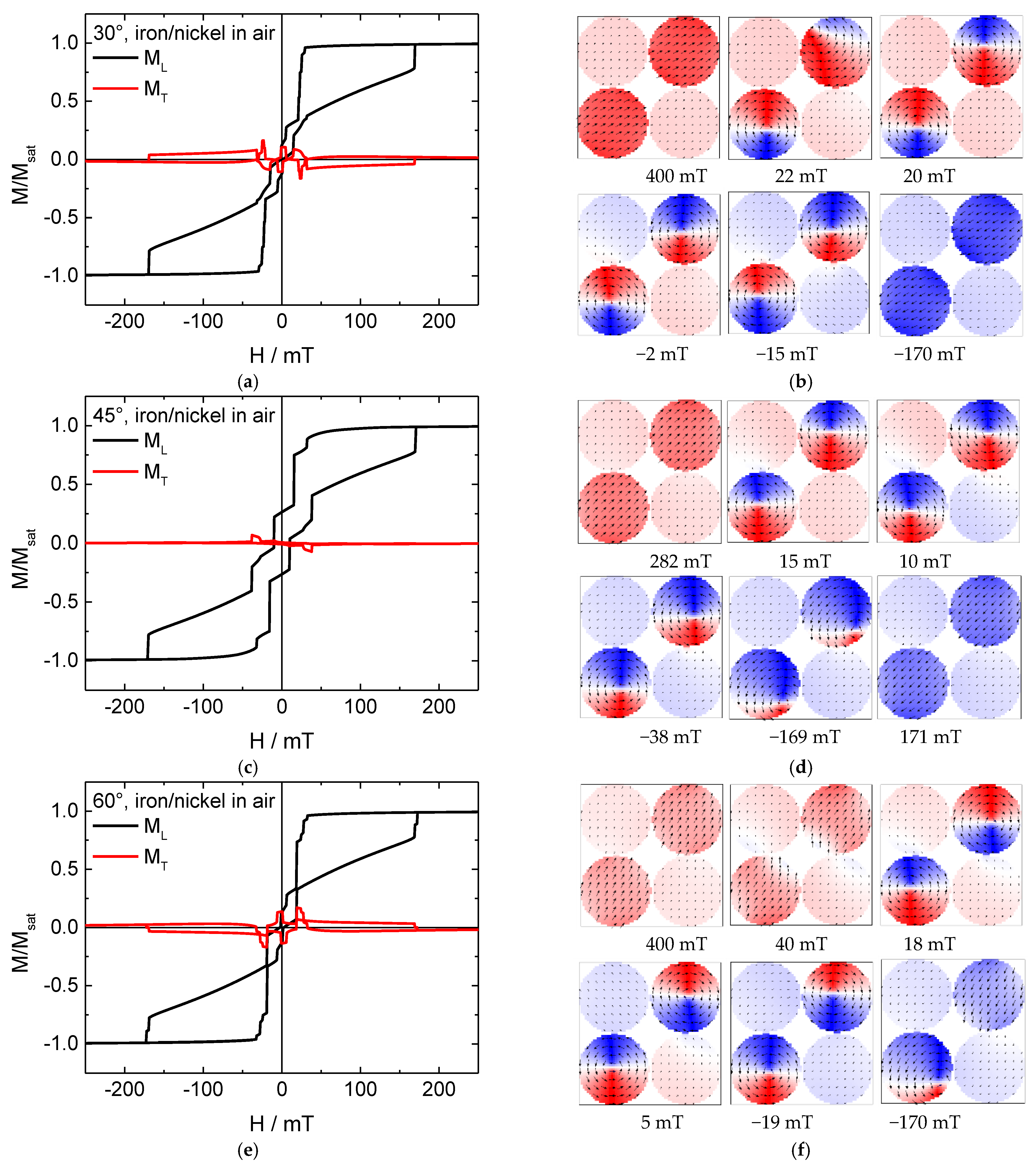
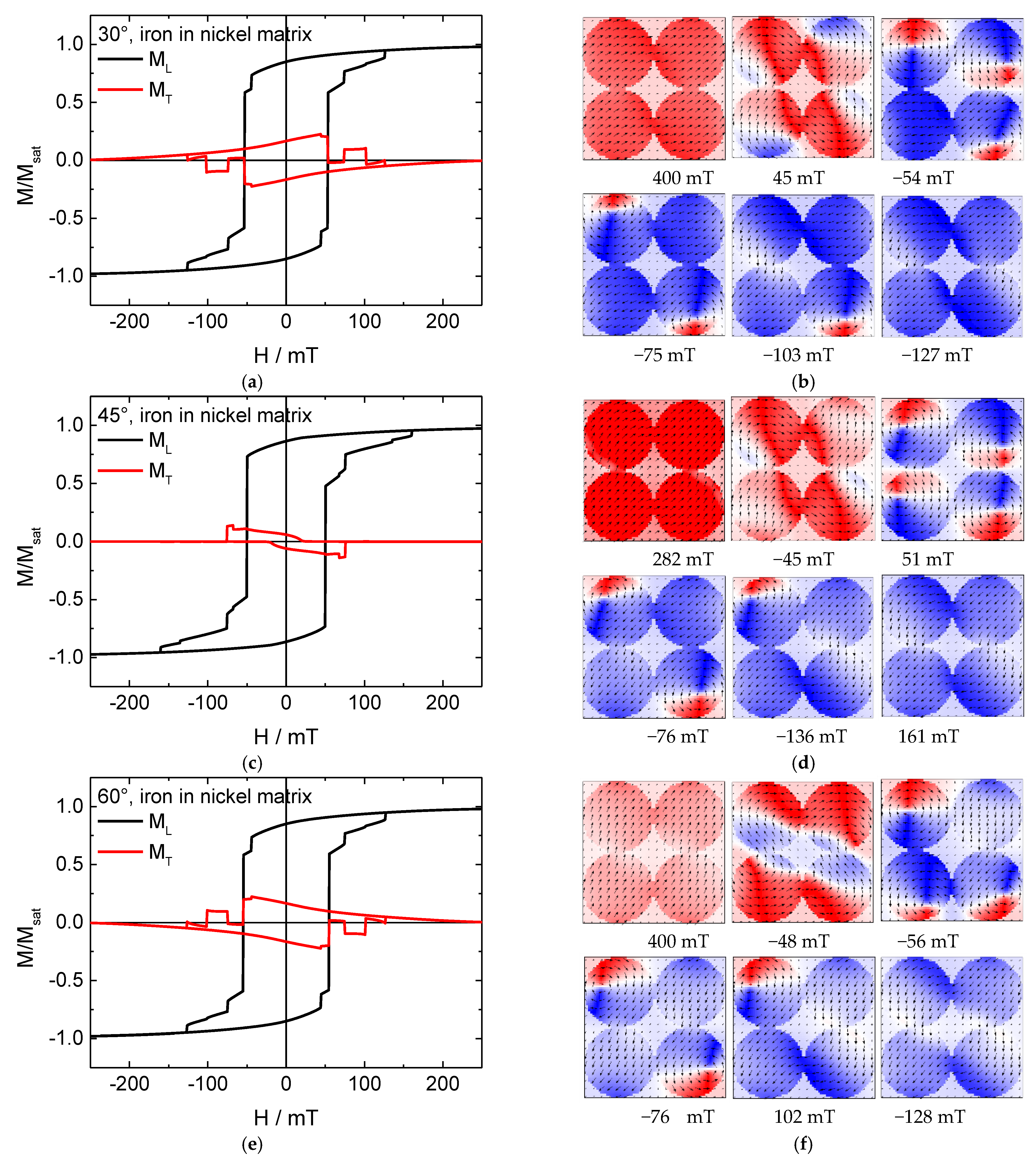
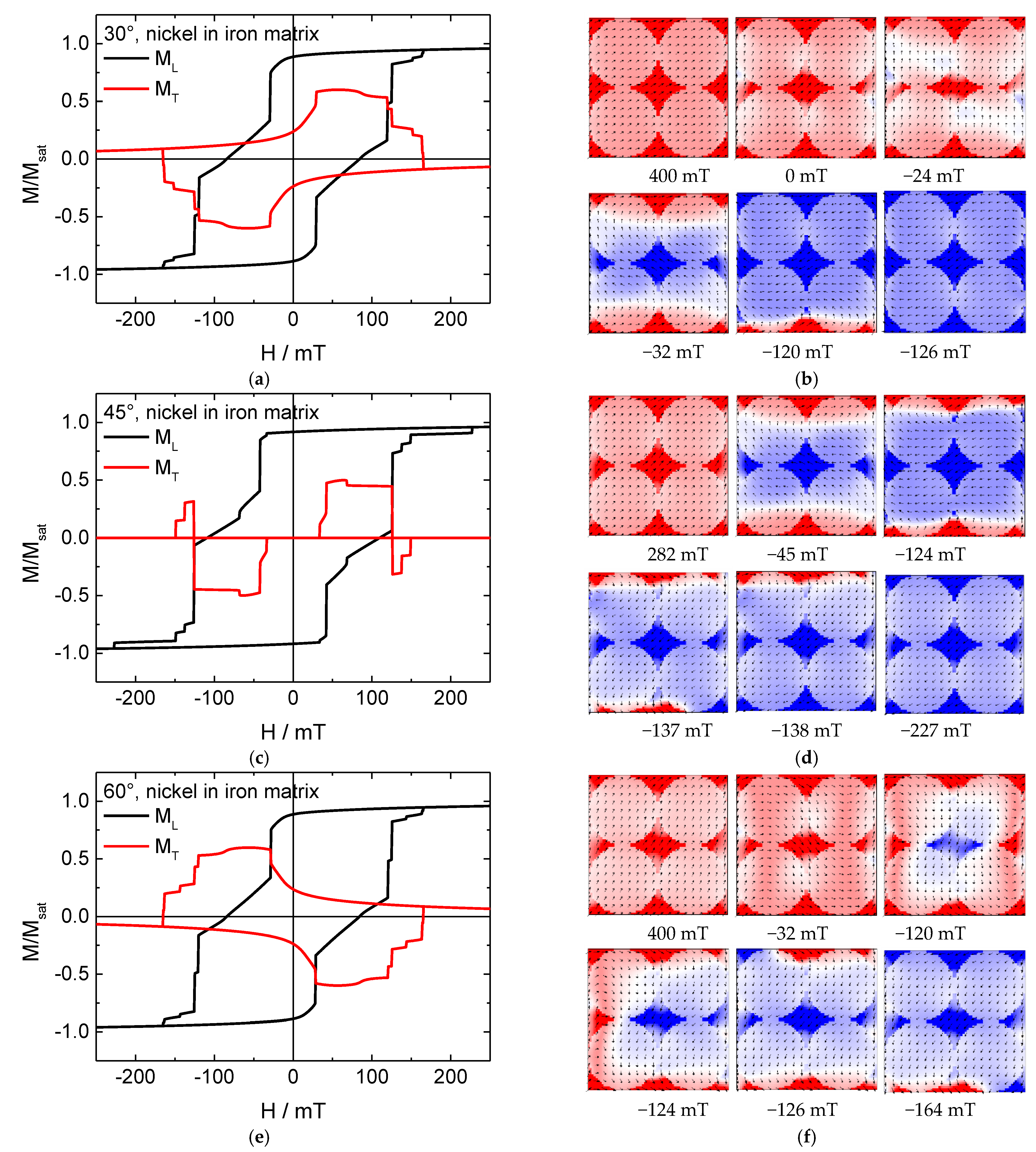
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nogués, J.; Sort, J.; Langlais, V.; Skumryev, V.; Surinach, S.; Munoz, J.S.; Baro, M.D. Exchange bias in nanostructures. Phys. Rep. 2005, 422, 65–117. [Google Scholar] [CrossRef]
- Fokin, N.; Grothe, T.; Mamun, A.; Trabelsi, M.; Klöcker, M.; Sabantina, L.; Döpke, C.; Blachowicz, T.; Hütten, A.; Ehrmann, A. Magnetic properties of electrospun magnetic nanofiber mats after stabilization and carbonization. Materials 2020, 13, 1552. [Google Scholar] [CrossRef] [PubMed]
- Wachowiak, A.; Wiebe, J.; Bode, M.; Pietzsch, O.; Morgenstern, M.; Wiesendanger, R. Direct Observation of Internal Spin Structure of Magnetic Vortex Cores. Science 2002, 298, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Mejia-López, J.; Altbir, D.; Romero, A.H.; Batlle, X.; Roshchin, I.V.; Li, C.-P.; Schuller, I.K. Vortex state and effect of anisotropy in sub-100-nm magnetic nanodots. J. Appl. Phys. 2006, 100, 104319. [Google Scholar] [CrossRef]
- Vavassori, P.; Bovolenta, R.; Metlushko, V.; Ilic, B. Vortex rotation control in Permalloy disks with small circular voids. J. Appl. Phys. 2006, 99, 53902. [Google Scholar] [CrossRef]
- Guslienko, K.Y.; Aranda, G.R.; Gonzalez, J.M. Topological gauge field in nanomagnets: Spin-wave excitations over a slowly moving magnetization background. Phys. Rev. B 2010, 81, 014414. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Systematic study of magnetization reversal in square Fe nanodots of varying dimensions in different orientations. Hyperfine Interact. 2018, 239, 48. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Vortex and double-vortex nucleation during magnetization reversal in Fe nanodots of different dimensions. J. Magn. Magn. Mater. 2019, 475, 727–733. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Martínez-Goyeneche, L.; Álvarez-Alonso, P.; Fernández, A. Enhancement the perpendicular magnetic anisotropy of nanopatterned hard/soft bilayer magnetic antidot arrays for spintronic applications. Nanotechnology 2020, 31, 485708. [Google Scholar] [CrossRef]
- Verba, R.V.; Navas, D.; Bunyaev, S.A.; Hierro-Rodriguez, A.; Guslienko, K.Y.; Ivanov, B.A.; Kakazei, G.N. Helicity of magnetic vortices and skyrmions in soft ferromagnetic nanodots and films biased by stray radial fields. Phys. Rev. B 2020, 101, 064429. [Google Scholar] [CrossRef]
- Negusse, E.; Williams, C.M. Magnetically induced enhanced exchange spring effect in CoFe2O4/CoFe2/CoFe2O4 films. IEEE Trans. Magn. 2020, 56, 1–5. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Jiang, J.S.; Grimsditch, M.; Sowers, C.H.; Bader, S.D. Exchange-spring behavior in epitaxial hard/soft magnetic bilayers. Phys. Rev. B 1998, 58, 12193. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Jiang, J.S.; Bader, S.D. Hard/soft magnetic heterostructures: Model exchange-spring magnets. J. Magn. Magn. Mater. 1999, 200, 392–404. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Skomski, R. New magnets from interstitial intermetallics. Phys. Scr. 1993, T49, 315–321. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J.M.D. Nucleation field and energy product of aligned two-phase magnets—progress towards the ‘1 MJ/m³’ magnet. IEEE Trans. Magn. 1993, 29, 2860–2862. [Google Scholar] [CrossRef]
- Sawicki, M.; Bowden, G.J.; de Groot, P.A.J.; Rainford, B.D.; Beaujour, J.M.L. Engineering coercivity in epitaxially grown (110) films of DyFe2-YFe2 superlattices. Appl. Phys. Lett. 2000, 77, 573–575. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Park, H.-K.; Ju, Y.-W. Fabrication of the novel Fe2+αO3+α-CoFe2O4 composite fibers and their magnetic properties. J. Korean Ceram. Soc. 2020, 57, 423–431. [Google Scholar] [CrossRef]
- Zhang, X.; Kan, X.C.; Wang, M.; Rao, R.; Qian, N.X.; Zheng, G.H.; Ma, Y.Q. Mechanism of enhanced magnetization in CoFe2O4/La0.7Sr0.3MnO3 composites with different mass ratios. Ceram. Int. 2020, 46, 14847–14856. [Google Scholar] [CrossRef]
- Sudsom, D.; Juhász Junger, I.; Döpke, C.; Blachowicz, T.; Hahn, L.; Ehrmann, A. Micromagnetic Simulation of Vortex Development in Magnetic Bi-Material Bow-Tie Structures. Cond. Matter 2020, 5, 5. [Google Scholar] [CrossRef]
- Sudsom, D.; Blachowicz, T.; Hahn, L.; Ehrmann, A. Vortex nucleation and propagation in magnetic double-wedges and semi-squares for reliable quaternary storage systems. J. Magn. Magn. Mater. 2020, 514, 167294. [Google Scholar] [CrossRef]
- Sudsom, D.; Ehrmann, A. Micromagnetic simulations of magnetic particles embedded in magnetic or non-magnetic matrices. Presented at the 2nd International Online—Conference on Nanomaterials, 15–30 November 2020; Volume 15, p. 30. [Google Scholar]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide; Version 1.0; Interagency Report NISTIR 6376; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999. [Google Scholar]
- Gilbert, T.L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443–3449. [Google Scholar] [CrossRef]
- Xuan, D.N.; Döpke, C.; Blachowicz, T.; Ehrmann, A. Magnetization reversal in hexagonal nanomagnets. Act. Phys. Pol. 2020, 137, 395–403. [Google Scholar] [CrossRef]
- Dmytriiev, O.; Dvornik, M.; Mikhaylovskiy, R.V.; Franchin, M.; Fangohr, H.; Giovannini, L.; Montoncello, F.; Berkov, D.V.; Semenova, E.K.; Gorn, N.L.; et al. Calculation of high-frequency permeability of magnonic metamaterials beyond the macrospin approximation. Phys. Rev. B 2012, 86, 104405. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Wang, F.; Zhang, J.; Zhang, R.Q.; Wang, Z.F.; Xu, X.H. Design and micromagnetic simulation of the L10-FePt/Fe multilayer graded film. J. Appl. Phys. 2012, 111, 073910. [Google Scholar] [CrossRef]
- Berkov, D.V.; Gorn, N.L. Micromagnetic simulations of the magnetization precession induced by a spin-polarized current in a point-contact geometry (Invited). J. Appl. Phys. 2006, 99, 08Q701. [Google Scholar] [CrossRef]
- Dumas, R.K.; Liu, K. Temperature induced single domain-vortex state transition in sub-100 nm Fe nanodots. Appl. Phys. Lett. 2007, 91, 202501. [Google Scholar] [CrossRef]
- Dumas, R.K.; Li, C.-P.; Roshchin, I.V.; Schuller, I.K.; Liu, K. Magnetic fingerprints of sub-100 nm Fe dots. Phys. Rev. B 2007, 75, 134405. [Google Scholar] [CrossRef]
- Jung, J.-S.; Kim, E.-M.; Chae, W.-S.; Malkinski, L.M.; Lim, J.-H.; O’Connor, C.; Jun, J.-H. Electrodeposited nickel nanodots array on the silicon wafer. Bull. Korean Chem. Soc. 2008, 29, 2169–2171. [Google Scholar]
- Ramaswamy, S.; Gopalakrishnan, C.; Kumar, S.N.; Littleflower, A.; Ponnavaikko, M. Fabrication of Ni nanodots template by nanoporous polysulfone membrane: Structural and magnetic properties. Appl. Phys. A 2010, 98, 481–485. [Google Scholar] [CrossRef]
- Nasirpouri, F.; Nogaret, A.; Bending, S.J. Effect of size and configuration on the magnetization of nickel dot arrays. IEEE Trans. Magn. 2011, 47, 4695–4700. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sudsom, D.; Ehrmann, A. Micromagnetic Simulations of Fe and Ni Nanodot Arrays Surrounded by Magnetic or Non-Magnetic Matrices. Nanomaterials 2021, 11, 349. https://doi.org/10.3390/nano11020349
Sudsom D, Ehrmann A. Micromagnetic Simulations of Fe and Ni Nanodot Arrays Surrounded by Magnetic or Non-Magnetic Matrices. Nanomaterials. 2021; 11(2):349. https://doi.org/10.3390/nano11020349
Chicago/Turabian StyleSudsom, Devika, and Andrea Ehrmann. 2021. "Micromagnetic Simulations of Fe and Ni Nanodot Arrays Surrounded by Magnetic or Non-Magnetic Matrices" Nanomaterials 11, no. 2: 349. https://doi.org/10.3390/nano11020349
APA StyleSudsom, D., & Ehrmann, A. (2021). Micromagnetic Simulations of Fe and Ni Nanodot Arrays Surrounded by Magnetic or Non-Magnetic Matrices. Nanomaterials, 11(2), 349. https://doi.org/10.3390/nano11020349






