Granular Hall Sensors for Scanning Probe Microscopy
Abstract
1. Introduction
2. Results and Discussion
2.1. Sample Composition and Transport Regime
2.2. Magneto-Transport Properties
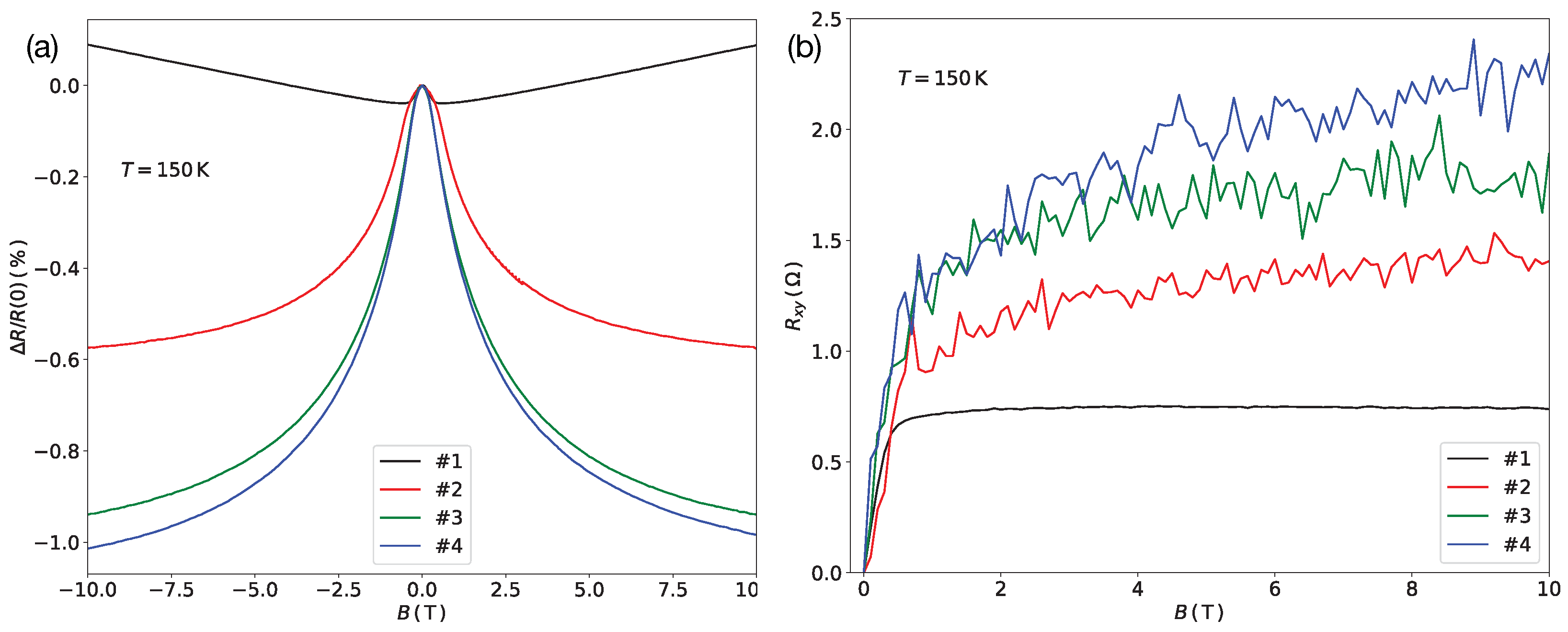
2.2.1. Magneto-Resistance and Hall Effect
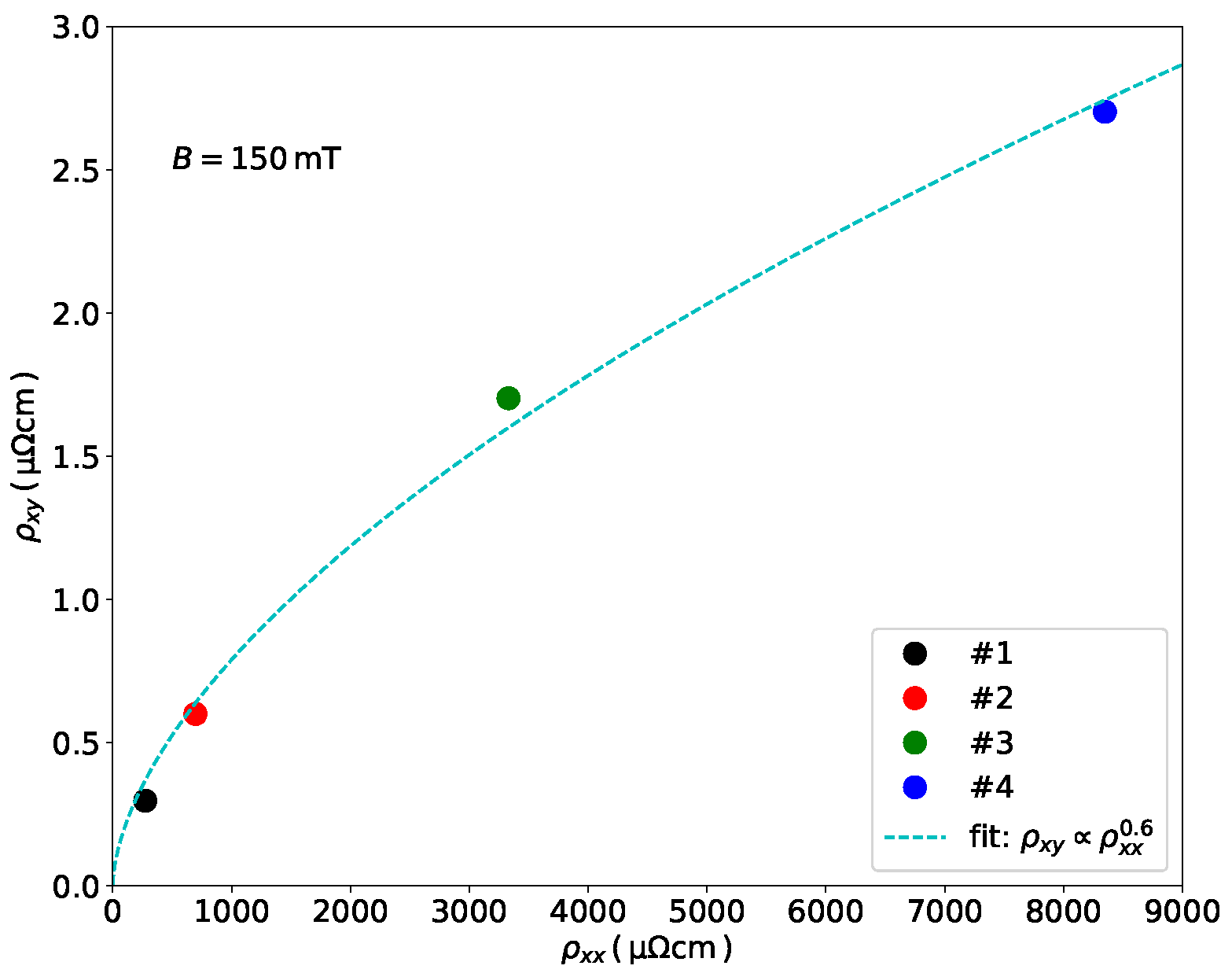
2.2.2. Scaling Behavior
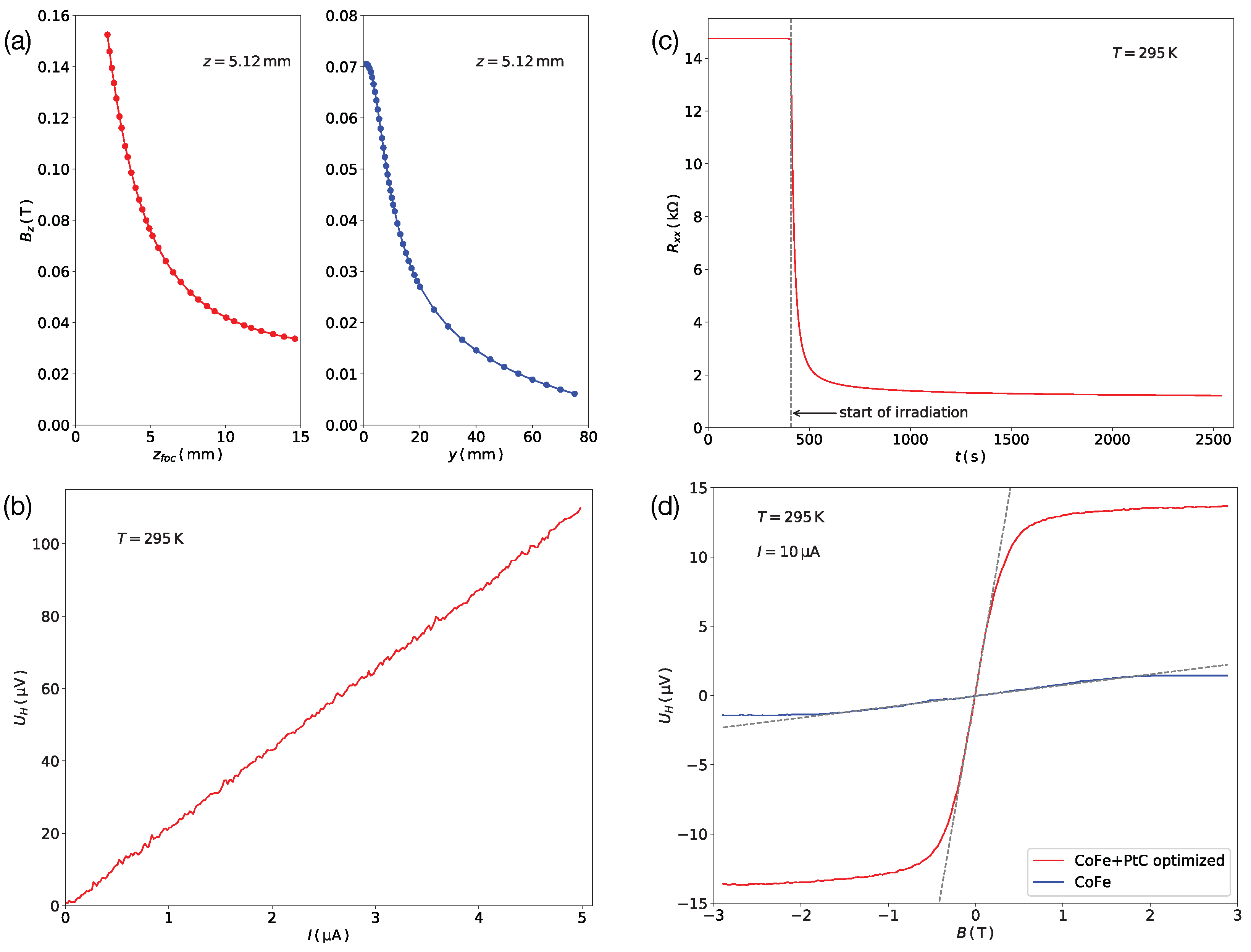
2.2.3. In Situ Measurements and Optimization
2.3. Scanning Hall Probe Microscopy
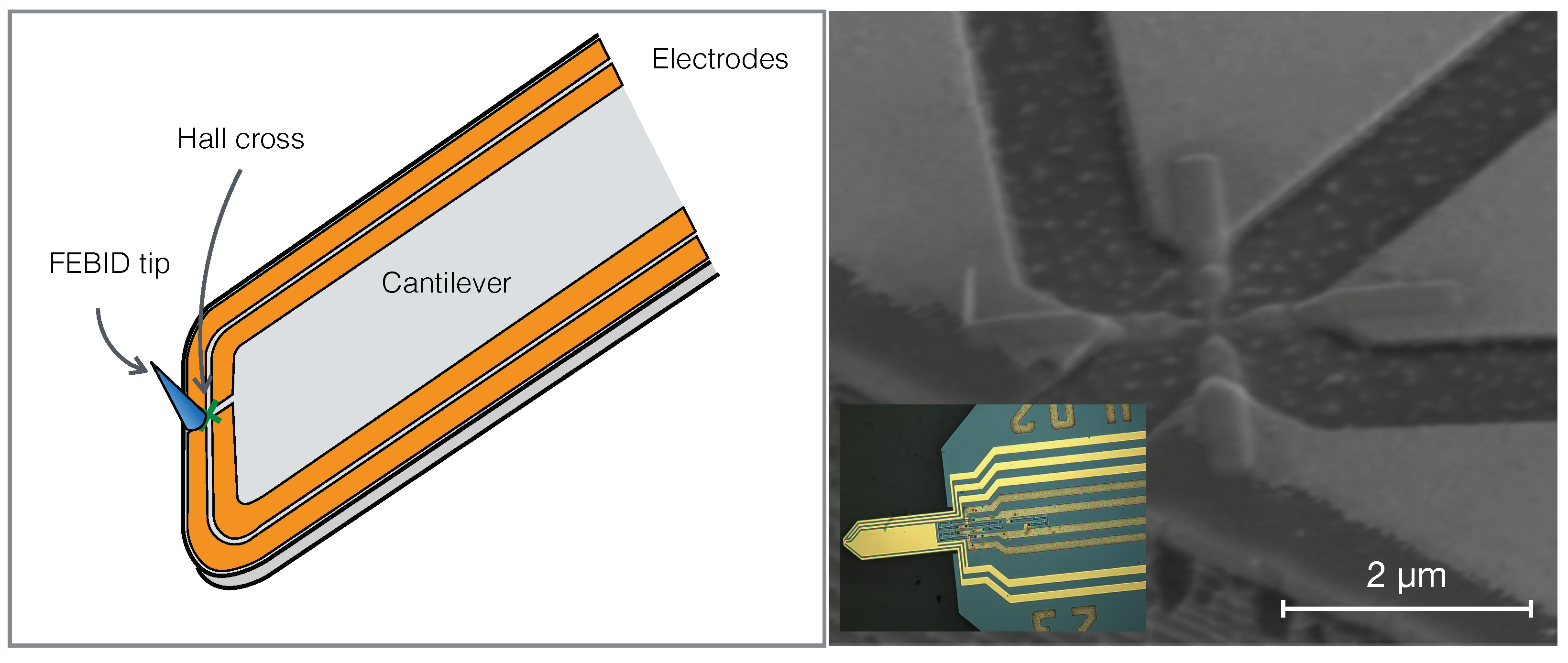
2.3.1. Probe Geometry
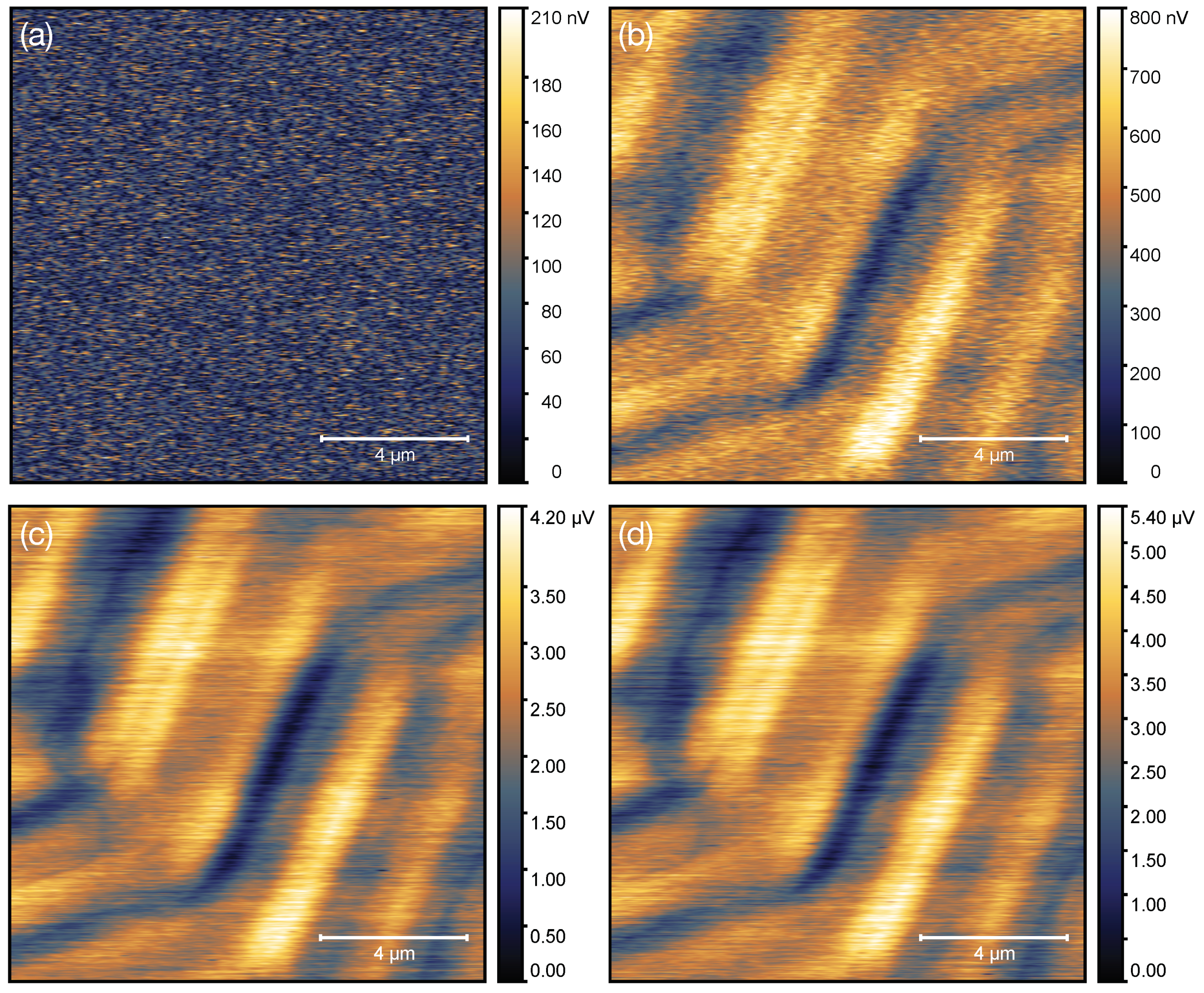
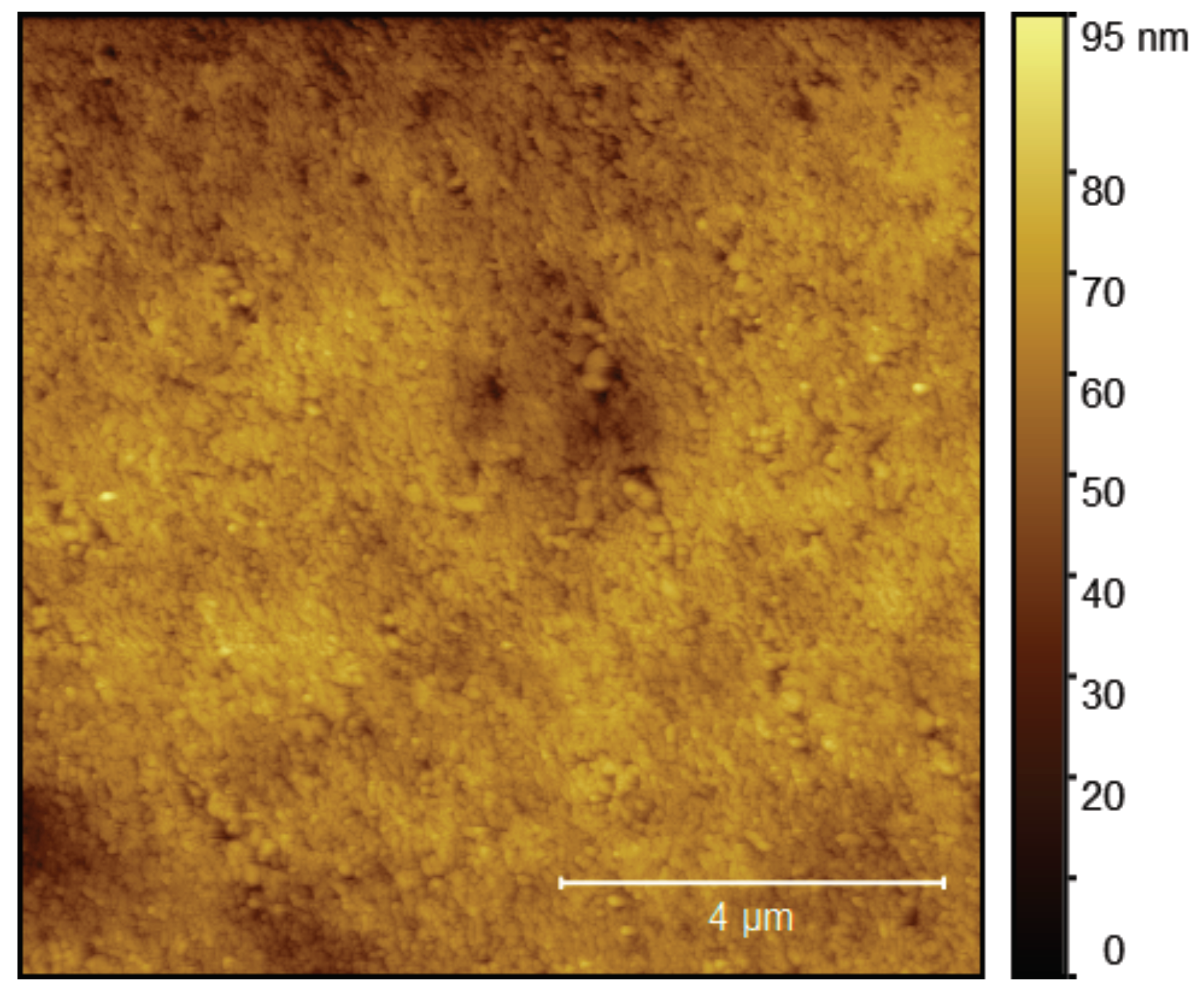
2.3.2. Imaging Results
3. Materials and Methods
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MFM | Magnetic force microscopy |
| SSQM | Scanning SQUID microscopy |
| SHPM | Scanning Hall probe microscopy |
| GFM | Granular ferromagnet |
| OHE | Ordinary Hall effect |
| EHE | Extraordinary Hall effect |
| FEBID | Focused electron beam induced deposition |
| GIS | Gas injection system |
| SEM | Scanning electron microcope |
| EDX | Energy-dispersive X-ray spectroscopy |
| AFM | Atomic force microscopy |
References
- Kazakova, O.; Puttock, R.; Barton, C.; Corte-León, H.; Jaafar, M.; Neu, V.; Asenjo, A. Frontiers of magnetic force microscopy. J. Appl. Phys. 2019, 125, 060901. [Google Scholar] [CrossRef]
- Koelle, D. A tip for better sensing. Nat. Nanotechnol. 2013, 8, 617. [Google Scholar] [CrossRef] [PubMed]
- Reith, P.; Renshaw Wang, X.; Hilgenkamp, H. Analysing magnetism using scanning SQUID microscopy. Rev. Sci. Instrum. 2017, 88, 123706. [Google Scholar] [CrossRef]
- Chong, B.K.; Zhou, H.; Mills, G.; Donaldson, L.; Weaver, J.M.R. Scanning Hall probe microscopy on an atomic force microscope tip. J. Vac. Sci. Technol. A 2001, 19, 1769. [Google Scholar] [CrossRef]
- Sandhu, A.; Masuda, H.; Oral, A.; Bending, S.J.; Yamada, A.; Konagai, M. Room temperature scanning Hall probe microscopy using GaAs/AlGaAs and Bi micro-hall probes. Ultramicroscopy 2002, 91, 97. [Google Scholar] [CrossRef]
- Brook, A.; Bending, S.; Pinto, J.; Oral, A.; Ritchie, D.; Beere, H.; Henini, M.; Springthorpe, A. Integrated piezoresistive sensors for atomic force-guided scanning Hall probe microscopy. Appl. Phys. Lett. 2003, 82, 3538. [Google Scholar] [CrossRef]
- Sandhu, A.; Kurosawa, K.; Dede, M.; Oral, A. 50 nm Hall Sensors for Room Temperature Scanning Hall Probe Microscopy. Jpn. J. Appl. Phys. 2004, 43, 777. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef]
- Denardin, J.C.; Knobel, M.; Zhang, X.X.; Pakhomov, A.B. Giant Hall effect in superparamagnetic granular films. J. Magn. Magn. Mater. 2003, 262, 15. [Google Scholar] [CrossRef]
- Teresa, J.M.D.; Fernández-Pacheco, A.; Córdoba, R.; Serrano-Ramón, L.; Sangiao, S.; Ibarra, M.R. Review of magnetic nanostructures grown by focused electron beam induced deposition (FEBID). J. Phys. D Appl. Phys. 2016, 49, 243003. [Google Scholar] [CrossRef]
- Huth, M.; Porrati, F.; Dobrovolskiy, O. Focused electron beam induced deposition meets materials science. Microelectron. Eng. 2018, 185–186, 9. [Google Scholar] [CrossRef]
- Gabureac, M.; Bernau, L.; Utke, I.; Boero, G. Granular Co–C nano-Hall sensors by focused-beam-induced deposition. Nanotechnology 2010, 21, 115503. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Córdoba, R.; Lavrijsen, R.; Fernández-Pacheco, A.; Ibarra, M.R.; Schoenaker, F.; Ellis, T.; Barcones-Campo, B.; Kohlhepp, J.T.; Swagten, H.J.M.; Koopmans, B.; et al. Giant anomalous Hall effect in Fe-based microwires grown by focused-electron-beam-induced deposition. J. Phys. D Appl. Phys. 2011, 45, 035001. [Google Scholar] [CrossRef]
- Porrati, F.; Sachser, R.; Schwalb, C.H.; Frangakis, A.S.; Huth, M. Tuning the electrical conductivity of Pt-containing granular metals by postgrowth electron irradiation. J. Appl. Phys. 2011, 109, 063715. [Google Scholar] [CrossRef]
- Plank, H.; Kothleitner, G.; Hofer, F.; Michelitsch, S.G.; Gspan, C.; Hohenau, A.; Krenn, J. Optimization of postgrowth electron-beam curing for focused electron-beam-induced Pt deposits. J. Vac. Sci. Technol. B 2011, 29, 051801. [Google Scholar] [CrossRef]
- Friedli, V.; Utke, I. Optimized molecule supply from nozzle-based gas injection systems for focused electron- and ion-beam induced deposition and etching: Simulation and experiment. J. Phys. D Appl. Phys. 2009, 42, 125305. [Google Scholar] [CrossRef]
- Porrati, F.; Sachser, R.; Gazzadi, G.C.; Frabboni, S.; Huth, M. Fabrication of FeSi and Fe3Si compounds by electron beam induced mixing of [Fe/Si]2 and [Fe3/Si]2 multilayers grown by focused electron beam induced deposition. J. Appl. Phys. 2016, 119, 234306. [Google Scholar] [CrossRef]
- Sachser, R.; Porrati, F.; Schwalb, C.H.; Huth, M. Universal Conductance Correction in a Tunable Strongly Coupled Nanogranular Metal. Phys. Rev. Lett. 2011, 107, 206803. [Google Scholar] [CrossRef]
- Porrati, F.; Pohlit, M.; Müller, J.; Barth, S.; Biegger, F.; Gspan, C.; Plank, H.; Huth, M. Direct writing of CoFe alloy nanostructures by focused electron beam induced deposition from a heteronuclear precursor. Nanotechnology 2015, 26, 475701. [Google Scholar] [CrossRef]
- Schwalb, C.H.; Grimm, C.; Baranowski, M.; Sachser, R.; Porrati, F.; Reith, H.; Das, P.; Müller, J.; Völklein, F.; Kaya, A.; et al. Tunable Strain Sensor Using Nanogranular Metals. Sensors 2010, 10, 9847–9856. [Google Scholar] [CrossRef]
- Gerber, A.; Milner, A.; Finkler, A.; Karpovski, M.; Goldsmith, L.; Tuaillon-Combes, J.; Boisron, O.; Mélinon, P.; Perez, A. Correlation between the extraordinary Hall effect and resistivity. Phys. Rev. B 2004, 69, 224403. [Google Scholar] [CrossRef]
- Xiong, P.; Xiao, G.; Wang, J.Q.; Xiao, J.Q.; Jiang, J.S.; Chien, C.L. Extraordinary Hall effect and giant magnetoresistance in the granular Co-Ag system. Phys. Rev. Lett. 1992, 69, 3220. [Google Scholar] [CrossRef] [PubMed]
- Bartov, D.; Segal, A.; Karpovski, M.; Gerber, A. Absence of the ordinary and extraordinary Hall effects scaling in granular ferromagnets at metal-insulator transition. Phys. Rev. B 2014, 90, 144423. [Google Scholar] [CrossRef]
- Meier, H.; Kharitonov, M.Y.; Efetov, K.B. Anomalous Hall effect in granular ferromagnetic metals and effects of weak localization. Phys. Rev. B 2009, 80, 045122. [Google Scholar] [CrossRef]
- Porrati, F.; Begun, E.; Winhold, M.; Schwalb, C.; Sachser, R.; Frangakis, A.S.; Huth, M. Room temperature L10phase transformation in binary CoPt nanostructures prepared by focused-electron-beam-induced deposition. Nanotechnology 2012, 23, 185702. [Google Scholar] [CrossRef] [PubMed]
- Dobrovolskiy, O.V.; Kompaniiets, M.; Sachser, R.; Porrati, F.; Gspan, C.; Plank, H.; Huth, M. Tunable magnetism on the lateral mesoscale by post-processing of Co/Pt heterostructures. Beilstein J. Nanotechol. 2015, 6, 1082. [Google Scholar] [CrossRef] [PubMed]
- Winhold, M. Focused Electron-Beam-Induced Deposition—From Process Optimization to Cantilever-Based Strain-Sensing Applications Using Nanogranular Tunneling Resistors. Ph.D. Thesis, Goethe University, Frankfurt am Main, Germany, 2016. [Google Scholar]
- Yablon, D.; Werten, P.; Winhold, M.; Schwalb, C.H. Cross-platform integration of AFM with SEM: Offering the best of both worlds. Microsc. Anal. 2017, 31, 14–18. [Google Scholar]
- Kreith, J.; Strunz, T.; Fantner, E.J.; Fantner, G.E.; Cordill, M.J. A versatile atomic force microscope integrated with a scanning electron microscope. Rev. Sci. Instrum. 2017, 88, 053704. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sachser, R.; Hütner, J.; Schwalb, C.H.; Huth, M. Granular Hall Sensors for Scanning Probe Microscopy. Nanomaterials 2021, 11, 348. https://doi.org/10.3390/nano11020348
Sachser R, Hütner J, Schwalb CH, Huth M. Granular Hall Sensors for Scanning Probe Microscopy. Nanomaterials. 2021; 11(2):348. https://doi.org/10.3390/nano11020348
Chicago/Turabian StyleSachser, Roland, Johanna Hütner, Christian H. Schwalb, and Michael Huth. 2021. "Granular Hall Sensors for Scanning Probe Microscopy" Nanomaterials 11, no. 2: 348. https://doi.org/10.3390/nano11020348
APA StyleSachser, R., Hütner, J., Schwalb, C. H., & Huth, M. (2021). Granular Hall Sensors for Scanning Probe Microscopy. Nanomaterials, 11(2), 348. https://doi.org/10.3390/nano11020348






