Unconventional Thermal and Magnetic-Field-Driven Changes of a Bipartite Entanglement of a Mixed Spin-(1/2,S) Heisenberg Dimer with an Uniaxial Single-Ion Anisotropy
Abstract
:1. Introduction
2. Model and Method
3. Results and Discussion
3.1. Quantum Negativity
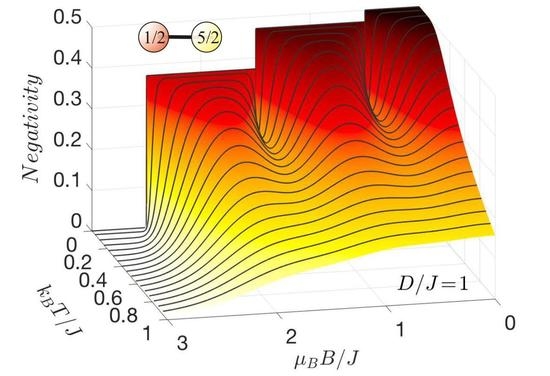
3.2. The Thermal Negativity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Density Matrices
Appendix A.1. Density Matrix of the Mixed Spin-(1/2,1) Heisenberg Dimer
Appendix A.2. Density Matrix of the Mixed Spin-(1/2,3/2) Heisenberg Dimer
Appendix A.3. Density Matrix of the Mixed Spin-(1/2,2) Heisenberg Dimer
Appendix A.4. Density Matrix of the Mixed Spin-(1/2,5/2) Heisenberg Dimer
Appendix B. The Explicit Form of the Eigenvalues
Appendix C. Density Matrices Partially Transposed with Respect the Spin-1/2 Subsystem
Appendix C.1. Partially Transposed Density Matrix of the Mixed Spin-(1/2,1) Heisenberg Dimer
Appendix C.2. Partially Transposed Density Matrix of the Mixed Spin-(1/2,3/2) Heisenberg Dimer
Appendix C.3. Partially Transposed Density Matrix of the Mixed Spin-(1/2,2) Heisenberg Dimer
Appendix C.4. Partially Transposed Density Matrix of the Mixed Spin-(1/2,5/2) Heisenberg Dimer
References
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, T.; Fujisawa, T.; Cheong, H.D.; Jeong, Y.H.; Hirayama, Y. Coherent Manipulation of Electronic States in a Double Quantum Dot. Phys. Rev. Lett. 2003, 91, 226804. [Google Scholar] [CrossRef] [Green Version]
- Shulman, M.D.; Dial, O.E.; Harvey, S.P.; Bluhm, H.; Umansky, V.; Yacoby, A. Demonstration of entanglement of electrostatically coupled singlet-triplet qubits. Science 2012, 336, 202–205. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Simmons, C.B.; Ward, D.R.; Prance, J.R.; Wu, X.; Koh, T.S.; Gamble, J.K.; Savage, D.E.; Lagally, M.G.; Friesen, M.; et al. Fast coherent manipulation of three-electron states in a double quantum dot. Nat. Commun. 2014, 5, 3020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, N.C.; Van Meter, R.; Fowler, A.G.; McMahon, P.L.; Kim, J.; Ladd, T.D.; Yamamoto, Y. Layered Architecture for Quantum Computing. Phys. Rev. X 2012, 2, 031007. [Google Scholar] [CrossRef] [Green Version]
- Delbecq, M.R.; Nakajima, T.; Stano, P.; Otsuka, T.; Amaha, S.; Yoneda, J.; Takeda, K.; Allison, G.; Ludwig, A.; Wieck, A.D.; et al. Quantum Dephasing in a Gated GaAs Triple Quantum Dot due to Nonergodic Noise. Phys. Rev. Lett. 2016, 116, 046802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watson, T.F.; Philips, S.G.J.; Kawakami, E.; Ward, D.R.; Scarlino, P.; Veldhorst, M.; Savage, D.E.; Lagally, M.G.; Friesen, M.; Coppersmith, S.N.; et al. A programmable two-qubit quantum processor in silicon. Nature (London) 2018, 555, 633–637. [Google Scholar] [CrossRef] [Green Version]
- Berger, C.; Huttner, U.; Mootz, M.; Kira, M.; Koch, S.W.; Tempel, J.S.; Assmann, M.; Bayer, M.; Mintairov, A.M.; Merz, J.L. Quantum-Memory Effects in the Emission of Quantum-Dot Microcavities. Phys. Rev. Lett. 2014, 113, 093902. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Holloway, G.W.; Benjamin, S.C.; Briggs, G.A.D.; Baugh, J.; Mol, J.A. Double quantum dot memristor. Phys. Rev. B 2017, 96, 075446. [Google Scholar] [CrossRef] [Green Version]
- Gunlycke, D.; Kendon, V.M.; Vedral, V.; Bose, S. Thermal concurrence mixing in a one-dimensional Ising model. Phys. Rev. A 2001, 64, 423021. [Google Scholar] [CrossRef] [Green Version]
- Arnesen, M.C.; Bose, S.; Vedral, V. Natural Thermal and Magnetic Entanglement in the 1D Heisenberg Model. Phys. Rev. Lett. 2001, 87, 017901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X. Entanglement in the quantum Heisenberg XY model. Phys. Rev. A 2001, 64, 123131. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Fu, H.; Solomon, A.I. Thermal entanglement in three-qubit Heisenberg models. J. Phys. A 2001, 34, 11307. [Google Scholar] [CrossRef]
- Wang, X. Threshold temperature for pairwise and many-particle thermal entanglement in the isotropic Heisenberg model. Phys. Rev. A 2002, 66, 044305. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Song, H.S.; Guo, Y.Q.; Li, C. Enhanced thermal entanglement in an anisotropic Heisenberg XYZ chain. Phys. Rev. A 2003, 68, 024301. [Google Scholar] [CrossRef] [Green Version]
- Asoudeh, M.; Karimipour, V. Thermal entanglement of spins in the Heisenberg model at low temperatures. Phys. Rev. A 2004, 70, 052307. [Google Scholar] [CrossRef] [Green Version]
- Canosa, N.; Rossignoli, R. Global entanglement in XXZ chains. Phys. Rev. A 2006, 73, 022347. [Google Scholar] [CrossRef] [Green Version]
- Ananikian, N.S.; Ananikyan, L.N.; Chakhmakhchyan, L.A.; Rojas, O. Thermal entanglement of a spin-1/2 Ising-Heisenberg model on a symmetrical diamond chain. J. Phys. Condens. Matter 2012, 24, 256001. [Google Scholar] [CrossRef] [Green Version]
- Torrico, J.; Rojas, M.; De Souza, S.M.; Rojas, O.; Ananikian, N.S. Pairwise thermal entanglement in the Ising-XYZ diamond chain structure in an external magnetic field. EPL 2014, 108, 50007. [Google Scholar] [CrossRef] [Green Version]
- Luitz, D.J.; Laflorencie, N.; Alet, F. Many-body localization edge in the random-field Heisenberg chain. Phys. Rev. B 2015, 91, 081103. [Google Scholar] [CrossRef] [Green Version]
- Rojas, O.; Rojas, M.; de Souza, S.M.; Torrico, J.; Strečka, J.; Lyra, M.L. Thermal entanglement in a spin-1/2 Ising-XYZ distorted diamond chain with the second-neighbor interaction between nodal Ising spins. Phys. A 2017, 486, 367–377. [Google Scholar] [CrossRef]
- Zad, H.A.; Ananikian, N. Thermal entanglement in the mixed-spin Ising-Heisenberg double sawtooth frustrated ladder. Solid State Commun. 2018, 276, 24–27. [Google Scholar]
- Souza, F.; Lyra, M.L.; Strečka, J.; Pereira, M.S.S. Magnetization processes and quantum entanglement in a spin-1/2 Ising-Heisenberg chain model of a heterotrimetallic Fe-Mn-Cu coordination polymer. J. Magn. Magn. Mater 2019, 471, 423–431. [Google Scholar] [CrossRef]
- Veríssimo, L.M.; Pereira, M.S.S.; Strečka, J.; Lyra, M.L. Kosterlitz-Thouless and Gaussian criticalities in a mixed spin-(1/2,5/2,1/2) Heisenberg branched chain with exchange anisotropy. Phys. Rev. B 2019, 99, 134408. [Google Scholar] [CrossRef]
- Karl<sup>′</sup>ová, K.; Strečka, J.; Lyra, M.L. Breakdown of intermediate one-half magnetization plateau of spin-1/2 Ising-Heisenberg and Heisenberg branched chains at triple and Kosterlitz-Thouless critical points. Phys. Rev. E 2019, 100, 042127. [Google Scholar]
- Wang, X.; Wang, Z.D. Thermal entanglement in ferrimagnetic chains. Phys. Rev. A 2006, 73, 064302. [Google Scholar] [CrossRef] [Green Version]
- Čenčariková, H.; Strečka, J. Unconventional strengthening of the bipartite entanglement of a mixed spin-(1/2,1) Heisenberg dimer achieved through Zeeman splitting. Phys. Rev. B 2020, 102, 184419. [Google Scholar] [CrossRef]
- Vargová, H.; Strečka, J.; Tomašovičová, N. Effect of an uniaxial single-ion anisotropy on the quantum and thermal entanglement of a mixed spin-(1/2,S) Heisenberg dimer. arXiv 2021, arXiv:2107.14620. [Google Scholar]
- Sun, Z.; Wang, X.; Hu, A.; Li, Y.-Q. Entanglement properties in (1/2,1) mixed-spin Heisenberg systems. Physica A 2006, 370, 483–500. [Google Scholar] [CrossRef] [Green Version]
- Hao, X.; Zhu, S. Entanglement in a quantum mixed-spin chain. Phys. Lett. A 2007, 366, 206–210. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.-L.; Huang, X.-L.; Song, H.-S. Effects of anisotropy and external magnetic field on the thermal entanglement in a (1/2,1) mixed-spin Heisenberg model. Phys. Scr. 2007, 76, 327. [Google Scholar] [CrossRef]
- Wang, F.; Fu, L.-P.; Guo, K.-T. Anisotropy and Magnetic Field Effects on Entanglement of a Two-Spin (1/2,1) Mixed-Spin Heisenberg XY Chain. Commun. Theor. Phys. 2008, 50, 341. [Google Scholar]
- Huang, H.; Wang, X.; Sun, Z.; Yang, G. Entanglement properties in mixed spin-(1,s) systems. Physica A 2008, 387, 2736–2744. [Google Scholar] [CrossRef]
- Li, S.-S.; Ren, T.-Q.; Kong, X.-M.; Liu, K. Thermal entanglement in the Heisenberg XXZ model with Dzyaloshinskii–Moriya interaction. Physica A 2012, 391, 35–41. [Google Scholar] [CrossRef]
- Xu, S.; Song, X.; Ye, L. Measurement-induced disturbance and negativity in mixed-spin XXZ model. Quantum Inf. Process. 2014, 13, 1013–1024. [Google Scholar] [CrossRef]
- Zhou, C.-B.; Xiao, S.-Y.; Zhang, C.; Wu, G.; Ran, Y.-Q. Entanglement in Mixed-Spin (1/2, 3/2) Heisenberg XXZ Model with Dzyaloshinskii–Moriya Interaction. Int. J. Theor. Phys. 2016, 55, 875–885. [Google Scholar] [CrossRef]
- Zhou, C.-B.; Xiao, S.-Y.; Zhang, C.; Wu, G.; Ran, Y.-Q. Influence of Dzyaloshinskii–Moriya interaction on measurement-induced disturbance in a mixed-spin Heisenberg XXZ model with an inhomogeneous magnetic field. Physica B 2015, 477, 40–44. [Google Scholar] [CrossRef]
- Guo, K.-T.; Xiang, S.-H.; Xu, H.-Y.; Li, X.-H. Thermal entanglement of the mixed spin-1/2 and spin-5/2 Heisenberg model under an external magnetic field. Quantum Inf. Process. 2014, 13, 1511–1521. [Google Scholar] [CrossRef]
- Adamyan, Z.A.; Muradyana, S.A.; Ohanyan, V.R. Quantum Entanglement in Spin Dimers: Effects of a Magnetic Field and Heterogeneous g-Factors. Contemp. Phys. 2020, 55, 292–298. [Google Scholar] [CrossRef]
- Guo, K.-T.; Liang, M.-C.; Xu, H.-Y.; Zhu, C.-B. Entanglement in a two-spin (1/2, 3/2) mixed-spin Heisenberg XXZ chain with an inhomogeneous external magnetic field. J. Phys. A Math. Theor. 2010, 43, 505301. [Google Scholar] [CrossRef]
- Guo, K.-T.; Liang, M.-C.; Xu, H.-Y.; Zhu, C.-B. Entanglement in a two-spin (1/2,3/2) mixed-spin Heisenberg XX chain with an inhomogeneous external magnetic field. Sci. China Phys. Mech. Astron. 2011, 54, 491–495. [Google Scholar] [CrossRef]
- Yang, G.-H.; Zhou, L. Entanglement properties of a two-qubit, mixed-spin, Heisenberg chain under a nonuniform magnetic field. Phys. Scr. 2008, 78, 025703. [Google Scholar] [CrossRef]
- Wang, F.; Jia, H.; Zhang, H.; Zhang, X.; Chang, S. Thermal entanglement in a mixed-spin Heisenberg XXZ model under a nonuniform external magnetic field. Sci. China Ser. G 2009, 52, 1919–1924. [Google Scholar] [CrossRef]
- Han, S.D.; Tüfekçi, T.; Spiller, T.P. Entanglement in (1/2,1) Mixed-Spin XY Model with Long-Range Interaction. Int. J. Theor. Phys. 2017, 56, 1474–1483. [Google Scholar] [CrossRef]
- Solano-Carrilo, E.; Franco, R.; Silva-Valencia, J. Entanglement and quantum phase transition in a mixed-spin Heisenberg chain with single-ion anisotropy. Physica A 2011, 390, 2208–2214. [Google Scholar] [CrossRef]
- Solano-Carrilo, E.; Franco, R.; Silva-Valencia, J. Pairwise entanglement and critical behavior of an anisotropic ferrimagnetic spin chain. Phys. Lett. A 2011, 375, 1032–1035. [Google Scholar] [CrossRef]
- Zhu, G.-Q. Average entanglement of spin 1 and 1/2 pair. Cent. Eur. J. Phys. 2009, 7, 135–140. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, X.; Xiong, H.-N. Entanglement, purity and fidelity in the anisotropy (1/2,1) mixed-spin system. Phys. A 2009, 388, 1337–1343. [Google Scholar] [CrossRef]
- Holleitner, A.W.; Knotz, K.; Myers, R.C.; Gossard, A.C.; Awschalom, D.D. Pinning a domain wall in (Ga,Mn)As with focused ion beam lithography. Appl. Phys. Lett. 2004, 85, 5622–5624. [Google Scholar] [CrossRef] [Green Version]
- Kahn, O.; Pei, Y.; Verdaguer, M.; Renard, J.P.; Sletten, J. Magnetic ordering of manganese(II) copper(II) bimetallic chains; design of a molecular based ferromagnet. J. Am. Chem. Soc. 1988, 110, 782–789. [Google Scholar] [CrossRef]
- Hagiwara, M.; Minami, K.; Narumi, Y.; Tatani, K.; Kindo, K. Magnetization Process of the S = 1/2 and 1 Ferrimagnetic Chain and Dimer. J. Phys. Soc. Jpn. 1999, 68, 2214–2217. [Google Scholar] [CrossRef]
- Hagiwara, M.; Minami, K.; Narumi, Y.; Tatani, K.; Kindo, K. Magnetic Properties of a Quantum Ferrimagnet: NiCu(pba)( D2O)3·2D2O. J. Phys. Soc. Jpn. 1998, 67, 2209–2211. [Google Scholar] [CrossRef] [Green Version]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargová, H.; Strečka, J. Unconventional Thermal and Magnetic-Field-Driven Changes of a Bipartite Entanglement of a Mixed Spin-(1/2,S) Heisenberg Dimer with an Uniaxial Single-Ion Anisotropy. Nanomaterials 2021, 11, 3096. https://doi.org/10.3390/nano11113096
Vargová H, Strečka J. Unconventional Thermal and Magnetic-Field-Driven Changes of a Bipartite Entanglement of a Mixed Spin-(1/2,S) Heisenberg Dimer with an Uniaxial Single-Ion Anisotropy. Nanomaterials. 2021; 11(11):3096. https://doi.org/10.3390/nano11113096
Chicago/Turabian StyleVargová, Hana, and Jozef Strečka. 2021. "Unconventional Thermal and Magnetic-Field-Driven Changes of a Bipartite Entanglement of a Mixed Spin-(1/2,S) Heisenberg Dimer with an Uniaxial Single-Ion Anisotropy" Nanomaterials 11, no. 11: 3096. https://doi.org/10.3390/nano11113096
APA StyleVargová, H., & Strečka, J. (2021). Unconventional Thermal and Magnetic-Field-Driven Changes of a Bipartite Entanglement of a Mixed Spin-(1/2,S) Heisenberg Dimer with an Uniaxial Single-Ion Anisotropy. Nanomaterials, 11(11), 3096. https://doi.org/10.3390/nano11113096