Enhanced Thermoelectric Performance of Polycrystalline Si0.8Ge0.2 Alloys through the Addition of Nanoscale Porosity
Abstract
:1. Introduction
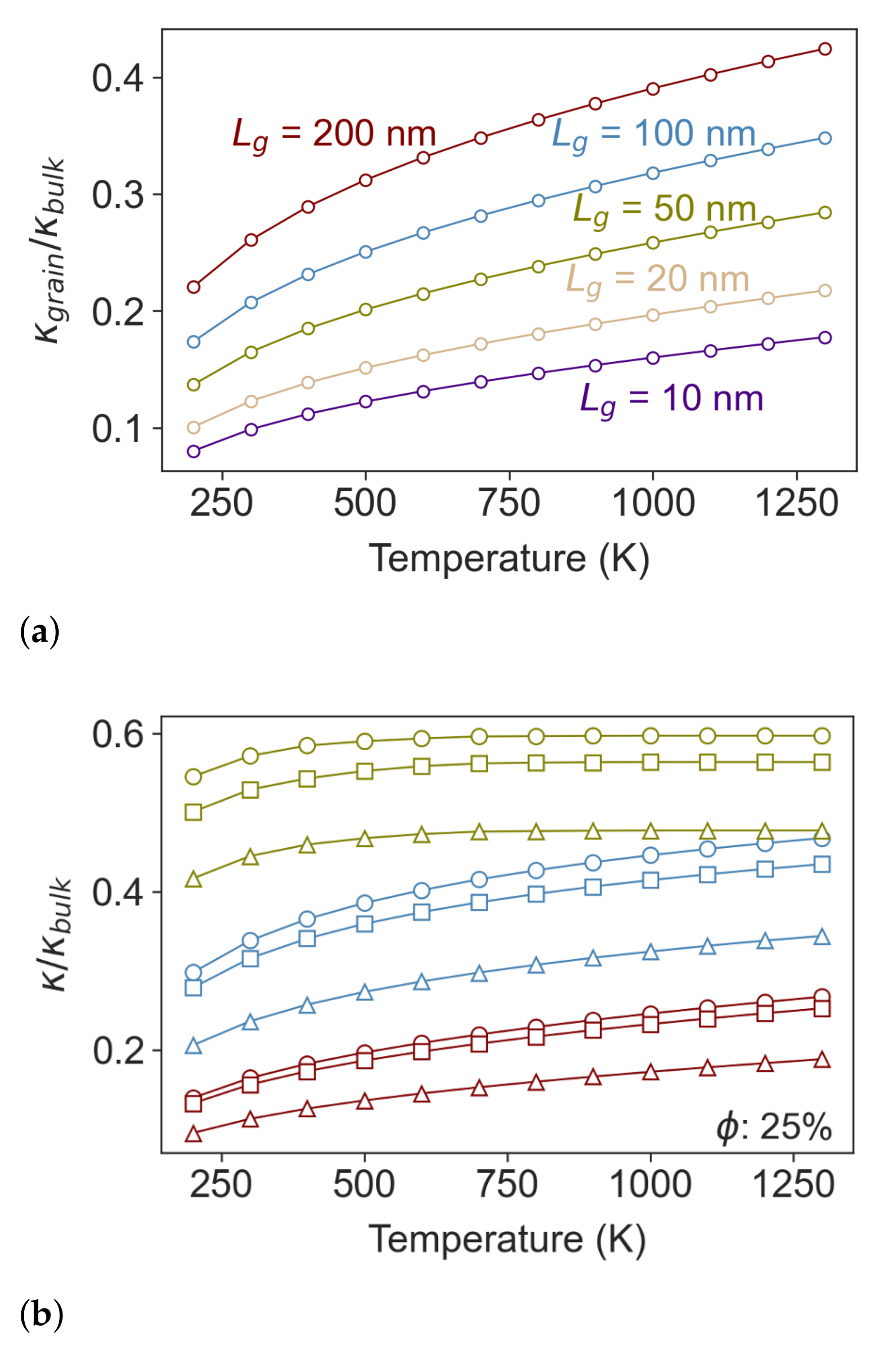
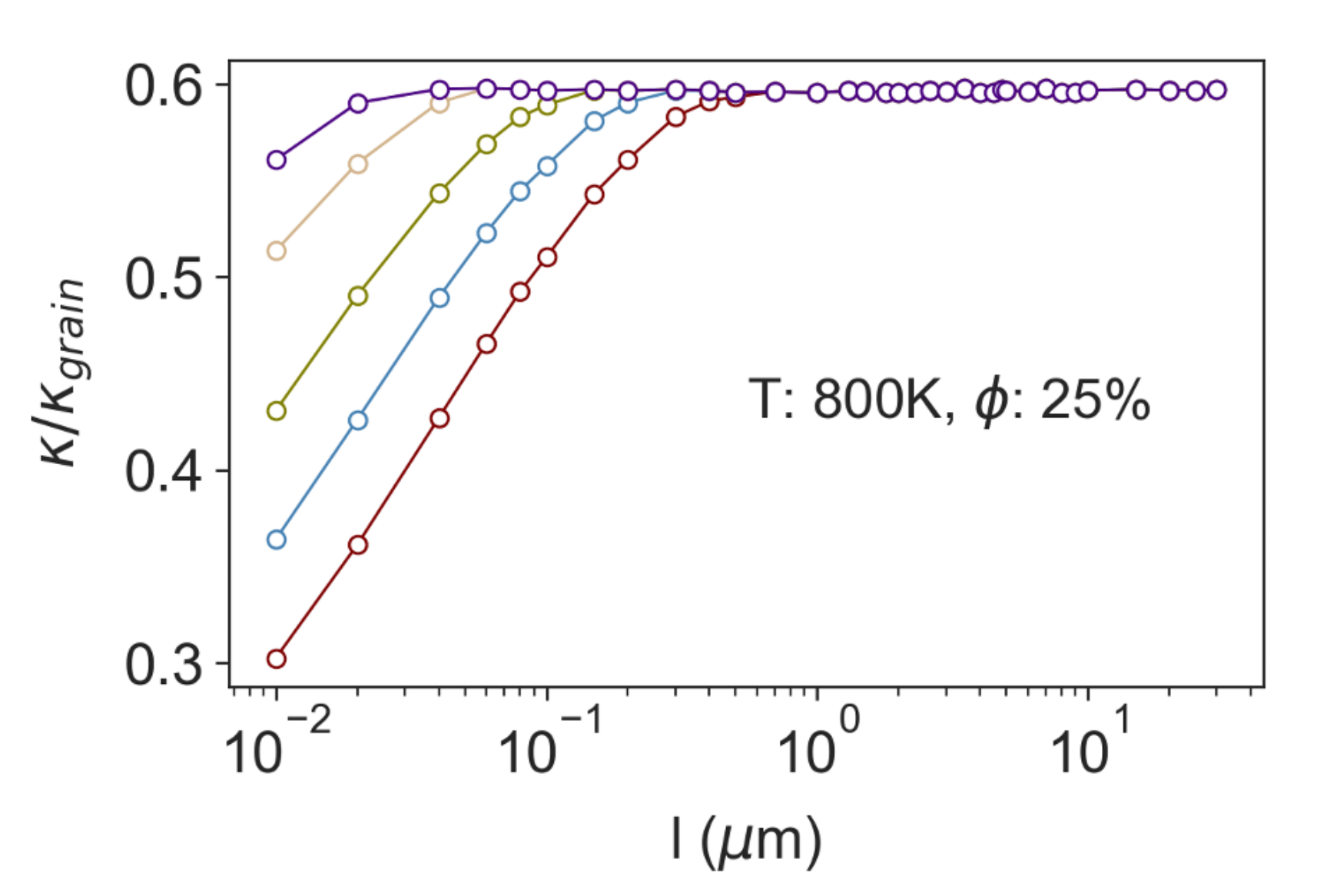
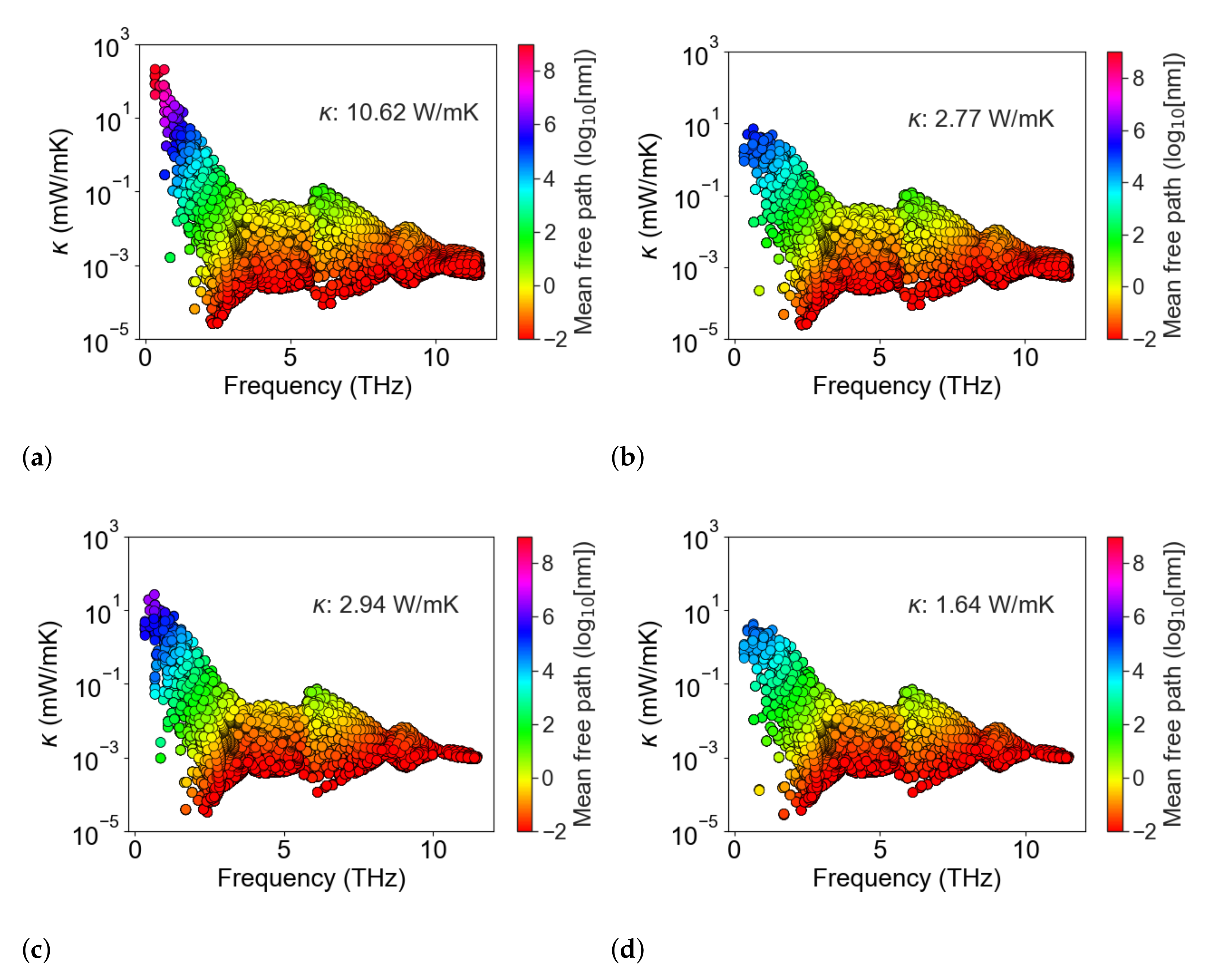
2. Thermal Transport in Nanoporous Si0.8Ge0.2
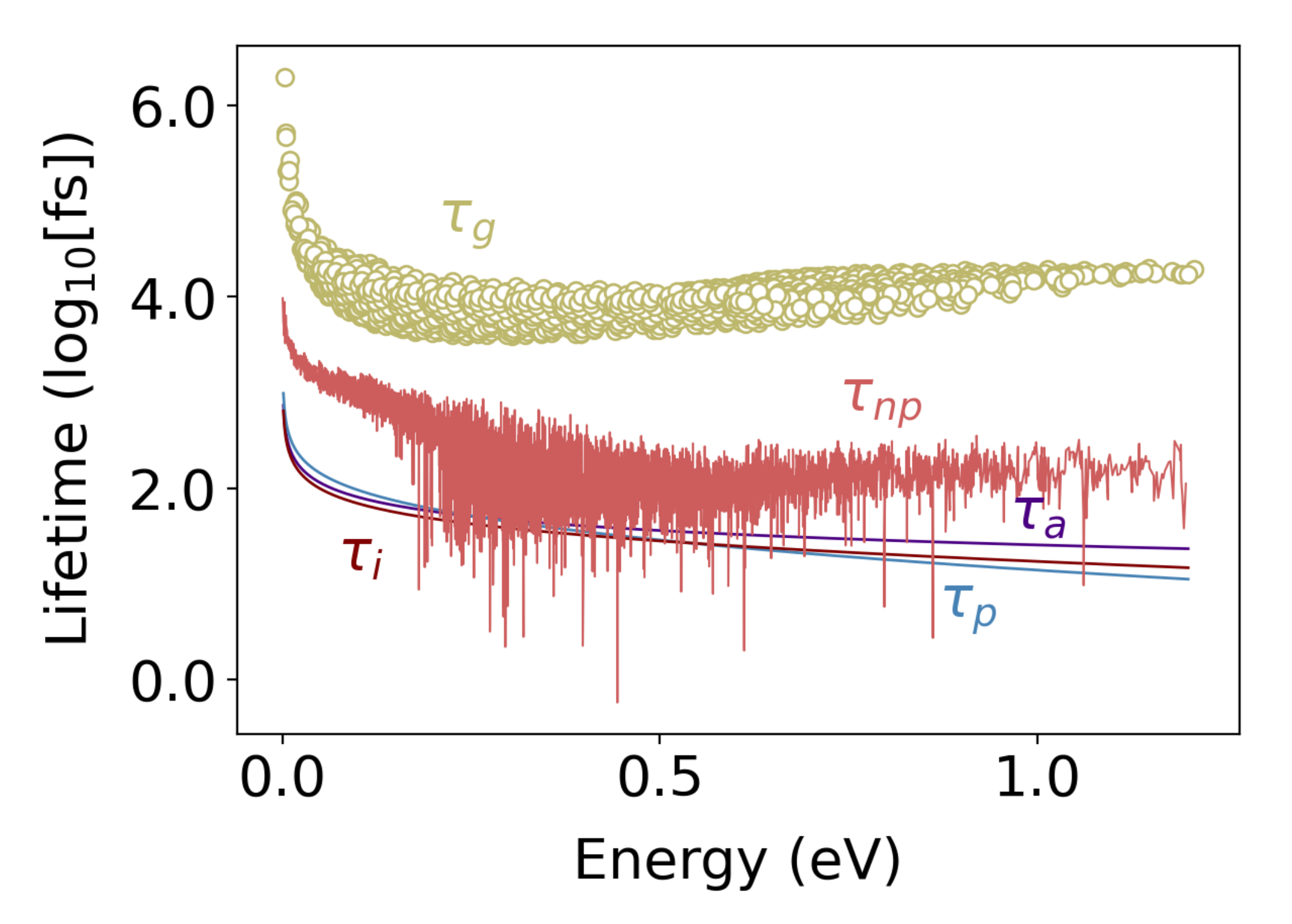
3. Charge Carriers Transport in Nanoporous Si0.8Ge0.2
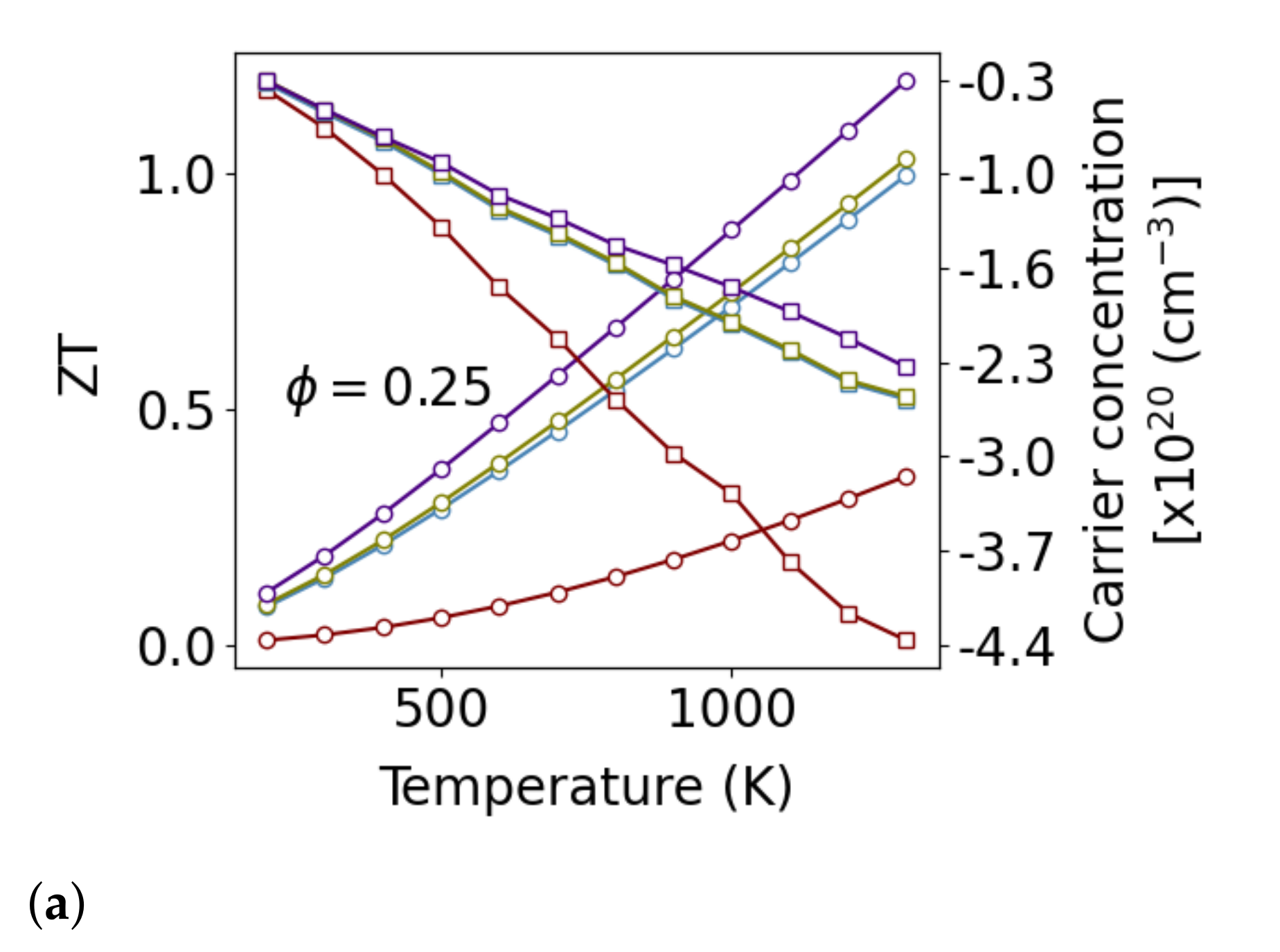
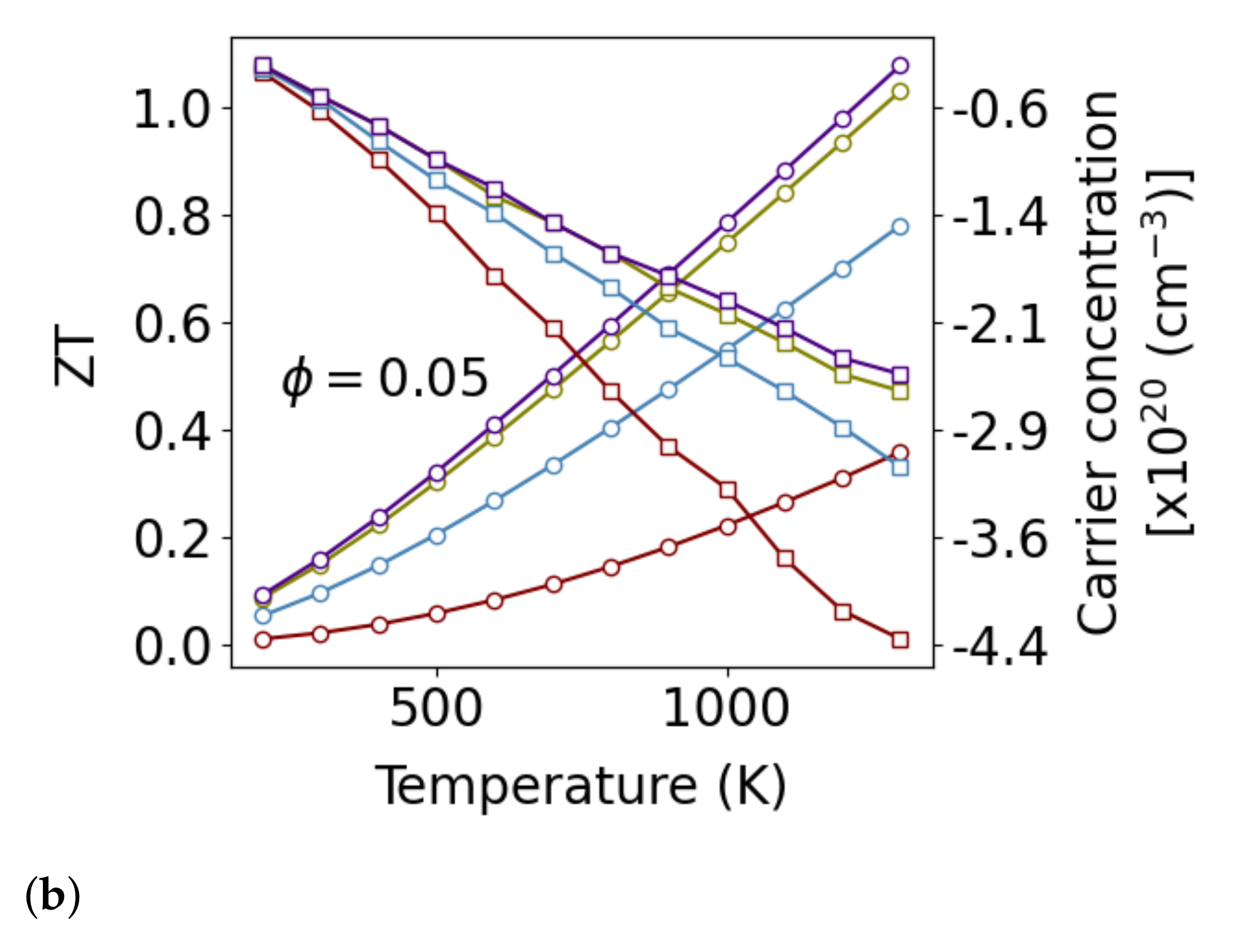
4. Thermoelectric of Nanoporous Polycrystalline Si0.8Ge0.2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
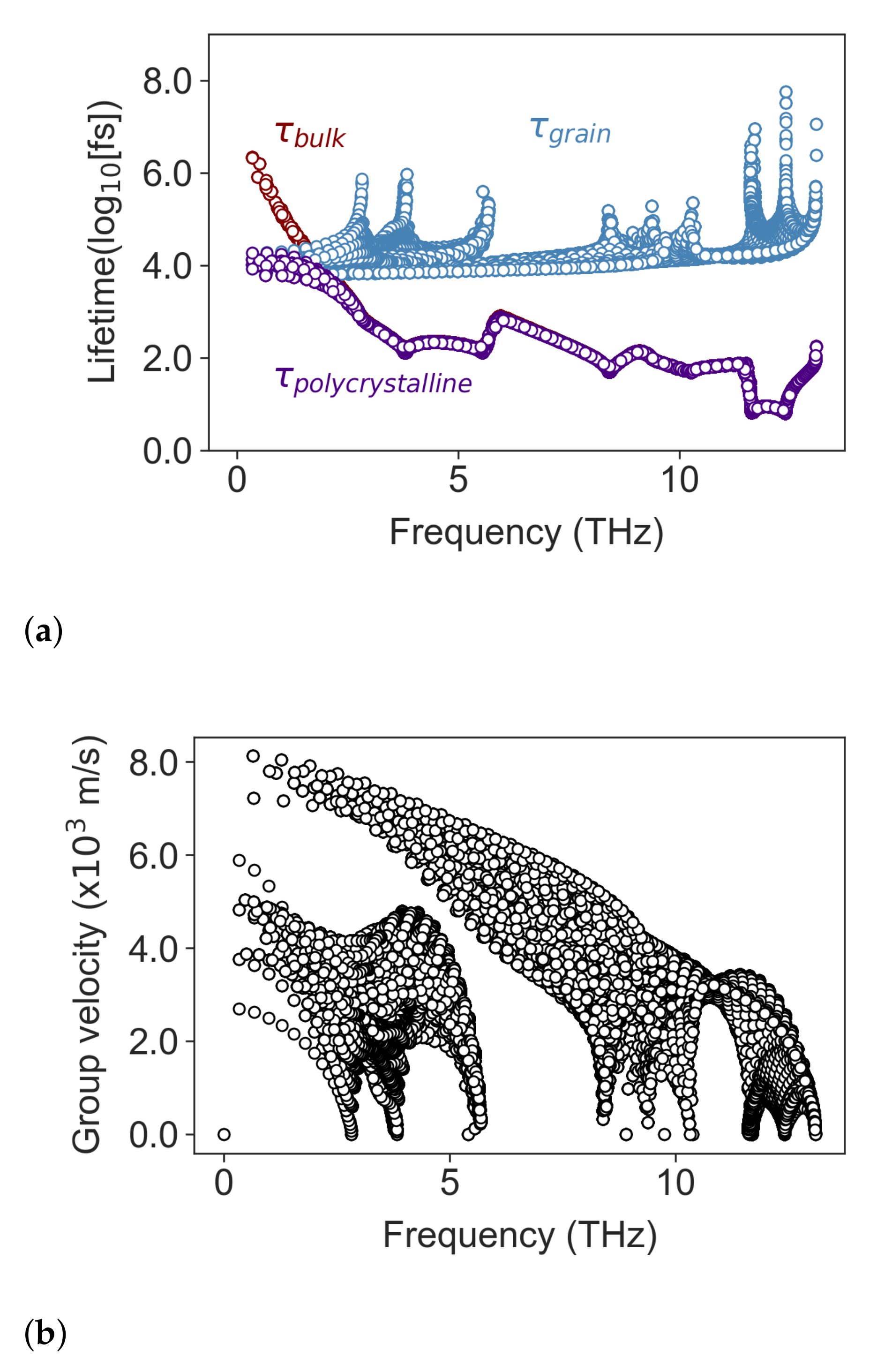
Appendix A.1. Importance of Pore’s Shape on Thermal Conductivity
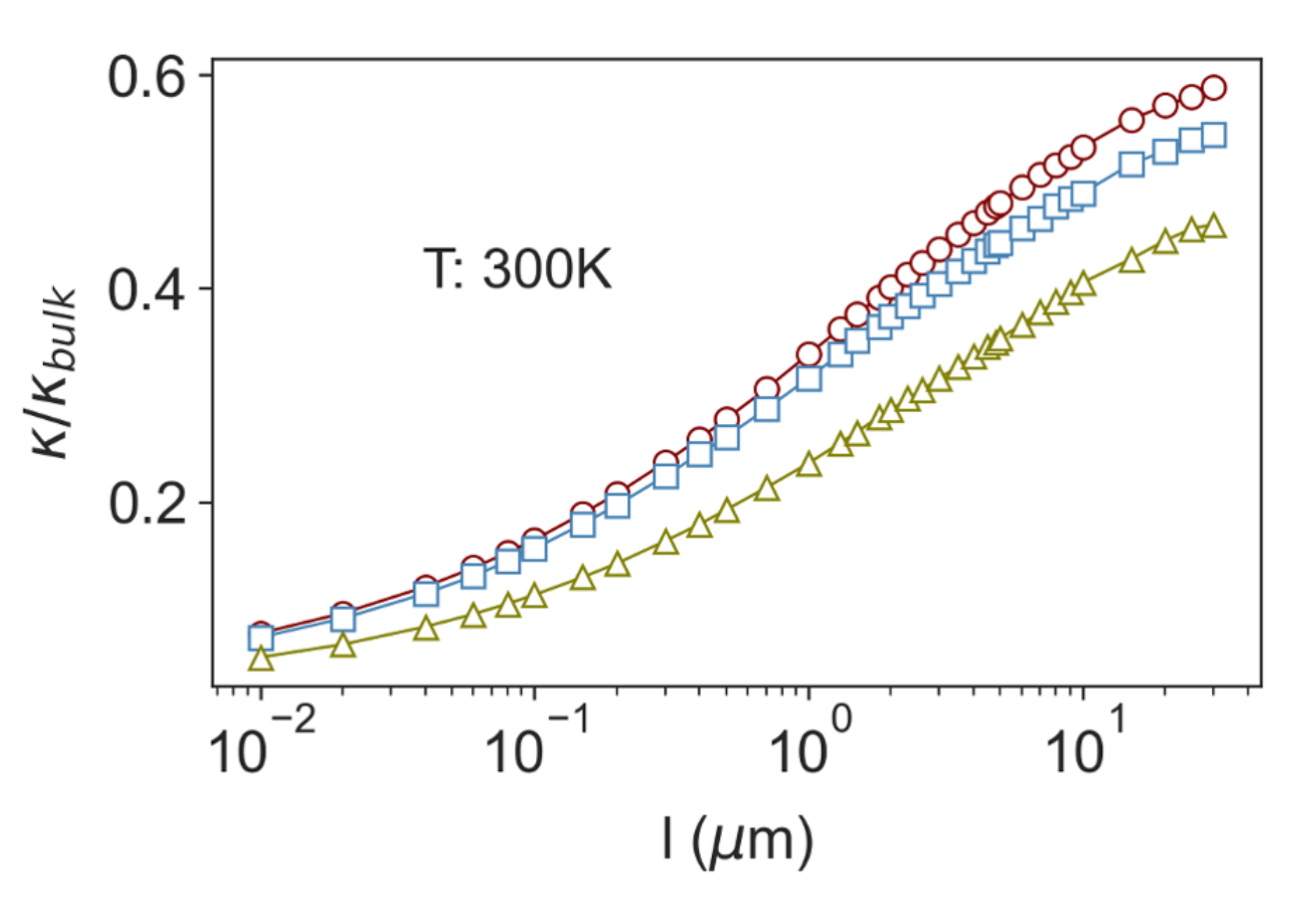

Appendix A.2. Importance of Electrical Contribution to Thermal Conductivity
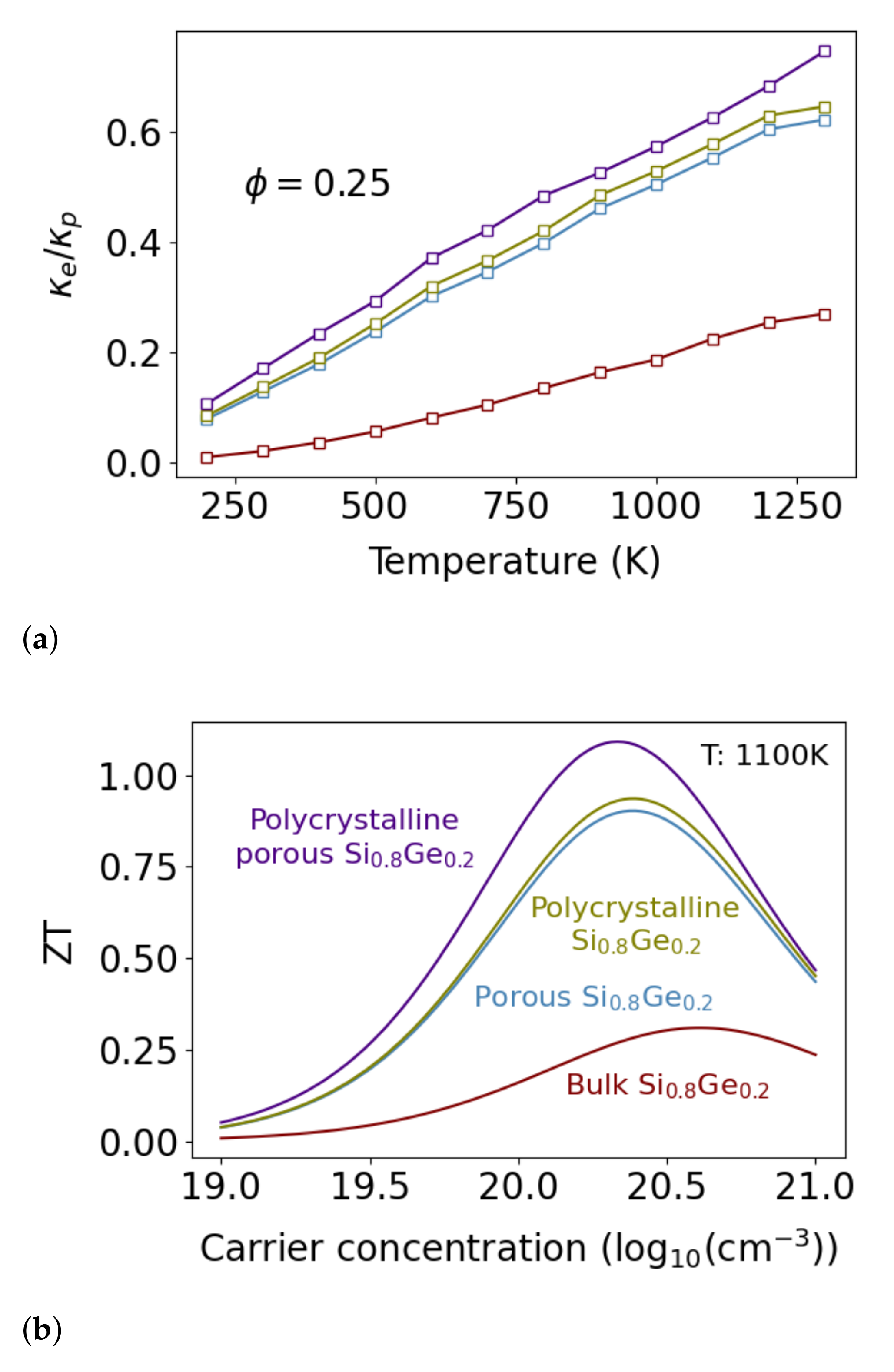
Appendix A.3. Temperature Dependency of the Electron Scattering Terms
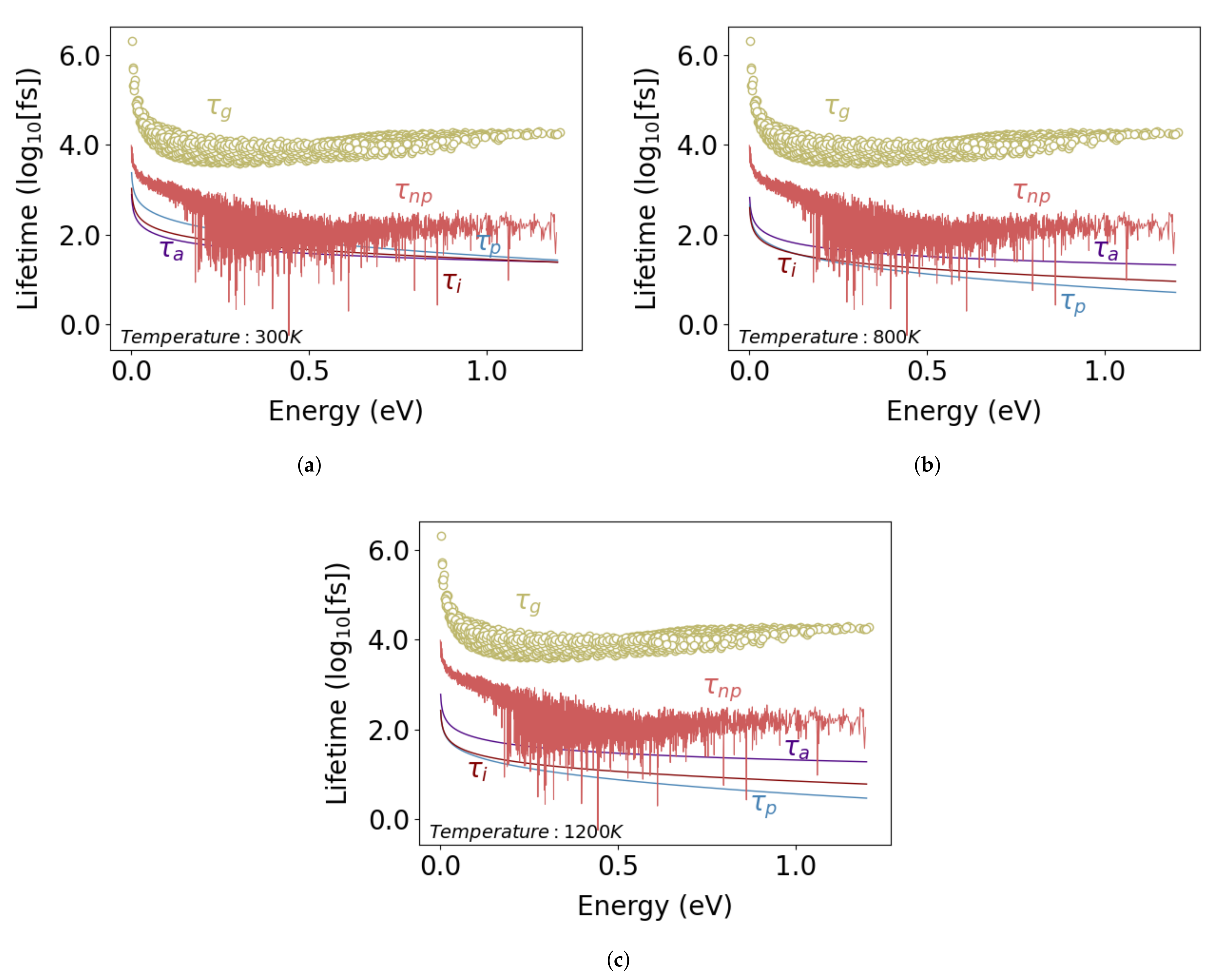
References
- Hosseini, S.H. Prediction of Thermal and Electrical Transport in Nanostructured Materials for Energy Conversion Applications. Ph.D. Thesis, University of California—Riverside, Riverside, CA, USA, 2021. [Google Scholar]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. In Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group; World Scientific: Singapore, 2011; pp. 101–110. [Google Scholar]
- Nolas, G.S.; Sharp, J.; Goldsmid, J. Thermoelectrics: Basic Principles and New Materials Developments; Springer Science & Business Media: New York, NY, USA, 2013; Volume 45. [Google Scholar]
- Riffat, S.B.; Ma, X. Thermoelectrics: A review of present and potential applications. Appl. Therm. Eng. 2003, 23, 913–935. [Google Scholar] [CrossRef]
- Vineis, C.J.; Shakouri, A.; Majumdar, A.; Kanatzidis, M.G. Nanostructured thermoelectrics: Big efficiency gains from small features. Adv. Mater. 2010, 22, 3970–3980. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Galli, G.A.; Grossman, J.C. Nanoporous Si as an efficient thermoelectric material. Nano Lett. 2008, 8, 3750–3754. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Grossman, J.C. Thermoelectric properties of nanoporous Ge. Appl. Phys. Lett. 2009, 95, 013106. [Google Scholar] [CrossRef]
- Romano, G.; Grossman, J.C. Phonon bottleneck identification in disordered nanoporous materials. Phys. Rev. B 2017, 96, 115425. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Yu, F.; Wang, B.; Zhao, H.; Chen, C.; Wang, D.; Ying, P.; Wu, Y.; Li, P.; Zhang, B.; et al. Porous bismuth antimony telluride alloys with excellent thermoelectric and mechanical properties. J. Mater. Chem. A 2021, 9, 4990–4999. [Google Scholar] [CrossRef]
- Zhao, X.; Deng, S.; Pan, W.; Qi, N.; Chen, Z.; Su, X.; Tang, X. Enhanced thermoelectric performance of tin oxide through antimony doping and introducing pore structures. J. Mater. Sci. 2021, 56, 2360–2371. [Google Scholar] [CrossRef]
- Wang, X.; Suwardi, A.; Zheng, Y.; Zhou, H.; Chien, S.W.; Xu, J. Enhanced thermoelectric performance of nanocrystalline indium tin oxide pellets by modulating the density and nanoporosity via spark plasma sintering. ACS Appl. Nano Mater. 2020, 3, 10156–10165. [Google Scholar] [CrossRef]
- Virtudazo, R.V.R.; Srinivasan, B.; Guo, Q.; Wu, R.; Takei, T.; Shimasaki, Y.; Wada, H.; Kuroda, K.; Bernik, S.; Mori, T. Improvement in the thermoelectric properties of porous networked Al-doped ZnO nanostructured materials synthesized via an alternative interfacial reaction and low-pressure SPS processing. Inorg. Chem. Front. 2020, 7, 4118–4132. [Google Scholar] [CrossRef]
- Li, S.; Wang, R.; Zhu, W.; Chu, M.; Huang, Z.; Zhang, Y.; Zhao, W.; Liu, F.; Luo, J.; Xiao, Y.; et al. Achieving High Thermoelectric Performance by Introducing 3D Atomically Thin Conductive Framework in Porous Bi2Te2. 7Se0. 3-Carbon Nanotube Hybrids. Adv. Electron. Mater. 2020, 6, 2000292. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Greaney, P.A.; Romano, G. Nondiffusive Correction Model to Estimate the Effective Thermal Conductivity in Nongray, Nanostructured Materials. arXiv 2021, arXiv:2105.10613. [Google Scholar]
- de Sousa Oliveira, L.; Hosseini, S.A.; Greaney, A.; Neophytou, N. Heat current anticorrelation effects leading to thermal conductivity reduction in nanoporous Si. Phys. Rev. B 2020, 102, 205405. [Google Scholar] [CrossRef]
- de Sousa Oliveira, L.; Neophytou, N. Large-scale molecular dynamics investigation of geometrical features in nanoporous Si. Phys. Rev. B 2019, 100, 035409. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Wang, H.T.; Lee, D.H.; Fardy, M.; Huo, Z.; Russell, T.P.; Yang, P. Holey silicon as an efficient thermoelectric material. Nano Lett. 2010, 10, 4279–4283. [Google Scholar] [CrossRef] [Green Version]
- De Boor, J.; Kim, D.; Ao, X.; Becker, M.; Hinsche, N.; Mertig, I.; Zahn, P.; Schmidt, V. Thermoelectric properties of porous silicon. Appl. Phys. A 2012, 107, 789–794. [Google Scholar] [CrossRef]
- Lee, H.; Vashaee, D.; Wang, D.; Dresselhaus, M.S.; Ren, Z.; Chen, G. Effects of nanoscale porosity on thermoelectric properties of SiGe. J. Appl. Phys. 2010, 107, 094308. [Google Scholar] [CrossRef]
- Vishwakarma, A.; Bathula, S.; Chauhan, N.S.; Bhardwaj, R.; Gahtori, B.; Srivastava, A.K.; Dhar, A. Facile synthesis of nanostructured n-type SiGe alloys with enhanced thermoelectric performance using rapid solidification employing melt spinning followed by spark plasma sintering. Curr. Appl. Phys. 2018, 18, 1540–1545. [Google Scholar] [CrossRef]
- Basu, R.; Bhattacharya, S.; Bhatt, R.; Roy, M.; Ahmad, S.; Singh, A.; Navaneethan, M.; Hayakawa, Y.; Aswal, D.; Gupta, S. Improved thermoelectric performance of hot pressed nanostructured n-type SiGe bulk alloys. J. Mater. Chem. A 2014, 2, 6922–6930. [Google Scholar] [CrossRef]
- Bathula, S.; Jayasimhadri, M.; Singh, N.; Srivastava, A.; Pulikkotil, J.; Dhar, A.; Budhani, R. Enhanced thermoelectric figure-of-merit in spark plasma sintered nanostructured n-type SiGe alloys. Appl. Phys. Lett. 2012, 101, 213902. [Google Scholar] [CrossRef]
- Perez-Taborda, J.A.; Rojo, M.M.; Maiz, J.; Neophytou, N.; Martin-Gonzalez, M. Ultra-low thermal conductivities in large-area Si-Ge nanomeshes for thermoelectric applications. Sci. Rep. 2016, 6, 32778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pei, Y.; LaLonde, A.; Iwanaga, S.; Snyder, G.J. High thermoelectric figure of merit in heavy hole dominated PbTe. Energy Environ. Sci. 2011, 4, 2085–2089. [Google Scholar] [CrossRef] [Green Version]
- Gelbstein, Y.; Dashevsky, Z.; Dariel, M. High performance n-type PbTe-based materials for thermoelectric applications. Phys. B Condens. Matter 2005, 363, 196–205. [Google Scholar] [CrossRef]
- Banik, A.; Biswas, K. A game-changing strategy in SnSe thermoelectrics. Joule 2019, 3, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Cho, S. A review of SnSe: Growth and thermoelectric properties. J. Korean Phys. Soc. 2018, 72, 841–857. [Google Scholar]
- Harter, J.R.; Hosseini, S.A.; Palmer, T.S.; Greaney, P.A. Prediction of thermal conductivity in dielectrics using fast, spectrally-resolved phonon transport simulations. Int. J. Heat Mass Transf. 2019, 144, 118595. [Google Scholar] [CrossRef] [Green Version]
- Romano, G. OpenBTE: A Solver for ab-initio Phonon Transport in Multidimensional Structures. arXiv 2021, arXiv:2106.02764. [Google Scholar]
- Duncan, R.A.; Romano, G.; Sledzinska, M.; Maznev, A.A.; Péraud, J.P.M.; Hellman, O.; Sotomayor Torres, C.M.; Nelson, K.A. Thermal transport in nanoporous holey silicon membranes investigated with optically induced transient thermal gratings. J. Appl. Phys. 2020, 128, 235106. [Google Scholar] [CrossRef]
- Romano, G.; Esfarjani, K.; Strubbe, D.A.; Broido, D.; Kolpak, A.M. Temperature-dependent thermal conductivity in silicon nanostructured materials studied by the Boltzmann transport equation. Phys. Rev. B 2016, 93, 035408. [Google Scholar] [CrossRef] [Green Version]
- Park, W.; Romano, G.; Ahn, E.C.; Kodama, T.; Park, J.; Barako, M.T.; Sohn, J.; Kim, S.J.; Cho, J.; Marconnet, A.M.; et al. Phonon conduction in silicon nanobeam labyrinths. Sci. Rep. 2017, 7, 6233. [Google Scholar] [CrossRef] [PubMed]
- Park, W.; Sohn, J.; Romano, G.; Kodama, T.; Sood, A.; Katz, J.S.; Kim, B.S.; So, H.; Ahn, E.C.; Asheghi, M.; et al. Impact of thermally dead volume on phonon conduction along silicon nanoladders. Nanoscale 2018, 10, 11117–11122. [Google Scholar] [CrossRef]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Carrete, J.; Vermeersch, B.; Katre, A.; van Roekeghem, A.; Wang, T.; Madsen, G.K.; Mingo, N. almaBTE: A solver of the space–time dependent Boltzmann transport equation for phonons in structured materials. Comput. Phys. Commun. 2017, 220, 351–362. [Google Scholar] [CrossRef] [Green Version]
- Arrigoni, M.; Carrete, J.; Mingo, N.; Madsen, G.K. First-principles quantitative prediction of the lattice thermal conductivity in random semiconductor alloys: The role of force-constant disorder. Phys. Rev. B 2018, 98, 115205. [Google Scholar] [CrossRef] [Green Version]
- Tamura, S.i. Isotope scattering of dispersive phonons in Ge. Phys. Rev. B 1983, 27, 858. [Google Scholar] [CrossRef] [Green Version]
- Hori, T.; Shiomi, J.; Dames, C. Effective phonon mean free path in polycrystalline nanostructures. Appl. Phys. Lett. 2015, 106, 171901. [Google Scholar] [CrossRef]
- Hua, C.; Minnich, A.J. Importance of frequency-dependent grain boundary scattering in nanocrystalline silicon and silicon–germanium thermoelectrics. Semicond. Sci. Technol. 2014, 29, 124004. [Google Scholar] [CrossRef]
- Yang, L.; Minnich, A.J. Thermal transport in nanocrystalline Si and SiGe by ab initio based Monte Carlo simulation. Sci. Rep. 2017, 7, 44254. [Google Scholar]
- Prasher, R. Transverse thermal conductivity of porous materials made from aligned nano-and microcylindrical pores. J. Appl. Phys. 2006, 100, 064302. [Google Scholar] [CrossRef]
- Romano, G.; Grossman, J.C. Toward phonon-boundary engineering in nanoporous materials. Appl. Phys. Lett. 2014, 105, 033116. [Google Scholar] [CrossRef] [Green Version]
- Eucken, A. W armeleitf ahigkeit keramischer feuerfester Stoffe-Berechnung aus der W armeleitf ahigkeit der Bestandteile. Forschung auf dem Gebiet des Ingenieurwesens 1932, 3, 16. [Google Scholar]
- Liu, L.C.; Huang, M.J. Thermal conductivity modeling of micro-and nanoporous silicon. Int. J. Therm. Sci. 2010, 49, 1547–1554. [Google Scholar] [CrossRef]
- Savvides, N.; Rowe, D. Precipitation of phosphorus from solid solutions in Si-Ge alloys and its effect on thermoelectric transport properties. J. Phys. D Appl. Phys. 1981, 14, 723. [Google Scholar] [CrossRef]
- Chen, G. Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Minnich, A.; Lee, H.; Wang, X.; Joshi, G.; Dresselhaus, M.; Ren, Z.; Chen, G.; Vashaee, D. Modeling study of thermoelectric SiGe nanocomposites. Phys. Rev. B 2009, 80, 155327. [Google Scholar] [CrossRef]
- Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Fischetti, M.V. Monte Carlo simulation of transport in technologically significant semiconductors of the diamond and zinc-blende structures. I. Homogeneous transport. IEEE Trans. Electron Devices 1991, 38, 634–649. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J.; Hafner, J. Theory of the crystal structures of selenium and tellurium: The effect of generalized-gradient corrections to the local-density approximation. Phys. Rev. B 1994, 50, 13181. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Ravich, Y.I.; Efimova, B.; Tamarchenko, V. Scattering of current carriers and transport phenomena in lead chalcogenides. Phys. Status Solidi (b) 1971, 43, 11–33. [Google Scholar] [CrossRef]
- Lundstrom, M. Fundamentals of Carrier Transport; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Mondal, M.; Gnatak, K. Effect of carrier degeneracy on the screening length in degenerate tetragonal semiconductors. Phys. Status Solidi (b) 1986, 135, 239–251. [Google Scholar] [CrossRef]
- Riffe, D.M. Temperature dependence of silicon carrier effective masses with application to femtosecond reflectivity measurements. JOSA B 2002, 19, 1092–1100. [Google Scholar] [CrossRef] [Green Version]
- Singh, J. Physics of Semiconductors and Their Heterostructures; McGraw-Hill College: New York, NY, USA, 1993. [Google Scholar]
- Vining, C.B. A model for the high-temperature transport properties of heavily doped n-type silicon-germanium alloys. J. Appl. Phys. 1991, 69, 331–341. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.A. Thermoelectric.py. 2019. Available online: https://github.com/ariahosseini/thermoelectric.py (accessed on 11 February 2021).
- Nag, B.R. Electron Transport in Compound Semiconductors; Springer Science & Business Media: New York, NY, USA, 2012; Volume 11. [Google Scholar]
- Hosseini, S.A.; Romano, G.; Greaney, P.A. Mitigating the Effect of Nanoscale Porosity on Thermoelectric Power Factor of Si. ACS Appl. Energy Mater. 2021, 4, 1915–1923. [Google Scholar] [CrossRef]
- Tarkhanyan, R.H.; Niarchos, D.G. Thermoelectric power factor in nano-to microscale porous composites. J. Mater. Res. 2015, 30, 2618–2627. [Google Scholar] [CrossRef]
- Taur, Y.; Ning, T.H. Fundamentals of Modern VLSI Devices; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Christensen, J.S. Dopant Diffusion in Si and SiGe. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2004. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, S.A.; Romano, G.; Greaney, P.A. Enhanced Thermoelectric Performance of Polycrystalline Si0.8Ge0.2 Alloys through the Addition of Nanoscale Porosity. Nanomaterials 2021, 11, 2591. https://doi.org/10.3390/nano11102591
Hosseini SA, Romano G, Greaney PA. Enhanced Thermoelectric Performance of Polycrystalline Si0.8Ge0.2 Alloys through the Addition of Nanoscale Porosity. Nanomaterials. 2021; 11(10):2591. https://doi.org/10.3390/nano11102591
Chicago/Turabian StyleHosseini, S. Aria, Giuseppe Romano, and P. Alex Greaney. 2021. "Enhanced Thermoelectric Performance of Polycrystalline Si0.8Ge0.2 Alloys through the Addition of Nanoscale Porosity" Nanomaterials 11, no. 10: 2591. https://doi.org/10.3390/nano11102591
APA StyleHosseini, S. A., Romano, G., & Greaney, P. A. (2021). Enhanced Thermoelectric Performance of Polycrystalline Si0.8Ge0.2 Alloys through the Addition of Nanoscale Porosity. Nanomaterials, 11(10), 2591. https://doi.org/10.3390/nano11102591






