1. Introduction
The thermodynamic state of a fluid in confinement is important for the understanding of adsorption to walls, chemical reactions, film formation and transport in porous media [
1,
2,
3,
4,
5,
6]. The molecular structuring at the walls and the forces between particles and walls are central. The change in thermodynamic properties upon confinement is substantial. This has been known for a long time [
1,
7]. Derjaguin considered the measurable force that attracts or repels two walls that are close together, and defined from this the disjoining pressure [
7]. The disjoining pressure has also been called the solvation pressure [
1]. When the walls are far apart, the disjoining pressure vanishes. It is not well known, however, how size and shape, as variables, affect the disjoining pressure or other properties of the confined fluid.
Confinement is considered to be important, for instance, in the context of CO
separation and sequestration by metal-organic frameworks [
2] or for adsorption in zeolites [
3]. The disjoining pressure is of interest when studying aggregation of colloidal particles, suspended or adsorbed [
4,
5,
6]. It is likely to be important also for film flow on the macroscale [
8].
More knowledge of confined fluids on the nanoscale is therefore needed. It may, for instance, help us solve the well-known up-scaling problem in porous media science [
9]. The central problem is to understand how to integrate properties on the pore scale to the macroscale where Darcy’s law applies. In order to account for shape and size effects, it was recently proposed to use the four Minkowski functionals [
10,
11,
12]. This simplifies the description of a representative elementary volume (REV). Another procedure using the grand potential for average variables in the REV was also proposed [
13,
14].
In this work, we want to further examine this procedure [
13,
14], by looking for a way to describe the confined fluid in a pore. We are looking for a way to deal with size- and shape-dependent variables in a systematic and general manner. Two thermodynamic approaches are common. The approach following Gibbs is most popular [
15,
16,
17,
18,
19]. However, the method of Hill may offer an attractive alternative [
20,
21,
22,
23,
24,
25], partly because it may provide an independent check on Gibbs procedure, but also because general geometric scaling relations are obtainable from Hill’s method. We will see that this is also the case in the present study.
We will pursue the method of Hill. This starts with the observation that a small system has surface energy comparable to its bulk energy. A consequence is that the properties are not Euler homogeneous. Hill proposed to deal with such systems in an original manner [
26]. His idea was to introduce an ensemble of replicas of the small systems, on which standard thermodynamics could be applied. Hill’s method has not gained much attention, in spite of a renewed effort to spur interests [
27,
28].
The long-range aim of this work is to contribute to the effort of finding variables that characterize the confined fluid, for instance in a REV. The grand potential offers one option to describe the pressure and other variables [
13,
14]. We will pursue this route and study a single-phase and single-component fluid in a slit pore using Hill’s method. The so-called integral and differential pressures introduced by Hill are central. Hill did not consider the disjoining pressure, however, it is a small system property and we will see that this concept has benefited from insights of nanothermodynamics. The purpose of this paper is to clarify the use of Hill’s nanothermodynamics, by applying the method to a fluid in a slit pore with walls of large surface areas. This is a well-studied case in the literature [
1,
29], and is well suited to bring out new results on the confined state, the disjoining pressure and other properties. Grand canonical Monte Carlo and molecular dynamics simulation techniques are well suited to investigate thermodynamic relations. We will use these tools to simulate a single-phase fluid in a slit pore in the grand canonical ensemble. A particular advantage of this technique is that the simulations offer a mechanical picture of the system.
Solid–fluid and fluid–fluid interactions are considered here, but not solid–solid interactions. The solid–solid interactions will have a large effect on the thermodynamic state of the system at very small slit pore heights. We do not consider quantum effects that follow from system smallness in this work. We will consider slit pores of height to 71, where is the thermal de Broglie wavelength.
Section 2.1 introduces the reader to Hill’s nanothermodynamics. We show in
Section 2.2 how this theory can be used to define size- and shape-dependent properties, and new Maxwell relations that follow from these. A definition of the disjoining pressure follows naturally in
Section 2.3. In order to be able to verify relations with molecular simulations as a tool, we need to identify the integral pressures and surface tension in terms of the mechanical pressure tensor components. This is done in
Section 2.4. In
Section 3 we describe the molecular simulations.
We proceed in
Section 4 to investigate relations in the theory, and illustrate them with numerical results. We compute the local mechanical and thermodynamic variables according to Hill; i.e., the integral and differential pressures, and the integral and differential surface tensions. The grand potential, or the replica energy, is equal to minus the integral pressure times the volume. The set of thermodynamic variables of the nanothermodynamic framework, in terms of mechanical properties, is found to be self-consistent. We offer concluding remarks in
Section 5.
3. Simulation Details
The thermodynamic state of slit pores of varying heights
h was investigated by using grand-canonical Monte Carlo (GCMC) [
41] in combination with molecular dynamic (MD) simulations with the Nosé–Hoover thermostat [
42]. This produced the grand canonical ensemble, i.e., constant chemical potential, temperature, volume and surface area. The GCMC method inserted and deleted fluid particles to and from the simulation box from an imaginary fluid particle reservoir at the same temperature and chemical potential. This controlled the chemical potential of the fluid in the slit pore. The MD procedure updated the positions and velocities of the fluid particles and controlled the temperature with the Nosé–Hoover thermostat.
The simulations were carried out using LAMMPS [
43]. The local mechanical pressure tensor was calculated by post-processing the particle trajectories with in-house software (available at D.O.I. 10.5281/zenodo.4405267). The chemical potential and temperature were kept constant at
and
. The critical temperature of the Lennard–Jones/spline fluid is
[
44]. All units in this work are in reduced Lennard–Jones units, see
Table 1 for a definition.
The simulation box was a rectangular cuboid of side lengths . The side lengths were chosen such that the surface area was large. Large in this context indicates large enough for , , , , and to be independent of the surface area . The simulation box size was decided such that the average number of fluid particles was approximately . The simulation box was periodic in the y- and z-directions, and non-periodic in the x-direction. This implies that the particles did not interact across the simulation box boundary in the x-direction.
The fluid–fluid and fluid–solid interaction was modeled with the Lennard-Jones/spline potential [
44]. The fluid–fluid and fluid–solid interactions were equal. The potential energy of a fluid–fluid or fluid–solid pair separated by a distance
r was
where
,
a,
b and
were chosen such that the potential energy and the force were continuous at the inflection point
and the cut-off
. The solid walls were placed at the simulation box boundaries
and
. The distance between the fluid and solids were
and
, where
is the
x-position of the fluid particle.
The dividing surfaces of the fluid–solid surfaces were chosen to be at
and
. The slit pore height was consequently determined to be
. Other choices of the dividing surface are possible, for example, the Gibbs dividing surface or the surface of tension. When
the fluid particle can interact with both solid walls. See
Figure 1 for an visualization of the simulation box for the case
.
The mechanical pressure tensor was calculated in thin rectangular cuboids, called layers
l, of side lengths
. The thickness of the layers was
and the number of layers was
. The diagonal components of the mechanical pressure tensor was calculated using Equations (
27)–(
29).
The kinetic energy was calculated as the sum of the kinetic energy for each fluid particle and the potential energy was calculated as the sum of the potential energy of each fluid–fluid and fluid–solid pairs,
The sums of the kinetic and potential energies were used to calculate the internal energy and entropy densities.
4. Results and Discussion
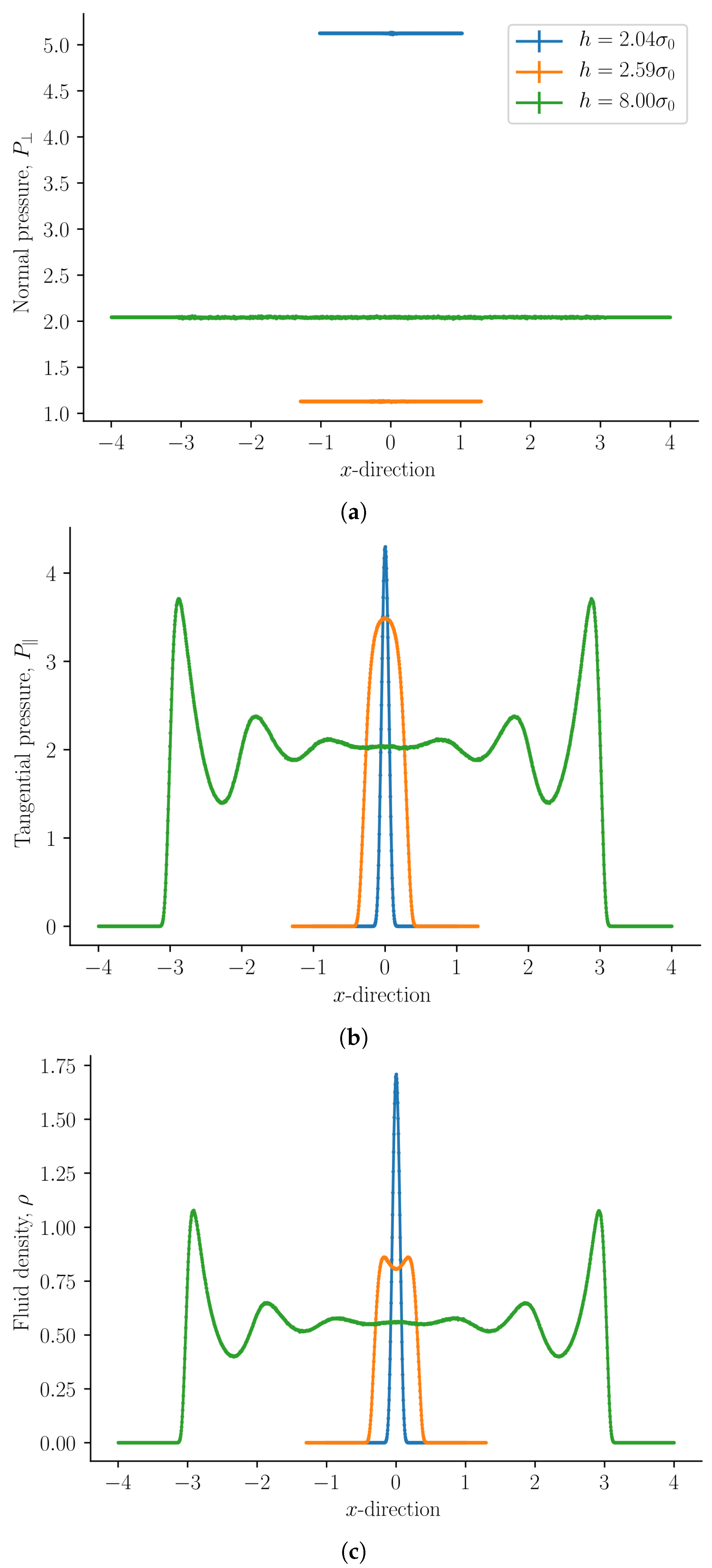
The normal mechanical pressure
is presented in
Figure 2a. It does not depend on the position
x, but it depends strongly on the slit pore height
h. The figure shows a straight line of various lengths for each of the three heights, which reflect the slit pore height
h. The integral normal pressure was identified as this component,
. We see that it is always constant, as demanded by Equation (
31). For slit pore heights
we find that the normal mechanical pressure is equal to the bulk pressure. At
the normal mechanical pressure is at a global maximum and at
it has a local minimum for the given temperature and chemical potential. The normal mechanical pressures divided by the bulk pressure for the two cases are
and
, respectively. The global minimum, which is zero, is at
when no fluid particles fit in the slit pore. This is because solid–solid interactions and quantum effects are not considered in this work.
The tangential mechanical pressure
, illustrated in
Figure 2b, depends in contrast on the position
x as well as on the slit pore height
h. The integral pressure is the average of
, see Equation (
34). The tangential mechanical pressure follows the trend of the fluid number density, compare
Figure 2b,c. For pore sizes
the tangential mechanical pressure is constant and equal to the bulk pressure
in the center of the pore. This indicates that the pore is large enough to accommodate bulk liquid in the center. The fluid is highly structured close to the fluid–solid surface [
1]. As the slit pore height is decreased, fluid structures on the two sides overlap. When regions of structured fluids overlap, repulsive and attractive forces between the surfaces appear, and the disjoining pressure becomes non-zero.
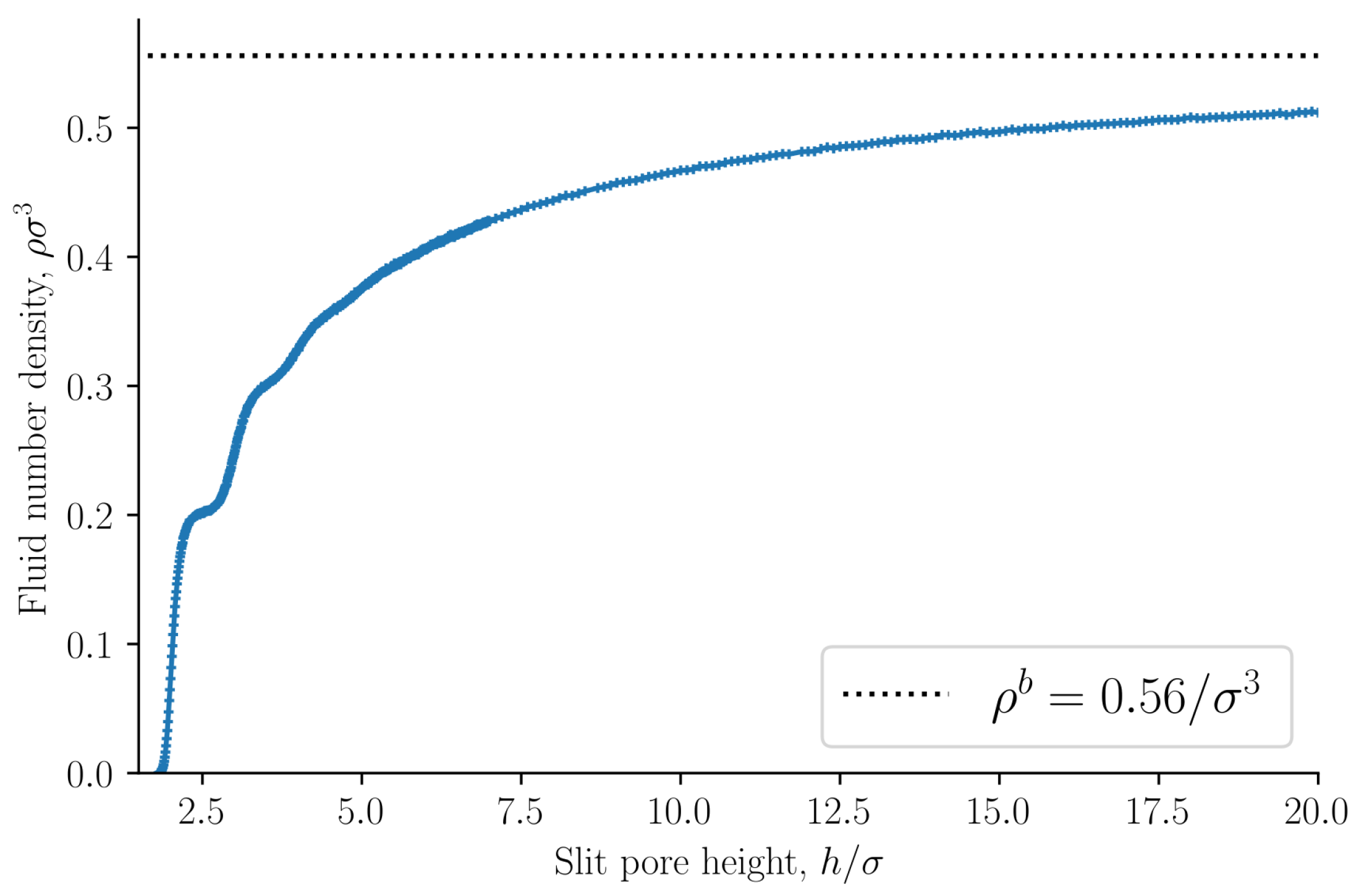
The fluid number density
is presented in
Figure 3 as a function of the slit pore height
h. The bulk fluid number density
in equilibrium with the slit pore is shown as a dashed line. The fluid number density converges to the bulk value as the slit pore height approaches infinity. The volume
V depends on the choice of the fluid–solid dividing surfaces. We have chosen the dividing surfaces to be at
and
. The choice of the dividing surface determines how rapidly the slit pore values converge to the bulk values. A dividing surface closer to the fluid phase will reduce the volume and consequently the slit pore values will converge faster to the bulk values. Other choices of the dividing surface are possible.
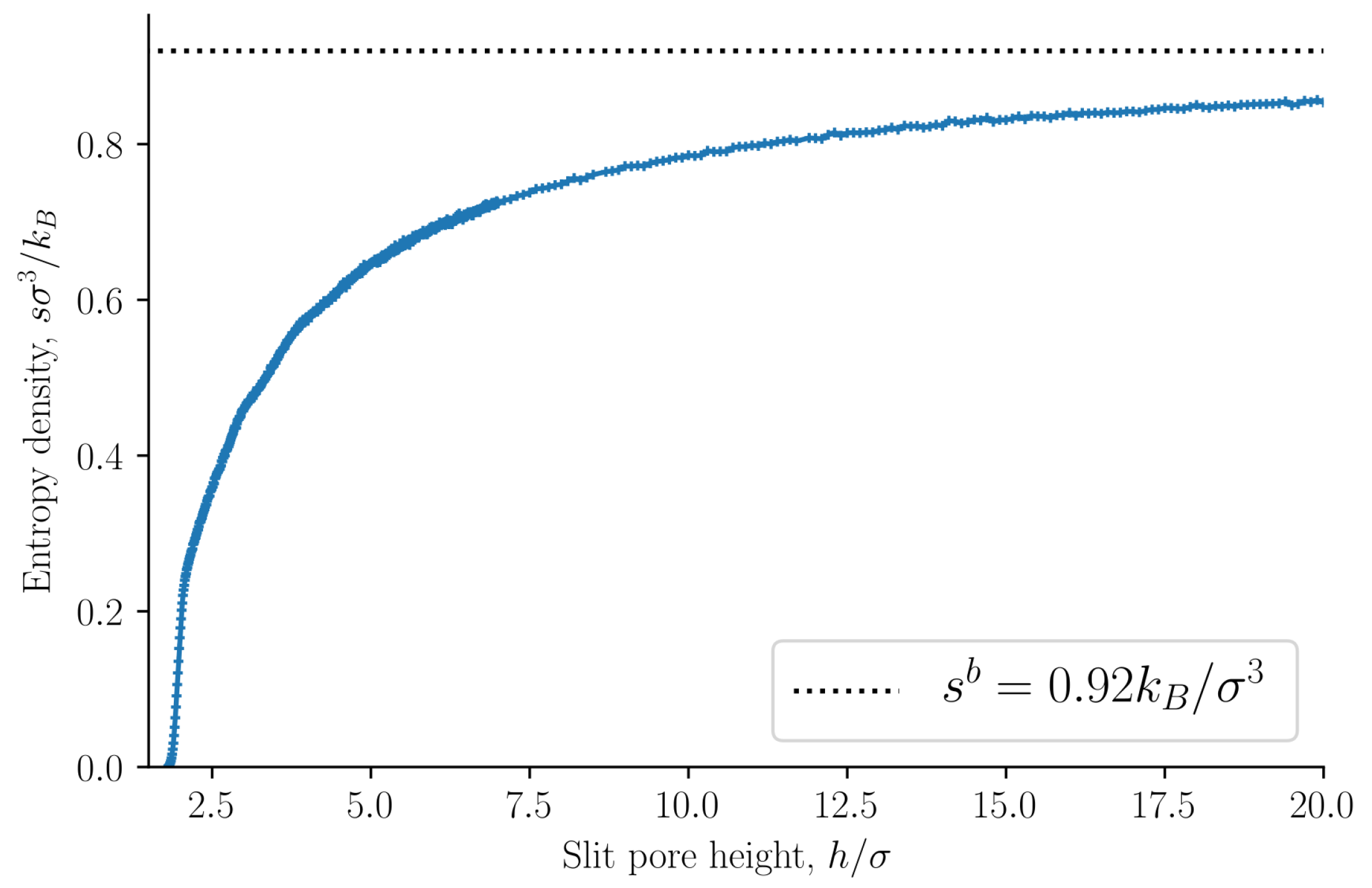
The entropy density is presented in
Figure 4 as a function of the slit pore height
h. The entropy density is a monotonically increasing function of the height
h. This confirms the observation by Israelachvili [
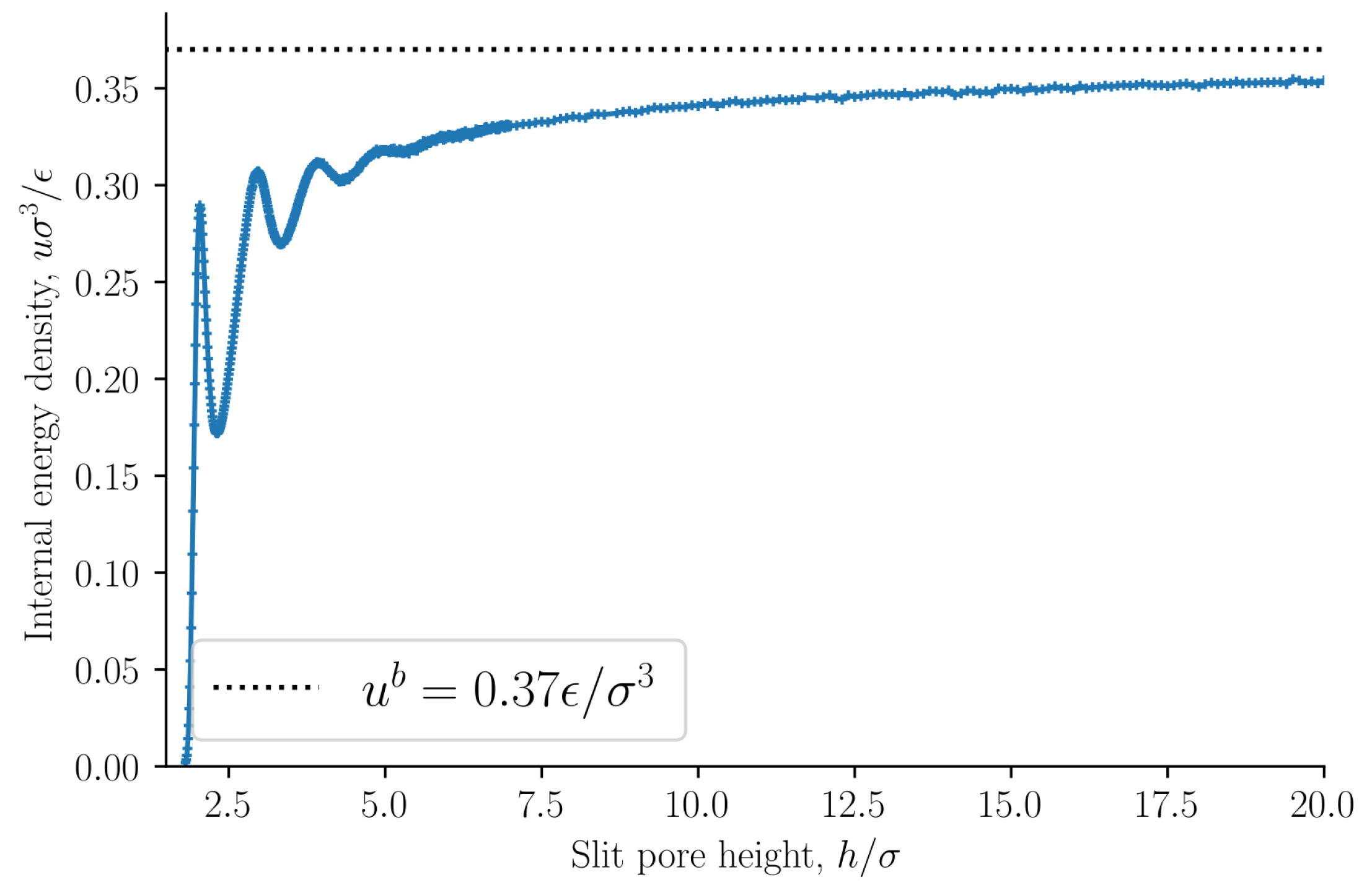
1] that the origin of the oscillations of the disjoining pressure as a function of the height is not entropic. As a further confirmation of this point, we find that the internal energy density oscillates with a period equal to the particle diameter, see
Figure 5. The oscillating forces or pressures are thus of energetic origin. The bulk entropy and internal energy densities are shown as dashed lines. The entropy and internal energy densities of the slit pore converge to the bulk values as the slit pore height is increased.
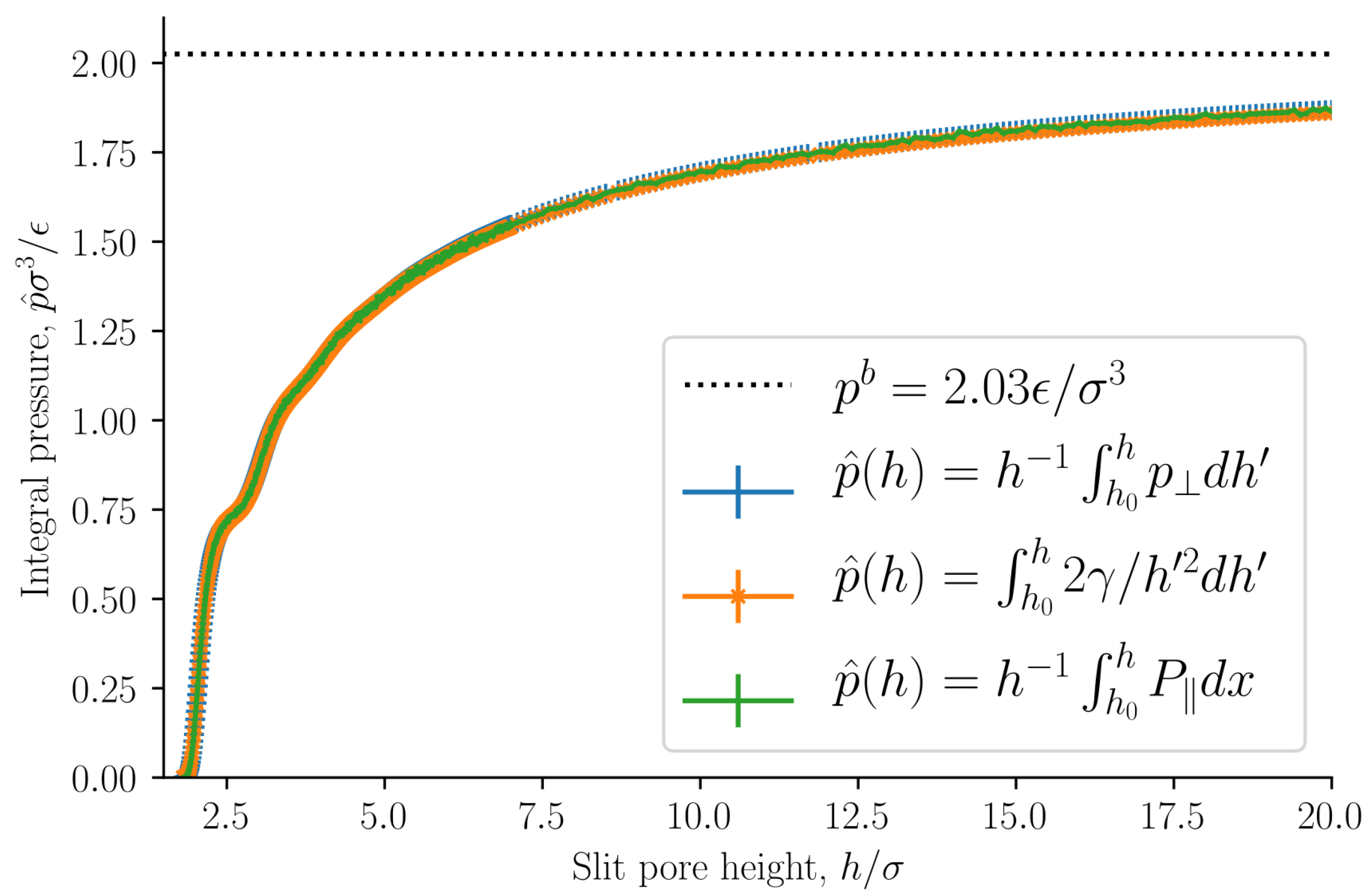
The integral pressure is equal to the volume average tangential mechanical pressure
. It is of special interest because it is equal to minus the grand potential divided by volume
, or the replica energy density. The grand potential is the starting point for the definition of the average thermodynamic properties of the REV [
13]. The integral pressure is presented in
Figure 6 as a function of the slit pore height
h. The integral pressure converges to the bulk pressure
as the slit pore height approaches infinity, as expected. The bulk pressure is shown as a dashed line.
In previous works [
13,
14,
21] we argued that the gradient of the integral pressure is the driving force for mass flux. In another work [
23] we found the integral pressure of a two-phase system in a slit pore to be equal in the liquid and vapor in equilibrium. The identification of the integral pressure in this work is consistent with this interpretation. The gradient of the integral pressure is the driving force of the mass flux. For fluid flows tangential to the slit pore surfaces it is the gradient in the tangential mechanical pressure tensor component that gives the driving force when the system is out of equilibrium. In this work we identify the integral pressure as the average of the tangential mechanical pressure tensor components.
As stated in
Section 2.2, the integral and differential normal pressures and integral and differential surface tensions are expected to be equal when the surface area is large. If this is correct, the integral pressure can be computed as
The lower integration limit is
, at which point the integral pressure is in good approximation zero. The integral pressure computed from Equation (
39) is shown in
Figure 6. The curves are identical. This implies that the integral and differential normal pressures are equal. As we have already shown that the subdivision potential is zero
for large surface areas with this set of control variables, it follows that the integral and differential surface tensions are also equal. We will from now on refer to the integral normal pressure and integral surface tensions as the normal pressure and surface tension.
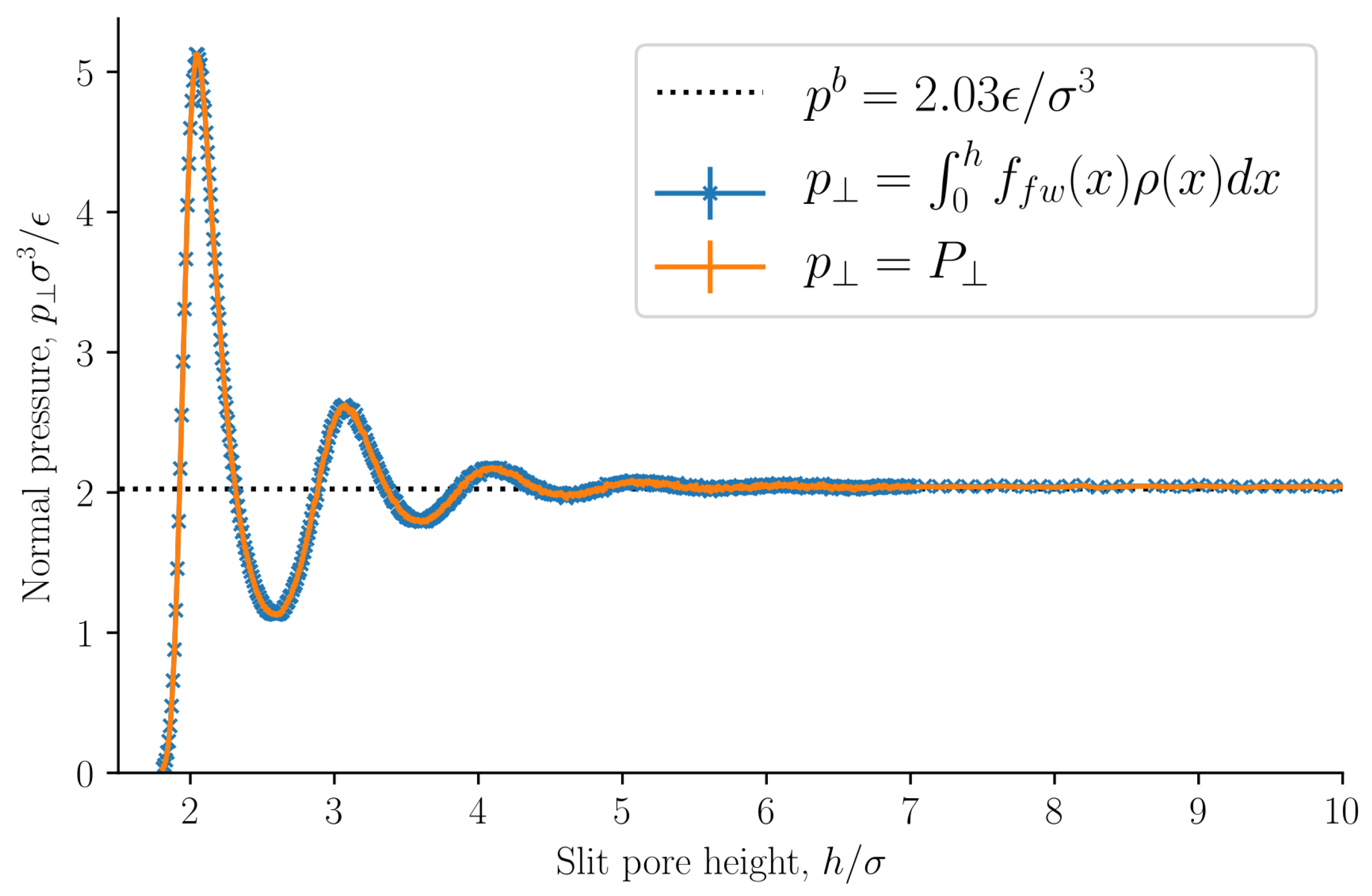
The normal pressure was identified as the normal mechanical pressure
in Equation (
31). It is presented in
Figure 7 as a function of the slit pore height
h. The normal pressure was also calculated from the local fluid density and the fluid–solid force using Equation (
32). The two methods of calculating the normal pressure agree, which indicates that we have calculated the mechanical pressure tensor correctly.
The normal pressure oscillates with a period equal to the fluid particle diameter at small heights
h. The oscillations decay as the height
h increases. Such oscillations have been observed in experiments and are well known, see for example Israelachvili [
1]. The oscillations are caused by the structuring of the fluid particles between the surfaces, and by the fact that the fluid particles all have the same diameter. As the height is increased above
the oscillations vanish and the normal pressure is constant and equal to the bulk pressure. The bulk pressure is shown as a dashed line in the figure. At heights
the fluid structuring near the walls do not overlap. At lower densities, smaller oscillations are expected with a faster decay. The normal pressure shows a similar trend to previous works [
15,
16,
40]. At very small heights, the solid–solid interaction will dominate and completely overshadow the fluid-fluid and fluid–solid interactions presented here. We have not included any solid–solid interaction in this work, and as a consequence the normal pressure approaches zero because there is no room for any fluid particles to enter the slit pore.
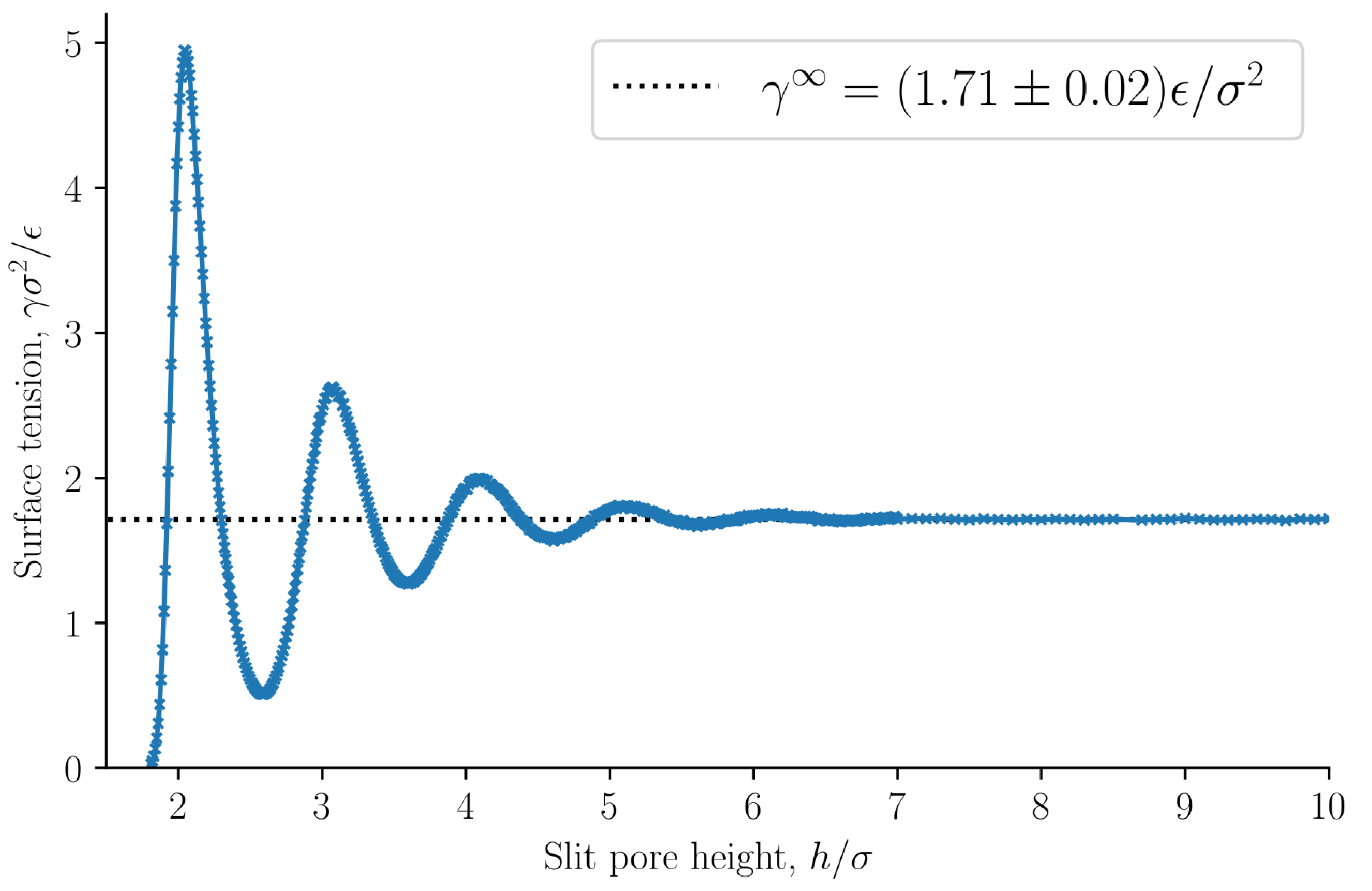
When
and
, it follows from Equation (
8) that the integral and differential surface tensions are equal
. The surface tension as a function of the slit pore height is presented in
Figure 8, see Equation (
33). The surface tension at infinite separation
is computed as the average surface tension of the slit pore, with height
, at which point the surface tension is independent of
h.
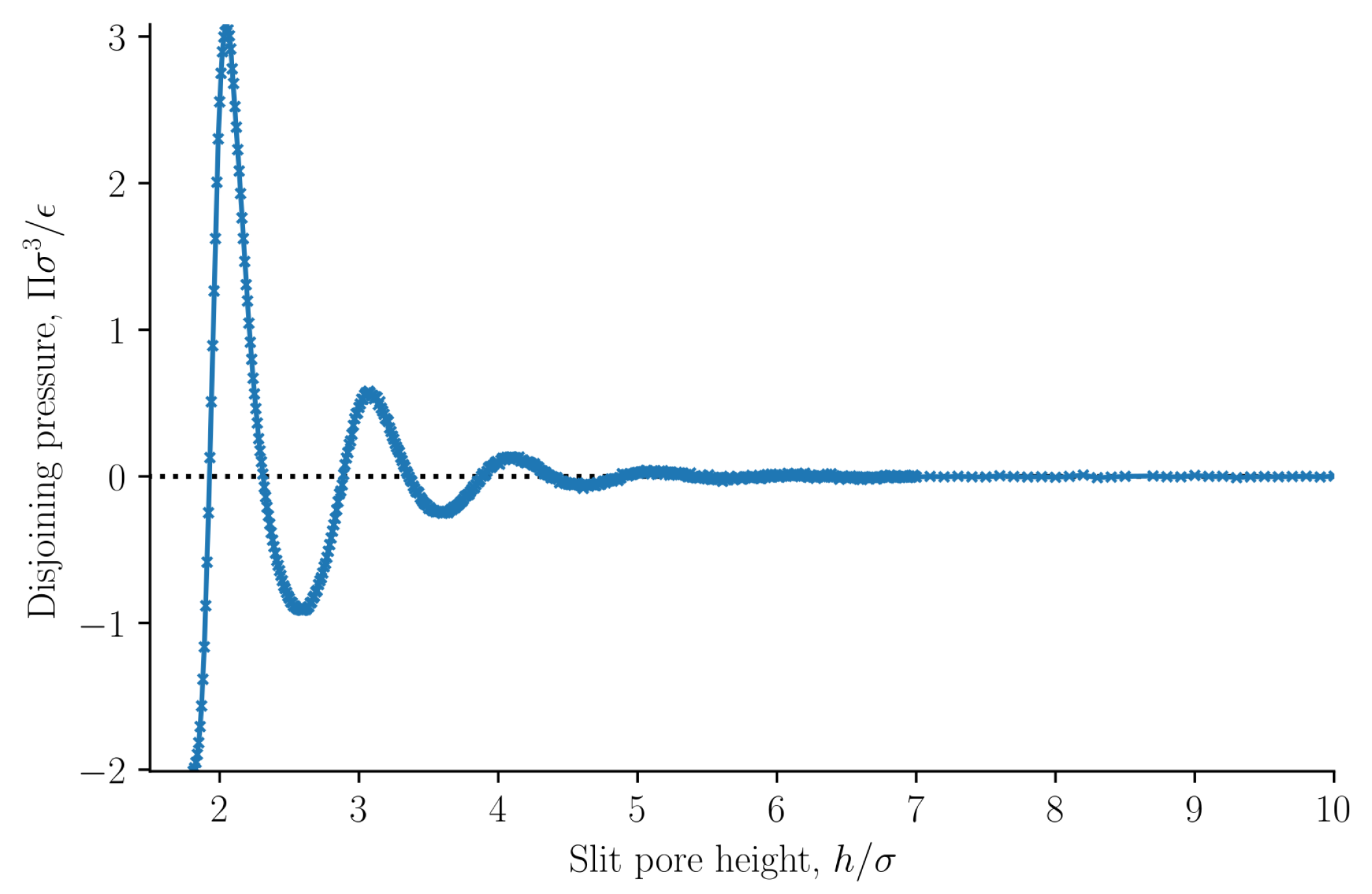
The disjoining pressure
was computed from Equation (
25), and is shown as a function of the slit pore height
h in
Figure 9. The disjoining pressure was here defined to be equal to the integral normal pressure minus the normal pressure at infinite separation. Because the integral and the differential normal pressures are the same and because the normal pressure at infinite separation is equal to the bulk pressure, in this case, the definition contain the commonly used definition of the disjoining pressure [
7,
29]. The normal pressure is constant for slit pore heights
. Consequently, the normal pressure at infinite separation can be calculated as the normal pressure when
. The normal pressure at infinite separation is equal to the pressure in a bulk fluid with the same temperature and chemical potential.
For the present case, we can claim that our definition of the disjoining pressure is equivalent to the common definition. Our definition is general, as it also covers the cases where the integral and the differential normal pressures are unequal. Examples where this is the case are given below.
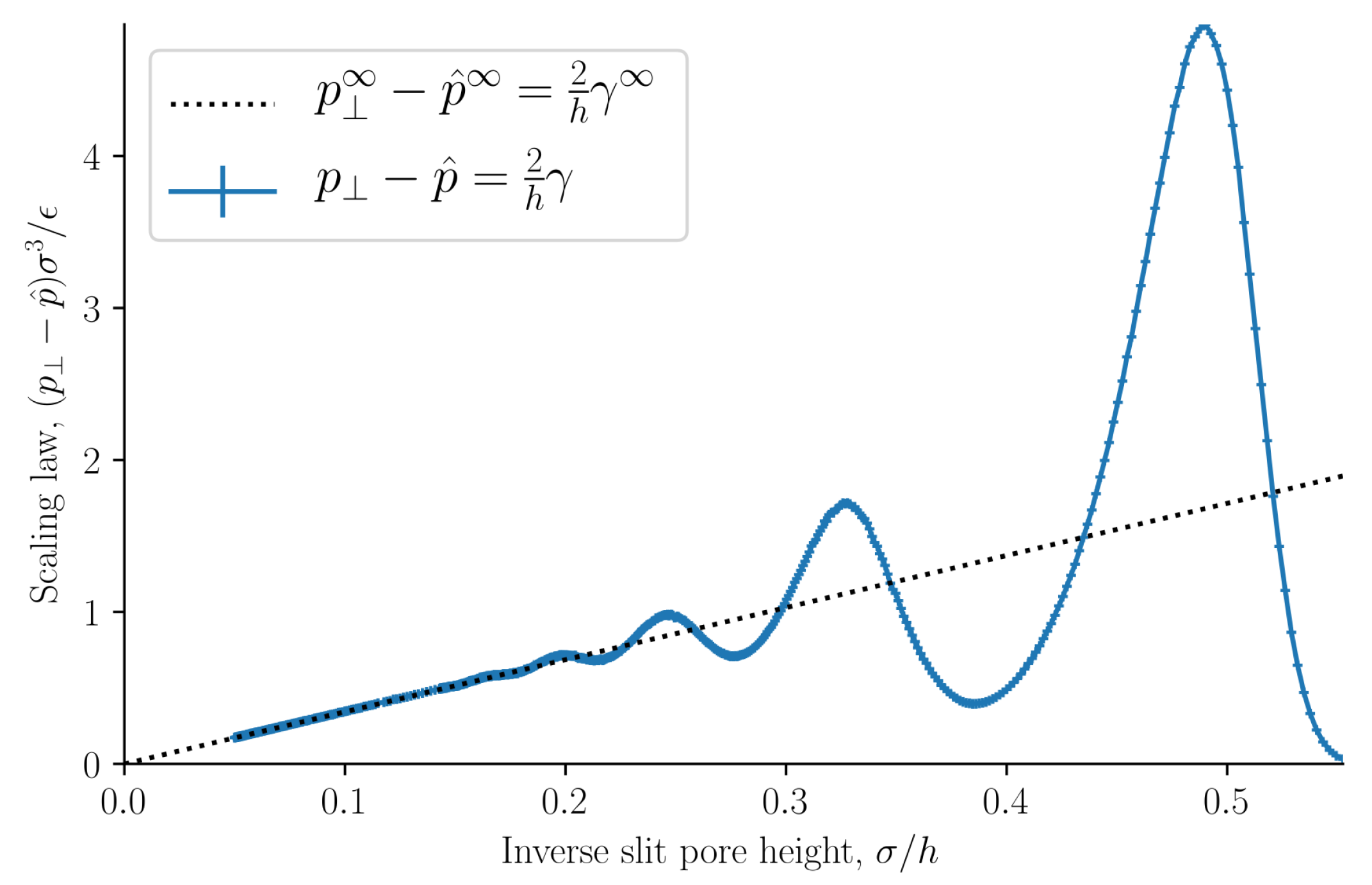
Figure 10 shows how the normal pressure minus the integral pressure scales with inverse slit pore height. It is equal to the scaling law presented in a previous work [
23]. The slope of this ideal curve is equal to two times the surface tension. When the inverse slit pore height approaches zero, i.e., when the walls are far apart, the normal pressure and integral pressures are equal as predicted. For pores that are so small that no bulk fluid can form in the center, the structuring at the walls starts to overlap, and a fluctuating difference is seen in the difference of the normal and integral pressures. In the region of the straight line, we have a scaling law, that relates states of different heights. At heights smaller than approximately
the scaling law breaks down, the difference of the two pressures starts to oscillate. There are positive and negative deviations from the law.
In our earlier work [
23], we studied liquid-vapor coexistence in a slit pore. In that work the surface area was not a control variable, and as a consequence the subdivision potential was found to be equal to two times the surface tension divided by the slit pore height, see
Figure 10. Another reasonable set of control variables is the height
h instead of the volume
V. For a control variable set consisting of temperature, height, surface area and chemical potential, the differential normal pressure is equal to
The differential surface tensions is
For this set of control variables, the height
h is kept constant instead of the volume
V. The subdivision potential is accordingly
These relations also help us characterize the smallness of the slit pore with the large walls. The subdivision potential, introduced by Hill as a measure of smallness, deviates from zero in the last relation, also when the integral pressure does not depend on the size of the area, with height
h and surface area
as control variables. A dependency on the area is relevant when adsorption takes place on small spheres [
24]. A slit pore with large walls may be expected to be small for small heights
h, since the confined fluid is not bulk-like. However, we have seen that when we use volume
V and surface area
as control variables, the subdivision potential is zero for large surface areas. A zero subdivision potential means that the system also can be described perfectly using regular thermodynamics [
18]. It is nevertheless meaningful to define a non-zero integral pressure, because the integral pressure enters the grand potential. It, therefore, determines the thermodynamic properties of a REV. Away from equilibrium, it will create a driving force.
The grand potential or minus the integral pressure times the volume are equal to the replica energy. The replica energy is not zero in the present case. Clearly, we have here an example where smallness is brought out in Hill’s terms through the replica potential.