Statistical Mechanics at Strong Coupling: A Bridge between Landsberg’s Energy Levels and Hill’s Nanothermodynamics
Abstract
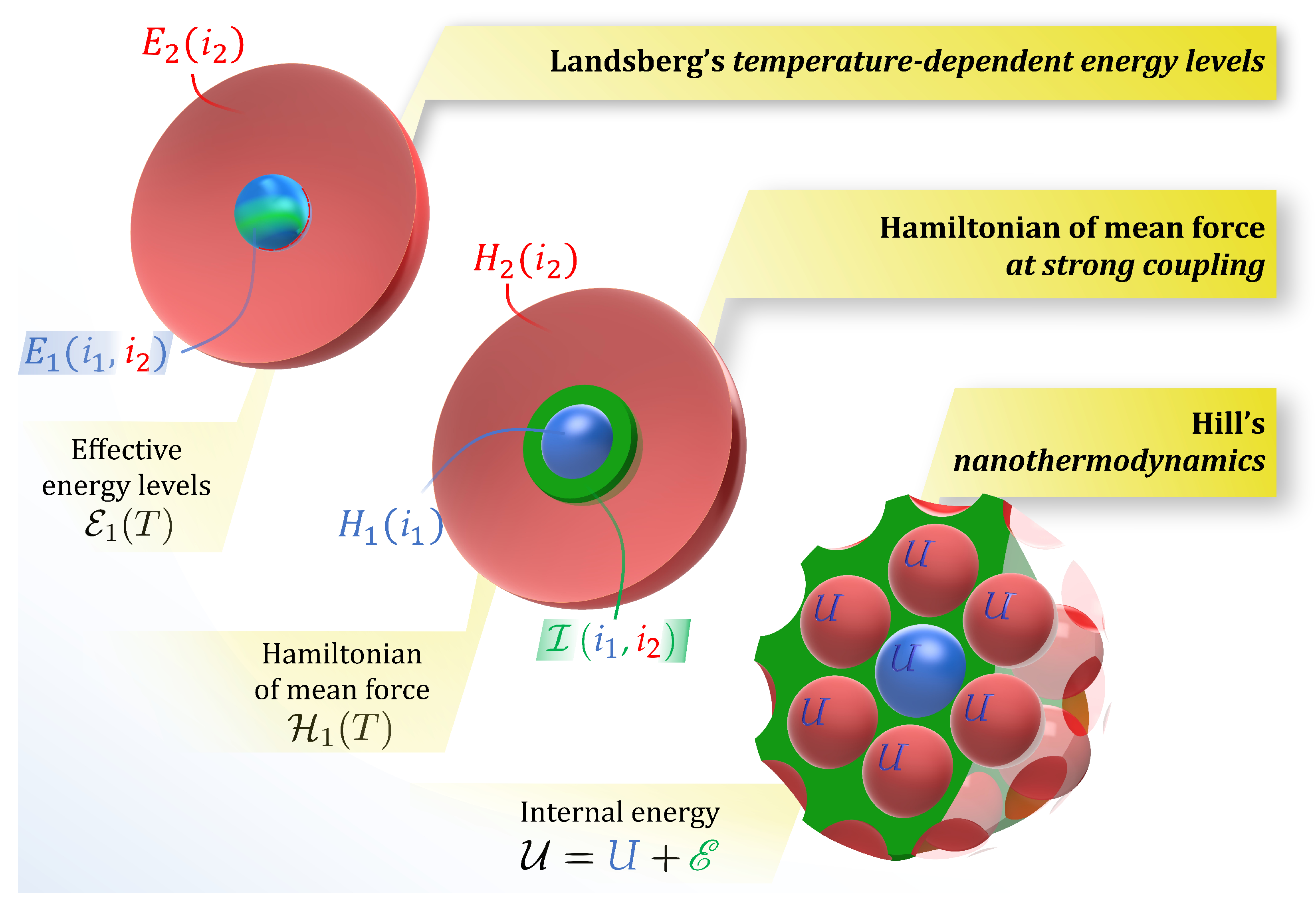
1. Introduction
2. ‘Temperature-Dependent’ Energy Levels and the Hamiltonian of Mean Force
3. Strong Coupling and Hill’s Nanothermodynamics
3.1. Hill’s Subdivision Potential
3.2. Statistical Mechanics at Strong Coupling
Generalization to Other Ensembles
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Campa, A.; Dauxois, T.; Fanelli, D.; Ruffo, S. Physics of Long-Range Interacting Systems; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Latella, I.; Peréz-Madrid, A.; Campa, A.; Casetti, L.; Ruffo, S. Thermodynamics of Nonadditive Systems. Phys. Rev. Lett. 2015, 114, 230601. [Google Scholar] [CrossRef] [PubMed]
- de Miguel, R.; Rubí, J.M. Strong Coupling and Nonextensive Thermodynamics. Entropy 2020, 22, 975. [Google Scholar] [CrossRef] [PubMed]
- Rushbrooke, G.S. On the statistical mechanics of assemblies wose energy-levels depend on temperature. Trans. Faraday Soc. 1940, 36, 1055. [Google Scholar] [CrossRef]
- Landsberg, P.T. Statitical Mechanics of Teperature-Dependent Energy Levels. Phys. Rev. 1954, 95, 643. [Google Scholar]
- Elcock, E.W.; Landsberg, P.T. Temperature Dependent Energy Levels in Statistical Mechanics. Proc. Phys. Soc. Lond. Sect. B 1957, 70, 161. [Google Scholar] [CrossRef]
- Cuden, C.B. The Temperature Dependence of the Energy Gaps in Semiconductors. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1969. [Google Scholar] [CrossRef]
- Bendt, P.J.; Cowan, R.D.; Yarnell, J.L. Excitations in Liquid Helium: Thermodynamic Calculations. Phys. Rev. 1959, 113, 1386. [Google Scholar] [CrossRef]
- Donnelly, R.J.; Roberts, P.H. A theory of temperature-dependent energy levels: Thermodynamic properties og He II. Low Temp. Phys. 1977, 27, 687. [Google Scholar] [CrossRef]
- Allen, P.V.; Heine, V. Theory of the temperature dependence of electronic band structures. J. Phys. C Solid State Phys. 1976, 9, 2305. [Google Scholar] [CrossRef]
- Patrick, C.E.; Giustino, F. Unified theory of electron-phonon renormalization and phono-assisted optical absorption. J. Phys. Condens. Matter 2014, 26, 365503. [Google Scholar] [CrossRef]
- Dykman, M.I.; Kono, K.; Kostantinov, D.; Lea, M.J. Ripplonic Lamb Shift for Electrons on Liquid Helium. Phys. Rev. Lett. 2017, 119, 256802. [Google Scholar] [CrossRef]
- Erez, A.; Meir, Y. Effect of amplitude fluctuations on the Berezinskii-Kosterlitz-Thouless transition. Phys. Rev. B 2013, 88, 184510. [Google Scholar] [CrossRef]
- Kolář, M.; Ryabov, A.; Filip, R. Optomechanical oscillator controlled by variatioons in its heat bath temperature. Phys. Rev. A 2017, 95, 042105. [Google Scholar] [CrossRef]
- Yamano, T. Efficiencies of thermodynamics when temperature-dependent energy levels exist. Phys. Chem. Chem. Phys. 2016, 18, 7011. [Google Scholar] [CrossRef]
- Yamano, T. Effect of temperature-dependent energy levels on exergy. J. Phys. Commun. 2017, 1, 055007. [Google Scholar] [CrossRef]
- de Miguel, R.; Rubí, J.M. Thermodynamics far from the thermodynamic limit. J. Phys. Chem. B 2017, 121, 10429–10434. [Google Scholar] [CrossRef] [PubMed]
- Shental, O.; Kanter, I. Shannon meets Carnot: Generalized second thermodynamic law. Europhys. Lett. 2009, 85, 10006. [Google Scholar] [CrossRef][Green Version]
- Hill, T.L. Thermodynamics of Small Systems. J. Chem. Phys. 1962, 36, 3182. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems, Parts I & II; Dover: New York, NY, USA, 2013. [Google Scholar]
- Hill, T.L. Perspective: Nanothermodynamics. Nano Lett. 2001, 1, 111. [Google Scholar] [CrossRef]
- Hill, T.L. A different Approach to Nanothermodynamics. Nano Lett. 2001, 1, 273. [Google Scholar] [CrossRef]
- Bedeaux, D.; Kjelstrup, S.; Schnell, S.K. Nanothermodynamics—General Theory; PoreLab: Trondheim, Norway, 2020. [Google Scholar]
- Rubí, J.M.; Bedeaux, D.; Kjelstrup, S. Thermodynamics for Single-Molecule Stretching Experiments. J. Phys. Chem. B 2006, 110, 12733. [Google Scholar] [CrossRef][Green Version]
- Quian, H. Hill’s small systems nanothermodynamics: A simple macromolecular partition problem with a statistical perspective. J. Biol. Phys. 2012, 38, 201. [Google Scholar] [CrossRef][Green Version]
- Chamberlin, R.V. The BigWorld of Nanothermodynamics. Entropy 2015, 17, 52. [Google Scholar] [CrossRef]
- Galteland, O.; Bedeaux, D.; Hafskjold, B.; Kjelstrup, S. Pressures Inside a Nano-Porous Medium. The Case of a Single Phase Fluid. Front. Phys. 2019, 7, 60. [Google Scholar] [CrossRef]
- Rauter, M.T.; Galteland, O.; Erdõs, M.; Moultos, O.A.; Vlugt, T.J.H.; Schnell, S.; Bedeaux, D.; Kjelstrup, S. Two-Phase Equilibrium Conditions in Nanopores. Nanomaterials 2020, 10, 608. [Google Scholar] [CrossRef] [PubMed]
- Strøm, B.A.; He, J.; Bedeaux, D.; Kjelstrup, S. When Thermodynamic Properties of Adsorbed Films Depend on Size: Fundamental Theory and Case Study. Nanomaterials 2020, 10, 1691. [Google Scholar] [CrossRef]
- Talkner, P.; Hanggi, P. Colloquium: Statistical mechanics and thermodynamics at strong coupling: Quantum and classical. Rev. Mod. Phys. 2020, 92, 041002. [Google Scholar] [CrossRef]
- Kolář, M.; Ryabov, A.; Filip, R. Heat capacities of thermally manipulated mechanical oscillator at strong coupling. Sci. Rep. 2019, 9, 10855. [Google Scholar] [CrossRef] [PubMed]
- de Miguel, R.; Rubí, J.M. Negative thermophoretic force in the strong coupling regime. Phys. Rev. Lett. 2019, 123, 200602. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, G.; Engineer, M. Temperature dependence of the polaron. Phys. Rev. B 1975, 12, 5472. [Google Scholar] [CrossRef]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, 3rd ed.; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Talkner, P.; Hanggi, P. Open system trajectories specify fluctuating work but not heat. Phys. Rev. E 2016, 94, 022143. [Google Scholar] [CrossRef]
- Seifert, U. First and Second Law of Thermodynamics at Strong Coupling. Phys. Rev. Lett. 2016, 116, 020601. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Stochastic and Macroscopic Thermodynamics of Strongly Coupled Systems. Phys. Rev. X 2017, 7, 011008. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Miguel, R.; Rubí, J.M. Statistical Mechanics at Strong Coupling: A Bridge between Landsberg’s Energy Levels and Hill’s Nanothermodynamics. Nanomaterials 2020, 10, 2471. https://doi.org/10.3390/nano10122471
de Miguel R, Rubí JM. Statistical Mechanics at Strong Coupling: A Bridge between Landsberg’s Energy Levels and Hill’s Nanothermodynamics. Nanomaterials. 2020; 10(12):2471. https://doi.org/10.3390/nano10122471
Chicago/Turabian Stylede Miguel, Rodrigo, and J. Miguel Rubí. 2020. "Statistical Mechanics at Strong Coupling: A Bridge between Landsberg’s Energy Levels and Hill’s Nanothermodynamics" Nanomaterials 10, no. 12: 2471. https://doi.org/10.3390/nano10122471
APA Stylede Miguel, R., & Rubí, J. M. (2020). Statistical Mechanics at Strong Coupling: A Bridge between Landsberg’s Energy Levels and Hill’s Nanothermodynamics. Nanomaterials, 10(12), 2471. https://doi.org/10.3390/nano10122471





