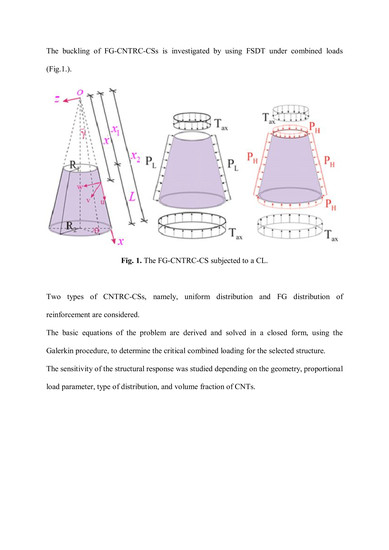
Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading
Abstract
:1. Introduction
2. Formulation of the Problem
3. The Governing Equations
4. Solution Procedure
5. Results and Discussion
5.1. Introduction
5.2. Comparative Evaluation
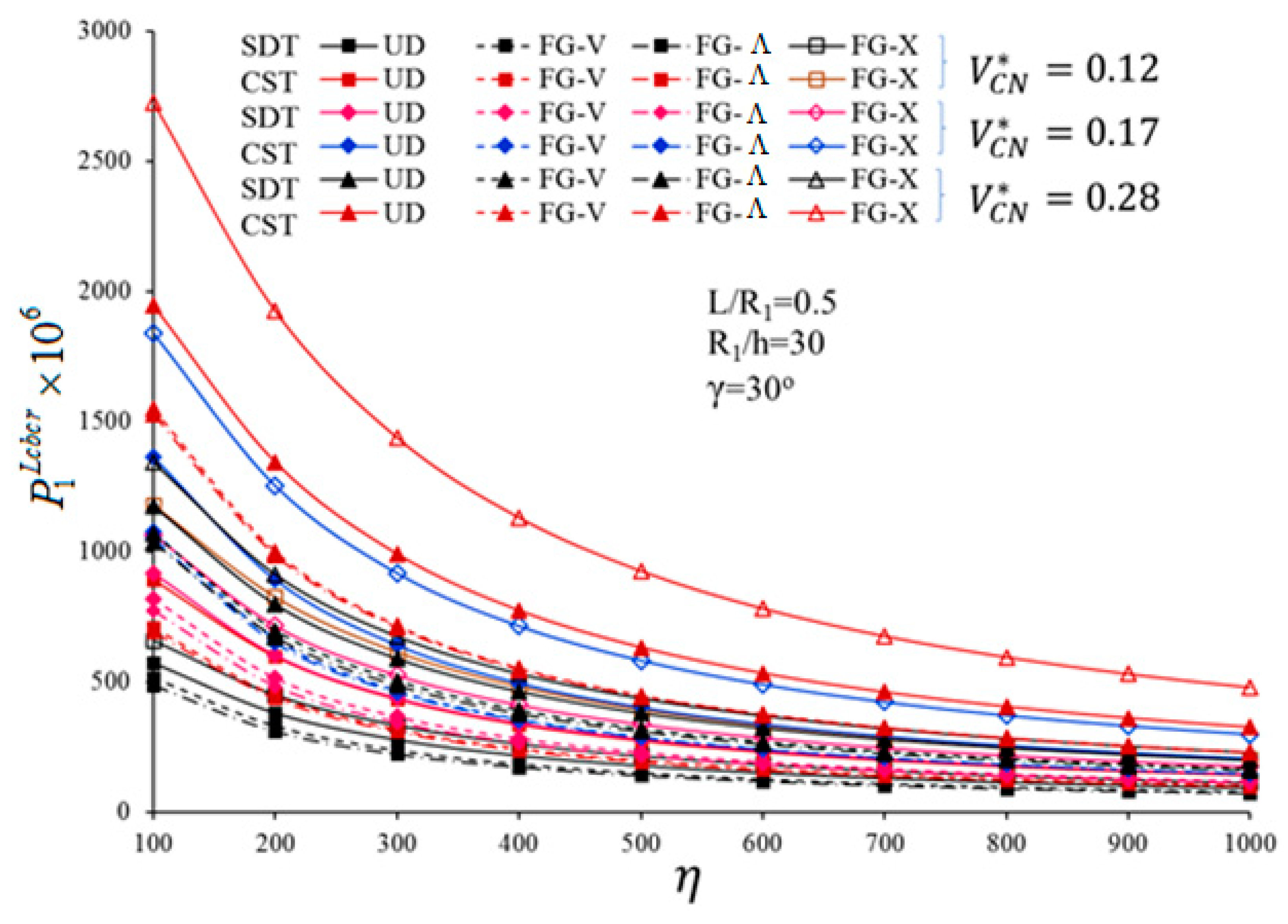
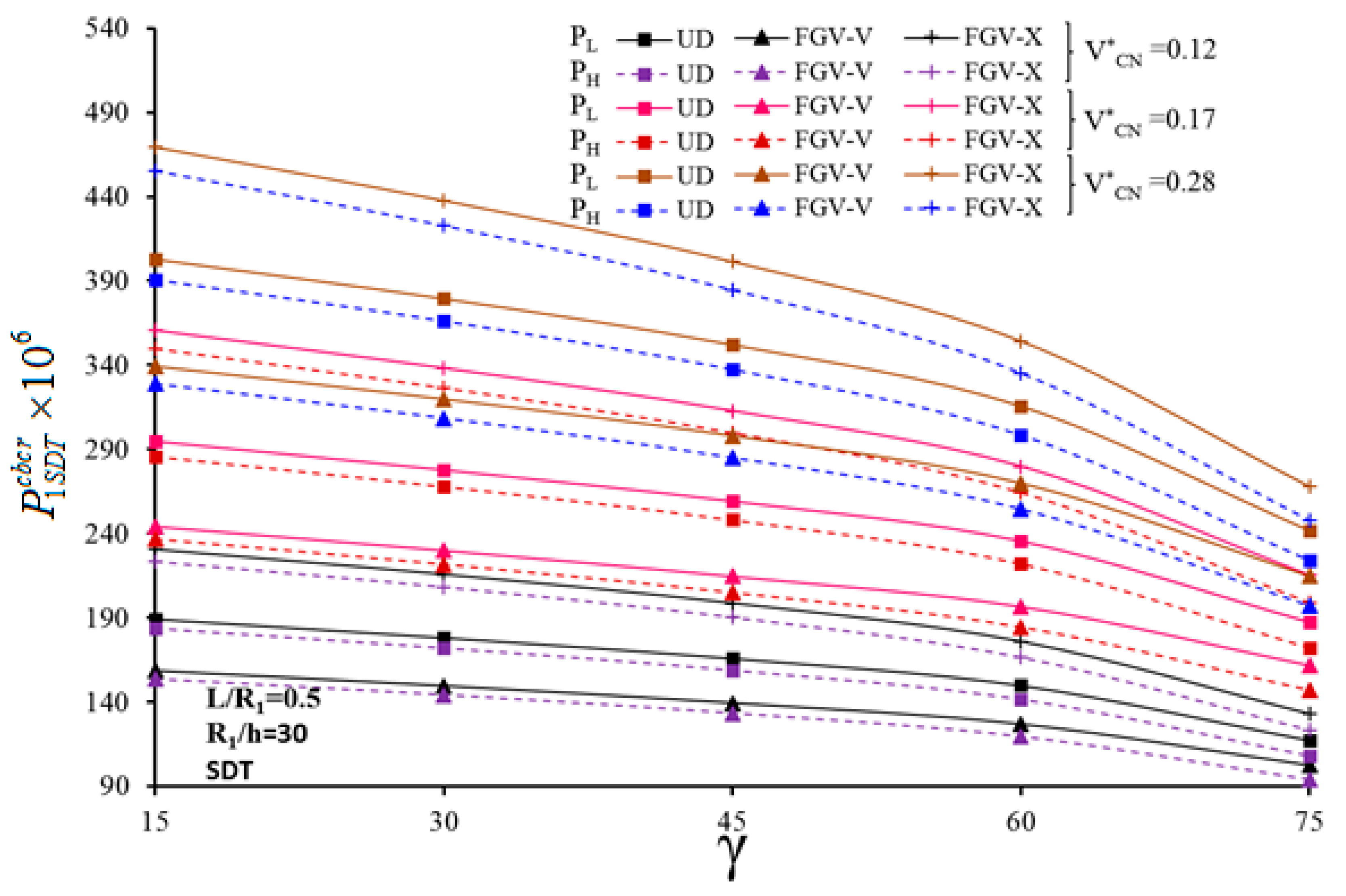
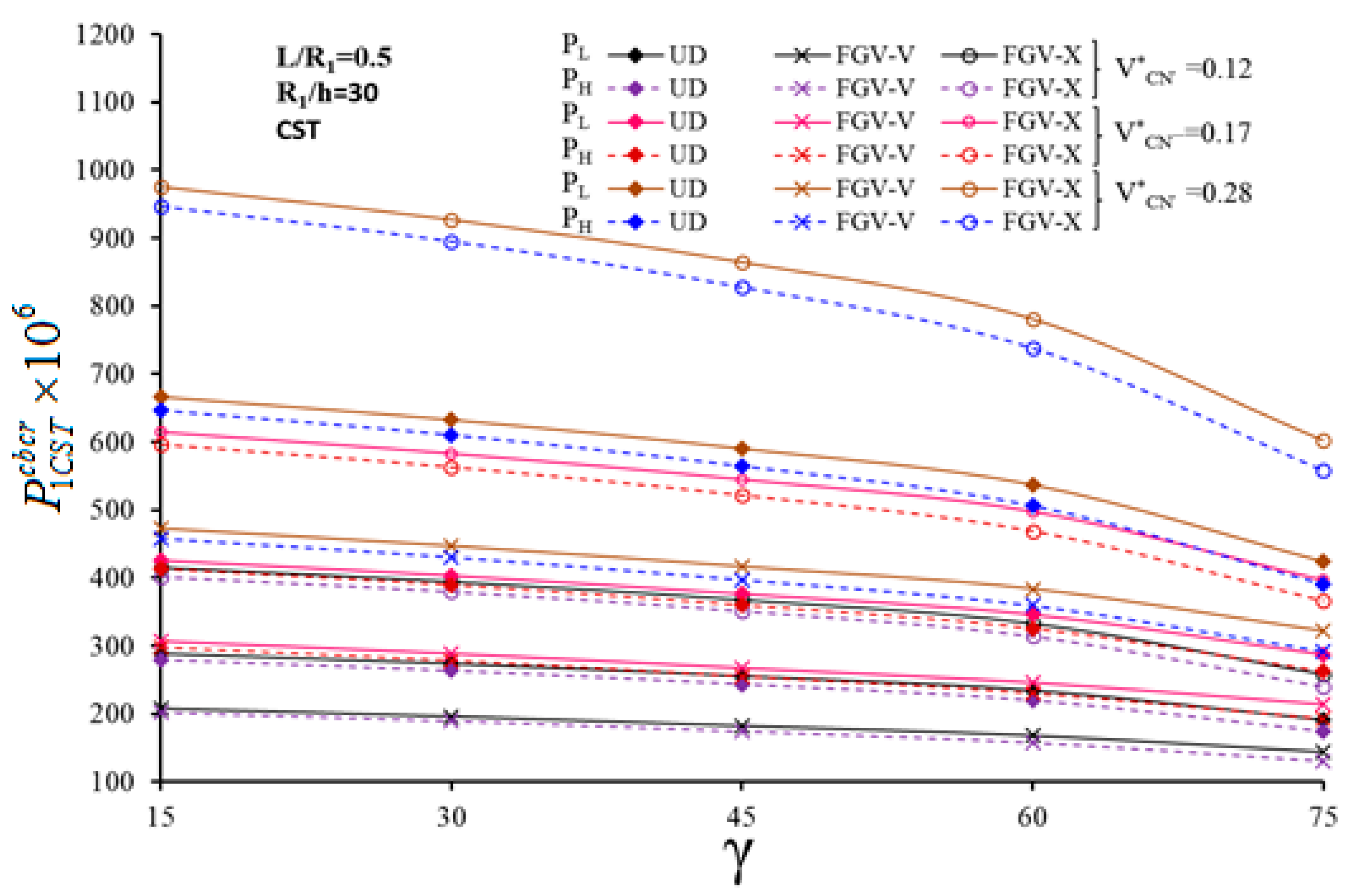
5.3. Analysis of Combined Buckling Loads
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Shen, H.S.; Chen, T.Y. Buckling and postbuckling behaviour of cylindrical shells under combined external pressure and axial compression. Thin-Walled Struct. 1991, 12, 321–334. [Google Scholar] [CrossRef]
- Winterstetter, T.A.; Schmidt, H. Stability of circular cylindrical steel shells under combined loading. Thin-Walled Struct. 2002, 40, 893–910. [Google Scholar] [CrossRef]
- Tafresi, A.; Bailey, C.G. Instability of imperfect composite cylindrical shells under combined loading. Compos. Struct. 2007, 80, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Ajdari, M.A.B.; Jalili, S.; Jafari, M.; Zamani, J.; Shariyat, M. The analytical solution of the buckling of composite truncated conical shells under combined external pressure and axial compression. J. Mech. Sci. Technol. 2012, 26, 2783–2791. [Google Scholar] [CrossRef]
- Sofiyev, A.H. On the buckling of composite conical shells resting on the Winkler–Pasternak elastic foundations under combined axial compression and external pressure. Compos. Struct. 2014, 113, 208–215. [Google Scholar] [CrossRef]
- Shen, H.S.; Noda, N. Postbuckling of FGM cylindrical shells under combined axial and radial mechanical loads in thermal environments. Int. J. Solid Struct. 2005, 42, 4641–4662. [Google Scholar] [CrossRef]
- Sofiyev, A.H. The buckling of FGM truncated conical shells subjected to combined axial tension and hydrostatic pressure. Compos. Struct. 2010, 92, 488–498. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Buckling analysis of FGM circular shells under combined loads and resting on the Pasternak type elastic foundation. Mech. Res. Commun. 2010, 37, 539–544. [Google Scholar] [CrossRef]
- Khazaeinejad, P.; Najafizadeh, M.M.; Jenabi, J.; Isvandzibaei, M.R. On the buckling of functionally graded cylindrical shells under combined external pressure and axial compression. J. Press. Vessel Technol. 2010, 132, 064501. [Google Scholar] [CrossRef]
- Huang, H.; Han, Q.; Feng, N.; Fan, X. Buckling of functionally graded cylindrical shells under combined loads. Mech. Adv. Mater. Struct. 2011, 18, 337–346. [Google Scholar] [CrossRef]
- Wu, C.P.; Chen, Y.C.; Peng, S.T. Buckling analysis of functionally graded material circular hollow cylinders under combined axial compression and external pressure. Thin-Walled Struct. 2013, 69, 54–66. [Google Scholar] [CrossRef]
- Shen, H.S.; Wang, H. Nonlinear bending and postbuckling of FGM cylindrical panels subjected to combined loadings and resting on elastic foundations in thermal environments. Compos. B Eng. 2015, 78, 202–213. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, H.; Han, Q. Buckling of elastoplastic functionally graded cylindrical shells under combined compression and pressure. Compos. B Eng. 2015, 69, 120–126. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoglu, N. The stability of FGM truncated conical shells under combined axial and external mechanical loads in the framework of the shear deformation theory. Compos. B Eng. 2016, 92, 463–476. [Google Scholar] [CrossRef]
- Iijima, S. Synthesis of carbon nanotubes. Nature 1994, 354, 56–58. [Google Scholar] [CrossRef]
- Kit, O.O.; Tallinen, T.; Mahadevan, L.; Timonen, J.; Koskinen, P. Twisting graphene nanoribbons into carbon nanotubes. Phys. Rev. B 2012, 85, 085428. [Google Scholar] [CrossRef]
- Lim, H.E.; Miyata, Y.; Kitaura, R.; Nishimura, Y.; Nishimoto, Y.; Irle, S.; Warner, J.H.; Kataura, H.; Shinohara, H. Growth of carbon nanotubes via twisted graphene nanoribbons. Nat. Commun. 2013, 4, 2548. [Google Scholar] [CrossRef]
- Bouaziz, O.; Kim, H.S.; Estrin, Y. Architecturing of metal-Based composites with concurrent nanostructuring: A new paradigm of materials design. Adv. Eng. Mater. 2013, 15, 336–340. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Estrin, Y.; Kulagin, R. Synthesis of hybrid materials by severe plastic deformation: a new paradigm of SPD processing. Adv. Eng. Mater. 2015, 17, 1853–1861. [Google Scholar] [CrossRef]
- Estrin, Y.; Beygelzimer, Y.; Kulagin, R. Design of architectured materials based on mechanically driven structural and compositional patterning. Adv. Eng. Mater. 2019, 21, 1900487. [Google Scholar] [CrossRef]
- Ashrafi, B.; Hubert, P.; Vengallatore, S. Carbon nanotube-Reinforced composites as structural materials for micro actuators in micro electromechanical systems. Nanotechnology 2006, 17, 4895–4903. [Google Scholar] [CrossRef]
- Rafiee, M.; Yang, J.; Kitipornchai, S. Thermal bifurcation buckling of piezoelectric carbon nanotube reinforced composite beams. Comput. Math. Appl. 2013, 66, 1147–1160. [Google Scholar] [CrossRef]
- Araneo, R.; Bini, F.; Rinaldi, A.; Notargiacomo, A.; Pea, M.; Celozzi, S. Thermal-Electric model for piezoelectric ZnO nanowires. Nanotechnology 2015, 26, 265402. [Google Scholar] [CrossRef]
- Ng, T.Y.; Lam, K.Y.; Liew, K.M. Effects of FGM materials on the parametric resonance of plate structures. Comput. Meth. Appl. Mech. Eng. 2000, 190, 953–962. [Google Scholar] [CrossRef]
- Praveen, G.N.; Reddy, J.N. Nonlinear transient thermo elastic analysis of functionally graded ceramic–Metal plates. Int. J. Solids Struct. 1998, 33, 4457–4476. [Google Scholar] [CrossRef]
- He, X.Q.; Ng, T.Y.; Sivashanker, S.; Liew, K.M. Active control of FGM plates with integrated piezoelectric sensors and actuators. Int. J. Solids Struct. 2001, 38, 1641–1655. [Google Scholar] [CrossRef]
- Tornabene, F. Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-Parameter power-law distribution. Comput. Meth. Appl. Mech. Eng. 2009, 198, 2911–2935. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Inman, D.J. 2-D differential quadrature solution for vibration analysis of functionally graded conical, cylindrical shell and annular plate structures. J. Sound Vib. 2009, 328, 259–290. [Google Scholar] [CrossRef]
- Akbari, M.; Kiani, Y.; Aghdam, M.M.; Eslami, M.R. Free vibration of FGM Levy conical panels. Compos. Struct. 2015, 116, 732–746. [Google Scholar] [CrossRef]
- Zhao, X.; Liew, K.M. Free vibration analysis of functionally graded conical shell panels by a meshless method. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Jooybar, N.; Malekzadeh, P.; Fiouz, A.; Vaghefi, M. Thermal effect on free vibration of functionally graded truncated conical shell panels. Thin-Walled Struct. 2016, 103, 45–61. [Google Scholar] [CrossRef]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration study of composite conical panels reinforced with FG-CNTs. Eng. Struct. 2018. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Postbuckling of nanotube-Reinforced composite cylindrical shells under combined axial and radial mechanical loads in thermal environment. Compos. B Eng. 2013, 52, 311–322. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M.; Bahrami, M. Nonlinear buckling and postbuckling behavior of cylindrical nano-Shells subjected to combined axial and radial compressions incorporating surface stress effects. Compos. B Eng. 2015, 79, 676–691. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Malakzadeh, P. Dynamic stability of rotating FG-CNTRC cylindrical shells under combined static and periodic axial loads. Int. J. Struct. Stab. Dyn. 2018, 18. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotube reinforced composites: A review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Jam, J.E.; Kiani, Y. Buckling of pressurized functionally graded carbon nanotube reinforced conical shells. Compos. Struct. 2015, 125, 586–595. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Thermal buckling of temperature dependent FG-CNT reinforced composite conical shells. Aerosp. Sci. Technol. 2015, 47, 42–53. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J. Numerical study on the buckling and vibration of functionally graded carbon nanotube-Reinforced composite conical shells under axial loading. Compos. B Eng. 2016, 95, 196–208. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Shojaei, M.F.; Hasrati, E. Buckling analysis of axially-Loaded functionally graded carbon nanotube-Reinforced composite conical panels using a novel numerical variational method. Compos. Struct. 2016, 157, 398–411. [Google Scholar] [CrossRef]
- Mehri, M.; Asadi, H.; Wang, Q. Buckling and vibration analysis of a pressurized CNT reinforced functionally graded truncated conical shell under an axial compression using HDQ method. Comput. Meth. Appl. Mech. Eng. 2016, 303, 75–100. [Google Scholar] [CrossRef]
- Fan, J.; Huang, J.; Ding, J. Free vibration of functionally graded carbon nanotube-Reinforced conical panels integrated with piezoelectric layers subjected to elastically restrained boundary conditions. Adv. Mech. Eng. 2017, 9, 1–17. [Google Scholar] [CrossRef]
- Belal Ahmed Mohamed, M.S.; Zishun, L.; Kim, M.L. Active control of functionally graded carbon nanotube-Reinforced composite plates with piezoelectric layers subjected to impact loading. J. Vib. Contr. 2019, 0, 1–18. [Google Scholar]
- Kiani, Y. Buckling of functionally graded graphene reinforced conical shells under external pressure in thermal environment. Compos. B Eng. 2019, 156, 128–137. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Türkaslan-Esencan, B.; Bayramov, R.P.; Salamci, M.U. Analytical solution of stability of FG-CNTRC conical shells under external pressures. Thin-Walled Struct. 2019, 144. [Google Scholar] [CrossRef]
- Ambartsumian, S.A. Theory of Anisotropic Shells; TT F-118; NASA: Washington, DC, USA, 1964.
- Volmir, A.S. Stability of Elastic Systems; Nauka: Moscow, Russia, 1967. [Google Scholar]
- Eslami, M.R. Buckling and Postbuckling of Beams, Plates and Shells; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]

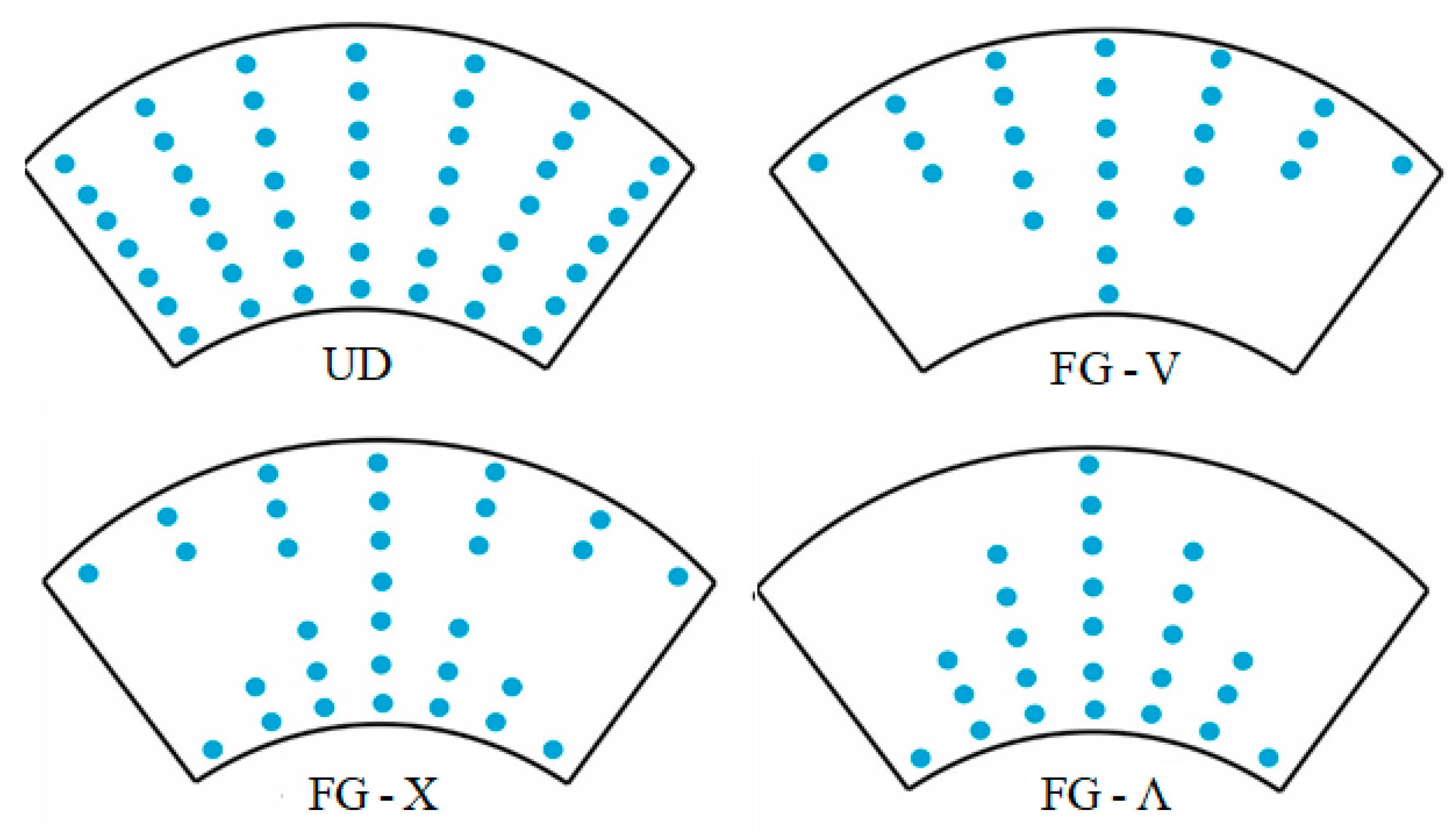

| CWCNT | Matrix (PMMA) | |
|---|---|---|
| Geometrical properties | , , | |
| Material properties | ||
| CNT efficiency parameter | for ; for ; for . |
| η = 750 | η = 140 | |||
|---|---|---|---|---|
| Shen and Xiang [33] | ||||
| 0.12 | 118.848 | 0.285 | 0.112 | 0.218 |
| 0.17 | 196.376 | 0.484 | 0.190 | 0.370 |
| 0.28 | 247.781 | 0.616 | 0.242 | 0.470 |
| Present study | ||||
| 0.12 | 117.840 | 0.281 | 0.111 | 0.2181 |
| 0.17 | 197.515 | 0.479 | 0.188 | 0.3711 |
| 0.28 | 247.062 | 0.613 | 0.2414 | 0.4756 |
| γ | 10° | 20° | 30° | |
| Jam and Kiani [37] | UD | 31.11(8) | 24.31(9) | 19.00(9) |
| FG-X | 34.53(8) | 27.24(9) | 21.38(9) | |
| FG-V | 32.41(8) | 25.19(9) | 19.52(10) | |
| Present study | UD | 31.01(8) | 23.91(9) | 18.23(10) |
| FG-X | 34.38(8) | 26.69(9) | 20.49(10) | |
| FG-V | 32.40 (8) | 24.97 (9) | 19.77 (10) | |
| R1/h | Types | |||||
|---|---|---|---|---|---|---|
| 0.12 | 30 | UD | 178.227(8) | 273.320(7) | 172.051(8) | 263.619(6) |
| FGV-V | 149.371(7) | 196.380(5) | 144.088(7) | 189.196(5) | ||
| FGV-X | 215.601(9) | 393.913(8) | 208.297(9) | 380.032(7) | ||
| 50 | UD | 83.296(9) | 96.267(9) | 78.996(9) | 91.297(9) | |
| FGV-V | 68.684(8) | 72.655(8) | 65.013(8) | 68.772(8) | ||
| FGV-X | 107.856(10) | 134.647(10) | 102.492(10) | 127.951(10) | ||
| 70 | UD | 44.157(11) | 46.897(11) | 41.493(11) | 44.068(11) | |
| FGV-V | 37.515(10) | 37.035(10) | 35.124(9) | 34.636(9) | ||
| FGV-X | 57.660(12) | 63.714(12) | 54.360(12) | 60.067(12) | ||
| 90 | UD | 26.050(12) | 26.743(12) | 24.320(12) | 24.967(12) | |
| FGV-V | 22.882(11) | 21.902(11) | 21.266(11) | 20.355(11) | ||
| FGV-X | 33.770(13) | 35.488(13) | 31.663(13) | 33.274(13) | ||
| 0.17 | 30 | UD | 277.753(7) | 403.421(6) | 267.928(7) | 388.892(6) |
| FGV-D | 216.472(7) | 285.441(6) | 208.815(7) | 275.161(6) | ||
| FGV-X | 337.997(8) | 582.930(7) | 326.283(8) | 562.312(7) | ||
| 50 | UD | 127.380(9) | 144.108(9) | 120.804(9) | 136.614(8) | |
| FGV-V | 104.824(8) | 108.979(8) | 99.222(8) | 103.074(7) | ||
| FGV-X | 166.556(10) | 202.672(9) | 157.999(9) | 192.209(9) | ||
| 70 | UD | 67.718(10) | 71.100(10) | 63.421(10) | 66.589(10) | |
| FGV-V | 57.633(9) | 56.330(9) | 53.797(9) | 52.580(9) | ||
| FGV-X | 89.216(11) | 97.309(11) | 83.834(11) | 91.439(11) | ||
| 90 | UD | 40.167(12) | 40.992(12) | 37.468(11) | 38.204(11) | |
| FGV-V | 35.470(11) | 33.809(11) | 32.965(11) | 31.366(10) | ||
| FGV-X | 52.637(13) | 54.879(13) | 49.194(12) | 51.292(12) | ||
| 0.28 | 30 | UD | 379.351(8) | 632.214(7) | 366.204(8) | 609.852(7) |
| FGV-V | 319.603(7) | 446.857(6) | 308.298(7) | 430.763(6) | ||
| FGV-X | 437.545(9) | 927.004(8) | 422.721(9) | 894.878(8) | ||
| 50 | UD | 182.000(10) | 218.225(10) | 172.950(10) | 207.373(10) | |
| FGV-V | 148.010(9) | 162.024(8) | 140.108(8) | 153.364(8) | ||
| FGV-X | 234.684(10) | 314.925(11) | 223.013(10) | 299.268(10) | ||
| 70 | UD | 96.385(12) | 104.268(12) | 90.694(11) | 98.163(11) | |
| FGV-V | 79.650(10) | 80.897(10) | 74.597(10) | 75.765(10) | ||
| FGV-X | 128.856(12) | 148.054(12) | 121.480(12) | 139.579(12) | ||
| 90 | UD | 56.322(13) | 58.452(13) | 52.808(13) | 54.805(13) | |
| FGV-V | 47.930(12) | 47.203(11) | 44.628(11) | 43.870(11) | ||
| FGV-X | 76.299(13) | 82.031(14) | 71.538(13) | 76.978(13) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofiyev, A.H.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading. Nanomaterials 2020, 10, 419. https://doi.org/10.3390/nano10030419
Sofiyev AH, Tornabene F, Dimitri R, Kuruoglu N. Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading. Nanomaterials. 2020; 10(3):419. https://doi.org/10.3390/nano10030419
Chicago/Turabian StyleSofiyev, Abdullah H., Francesco Tornabene, Rossana Dimitri, and Nuri Kuruoglu. 2020. "Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading" Nanomaterials 10, no. 3: 419. https://doi.org/10.3390/nano10030419
APA StyleSofiyev, A. H., Tornabene, F., Dimitri, R., & Kuruoglu, N. (2020). Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading. Nanomaterials, 10(3), 419. https://doi.org/10.3390/nano10030419