A Legendre–Fenchel Transform for Molecular Stretching Energies
Abstract
1. Introduction
2. Method
2.1. Simulation Details
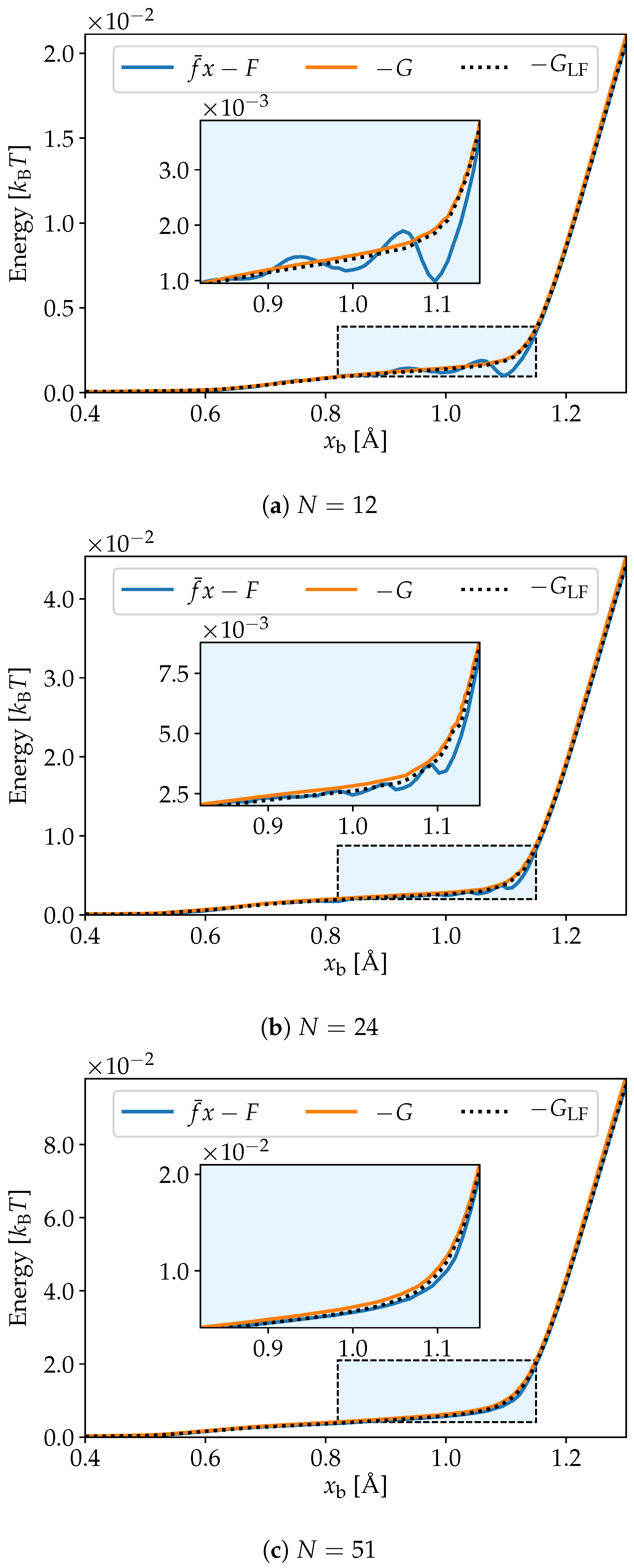
2.2. Energy Transforms
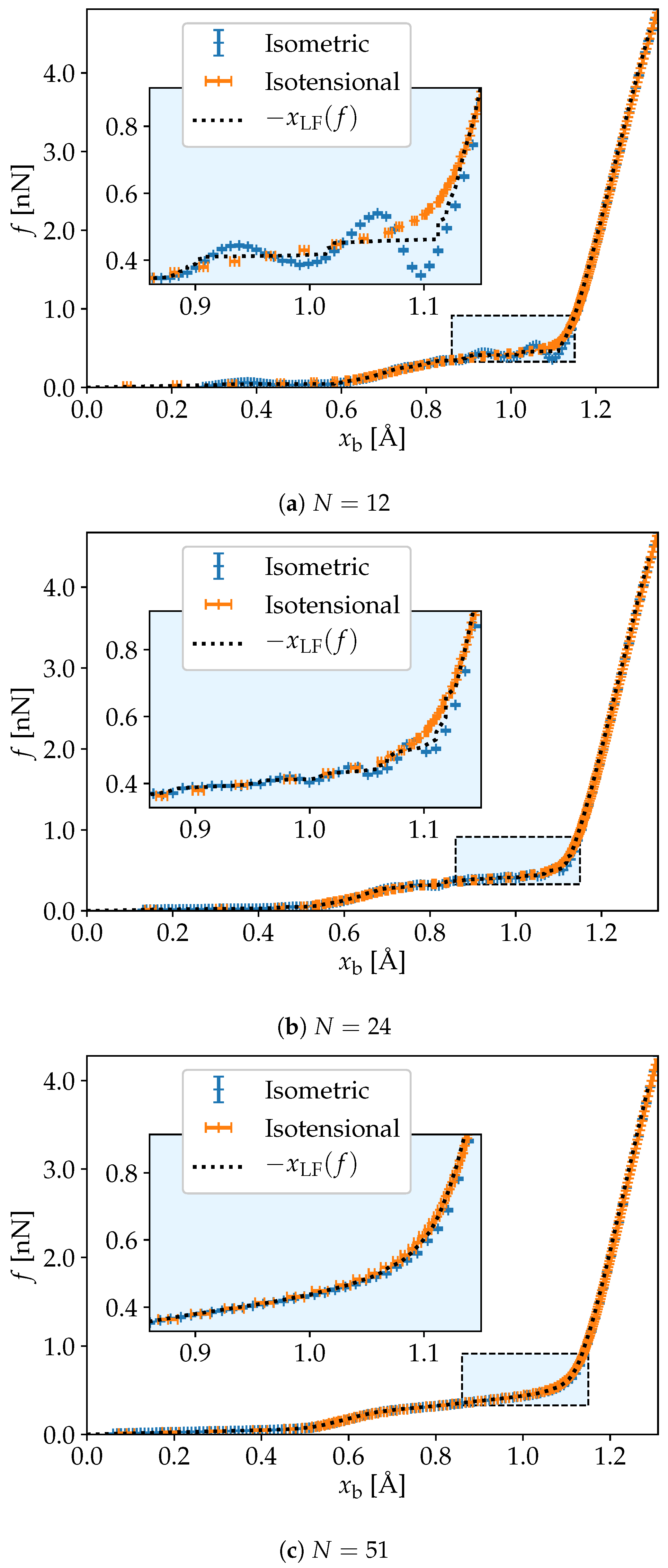
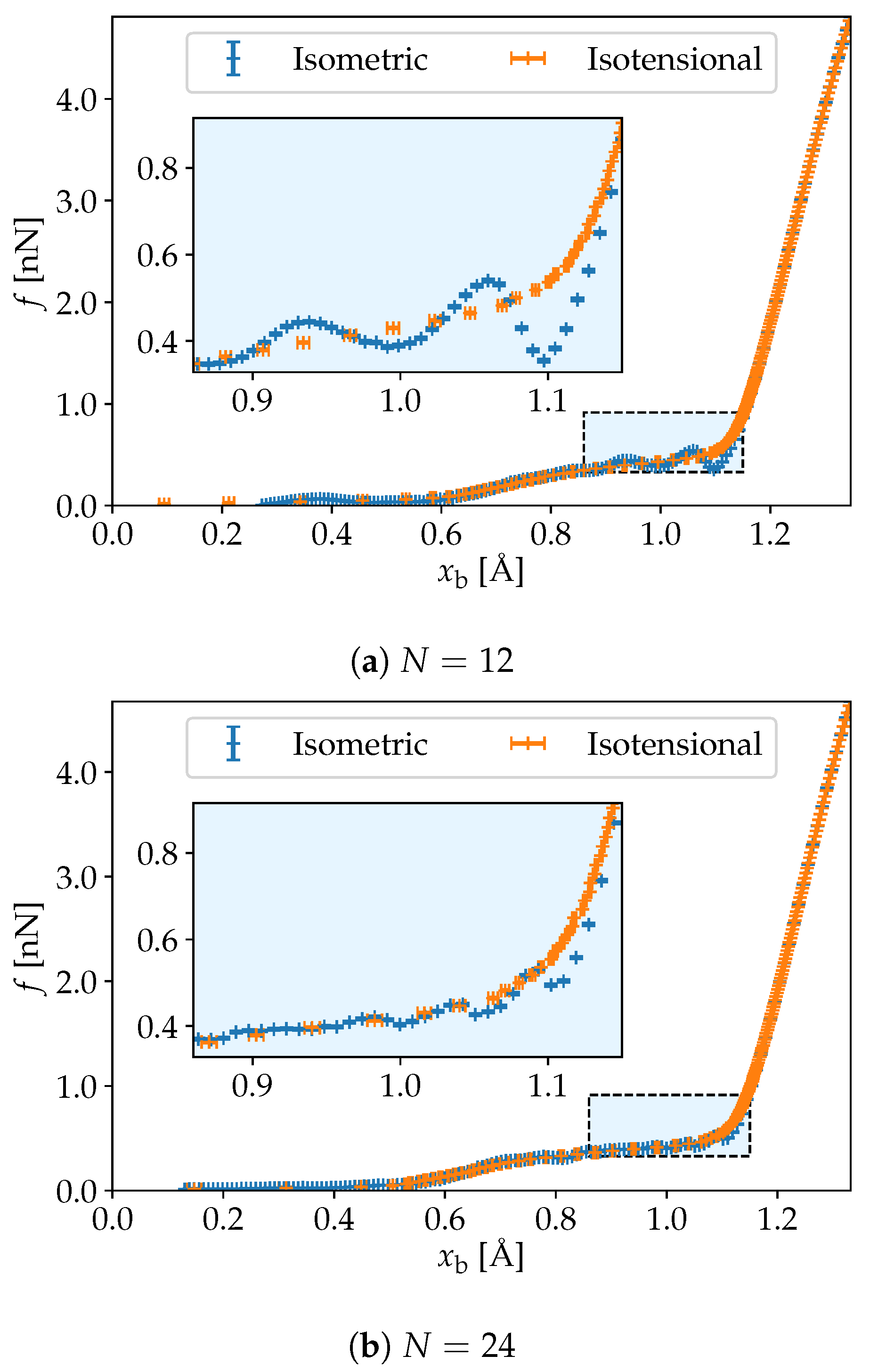
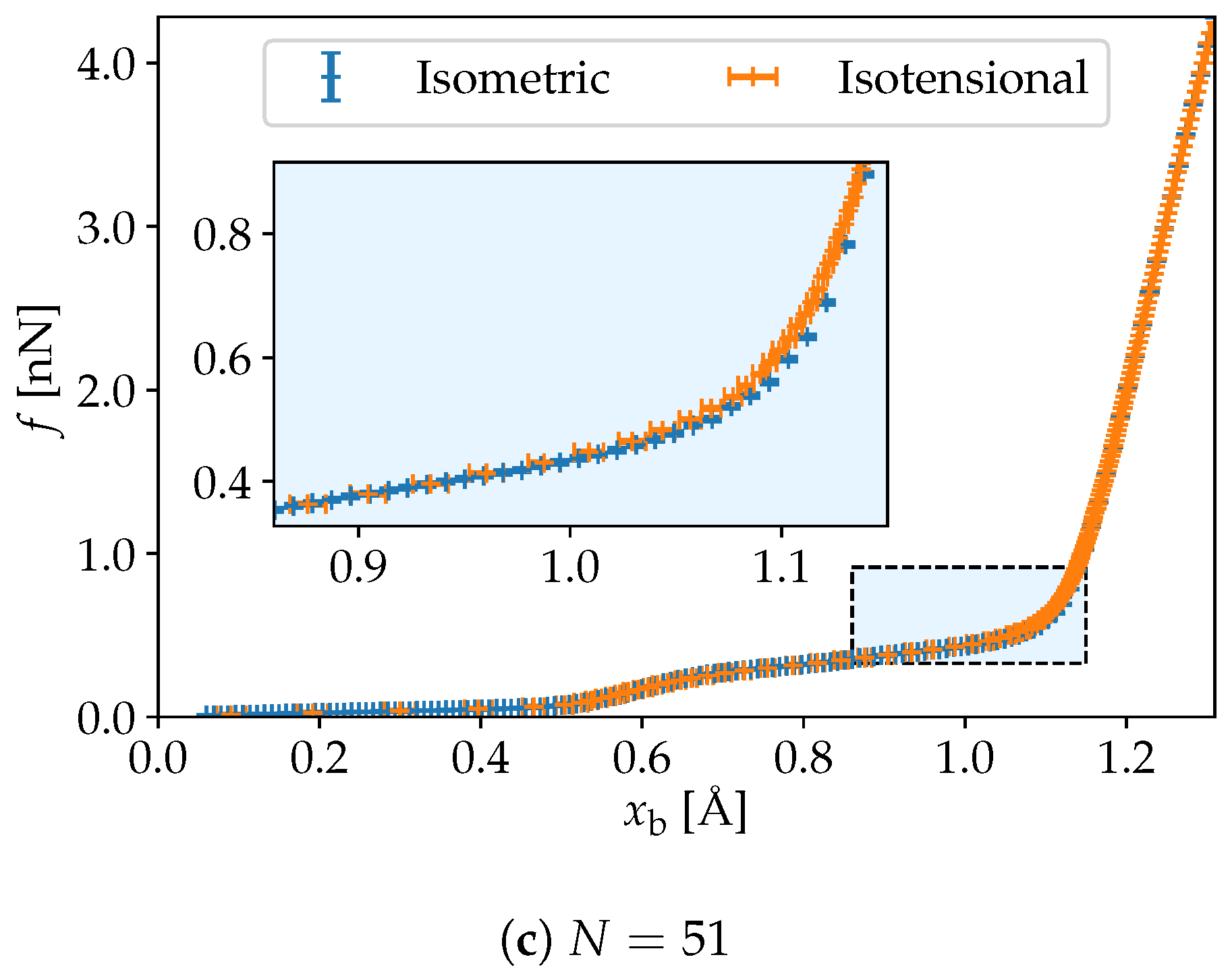
3. Simulation Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hill, T.L. Thermodynamics of Small Systems; W.A. Benjamin Inc.: New York, NY, USA, 1963; p. 210. [Google Scholar]
- Bedeaux, D.; Kjelstrup, S.; Schnell, S.K. Nanothermodynamics—General Theory, 1st ed.; PoreLab: Trondheim, Norway, 2020. [Google Scholar]
- Campa, A.; Dauxois, T.; Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 2009, 480, 57–159. [Google Scholar] [CrossRef]
- Bouchet, F.; Gupta, S.; Mukamel, D. Thermodynamics and dynamics of systems with long-range interactions. Phys. A Stat. Mech. Its Appl. 2010, 389, 4389–4405. [Google Scholar] [CrossRef]
- Campa, A.; Dauxois, T.; Fanelli, D.; Ruffo, S. Physics of Long-Range Interacting Systems; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Latella, I.; Pérez-Madrid, A. Local thermodynamics and the generalized Gibbs-Duhem equation in systems with long-range interactions. Phys. Rev. E 2013, 88, 42135. [Google Scholar] [CrossRef]
- Latella, I.; Pérez-Madrid, A.; Campa, A.; Casetti, L.; Ruffo, S. Thermodynamics of Nonadditive Systems. Phys. Rev. Lett. 2015, 114, 230601. [Google Scholar] [CrossRef]
- Gross, D.H.E. Microcanonical Thermodynamics; World Scientific: Singapore, 2001. [Google Scholar]
- Chomaz, P.; Gulminelli, F. Phase Transitions in Finite Systems. In Dynamics and Thermodynamics of Systems with Long Range Interactions; Dauxois, T., Ruffo, S., Arimondo, E., Wilkens, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 602, pp. 68–129. [Google Scholar]
- Süzen, M.; Sega, M.; Holm, C. Ensemble inequivalence in single-molecule experiments. Phys. Rev. E 2009, 79, 051118. [Google Scholar] [CrossRef]
- Bering, E.; Kjelstrup, S.; Bedeaux, D.; Miguel Rubi, J.; de Wijn, A.S. Entropy Production beyond the Thermodynamic Limit from Single-Molecule Stretching Simulations. J. Phys. Chem. B 2020, 124, 8909–8917. [Google Scholar] [CrossRef] [PubMed]
- Keller, D.; Swigon, D.; Bustamante, C. Relating Single-Molecule Measurements to Thermodynamics. Biophys. J. 2003, 84, 733–738. [Google Scholar] [CrossRef]
- Monge, A.M.; Manosas, M.; Ritort, F. Experimental test of ensemble inequivalence and the fluctuation theorem in the force ensemble in DNA pulling experiments. Phys. Rev. E 2018, 98, 032146. [Google Scholar] [CrossRef]
- Rockafellar, T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1972. [Google Scholar]
- Ellis, R.; Haven, K.; Turkington, B. Large Deviation Principles and Complete Equivalence and Nonequivalence Results for Pure and Mixed Ensembles. J. Stat. Phys. 2000, 101, 999–1064. [Google Scholar] [CrossRef]
- Touchette, H. The large deviation approach to statistical mechanics. Phys. Rep. 2009, 478, 1–69. [Google Scholar] [CrossRef]
- Bering, E.; de Wijn, A.S. Stretching and breaking of PEO nanofibres. A classical force field and ab initio simulation study. Soft Matter 2020, 16, 2736–2752. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Depa, P.; Sakai, V.G.; Maranas, J.K.; Lynn, J.W.; Peral, I.; Copley, J.R.D. A comparison of united atom, explicit atom, and coarse-grained simulation models for poly(ethylene oxide). J. Chem. Phys. 2006, 124, 234901(11). [Google Scholar] [CrossRef] [PubMed]
- van Zon, A.; Mos, B.; Verkerk, P.; de Leeuw, S. On the dynamics of PEO-NaI polymer electrolytes. Electrochim. Acta 2001, 46, 1717–1721. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D.; Thomas, J.O. Molecular dynamics simulation of crystalline poly(ethylene oxide). J. Chem. Phys. 1994, 101, 10064. [Google Scholar] [CrossRef]
- Beyer, M.K. The mechanical strength of a covalent bond calculated by density functional theory. J. Chem. Phys. 2000, 112, 7307–7312. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Steinbach, P.J.; Brooks, B.R. Protein simulation below the glass-transition temperature. Dependence on cooling protocol. Chem. Phys. Lett. 1994, 226, 447–452. [Google Scholar] [CrossRef]
- Hill, T.L. An Introduction to Statistical Thermodynamics; Dover Publications Inc.: New York, NY, USA, 1986. [Google Scholar]
- Campa, A.; Casetti, L.; Latella, I.; Pérez-Madrid, A.; Ruffo, S. Concavity, Response Functions and Replica Energy. Entropy 2018, 20, 907. [Google Scholar] [CrossRef]
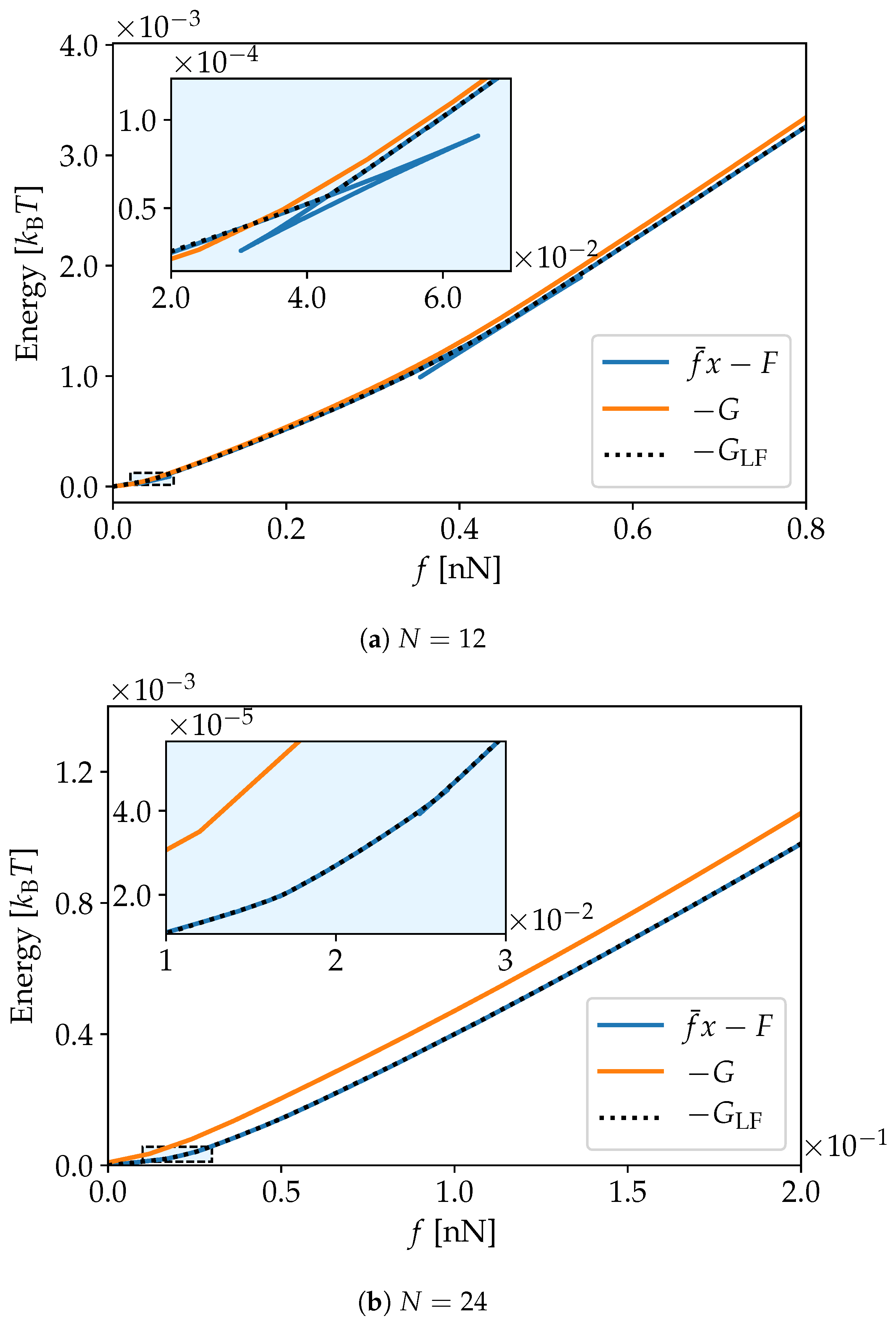
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bering, E.; Bedeaux, D.; Kjelstrup, S.; de Wijn, A.S.; Latella, I.; Rubi, J.M. A Legendre–Fenchel Transform for Molecular Stretching Energies. Nanomaterials 2020, 10, 2355. https://doi.org/10.3390/nano10122355
Bering E, Bedeaux D, Kjelstrup S, de Wijn AS, Latella I, Rubi JM. A Legendre–Fenchel Transform for Molecular Stretching Energies. Nanomaterials. 2020; 10(12):2355. https://doi.org/10.3390/nano10122355
Chicago/Turabian StyleBering, Eivind, Dick Bedeaux, Signe Kjelstrup, Astrid S. de Wijn, Ivan Latella, and J. Miguel Rubi. 2020. "A Legendre–Fenchel Transform for Molecular Stretching Energies" Nanomaterials 10, no. 12: 2355. https://doi.org/10.3390/nano10122355
APA StyleBering, E., Bedeaux, D., Kjelstrup, S., de Wijn, A. S., Latella, I., & Rubi, J. M. (2020). A Legendre–Fenchel Transform for Molecular Stretching Energies. Nanomaterials, 10(12), 2355. https://doi.org/10.3390/nano10122355