1. Introduction
Adsorption is a central process in nature and in engineering. An important case in nature is adsorption on particles in the atmosphere. It has been recognized for many years that the representation of cloud processes is a significant source of uncertainty in climate models. Many interactions among particles in the atmosphere, clouds and precipitation are relevant for such processes and are the focus of a large area of climate change research [
1]. The particles may vary in type, size and shape, and may originate from phenomena such as forest fires and volcanic eruptions, or from human activity such as industry and transportation. They follow the rising air through expansion and cooling, and serve, among other things, as condensation and ice nucleation sites. The initiation of condensation on particles begins with the adsorption or absorption of molecules from the surrounding air. Therefore, the development of more accurate climate models will benefit from a better understanding of these processes for small, curved particles. Although we use herein condensation on particles in the atmosphere as an important application, the focus of this work is on the fundamentals of adsorption on small systems in general.
A substantial amount of research from the 1930s onward on size-effects in thermodynamics may be found, for instance, in the literature on nucleation [
2,
3,
4,
5,
6,
7,
8]. The majority of the work is based on Gibbs’ theory of heterogeneous systems [
9]. However, there exists an alternative to the method of Gibbs, developed by Hill in the early 1960s [
10]. Hill’s method distinguishes itself by the fact that it is a unified and systematic approach to the treatment of all small systems, and does not require the concept of dividing surfaces to be introduced at the outset. The equivalence of Hill’s and Gibbs’ method in its most general form for the description of curved surfaces has recently been verified [
11]. The method is a generalization of macroscopic thermodynamics to small systems, and thus contains conventional thermodynamics as a special case in the macroscopic limit. By generalizing the fundamental differential equations traditionally used in thermodynamics, the whole internal structure of thermodynamic relations for small systems follows naturally by the familiar methods such as Euler integration, which otherwise would not apply for size dependent systems. The analogue of the Gibbs–Duhem equation for small systems is then readily available, and relations describing the size- and shape-dependence of all intensive properties follow. This has motivated us to describe adsorption on small systems using Hill’s theory to provide a solid foundation for the present and similar investigations. The aim of the study was thus to present a set of equations for adsorption on a small adsorbent, alternative to existing theories, most prominently Gibbs, and illustrate the set using molecular simulations of CO
adsorption on a small sphere of graphite.
In conventional thermodynamics an adsorption system may be described in several ways, one of which considers the system to be the adsorbed phase only. The adsorbent properties are then subtracted from the properties of the surroundings, with the exception of the interaction energy with the adsorbed phase [
12]. This view recognizes the asymmetric nature of the system and leads naturally to thermodynamic properties per film molecule. Another approach is to treat the system as a solution of adsorbent and adsorbate [
13]. This application is referred to as solution thermodynamics. Though both approaches may be applied, the potential usefulness of one over the other relates to the possible interchange of adsorbent and adsorbate components. In the asymmetric approach, hereafter referred to as adsorption thermodynamics, the focus is on obtaining thermodynamic properties and relations for the adsorbed phase. In the systems typically considered, the properties are categorized as extensive or intensive depending on whether they are proportional to or independent of the size of the film. Therefore, even though the size is necessary in order to completely characterize the film, the nature of the film appears to be independent of it. As a consequence, the differential thermodynamic relations for the adsorbed phase are Euler homogeneous and of first degree in the extensive properties [
14]. The relations are therefore directly integrable by the theorem of Euler.
For small systems, the statements above must be modified. The properties normally referred to as intensive are no longer independent of size, so the conventional use of the terms intensive and extensive must now refer to properties that obtain the implied characteristics in the macroscopic limit. The differential thermodynamic relations for a single system are no longer linear homogeneous functions, and can not be directly integrated as before. As the nature of the film now depends on its size and shape, it becomes of interest to systematically investigate the effects of size and shape in a framework that allows for this in a general way. This is possible in the thermodynamic theory of small systems, or nanothermodynamics, as developed by Terrell L. Hill [
10], and is the precise reason why we would like to advocate this method. For a more recent text on the method, see Bedeaux et al. [
15].
To be able to recognize these differences is important, because it enables us to compare energies of systems that vary in size. Consider two nanoparticles at ambient conditions. One is slightly larger than the other, but they are otherwise identical. The particles do not have bare surfaces; molecules will be adsorbed from the environment—for instance, adsorption of CO
on the surfaces of the particles (not adsorption of nano-sized particles on a macroscopic surface). A central question is then: how do the thermodynamic properties of the adsorbed phase differ between the two cases? This is an important question because the adsorbed phase is an interface through which the particle interacts with its environment. Some forms of energy transfer and some forms of interactions are strongly influenced by the presence of adsorbed phases. Not only would size affect the intensive properties, but depending on the constraints on the system, intensive properties may suffice to determine the system size. At length scales where properties typically are size- and shape-dependent, the nanothermodynamics of Hill may help us investigate the interplay between the nature of a system and its size. This is not to say that other approaches may not be successful (see, e.g., [
3]), but the corresponding overarching relations (e.g., Maxwell relations) may be less obvious in these. Therefore, the existence of an alternative method may be useful per se.
Our aim was, therefore, to establish operational thermodynamic relations that enable investigations of thin film properties from a nanothermodynamic perspective. Our work has its basis in the work of Hill on nanothermodynamics [
10] and papers V [
16] and IX [
13] in the series on statistical mechanics of adsorption. The relations were applied to molecular simulations of CO
adsorption on a spherical graphite-like adsorbent, and to CO
adsorption on a generic adsorbent with a strong interaction potential. The purpose of the generic adsorbent case was to observe size effects that were thought to possibly occur when there is significant adsorption on very small particles. The outcome was meant to give a foundation for future, similar developments. The contribution of this work is to clarify and extend the work of Hill on nanothermodynamics and provide a new application.
This paper is organized as follows: In
Section 2 we derive general thermodynamic relations for a single-component adsorbent with a single-component adsorbed phase. As the application of Hill’s nanothermodynamics is rather limited so far, we considered it necessary to recapitulate the central hypothesis and basis. Readers that are mainly interested in the operational relations and their application may skip this section. Readers that are interested in a comprehensive description of the theory and philosophy of nanothermodynamics are referred to the original work [
17] or the recent work [
15].
In
Section 3 we use the relations to derive operational equations that in turn are applied to the chosen cases. We make simplifying assumptions for the adsorbent, select a reference state typical of adsorption thermodynamics and introduce the condition of equilibrium between the film and the gas. We also derive relations for the dependence of intensive properties on size.
In
Section 4 we describe the details of the simulation setup and the methodology for the simulations and the thermodynamic analysis. In
Section 5 and
Section 6 we present and discuss the simulation results, demonstrating the size dependence of a few select thermodynamic properties. We compare the integral free energy per unit area to the differential change in free energy with respect to the change in area. These are properties that are equal in the macroscopic limit. We compare the enthalpy per molecule to the entropy per molecule times temperature, which are also properties that are equal in the macroscopic limit. Finally, in
Section 7 we make concluding remarks and propose directions for future work.
5. Results
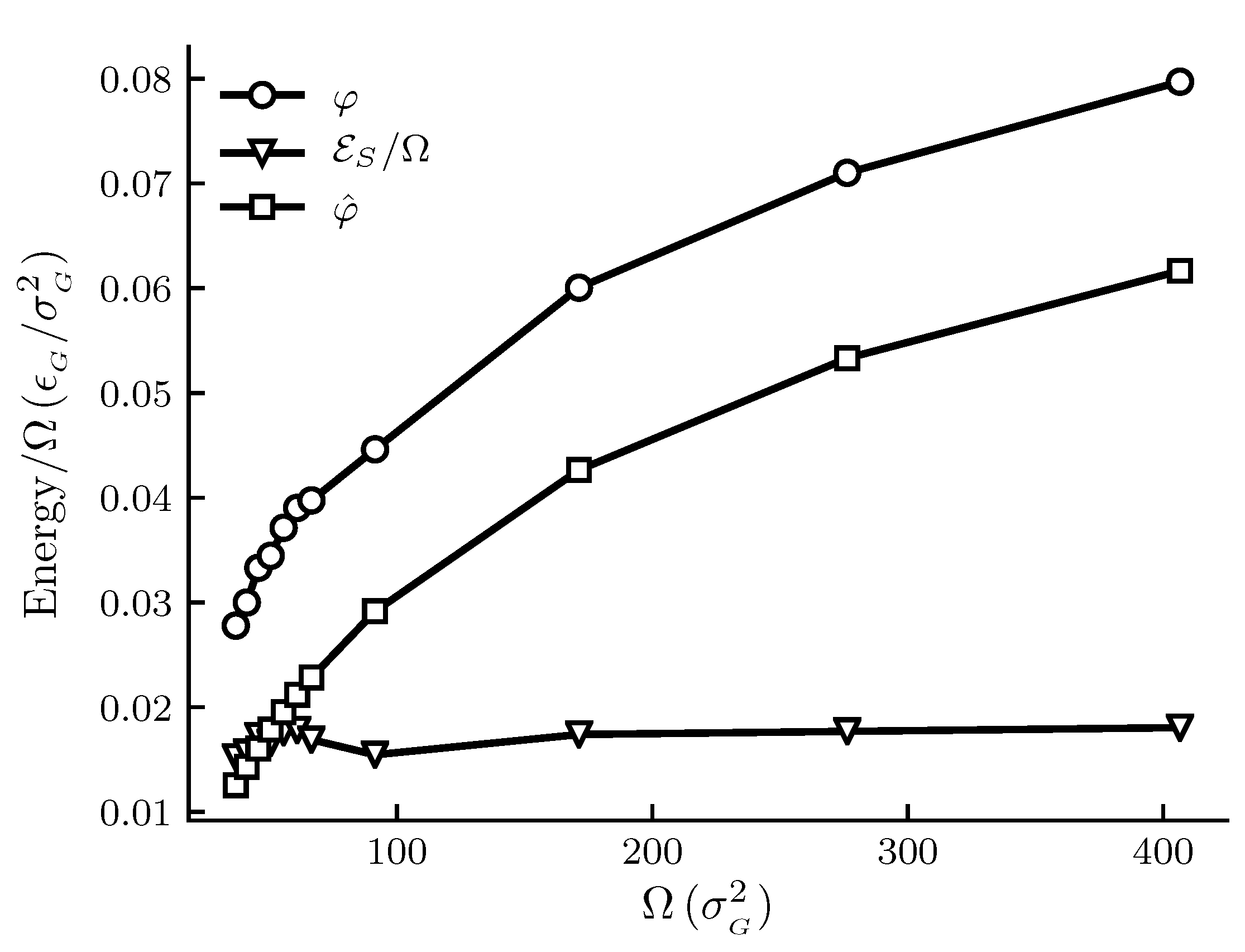
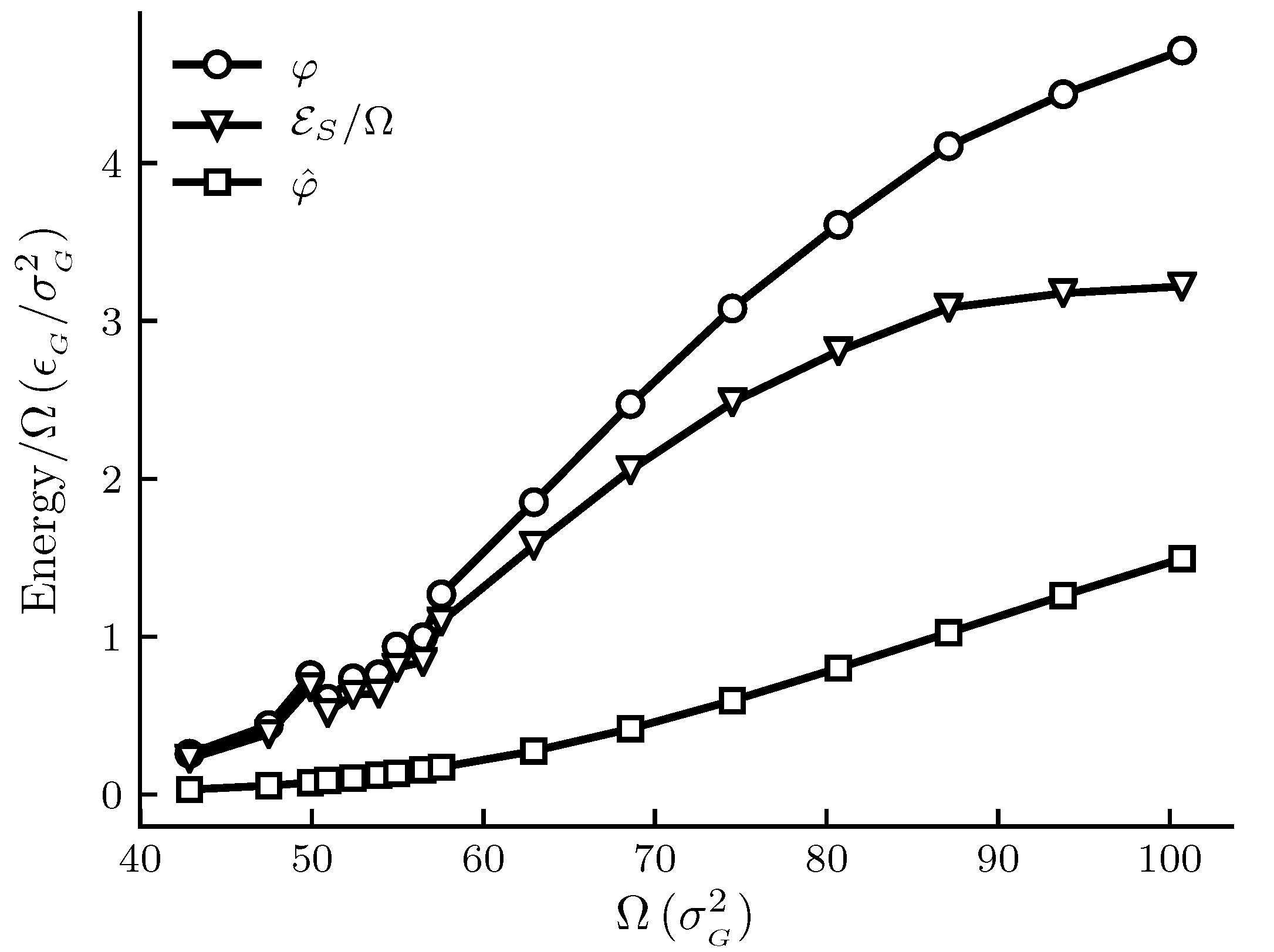
The calculated results are shown in
Figure 1,
Figure 2,
Figure 3 and
Figure 4. The figures show
,
and
and other thermodynamic properties as functions of the adsorbent area
at constant temperature and pressure. All quantities are given in reduced units.
Figure 1 and
Figure 2 are the results for the graphite adsorbent case.
Figure 3 and
Figure 4 are the results for the generic adsorbent case representing very small adsorbents with strong interaction potentials. It is clear from the figures that all properties shown depend on the system size (area). To place our experiment in context with macroscopic thermodynamics, consider an infinite flat film adsorbed on a flat adsorbent. The intensive thermodynamic properties of this film do not depend on the surface area. There is then no difference between the integral spreading pressure
and the differential spreading pressure
, and
. The results documented show that we are far away from this limit, since there is an observable difference between integral and differential properties. The systems can thus be considered as small in Hill’s sense.
Figure 1 shows how the spreading pressures,
and
, and the subdivision potential depend on system size for the graphite adsorbent case. The area range corresponds approximately to an adsorbent radius between 6 and 25 × 10
m. We can see that the trend for
and
has an initially steep increase, after which the rate of increase goes down. At the upper limit of the area range there is still a significant difference between
and
. The subdivision potential per unit area
, or the deviation from the corresponding macroscopic system, appears fairly constant; however, these results are still consistent with the theoretical prediction that
and
approaches zero in the macroscopic limit; see discussion below.
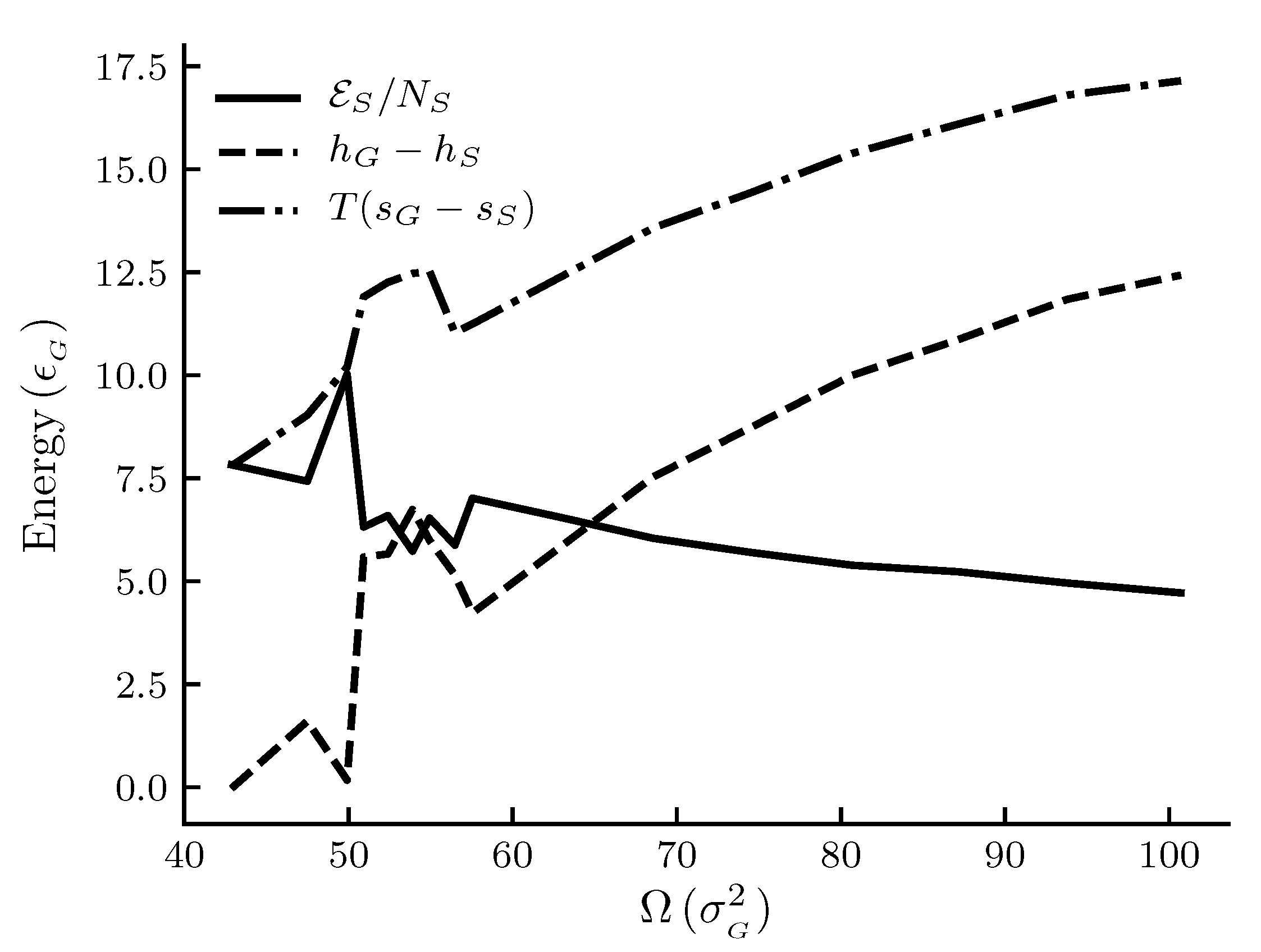
Figure 2 shows the size dependence of the entropy and the enthalpy per film molecule relative to the gas, and the difference
between the two as given by Equation (
39) for the graphite adsorbent case. We see that, in general, there is less entropy and enthalpy per film molecule as the adsorbent becomes larger. The rate at which the properties decrease with increasing size goes down. The difference
, or the deviation from the corresponding macroscopic system, decreases as the adsorbent area becomes larger. This is expected.
Figure 3 shows how the spreading pressures,
and
, and the subdivision potential depend on system size for the generic adsorbent case. We see that the general trend for all three curves is an initial increase to an inflection point, after which the rate of increase goes down. At the upper limit of the area range there is still a significant difference between
and
, and the subdivision potential per unit area
has not started to decrease towards zero at that point. However, the results are still consistent with the theoretical prediction that
and
approaches zero in the macroscopic limit; see discussion below. Special is a local deviation from the overall trend of the curves for adsorbent areas
. This is more clearly seen in the enthalpy and entropy curves of
Figure 4 for the same range of areas.
Figure 4 shows the size dependence of the entropy and the enthalpy per film molecule relative to the gas, and the difference
between the two as given by Equation (
39). We see that, in general, there is less entropy and enthalpy per film molecule as the adsorbent becomes larger. The rate at which the properties decrease with increasing size goes down. The difference
, or the deviation from the corresponding macroscopic system, decreases as the adsorbent area becomes larger. This is expected.
A local maximum in the entropy of the gas relative to the entropy of the film for adsorbent areas
is special, as is a corresponding maximum in the gas enthalpy relative to the film enthalpy. The quantities are plotted as
and
for convenience so that all quantities are positive. Thus we observed a minimum in the film entropy relative to the gas
and a minimum in the film enthalpy relative to the gas
. From the results, the areas around reduced units 55 appear special. Compared to
Figure 2 it appears that there is local deviation from the general trend in the curves for the graphite adsorbent in this range of areas, but to a much smaller extent than for the generic adsorbent. A thermodynamic analysis alone will not reveal any particular reason for such a behavior. Several explanations can be thought of, as discussed below.
6. Discussion
In the simulations we changed the size of the adsorbent while keeping the temperature and chemical potential of the gas constant. As the gas is macroscopic, this is equivalent to controlling the temperature and pressure. In effect, as long as the gas is macroscopic it is unaffected by the size of the adsorbent. In cases where the gas is no longer macroscopic, such as in confinement, the gas phase must also be treated as a small system where all three of the variables T, p and are independent.
When we increase the size of the adsorbent, there are two direct changes to the composite system: (1) the strength of the external field increases, and (2) the surface becomes less curved. For the present systems, the two changes were coupled to the size of the adsorbent, so we cannot isolate the individual effects. However, if one would like to do so, one could study different adsorbent materials at the same size.
The strength of the external field felt by an adsorbed molecule comes from integrating the pairwise sum over all atoms that would constitute the adsorbent, resulting in Equation (
55). Therefore, an increase in the field strength is analogous to the introduction of more adsorbent atoms. This leads to a larger total interaction energy for the film, but is to some extent counteracted by the fact that with increasing size, a larger fraction of the adsorbent atoms would be at a greater distance from a given adsorbed molecule. As the pair potential is inversely proportional to the separation distance by
, the greater distance leads to a plateau in the total interaction energy in the large size limit.
To further discuss the effect of the presence of the adsorbent and its size on the film, we give an illustration of four related systems divided into two groups. The first group consists of two systems that have flat surfaces, while the second group consists of two systems with curved surfaces. In each group one of the systems has the condensed phase in the presence of an adsorbent while the other has a free condensed phase. The comparison of free and adsorbed systems within a group focuses on the effects of the adsorbent, while the comparison of spherical and flat systems between the groups focuses on the effects of size. We found the analogy of the systems in the second group to the more simple systems in the first group helpful.
In the first case, consider a single-component bulk liquid with a flat surface, in equilibrium with its own vapor. The nature of this system is completely characterized by the temperature. This means that there is only one pressure for a given temperature T at which the equilibrium state can exist. If we now extend the definition of the system and let the liquid be adsorbed onto a flat adsorbent surface, the situation becomes different. If the pressure is below for the given temperature, the phase will start to evaporate. However, the evaporation will not necessarily continue until there is only gas left. This is because the evaporation will reach a point at which the field of force from the adsorbent is felt in such a way that no part of the phase maintains the properties of bulk. Beyond this point there is a non-zero free energy change associated with adsorption/desorption, and the amount of adsorbed material may adjust to satisfy the equilibrium condition while T and p remain independent. The condensed phase may therefore be in equilibrium with the vapor at pressures below .
Now consider the analogous case of a single-component spherical liquid droplet of area
in equilibrium with its own vapor. The (unstable) equilibrium state is characterized by
T and
. This means that for a given temperature and area there is only one pressure
at which the equilibrium state can exist. The equilibrium pressure
for this system is larger than
due to the curvature and the Laplace pressure. If we let the liquid be an adsorbed phase on a spherical adsorbent, as in our simulations, the situation changes again. The system has three independent variables. The equilibrium state may be characterized by
T,
and
p as in Equation (
21). Compared to the droplet at the same temperature, we set the adsorption such that the two physical systems are equal in size as characterized by
. There is one more independent variable to fix. Therefore, unlike for the droplet we have many possible equilibrium pressures for a given adsorption (as determined by
) if we let
be different in each case. In
Figure 1,
Figure 2,
Figure 3 and
Figure 4 we have many adsorptions for a given pressure because the area is different in each case. For given values of
T and
there is a limit pressure
at which bulk condensation starts. This limit becomes lower for larger
until it reaches
for a large flat adsorbent. In other words, a given adsorbent size imposes a limit on the vapor pressure required for bulk condensation. This has previously been observed with a statistical model [
28]. As the limit changes with size, this implies that a change in size of the adsorbent for
may induce bulk condensation if
drops below
p. For
there is naturally no adsorbent size that will induce bulk condensation. After bulk condensation starts, the saturation pressure decreases gradually towards
because the curvature of the growing condensed phase decreases and approaches zero.
To summarize, for the first system we only have to fix the temperature in order to fix the equilibrium state. In the second system we have, in addition, to fix the pressure. In the third system we have to fix the temperature and the area of the adsorbent. In the last system we have to fix the temperature, the area and the pressure.
For our simulations the illustration above implies that for pressures , we may have a flat and a spherical adsorbed film in equilibrium at the same temperature and pressure. They will in general have different thermodynamic properties. For instance, the adsorption differs as discussed above. By increasing the adsorbent size, the bulk condensation pressure limit approaches from above and the thermodynamic properties approach the values for a flat film. For pressures , the spherical film may be in equilibrium but there is no possible corresponding flat system because . An increase of adsorbent size may cause the bulk condensation pressure limit to pass through p, at which point the adsorption diverges.
In
Figure 1 and
Figure 3 the pressures are below
for the given temperature. We would therefore expect the curves for
and
to eventually coincide at the plateau value for a flat adsorbed film at the given temperature and pressure. This occurs when the slope of the
curve is zero, which is consistent with the relation
and Equation (
44) as
. The curve for
in
Figure 3 is s-shaped and consistent with the approach to a plateau value. According to Equation (
44), the s-shaped curve of
gives a bell-shaped curve for
, with a peak value at the inflection point of
, and ending at
. The expected curve for
would according to the relation
also have a peak before decreasing towards the plateau value of
. The same reasoning applies to
Figure 1, however the shapes of the curves are stretched out and harder to identify. Thus, although the eventual decrease in
towards zero is not observed for the limited area ranges in
Figure 1 and
Figure 3, the results are consistent with the macroscopic limit relations
and
. More experiments are needed for further confirmations.
The trends in the entropy and enthalpy curves in
Figure 2 and
Figure 4 are reasonable, when we consider the discussion above on the change in total interaction energy with size. With a larger interaction energy, the molecules are more tightly bound to the surface, and there are less possible configurations of the system available. The adsorbed phase is then more ordered, and the entropy becomes lower. In the macroscopic limit where the film is flat
and
by Equation (
39). The trends of the curves for
are consistent with this. More experiments are needed for further confirmations.
For the very small adsorbent with a strong interaction potential(cf.
Figure 4), we can observe a peak in the entropy and enthalpy, and there is a corresponding effect in
Figure 3. A minimum in the entropy of an adsorbed molecule, when plotted against the adsorption or pressure, is well known in systems where the interaction of the adsorbate with the adsorbent is strong. This is related to the decrease in the number of configurations available to the system as the first adsorption layer is filled and a subsequent increase following the initiation of adsorption in a second layer. No film density variation consistent with this was observed. The peak we see in
Figure 4 was also observed for the same areas for a range of different adsorptions, indicating that it does not have the same origin as discussed above. These were observations from curves showing the same qualitative behavior but at different pressures than the ones shown here. The start of the second layer was estimated by the location of the minimum in the entropy when plotted against the adsorption (not shown here). The local minimum we observe may thus best be related to available configurations of the system in other ways, such as the change in structure and arrangement of the molecules on the surface. The type of entropy we are showing in
Figure 4 is the entropy per molecule
(relative to the gas). As emphasized by Hill [
16], this type of entropy, as opposed to the differential entropy
is the correct one to discuss in relation to the degree of order of the adsorbed molecules. More information on the spatial arrangement of the adsorbed molecules may allow this question to be investigated further.
7. Conclusions and Perspectives
We have seen in this work how we can deal with size as a variable in a systematic manner. The common thermodynamic equations for adsorption were changed in three ways.
Using the procedure of Hill, we have calculated the integral spreading pressure from adsorption isotherm data for a fixed adsorbent size, using Equation (
46). The equation has the same form as the one usually encountered in adsorption thermodynamics, the integral form of Equation (
26) in [
13], with the important distinction that
and
in Hill’s description are not the same functions for small systems. Equation (
46) is valid for systems of any size.
Similarly, we have shown how to obtain the entropy and the enthalpy per film molecule by Equations (
36) and (
39). Equation (
36) is the same as the one usually encountered in adsorption thermodynamics, Equation (
21) in [
13], except for the important fact that the function that is kept constant when we take the derivative is now
instead of
.
This entropy is the entropy typically discussed in relation to the degree of order of the adsorbed molecules. Equation (
39) differs from the usual equation by the term
. We observe that for a small system
because
. The expressions referred to above, become the usual expressions in the macroscopic limit where
and
.
The effects of size on intensive variables is a feature of Hill’s nanothermodynamics [
17], and may be expressed in terms of
and derivatives of
by Equations (
41)–(
45). By the subdivision potential, we have a direct measure of the system smallness, and we can see from the numerical data that the value is significant in all relevant properties.
On this basis, we can suggest some possible directions for future work. The adsorbent may be modeled explicitly as a collection of atoms instead of as an integrated potential. This may allow the investigation of adsorption on a non-smooth surface with adsorption sites. By allowing the adsorbent to be compressible, it may be possible to observe how the film is affected by a phase transition in the adsorbent for different sizes. By modeling the adsorbate as all-atom molecules instead of coarse-grained particles, it may be possible to study changes in the molecular orientation and structure of adsorbing layers induced by the adsorbent size.