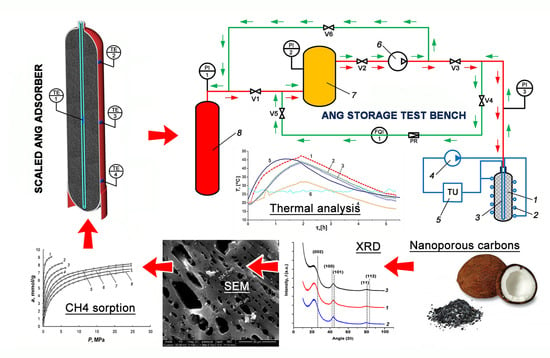
Thermodynamic Behaviors of Adsorbed Methane Storage Systems Based on Nanoporous Carbon Adsorbents Prepared from Coconut Shells
Abstract
1. Introduction
2. Materials and Methods
2.1. Adsorbent
2.2. Adsorptive
2.3. Methods
Structural Characterization of Coconut Shell (CNS)-Derived Carbon Adsorbents
- semi-automatic adsorption weight vacuum unit (from 5 Pa to 0.1 MPa, gravimetric method; the accuracy of ±1.5% with a confidence level of 0.95) [50];
- universal adsorption-dilatometer setup (0.1–6 MPa, volumetric method, the accuracy of ±3% with a confidence level of 0.95) [51];
- original volumetric-gravimetric high-pressure setup (0.2–25 MPa, the accuracy ±5% with a confidence level of 0.95) [52].
2.4. Experimental Test Bench and Approach to Study the Heat Effects of Methane Charge/Discharge Processes in the Adsorbed Natural Gas (ANG) System
3. Results and Discussion
3.1. Porous Structure of CNS-Derived Carbon Adsorbents
3.2. Morphology and Chemical Composition of CNS-Derived Carbon Adsorbents
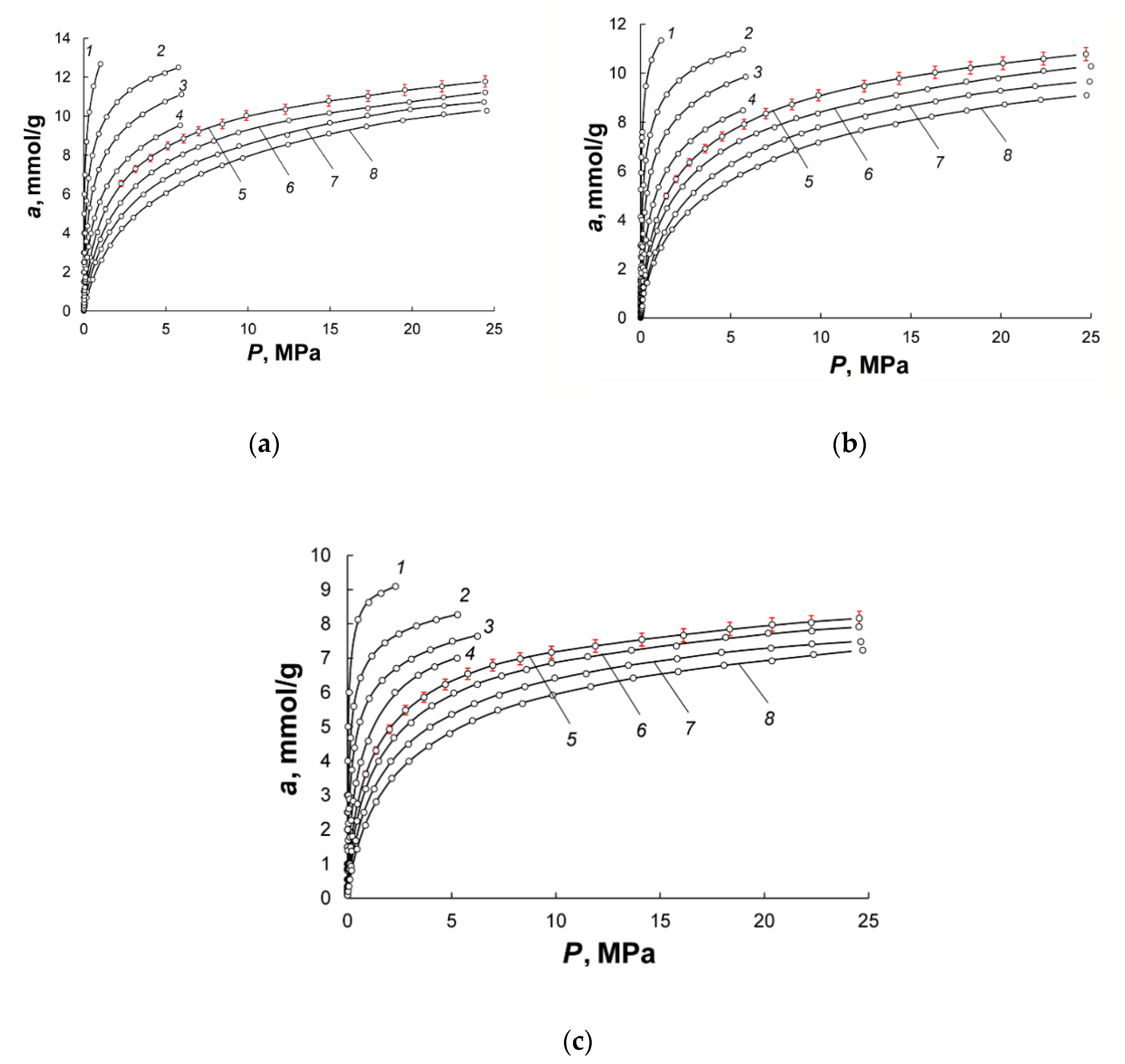
3.3. Methane Adsorption on the CNS-Derived Carbon Adsorbents
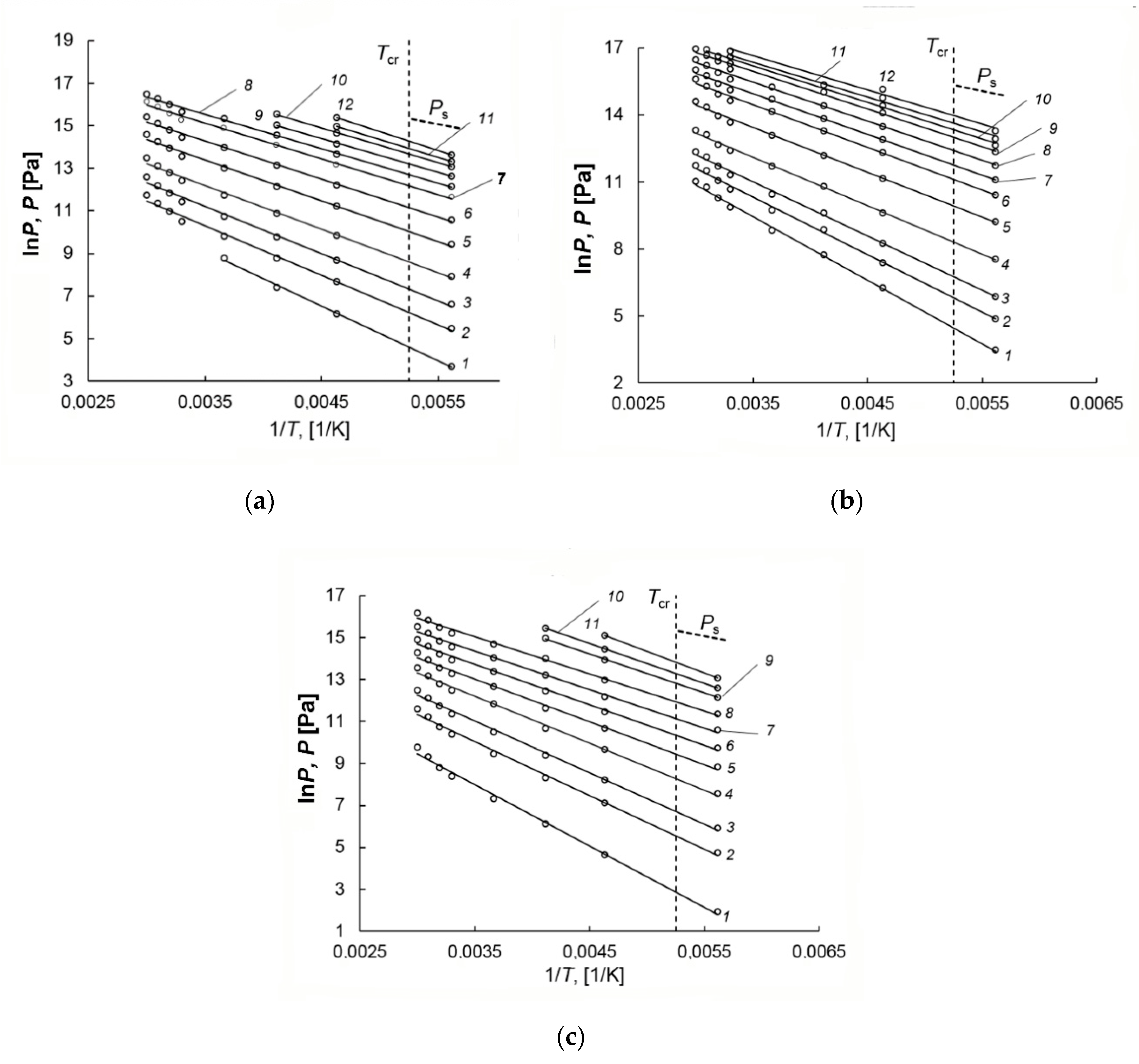
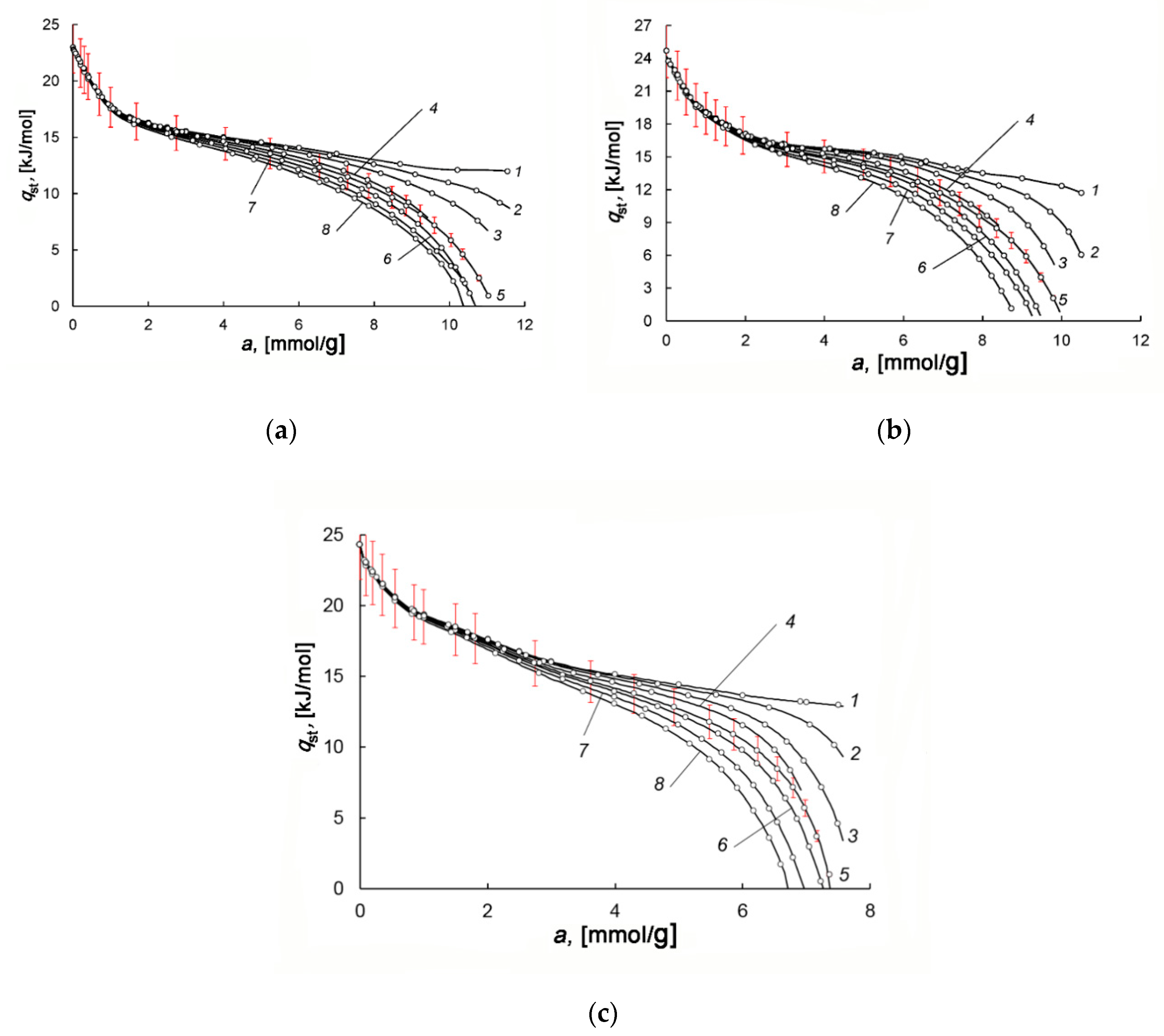
3.4. Differential Molar Isosteric Heat of Methane Adsorption on the CNS-Derived Carbon Adsorbents
3.5. Thermodynamic Characteristics of the Adsorption Storage System
3.6. Mathematical Model of the Gas Charge/Discharge Processes in the ANG System
3.7. Experimental Study of Energy and Capacity Parameters of the ANG System
- thermal insulation regime realized by thermal insulation and in the absence of forced heating and cooling. The initial period of charge and discharge proceeds under nearly adiabatic conditions;
- hermal regulation regime realized by forced cooling and heating using a coolant with a temperature close to the ambient.
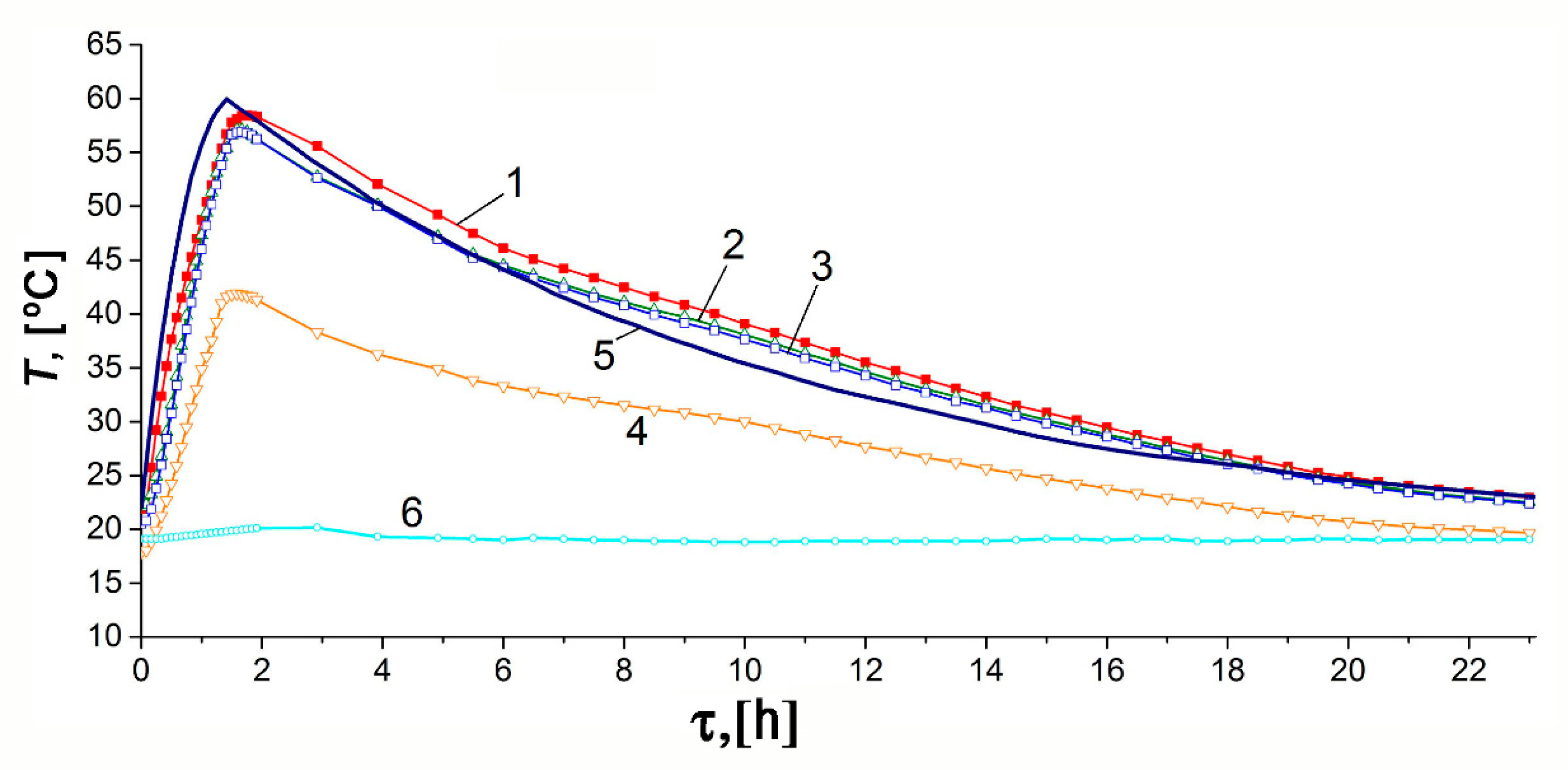
3.7.1. The Charge/Discharge Processes under the Thermal Insulation Conditions: Model and Experimental Data
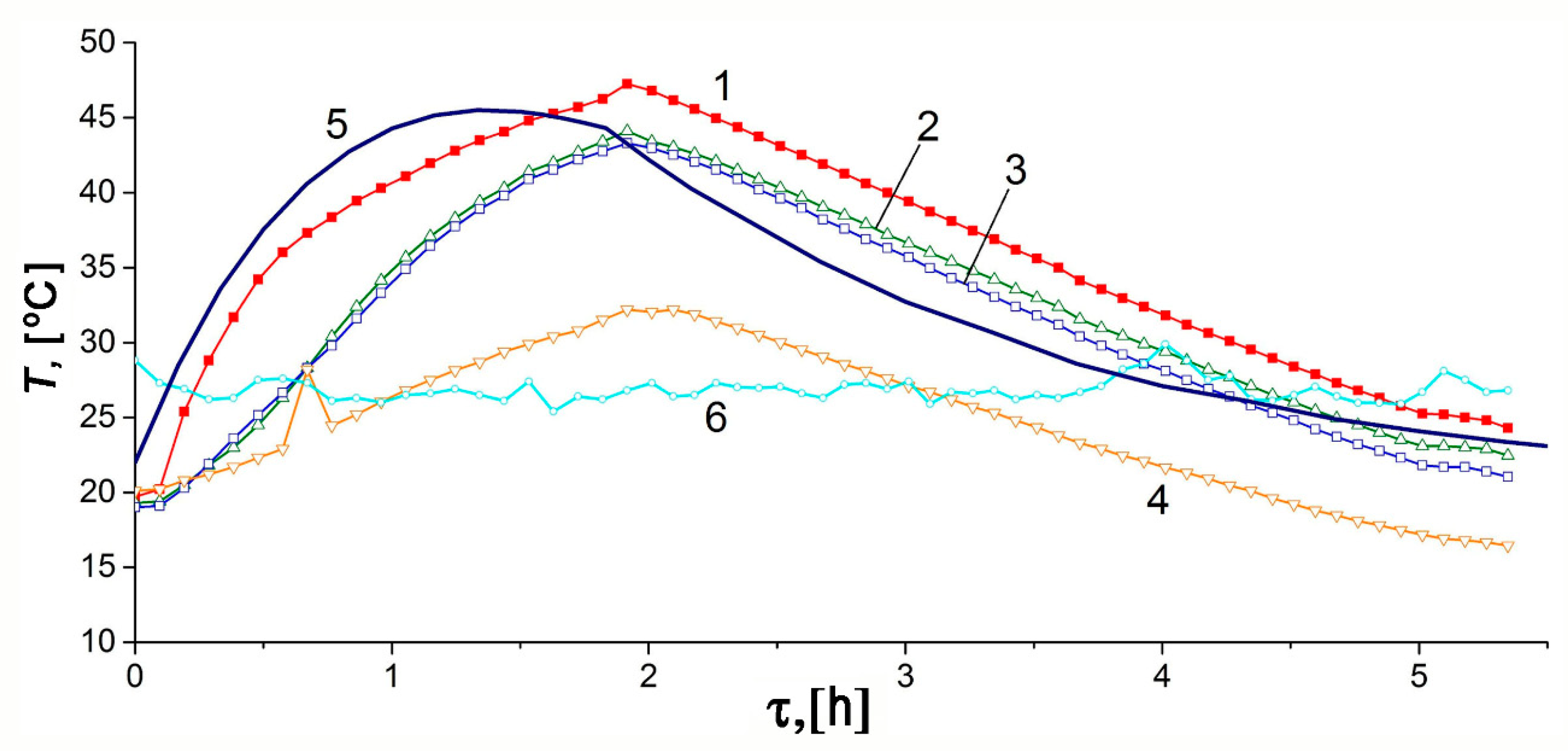
3.7.2. The Charge/Discharge of the ANG System under the Thermal Regulation Conditions: Model and Experimental Data
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Menon, V.C.; Komarneni, S. Porous Adsorbents for Vehicular Natural Gas Storage: A Review. J. Porous Mater. 1998, 5, 43–58. [Google Scholar] [CrossRef]
- Desantis, D.; Mason, J.A.; James, B.D.; Houchins, C.; Long, J.R.; Veenstra, M. Techno-economic Analysis of Metal-Organic Frameworks for Hydrogen and Natural Gas Storage. Energy Fuels. 2017, 31, 2024–2032. [Google Scholar] [CrossRef]
- Cook, T.L.; Komodromos, C.; Quinn, D.F.; Ragan, S. Adsorbent storage for natural gas vehicles. In Carbon Materials for Advanced Technologies, 1st ed.; Burchell, T.D., Ed.; Elsevier Science Ltd.: Oxford, UK, 1999; pp. 269–302. [Google Scholar]
- Broom, D.P.; Thomas, K.M. Gas adsorption by nanoporous materials: Future applications and experimental challenges. MRS Bulletin. 2014, 38, 412–421. [Google Scholar] [CrossRef]
- Tsivadze, A.Y.; Aksyutin, O.E.; Ishkov, A.G.; Men’shchikov, I.E.; Fomkin, A.A.; Shkolin, A.V.; Khozina, E.V.; Grachev, V.A. Porous carbon-based adsorption systems for natural gas (methane) storage. Russ. Chem. Rev. 2018, 87, 950–983. [Google Scholar] [CrossRef]
- Vilardi, G.; Bassano, C.; Deiana, P.; Verdone, N. Exergy and energy analysis of biogas upgrading by pressure swing adsorption: Dynamic analysis of the process. Energy Convers. Manag. 2020, 226, 113482. [Google Scholar] [CrossRef]
- Conchi, O.; Ania, C.O.; Raymundo-Piñero, E. Nanoporous Carbons with Tuned Porosity. In Nanoporous Materials for Gas Storage, 1st ed.; Kaneko, K., Rodríguez-Reinoso, F., Eds.; Springer Nature Pte Ltd.: Singapore, 2019; pp. 7–12. [Google Scholar]
- Kumar, K.V.; Preuss, K.; Titirici, M.M.; Rodríguez-Reinoso, F. Nanoporous Materials for the Onboard Storage of Natural Gas. Chem. Rev. 2017, 117, 1796–1825. [Google Scholar] [CrossRef]
- Mahmoud, E. Evolution of the Design of CH4 Adsorbents. Surfaces 2020, 3, 32. [Google Scholar] [CrossRef]
- Dubinin, M.M. Physical Adsorption of Gases and Vapors in Micropores. In Progress Surface Membrane Science, 1st ed.; Cadenhead, D.A., Danielli, J.F., Rosenberg, M.D., Eds.; Academic Press: New York, NY, USA, 1975; Volume 9, pp. 1–70. [Google Scholar]
- Anuchin, K.M.; Fomkin, A.A.; Korotych, A.P.; Tolmachev, A.M. Adsorption concentration of methane. Dependence of adsorbate density on the width of slit-shaped micropores in activated carbons. Prot. Met. Phys. Chem. Surf. 2014, 50, 173–177. [Google Scholar] [CrossRef]
- Men’shchikov, I.E.; Fomkin, A.A.; Shkolin, A.V.; Yakovlev, V.Y.; Khozina, E.V. Optimization of structural and energy characteristics of adsorbents for methane storage. Russ. Chem. Bull. 2018, 67, 1814–1822. [Google Scholar] [CrossRef]
- Fenelonov, V.B. Poristyi Uglerod (Porous Carbon); Boreskov Institute of Catalysis SB RAS: Novosibirsk, Russia, 1995; 518p. (In Russian) [Google Scholar]
- Vasiliev, L.L.; Kanonchik, L.E.; Mishkinis, D.A.; Rabetsky, M.I. Adsorbed natural gas storage and transportation vessels. Int. J. Therm. Sci. 2000, 39, 1047–1055. [Google Scholar] [CrossRef]
- Menéndez-Díaz, J.A.; Martín-Gullón, I. Types of carbon adsorbents and their production. In Activated Carbon Surfaces in Environmental Remediation, Interface Science and Technology; Bandosz, T.J., Ed.; Elsevier Science Publishing Co Inc.: San Diego, CA, USA, 2006; Volume 7, pp. 1–48. [Google Scholar]
- Ukanwa, K.S.; Patchigolla, K.; Sakrabani, R.; Anthony, E.; Mandavgane, S. A Review of Chemicals to Produce Activated Carbon from Agricultural Waste Biomass. Sustainability 2019, 11, 6204. [Google Scholar] [CrossRef]
- Park, J.E.; Lee, G.B.; Hwang, S.Y.; Kim, J.H.; Hong, B.; Kim, H.; Kim, S. The Effects of Methane Storage Capacity Using Upgraded Activated Carbon by KOH. Appl. Sci. 2018, 8, 1596. [Google Scholar] [CrossRef]
- Donald, J.; Ohtsuka, Y.; Xu, C. Effects of activation agents and intrinsic minerals on pore development in activated carbons derived from a Canadian peat. Mater. Lett. 2011, 65, 744–747. [Google Scholar] [CrossRef]
- Yan-Yan, F.; Wen, Y.; Wei, C. K2S-activated carbons developed from coal and their methane adsorption behaviors. Chin. Phys. B 2014, 23, 108201. [Google Scholar]
- Machnikowski, J.; Kierzek, K.; Lis, K.; Machnikowska, H.; Czepirski, L. Tailoring Porosity Development in Monolithic Adsorbents Made of KOH-Activated Pitch Coke and Furfuryl Alcohol Binder for Methane Storage. Energ Fuel. 2010, 10, 3410–3414. [Google Scholar] [CrossRef]
- Azevedo, D.C.; Araújo, J.C.S.; Bastos-Neto, M.; Torres, A.E.B.; Jaguaribe, E.F.; Cavalcante, C.L. Microporous activated carbon prepared from coconut shells using chemical activation with zinc chloride. Micropor. Mesopor. Mater. 2007, 100, 361–364. [Google Scholar] [CrossRef]
- Rios, R.B.; Silva, F.W.M.; Torres, A.E.B.; Azevedo, D.C.S.; Cavalcante, C.L., Jr. Adsorption of methane in activated carbons obtained from coconut shells using H3PO4 chemical activation. Adsorpt. J. 2009, 15, 271–277. [Google Scholar] [CrossRef]
- Nasri, N.S.; Sidik, H.U.; Zaini, M.A.A.; Rashid, N.M.; Majid, Z.A.; Chelliapan, S.; Kumar, T.; Zain, H.M.; Mohsin, R.; Zaini, N. Methane and Natural Gases Kinetic and Equilibrium Adsorption Comparison on Synthesised Porous Coconut Shell Kernel Activated Carbon. Chem. Eng. Trans. 2019, 72, 61–66. [Google Scholar]
- Mota, J.P. Adsorbed natural gas technology. In Recent Advances in Adsorption Processes for Environmental Protection and Security, Proceedings of the NATO Advanced Research Workshop, Kyiv, Ukraine, 9−12 September, 2006; Mota, J.P., Luibchik, S., Eds.; Springer Science+Business Media BV: Dordrecht, The Netherlands, 2008; pp. 177–192. [Google Scholar]
- Chang, K.J.; Talu, O. Behavior and performance of adsorptive natural gas storage cylinders during discharge. Appl. Therm. Eng. 1996, 16, 359–374. [Google Scholar] [CrossRef]
- Mota, J.P.B.; Saatdjian, E.; Tondeur, D. A Simulation Model of a High-Capacity Methane Adsorptive Storage System. Adsorpt. J. 1995, 1, 17–27. [Google Scholar] [CrossRef]
- Mota, J.P.B.; Rodrigues, A.E.; Saatdjian, E.; Tondeur, D. Dynamics of natural gas adsorption storage systems employing activated carbon. Carbon 1997, 35, 1259–1270. [Google Scholar] [CrossRef]
- Babenko, V.A.; Kanonchik, L.E. Mathematical modeling of a cylinder with a sorbent and natural gas. J. Eng. Phys. Therm. 2000, 73, 516–527. [Google Scholar] [CrossRef]
- Khorashadizadeh, M.; Shahrak, M.N.; Shahsavand, A. Reliable modeling of discharge process for adsorbed natural gas storage tanks. Korean J. Chem. Eng. 2014, 31, 1994–2002. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, Q.; Gu, A.; Lu, X. Experimental studies of the performance of adsorbed natural gas storage system during discharge. Appl. Therm. Eng. 2004, 25, 591–601. [Google Scholar] [CrossRef]
- Ridha, F.N.; Yunus, R.M.; Rashid, M.; Ismail, A.F. Thermal analysis of adsorptive natural gas storages during dynamic charge phase at room temperature. Exper. Therm. Fluid Sci. 2007, 32, 14–22. [Google Scholar] [CrossRef]
- Feroldi, M.; Neves, A.C.; Borba, C.E.; Alves, H.J. Methane storage in activated carbon at low pressure under different temperatures and flow rates of charge. J. Clean. Prod. 2018, 172, 921–926. [Google Scholar] [CrossRef]
- Strizhenov, E.M.; Chugaev, S.S.; Zherdev, A.A. Mathematical model of the process of circuit charging of an adsorption methane storage system. Chem. Pet. Eng. 2019, 54, 760–770. [Google Scholar] [CrossRef]
- Vasil’ev, L.L.; Kanonchik, L.E.; Mishkinis, D.A.; Rabetskii, M.I. Adsorption Systems of Natural Gas Storage and Transportation at Low Pressures and Temperatures. J. Eng. Thermophys. Rus. 2003, 76, 987–995. [Google Scholar] [CrossRef]
- Saez, A.; Toledo, M. Thermal effect of the adsorption heat on an adsorbed natural gas storage. Appl. Therm. Eng. 2008, 29, 2617–2623. [Google Scholar] [CrossRef]
- Ybyraiymkul, D.; Ng, K.C.; Kaltayev, A. Experimental and numerical study of effect of thermal management on storage capacity of the adsorbed natural gas vessel. Appl. Therm. Eng. 2017, 125, 523–531. [Google Scholar] [CrossRef]
- Strizhenov, E.M.; Zherdev, A.A.; Petrochenko, R.V.; Zhidkov, D.A.; Kuznetsov, R.A.; Chugaev, S.S.; Podchufarov, A.A.; Kurnasov, D.V. A Study of Methane Storage Characteristics of Compacted Adsorbent AU-1. Chem. Pet. Eng. 2017, 52, 838–845. [Google Scholar] [CrossRef]
- Strizhenov, E.M.; Zherdev, A.A.; Podchufarov, A.A.; Chugaev, S.S.; Kuznetsov, R.A.; Zhidkov, D.A. Capacity and thermodynamic nomograph for an adsorption methane storage system. Chem. Pet. Eng. 2016, 51, 812–818. [Google Scholar] [CrossRef]
- Chugaev, S.S.; Strizhenov, E.M.; Zherdev, A.A.; Kuznetsov, R.A.; Podchufarov, A.A.; Zhidkov, D.A. Fire- and Explosion-Safe Low-Temperature Filling of an Adsorption Natural Gas Storage System. Chem. Pet. Eng. 2017, 52, 846–854. [Google Scholar] [CrossRef]
- Chkhaidze, E.V.; Fomkin, A.A.; Serpinskii, V.V.; Tsitsishvili, G.V.; Dubinin, M.M. Methane adsorption on a microporous carbon adsorbent in the precritical and hypercritical regions. Russ. Chem. Bull. 1986, 35, 847–849. [Google Scholar] [CrossRef]
- Strizhenov, E.M.; Fomkin, A.A.; Zherdev, A.A.; Pribylov, A.A. Adsorption of methane on AU-1 microporous carbon adsorbent. Prot. Met. Phys. Chem. Surf. 2012, 48, 614–619. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A.; Tsivadze, A.Y.; Anuchin, K.M.; Men’shchikov, I.E.; Pulin, A.L. Experimental Study and Numerical Modeling: Methane Adsorption in Microporous Carbon Adsorbent over the Subcritical and Supercritical Temperature Regions. Prot. Met. Phys. Chem. Surf. 2016, 52, 955–963. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A.; Men’shchikov, I.E.; Strizhenov, E.M.; Pulin, A.L.; Khozina, E.V. Monolithic microporous carbon adsorbent for low-temperature natural gas storage. Adsorption 2019, 25, 1559–1573. [Google Scholar] [CrossRef]
- ISO 697:1981. Surface Active Agents. Washing Powders. Determination of Apparent Density. Method by Measuring the Mass of a Given Volume; International Organization for Standardization: Geneva, Switzerland, Publication date: 1981–2003.
- ISO 60:1977. Plastics. Determination of Apparent Density of Material that can be Poured from a Specified Funnel; International Organization for Standardization: Geneva, Switzerland, 1977–2008.
- Sychev, V.V.; Vasserman, A.A.; Zagoruchenko, V.A.; Kozlov, A.D.; Spiridonov, G.A.; Tzymarnyi, V.A. Thermodynamic Properties of Methane; Izd. Standartov: Moscow, Russia, 1979; 349p. (In Russian) [Google Scholar]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Kiselev, A.V. New Adsorption Method for the Determination of Surface of Adsorbent. Uspekhi Khimii 1945, XVI, 367–394. (In Russian) [Google Scholar]
- Ravikovitch, P.I.; Vishnyakov, A.; Russo, R.; Neimark, A.V. Unified approach to pore size characterization of microporous carbonaceous materials from N2, Ar, and CO2 adsorption isotherms. Langmuir 2000, 16, 2311–2320. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A.; Pulin, A.L.; Yakovlev, V.Y. A technique for measuring an adsorption-induced deformation. Instrum. Exp. Tech. 2008, 51, 150–155. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Shkolin, A.V.; Men’shchikov, I.E.; Pulin, A.L.; Pribylov, A.A.; Smirnov, I.A. Measurement of adsorption of methane at high pressures for alternative energy systems. J. Meas. Tech. 2016, 58, 1387–1391. [Google Scholar] [CrossRef]
- Pribylov, A.A.; Serpinskii, V.V.; Kalashnikov, S.M. Adsorption of gases by microporous adsorbents under pressures up to hundreds of megapascals. Zeolites 1991, 11, 846–849. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Seliverstova, I.I.; Serpinskii, V.V. Determination of the parameters of the microprobe structure of solid adsorbents. Communication 1. Method of determination of the specific volume of totally microporous adsorbents. Russ. Chem. Bull. 1986, 35, 256–259. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Oliver, J.P.; Rodrigues-Reinoso, F.; Rouquerol, J.; Sing, K. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Achaw, O.-W.; Afrane, G. The evolution of pore structure of coconut shells during the preparation of coconut shell-based activated carbons. Micropor. Mesopor. Mat. 2008, 112, 284–290. [Google Scholar] [CrossRef]
- Marsh, H.; Rodríguez-Reinoso, F. SEM and TEM Images of Structures in Activated Carbons in Activated Carbon, 1st ed.; Elsevier Ltd.: London, UK, 2006; pp. 366–382. [Google Scholar]
- Leman, A.S.; Shahidan, S.; Senin, M.S.; Hannan, N.I.R.R. A preliminary study on chemical and physical properties of coconut shell powder as a filler in concrete. IRIS IOP Conf. Ser. Mater. Sci. Eng. 2016, 160, 012059. [Google Scholar] [CrossRef]
- Rutman, A.M.; Skakov, Y.A. Radial distribution functions of atoms and interference functions of partly ordered carbon materials. I. Influence of edge atoms of disperse layers. Sov. Phys. Cryst. 1989, 34, 338–341. [Google Scholar]
- Fujimoto, H. Theoretical X-ray scattering intensity of carbons with turbostratic stacking and AB stacking structures. Carbon 2003, 41, 1585–1592. [Google Scholar] [CrossRef]
- Shiryaev, A.A.; Voloshchuk, A.M.; Volkov, V.V.; Averin, A.A.; Artamonova, S.D. Nanoporous active carbons at ambient conditions: A comparative study using X-ray scattering and diffraction, Raman spectroscopy and N2 adsorption. IOP J. Phys. Conf. Ser. 2017, 848, 012009. [Google Scholar] [CrossRef]
- Guinier, A. La diffraction des rayons X aux tres petits angles: Application a l’etude de phenomenes ultramicroscopiques. Ann. Phys. 1939, 11, 161–237. [Google Scholar] [CrossRef]
- Bakaev, V.A. The statistical thermodynamics of adsorption equilibriums in the case of zeolites. Dokl. Acad. Nauk SSSR Dokl.Chem. Engl. Transl. 1966, 167, 369–372. [Google Scholar]
- Tolmachev, A.M. Adsorption of Gases, Vapors, and Solutions: I. Thermodynamics of Adsorption. Prot. Met. Phys. Chem. Phys. Surf. 2010, 46, 955–963. [Google Scholar] [CrossRef]
- Bering, B.P.; Zhukovskaya, E.G.; Rakhmukov, B.K.; Serpinskii, V.V. Adsorption in micropores. Communication 1. Theoretical aspects. Izv. Akademii Nauk SSSR Ser. Khim. 1967, 8, 1656–1659. (In Russian) [Google Scholar]
- Bering, B.P.; Zhukovskaya, E.G.; Rakhmukov, B.K.; Serpinskii, V.V. Adsorption in micropores. Communication 2. Experimental isosteres of adsorption. Izv. Akademii Nauk SSSR Ser. Khim. 1967, 16, 1662–1669. [Google Scholar]
- Bering, B.P.; Zhukovskaya, E.G.; Rakhmukov, B.K.; Serpinskii, V.V. Adsorption in micropores. Communication 3. Methods of calculation of parameters of adsorption equilibrium. Izv. Akademii Nauk SSSR Ser. Khim. 1968, 17, 30–36. [Google Scholar]
- Barrer, R.M.; Papadopoulos, R. The sorption of krypton and xenon in zeolites at high pressures and temperatures I. Chabazite. Proc. Roy. Soc. Lond. Ser.A, Math Phys. Sci. 1972, 326, 315–330. [Google Scholar]
- Fomkin, A.A. Adsorbzija Ar na Zeolite NaX. In Adsorbzija v Mikroporach; Dubinin, M.M., Serpinsky, V.V., Eds.; Nauka: Moscow, Russia, 1983; pp. 98–99. [Google Scholar]
- Fomkin, A.A. Adsorption of Gases, Vapors and Liquids by Microporous Adsorbents. Adsorption 2005, 11, 425–436. [Google Scholar] [CrossRef]
- Bülow, M.; Shen, D.; Jale, S. Measurement of sorption equilibria under isosteric conditions: The principles, advantages and limitations. Appl. Surf. Sci. 2002, 196, 157–172. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Pribylov, A.A.; Tkachev, A.G.; Memetov, N.R.; Melezhik, A.V.; Kucherova, A.E.; Shubin, I.N.; Shkolin, A.V.; Men’shchikov, I.E.; Pulin, A.L.; et al. Methane Adsorption in Microporous Carbon Adsorbent with a Bimodal Pore Size Distribution. Prot. Met. Phys. Chem. Surf. 2020, 56, 1–5. [Google Scholar] [CrossRef]
- Potapov, S.V.; Fomkin, A.A.; Sinitsyn, V.A.; Shkolin, A.V. Xenon Adsorption on Microporous Adsorbents At Higher Pressures. Prot. Met. Phys. Chem. Surf. 2010, 46, 644–647. [Google Scholar] [CrossRef]
- Fomkin, A.A.; Serpinsky, V.V.; Bering, B.P. Investigation of the adsorption of xenon on NaX zeolite within a broad range of pressures and temperatures. Russ. Chem. Bull. 1975, 24, 1147–1150. [Google Scholar] [CrossRef]
- Bakaev, V.A. One possible formulation of the thermodynamics of sorption equilibrium. Bull. Acad. Sci. USSR Div. Chem. Sci. 1971, 20, 2516–2520. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A. Thermodynamics of methane adsorption on the microporous carbon adsorbent ACC. Russ. Chem. Bull. 2008, 57, 1799–1805. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A. Measurement of Carbon-Nanotube Adsorption of Energy-Carrier Gases for Alternative Energy Systems. Meas. Techn. 2018, 61, 395–401. [Google Scholar] [CrossRef]
- Bakaev, V.A. Molecular Theory of Physical Adsorption. Ph.D. Thesis, Moscow State University, Moscow, Russia, May 1990. (In Russian). [Google Scholar]
- Novikova, S.I. Teplovoe Rasshirenie Tverdykh Tel (Heat Expansion of Solids); Nauka: Moscow, Russia, 1974; p. 293. (In Russian) [Google Scholar]
- Dunne, J.A.; Rao, M.; Sircar, S.; Gorte, R.J.; Myers, A.L. Calometric Heats of Adsorption and Adsorption Isotherms. 2. O2, N2, Ar, CO2, CH4, C2H6, and SF6 on NaX, H-ZSM-5, and Na-ZSM-5 Zeolites. Langmuir 1996, 12, 5896–5904. [Google Scholar] [CrossRef]
- Sircar, S.; Mohr, R.; Ristic, C.; Rao, M.B. Isosteric Heat of Adsorption: Theory and Experiment. J. Phys. Chem. B 1999, 103, 6539–6546. [Google Scholar] [CrossRef]
- Men’shchikov, I.E.; Shkolin, A.V.; Khozina, E.V.; Fomkin, A.A. Thermodynamics of Adsorbed Methane Storage Systems Based on Peat-Derived Activated Carbons. Nanomaterials. 2020, 10, 1379. [Google Scholar] [CrossRef]
- Tykodi, R.J.; Aston, J.G.; Schreiner, G.D.L. Thermodynamic Properties of Neon Adsorbed on Titanium Dioxide. J. Am. Chem. Soc. 1955, 77, 2168–2171. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A.; Potapov, S.V. Thermodynamics of krypton adsorption on microporous carbon adsorbent at high pressures. Russ. Chem. Bull. 2017, 66, 607–613. [Google Scholar] [CrossRef]










| Sample | W0, cm3/g | x0, nm | E0, kJ/mol | SBET, m2/g | WS, cm3/g | Wmeso, cm3/g | d, g/L | ∆, mm | Ω, wt.% |
|---|---|---|---|---|---|---|---|---|---|
| AC-90S | 0.64 | 0.58 */0.79 ** | 20.1 */15.1 ** | 1470 | 0.66 | 0.02 | 380 | 0.7−1.1 | 65 |
| AC-90L | 0.54 | 0.56 */0.64 ** | 21.6 */18.8 ** | 1270 | 0.55 | 0.01 | 465 | 0.9−2.4 | 60 |
| AC-60L | 0.44 | 0.59 | 20.3 | 1020 | 0.44 | 0.00 | 530 | 1.9−3.0 | 48 |
| Sample | C | O | K |
|---|---|---|---|
| AC-90S | 92.0 | 6.0 | 2.0 |
| AC-90L | 93.0 | 6.5 | 0.5 |
| AC-60L | 96.0 | 3.5 | 0.5 |
| Parameters and Indicators of the Discharge Process | Discharge Conditions | |
|---|---|---|
| Thermal Insulation | Thermal Regulation | |
| Initial pressure, MPa | 9.94 | 10.04 |
| Initial adsorber temperature (TE1 reading), °C | 22.7 | 20.9 |
| Final pressure, MPa | 0.1 | 0.1 |
| Final temperature after the termination of the discharge cycle (TE1 reading), °C | 24.2 | 24.5 |
| Delivered natural gas (experimental), m3 (STP) | 14.8 | 15.2 |
| Delivered natural gas (model), m3(STP) | 15.7 | 15.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men’shchikov, I.E.; Shkolin, A.V.; Strizhenov, E.M.; Khozina, E.V.; Chugaev, S.S.; Shiryaev, A.A.; Fomkin, A.A.; Zherdev, A.A. Thermodynamic Behaviors of Adsorbed Methane Storage Systems Based on Nanoporous Carbon Adsorbents Prepared from Coconut Shells. Nanomaterials 2020, 10, 2243. https://doi.org/10.3390/nano10112243
Men’shchikov IE, Shkolin AV, Strizhenov EM, Khozina EV, Chugaev SS, Shiryaev AA, Fomkin AA, Zherdev AA. Thermodynamic Behaviors of Adsorbed Methane Storage Systems Based on Nanoporous Carbon Adsorbents Prepared from Coconut Shells. Nanomaterials. 2020; 10(11):2243. https://doi.org/10.3390/nano10112243
Chicago/Turabian StyleMen’shchikov, Ilya E., Andrey V. Shkolin, Evgeny M. Strizhenov, Elena V. Khozina, Sergey S. Chugaev, Andrey A. Shiryaev, Anatoly A. Fomkin, and Anatoly A. Zherdev. 2020. "Thermodynamic Behaviors of Adsorbed Methane Storage Systems Based on Nanoporous Carbon Adsorbents Prepared from Coconut Shells" Nanomaterials 10, no. 11: 2243. https://doi.org/10.3390/nano10112243
APA StyleMen’shchikov, I. E., Shkolin, A. V., Strizhenov, E. M., Khozina, E. V., Chugaev, S. S., Shiryaev, A. A., Fomkin, A. A., & Zherdev, A. A. (2020). Thermodynamic Behaviors of Adsorbed Methane Storage Systems Based on Nanoporous Carbon Adsorbents Prepared from Coconut Shells. Nanomaterials, 10(11), 2243. https://doi.org/10.3390/nano10112243