The Thermoelectric Properties of Monolayer MAs2 (M = Ni, Pd and Pt) from First-Principles Calculations
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussions
3.1. Crystal and Electronic Structures
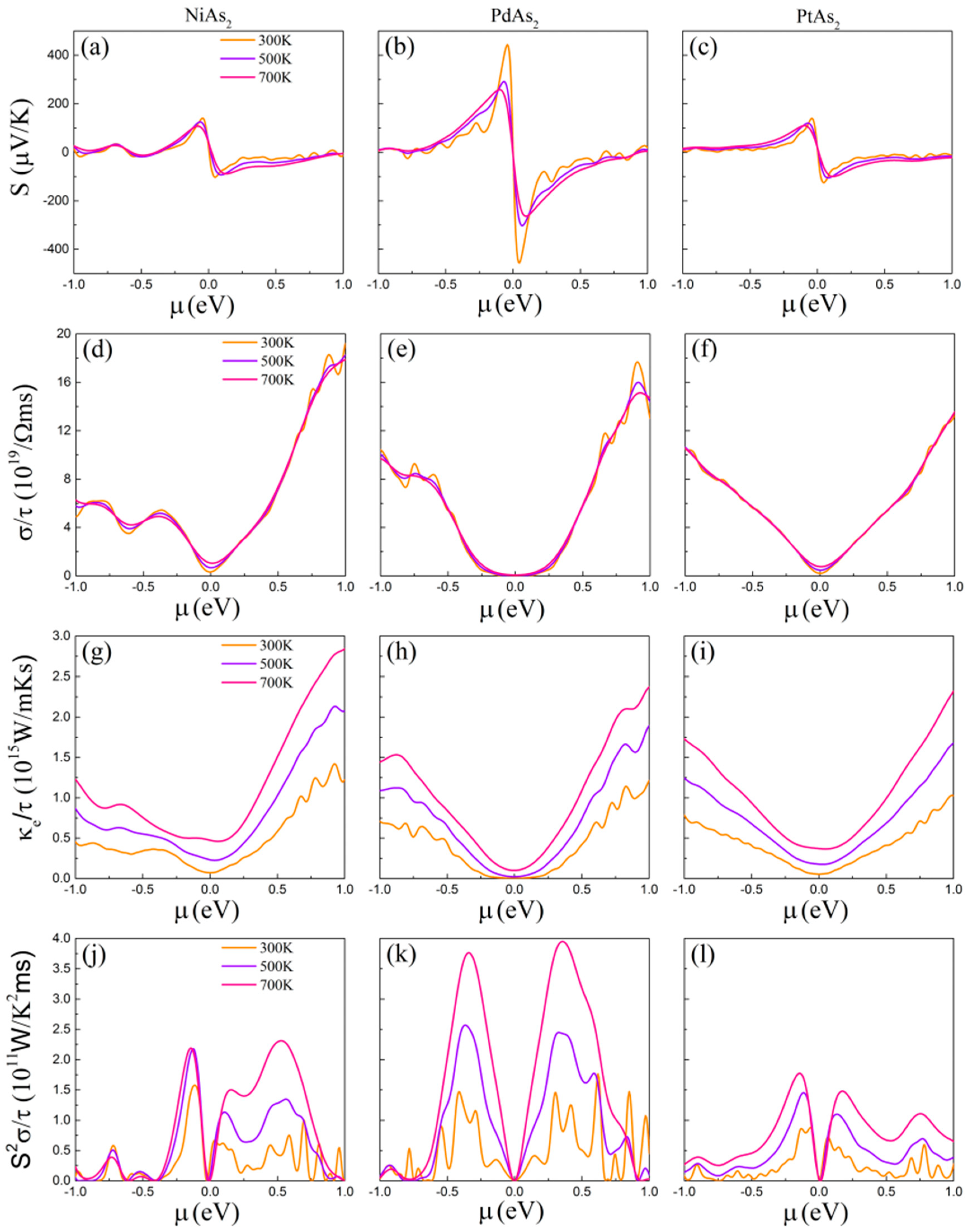
3.2. Electrical Transport Properties
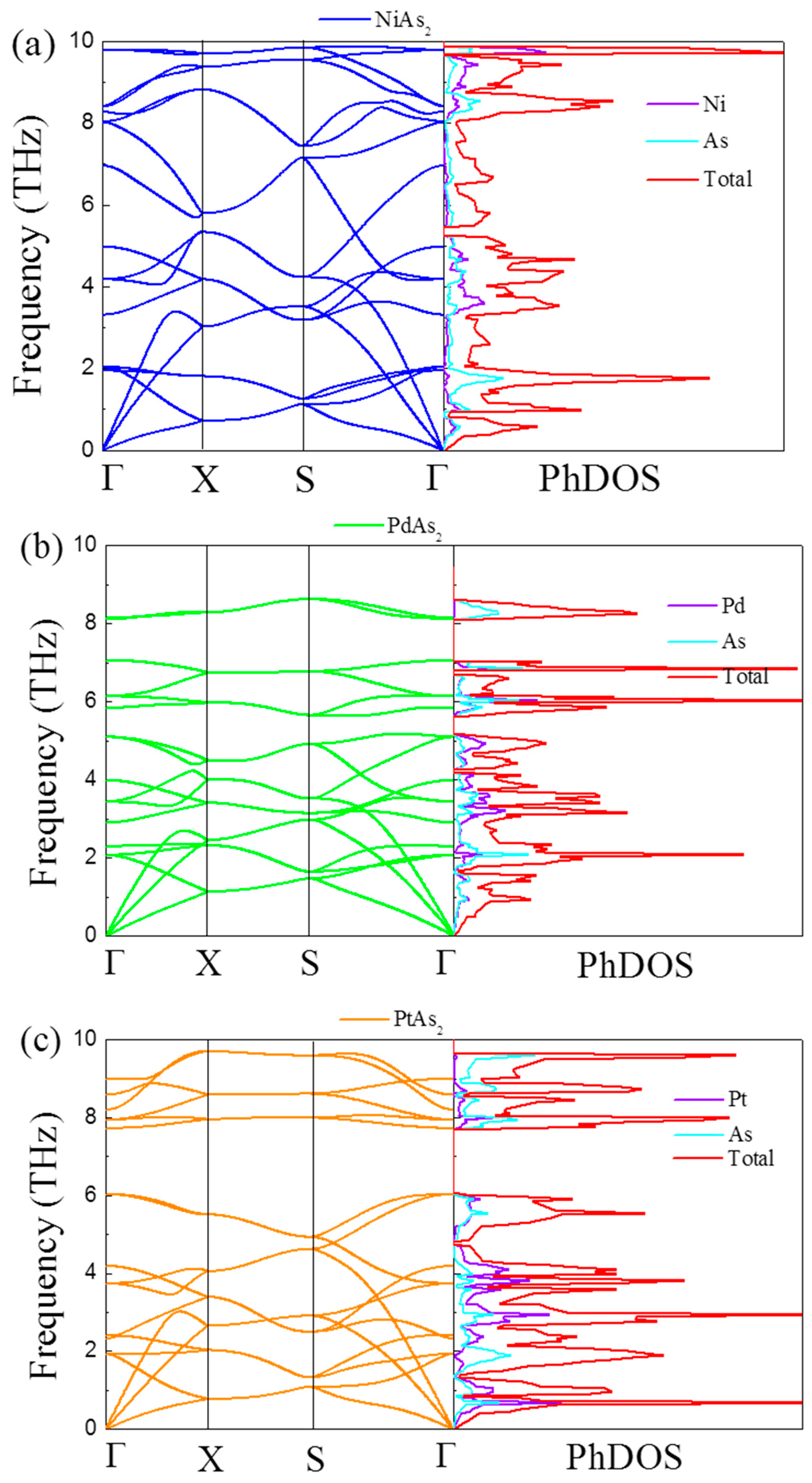
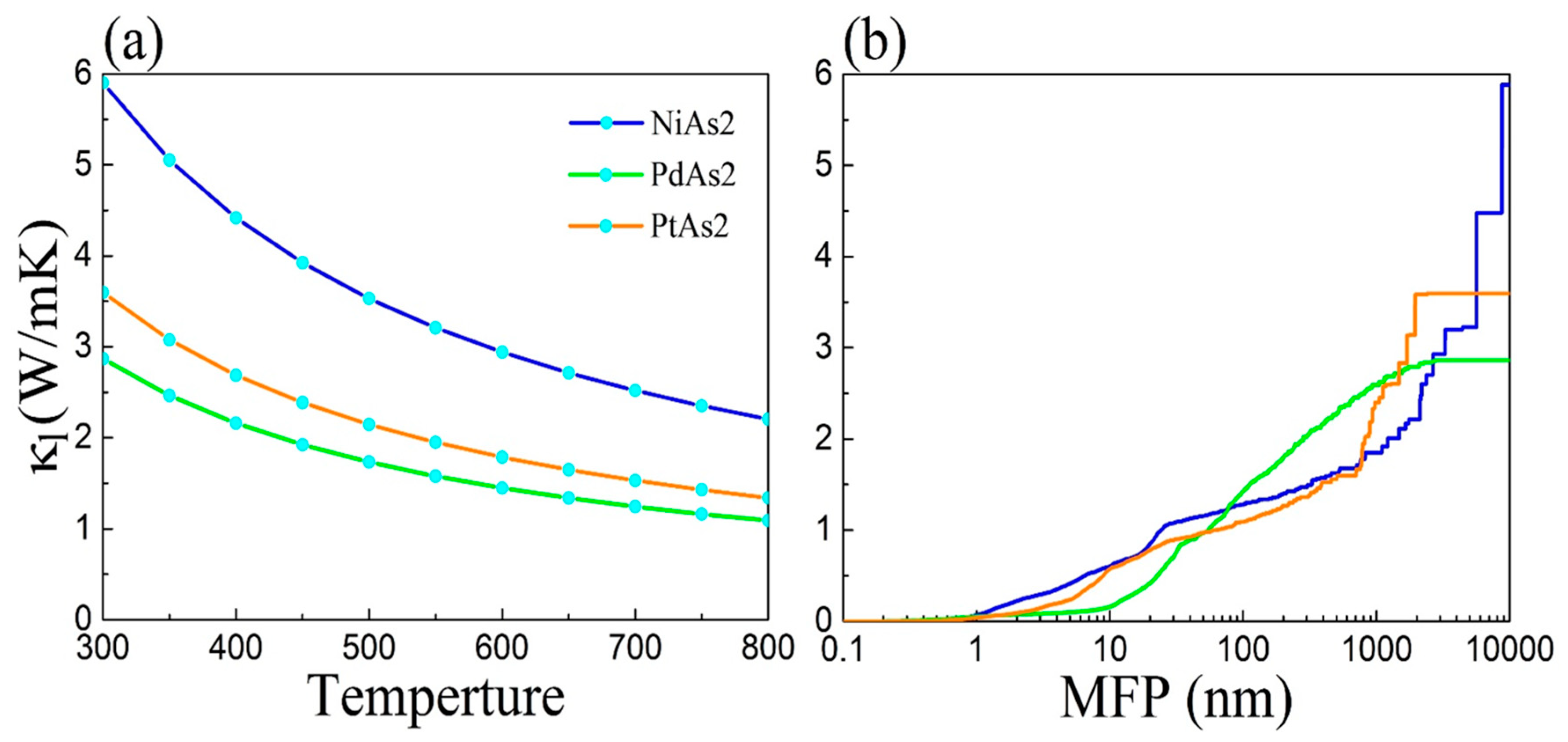
3.3. Thermal Transport Properties
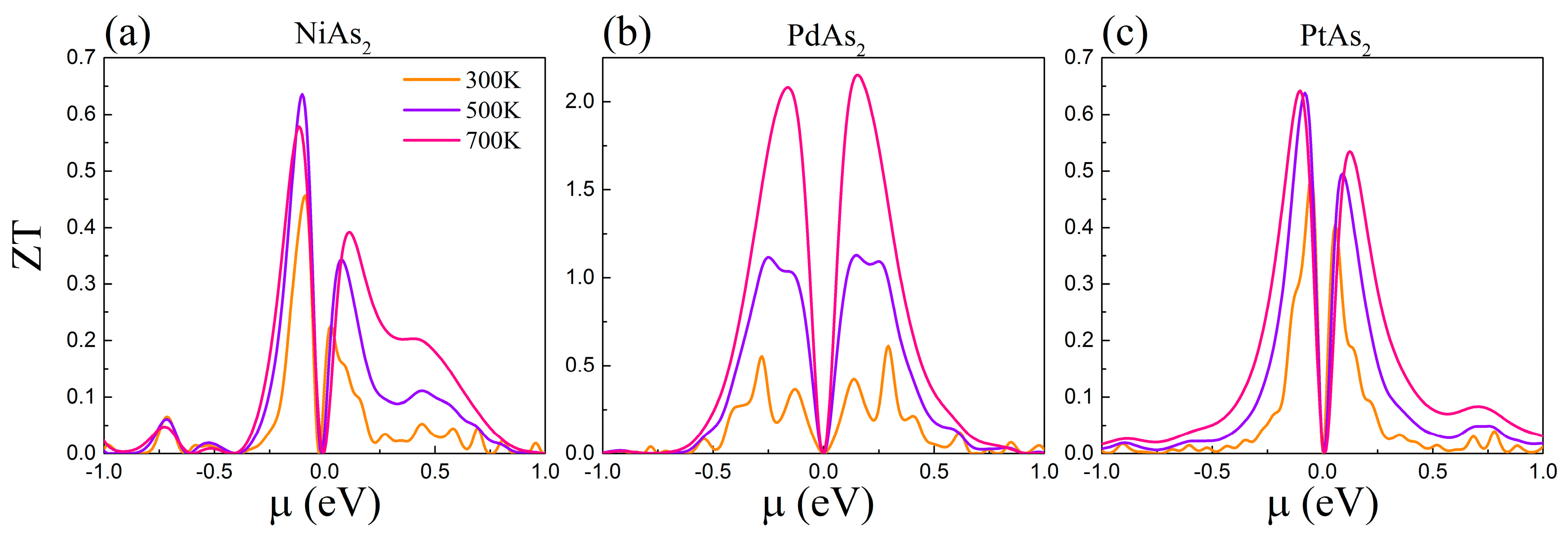
3.4. Thermoelectric Figure of Merit (ZT)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Disalvo, F.J. Thermoelectric cooling and power generation. Science 1999, 285, 703–706. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Tritt, T. Advances in thermoelectric materials research: Looking back and moving forward. Science 2017, 357, eaak9997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, X.; Liu, P.; Zhang, J.; Zhang, P.; Zhou, W.-X.; Xie, G.; Wang, B. Monolayer SnP3: An excellent p-type thermoelectric material. Nanoscale 2019, 11, 19923–19932. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; de la Mata, M.; Li, Z.; Belarre, F.J.; Arbiol, J.; Khor, K.A.; Poletti, D.; Zhu, B.; Yan, Q.; Xiong, Q. Enhanced thermoelectric performance of solution-derived bismuth telluride based nanocomposites via liquid-phase Sintering. Nano Energy 2016, 30, 630–638. [Google Scholar] [CrossRef]
- Tang, L.P.; Tang, L.M.; Geng, H.; Yi, Y.P.; Wei, Z.; Chen, K.Q.; Deng, H.X. Tuning transport performance in two-dimensional metal-organic framework semiconductors: Role of the metal d band. Appl. Phys. Lett. 2018, 112, 1–6. [Google Scholar] [CrossRef]
- Pei, Y.; Wang, H.; Snyder, G. Band Engineering of Thermoelectric Materials. Adv. Mater. 2012, 24, 6125–6135. [Google Scholar] [CrossRef]
- Dun, C.; Hewitt, C.A.; Li, Q.; Guo, Y.; Jiang, Q.; Xu, J.; Marcus, G.; Schall, D.C.; Carroll, D.L. Self-Assembled Heterostructures: Selective Growth of Metallic Nanoparticles on V2–VI3 Nanoplates. Adv. Mater. 2017, 29, 1–8. [Google Scholar] [CrossRef]
- Zeng, Y.-J.; Wu, D.; Cao, X.-H.; Zhou, W.-X.; Tang, L.-M.; Chen, K.-Q. Nanoscale Organic Thermoelectric Materials: Measurement, Theoretical Models, and Optimization Strategies. Adv. Funct. Mater. 2020, 30, 1903873. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Bo, T.; Zhu, X.; Wang, Z.; Wu, J.; Li, Y.; Wang, B.T. Two-dimensional tetragonal Ti2BN: A novel potential anode material for Li-ion batteries. Appl. Surf. Sci. 2020, 513, 145821. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Bo, T.; Zhang, J.; Lu, Z.; Wang, Z.; Li, Y.; Wang, B.T. Novel two-dimensional tetragonal vanadium carbides and nitrides as promising materials for Li-ion batteries. Phys. Chem. Chem. Phys. 2019, 21, 19513–19520. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An unexplored 2D semiconductor with a high hole mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Medrano Sandonas, L.; Teich, D.; Gutierrez, R.; Lorenz, T.; Pecchia, A.; Seifert, G.; Cuniberti, G. Anisotropic Thermoelectric Response in Two-Dimensional Puckered Structures. J. Phys. Chem. 2016, 120, 18841–18849. [Google Scholar] [CrossRef]
- Sun, X.; Cronin, S.B.; Liu, J.; Wang, K.L.; Koga, T.; Dresselhaus, M.S.; Chen, G. Experimental study of the effect of the quantum well structures on the thermoelectric figure of merit in Si/Si1-xGex system. In Proceedings of the 18th International Conference on Thermoelectrics, Baltimore, MD, USA, 29 August–2 September 1999; pp. 652–655. [Google Scholar]
- Hicks, L.D.; Harman, T.C.; Dresselhaus, M.S. Use of quantum-well superlattices to obtain a high figure of merit from nonconventional thermoelectric materials. Appl. Phys. Lett. 1993, 63, 3230–3232. [Google Scholar] [CrossRef]
- Sun, X.; Dresselhaus, M.S.; Wang, K.L.; Tanner, M.O. Effect of quantum-well structures on the thermoelectric figure of merit in the Si/Si1−xGex system. MRS Online Proc. Libr. Arch. 1997, 452, 261–266. [Google Scholar] [CrossRef]
- Li, Z.W. Thermoelectric properties of carbon nanotube/silicone rubber composites. J. Exp. Nanosci. 2017, 12, 188–196. [Google Scholar] [CrossRef]
- Imae, I.; Kataoka, H.; Harima, Y. Flexible thermoelectric materials based on conducting polymers doped with silicone polymer electrolyte. Mol. Cryst. Liq. Cryst. 2019, 685, 100–106. [Google Scholar] [CrossRef]
- Kou, L.; Chen, C.; Smith, S.C. Phosphorene: Fabrication, Properties, and Applications. J. Phys. Chem. Lett. 2015, 6, 2794–2805. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Liu, H.J.; Cheng, L.; Wei, J.; Liang, J.H.; Fan, D.D.; Shi, J.; Tang, X.F.; Zhang, Q.J. Phosphorene nanoribbon as a promising candidate for thermoelectric applications. Sci. Rep. 2014, 4, 1–8. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Shao, H.; Ni, G.; Li, J.; Lu, H.; Zhang, R.; Peng, B.; Zhu, Y.; Zhu, H.; et al. First-principles study on the electronic, optical, and transport properties of monolayer α- and β-GeSe. Phys. Rev. 2017, 96, 245421. [Google Scholar] [CrossRef] [Green Version]
- Jeong, G.; Jaung, Y.H.; Kim, J.; Song, J.Y.; Shin, B. Sn1-xSe thin films with low thermal conductivity: Role of stoichiometric deviation in thermal transport. J. Mater. Chem. 2018, 6, 10083–10087. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef] [Green Version]
- Shao, Y.; Shao, M.; Kawazoe, Y.; Shi, X.; Pan, H. Exploring new two-dimensional monolayers: Pentagonal transition metal borides/carbides (penta-TMB/Cs). J. Mater. Chem. 2018, 6, 10226–10232. [Google Scholar] [CrossRef]
- Liu, H.; Qin, G.; Lin, Y.; Hu, M. Disparate strain dependent thermal conductivity of two-dimensional penta-structures. Nano Lett. 2016, 16, 3831–3842. [Google Scholar] [CrossRef]
- Shojaei, F.; Hahn, J.R.; Kang, H.S. Electronic structure and photocatalytic band offset of few-layer GeP2. J. Mater. Chem. 2017, 5, 22146–22155. [Google Scholar] [CrossRef]
- Qian, S.; Sheng, X.; Xu, X.; Wu, Y.; Lu, N.; Qin, Z.; Feng, E.; Huang, W.; Zhou, Y.; Zhang, C.; et al. Penta-MX2(M = Ni, Pd and Pt, X = P and As) monolayers: Direct band-gap semiconductors with high carrier mobility. J. Mater. Chem. 2019, 7, 3569–3575. [Google Scholar] [CrossRef]
- Kresse, G.; Marsman, M.; Furthmüller, J. Vienna Ab initio Simulation Package (VASP), The Guide. In Computational Materials Physics; Faculty of Physics, Universität Wien: Vienna, Austria, 2014. [Google Scholar]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. Condens Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. 1981, 23, 5048–5079. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.-C.; Qin, G.; Fang, W.-Z.; Cui, H.-J.; Zheng, Q.-R.; Yan, Q.-B.; Su, G. Tinselenidene: A Two-dimensional Auxetic Material with Ultralow Lattice Thermal Conductivity and Ultrahigh Hole Mobility. Sci. Rep. 2016, 6, 19830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bardeen, J.; Shockley, W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72. [Google Scholar] [CrossRef]
- Chaput, L.; Pécheur, P.; Scherrer, H. Thermopower, Hall tensor, and relaxation time approximation for elemental zinc. Phys. Rev. 2007, 75, 1–5. [Google Scholar] [CrossRef]
- Yuan, H.; Li, Z.; Yang, J. Atomically thin semiconducting penta-PdP2 and PdAs2 with ultrahigh carrier mobility. J. Mater. Chem. 2018, 6, 9055–9059. [Google Scholar] [CrossRef]
- Pan, X.L.; Zhao, Y.Q.; Zeng, Z.Y.; Chen, X.R.; Chen, Q.F. Electronic, elastic, optical and thermal transport properties of penta-PdAs2 monolayer: First-principles study. Solid State Commun. 2020, 307, 113802. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, G.; Zhang, Y.W. Polarity-Reversed Robust Carrier Mobility in Monolayer MoS2 Nanoribbons. J. Am. Chem. Soc. 2014, 136, 6269–6275. [Google Scholar] [CrossRef] [Green Version]
- Lan, Y.-S.; Chen, X.-R.; Hu, C.-E.; Cheng, Y.; Chen, Q.-F. Penta-PdX2 (X = S, Se, Te) monolayers: Promising anisotropic thermoelectric materials. J. Mater. Chem. 2019, 7, 11134–11142. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, Y.-Q.; Zeng, Z.-Y.; Chen, X.-R.; Geng, H.-Y. Anisotropic thermoelectric properties of Weyl semimetal NbX (X = P and As): A potential thermoelectric material. Phys. Chem. Chem. Phys. 2019, 21, 15167–15176. [Google Scholar] [CrossRef]
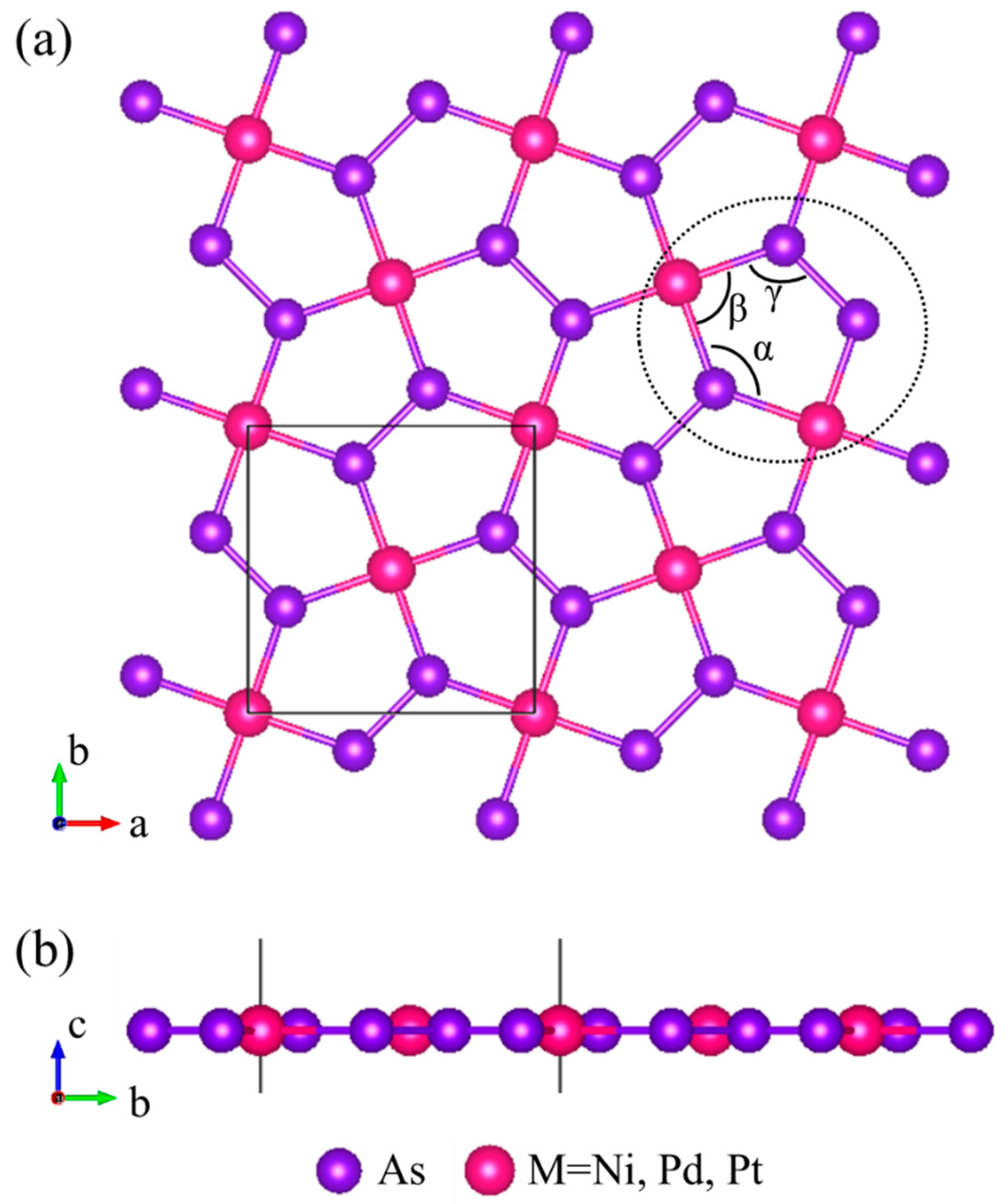
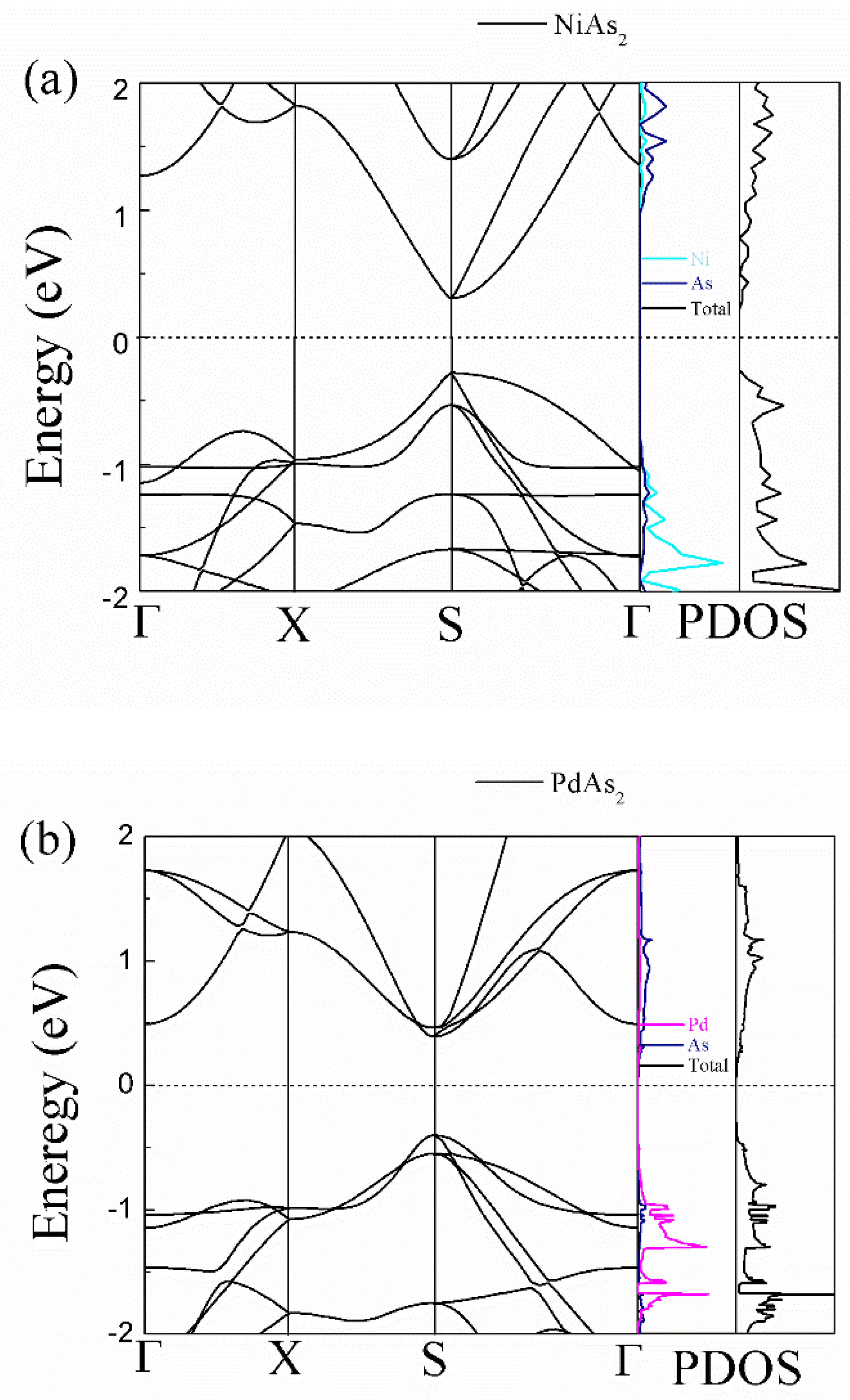
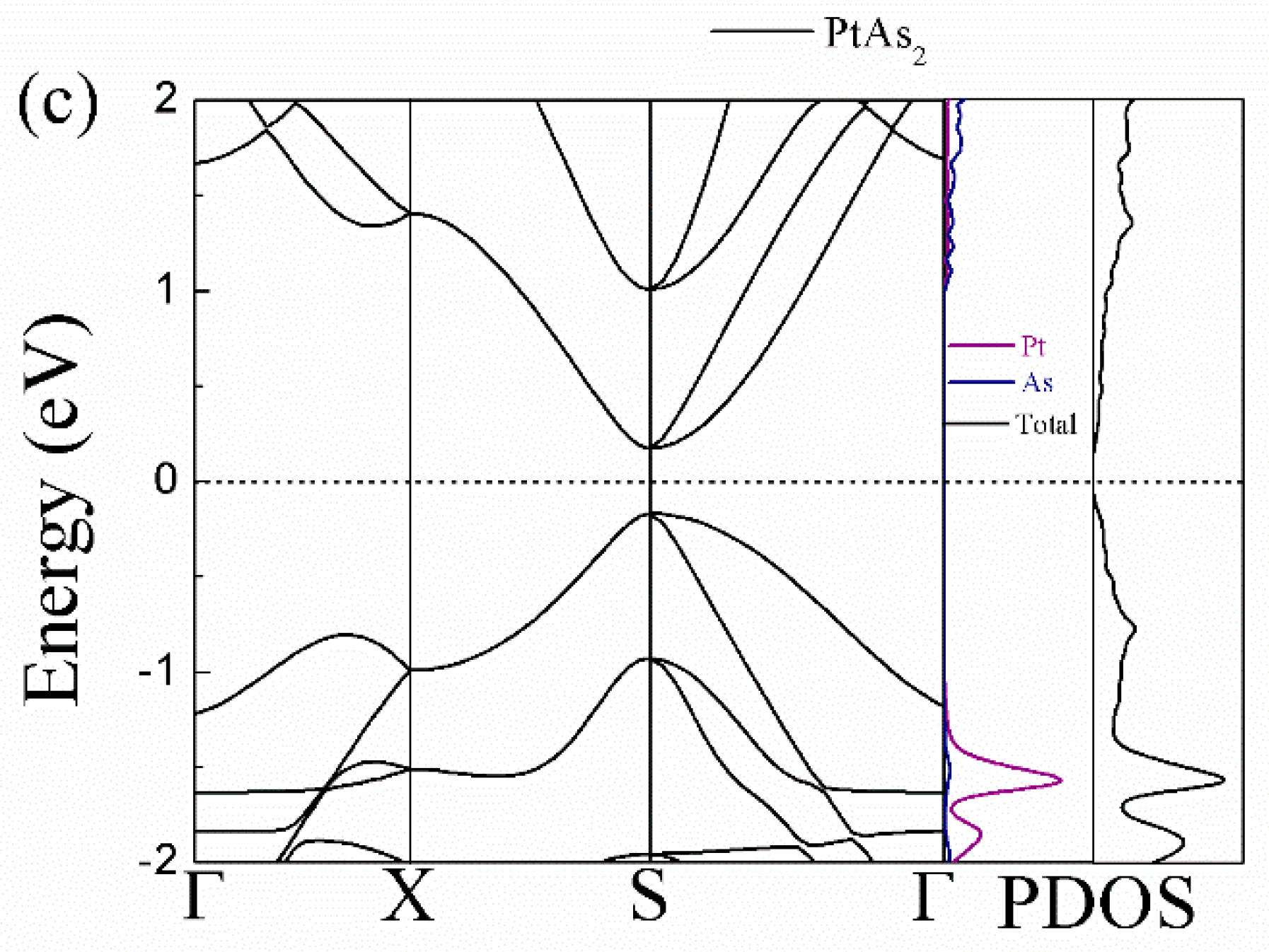

| LC (Å) | α (deg) | β (deg) | γ (deg) | |
|---|---|---|---|---|
| NiAs2 | 5.89 | 132.64 | 90 | 113.68 |
| PdAs2 | 6.19 | 129.39 | 90 | 115.30 |
| PtAs2 | 6.16 | 129.78 | 90 | 115.11 |
| Carriers Type | El (eV) | C2D (J/m2) | m*/m0 | μ (104 cm2/Vs) | τ (ps) | |
|---|---|---|---|---|---|---|
| NiAs2 | electorn | 2.2 | 100 | 0.14 | 1.47 | 1.17 |
| hole | 1.68 | 100 | 0.16 | 1.93 | 1.76 | |
| PdAs2 | electorn | 1.52 | 93 | 0.21 | 1.27 | 1.51 |
| hole | 0.69 | 93 | 0.09 | 34.27 | 1.75 | |
| PtAs2 | electorn | 1.41 | 117 | 0.07 | 17.07 | 6.79 |
| hole | 2.33 | 117 | 0.08 | 4.80 | 2.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Q.-L.; Yang, H.-Y.; Wu, Y.-Y.; Liu, Y.-B.; Li, Y.-H. The Thermoelectric Properties of Monolayer MAs2 (M = Ni, Pd and Pt) from First-Principles Calculations. Nanomaterials 2020, 10, 2043. https://doi.org/10.3390/nano10102043
Wei Q-L, Yang H-Y, Wu Y-Y, Liu Y-B, Li Y-H. The Thermoelectric Properties of Monolayer MAs2 (M = Ni, Pd and Pt) from First-Principles Calculations. Nanomaterials. 2020; 10(10):2043. https://doi.org/10.3390/nano10102043
Chicago/Turabian StyleWei, Qiang-Lin, Heng-Yu Yang, Yi-Yuan Wu, Yi-Bao Liu, and Yu-Hong Li. 2020. "The Thermoelectric Properties of Monolayer MAs2 (M = Ni, Pd and Pt) from First-Principles Calculations" Nanomaterials 10, no. 10: 2043. https://doi.org/10.3390/nano10102043





