Depth-Sensing Indentation as a Micro- and Nanomechanical Approach to Characterisation of Mechanical Properties of Soft, Biological, and Biomimetic Materials
Abstract
1. Introduction
2. Depth-Sensing Indentation: Conventional Approaches
2.1. DSI by Sharp Indenters: The BASh Formula and the Oliver–Pharr Approach
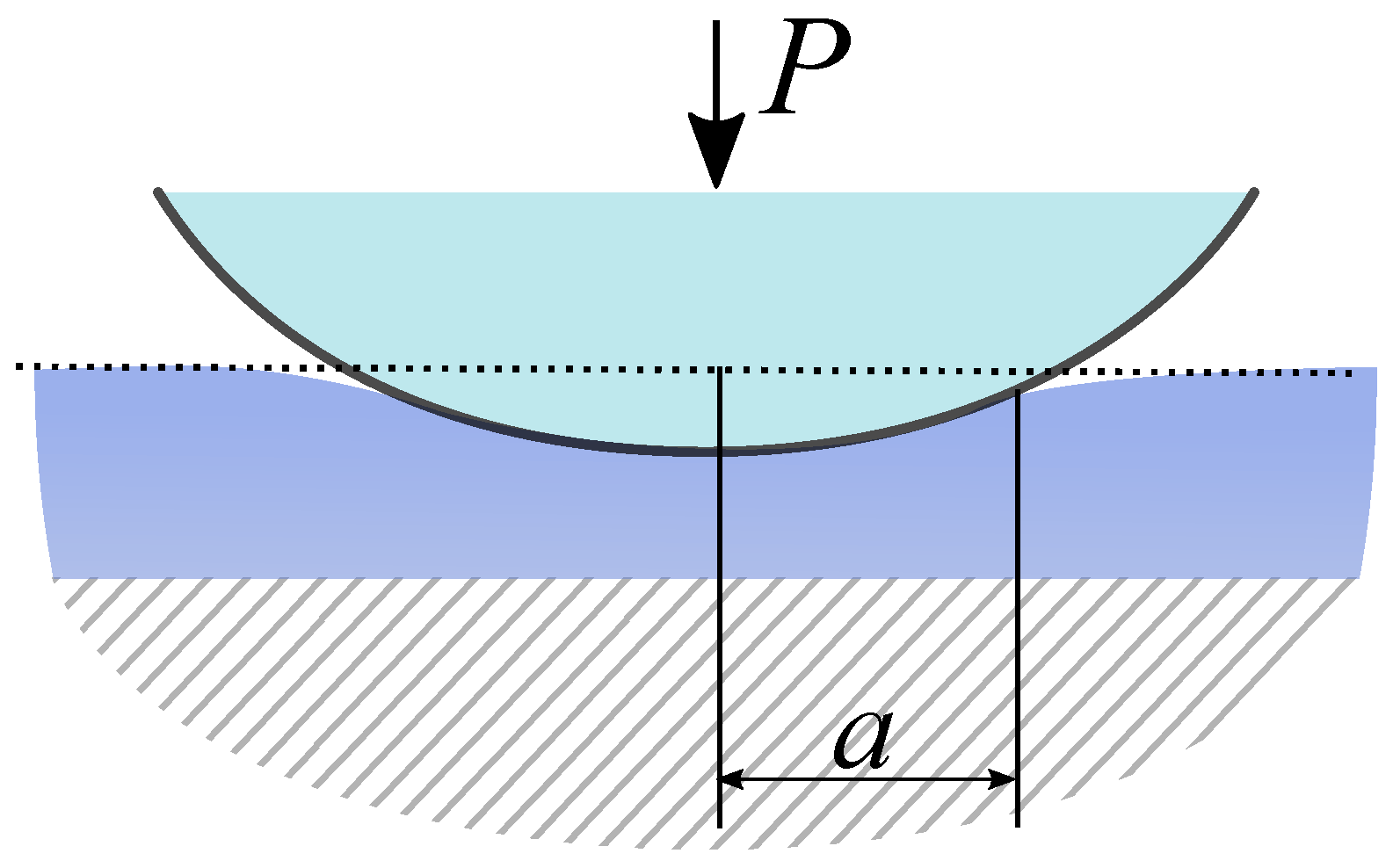
2.2. Adhesion in Depth-Sensing Indentation, and the Conventional Use of Spherical Indenters
3. The BG Method
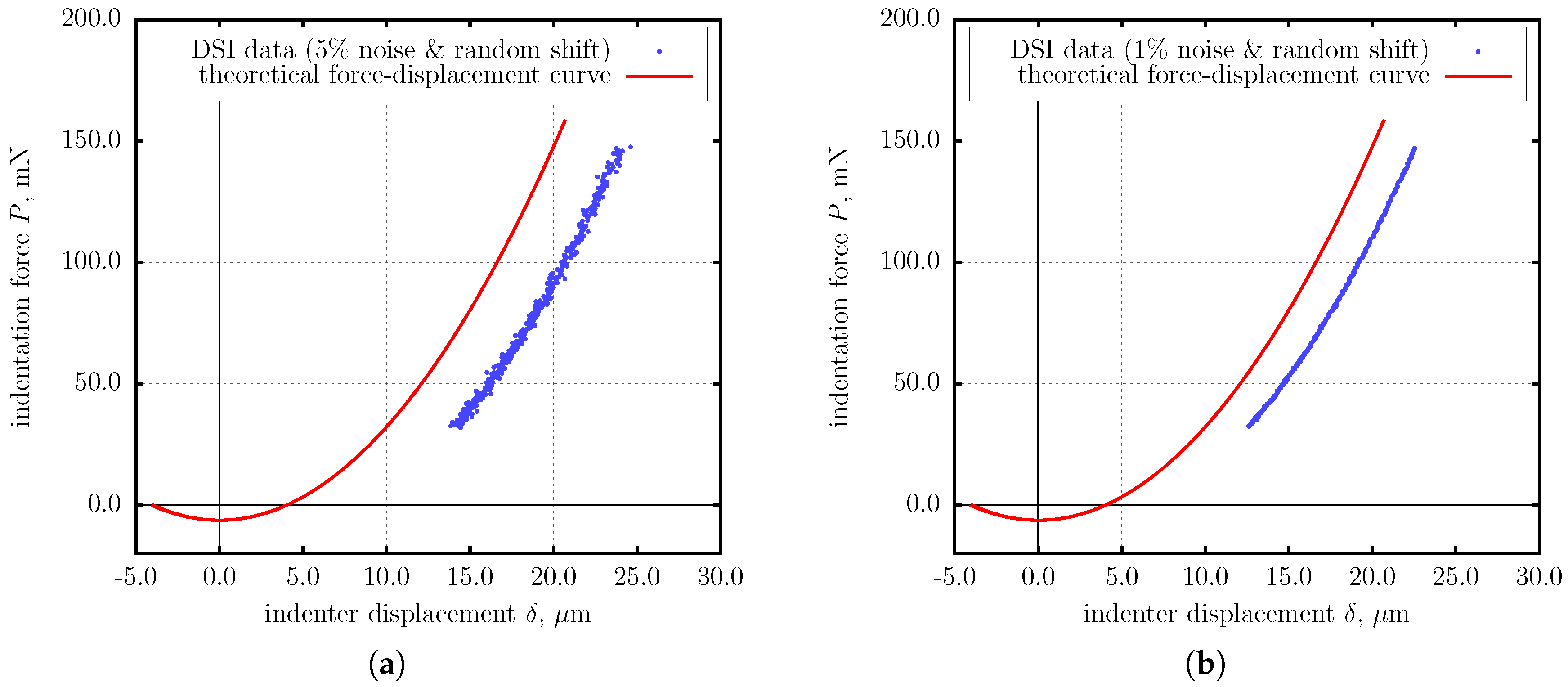
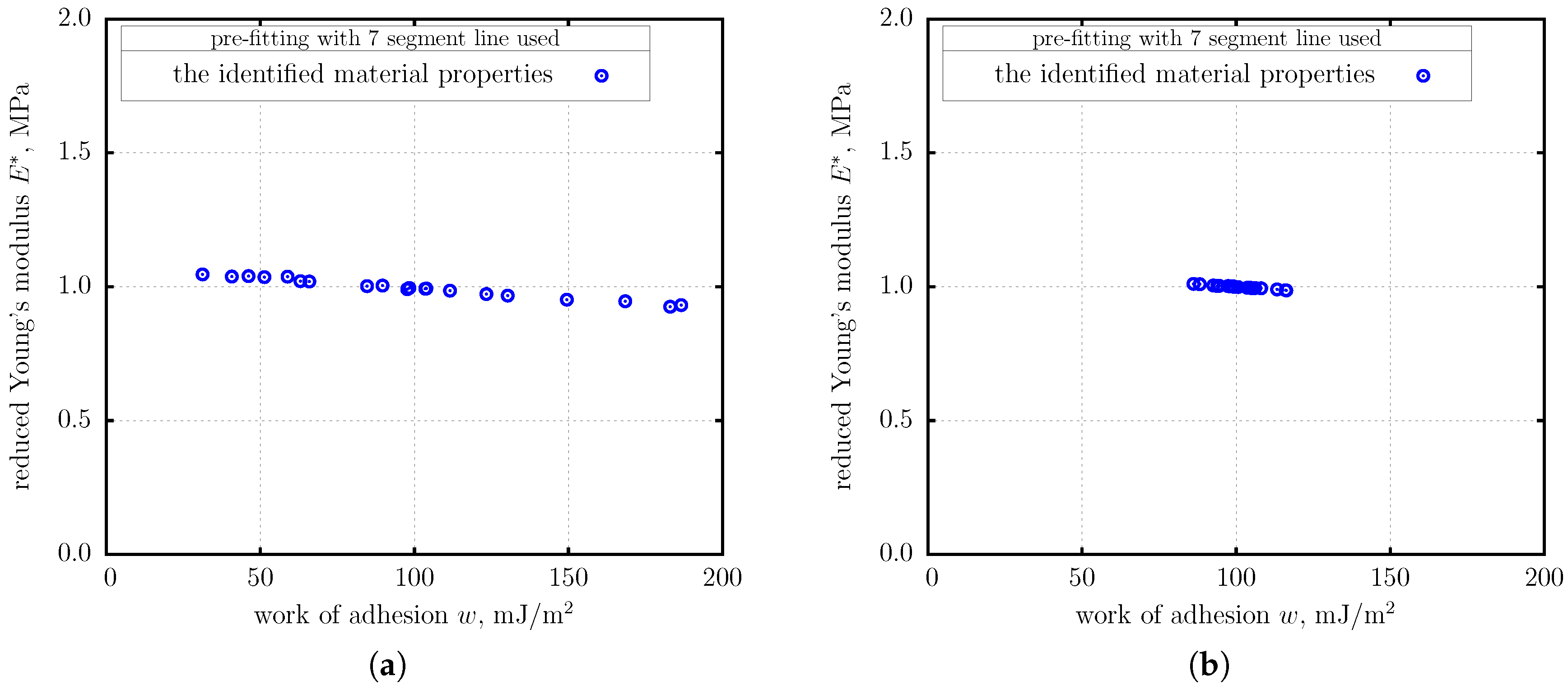
4. The Extended BG (eBG) Method
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Meyers, M.A.; Chen, P.Y.; Lin, A.Y.M.; Seki, Y. Biological materials: Structure and mechanical properties. Progress Mater. Sci. 2008, 53, 1–206. [Google Scholar] [CrossRef]
- Wu, P.H.; Aroush, D.R.B.; Asnacios, A.; Chen, W.C.; Dokukin, M.E.; Doss, B.L.; Durand-Smet, P.; Ekpenyong, A.; Guck, J.; Guz, N.V.; et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 2018, 15, 491–498. [Google Scholar] [CrossRef] [PubMed]
- ASTM. International Standard ASTM E111-17. Standard Test Method for Young’s Modulus, Tangent Modulus, and Chord Modulus; ASTM E111-17; ASTM: West Conshohocken, PA, USA, 2017. [Google Scholar]
- International Organization for Standardization. International Standard ISO 527-1. Plastics—Determination of Tensile Properties—Part 1: General Principles; ISO527-1; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- ASTM. International Standard ASTM E132-17. Standard Test Method for Poisson’s Ratio at Room Temperature; ASTM E132-17; ASTM: West Conshohocken, PA, USA, 2017. [Google Scholar]
- International Organization for Standardization. International Standard ISO 29862. Self Adhesive Tapes—Determination of Peel Adhesion Properties; ISO 29862; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Kang, W.; Merrill, M.; Wheeler, J.M. In situ thermomechanical testing methods for micro/nano-scale materials. Nanoscale 2017, 9, 2666–2688. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Mukherjee, S.; Howe, J.Y.; Perovic, D.D.; Sun, Y.; Singh, C.V.; Filleter, T. Nonlinear fracture toughness measurement and crack propagation resistance of functionalized graphene multilayers. Sci. Adv. 2018, 4, eaao7202. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Howe, J.Y.; Perovic, D.; Filleter, T.; Sun, Y. In situ TEM tensile testing of carbon-linked graphene oxide nanosheets using a MEMS device. Nanotechnology 2016, 27, 28LT01. [Google Scholar] [CrossRef] [PubMed]
- Alekya, B.; Rao, S.; Pandya, H.J. Engineering approaches for characterizing soft tissue mechanical properties: A review. Clin. Biomech. 2019, 69, 127–140. [Google Scholar]
- Peisker, H.; Michels, J.; Gorb, S. Evidence for a material gradient in the adhesive tarsal setae of the ladybird beetle Coccinella septempunctata. Nat. Commun. 2013, 4, 1661. [Google Scholar] [CrossRef]
- Barbakadze, N.; Enders, S.; Gorb, S.; Arzt, E. Local mechanical properties of the head articulation cuticle in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae). J. Exp. Biol. 2006, 209, 722–730. [Google Scholar] [CrossRef]
- Griffin, M.; Premakumar, Y.; Seifalian, A.; Butler, P.E.; Szarko, M. Biomechanical Characterization of Human Soft Tissues Using Indentation and Tensile Testing. J. Vis. Exp. 2016, 118, 54872. [Google Scholar] [CrossRef]
- Bhushan, B.; Li, X. Nanomechanical characterisation of solid surfaces and thin films. Int. Mater. Rev. 2003, 48, 125–164. [Google Scholar] [CrossRef]
- Purtov, J.; Gorb, E.; Steinhart, M.; Gorb, S. Measuring of the hardly measurable: Adhesion properties of anti-adhesive surfaces. Appl. Phys. A 2013, 111, 183–189. [Google Scholar] [CrossRef]
- Pepelyshev, A.; Borodich, F.; Galanov, B.; Gorb, E.; Gorb, S. Adhesion of Soft Materials to Rough Surfaces: Experimental Studies, Statistical Analysis and Modelling. Coatings 2018, 8, 350. [Google Scholar] [CrossRef]
- Galanov, B.A. Models of adhesive contact between rough elastic bodies. Int. J. Mech. Sci. 2011, 53, 968–977. [Google Scholar] [CrossRef]
- Polyakov, B.; Vlassov, S.; Dorogin, L.M.; Kulis, P.; Kink, I.; Lohmus, R. The effect of substrate roughness on the static friction of CuO nanowires. Surf. Sci. 2012, 606, 1393–1399. [Google Scholar] [CrossRef]
- Deng, W.; Kesari, H. Molecular statics study of depth-dependent hysteresis in nano-scale adhesive elastic contacts. Model. Simul. Mater. Sci. Eng. 2017, 25, 055002. [Google Scholar] [CrossRef]
- Medina, S.; Dini, D. A numerical model for the deterministic analysis of adhesive rough contacts down to the nano-scale. Int. J. Solids Struct. 2014, 51, 2620–2632. [Google Scholar] [CrossRef]
- Grierson, D.S.; Flater, E.E.; Carpick, R.W. Accounting for the JKR–DMT transition in adhesion and friction measurements with atomic force microscopy. J. Adhes. Sci. Technol. 2005, 19, 291–311. [Google Scholar] [CrossRef]
- Kendall, K. Molecular Adhesion and Its Applications; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2001. [Google Scholar]
- Kohn, J.C.; Ebenstein, D.M. Eliminating adhesion errors in nanoindentation of compliant polymers and hydrogels. J. Mech. Behav. Biomed. Mater. 2013, 20, 316–326. [Google Scholar] [CrossRef]
- Gorb, S.; Jiao, Y.; Scherge, M. Ultrastructural architecture and mechanical properties of attachment pads in Tettigonia viridissima (Orthoptera Tettigoniidae). J. Comp. Physiol. 2000, 186, 821–831. [Google Scholar] [CrossRef]
- Kovalev, A.; Filippov, A.; Gorb, S. Slow viscoelastic response of resilin. J. Comp. Physiol. 2018, 204, 409–417. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1580. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Maugis, D. Contact, Adhesion and Rupture of Elastic Solids; Springer-Verlag: Berlin, Germany, 2000. [Google Scholar]
- Kalei, G.N. Some results of microhardness test using the depth of impression (in Russian). Mashinovedenie 1968, 4, 105–107. [Google Scholar]
- Khrushchov, M.M.; Berkovich, E.S. Devices PMT-2 and PMT-3 for Microhardness Testing (in Russian); USSR Academy of Sciences Publising: Moscow, Russia, 1950. [Google Scholar]
- Borodich, F.M.; Keer, L.M.; Korach, C.S. Analytical study of fundamental nanoindentation test relations for indenters of non-ideal shapes. Nanotechnology 2003, 14, 803–808. [Google Scholar] [CrossRef]
- Kindrachuk, V.M.; Galanov, B.A.; Kartuzov, V.V.; Dub, S.N. On elastic nanoindentation of coated half-spaces by point indenters of non-ideal shapes. Nanotechnology 2006, 17, 1104–1111. [Google Scholar] [CrossRef] [PubMed]
- Bulychev, S.I.; Alekhin, V.P.; Shorshorov, M.K.; Ternovskii, A.P.; Shnyrev, G.D. Determination of Young’s modulus according to indentation diagram (in Russian). Ind. Lab. 1975, 41, 1409–1412. [Google Scholar]
- Borodich, F.M. The Hertz-type and adhesive contact problems for depth-sensing indentation. Adv. App. Mech. 2014, 47, 225–366. [Google Scholar]
- ISO. International Standard ISO 14577-1:2015. Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method; ISO14577-1; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Giannakopoulos, A.; Suresh, S. Determination of elastoplastic properties by instrumented sharp indentation. Scr. Mater. 1999, 40, 1191–1198. [Google Scholar] [CrossRef]
- Borodich, F.M.; Keer, L.M. Evaluation of elastic modulus of materials by adhesive (no-slip) nanoindentation. Proc. R. Soc. Lond. A 2004, 460, 507–514. [Google Scholar] [CrossRef]
- Chaudhri, M.M.; Lim, Y.Y. Nanoindentation Techniques: A Critical Assessment of the Current Methods of Data Analysis. Key Eng. Mater. 2007, 345–346, 1107–1114. [Google Scholar] [CrossRef]
- Galanov, B.A.; Dub, S.N. Critical comments to the Oliver–Pharr measurement technique of hardness and elastic modulus by instrumented indentations and refinement of its basic relations. J. Superhard Mater. 2017, 39, 373–389. [Google Scholar] [CrossRef]
- Kossovich, E.L.; Borodich, F.M.; Epshtein, S.A.; Galanov, B.A.; Minin, M.G.; Prosina, V.A. Mechanical, structural and scaling properties of coals: Depth-sensing indentation studies. App. Phys. A 2019, 125, 195. [Google Scholar] [CrossRef]
- Argatov, I.I.; Borodich, F.M.; Epshtein, S.A.; Kossovich, E.L. Understanding of material properties of thin films attached to substrates: Depth-sensing unloading of elasto-plastic and elasto-brittle materials. Mech. Mater. 2017, 114, 172–179. [Google Scholar] [CrossRef]
- Galanov, B.A.; Grigor’ev, O.N.; Mil’man, Y.V.; Ragozin, I.P. Determination of the hardness and Young’s modulus from the depth of penetration of a piramidal indentor. Strength Mater. 1983, 15, 1624–1628. [Google Scholar] [CrossRef]
- Galanov, B.A.; Grigor’ev, O.N.; Mil’man, Y.V.; Ragozin, I.P.; Trefilov, V.I. Determination of the hardness and Young’s modulus with elastoplastic penetration of indentors into materials. Sov. Phys. Dokl. 1984, 29, 146–147. [Google Scholar]
- Borodich, F.M.; Keer, L.M. Contact problems and depth-sensing nanoindentation for frictionless and frictional boundary conditions. Int. J. Solids Struct. 2004, 41, 2479–2499. [Google Scholar] [CrossRef]
- Enders, S.; Barbakadse, N.; Gorb, S.; Arzt, E. Exploring Biological Surfaces by Nanoindentation. J. Mater. Res. 2004, 19, 880–887. [Google Scholar] [CrossRef]
- Arzt, E.; Enders, S.; Gorb, S. Towards a micromechanical understanding of biological surface devices. Zeitschrift für Metallkunde 2002, 93, 345–351. [Google Scholar] [CrossRef]
- Klein, M.C.; Deuschle, J.; Gorb, S. Material properties of the skin of the Kenyan sand boa Gongylophis colubrinus (Squamata, Boidae). J. Comp. Physiol. A 2010, 196, 659–668. [Google Scholar] [CrossRef]
- Klein, M.C.; Gorb, S. Epidermis architecture and material properties of the skin of four snake species. J. R. Soc. Interface 2012, 3140–3155. [Google Scholar] [CrossRef]
- Huber, G.; Orso, S.; Spolenak, R.; Wegst, U.; Enders, S.; Gorb, S.; Arzt, E. Mechanical properties of a single gecko seta. Int. J. Mater. Res. 2008, 99, 1113–1118. [Google Scholar] [CrossRef]
- Schwendicke, F.; Eggers, K.; Meyer-Lueckel, H.; Dörfer, C.; Kovalev, A.; Gorb, S.; Paris, S. In vitro Induction of Residual Caries Lesions in Dentin: Comparative Mineral Loss and Nano-Hardness Analysis. Caries Res. 2015, 49, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Krings, W.; Kovalev, A.; Glaubrecht, M.; Gorb, S. Differences in the Young modulus and hardness reflect different functions of teeth within the taenioglossan radula of gastropods. Zoology 2019, 137, 125713. [Google Scholar] [CrossRef] [PubMed]
- Rundlöf, M.; Karlsson, M.; Wågberg, L.; Poptoshev, E.; Rutland, M.; Claesson, P. Application of the JKR Method to the Measurement of Adhesion to Langmuir-Blodgett Cellulose Surfaces. J. Colloid Interface Sci. 2000, 230, 441–447. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Carrillo, F.; Gupta, S.; Balooch, M.; Marshall, S.; Marshall, G.; Pruitt, L.; Puttlitz, C. Nanoindentation of polydimethylsiloxane elastomers: Effect of crosslinking, work of adhesion, and fluid environment on elastic modulus. J. Mater. Res. 2005, 20, 2820–2830. [Google Scholar] [CrossRef]
- Wahl, K.J.; Asif, S.A.S.; Greenwood, J.A.; Johnson, K.L. Oscillating adhesive contacts between micron-scale tips and compliant polymers. J. Colloid Interface Sci. 2006, 296, 178–188. [Google Scholar] [CrossRef]
- Ebenstein, D.M.; Wahl, K.J. A comparison of JKR-based methods to analyze quasi-static and dynamic indentation force curves. J. Colloid Interface Sci. 2006, 298, 652–662. [Google Scholar] [CrossRef]
- Yu, Y.; Sanchez, D.; Lu, N. Work of adhesion/separation between soft elastomers of different mixing ratios. J. Mater. Res. 2015, 30, 2702–2712. [Google Scholar] [CrossRef]
- Goodwyn, P.; Peressadko, A.; Schwarz, H.; Kastner, V.; Gorb, S. Material structure, stiffness, and adhesion: Why attachment pads of the grasshopper (Tettigonia viridissima) adhere more strongly than those of the locust (Locusta migratoria) (Insecta: Orthoptera). J. Comp. Physiol. A 2006, 192, 1233–1243. [Google Scholar] [CrossRef]
- Bußhardt, P.; Wolf, H.; Gorb, S. Adhesive and frictional properties of attachment pads in two species of stick insects (Phasmatoidea) with smooth and nubbly euplantulae. Zoology 2012, 115, 135–141. [Google Scholar] [CrossRef]
- Eichler-Volf, A.; Xue, L.; Kovalev, A.; Gorb, E.; Gorb, S.; Steinhart, M. Nanoporous Monolithic Microsphere Arrays Have Anti-Adhesive Properties Independent of Humidity. Materials 2016, 9, 373. [Google Scholar] [CrossRef]
- Xue, L.; Kovalev, A.; Eichler-Volf, A.; Steinhart, M.; Gorb, S. Humidity-enhanced wet adhesion on insect-inspired fibrillar adhesive pads. Nat. Commun. 2015, 6, 6621. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 1971, 324, 301–313. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Muller, V.M.; Toporov, Y.P. Effect of contact deformations on adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Beach, E.R.; Tormoen, G.W.; Drelich, J.; Han, R. Pull-off force measurements between rough surfaces by atomic force microscopy. J. Colloid Interface Sci. 2002, 247, 84–99. [Google Scholar] [CrossRef] [PubMed]
- Borodich, F.M.; Galanov, B.A. Non-direct estimations of adhesive and elastic properties of materials by depth-sensing indentation. Proc. R. Soc. London A 2008, 464, 2759–2776. [Google Scholar] [CrossRef]
- Sirghi, L.; Rossi, F. Adhesion and elasticity in nanoscale indentation. App. Phys. Lett. 2006, 89, 243118. [Google Scholar] [CrossRef]
- Borodich, F.M.; Galanov, B.A.; Gorb, S.N.; Prostov, M.Y.; Prostov, Y.I.; Suarez-Alvarez, M.M. Evaluation of adhesive and elastic properties of materials by depth-sensing indentation of spheres. J. App. Phys. A Mater. Sci. Process. 2012, 108, 13–18. [Google Scholar] [CrossRef]
- Borodich, F.M.; Galanov, B.A.; Gorb, S.N.; Prostov, M.Y.; Prostov, Y.I.; Suarez-Alvarez, M.M. An inverse problem for adhesive contact and non-direct evaluation of material properties for nanomechanics applications. Nanoscale Syst. Math. Model. Theory Appl. 2012, 1, 80–92. [Google Scholar] [CrossRef][Green Version]
- Borodich, F.M.; Galanov, B.A.; Gorb, S.N.; Prostov, M.Y.; Prostov, Y.I.; Suarez-Alvarez, M.M. Evaluation of Adhesive and Elastic Properties of Polymers by the BG Method. Macromol. React. Eng. 2013, 7, 555–563. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Chong, E.; Zak, S. An Introduction to Optimization; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Tabor, D. Surface forces and surface interactions. J. Colloid Interface Sci. 1977, 58, 2–13. [Google Scholar] [CrossRef]
- Muller, V.M.; Yushchenko, V.S.; Derjaguin, B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane. J. Colloid Interface Sci. 1980, 77, 91–101. [Google Scholar] [CrossRef]
- Domke, J.; Radmacher, M. Measuring the elastic properties of thin polymer films with the atomic microscope. Langmuir 1998, 14, 3320–3325. [Google Scholar] [CrossRef]
- Dimitriadis, E.K.; Horkay, F.; Maresca, J.; Kachar, B.; Chadwick, R.S. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys. J. 2002, 82, 2798–2810. [Google Scholar] [CrossRef]
- Sirghi, L.; Ponti, J.; Broggi, F.; Rossi, F. Probing elasticity and adhesion of live cells by atomic force microscopy indentation. Eur. Biophys. J. 2008, 37, 935–945. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Siamantouras, E.; Liu, K.K.; Liu, X. Determination of work of adhesion of biological cell under AFM bead indentation. J. Mech. Behav. Biomed. Mater. 2016, 56, 77–86. [Google Scholar] [CrossRef] [PubMed]
- Bouchonville, N.; Meyer, M.; Gaude, C.; Gay, E.; Ratel, D.; Nicolas, A. AFM mapping of the elastic properties of brain tissue reveals kPa μm(-1) gradients of rigidity. Soft Matter 2016, 12, 6232–6239. [Google Scholar] [CrossRef]
- Notbohm, J.; Poon, B.; Ravichandran, G. Analysis of nanoindentation of soft materials with an atomic force microscope. J. Mater. Res. 2012, 27, 229–237. [Google Scholar] [CrossRef]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Robust strategies for automated AFM force curve analysis-I. Non-adhesive indentation of soft, inhomogeneous materials. J. Biomech. Eng. 2007, 129, 430–440. [Google Scholar] [CrossRef]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Robust strategies for automated AFM force curve analysis-II. Adhesion-influenced indentation of soft, elastic materials. J. Biomech. Eng. 2007, 129, 904–912. [Google Scholar] [CrossRef]
- Bouchonville, N.; Nicolas, A. Quantification of the Elastic Properties of Soft and Sticky Materials Using AFM. Methods Mol. Biol. 2019, 1886, 281–290. [Google Scholar]
- Perepelkin, N.; Argatov, I.; Borodich, F. Evaluation of elastic and adhesive properties of solids by depth-sensing indentation (in press). J. Adhes. 2019. [CrossRef]
- Argatov, I.I.; Sabina, F.J. Asymptotic analysis of the substrate effect for an arbitrary indenter. Q. J. Mech. Appl. Math. 2013, 66, 75–95. [Google Scholar] [CrossRef]
- Argatov, I.I.; Borodich, F.M.; Popov, V.L. JKR adhesive contact for a transversely isotropic layer of finite thickness. J. Phys. D Appl. Phys. 2016, 49, 045307. [Google Scholar] [CrossRef]
- Borodich, F.M.; Galanov, B.A.; Perepelkin, N.V.; Prikazchikov, D.A. Adhesive contact problems for a thin elastic layer: Asymptotic analysis and the JKR theory. Math. Mech. Solids 2019, 24, 1405–1424. [Google Scholar] [CrossRef]
- Erbaş, B.; Aydın, Y.E.; Borodich, F.M. Indentation of thin elastic films glued to rigid substrate: Asymptotic solutions and effects of adhesion. Thin Solid Film. 2019, 683, 135–143. [Google Scholar] [CrossRef]
- Sergici, A.O.; Adams, G.G.; Müftü, S. Adhesion in the contact of a spherical indenter with a layered elastic half-space. J. Mech. Phys. Sol. 2006, 54, 1843–1861. [Google Scholar] [CrossRef]
- Stan, G.; Adams, G.G. Adhesive contact between a rigid spherical indenter and an elastic multi-layer coated substrate. Int. J. Sol. Struct. 2016, 87, 1–10. [Google Scholar] [CrossRef]
- Jin, F.; Guo, X.; Gao, H. Adhesive contact on power-law graded elastic solids: The JKR–DMT transition using a double-Hertz model. J. Mech. Phys. Sol. 2013, 61, 2473–2492. [Google Scholar] [CrossRef]
- Sridhar, I.; Johnson, K.L.; Fleck, N.A. Adhesion mechanics of the surface force apparatus. J. Phys. D Appl. Phys. 1997, 30, 1710–1719. [Google Scholar] [CrossRef]
- Johnson, K.L.; Sridhar, I. Adhesion between a spherical indenter and an elastic solid with a compliant elastic coating. J. Phys. D Appl. Phys. 2001, 34, 683–689. [Google Scholar] [CrossRef]
- Sridhar, I.; Zheng, Z.W.; Johnson, K.L. A detailed analysis of adhesion mechanics between a compliant elastic coating and a spherical probe. J. Phys. D Appl. Phys. 2004, 37, 2886–2895. [Google Scholar] [CrossRef]
- Perepelkin, N.; Kovalev, A.; Gorb, S.; Borodich, F. Estimation of the elastic modulus and the work of adhesion of soft materials using the extended Borodich-Galanov (BG) method and depth sensing indentation. Mech. Mat. 2019, 129, 198–213. [Google Scholar] [CrossRef]
- Ahn, S.J. Least Squares Orthogonal Distance Fitting of Curves and Surfaces in Space; Springer: Berlin, Germany, 2004. [Google Scholar]
- Boggs, P.T.; Byrd, R.H.; Schnabel, R.B. A stable and efficient algorithm for nonlinear orthogonal distance regression. SIAM J. Sci. Stat. Comput. 1987, 8, 1052–1078. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perepelkin, N.V.; Borodich, F.M.; Kovalev, A.E.; Gorb, S.N. Depth-Sensing Indentation as a Micro- and Nanomechanical Approach to Characterisation of Mechanical Properties of Soft, Biological, and Biomimetic Materials. Nanomaterials 2020, 10, 15. https://doi.org/10.3390/nano10010015
Perepelkin NV, Borodich FM, Kovalev AE, Gorb SN. Depth-Sensing Indentation as a Micro- and Nanomechanical Approach to Characterisation of Mechanical Properties of Soft, Biological, and Biomimetic Materials. Nanomaterials. 2020; 10(1):15. https://doi.org/10.3390/nano10010015
Chicago/Turabian StylePerepelkin, Nikolay V., Feodor M. Borodich, Alexander E. Kovalev, and Stanislav N. Gorb. 2020. "Depth-Sensing Indentation as a Micro- and Nanomechanical Approach to Characterisation of Mechanical Properties of Soft, Biological, and Biomimetic Materials" Nanomaterials 10, no. 1: 15. https://doi.org/10.3390/nano10010015
APA StylePerepelkin, N. V., Borodich, F. M., Kovalev, A. E., & Gorb, S. N. (2020). Depth-Sensing Indentation as a Micro- and Nanomechanical Approach to Characterisation of Mechanical Properties of Soft, Biological, and Biomimetic Materials. Nanomaterials, 10(1), 15. https://doi.org/10.3390/nano10010015





