Abstract
Contracting cancer typically induces a state of terror among the individuals who are affected. Exploring how glucose excess, estrogen excess, and anxiety work together to affect the speed at which breast cancer cells multiply and the immune system’s response model is necessary to conceive of ways to stop the spread of cancer. This paper proposes a mathematical model to investigate the impact of psychological panic, glucose excess, and estrogen excess on the interaction of cancer and immunity. The proposed model is precisely described. The focus of the model’s dynamic analysis is to identify the potential equilibrium locations. According to the analysis, it is possible to establish four equilibrium positions. The stability analysis reveals that all equilibrium points consistently exhibit stability under the defined conditions. The transcritical bifurcation occurs when the glucose excess is taken as a bifurcation point. Numerical simulations are employed to validate the theoretical study, which shows that psychological panic, glucose excess, and estrogen excess could be significant contributors to the spread of tumors and weakness of immune function.
1. Introduction
A group of disorders collectively referred to as cancer are those in which cells divide uncontrollably at a faster rate than healthy cells and have the potential to metastasize to other parts of the body [1]. The data indicate that the number of fatalities caused by cancer was approximately 8.2 million in the year 2010. It is anticipated that the mortality rate attributed to cancer will persistently increase, resulting in approximately 13 million fatalities by the year 2030 [2]. Breast cancer is the second most frequent type of cancer in women, second only to skin cancers, among many others. A little under 12% of women will develop invasive breast cancer in their lifetime [3]. There are three primary risk factors for breast cancer: genetic factors (such as family history), hormonal imbalance (namely estrogen), and environmental factors (including alcohol intake, poor diet, exposure to toxins, smoking, etc.) [4]. In order to study the dynamic behavior of cancer cells in the presence of different stimuli, numerous mathematical models have been developed throughout the years. For instance, Dehingia et al. developed a mathematical model to assess the impact of obesity on tumor growth and immune response, considering it as a risk factor in a study demonstrating that the accumulated fat in the body of an obese individual significantly contributes to the formation of tumors, hence elevating the risk factors associated with survival [5]. An elevation in estrogen levels could potentially expedite the rate of tumor formation [6,7]. Sorofa et al. [8] evaluated how estrogen affects the dynamics of normal immunological cells and breast cancer. The results showed that elevated estrogen levels can slow immune system development and enhance tumor initiation.
It has been demonstrated that the majority of the energy for breast cancer cells comes from glycolysis wherein glucose is transformed to lactate for energy throughout the glycolysis process [9,10]. Multiple studies have verified that cancer cells have a high need for glucose as a source of nourishment. Therefore, the effect of glucose is incorporated into the tumor model to assess its impact on breast cancer cells. For instance, Sun et al. investigated the impact of glucose deprivation on the apoptosis of breast cancer cells in a study demonstrating that consuming an excessive amount of glucose can promote the development and proliferation of cancer cells, whereas restricting glucose consumption can decrease and suppress the growth of cancer cells [11]. A pathological state and impaired functionality of the immune system may result from a high glucose intake. However, maintaining an adequate amount of glucose is critical for the functioning of the immune system. As a result, the infiltration of a substantial amount of glucose into immune cells may have detrimental effects on the immune system. Consequently, this results in compromised immune system functionality, which initiates pathological conditions [12]. Alharbi et al. created a model that offers a fundamental understanding of the process of breast cancer in patients who already have risk factors related to hyperglycemia. They determined that their findings have the potential to be advantageous for the future delivery and treatment of breast cancer drugs [13].
On the other hand, a growing body of literature highlights the use of mathematical models for investigating the effects of anxiety on disease transmission [14,15]. Research in the medical field has shown that emotional distress might hasten the metastasis of cancer cells in a patient. Stress on a psychological level widens and thickens blood vessels, which in turn speeds up the migration of cancer cells and makes disease spreading easier [16]. According to recent research, hormones produced by stress accelerate cancer cell growth in the “lymphatic system”, which in turn makes it easier for these cells to spread to other parts of the body, a process known as metastasis [17,18,19].
To sum up, most of the prior research has shown that a high-glucose diet and high estrogen levels might promote the growth and proliferation of breast cancer cells, making it more likely that the disease would progress rapidly. The impact of high estrogen levels and glucose on the human immune system, on the other hand, has been the subject of very few investigations. Experimental evidence suggests that immune cells are vulnerable to the harmful effects of either high or low blood glucose levels as well as high estrogen levels [8,20]. Moreover, there is a lack of research regarding the impact of anxiety on the immune cells–breast cancer model. Therefore, we must investigate this phenomenon, as it plays a role in minimizing the occurrence of disastrous situations. Hence, this investigation is focused on examining the influence of anxiety on immune-compromised cancer patients, which may serve as a substantial factor in the proliferation of tumors and the impairment of immune system efficacy.
This research aims to investigate the dynamics of the immune cells–breast cancer model as a result of the combined influence of the psychological panic factor, increased glucose consumption, and high estrogen levels and their harmful effects on normal, cancer, and immune cells. Considering these effects, we propose a PPIGCNE model of psychological panic–immune–glucose–cancer–normal estrogen interaction. This paper’s findings provide additional context for [8] by
- (1)
- Analyzing the impact of glucose as a risk factor on the progression of breast cancer.
- (2)
- Examining the influence of psychological panic on the immune system of breast cancer patients, which may play a key role in the progression of malignancies and the impairment of immune function.
Following a description of the model’s construction, we intend to determine how the above effects impact the dynamics of a PPIGCNE model. Furthermore, this paper will explore the understanding of the nonlinear dynamics exhibited by our model through the utilization of various methodologies, including stability and bifurcation analysis techniques. In conclusion, we will validate the precision of our analytical findings through a numerical simulation of the proposed system.
2. Assumptions of the Model
In this part, we will construct a model by integrating many experimental investigations and mathematical models [21,22,23] that elucidate the dynamics of tumor progression. The psychological panic, increased glucose consumption, and high estrogen levels interaction model are formulated. The dynamics of the PPIGCNE model significantly influence the development of breast cancer, making it a substantial risk factor. Furthermore, we analyze the interactions among the above factors with breast tumor cells. The relationships between immune cells , cancer cells , normal (breast) cells , and the effect of estrogen , are depicted in Figure 1.
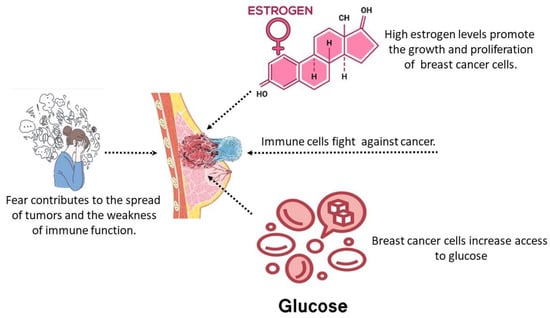
Figure 1.
Schematic sketch of the PPIGCNE model.
The response of the immune system is critical for safeguarding breast tissue against malignant tumors and ensuring an appropriate response upon tumor cell recognition. Tumor cell presence stimulates the activation of the immune system. The dynamic representation of immune cells is
The term denotes the consistent generation of immune cells within the organism, which is negatively influenced by the psychological fear factor in the presence of cancer. The fear function is integrated using the decreasing function , a concept that Wang et al. [24] first proposed. Given its biological implications, is deemed suitable since
In (1), , denoted by the Michaelis–Menten term [25], indicates the presence of tumor cells that elicit an immune response [26]. denotes the measure of the impact of tumor cells on immune cells by suppressing the immune response with cancer cells [26]. refers to the rate of immune suppression induced by estrogen [8]. refers to the decline of immune cells due to excess glucose and natural death rate [13].
The breast cancer cells T(t) consist of aberrant cells characterized by inflammation and fast proliferation of breast cells, leading to the formation of tumors. Therefore, we define the equation representing the tumor as:
The term represents the logistic tumor cell’s growth function, where is the breast cancer intrinsic growth rate and stands for the carrying capacity of breast cancer cells. The term means eradicating cancerous cells by the body’s immune system. The outcome of DNA damage caused by estrogen is that normal cells that have been harmed will transform into tumor cells, causing the tumor cell population to increase at a rate of . This leads to a growth factor of on the tumor cell population [8]. designates the death rate of cancer breast cells. indicates the formation of new cancer cells due to elevated glucose levels within the patient’s body [13].
Healthy breast cells possess unmodified DNA that governs the activities of all breast cells during their growth, division, and demise [27]. Healthy breast cells and malignant breast cells compete for nutrition and other resources. Healthy breast cells are depicted by
The term represents the logistic healthy breast cell growth function. The term represents the degradation rate of healthy breast cells caused by tumor cells. The decrease in healthy breast cells due to a higher level of estrogen causes the conversion of normal cells into tumor cells, which occurs at a rate of [8].
Estrogen, a female steroid hormone, is produced at low levels by the placenta in women and the testes in men. It serves several important purposes, including facilitating sexual development, controlling a woman’s menstrual cycle, and managing the physical changes associated with puberty. Therefore, it is regarded as a crucial hormone for the optimal transformation of the breast tissues. Estrogen is recognized as a risk factor that is linked to the development of breast cancer. Estrogen has a role in activating other hormones, such as relaxin, which in turn stimulates the proliferation of breast cells [28]. Estrogen has promoted the proliferation of tumor cells when tumor cells are present. It functions as a carcinogen by damaging DNA and converting normal epithelial cells into cancerous tumor cells [29,30]. The dynamics of estrogen can be described as follows:
where represents the rate at which increased estrogen is produced, and represents the rate at which estrogen is being washed out from the body system.
Upon careful evaluation of these factors, we propose the subsequent set of differential equations to determine the behavior of breast cancer cells:
The model’s parameters and their interpretations are clarified in Table 1.

Table 1.
The interpretations of the PPIGCNE model’s parameters.
3. Dynamical Evaluation Results
3.1. Positivity and Boundedness of the Solution
In the following theorems, the positivity and uniformly bounded of all the solutions of the PPIGCNE model in are confirmed.
Theorem 1.
All of the solutions of the PPIGCNE model and with the initial conditions are positively invariant.
Proof of Theorem 1.
Let and , where and . Then the PPIGCNE system becomes:
with . It is clear for any , such that , then (for ). Now for any solution of with , say , is such that , for all . Thus, the PPIGCNE system is positively invariant [31]. □
Theorem 2.
All the solutions of the PPIGCNE model are uniformly bounded.
Proof of Theorem 2.
Let be an initial condition for the PPIGCNE, then, by using the Bernoulli method, we obtain
Thus,
Using the standard comparison theory [32] on the last equation of the PPIGCNE, we obtain
From the second equation of the PPIGCNE, we have
Using the Bernoulli method, we obtain
Thus,
Now, by using the standard comparison theory [32], we obtain
Therefore, the corresponding domain region for the PPIGCNE model is
3.2. Existence of Equilibria
Resetting the left-hand side of the PPIGCNE model to zero will bring the solutions of the model equations to equilibrium:
- Tumor and breast cells-free equilibrium point , where and . It is important to mention that the expression remains constant for all equilibrium points that have in their composition.
- Tumor-free equilibrium point , where and . For , we must have
In biological terms, this point refers to a healthy case because the tumor vanishes while the immune system and normal cells remain. The following justifies this point. The low estrogen level causes the tumor environment to be improper for growth, hence promoting the eradication of cancer cells by immune cells.
- 3.
- Breast cells-free equilibrium point , where and is the root of the following equation:whereClearly,.Thus, if any of the following criteria holds, then has a unique positive root, say , in the interval according to the intermediate value theoremFor , we must havewhere . Biologically, condition (9) means this point is classed as a glucose risk. This is because the level of glucose (g) is higher than the rate of tumor growth, which is a factor that leads to the growth of cancer cells at a rate that is significantly higher than that of normal cells. As a result of the spread of the tumor, the patient is placed in a severe situation, which ultimately results in either a mastectomy or the patient’s death.
- 4.
- The coexisting point , where , , and,,, and is a root of the following equationwhereClearly,.Thus, if the following criteria hold, then has a unique positive root, say , in the interval according to the intermediate value theoremFor and , we must haveThe coexisting point signifies the stage of interaction among immune cells, malignant, normal, and estrogen. Every cell engages in a fierce struggle for survival during this phase. Tumor appearance triggers the activation of immune cells.
3.3. Stability Analysis
The local stability behavior around the previous equilibrium points is examined in this section. The Jacobian matrix of PPIGCNE model can be expressed as follows:
where , ,
- , , ,
- , , , ,
- , , .
The local analysis of the PPIGCNE system at the three equilibrium points mentioned above is computed as
- (1)
- The Jacobian matrix at is given as:
The eigenvalues of are , , and . Then, is a locally asymptotic stable if
where . Condition (13) shows a mastectomy could happen when the rate of decrease in healthy breast cells caused by a higher estrogen level is greater than the healthy breast cell’s intrinsic growth rate. Further, from a biological standpoint, condition (14) means that cancer cells are dependent on their capacity to absorb glucose and reproduce. Consequently, a glucose rate that is lower than will substantially inhibit cancer cells, thereby reducing their strength and ability to reproduce and spread. Conversely, for , is a saddle point. For , then has zero eigenvalue, making a nonhyperbolic point.
- (2)
- The Jacobian matrix at is given as:
The eigenvalues of are
,
.
That means is a locally asymptotical stable point if, and only if, the following conditions are satisfied:
where .
- (3)
- The Jacobian matrix at is given as:
Then, has the following eigenvalues
That means is a locally asymptotical stable point if, and only if, the following conditions hold:
- (4)
- The Jacobian matrix at can be written as:
- ,
- .
- So, the characteristic equation of can be written as:
- Thus, according to the Routh–Hurwitz rule, will be asymptotically stable if
Theorem 3.
is a global asymptotic stable provided the following conditions hold:
where .
Proof of Theorem 3.
Let us contemplate the positive definite function given below:
Thus,
Therefore,
Then, can be transformed into a negative definite form under conditions (20). Hence, is a Lyapunov function and is a GAS. □
Thus, the cancer-free steady state fulfills the requirements for local stability, rendering the point globally stable. From a biological perspective, the immune system refers to the process of selectively eliminating tumor cells if conditions (20) are met.
3.4. Transcritical Bifurcation
A transcritical bifurcation occurs when two equilibrium points collide and exchange their stability. In the following theorems, we will investigate the possibility of a transcritical split occurring. Many scholars use Sotomayor’s theorem to determine the existence of transcritical bifurcation TB, for instance, see [31,32,33,34,35,36,37,38]. For this determination, the PPIGCNE model can be rephrased in the following vector forms:
where are the equations on the right-hand side of the PPIGCNE system. We possess the subsequent outcomes concerning the local bifurcation around the breast cells-free equilibrium point . Now, for non-zero vector :
The following theorem determines the TB of the PPIGCNE model near .
Theorem 4.
For , the PPIGCNE model, at has a transcritical bifurcation if the following conditions are met
Proof of Theorem 4.
The PPIGCNE model, at , has a zero eigenvalue, say at , where can be calculated using the subsequent equation:
Here, is given in the local stability of . The Jacobian matrix , becomes:
where and . Now, let and represent the eigenvectors corresponding to the zero eigenvalue of and , respectively. Direct computation gives and , where . Then,
So, and hence,
Therefore, transcritical bifurcation requirements are met under condition 21. □
3.5. Numerical Simulation and Discussions
Numerical verification is essential for completing analytical studies. In this section, we visually confirmed the accuracy of our analytical findings for the PPIGCNE system using the software MATLAB R2021b [39,40,41,42,43,44]. The simulations were conducted using the parameter values specified in Table 1. The equilibrium values corresponding to the data given in Table 1 are and . See Figure 2.
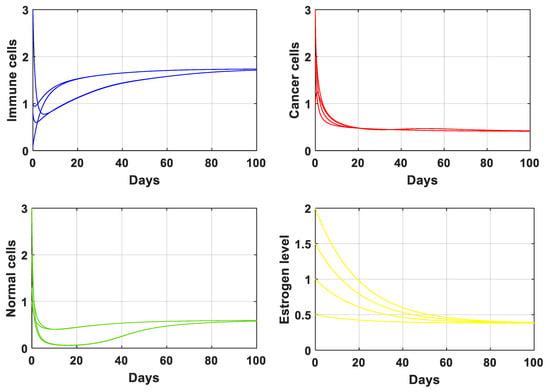
Figure 2.
The solution of the PPIGCNE system with the data is given in Table 1. The initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and ng/mL.
We will now examine three scenarios in order to understand the dynamic behavior of the PPIGCNE model and evaluate the impact of the psychological scare, high levels of estrogen, and high levels of glucose on tumor progression. The results of the three cases will then be compared. The following three cases are:
- (a)
- The effect of a psychological panic
The objective of this case is to demonstrate the impact of psychological scare levels on the interaction between immune cells and breast cancer cells. Figure 3 explains the performance of the PPIGCNE model with various values of the psychological panic rate from cancer, i.e., . Psychological panic has been discovered to have a negative impact on the immune system’s efficiency. Increased stress leads to a significant decline in immune cells. As a result, the tumor cells grow faster. Notwithstanding the notable decline in immune system efficacy, the PPIGCNE model, despite the excess in psychological scare levels, did not attain chaos, but it came close asymptotically to the coexisting point . Furthermore, Figure 4 illustrates the impact of psychological distress on the functionality of immune cells and the rate of malignant cell growth and division with more precisely rendered. To mitigate the health risks faced by breast cancer patients, psychiatric treatment is needed. Further, some external strategies are needed to improve the immune system’s performance.
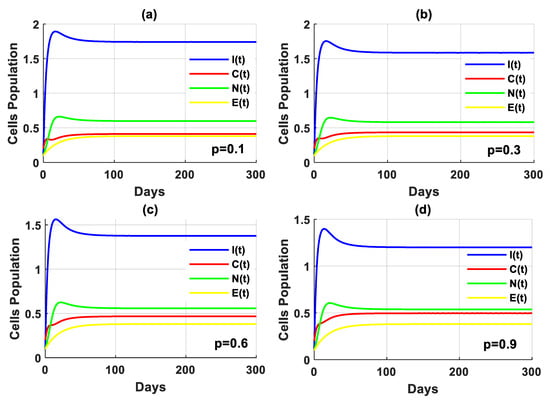
Figure 3.
The solution of the PPIGCNE system with various values of psychological scare rate and the initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and ng/mL.
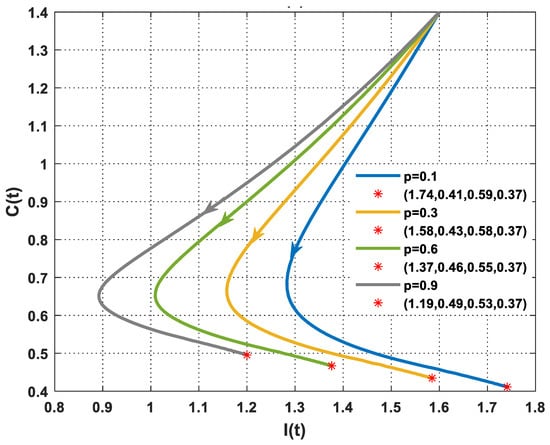
Figure 4.
The dynamics of immune and cancer cells with various values of and the initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and . represents the final state of the solution and the number in the bracket denotes the equilibrium point with different values of .
- (b)
- The impact of glucose excess
In the absence of tumor cells, the impact of excess glucose was observed to impair the functionality of the immune system (Figure 5). Furthermore, the solution of the PPIGCNE system, for various values of , initially experiences growth before converging asymptotically to the free cancer point . Furthermore, there was a significant drop in immune cells in the presence of tumor cells, as illustrated in Figure 6. In addition, the solution of the PPIGCNE system, as a consequence of excess glucose, drops off into the breast cells-free equilibrium point for . This result confirms the outcome of Theorem 4 which states that the PPIGCNE system faces a transcritical bifurcation at the glucose parameter (please see Figure 6). The above ultimately results in either the patient’s death or a mastectomy. Based on the findings, it can be inferred that there exists a direct correlation between elevated glucose levels and the proliferation and rate of division of cancer cells. Conversely, an inverse relationship can be observed between increased glucose levels and the immune system’s response to combat malignant cells. Please see Figure 7 for a better idea of what happens when glucose levels are high, both when there are no cancer cells and when there are.
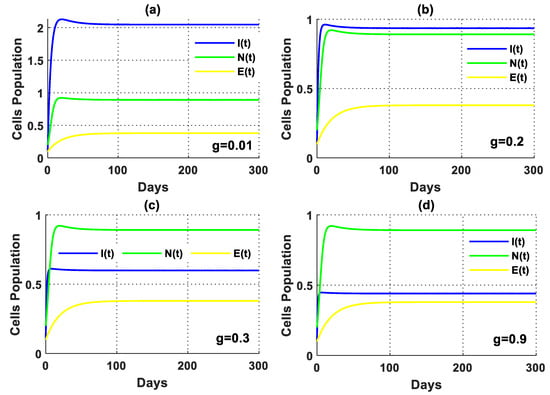
Figure 5.
The solution of the PPIGCNE system in the absence of tumor cells with various values of and the initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and .
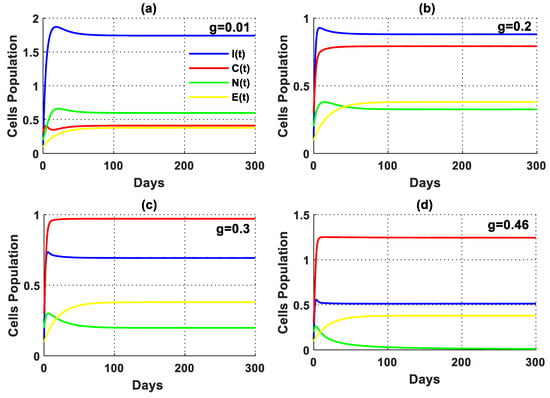
Figure 6.
The solution of the PPIGCNE system with various values of and the initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and .
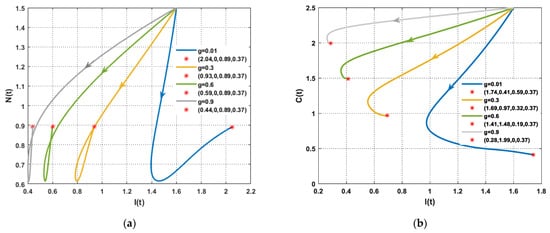
Figure 7.
The performance of the PPIGCNE system with various values of (a) The dynamics of immune and normal cells in the absence of tumor cells with various values of and the initial conditions are and ng/mL. (b) The dynamics of immune and cancer cells with various values of and the initial conditions are and ng/mL.
- (c)
- The impact of estrogen excess
In this scenario, the simulation is conducted by varying the values of the rate of higher estrogen production both in the absence and presence of tumor cells. In the absence of tumor cells, the solution of the PPIGCNE system approaches asymptotically to the free tumor equilibrium point with various values (see Figure 8). While in the presence of tumor cells, the solution of the PPIGCNE system converges to the coexisting point when . For , the solution of the PPIGCNE system settles down asymptotically to the breast cells-free equilibrium point . Please see Figure 9. The numerical solutions generally showed that in the presence of excess estrogen, immune cells, and normal cells decrease, with normal cells being the most affected (see Figure 10a), while tumor cells grow (see Figure 10b).
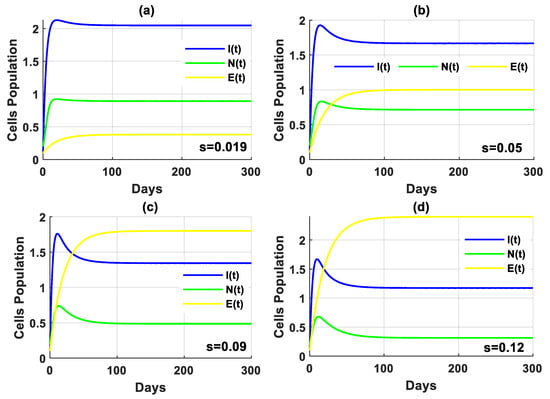
Figure 8.
The solution of the PPIGCNE system in the absence of tumor cells with various values of and the initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and ng/mL.
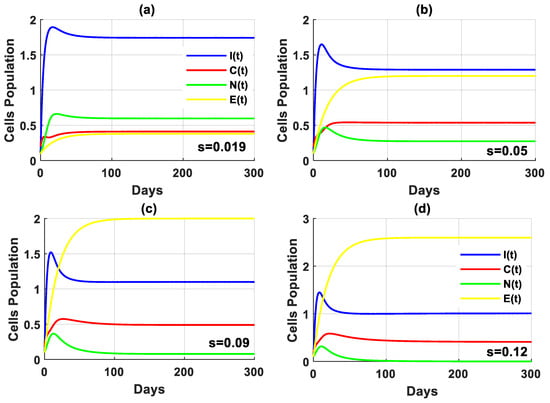
Figure 9.
The solution of the PPIGCNE system with various values of and the initial conditions of immune cells, breast cancer cells, normal cells, and estrogen level are and ng/mL.
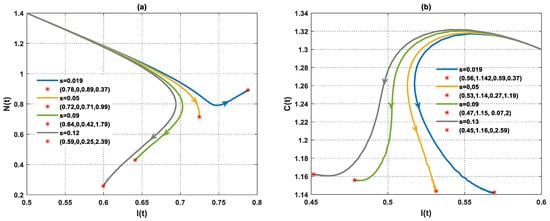
Figure 10.
The performance of the PPIGCNE system with various values of (a) The dynamics of immune and normal cells in the absence of tumor cells with various values of and the initial conditions are and ng/mL. (b) The dynamics of immune and cancer cells with various values of and the initial conditions are and ng/mL.
Remark 1.
The biological interpretation of the initial values that are smaller than one in a cancer system that have been used in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 refer to a parameter associated with cancer cell development or spread, such as the proliferation rate or growth factor in a mathematical model. If this initial value is less than one, cell division is slower than cancer cell death. This may imply a less aggressive cancer initially (and vice versa if the initial value is greater than one). The same interpretation is for the rest of the variables.
4. Conclusions
The dynamics of breast cancer in the presence of psychological scare, glucose excess, and estrogen excess have been presented in the form of a system of differential equations. The positivity and boundedness of the proposed system were established. Conditions of existence and local stability of the possible equilibria were illustrated. The global stability around the free breast cancer equilibrium point has been studied. The necessary threshold of glucose level to achieve a state of health has been determined. In terms of mathematics, this threshold is equivalent to a transcritical bifurcation. The numerical simulations validated the analytical findings. Precisely, the threshold value for the transcritical bifurcation was calculated, indicating the point at which normal cells (breast cells) transition from persisting to eradicating. The development of breast cancer in an individual relies on the immune system’s capacity to fight against tumor cells. It has been determined that an abundance of estrogen and glucose in the body leads to instability. This suggests that an increase in the amount of estrogen and glucose leads to a higher rate of tumor growth, thereby contributing to the development of breast cancer. It can be inferred that unregulated levels of estrogen and glucose can result in an immune system that is unable to effectively combat cancer cells, leading to a failure to control the disease. The results of the findings in this research could potentially result in the development of an optimal protocol for cancer therapy, which would greatly assist oncologists in their practice.
Our upcoming research will focus on augmenting the immune system through regular vitamin intake.
Author Contributions
Conceptualization, Z.A.; Data curation, S.J.; Formal analysis, S.J.; Funding acquisition, A.A.L.; Investigation, Z.A. and B.B.; Methodology, Z.A. and S.J.; Project administration, A.H.A.; Resources, B.B. and A.A.L.; Software, A.H.A.; Supervision, F.G.; Validation, B.B. and F.G.; Visualization, A.H.A.; Writing—original draft, Z.A. and S.J.; Writing—review & editing, A.H.A., F.G. and A.A.L. All authors have read and agreed to the published version of the manuscript.
Funding
The publication of this research was supported by the University of Oradea.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abernathy, K.; Abernathy, Z.; Baxter, A.; Stevens, M. Global dynamics of a breast cancer competition model. Differ. Equ. Dyn. Syst. 2020, 28, 791–805. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Action Plan for the Prevention and Control of Noncommunicable Diseases 2013–2020; World Health Organization: Geneva, Switzerland, 2013. [Google Scholar]
- Tarver, T. American cancer society. cancer facts and figures 2014. J. Consum. Health Internet 2012, 16, 366–367. [Google Scholar] [CrossRef]
- Patel, M.; Nagl, S. The Role of Model Integration in Complex Systems Modelling: An Example from Cancer Biology; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 3642156037. [Google Scholar]
- Dehingia, K.; Yao, S.-W.; Sadri, K.; Das, A.; Sarmah, H.K.; Zeb, A.; Inc, M. A study on cancer-obesity-treatment model with quadratic optimal control approach for better outcomes. Results Phys. 2022, 42, 105963. [Google Scholar] [CrossRef]
- Alnahdi, A.S.; Idrees, M. Nonlinear dynamics of estrogen receptor-positive breast cancer integrating experimental data: A novel spatial modeling approach. Math. Biosci. Eng. 2023, 20, 21163–21186. [Google Scholar] [CrossRef] [PubMed]
- Miziak, P.; Baran, M.; Błaszczak, E.; Przybyszewska-Podstawka, A.; Kałafut, J.; Smok-Kalwat, J.; Dmoszyńska-Graniczka, M.; Kiełbus, M.; Stepulak, A. Estrogen Receptor Signaling in Breast Cancer. Cancers 2023, 15, 4689. [Google Scholar] [CrossRef] [PubMed]
- Mufudza, C.; Sorofa, W.; Chiyaka, E.T. Assessing the effects of estrogen on the dynamics of breast cancer. Comput. Math. Methods Med. 2012, 2012, 473572. [Google Scholar] [CrossRef] [PubMed]
- Almeida, L.; Denis, J.A.; Ferrand, N.; Lorenzi, T.; Prunet, A.; Sabbah, M.; Villa, C. Evolutionary dynamics of glucose-deprived cancer cells: Insights from experimentally informed mathematical modelling. J. R. Soc. Interface 2024, 21, 20230587. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, A.M.; Martel, F. Targeting glucose transporters for breast cancer therapy: The effect of natural and synthetic compounds. Cancers 2020, 12, 154. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Sun, Y.; Rong, X.; Bai, L. High glucose promotes breast cancer proliferation and metastasis by impairing angiotensinogen expression. Biosci. Rep. 2019, 39, BSR20190436. [Google Scholar] [CrossRef]
- Shomali, N.; Mahmoudi, J.; Mahmoodpoor, A.; Zamiri, R.E.; Akbari, M.; Xu, H.; Shotorbani, S.S. Harmful effects of high amounts of glucose on the immune system: An updated review. Biotechnol. Appl. Biochem. 2021, 68, 404–410. [Google Scholar] [CrossRef]
- Alblowy, A.H.; Maan, N.; Alharbi, S.A. Role of glucose risk factors on human breast cancer: A nonlinear dynamical model evaluation. Mathematics 2022, 10, 3640. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Abboubakar, H.; Khan, A.; Abdeljawad, T. Mathematical modeling of the COVID-19 epidemic with fear impact. AIMS Math. 2023, 8, 6447–6465. [Google Scholar] [CrossRef]
- Doshi, D.; Karunakar, P.; Sukhabogi, J.R.; Prasanna, J.S.; Mahajan, S.V. Assessing coronavirus fear in Indian population using the fear of COVID-19 scale. Int. J. Ment. Health Addict. 2021, 19, 2383–2391. [Google Scholar] [CrossRef] [PubMed]
- Vrinten, C.; McGregor, L.M.; Heinrich, M.; von Wagner, C.; Waller, J.; Wardle, J.; Black, G.B. What do people fear about cancer? A systematic review and meta-synthesis of cancer fears in the general population. Psycho-Oncology 2017, 26, 1070–1079. [Google Scholar] [CrossRef] [PubMed]
- Niknamian, S. The Impact of Stress, Anxiety, Fear and Depression in The Cause of Cancer in Humans. Am. J. Biomed. Sci. Res. 2019, 3, 363–370. [Google Scholar] [CrossRef]
- Gormley, M.; Knobf, M.T.; Vorderstrasse, A.; Aouizerat, B.; Hammer, M.; Fletcher, J.; D’Eramo Melkus, G. Exploring the effects of genomic testing on fear of cancer recurrence among breast cancer survivors. Psycho-Oncology 2021, 30, 1322–1331. [Google Scholar] [CrossRef] [PubMed]
- Lebel, S.; Tomei, C.; Feldstain, A.; Beattie, S.; McCallum, M. Does fear of cancer recurrence predict cancer survivors’ health care use? Support. Care Cancer 2013, 21, 901–906. [Google Scholar] [CrossRef] [PubMed]
- Von Ah Morano, A.E.; Dorneles, G.P.; Peres, A.; Lira, F.S. The role of glucose homeostasis on immune function in response to exercise: The impact of low or higher energetic conditions. J. Cell Physiol. 2020, 235, 3169–3188. [Google Scholar] [CrossRef] [PubMed]
- Jawad, S.; Winter, M.; Rahman, Z.-A.S.A.; Al-Yasir, Y.I.A.; Zeb, A. Dynamical Behavior of a Cancer Growth Model with Chemotherapy and Boosting of the Immune System. Mathematics 2023, 11, 406. [Google Scholar] [CrossRef]
- Tang, T.-Q.; Shah, Z.; Bonyah, E.; Jan, R.; Shutaywi, M.; Alreshidi, N. Modeling and Analysis of Breast Cancer with Adverse Reactions of Chemotherapy Treatment through Fractional Derivative. Comput. Math. Methods Med. 2022, 2022, 5636844. [Google Scholar] [CrossRef]
- Alharbi, S.A.; Rambely, A.S. A New ODE-Based Model for Tumor Cells and Immune System Competition. Mathematics 2020, 8, 1285. [Google Scholar] [CrossRef]
- Wang, X.; Zanette, L.; Zou, X. Modelling the fear effect in predator–prey interactions. J. Math. Biol. 2016, 73, 1179–1204. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef] [PubMed]
- De Pillis, L.G.; Radunskaya, A. A mathematical tumor model with immune resistance and drug therapy: An optimal control approach. Comput. Math. Methods Med. 2001, 3, 79–100. [Google Scholar] [CrossRef]
- Gatenby, R.A. The potential role of transformation-induced metabolic changes in tumor-host interaction. Cancer Res. 1995, 55, 4151–4156. [Google Scholar] [PubMed]
- Abdulkream Alharbi, S.; Dehingia, K.; Jahman Alqarni, A.; Alsulami, M.; Al Qarni, A.A.; Das, A.; Hinçal, E. A study on ODE-based model of risk breast cancer with body mass. Appl. Math. Sci. Eng. 2023, 31, 2259059. [Google Scholar] [CrossRef]
- Ouifki, R.; Oke, S.I. Mathematical model for the estrogen paradox in breast cancer treatment. J. Math. Biol. 2022, 84, 28. [Google Scholar] [CrossRef]
- Das, A.; Dehingia, K.; Ray, N.; Sarmah, H.K. Stability analysis of a targeted chemotherapy-cancer model. Math. Model. Control 2023, 3, 116–126. [Google Scholar] [CrossRef]
- Sahoo, B.; Poria, S. Diseased prey predator model with general Holling type interactions. Appl. Math. Comput. 2014, 226, 83–100. [Google Scholar] [CrossRef]
- Hubbard, J.H.; West, B.H. Differential Equations: A Dynamical Systems Approach: Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2013; Volume 5. [Google Scholar]
- Alebraheem, J.; Ibrahim, T.Q.; Arif, G.E.; Hamdi, A.A.; Bazighifan, O.; Ali, A.H. The stabilizing effect of small prey immigration on competitive predator-prey dynamics. Math. Comput. Model. Dyn. Syst. 2024, 30, 605–625. [Google Scholar] [CrossRef]
- Ahmed, M.; Jawad, S. Bifurcation Analysis of the Role of Good and Bad Bacteria in the Decomposing Toxins in the Intestine with the Impact of Antibiotic and Probiotics Supplement. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2024; Volume 3097. [Google Scholar]
- Bassim, W.B.; Salem, A.J.; Ali, A.H. A new analytical study of prey-predator dynamical systems involving the effects of Hide-and-Escape and predation skill augmentation. Results Control Optim. 2024, 16, 100449. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Jawad, S.; Majeed, S.J.; Nisar, K.S. Impact of wind flow and global warming in the dynamics of prey-predator model. Results Control Optim. 2024, 15, 100424. [Google Scholar] [CrossRef]
- Jawad, S.R.; Al Nuaimi, M. Persistence and bifurcation analysis among four species interactions with the influence of competition, predation and harvesting. Iraqi J. Sci. 2023, 64, 1369–1390. [Google Scholar] [CrossRef]
- Hassan, S.K.; Jawad, S.R. The Effect of Mutual Interaction and Harvesting on Food Chain Model. Iraqi J. Sci. 2022, 63, 2641–2649. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Jawad, S.; Shah, K.; Abdeljawad, T. How does media coverage affect a COVID-19 pandemic model with direct and indirect transmission? J. Math. Comput. Sci. 2024, 35, 169–181. [Google Scholar] [CrossRef]
- Ali, A.; Jawad, S. Stability analysis of the depletion of dissolved oxygen for the Phytoplankton-Zooplankton model in an aquatic environment. Iraqi J. Sci. 2024, 65, 2736–2748. [Google Scholar] [CrossRef]
- Mondal, B.; Thirthar, A.A.; Sk, N.; Alqudah, M.A.; Abdeljawad, T. Complex dynamics in a two species system with Crowley–Martin response function: Role of cooperation, additional food and seasonal perturbations. Math. Comput. Simul. 2024, 221, 415–434. [Google Scholar] [CrossRef]
- Pakhira, R.; Mondal, B.; Thirthar, A.A.; Alqudah, M.A.; Abdeljawad, T. Developing a fuzzy logic-based carbon emission cost-incorporated inventory model with memory effects. Ain Shams Eng. J. 2024, 15, 102746. [Google Scholar] [CrossRef]
- Thirthar, A.A. A mathematical modelling of a plant-herbivore community with additional effects of food on the environment. Iraqi J. Sci. 2023, 64, 3551–3566. [Google Scholar] [CrossRef]
- Sk, N.; Mondal, B.; Thirthar, A.A.; Alqudah, M.A.; Abdeljawad, T. Bistability and tristability in a deterministic prey–predator model: Transitions and emergent patterns in its stochastic counterpart. Chaos Solitons Fractals 2023, 176, 114073. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).