Study of the Sloshing Dynamics in Partially Filled Rectangular Tanks with Submerged Baffles Using VOF and LES Turbulence Methods for Different Impact Angles
Abstract
1. Introduction
2. Numerical Model
2.1. Governing Equations
2.2. Volume of Fluid (VOF)
2.3. Sloshing Natural Frequency
3. Simulation Setup
3.1. Tank Schematic and Mesh
3.2. Method of Solution
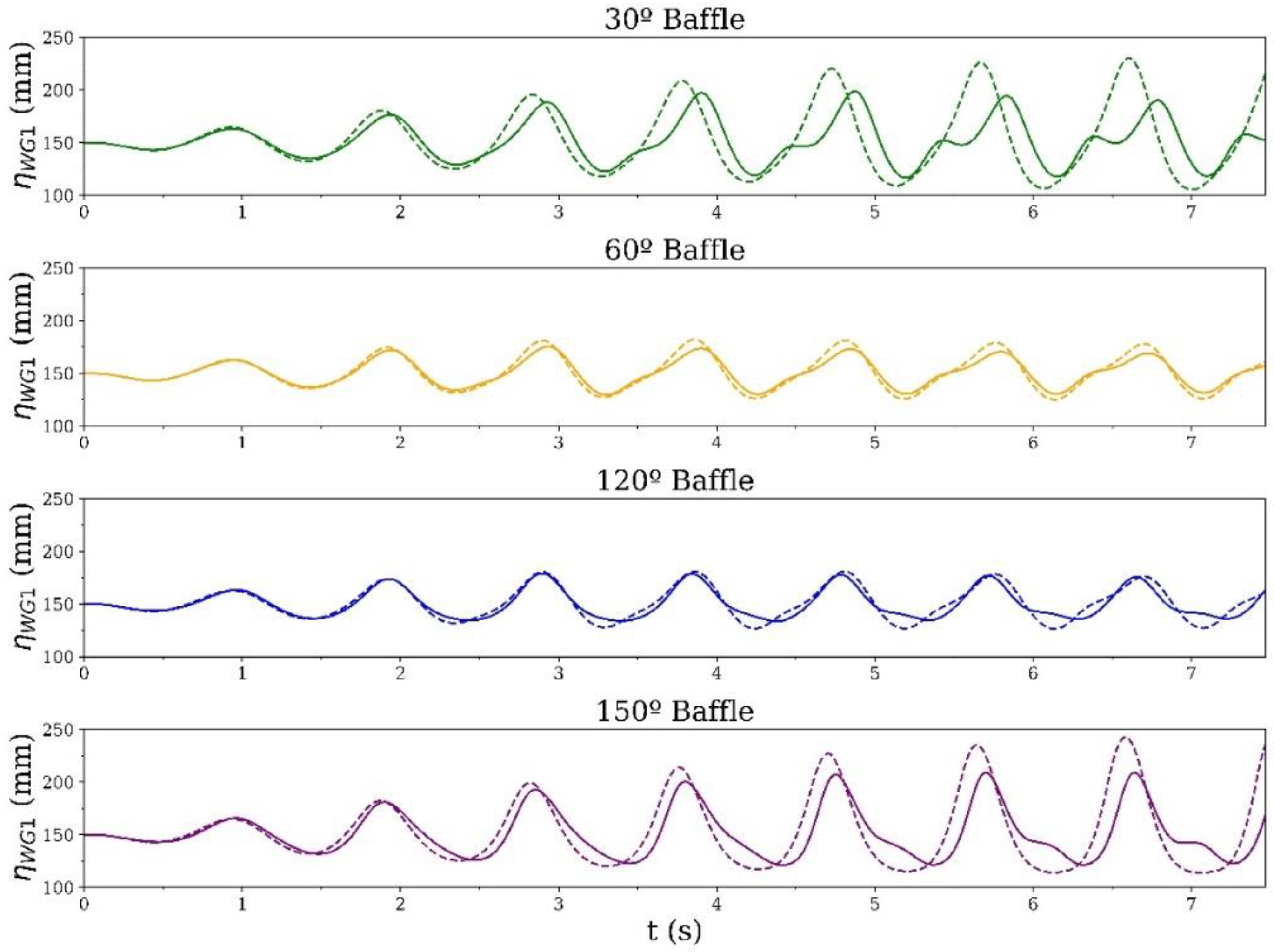
3.3. Model Validation
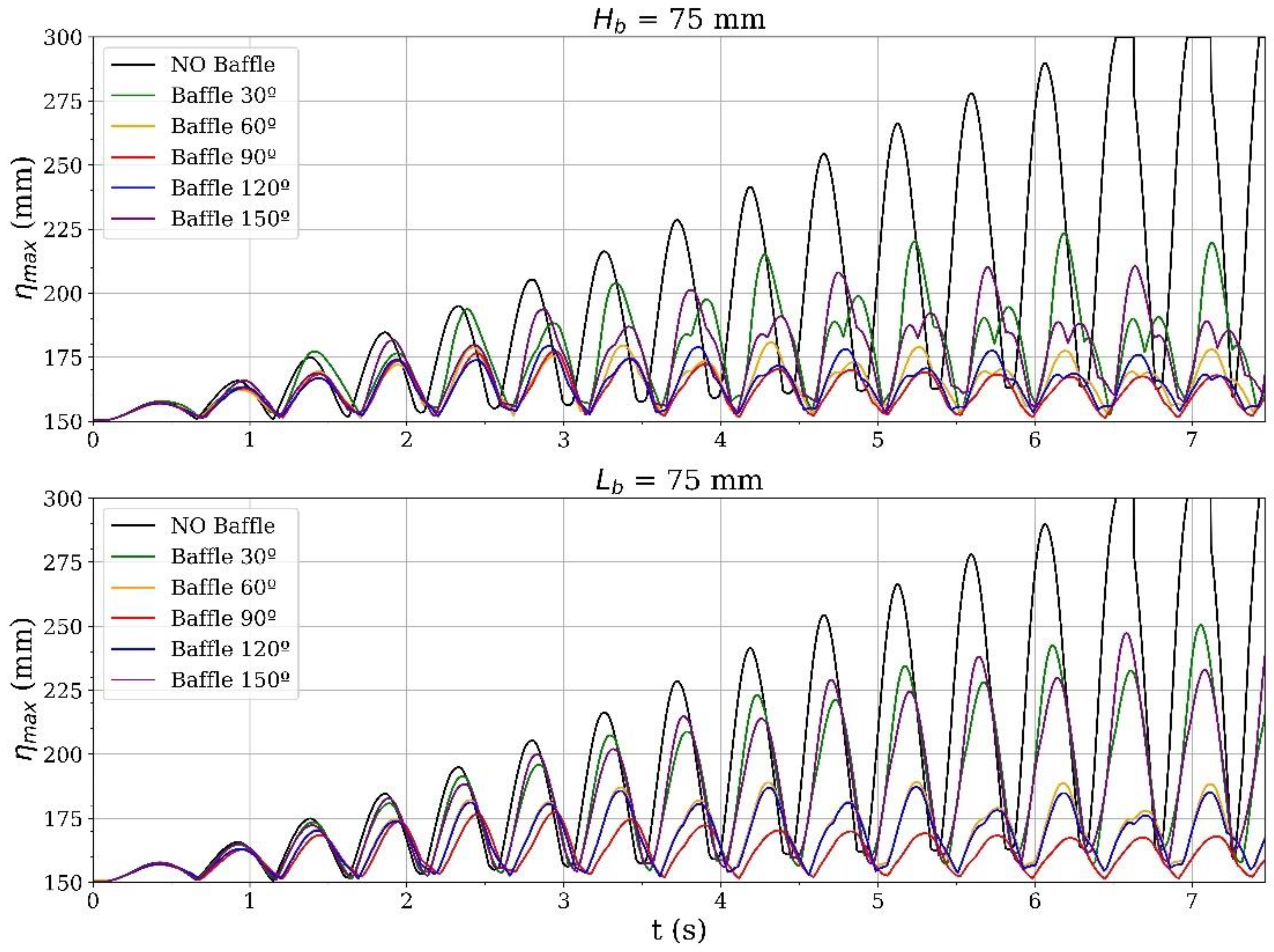
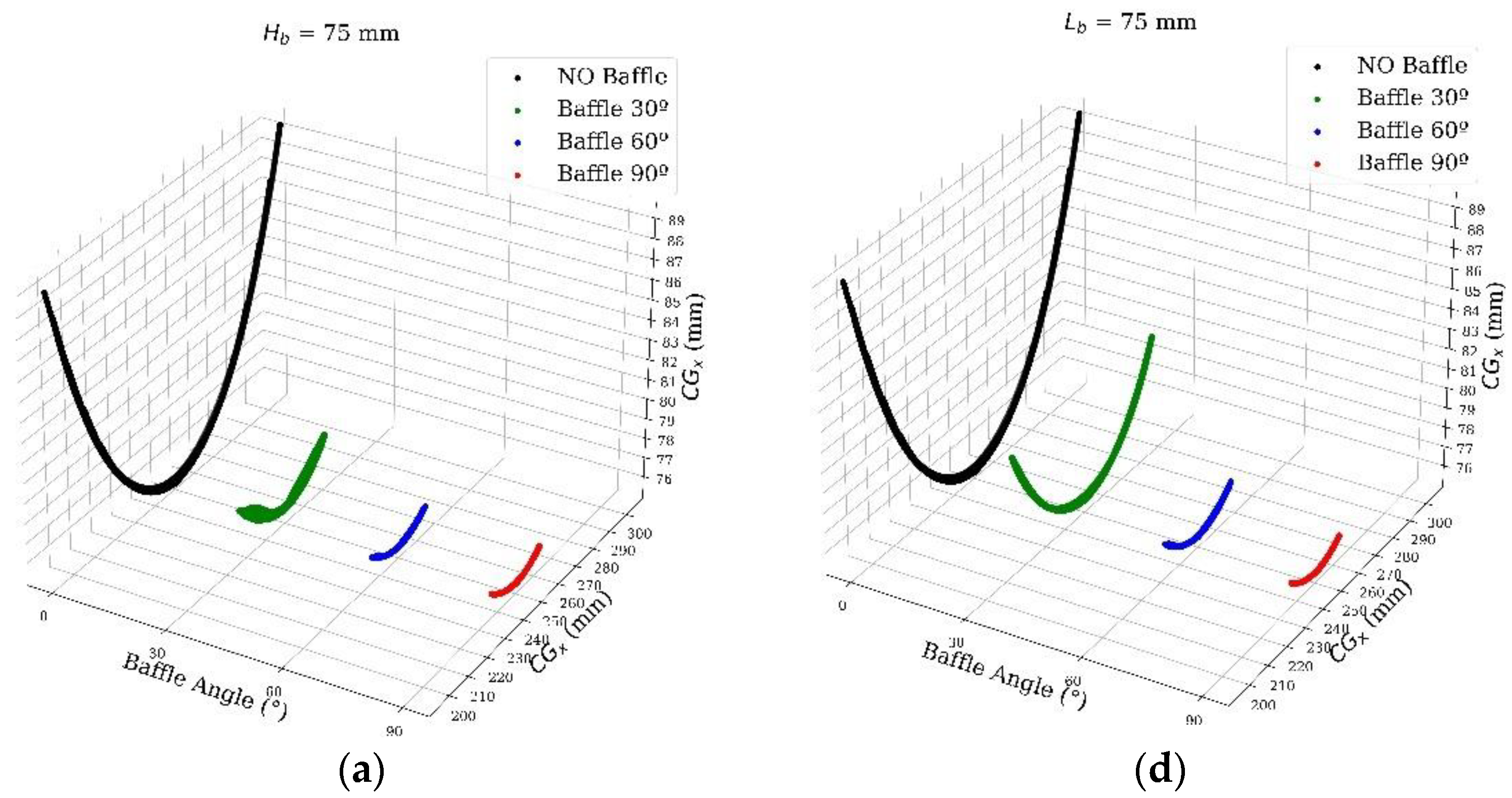
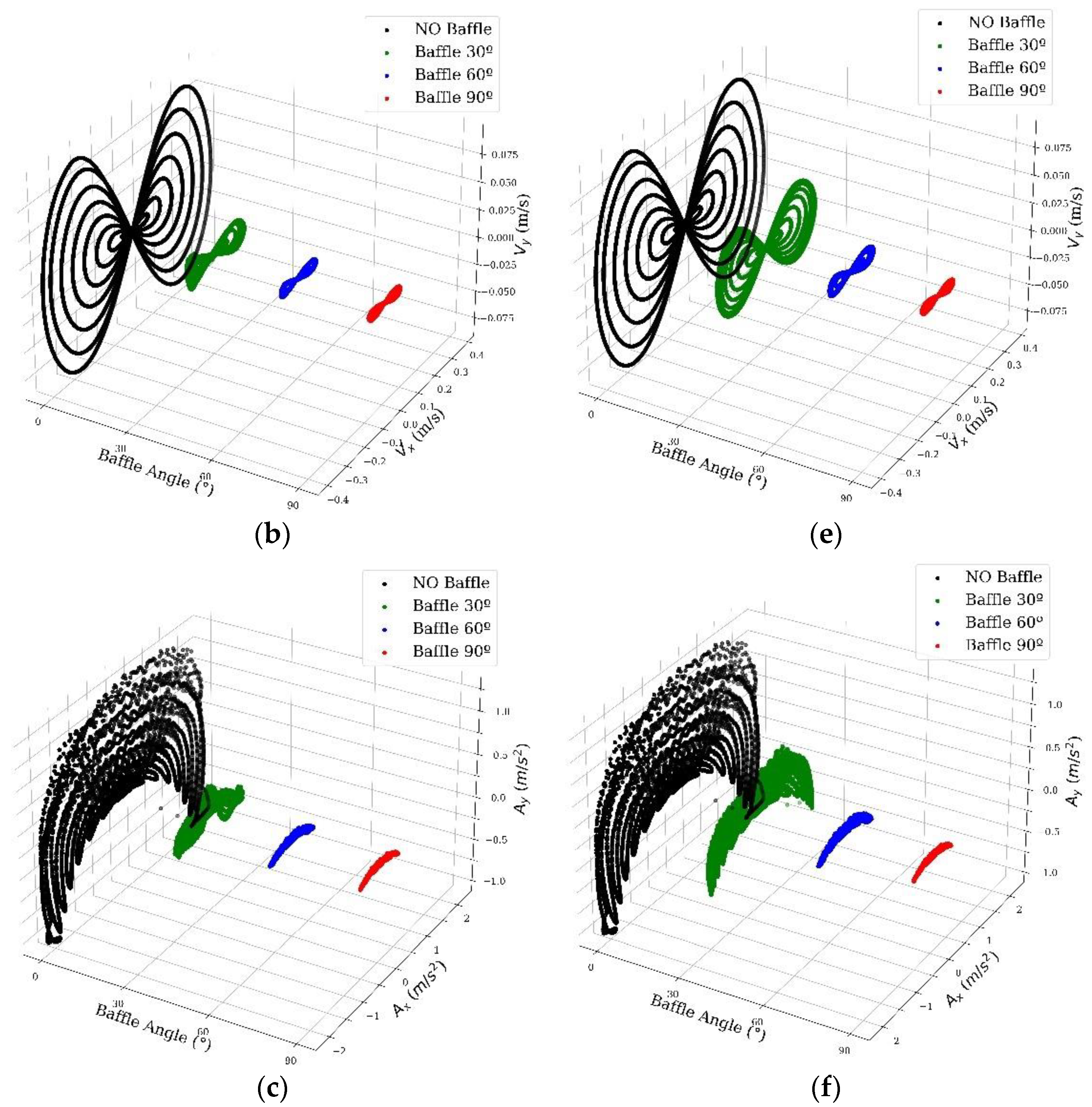
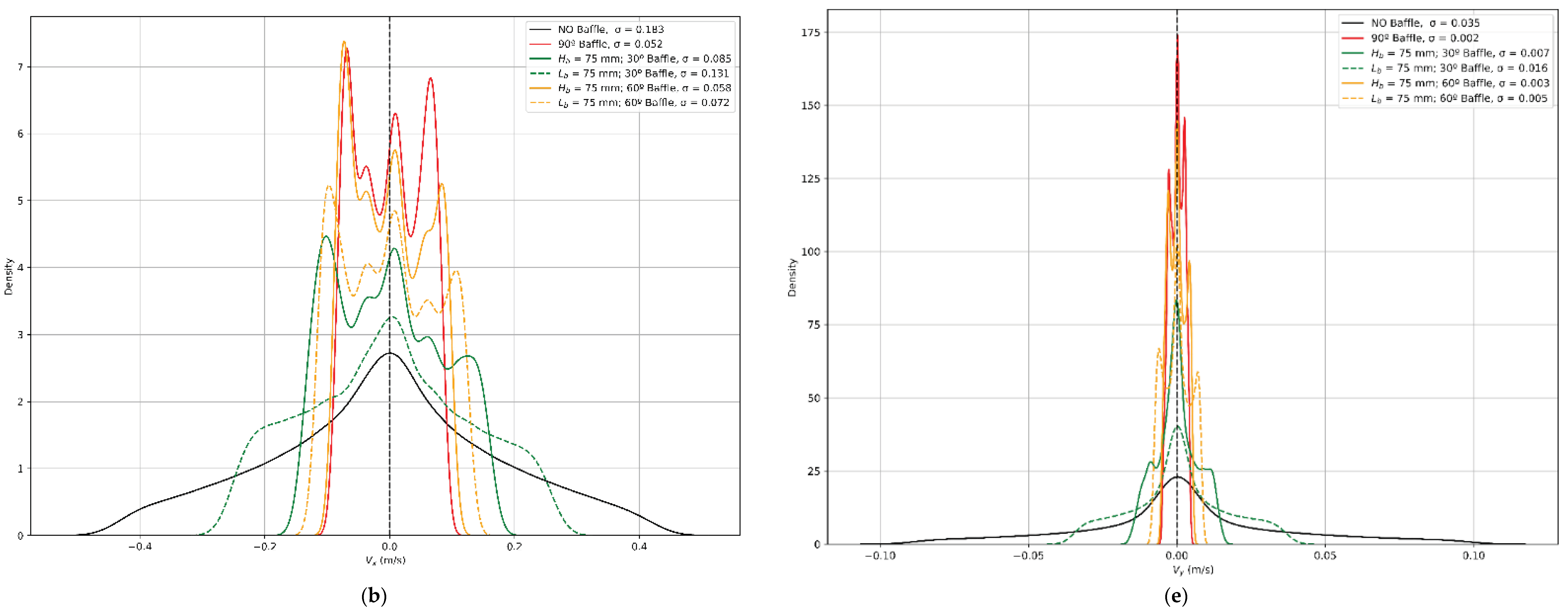
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Xue, M.A.; Chen, Y.; Zheng, J.; Qian, L.; Yuan, X. Fluid dynamics analysis of sloshing pressure distribution in storage vessels of different shapes. Ocean Eng. 2019, 192, 106582. [Google Scholar] [CrossRef]
- Craig, K.J.; Kingsley, T.C. Design optimization of containers for sloshing and impact. Struct. Multidiscip. Optim. 2007, 33, 71–87. [Google Scholar] [CrossRef]
- Kandasamy, T. An Analysis of Baffles Designs for Limiting Fluid Slosh in Partly Filled Tank Trucks. Open Transp. J. 2010, 4, 23–32. [Google Scholar] [CrossRef]
- Goudarzi, M.A.; Sabbagh-Yazdi, S.R.; Marx, W. Investigation of sloshing damping in baffled rectangular tanks subjected to the dynamic excitation. Bull. Earthq. Eng. 2010, 8, 1055–1072. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Aghabeigi, M. Sloshing characteristics in half-full horizontal elliptical tanks with vertical baffles. Appl. Math. Model. 2012, 36, 57–71. [Google Scholar] [CrossRef]
- Zheng, X.L.; Li, X.S.; Ren, Y.Y.; Wang, Y.N.; Ma, J. Effects of transverse baffle design on reducing liquid sloshing in partially filled tank vehicles. Math. Probl. Eng. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Hosseini, M.; Vosoughifar, H.; Farshadmanesh, P. Simplified Dynamic Analysis of Sloshing in Rectangular Tanks with Multiple Vertical Baffles. J. Water Sci. Res. 2013, 5, 19–30. [Google Scholar]
- Bautista-Jacobo, J.L.; Rodríguez-Morales, E.; Montes-Rodríguez, J.J.; Gámez-Cuatzín, H. Effect of Baffles on the Sloshing in Road Tankers Carrying LPG: A Comparative Numerical Study. Math. Probl. Eng. 2015, 2015, 35947. [Google Scholar] [CrossRef]
- Shreeharsha, H.V.; Shivakumar, S.G.; Mallikarjun, S.G. Simulation of Sloshing in Rigid Rectangular Tank and a Typical Aircraft Drop Tank. J. Aeronaut. Aerosp. Eng. 2017, 6, 1–9. [Google Scholar] [CrossRef]
- Khezzar, L.; Seibi, A.; Goharzadeh, A. Water sloshing in rectangular tanks—An experimental investigation\& numerical simulation. Int. J. Eng. 2009, 3, 174–184. [Google Scholar]
- Demirel, E.; Aral, M.M. Liquid sloshing damping in an accelerated tank using a novel slot-baffle design. Water 2018, 10, 1565. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Ho-Huu, V.; Nguyen, T.K. Optimal design of circular baffles on sloshing in a rectangular tank horizontally coupled by structure. Water 2018, 10, 1504. [Google Scholar] [CrossRef]
- Dinçer, A.E. Investigation of the sloshing behavior due to seismic excitations considering two-way coupling of the fluid and the structure. Water 2019, 11, 2664. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.A.; Jiang, Z. Experimental investigation of parametric sloshing in a tank with vertical baffles. Ocean Eng. 2020, 213, 107783. [Google Scholar] [CrossRef]
- Guan, Y.; Yang, C.; Chen, P.; Zhou, L. Numerical investigation on the effect of baffles on liquid sloshing in 3D rectangular tanks based on nonlinear boundary element method. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 399–413. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Liquid Sloshing Dynamics: Theory and Applications; Cambridge University Press: Cambridge, UK, 2005; Volume 1, p. 970. Available online: https://books.google.com/books?id=ctvhvH74ZzEC (accessed on 15 May 2021).
- Xue, M.A.; Zheng, J.; Lin, P. Numerical simulation of sloshing phenomena in cubic tank with multiple baffles. J. Appl. Math. 2012, 2012, 1–21. [Google Scholar] [CrossRef]
- Joshi, A.Y.; Bansal, A.; Rakshit, D. Effects of Baffles on Sloshing Impact Pressure of a Chamfered Tank. Procedia Eng. 2017, 173, 940–947. [Google Scholar] [CrossRef]
- Saravanan, G.; Sannasiraj, S.A.; Sundar, V. Asymptotic Analysis of Sloshing in a Rectangular Tank. Int. J. Ocean Clim. Syst. 2014, 5, 89–103. [Google Scholar] [CrossRef]
- Pandit, A.; Biswal, K.C. Sloshing response of partially filled rectangular tank under periodic horizontal ground motion. MATEC Web Conf. 2018, 172, 1–5. [Google Scholar] [CrossRef][Green Version]
- Xue, M.; Lin, P.Z.; Zheng, J.H.; Ma, Y.X.; Yuan, X.L.; Nguyen, V.T. Effects of perforated baffle on reducing sloshing in rectangular tank: Experimental and numerical study. China Ocean Eng. 2013, 27, 615–628. [Google Scholar] [CrossRef]
- Okamoto, T.; Kawahara, M. Two-dimensional sloshing analysis by Lagrangian finite element method. Int. J. Numer. Methods Fluids 1990, 11, 453–477. [Google Scholar] [CrossRef]
- Tahmasebi, M.K.; Shamsoddini, R.; Abolpour, B. Performances of Different Turbulence Models for Simulating Shallow Water Sloshing in Rectangular Tank. J. Mar. Sci. Appl. 2020, 19, 381–387. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. A Finite Volume approximation of the Navier-Stokes equations with nonlinear filtering stabilization. Comput. Fluids 2019, 187, 27–45. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. A POD-Galerkin reduced order model for a LES filtering approach. J. Comput. Phys. 2021, 436, 110260. [Google Scholar] [CrossRef]








| hmax RMS | WG1 RMS | WG2 RMS | WG3 RMS | xmax RMS | ||
|---|---|---|---|---|---|---|
| Lb | −0.46 | −0.58 | 0.61 | −0.49 | 0.098 | |
| Hb | −0.92 | −0.96 | 0.94 | −0.92 | 0.92 | |
| Cb | −0.014 | −0.16 | 0.15 | −0.05 | −0.3 | |
| CGx min | CGx max | CGx RMS | CGy min | CGy max | CGy RMS | |
| Lb | 0.56 | −0.58 | −0.38 | 0.94 | −0.66 | −0.51 |
| Hb | 0.88 | −0.97 | −0.73 | 0.62 | −0.96 | −0.94 |
| Cb | 0.18 | −0.15 | −0.036 | 0.89 | −0.27 | −0.073 |
| Vx min | Vx max | Vx RMS | Vy min | Vy max | Vy RMS | |
| Lb | 0.6 | −0.6 | −0.54 | 0.66 | −0.66 | −0.63 |
| Hb | 0.97 | −0.97 | −0.96 | 0.96 | −0.96 | −0.97 |
| Cb | 0.17 | −0.17 | −0.091 | 0.27 | −0.26 | −0.22 |
| Ax min | Ax max | Ax RMS | Ay min | Ay max | Ay RMS | |
| Lb | 0.56 | −0.56 | −0.54 | 0.7 | −0.57 | −0.61 |
| Hb | 0.96 | −0.96 | −0.96 | 0.98 | −0.93 | −0.96 |
| Cb | 0.12 | −0.12 | −0.093 | 0.3 | −0.16 | −0.2 |
| s CGx | s CGy | s Vx | s Vy | s Ax | s Ay | |
| Lb | −0.53 | −0.65 | −0.54 | −0.63 | −0.55 | −0.61 |
| Hb | −0.96 | −0.97 | −0.96 | −0.97 | −0.87 | −0.96 |
| Cb | −0.086 | −0.25 | −0.088 | −0.22 | −0.14 | −0.2 |
| FLW min | FLW max | FLW RMS | FRW min | FRW max | FRW RMS | |
| Lb | 0.61 | −0.59 | 0.43 | 0.56 | −0.57 | −0.71 |
| Hb | 0.97 | −0.94 | 0.88 | 0.96 | −0.96 | −0.98 |
| Cb | 0.19 | −0.19 | 0.014 | 0.12 | −0.14 | −0.31 |
| s FLW | s FRW | |||||
| Lb | −0.5 | −0.5 | ||||
| Hb | −0.94 | −0.94 | ||||
| Cb | −0.059 | −0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallés Rebollo, X.; Sadeghi, E.; Kusano, I.; García-Granada, A.-A. Study of the Sloshing Dynamics in Partially Filled Rectangular Tanks with Submerged Baffles Using VOF and LES Turbulence Methods for Different Impact Angles. Computation 2022, 10, 225. https://doi.org/10.3390/computation10120225
Vallés Rebollo X, Sadeghi E, Kusano I, García-Granada A-A. Study of the Sloshing Dynamics in Partially Filled Rectangular Tanks with Submerged Baffles Using VOF and LES Turbulence Methods for Different Impact Angles. Computation. 2022; 10(12):225. https://doi.org/10.3390/computation10120225
Chicago/Turabian StyleVallés Rebollo, Xavier, Ehsan Sadeghi, Ibuki Kusano, and Andrés-Amador García-Granada. 2022. "Study of the Sloshing Dynamics in Partially Filled Rectangular Tanks with Submerged Baffles Using VOF and LES Turbulence Methods for Different Impact Angles" Computation 10, no. 12: 225. https://doi.org/10.3390/computation10120225
APA StyleVallés Rebollo, X., Sadeghi, E., Kusano, I., & García-Granada, A.-A. (2022). Study of the Sloshing Dynamics in Partially Filled Rectangular Tanks with Submerged Baffles Using VOF and LES Turbulence Methods for Different Impact Angles. Computation, 10(12), 225. https://doi.org/10.3390/computation10120225







