Abstract
A business process or workflow is an assembly of tasks that accomplishes a business goal. Business process management is the study of the design, configuration/implementation, enactment and monitoring, analysis, and re-design of workflows. The traditional methodology for the re-design and improvement of workflows relies on the well-known sequence of extract, transform, and load (ETL), data/process warehousing, and online analytical processing (OLAP) tools. In this paper, we study the ad hoc queryiny of process enactments for (data-centric) business processes, bypassing the traditional methodology for more flexibility in querying. We develop an algebraic query language based on “incident patterns” with four operators inspired from Business Process Model and Notation (BPMN) representation, allowing the user to formulate ad hoc queries directly over workflow logs. A formal semantics of this query language, a preliminary query evaluation algorithm, and a group of elementary properties of the operators are provided.
1. Introduction
According to Gartner, business process (BP) improvement is the top business strategy in enterprise systems [1]. The design and adjustment of workflows relies on the analysis of past workflow executions, and thus the ability to query characteristics of past executions is key for BP improvement. This paper initiates the development of a query language for ad hoc exploration of BP execution logs.
Although analyzing workflow execution has been studied variously and used in practice, directly querying workflow logs is a new approach. The state-of-the-art design/development methodology for BP/workflow management systems places the data needed for analysis in process logs, activity logs, data stores, process models, and even execution engines [2,3]. In the past two decades, the database community invested significant effort into data warehousing and business intelligence (BI) to help enterprises with their analysis of workflow executions. A centerpiece of data/process warehouse/BI techniques is extract, transform, load (ETL): extract data from various databases storing workflow execution data, transform them into suitable forms (e.g., relations), and load the data into a data warehouse. Online analytic processing (OLAP) tools are then used for process analysis [4,5].
Figure 1 illustrates the traditional framework as described in [6]. The workflow engine schedules and manages executions of workflow instances (enactments). The effects of these executions are stored in multiple databases. ETL tools extract data of interest, then transform and store them in a data warehouse. Online analytics processing (OLAP) is then applied to the data in the data warehouse.
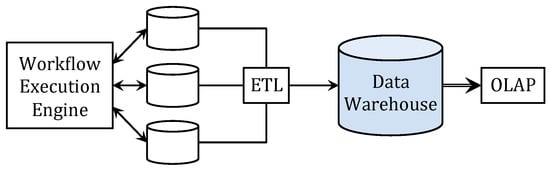
Figure 1.
Traditional framework using extract, transform, load (ETL)/online analytic processing (OLAP).
ETL/OLAP is seriously challenged as enterprises demand more flexible process analytics. ETL aims at specific types of analysis, often with queries centered around summaries over data cubes [6]. This is effective only when relevant data are extracted. For example, if timestamps are not extracted, analysis of activity duration is not possible, or if drug prescriptions are not available in the data warehouse, it is impossible to detect healthcare fraud (e.g., patients being over-prescribed drugs and selling them in the underground market) through these ETL analytics.
Figure 2 illustrates the approach for the flexible process analysis we develop in this paper. While the workflow engine advances workflow instances, it also records the key actions in a workflow (execution) log in addition to the relevant databases. The log faithfully records the execution traces for all active instances in their execution order. Queries can then be formulated against the log, and the user is empowered to pose ad hoc queries over the log to learn about and explore past workflow executions. Since there is no prior data selection nor filtering, log queries allow the user to formulate a much richer class of queries.
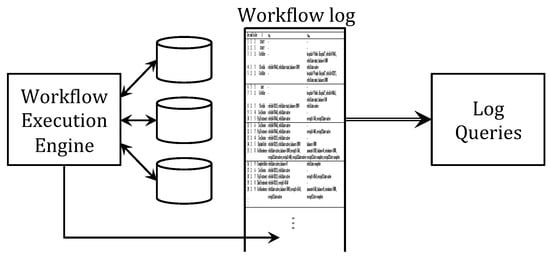
Figure 2.
Our framework for flexible process analysis.
This paper develops an algebraic query language based on “incident patterns” for process analytics. Intuitively, an incident pattern describes a temporally related set of activity executions within a single workflow instance, allowing the user to reason about temporal relationships between the activity executions. Inspired by Business Process Model and Notation (BPMN) gateways, four operators are used to formulate temporal relationships: consecutive, sequential, choice, and parallel operators, whose formal semantics are defined in this paper. A query evaluation algorithm and algebraic properties of the operators are also presented.
This paper is organized as follows. Section 2 gives the formal definitions of workflow log, incident patterns, and incident instances. Section 3 presents a query evaluation algorithm. Section 4 provides properties concerning incident patterns. Section 5 discusses related work. Finally, Section 6 concludes the paper.
2. Logs and Incidents
In this section, we introduce key concepts needed for the log query language and the technical discussions, including a “log record”, “log”, “incident pattern”, “incident instance”, and “incident set”. Log records are fundamental units of logs, with each log record corresponding to data generated by the execution of one activity in a workflow instance. Incident patterns serve as query expressions in the log query language presented in this paper.
We start with a formal exposition that will serve as the basis for both the syntax of the query language and its semantics. We assume the existence of the following pairwise disjoint, countably infinite sets:
- of attribute names,
- of activity names,
- of values, and
- of (positive) natural numbers.
We assume that logs are generated by workflows that include data attributes or variables. Such workflows include data-centric workflow systems (such as Barcelona/GSM [7]) or activity-centric workflows that have data variables (such as YAWL [8], jBPM [9], etc.). Specifically, every workflow has a set of attributes and a set of activities. An attribute is either undefined, denoted as ⊥, or has a value in . A map is a mapping whose domain is finite (i.e., a mapping defines values only for a finite set of attributes).
At runtime, a workflow model can have multiple workflow instances (or enactments); each instance has a distinct identifier called a (workflow) instance id.
A workflow “log” faithfully records the effects of workflow executions at runtime, logging data about workflow instances, decisions made, external systems interactions, etc. In particular, a workflow log keeps the information about changes to data values. There is no standard structure for workflow logs for collecting and maintaining results from workflow execution. For example, in the health management application system we examined with the team at Shan Dong University in China, workflow logging is accomplished through three separate logs for activities, workflow instance launches and completions, and business operations. Workflow management systems such as jBPM often provide mechanisms for workflow instance logging, but the primary goal of these systems is to support reasoning about business operations rather than to support querying data concerning workflow instances and executions.
To formulate the notion of a log for our study, we first define a “log record” (i.e., an entry in a log), using a relation signature over the domain.
Definition 1.
A log record is a tuple where
- is a log sequence number,
- is a workflow instance id identifying the workflow instance to which this log record belongs,
- is an instance-specific log sequence number (unique within each instance),
- is an activity name,
- is an input map over the attributes read by activity t, and
- is an output map over the attributes written by activity t.
To simplify technical discussions, we use the following functions to extract components of a log record: for each log record l, is its log sequence number, the workflow instance id, the instance-specific log sequence number, the activity name, the input map, and the output map.
Example 1.

Consider a system that manages referrals made at a medical clinic. Workflow activity instances in this system can be captured by log records, creating a collection of log records as shown in Figure 3. The log record with “” in the figure is the following log record from this system:

Figure 3.
An initial segment of a medical clinic referral log.
This log record l is the fourth log record in the log (). It belongs to the workflow instance with id 1 (). It was produced by the third activity executed in the workflow instance (), where this activity is named CheckIn (). Finally, , which means that the activity CheckIn reads attribute referId having value , attribute referState having value start, and attribute balance having value 1000, and indicates that CheckIn activity updates the value of referState to active.
In addition, we introduce two special log records start and end. A start log record is the first log record for a workflow instance. For all start log records l, and the activity name “start”. Similarly, an end log record is the last log record for a workflow instance with activity name “end”. In all start and end log records, the input and output maps are empty.
Definition 2.
A log L is a nonempty finite set of log records that satisfies all of the following conditions:
- 1.
- There is a bijection between the first natural numbers and the set of all log sequences numbers present in the log records in L, and
For each log record ,
- 2.
- iff = start (each workflow instance begins with a start record),
- 3.
- If , then there is a log record such that , , and (for each workflow instance, is consecutive), and
- 4.
- If end, for all log records , implies (end is the last record for each workflow instance).
In the above definition, Condition (1) ensures a total ordering on the log records in the log through their log sequence numbers. Conditions (2) and (3) together guarantee that the first and only the first log record of every workflow is a start record. Condition (3) further insists that the instance-specific log sequence numbers of each workflow instance is also an initial segment of the natural numbers starting from 1. Condition (4) states that an end log record denotes the largest log sequence number and the largest instance-specific log sequence number among all log records of the same workflow instance.
Note that each workflow instance must have a start record in the log, but may not have an end record (the instance is not yet completed). Although a log is a set of log records by definition, when the context is clear, we view a log as a sequence of log records in the ascending order of their log sequence numbers.
Example 2.
College clinics in China usually lack the necessary staff and equipment to treat certain medical conditions and to perform intensive medical procedures such as cancer treatment, dental care, etc. For such cases, medical staff refer students to local hospitals for proper care. Each referral has a fixed budget that is the maximum reimbursable amount of the medical cost, where the maximum allowed reimbursement may be different for different medical conditions. The referral process always starts when a student gets a referral from a doctor in a college clinic. Then, the student checks in at the referred hospital, where doctors provide further diagnoses and treatment. The student pays fees and get receipts for treatment. After receiving the receipts, the student may go to the refund center in her college clinic for reimbursement if the referral status remain active. Additionally, the referral—including the balance—can be updated if a diagnosis made at the referred hospital differs from the original diagnoses made in the college clinic. When this happens, the new balance may be used for all receipts after such an update. The student can request to terminate the active referral at any time.
Figure 3 shows an initial portion of a log of a clinic referral system. We can identify three workflow instances running, as the column wid—which stores ids of workflow instances—has three distinct values. Every workflow instance always starts with a start log record. Each subsequent log record of that instance contains the name of a workflow activity in the column t, and input, output maps for attributes being read and written as shown in the column , , respectively.
Querying the log shown in Figure 3 would allow doctors and administrators in the college clinic to make improvements to the current referral process. A doctor might wonder if there are any students who update their referrals before they receive a reimbursement. Specifically, consider the question “Are there any students who update their referral before they receive a reimbursement for associated medical care?”. This can be reformulated as a question about the log, “Is there a workflow instance in which a log record of the UpdateRefer activity has a lower instance-specific log sequence number than a log record of the GetReimburse activity?” In the example log in Figure 3, the answer is “yes”: for workflow instance with wid 2, there is a log record for an UpdateRefer activity with and another log record for a GetReimburse activity with .
Note that the above query examines only temporal relationships of records in the log rather than values of attributes (e.g., balance, hospital). In order to identify anomalous temporal relationships, the user can formulate potential patterns of activity ordering in a workflow instance as they occur in workflow log. This ad hoc nature of querying the log empowers the user to perform flexible analysis of the past and current workflow executions. We aim at developing a query language capable of examining activities and formulating temporal constraints among activities.
Consider again the query “Are there any students who update their referral before they receive a reimbursement for associated medical care?” discussed in the above. The query concerns two activities GetReimburse and UpdateRefer, as well as the temporal relationship that UpdateRefer occurs before GetReimburse. To capture this relationship, we introduce the key notion of an “incident pattern”.
Definition 3.
An (incident) pattern is an expression in one of the following forms (assuming and are incident patterns)
- activity patterns (atomic): t, , where is an activity name,
- consecutive pattern: ( and are consecutively executed),
- sequential pattern: ( is executed before ),
- choice pattern: (one of and is executed), and
- parallel pattern: ( and are executed in parallel and share no log records).
For the remainder of this paper, we refer to an incident pattern simply as a pattern. Intuitively, each atomic pattern “matches” an activity that has been executed. If the pattern is positive (t), the matching activity has the activity name t; if the pattern is negative (), the matching activity has an activity name other than t. A pattern composed using at least one of the four operators is called a composite pattern. Matching a composite pattern requires a workflow instance matching each pattern used in the composition, and these matches satisfy an additional constraint. For a consecutive operator, one match must follow the other immediately in the workflow instance. A sequential operator is similar, but with a relaxed condition there could be a gap between the two matches. A choice pattern simply matches one of the matches. And finally, For a parallel pattern, a match is a “shuffle” of the two matches (i.e., keeping their original order).
Using patterns, we can now express the above query, “Are there any students who update their referral before they are reimbursed for associated medical care?”. The pattern for this query is simply a sequential composition:
UpdateRefer ⊙ GetReimburse where UpdateRefer and GetReimburse are the activity names corresponding to the actions specified in the above query.
Clearly, the notion of a “match” in the above discussion is intuitive and rather informal. In the following we define the notion of an “incident instance” that precisely captures the informal concept of a match. In general, an “incident instance” is a set of log records that satisfies all conditions in a pattern.
Definition 4.
Given a log L and a pattern p, an incident (instance) o of p in L is a set of log records in L with three functions , , and , recursively defined as follows.
- Atomic: if where is an activity name, then o is an incident of p whenever is a singleton set of a log record such that ;if where is an activity name, then o is an incident of p whenever is a singleton set of a log record such that .In both cases, we define , , and finally ,
- Consecutive: if , then o is an incident of p whenever is an incident of (), , , and .Also, we define , , and .
- Sequential: if , o is an incident of p whenever is an incident of (), , , and .We define , , and .
- Choice: if , o is an incident of p whenever o is an incident of or .
- Parallel: if , o is an incident of p whenever is an incident of (), , , and .We define , , and .
Let denote the set of all incidents of p in L.
Definition 4 provides a semantics for patterns. Specifically, each incident of a pattern in a log L is a subset of L. Incidents of atomic patterns are singleton sets with the record satisfying the activity condition. Incidents of a consecutive, sequential, and parallel pattern are simply a union of incidents of the sub-patterns used in the operators with additional constraints the instance-specific log sequence numbers must be consecutive (consecutive) or preceding (sequential), or the incidents must be disjoint (parallel). For a choice pattern, incidents are simply the incidents of a sub-pattern.
Example 3.
Consider again the query, “Are there any students who update their referral before they receive their reimbursement?”. The query is expressed as the pattern
Since the pattern contains two activity names, each incident of this pattern must contain two log records with activities UpdateRefer and GetReimburse, respectively. In addition, by the definition of incidents for sequential operator ⊙, the workflow ids of these two log records must the same (the referral and reimbursement to correspond to the same workflow instance). Furthermore (and more importantly), the instance-specific log sequence number of the UpdateRefer log record must be less than that of the GetReimburse log record. Combining the above conditions, the partial log example in Figure 3 only contains one incident of this pattern: .
Consider another incident pattern “SeeDoctor ⊙ (UpdateRefer ⊙ GetReimburse)”. This pattern captures situations where a student sees a doctor, updates their referral, then gets reimbursed. There is one incident of this pattern: shown in Figure 3.
We provide the following definition of equivalence that is used in the discussions on properties of patterns in Section 4.
Definition 5.
Two patterns and are equivalent, denoted as , if , for all logs L.
3. Query Evaluation
To use incident patterns as log queries in the exploration of logged workflow executions, patterns must be evaluated. In this section, we focus on the evaluation of a specific query on a given log. This is formulated in the following way: given a pattern p and a log L, find incident set .
By Definition 5, all equivalent patterns will produce the same incident set on the same log. One strategy for evaluating a query p would transform p into an equivalent query and evaluate . Theorems in Section 4 present statements of equivalence in the form of algebraic laws. Along with the observations later in this section, these could be used to transform queries as a first step in query optimization. This section presents an algorithm for the evaluation of a given query without optimizations.
3.1. Evaluation of Pattern Composition Operators
In this section, we discuss the evaluation of individual pattern composition operators. According to Definition 4, composing incidents for the operators is rather straightforward. Algorithm 1 shows detailed steps of composition for the four operators.
For evaluating pattern for some operator , incidents sets and are used. These sets are further assumed to be sorted by the value of the function (as defined in Definition 4), which corresponds to the earliest instance-specific log sequence number of the log record for each incident. This ordering is readily available in atomic incidents and is easily preserved in the evaluation process for composite patterns. For simplicity, we assume the log contains just one workflow id, as incidents never contain log records corresponding to multiple workflow instances. Relaxing this assumption can be done easily.
| Algorithm 1 Composite pattern operator evaluation algorithms | |
| Input: Incident sets inc1, inc2 | |
| Output: Incident set incL | |
| 1: | function Consecutive-Eval(inc1, inc2) |
| 2: | |
| 3: | for inc1, inc2 do |
| 4: | if then |
| 5: | .append(); |
| 6: | return |
| 7: | function Sequential-Eval(inc1, inc2) |
| 8: | |
| 9: | for inc1, inc2 do |
| 10: | if then |
| 11: | .append(); |
| 12: | return |
| 13: | function Choice-Eval(inc1, inc2) |
| 14: | |
| 15: | for inc1, inc2 do |
| 16: | if then |
| 17: | for ; i++; do |
| 18: | if o1[i] ≠ o2[i] then |
| 19: | break; |
| 20: | if then |
| 21: | .append(); |
| 22: | .append(); |
| 23: | return |
| 24: | function Parallel-Eval(inc1, inc2) |
| 25: | |
| 26: | for inc1, inc2 do |
| 27: | overlap ← False |
| 28: | for , do |
| 29: | if then |
| 30: | overlap = True |
| 31: | break; |
| 32: | if overlap = False then |
| 33: | .append(); |
| 34: | return |
The evaulation algorithms for four composition operators are shown as four functions in Algorithm 1.
- In the evaluation of a consecutive pattern , two pointers iterate over and , respectively. For each pair and , if , add to . If , the evaluation has time complexity and produces at most results.
- In the evaluation of a sequential pattern , two pointers iterate over and , respectively. For each pair and , if , add to . If , the evaluation has time complexity , and produces at most results.
- The evaluation of a choice pattern produces the set union of the input sets and . This requires the identification of duplicated incidents (i.e., sets of log records that are incidents of both and , and exclude the duplicates in the output set). If and are the number of activity names in and , respectively, checking that an incident of and an incident of are not identical is linear in . The time complexity of evaluating choice pattern p is thus . There are incidents in , with the maximum size occurring when the log contains one workflow instance and and share no incidents.
- The incident set of a parallel pattern contains the union of all pairs of incidents and such that and share no log records. Each incident is a sequence of log records ordered by their log sequence numbers. Assuming incidents are sorted, checking that two incidents are disjoint is linear in the number of activity names of the two incident. Letting be the number of activity names in pattern resp., the time complexity of evaluating a parallel pattern is . There are incidents in , with the maximal case occurring when the log contains one workflow instance and all pairs of incidents , are disjoint.
We summarize the above analysis in the following lemma.
Lemma 1.
Let L be a log, , two incident patterns, and , incident sets of and on L, respectively. Let and . The following hold:
- can be computed in time and has size at most .
- can be computed in time and has size at most .
- can be computed in time , where is the number of activity names in , and has size at most .
- can be computed in time , and has size at most .
In the evaluation of a choice pattern , checking for duplication in the output set is only necessary when and contain the same multiset of activity names. Letting be the multiset of activity names in pattern , resp., determining the equality of two incidents of and is linear in if . This equality can be determined in before the inspection of any incidents of the input sets. Otherwise, if the patterns do not contain the same multiset of activity names, the incident set of a choice pattern is the union of the disjoint sets and , and can be calculated in .
3.2. Evaluation of Incident Pattern Queries
Based on the algorithms for the evaluation of the operators, we present an algorithm for the evaluation of composite patterns. Our pattern evaluation strategy constructs an “incident tree”, and performs a post-order evaluation of the tree.
Definition 6.
An incident tree is a binary tree with two types of nodes—namely operator and activity nodes—such that:
- An operator node has both left and right child nodes, and is labeled with a pattern operator, and
- An activity node is a leaf node, labeled with an activity name for positive atomic patterns, adding “¬” before the activity name in the case of negative activity patterns.
Example 4.
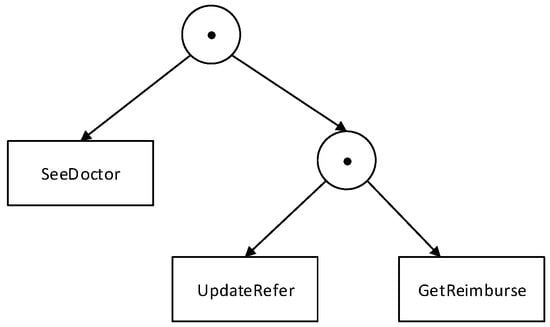
To illustrate incident trees, we use rectangles to represent activity nodes and circles for operator nodes. Figure 4 shows an incident tree for the pattern SeeDoctor ⊙ (UpdateRefer ⊙ GetRimburse).

Figure 4.
An incident tree for SeeDoctor ⊙ (UpdateRefer⊙ GetRimburse).
We perform a single pass scan over a pattern to build the corresponding incident tree, using the stack-based shunting-yard algorithm [10] (introduced by Edsger Dijkstra in 1961), which converts an expression in infix notation to postfix notation. Similar procedures are used to convert infix expressions to Reverse Polish notation [11].
The incident tree evaluation is performed starting with the leaf nodes and passing the incident sets for each subtree to its parent. More specifically, we process nodes according to post-order traversal of the incident tree, yielding an incident set for the given incident pattern at the root of the incident tree. An implementation is given in Algorithm 2.
In Algorithm 2, if the root node is a leaf, all log records with a matching (or un-matching) activity name are added to the output set . An index structure for each workflow id and activity is used to generate log records for an activity node in constant time. Otherwise, the root corresponds to a composite pattern, so a post-order evaluation is performed in lines 7 and 8. After the evaluation of incidents sets of the left and right subtrees, line 9 combines the results with the operator-specific function depending on the type of the root node. The function Operator-Eval invokes operator-specific algorithms discussed earlier in this section and formalized in Algorithm 1 to generate incident sets.
| Algorithm 2 Incident tree evaluation algorithm | |
| Input: Incident TreeNode , dictionary | |
| Output: Incident Set | |
| 1: | function Eval–Incident–Tree |
| 2: | ; |
| 3: | if root.type == ATOMIC then |
| 4: | for widSet do |
| 5: | if root.negated = False then |
| 6: | .append(LogRecordsDict[i](lr.activity_name = root.activity_name)); |
| 7: | else |
| 8: | .append(LogRecordsDict[i](lr.activity_name != root.activity_name)); |
| 9: | else |
| 10: | EvalIncidentTree(root.left, LogRecordsDict); |
| 11: | EvalIncidentTree(root.right, LogRecordsDict); |
| 12: | |
| 13: | for widSet do |
| 14: | OperatorEval(root.type, , ); |
| 15: | return incL |
Example 5.
For the incident tree in Figure 4, the evaluation Algorithm 3 starts at the leaf nodes SeeDoctor, UpdateRefer, and GetReimburse. A set of log records for each activity node is generated from the workflow log. In each set, the activity names in the log records are identical to the label of the corresponding activity node. For instance, the incidents of activity node SeeDoctor are incL .
The incident set for each leaf node is passed to its parent, the operator node at depth 2 in Figure 4. The evaluation proceeds by invoking the algorithm for the sequential operator, constructing the incident set; here, it is . Similarly, the result is passed to the root, which is also labelled with the sequential operator. The root performs the same operation and generates the final output .
| Algorithm 3 Incident tree generation algorithm | |
| Input: Incident pattern p (in postfix notation) | |
| Output: Incident Tree T, dictionary LogRecordsDict | |
| 1: | function BuildIncidentTree |
| 2: | TreeNode root ← new TreeNode(); |
| 3: | root.type ← p.type; ▹ operator_type {ATOMIC, CONS, SEQU, CHOICE, PARA} |
| 4: | if root.type==ATOMIC then |
| 5: | root.activity_name |
| 6: | root.negative = p.negative; ▹ p.negative is true iff p is a negative activity pattern |
| 7: | else |
| 8: | root.left ← EvalPattern(p.left_pattern); |
| 9: | root.right ← EvalPattern(p.right_pattern); |
| 10: | dictionary LogRecordsDict ; ▹ a dictionary mapping wid to log records of that wid |
| 11: | widSet |
| 12: | for do |
| 13: | LogRecordsDict[lr.wid].append(lr); |
| 14: | widSet + = lr.wid |
| 15: | return root, LogRecordsDict; |
Theorem 1.
Let L be a log with m log records and k the number of operators in a pattern p. The time complexity of evaluating p is .
Proof.
Let t be an activity name. The worst case time complexity for evaluation arises with pattern , which forms a left-deep incident tree with each leaf producing an incident set of size . An incident set produced by a node at depth d will have log records, indicating that the k⊕ operators with time complexity will have times , where . Thus, the overall time complexity is at most . ☐
4. Properties of Incident Operators
Incident patterns are algebraic expressions with four binary operators. In this section, we examine algebraic properties of the four pattern operators. The main results in the section establish commutative, associative, and distributive properties, which could serve as a basis for query optimization. For example, an associative law concerning an operator would allow the optimizer to choose between left-to-right and right-to-left evaluation paths. Although the study of query optimization techniques is beyond the scope of this paper, we believe that the log query evaluation algorithm presented in Section 3 can be significantly optimized.
Theorem 2 in the following states that all operators are associative.
Theorem 2.
for all patterns and all operators .
Proof.
Let L be an arbitrary log. It must be shown that for patterns , , . We prove the associativity of each operator individually.
- (Consecutive operator.) Suppose . According to Definition 4, , where are incidents of , , resp., , and . The same definition further implies that there are two incidents such that is an incident of . Thus, the three incidents have the following properties: , , , and is an incident of for .From these incidents, we construct an incident of as follows. Let . From the properties listed above, is an incident of . This, together with and , establishes that . Observing that , it follows .It must also hold that incidents of the right hand side, elements of , are incidents of the left hand side, elements of . This case is symmetric.
- (Sequential operator.) The proof is nearly identical to the proof for the consecutive operator, and can be formed by making the following replacements:
- becomes ,
- becomes ,
- become , and
- becomes .
- (Choice operator.) Let o be an incident of . Using the definition of the choice operator, this occurs if and only if o is an incident of or o is an incident of . Applying the same deconstruction to , o is an incident of if o is an incident or an incident of . This results in three cases for o: (1) , (2) , or (3) . The statement can be deconstructed into the same three cases using nearly identical reasoning. Therefore, .
- (Parallel operator.) If o is an incident of , there exists incidents and , such that and . The incident is an instance of pattern , which indicates there exists such that and . Since and , . By the disjointedness of and , we have . Because and , it follows that . Thus, membership in implies membership in . The proof for is symmetric.
☐
An operator is commutative if the ordering of its arguments is independent of the results of its evaluation. Theorem 3 below states that the choice operator ⊗ and parallel operator ⊕ are commutative.
Theorem 3.
For all patterns , and .
Proof.
Let L be an arbitrary log. We prove that for two patterns , the following holds: . Assuming that incident , o is an incident of or an incident of . If o is an incident of , o is an incident of . Similarly, if o is an incident of , . By assumption, o is an incident of or an incident of , so . It follows that . The other direction follows from a nearly identical proof. Thus, the choice operator is commutative.
For the parallel operator, consider incident o such that and such that and . By Definition 4, o is an incident of and also of . If no such incidents exist, then o is not an incident of nor . Thus, iff . It follows that the parallel operator is commutative. ☐
The consecutive and sequential operators are not commutative for a trivial reason. Indeed, sets of log records whose instance-specific log sequence numbers satisfy the ordering provided by the consecutive or sequential operators will surely fail the inverted ordering.
Theorem 4 in the following states that in queries containing only the consecutive ⊖ and sequential ⊙ operators, these operators have equal precedence, extending the associativity proven in Theorem 2.
Theorem 4.
For all patterns , the following all hold.
- 1.
- , and
- 2.
- .
Proof.
For Part 1, let L be an arbitrary log and incidents from sets , and , respectively. Then, is an incident of if and only if , , and . These conditions are necessary and sufficient for to be an incident of .
A proof for Part 2 can be obtained from the proof of Part 1 by replacing the statements and with and . ☐
Finally, Theorem 5 provides left- and right-distributive properties of all operators over the choice operator ⊗.
Theorem 5.
For , the following all hold.
- 1.
- (left-distributive), and
- 2.
- (right-distributive).
Proof.
We prove Part 1 for three operators, as the proof for the choice operator is trivial. Let L be an arbitrary log.
- (Consecutive operator.) Let . This is equivalent to such that , , , and . The choice operator yields two possible cases: (1) , or (2) . Because , in Case (1), o has necessary and sufficient properties such that . Similarly in Case (2), . Combining both cases of membership with the choice operator yields , because or .
- (Sequential operator.) A proof for the sequential operator is obtained by replacing the statement “” in the proof for the consecutive operator with “”.
- (Parallel operator.) Let . This is equivalent to such that , , , and . Rewriting by deconstructing the choice operator ⊗ yields or . Now observe that o has necessary and sufficient properties such that or , thus .
The proof of the right-distributive property in Part 2 is very similar to that of Part 1, and is thus omitted here. ☐
5. Related Work
In the field of business intelligence (BI), there is a growing collection of technologies for gathering, storing, accessing, and analyzing data, tools that help users make better decisions. Traditionally, the aim of research in BI has been to improve techniques in data management based on data warehousing and online analytic processing (OLAP) [6,12,13]. Since the early 1990s, focus has been on studying the integration of data from multiple sources using extract–transform–load (ETL) tools, effective/efficient data store, and support of multidimensional data analysis using OLAP. Due to recently increasing demands for faster decision making and the advent of the era of Big Data, an increased focus on real-time BI and business performance management, and pervasive BI has emerged in the research community [14]. Traditionally, ETL processes have been executed in an offline mode. Recently, the demand for real-time business needs has driven the optimization on ETL tools and near-real-time ETL design [15,16,17]. To provide front-end applications, OLAP [18] has been studied to support operations such as filtering, aggregation, pivoting, rollup, and drill-down on the multidimensional view of relational data. Traditional data warehousing has mainly been focused on structured data management and analysis. However, it barely considers business process during the analytic process.
The concepts of process-centric BI [19] and business process intelligence [20,21] were introduced to analyze data with business process information. In their work, after collecting data from business process instances, the traditional data analytic tools (e.g., OLAP and data mining techniques) are used to do further analysis. These developments have helped enterprises tremendously in process analytics. However, since data is tightly coupled with the process model and its execution engine, it is difficult to provide generic solutions for warehousing process data for different business processes. Additionally, it is not efficient to do runtime execution monitoring and analysis over a data warehousing approach.
Querying helps business process designers to understand, communicate upon, and enhance a business process. BPMN-Q (Business Process Model and Notation Querying) [22,23,24,25], BQL (Behavior Query Language) [26], and APQL (A Process-Model Query Language) [27] are query languages on business process models expressed in different modeling languages like BPMN, Business Process Execution Language (BPEL) [28] and Petri Net. These query languages focus on the static analysis of business process models which are mainly used at the process design stage other than execution history analysis.
Querying process models/traces has also been studied by Beeri, Milo, et al. [29,30]. In particular, three query languages were developed: BP-QL that focuses on finding process models using patterns [29,30,31,32], BP-EL and BP-Mon that allow querying over traces and/or process models. Key distinctions between their work and our approach are that (1) their traces are acyclic graphs reflecting the control flow structures, while ours is based on logs; and (2) their queries are graph patterns, while ours is based on four algebraic operations. We believe that querying logs directly is more natural in practice.
BP-SPARQL [33,34], which also focuses on trace analysis, is a declarative query language extended from SPARQL [35], a query language for Resource Description Framework (RDF) graphs. BP-SPARQL takes the process execution log of a system (with multiple process instances) and uses a data model—a graph with typed nodes representing entities, data objects with attributes and edges representing transitive relationship between two entities. While BP-SPARQL relies on an intermediate graph, our work analyzes the log directly.
There is also research focusing on event pattern analysis in field CEP (Complex Event Processing) and data streaming. ZStream [36] is a cost-based query processor for matching sequential patterns enriched with the operators sequence, conjunction, disjunction, negation, and Kleene closure. It uses tree-based query plans and a cost model to find the most efficient query evaluation plan. Similar systems include Aurora [37,38], Borealis [39], and TelegraphCQ [40]. Different from our work, these systems focus on streaming data and time window. There are also works extending SQL to process complex patterns in database systems, like DejaVu system [41], using finite state automata to extend SQL, and SQL_TS [42], using the Knuth–Morris–Pratt string matching algorithm for query optimization in database.
6. Conclusions
This paper presents a new query language that uses incident patterns to query enactments of business process stored as workflow logs. Four operators are used to formulate a temporal relationship between activities. Queries using incident patterns are not only more flexible than ETL/data warehousing, but also better support business experts to formulate their demands from different perspectives. The paper also provides a query evaluation algorithm, and explores the algebraic properties between these operators useful for developing further optimization techniques. There are many interesting questions that arise from this initial study. An immediate task is to develop query optimization techniques. Theorems 2–5 provide a first step in this study. Looking ahead, one may wonder how incident pattern query evaluation could compare to data warehousing queries. Clearly the naive approach sketched in this paper can be augmented with more advanced optimization techniques.
We also speculate that query languages for workflow log, such as those which make use of incident patterns, should be helpful in application problems such as detecting anomalous or malicious behavior, with applications in fraud detection, either through ad hoc queries or by constructing queries from business principles.
Acknowledgments
Work by the second author (I.M.) was supported by NSF Grant DGE-1258507.
Author Contributions
Yan Tang and Jianwen Su formulated the formal model for logs and incident operations. Yan Tang also developed the query evaluation algorithms. Isaac Mackey extended incident to allow negation and also was the lead contributor to complete all proof details.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Group, G. Gartner Newsroom. 2011. Available online: http://www.gartner.com/it/page.jsp?id=1740414 (accessed on 18 January 2018).
- Su, J.; Yang, J. Yank Your Data Out of My Engine: A New Approach to Workflow System Design. In Proceedings of the 8th International Workshop on Evolutionary Business Processes (EVL-BP), Adelaide, Australia, 21–25 September 2015. [Google Scholar]
- Sun, Y.; Su, J.; Yang, J. Universal Artifacts: A New Approach to Business Process Management (BPM) Systems. ACM Trans. Manag. Inf. Syst. 2016, 7, 3. [Google Scholar] [CrossRef]
- Dayal, U.; Castellanos, M.; Simitsis, A.; Wilkinson, K. Data integration flows for business intelligence. In Proceedings of the 12th the International Conference on Extending Database Technology (EDBT), Saint Petersburg, Russia, 24–26 March 2009; pp. 1–11. [Google Scholar]
- Wrembel, R.; Koncilia, C. Data Warehouse and OLAP: Concepts, Architectures and Solutions; IRM Press: Hershey, PA, USA, 2007. [Google Scholar]
- Chaudhuri, S.; Dayal, U.; Narasayya, V. An overview of business intelligence technology. Commun. ACM 2011, 54, 88–98. [Google Scholar] [CrossRef]
- Damaggio, E.; Hull, R.; Vaculin, R. On the Equivalence of incremental and fixpoint semantics for business artifacts with Guard-Stage-Milestone lifecycles. Inf. Syst. 2013, 38, 561–584. [Google Scholar] [CrossRef]
- Van der Aalst, W.; ter Hofstede, A. YAWL: Yet another workflow language. Inf. Syst. 2005, 30, 245–275. [Google Scholar] [CrossRef]
- Hanson, J. Manage Your Business Processes with JBoss jBPM. 2006. Available online: http://www.javaworld.com/javaworld/jw-05-2006/jw-0522-jbpm.html (accessed on 18 January 2018). (See also http://www.jboss.org/jbpm/).
- “Shunting-Yard Algorithm”. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Blueberry (accessed on 18 January 2018).
- Allen, W.M. Data Structures and Algorithm Analysis in C++; Pearson Education: Delhi, India, 2007. [Google Scholar]
- Chaudhuri, S.; Dayal, U. An Overview of Data Warehousing and OLAP Technology. SIGMOD Rec. 1997, 26, 65–74. [Google Scholar] [CrossRef]
- Berson, A.; Smith, S.J. Data Warehousing, Data Mining, and OLAP; McGraw-Hill, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Watson, H.J.; Wixom, B.H. The current state of business intelligence. Computer 2007, 40, 96–99. [Google Scholar] [CrossRef]
- Karakasidis, A.; Vassiliadis, P.; Pitoura, E. ETL queues for active data warehousing. In Proceedings of the 2nd International Workshop on Information Quality in Information Systems, Baltimore, MD, USA, 17 June 2005; ACM: New York, NY, USA, 2005; pp. 28–39. [Google Scholar]
- Luo, G.; Naughton, J.F.; Ellmann, C.J.; Watzke, M.W. Transaction reordering and grouping for continuous data loading. In International Workshop on Business Intelligence for the Real-Time Enterprise; Springer: Berlin/Heidelberg, Germany, 2006; pp. 34–49. [Google Scholar]
- Thiele, M.; Lehner, W. Real-time BI and situational analysis. In Business Intelligence Applications and the Web: Models, Systems and Technologies; IGI Global: Hershey, PA, USA, 2012; pp. 285–309. [Google Scholar]
- Thomsen, E. OLAP Solutions: Building Multidimensional Information Systems; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Bucher, T.; Gericke, A.; Sigg, S. Process-centric business intelligence. Bus. Process Manag. J. 2009, 15, 408–429. [Google Scholar] [CrossRef]
- Grigori, D.; Casati, F.; Castellanos, M.; Dayal, U.; Sayal, M.; Shan, M.C. Business process intelligence. Comput. Ind. 2004, 53, 321–343. [Google Scholar] [CrossRef]
- Castellanos, M.; Alves de Medeiros, K.; Mendling, J.; Weber, B.; Weitjers, A. Business process intelligence. Handb. Res. Bus. Process Mod. 2009, 456–480. [Google Scholar] [CrossRef]
- Awad, A. BPMN-Q: A Language to Query Business Processes. Enterprise Modelling and Information Systems Architectures—Concepts and Applications. In Proceedings of the 2nd International Workshop on Enterprise Modelling and Information Systems Architectures (EMISA’07), St. Goar, Germany, 8–9 October 2007; pp. 115–128. [Google Scholar]
- Awad, A.; Polyvyanyy, A.; Weske, M. Semantic Querying of Business Process Models. In Proceedings of the 12th International IEEE Enterprise Distributed Object Computing Conference, Munich, Germany, 15–19 September 2008; pp. 85–94. [Google Scholar]
- Awad, A.; Weidlich, M.; Weske, M. Specification, Verification and Explanation of Violation for Data Aware Compliance Rules. In Proceedings of the 7th International Joint Conference on Service-Oriented Computing (ICSOC-ServiceWave), Stockholm, Sweden, 24–27 November 2009; pp. 500–515. [Google Scholar]
- Sakr, S.; Awad, A. A framework for querying graph-based business process models. In Proceedings of the 19th International Conference on World Wide Web (WWW), Raleigh, NC, USA, 26–30 April 2010; pp. 1297–1300. [Google Scholar]
- Jin, T.; Wang, J.; Wen, L. Querying Business Process Models Based on Semantics. In Proceedings of the 16th International Conference on Database Systems for Advanced Applications (DASFAA), Hong Kong, China, 22–25 April 2011; pp. 164–178. [Google Scholar]
- Ter Hofstede, A.H.M.; Ouyang, C.; Rosa, M.L.; Song, L.; Wang, J.; Polyvyanyy, A. APQL: A Process-Model Query Language. In Proceedings of the First Asia Pacific Conference on Asia Pacific Business Process Management (AP-BPM), Beijing, China, 29–30 August 2013; pp. 23–38. [Google Scholar]
- Eshuis, R.; Grefen, P.W.P.J. Structural Matching of BPEL Processes. In Proceedings of the Fifth IEEE European Conference on Web Services (ECOWS), Halle, Germany, 26–28 November 2007; pp. 171–180. [Google Scholar]
- Beeri, C.; Eyal, A.; Kamenkovich, S.; Milo, T. Querying Business Processes. In Proceedings of the 32nd International Conference on Very Large Data Bases (VLDB), Seoul, Korea, 12–15 September 2006; pp. 343–354. [Google Scholar]
- Beeri, C.; Eyal, A.; Milo, T.; Pilberg, A. Monitoring Business Processes with Queries. In Proceedings of the 33rd International Conference on Very Large Data Bases (VLDB), Vienna, Austria, 23–27 September 2007; pp. 603–614. [Google Scholar]
- Beeri, C.; Eyal, A.; Kamenkovich, S.; Milo, T. Querying business processes with BP-QL. Inf. Syst. 2008, 33, 477–507. [Google Scholar] [CrossRef]
- Beeri, C.; Eyal, A.; Milo, T.; Pilberg, A. BP-Mon: Query-based monitoring of BPEL business processes. SIGMOD Rec. 2008, 37, 21–24. [Google Scholar] [CrossRef]
- Beheshti, S.; Benatallah, B.; Nezhad, H.R.M.; Sakr, S. A Query Language for Analyzing Business Processes Execution. In Proceedings of the 9th International Conference on Business Process Management (BPM), Clermont-Ferrand, France, 30 August–2 September 2011; pp. 281–297. [Google Scholar]
- Beheshti, S.; Sakr, S.; Benatallah, B.; Nezhad, H.R.M. Extending SPARQL to Support Entity Grouping and Path Queries. arXiv, 2012; arXiv:abs/1211.5817. [Google Scholar]
- SPARQL Query Language for RDF. 2008. Available online: https://www.w3.org/TR/rdf-sparql-query/ (accessed on 18 January 2018).
- Mei, Y.; Madden, S. Zstream: A cost-based query processor for adaptively detecting composite events. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009; ACM: New York, NY, USA, 2009; pp. 193–206. [Google Scholar]
- Abadi, D.J.; Carney, D.; Çetintemel, U.; Cherniack, M.; Convey, C.; Lee, S.; Stonebraker, M.; Tatbul, N.; Zdonik, S. Aurora: A new model and architecture for data stream management. VLDB J. 2003, 12, 120–139. [Google Scholar] [CrossRef]
- Carney, D.; Çetintemel, U.; Cherniack, M.; Convey, C.; Lee, S.; Seidman, G.; Stonebraker, M.; Tatbul, N.; Zdonik, S. Monitoring streams: A new class of data management applications. In Proceedings of the 28th International Conference on Very Large Data Bases, Hong Kong, China, 20–23 August 2002; pp. 215–226. [Google Scholar]
- Abadi, D.J.; Ahmad, Y.; Balazinska, M.; Cetintemel, U.; Cherniack, M.; Hwang, J.H.; Lindner, W.; Maskey, A.; Rasin, A.; Ryvkina, E.; et al. The Design of the Borealis Stream Processing Engine. In Proceedings of the 2005 CIDR Conference, Asilomar, CA, USA, 4–7 January 2005; Volume 5, pp. 277–289. [Google Scholar]
- Chandrasekaran, S.; Cooper, O.; Deshpande, A.; Franklin, M.J.; Hellerstein, J.M.; Hong, W.; Krishnamurthy, S.; Madden, S.R.; Reiss, F.; Shah, M.A. TelegraphCQ: Continuous dataflow processing. In Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data, San Diego, CA, USA, 9–12 June 2003; p. 668. [Google Scholar]
- Dindar, N.; Güç, B.; Lau, P.; Ozal, A.; Soner, M.; Tatbul, N. Dejavu: Declarative pattern matching over live and archived streams of events. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009; ACM: New York, NY, USA, 2009; pp. 1023–1026. [Google Scholar]
- Sadri, R.; Zaniolo, C.; Zarkesh, A.; Adibi, J. Expressing and optimizing sequence queries in database systems. ACM Trans. Database Syst. 2004, 29, 282–318. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).