Offset Free Tracking Predictive Control Based on Dynamic PLS Framework
Abstract
:1. Introduction
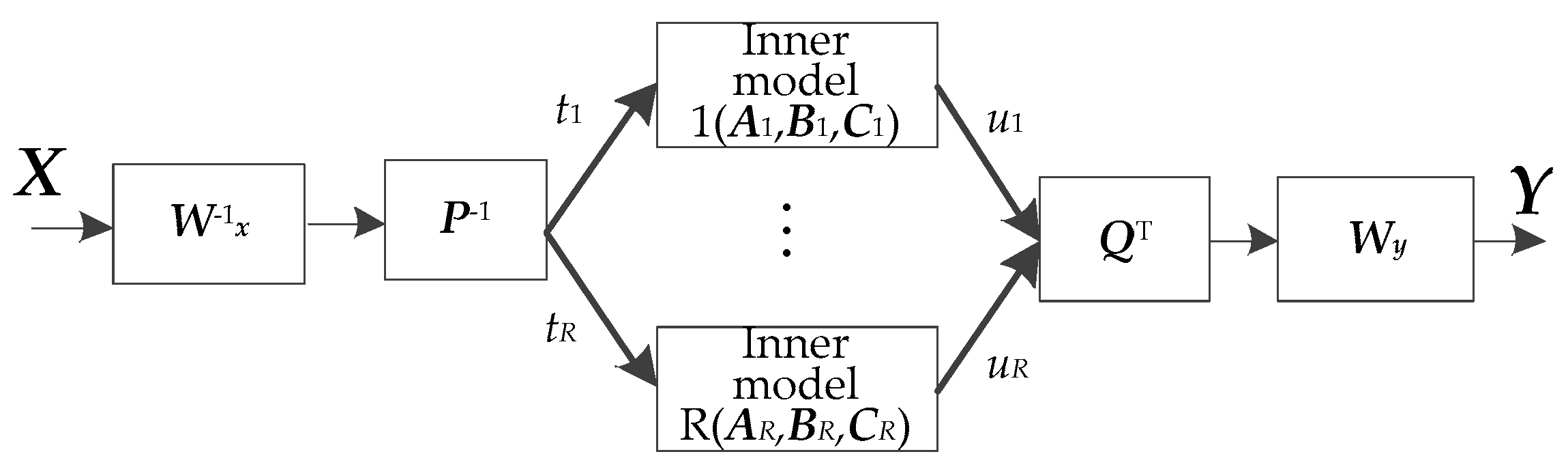
2. Dynamic PLS Model Description
3. Predictive Controller Design
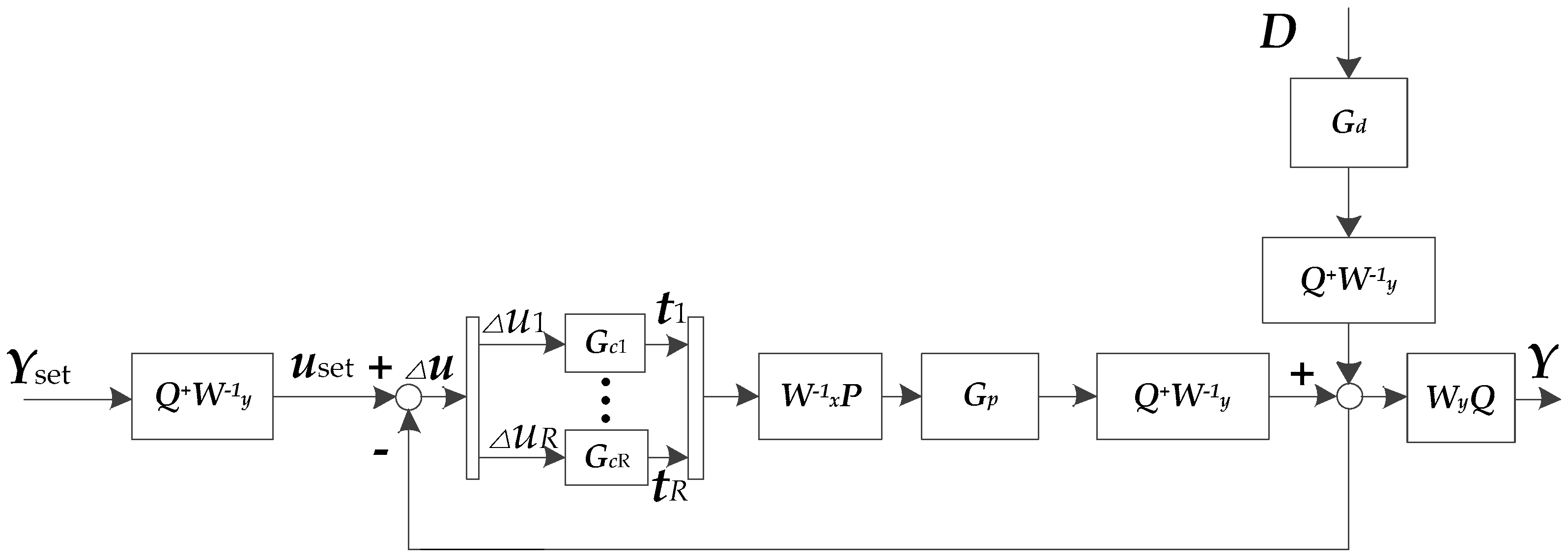
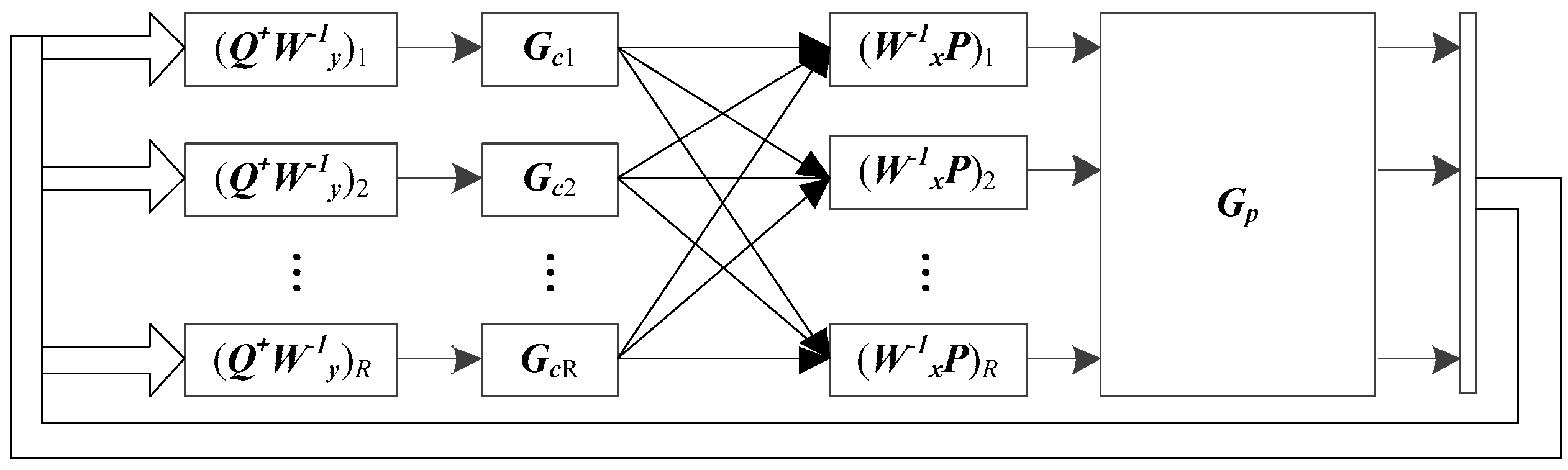
3.1. Dynamic PLS Control Framework
3.2. Equation of Prediction
3.3. Offset-Free Control
3.4. Stability Analysis
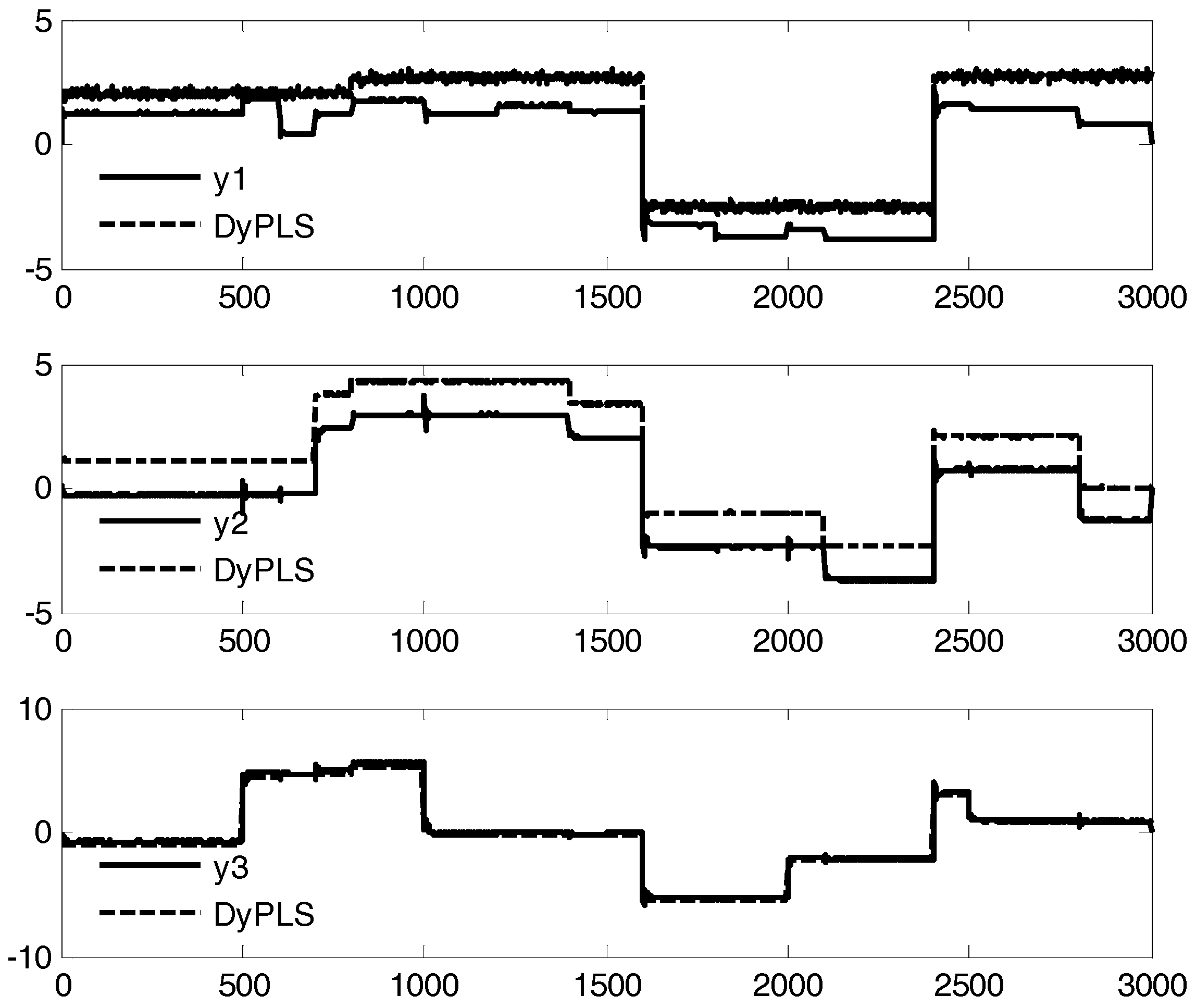
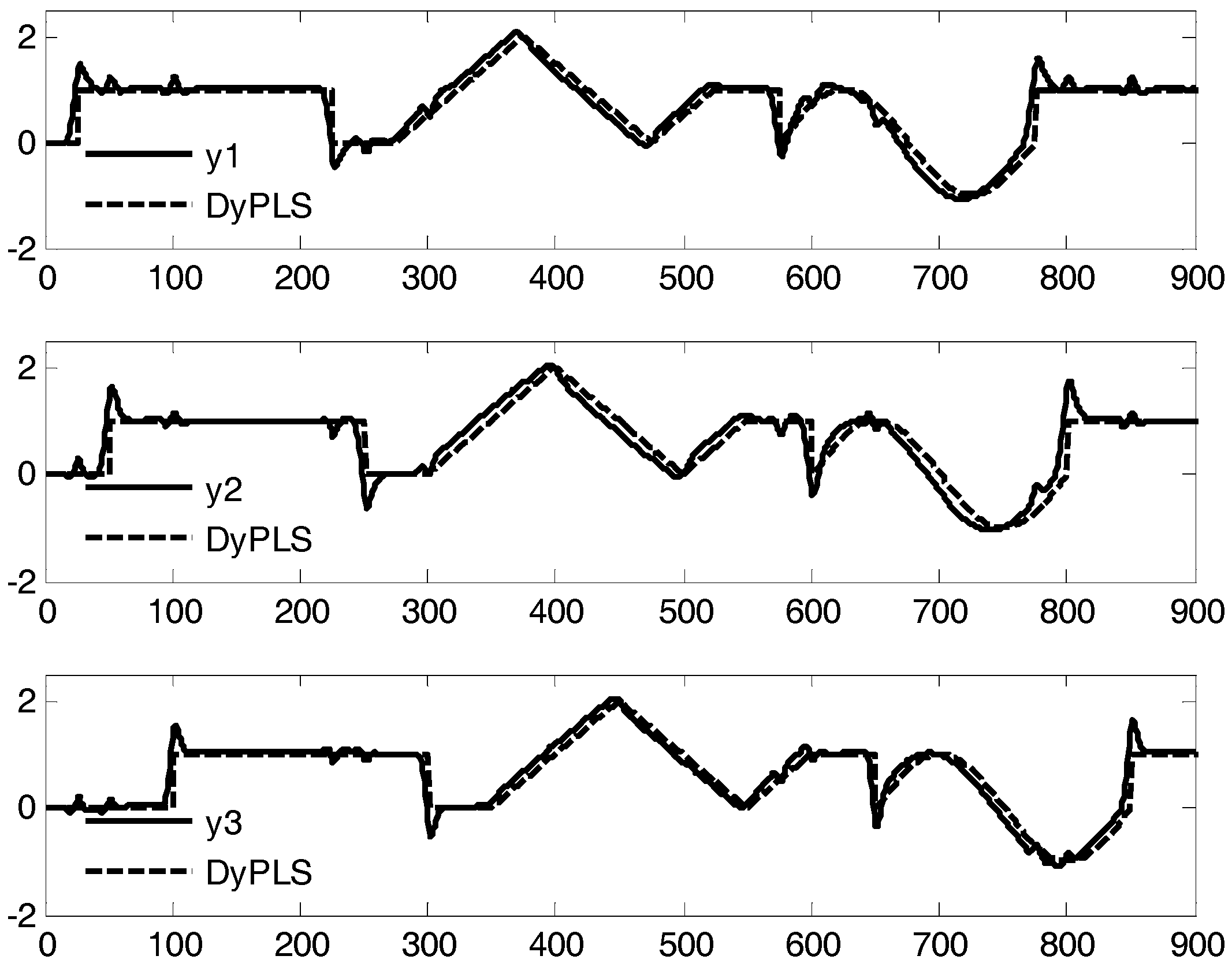
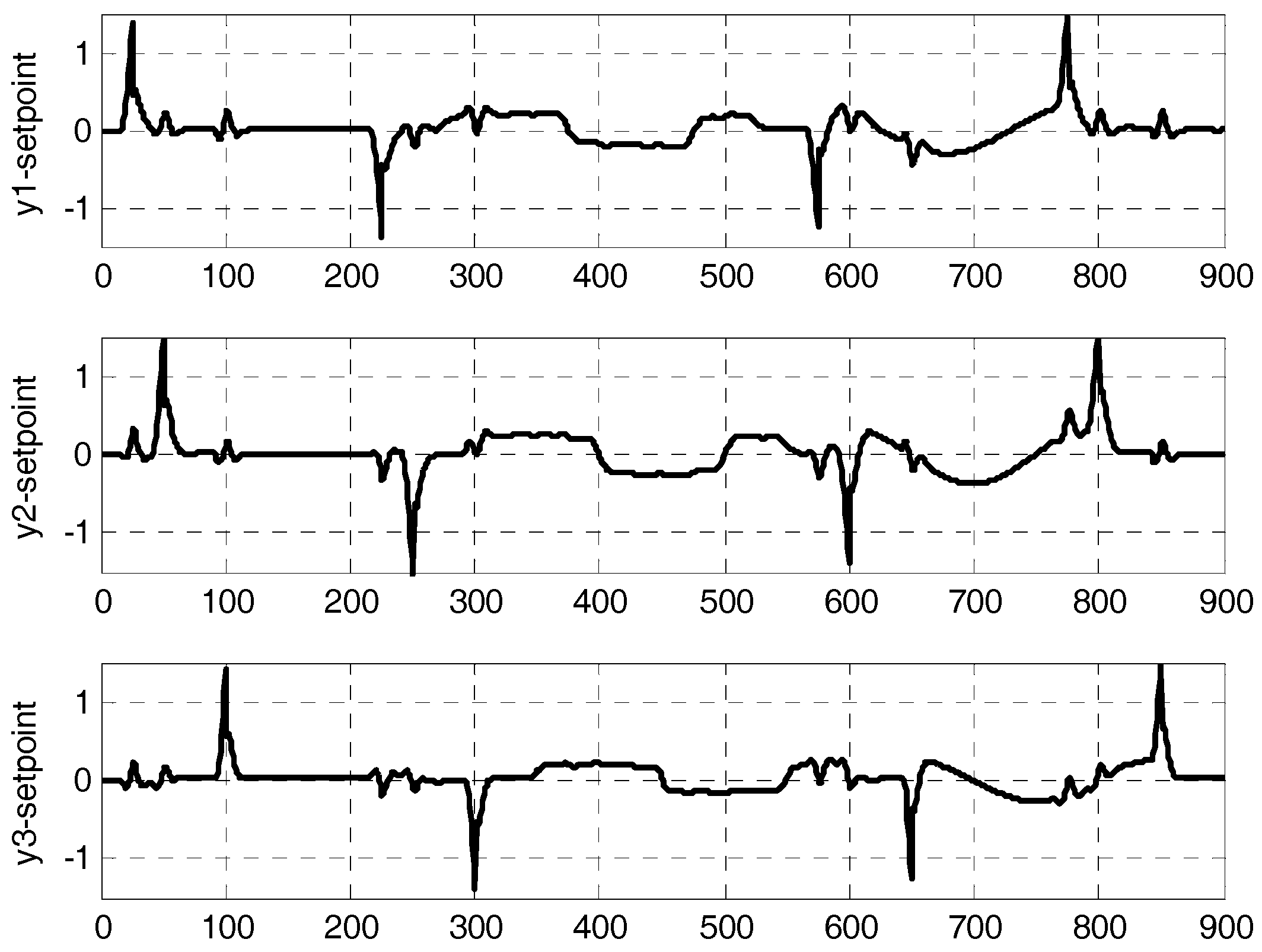
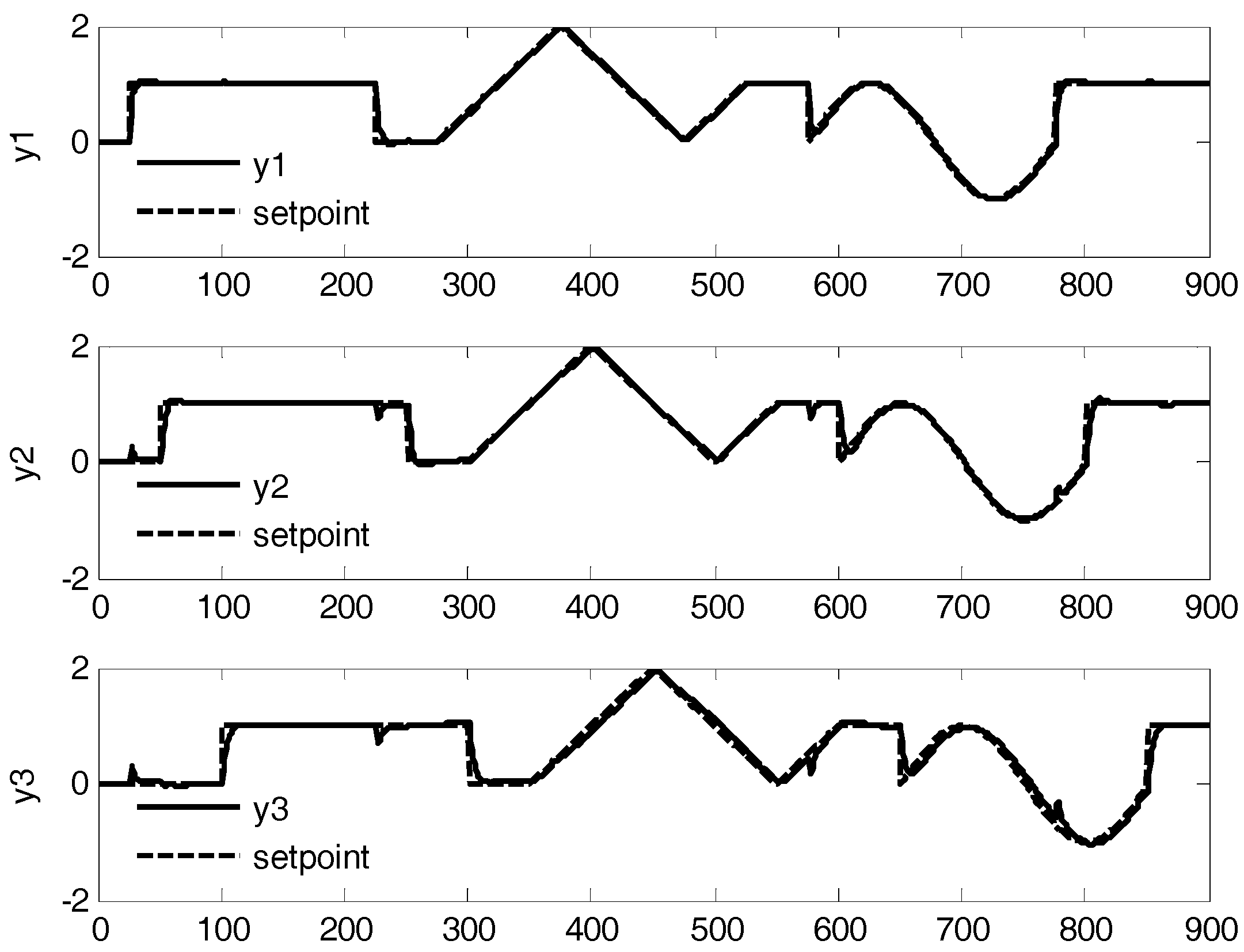
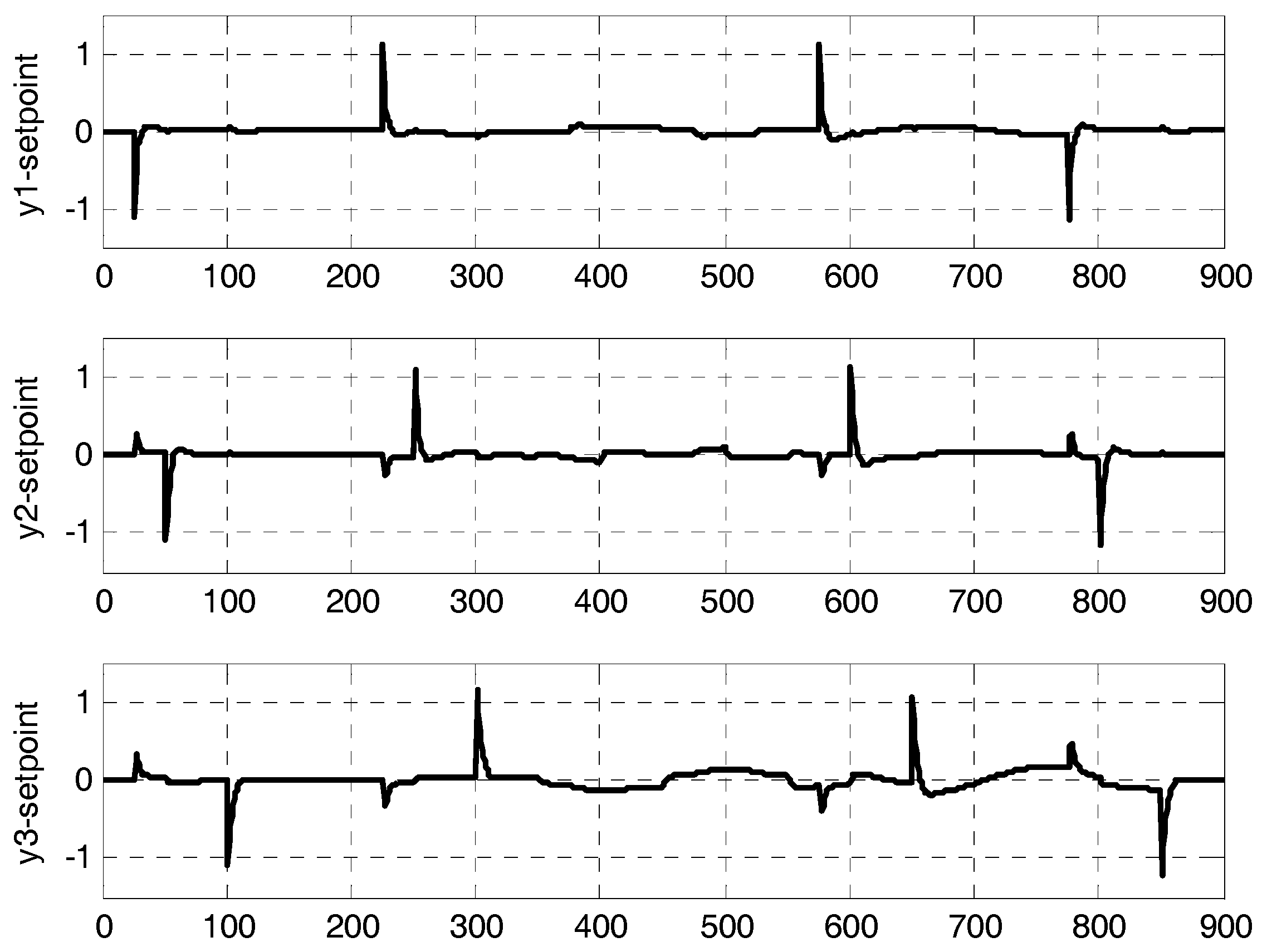
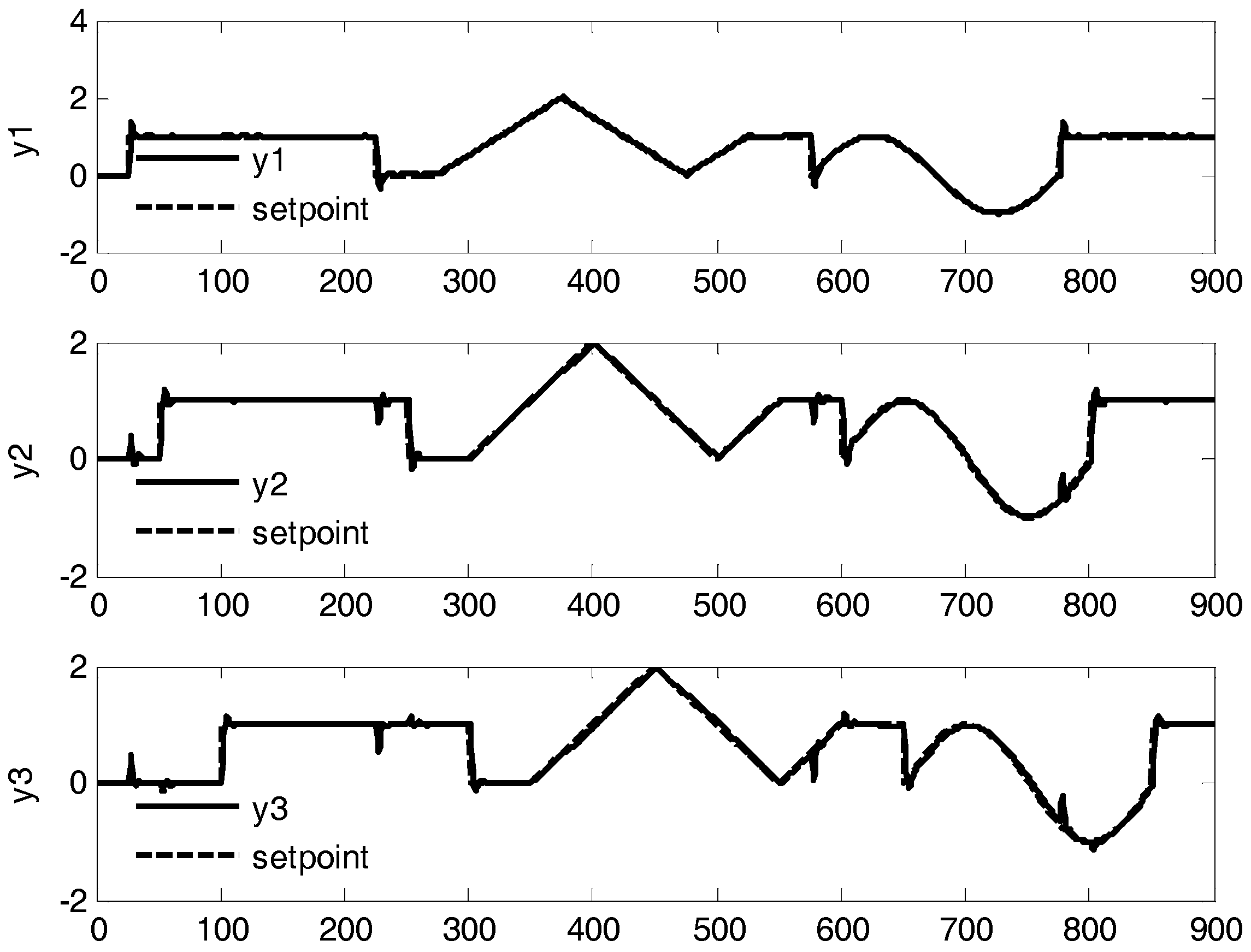
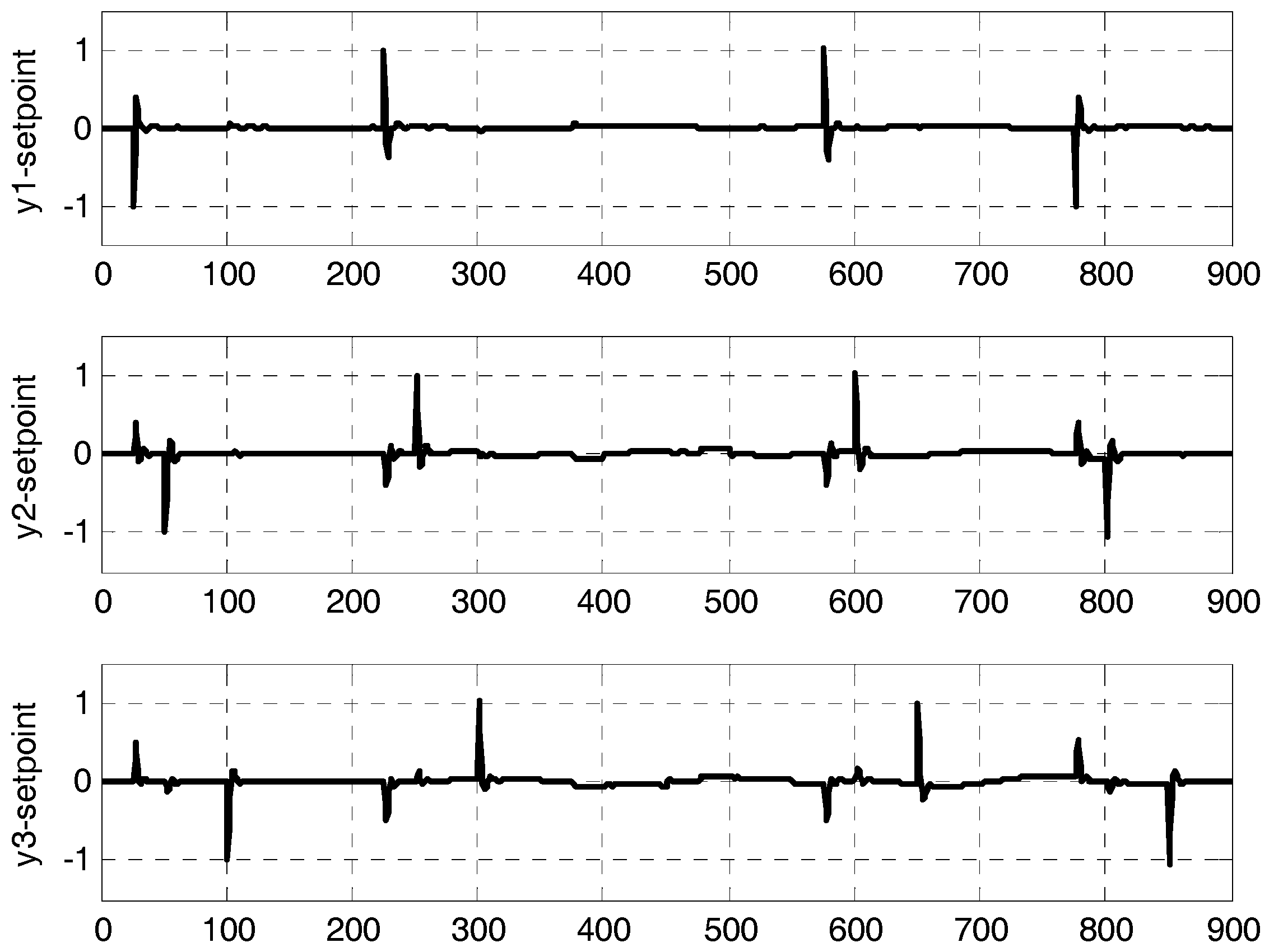
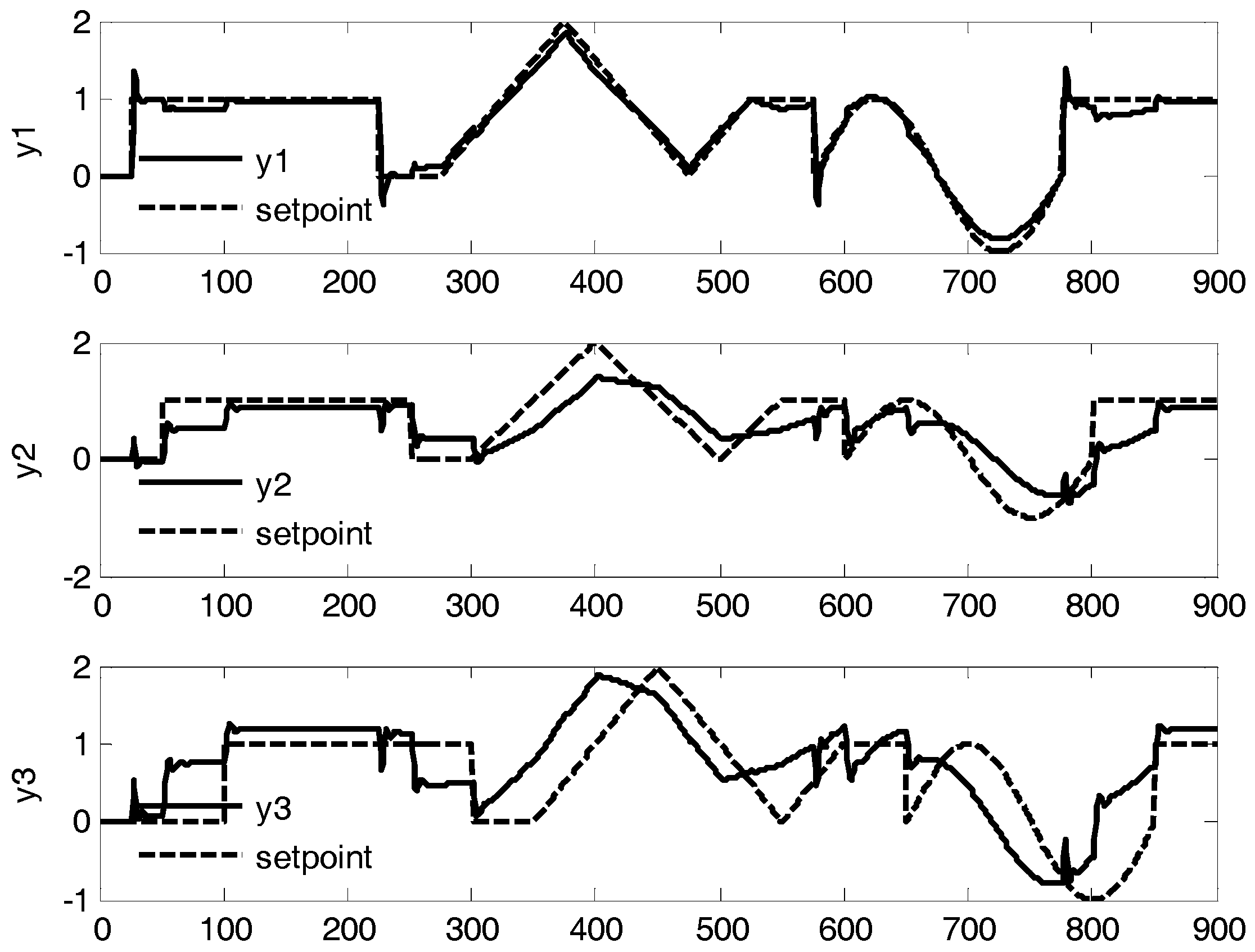
4. Case Study
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ge, X.H.; Yang, F.W.; Han, Q.L. Distributed networked control systems: A brief overview. Inf. Sci. 2017, 380, 117–131. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, C.L.; Hua, C.Q.; Zhu, S.Y.; Guan, X.P. Co-design of stabilisation and transmission scheduling for wireless control systems. IET Control Theory Appl. 2017, 11, 1767–1778. [Google Scholar] [CrossRef]
- Acuna-Bravo, W.; Canuto, E.; Agostani, M.; Bonadei, M. Proportional electro-hydraulic valves: An embedded model control solution. Control Eng. Pract. 2017, 62, 22–35. [Google Scholar] [CrossRef]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control Autom. Syst. 2011, 9, 415. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control; Springer Publishing Company, Incorporated: London, UK, 2013; pp. 2267–2274. [Google Scholar]
- Rahmani, M.A.; Alamir, M.; Gualino, D.; Rieu, V. Nonlinear dynamic model identification and mpc control of an organic rankine cycle (orc) based solar thermal power plant. In Proceedings of the 2015 European Control Conference, Linz, Austria, 15–17 July 2015. [Google Scholar]
- Ławryńczuk, M. Computationally efficient model predictive control algorithms. Stud. Syst. Decis. Control 2014, 3, 137–149. [Google Scholar]
- Lu, Q.; Shi, P.; Lam, H.K.; Zhao, Y. Interval type-2 fuzzy model predictive control of nonlinear networked control systems. IEEE Trans. Fuzzy Syst. 2015, 23, 2317–2328. [Google Scholar] [CrossRef]
- Yao, Y.; Gao, F. A survey on multistage/multiphase statistical modeling methods for batch processes. Annu. Rev. Control 2009, 33, 172–183. [Google Scholar] [CrossRef]
- Chi, Q.; Fei, Z.; Zhao, Z.; Zhao, L.; Liang, J. A model predictive control approach with relevant identification in dynamic pls framework. Control Eng. Pract. 2014, 22, 181–193. [Google Scholar] [CrossRef]
- Kaspar, M.H.; Ray, W.H. Chemometric methods for process monitoring and high-performance controller design. AIChE J. 1992, 38, 1593–1608. [Google Scholar] [CrossRef]
- Kaspar, M.H.; Ray, W.H. Dynamic pls modelling for process control. Chem. Eng. Sci. 1993, 48, 3447–3461. [Google Scholar] [CrossRef]
- Chen, J.; Cheng, Y.-C.; Yea, Y. Multiloop pid controller design using partial least squares decoupling structure. Korean J. Chem. Eng. 2005, 22, 173–183. [Google Scholar] [CrossRef]
- Laurí, D.; Martínez, M.; Salcedo, J.V.; Sanchis, J. Pls-based model predictive control relevant identification: Pls-ph algorithm. Chemom. Intell. Lab. Syst. 2010, 100, 118–126. [Google Scholar] [CrossRef]
- Hu, B.; Zheng, P.; Liang, J. Multi-loop internal model controller design based on a dynamic pls framework. Chin. J. Chem. Eng. 2010, 18, 277–285. [Google Scholar] [CrossRef]
- Hu, B.; Zhao, Z.; Liang, J. Multi-loop nonlinear internal model controller design under nonlinear dynamic pls framework using arx-neural network model. J. Process Control 2012, 22, 207–217. [Google Scholar] [CrossRef]
- LÜ, Y.; Liang, J. Multi-loop constrained iterative model predictive control using arx -pls decoupling structure. Chin. J. Chem. Eng. 2013, 21, 1129–1143. [Google Scholar] [CrossRef]
- Huusom, J.K.; Poulsen, N.K.; Jorgensen, S.B.; Jorgensen, J.B. Adaptive disturbance estimation for offset-free siso model predictive control. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; IEEE: New York, NY, USA, 2011; pp. 2417–2422. [Google Scholar]
- Muske, K.R.; Badgwell, T.A. Disturbance modeling for offset-free linear model predictive control. J. Process Control 2002, 12, 617–632. [Google Scholar] [CrossRef]
- Morari, M.; Maeder, U. Nonlinear offset-free model predictive control. Automatica 2012, 48, 2059–2067. [Google Scholar] [CrossRef]
- González, A.H.; Adam, E.J.; Marchetti, J.L. Conditions for offset elimination in state space receding horizon controllers: A tutorial analysis. Chem. Eng. Process. Process Intensif. 2008, 47, 2184–2194. [Google Scholar] [CrossRef]
- Betti, G.; Farina, M.; Scattolini, R. An mpc algorithm for offset-free tracking of constant reference signals. In Proceedings of the 2012 IEEE 51st Annual Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 5182–5187. [Google Scholar]
- Betti, G.; Farina, M.; Scattolini, R. A robust mpc algorithm for offset-free tracking of constant reference signals. IEEE Trans. Autom. Control 2013, 58, 2394–2400. [Google Scholar] [CrossRef]
- Pannocchia, G.; Gabiccini, M.; Artoni, A. Offset-free mpc explained: Novelties, subtleties, and applications. In Proceedings of the IFAC Conference on Nonlinear Model Predictive Control, Seville, Spain, 17–20 September 2015; pp. 342–351. [Google Scholar]
- Borrelli, F.; Morari, M. Offset free model predictive control. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 4663–4668. [Google Scholar]
- Maeder, U.; Borrelli, F.; Morari, M. Linear offset-free model predictive control. Automatica 2009, 45, 2214–2222. [Google Scholar] [CrossRef]
- Pannocchia, G.; Rawlings, J.B. Disturbance models for offset-free model-predictive control. AIChE J. 2003, 49, 426–437. [Google Scholar] [CrossRef]
- Maeder, U.; Morari, M. Offset-free reference tracking with model predictive control. Automatica 2010, 46, 1469–1476. [Google Scholar] [CrossRef]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Wold, S.; Sjostrom, M.; Eriksson, L. Pls-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Qin, S.J.; McAvoy, T.J. Nonlinear pls modeling using neural networks. Comput. Chem. Eng. 1992, 16, 379–391. [Google Scholar] [CrossRef]
- Lakshminaravanan, S.; Shah, S.L.; Nandakumar, K. Modeling and control of multivariable processes: Dynamic pls approach. AIChE J. 1997, 43, 2307–2322. [Google Scholar] [CrossRef]
- Qin, S.J. An overview of subspace identification. Comput. Chem. Eng. 2006, 30, 1502–1513. [Google Scholar] [CrossRef]
- Negenborn, R.R.; van Overloop, P.J.; Keviczky, T.; de Schutter, B. Distributed model predictive control of irrigation canals. Netw. Heterog. Media 2009, 4, 359–380. [Google Scholar] [CrossRef]
- Embirucu, M.; Fontes, C. Multirate multivariable generalized predictive control and its application to a slurry reactor for ethylene polymerization. Chem. Eng. Sci. 2006, 61, 5754–5767. [Google Scholar] [CrossRef]

| Symbol | Description | |
|---|---|---|
| input | x1 | monomer feed flow |
| x2 | solvent(n-hexane) feed flow | |
| x3 | catalyst feed flow | |
| x4 | gas recycle/monomer feed ratio | |
| output | y1 | production |
| y2 | slurry polymer | |
| y3 | catalyst efficiency |
| Conventional MPC | Conventional MPC in Dynamic PLS | Proposed Method | |
|---|---|---|---|
| ISE of y1 | 37.33 | 6.38 | 5.70 |
| ISE of y2 | 52.21 | 9.26 | 7.80 |
| ISE of y3 | 31.98 | 14.73 | 9.08 |
| Computing time (ms) | 87.23 | 63.87 | 64.37 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, J.; Yue, W.; Lin, L. Offset Free Tracking Predictive Control Based on Dynamic PLS Framework. Information 2017, 8, 121. https://doi.org/10.3390/info8040121
Xin J, Yue W, Lin L. Offset Free Tracking Predictive Control Based on Dynamic PLS Framework. Information. 2017; 8(4):121. https://doi.org/10.3390/info8040121
Chicago/Turabian StyleXin, Jin, Wang Yue, and Luo Lin. 2017. "Offset Free Tracking Predictive Control Based on Dynamic PLS Framework" Information 8, no. 4: 121. https://doi.org/10.3390/info8040121
APA StyleXin, J., Yue, W., & Lin, L. (2017). Offset Free Tracking Predictive Control Based on Dynamic PLS Framework. Information, 8(4), 121. https://doi.org/10.3390/info8040121






