A Novel Grey Prediction Model Combining Markov Chain with Functional-Link Net and Its Application to Foreign Tourist Forecasting

Abstract

Grey prediction models for time series have been widely applied to demand forecasting because only limited data are required for them to build a time series model without any statistical assumptions. Previous studies have demonstrated that the combination of grey prediction with neural networks helps grey prediction perform better. Some methods have been presented to improve the prediction accuracy of the popular GM(1,1) model by using the Markov chain to estimate the residual needed to modify a predicted value. Compared to the previous Grey-Markov models, this study contributes to apply the functional-link net to estimate the degree to which a predicted value obtained from the GM(1,1) model can be adjusted. Furthermore, the troublesome number of states and their bounds that are not easily specified in Markov chain have been determined by a genetic algorithm. To verify prediction performance, the proposed grey prediction model was applied to an important grey system problem—foreign tourist forecasting. Experimental results show that the proposed model provides satisfactory results compared to the other Grey-Markov models considered.

1. Introduction

Both time series and econometric methods have been commonly used for demand forecasting. However, prediction performance of econometric methods can be significantly influenced by incomplete information associated with explanatory factors; and models for time series, such as ARIMA [1] and Box-Jenkins models, usually require large size of samples to obtain reasonable prediction accuracy [2,3,4,5]. Neural networks, such as multilayer perceptron and support vector regression, have also been applied to demand forecasting [6,7]. Although the neural network has proven to be an efficient technique involving computational intelligence in representing complex nonlinear mappings, similar to econometric methods, multilayer perceptron and support vector regression suffer from incomplete information associated with input variables.

Grey prediction models [8] have the ability to characterize an unknown system with small data sets [9], without requiring conformance to statistical assumptions such as normality distribution. For time series prediction, GM(1,1) is among the most frequently used grey prediction models [10]. It requires only four recent samples to derive reliable and acceptable prediction accuracy [5], and has been widely applied to various decision problems involving management, economics, and engineering [2,3,4,11,12,13,14,15,16]. To better improve the prediction performance of the original GM(1,1) model, several versions combining with computational intelligence have been proposed, such as models with self-adaptive intelligence [17], neural-network-based grey prediction for electricity consumption prediction [18,19], PGM(1,1) using particle swarm optimization to determine the development coefficient [20], GM(1,1) models with online sequential extreme learning machine [21], an optimized nonlinear grey Bernoulli model [22], an adaptive GM(1,1) for electricity consumption [3], and grey wave forecasting through qualified contour sequences [23]. Literally, the combination of grey prediction and neural networks can better represent system dynamics with uncertainty and nonlinearity [21].

The GM(1,1) model with residual modification could be established to improve prediction accuracy of the original GM(1,1) model [7,9]. To modify the predicted values from the original model, a residual modification model is commonly set up by building the original GM(1,1) model, and then constructing the residual GM(1,1) model by a residual series [4,19]. As a matter of facts, construction of grey prediction models with residual modification all stemmed from the foundation of the GM(1,1) residual model. It is interesting that prediction accuracy obtained by the original GM(1,1) model can be effectively improved using the Markov chain to realize the residual model [24,25]. The Grey-Markov model, MCGM(1,1) uses the GM(1,1) model to get the basic trend of the original data, and then uses the Markov chain to fix residual errors generated by the GM(1,1) model. It has shown advantages over the GM(1,1) model, when the time series data fluctuated significantly [26,27]. Other related MCGM(1,1) studies, such as Hsu and Wen [28] and Hsu [29] used Markov chain sign estimation to modify residuals for the trans-Pacific air passenger market and the global integrated circuit industry. Hsu et al. [30] combined a Fourier grey model with Markov chain to predict turning time of the stock market. Kumar and Jain [31] applied MCGM(1,1) to predict conventional energy consumption. Li et al. [32] combined RGM(1,1) with the Markov chain for thermal electric power generation. Mao and Sun [33] applied MCGM(1,1) to fire accident prediction. Sun et al. [25] proposed a MCGM(1,1) variant using the Cuckoo search algorithm for foreign tourist arrivals prediction. Wang [34] showed the effectiveness of MCGM(1,1) for tourism demand prediction. Xie et al. [35] proposed a QP-Markov model to estimate the probability that one energy component can transit to another energy component.

However, for an MCGM(1,1)-based model, it is not easy to determine the number of states and their bounds for the Markov chain—these parameters are usually specified in advance through experience and the modification range for a predicted value derived by the original GM(1,1) model is identical to its corresponding predicted residual from the Markov chain. These more or less have an impact on prediction performance. Because of the advantage of combining grey prediction with neural networks, we propose a residual modification model based on neural networks, NN-Grey-Markov, incorporating a functional link net (FLN) with effective function approximation capability [36,37,38,39] to estimate the modification range with respect to a predicted residual obtained from the Markov chain. The genetic algorithm (GA) is employed to determine connection weights of an FLN, the number of states, and the bounds of each state, to construct the proposed grey prediction model with high prediction accuracy.

Foreign tourist forecasting can be recognized to be a grey system problem since several factors influence tourism demand in uncertain ways. That is, several factors such as exchange rate, security, and disease cause fluctuations in tourism demand but the precise manner of this effect is not clear. The variety of the international tourism market has meant foreign tourist prediction has been a challenging task for tourism administrators [25,40,41]. The global tourism industry has a significant impact on a nation’s economic development and foreign tourist forecasting plays a very important role when devising tourism development plans for cities or countries. It therefore makes us more intrigued to examine the prediction performance of the proposed residual modification model on foreign tourist forecasting.

The remainder of the paper is organized as follows: Section 2 introduces the MCGM(1,1) model and Section 3 presents the proposed NN-Grey-Markov model. Section 4 validates the prediction accuracy of the proposed grey prediction model for foreign tourist forecasting using two real cases. This paper is concluded with Section 5.

2. The MCGM(1,1) Model

2.1. Original GM(1,1) Model

By one time accumulated generating operation (1-AGO) [9], a new sequence, $x_{}^{(1)}$ = ($x_1^{(1)}$, $x_2^{(1)}$, …, $x_n^{(1)}$), can be generated from an original data sequence $x_{}^{(0)}$ = ($x_1^{(0)}$, $x_2^{(0)}$, …, $x_n^{(0)}$) as follows:

$$x_k^{(1)}={\displaystyle \sum _{j=1}^k{x}_k^{(0)}},k=1,2,\dots ,n$$

(1)

and $x_1^{(1)}$, $x_2^{(1)}$, …, $x_n^{(1)}$ can be approximated by a first-order whitenization differential equation,

$$\frac{d{\mathbf{x}}^{(1)}}{dt} +a{x}^{(1)}=b$$

(2)

where a is the developing coefficient and b is the control variable. Using 1-AGO is beneficial to identify regularity hidden in data sequences, even if the original data are finite, insufficient, and chaotic.

The predicted value, ${\widehat{x}}_k^{(1)}$, for $x_k^{(1)}$ can be obtained by solving the differential equation with initial condition $x_1^{(1)}$ = $x_1^{(0)}$,

$${\widehat{x}}_k^{(1)}=(x_1^{(0)}-\frac{b}{a})e^{-a\left(k-1\right)}+\frac{b}{a}$$

(3)

Thus, ${\widehat{x}}_1^{(1)}$ = $x_1^{(0)}$ holds, and a and b can be estimated from the grey difference equation

$$x_k^{(0)}+a{z}_k^{(1)}=b$$

(4)

where $z_k^{(1)}$ is the background value,

$$z_k^{(1)}=\alpha x_k^{(1)}+\left(1-\alpha \right)x_{k-1}^{(1)}$$

(5)

where α = 0.5 usually, for convenience. Using n − 1 grey difference equations (k = 2, 3, …, n), a and b can be derived using the ordinary least squares approach,

[a, b]^T = (B^TB)⁻¹B^Ty

(6)

where

$$B=\left[\begin{array}{cc}-z_2^{(1)}& 1\\ -z_3^{(1)}& 1\\ ⋮& ⋮\\ -z_n^{(1)}& 1\end{array}\right]$$

(7)

and

$$y={[x_2^{(0)},x_3^{(0)},\dots ,x_n^{(0)}]}^{\mathrm{T}}$$

(8)

Using the inverse AGO, the predicted value of $x_k^{(0)}$ is

$${\widehat{x}}_k^{(0)}={\widehat{x}}_k^{(1)}-{\widehat{x}}_{k-1}^{(1)},k=2,3,\dots ,n$$

(9)

Therefore,

$${\widehat{x}}_k^{(0)} =(1-e^a)(x_1^{(0)}-\frac{b}{a})e^{-a}{}^{(k-1)},k=2,3,\dots ,n$$

(10)

and ${\widehat{x}}_1^{(1)}$ = ${\widehat{x}}_1^{(0)}$ holds.

2.2. Residual Modification by Markov Chain

Let $\mathsf{\epsilon }$ = (${\epsilon }_1^{}$, ${\epsilon }_2^{}$, …, ${\epsilon }_n^{}$) denote the sequence of residual values, where

$${\epsilon }_k^{}=\left|x_k^{(0)}-{\widehat{x}}_k^{(0)}\right|,k=1,2,\dots ,n$$

(11)

Let [${\epsilon }_{\min }^{}$, ${\epsilon }_{\max }^{}$] denote the range of residuals, where ${\epsilon }_{\min }^{}$ and ${\epsilon }_{\max }^{}$ are the minimum and maximum values among ${\epsilon }_k^{}$, respectively. Then [${\epsilon }_{\min }^{}$, ${\epsilon }_{\max }^{}$] can be divided into r intervals (r ≥ 2), with each interval treated as a state. The state with lower bound ${\epsilon }_{\min }^{}$ is state 1, and state r is the state with upper bound ${\epsilon }_{\max }^{}$. Therefore, state of ${\epsilon }_k^{}$ can be determined depending on where it locates. It is not necessary to require intervals with equal length.

Subsequently, an m-step transition probability matrix P^(m) can be generated as follows:

$$P^{\left(m\right)}=\left[\begin{array}{cccc}{p}_{11}^{(m)}& p_{12}^{(m)}& \dots & p_{1r}^{(m)}\\ p_{21}^{(m)}& p_{22}^{(m)}& \dots & p_{2r}^{(m)}\\ ⋮& ⋮& \ddots & ⋮\\ p_{r1}^{(m)}& p_{r2}^{(m)}& \dots & p_{rr}^{(m)}\end{array}\right]$$

(12)

where $p_{ij}^{(m)}$ denotes the transition probability from state i to j (1 ≤ i, j ≤ r) by m steps,

$$p_{ij}^{(m)}=\frac{t_{ij}^{(m)}}{t_i}$$

(13)

where $t_{ij}^{(m)}$ denotes the number of transitions from state i to j by m steps, and t_i denotes the number of state i among the sequence of residual values. For each row in P^(m), the sum of elements equals one. However, $p_{ii}^{(m)}$ can be specified directly as one when the sum of elements in the row i equals zero. In other words, such a state is treated as an absorbing state.

The predicted residual value, ${\widehat{\epsilon }}_k^{(m)}$ can be computed if ${\epsilon }_k^{}$ locates in state i,

$${\widehat{\epsilon }}_k^{(m)}=p_{i1}^{(m)}{c}_1+p_{i2}^{(m)}{c}_2+\dots +p_{ir}^{(m)}{c}_r$$

(14)

where c_w (1 ≤ w ≤ r) is the center of state w, whose lower and upper bounds are l_w and u_w, respectively. Alternatively, c_w can be expressed as [25,32]

c_w = α_w l_w + (1 − α_w) u_w

(15)

Then ${\widehat{x}}_k^{(0)}$ can be revised as a new predicted value ${\tilde{x}}_k^{(0)}$ by adding the predicted residual ${\widehat{\epsilon }}_k^{(m)}$.

$${\tilde{x}}_k^{(0)}={\widehat{x}}_k^{(0)}+{\widehat{\epsilon }}_k^{(m)},k=1,2,\dots ,n$$

(16)

The Markov chain is used to modify the residuals generated by the GM(1,1) model. Sun et al. [25] and Mao and Sun [33] used the sequence of relative errors rather than the sequence of residual values.

3. The Proposed NN-Grey-Markov Model

Two issues must be addressed for the original Grey-Markov model. First, the modification range of ${\widehat{x}}_k^{(0)}$ in the original Grey-Markov model is restricted to ${\widehat{\epsilon }}_k^{(m)}$ with a positive sign, which may affect prediction accuracy of the residual modification models. To increase flexibility, the restriction may be relaxed by deriving the sign and modification range with respect to ${\widehat{\epsilon }}_k^{(m)}$. Second, the number of intervals, r, is fixed and usually specified in advance. To improve prediction accuracy it is reasonable to apply a GA—which is a powerful search and optimization method [42,43,44]—to automatically determine r and the lower and upper bounds of each interval. FLN is an appropriate tool to provide estimations for the sign and modification range, due to its effective function approximation capability.

Section 3.1 describes how to apply FLN to estimate the sign and modification range for each predicted residual, and Section 3.2 describes the construction of the proposed NN-Grey-Markov model using GA to determine the required parameters, including FLN connection weights, r and the lower and upper bounds of each interval.

3.1. Incorporating Functional-Link Net into the Proposed NN-Grey-Markov Model

For flexibility, it is reasonable to modify ${\widehat{x}}_k^{(0)}$ as ${\tilde{x}}_k^{(0)}$ by adding or subtracting ${\widehat{\epsilon }}_k^{(m)}$,

$${\tilde{x}}_k^{(0)}={\widehat{x}}_k^{(0)}+y_k{\widehat{\epsilon }}_k^{(m)},k=1,2,\dots ,n$$

(17)

where y_k ranges from −1 to 1 and can be interpreted as the degree to which ${\widehat{x}}_k^{(0)}$ can be adjusted. That is, if y_k is positive, the greater y_k, the more likely ${\widehat{x}}_k^{(0)}$ is to be adjusted toward ${\widehat{x}}_k^{(0)}$ + ${\widehat{\epsilon }}_k^{(m)}$. On the contrary, if y_k is negative, the smaller y_k, the more likely ${\widehat{x}}_k^{(0)}$ is to be adjusted toward ${\widehat{x}}_k^{(0)}$ − ${\widehat{\epsilon }}_k^{(m)}$. We estimated y_k with FLN using the hyperbolic tangent function,

$$\tanh \left(z\right)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

(18)

as the activation function, which has range (−1, 1).

An enhanced pattern with respect to a single input denoted by t_k, can be generated as (t_k, sin(πt_k), cos(πt_k), sin(2πt_k), cos(2πt_k), sin(4πt_k)) through a functional link, where t_k denotes the time period k with respect to ${\widehat{x}}_k^{(0)}$. Let θ be the bias to the output node. Then the actual output value, y_k, corresponding to (t_k, sin(πt_k), cos(πt_k), sin(2πt_k), cos(2πt_k), sin(4πt_k)) is

y_k = tanh(w₁t_k + w₂sin(πt_k) + w₃cos(πt_k) + w₄sin(2πt_k) + w₅cos(2πt_k) + w₆sin(4πt_k) + θ)

(19)

Although the components in the functional expansion representation can be unrestrictedly extended for t_k, this is not practical in real applications. (t_k, sin(πt_k), cos(πt_k), sin(2πt_k), cos(2πt_k), sin(4πt_k)) with respect to t_k is acceptable [37]. Hu [45] also demonstrated the superiority of applying residual modification using FLN to predict energy demand.

3.2. Constructing the Proposed NN-Grey-Markov Model

To construct the proposed grey prediction model with high prediction accuracy, we consider the mean absolute percentage error (MAPE), which is usually recommended to be used for modelling [46,47]. MAPE with respect to $x_{}^{(0)}$ is formulated as follows:

$$\mathrm{MAPE}=\frac{1}{n}{\displaystyle \sum _{k=1}^n\frac{\left|x_k^{(0)}-{\tilde{x}}_k^{(0)}\right|}{x_k^{(0)}}}\times 100\%$$

(20)

What we are aiming for is to set up a prediction model with high prediction accuracy. The problem can be formulated as maximizing the reciprocal of MAPE for constructing the prediction model. Using this fitness function, a real-valued GA was developed to automatically determine 7 + 2r parameters, including the connection weights (w₁, w₂, w₃, w₄, w₅, w₆), bias (θ), the number of intervals (r), partition points (p₁, p₂, …, p_r−1), and relative weights in respective intervals (α₁, α₂, …, α_r) for the proposed grey prediction model, where w₁, w₂, w₃, w₄, w₅, w₆, and θ range from −1 to 1, p₁, p₂, …, p_r−1 range from ${\epsilon }_{\min }^{}$ to ${\epsilon }_{\max }^{}$, and r range from 2 to 10. It is noted that u_r−1 = l_r = p_r−1 holds.

Let n_size and n_max denote the population size and maximum number of generations, respectively, and P_m denote the population in generation m (1 ≤ m ≤ n_max). After evaluating the fitness value of each chromosome in P_m, n_size new chromosomes were generated for P_m+1 by means of selection, crossover, and mutation. GA was performed for n_max generations. When the stopping condition was satisfied, the algorithm is terminated, and the best chromosome with maximum fitness value among consecutive generations can be used to examine the generalization ability of the NN-Grey-Markov model. These genetic operations are briefly described below.

3.2.1. Selection

Let chromosome u (1 ≤ u ≤ n_size) produced in P_m be represented as $w_{u,1}^m$$w_{u,2}^m$$w_{u,3}^m$$w_{u,4}^m$$w_{u,5}^m$$w_{u,6}^m$${\theta }_u^m$$r_u^m$$p_{u,1}^m$$p_{u,2}^m$…$p_{u,r-1}^m$${\alpha }_{u,1}^m$${\alpha }_{u,2}^m$…${\alpha }_{u,r}^m$. Two chromosomes from P_m were randomly selected by binary tournament selection, and the one with higher fitness was put into a mating pool. This process was repeated until n_size chromosomes were placed in the mating pool. n_size/2 pairs of chromosomes from the pool were then randomly selected, and offspring of the selected parents were reproduced by crossover and mutation.

3.2.2. Crossover

Crossover was applied to reproduce children by altering the parent chromosomal makeup. For two selected chromosomes, u ($w_{u,1}^m$$w_{u,2}^m$$w_{u,3}^m$$w_{u,4}^m$$w_{u,5}^m$$w_{u,6}^m$${\theta }_u^m$$r_u^m$$p_{u,1}^m$$p_{u,2}^m$…$p_{u,r-1}^m$${\alpha }_{u,1}^m$${\alpha }_{u,2}^m$…${\alpha }_{u,r}^m$) and v ($w_{v,1}^m$$w_{v,2}^m$$w_{v,3}^m$$w_{v,4}^m$$w_{v,5}^m$$w_{v,6}^m$${\theta }_v^m$$r_v^m$$p_{v,1}^m$$p_{v,2}^m$…$p_{v,r-1}^m$${\alpha }_{v,1}^m$${\alpha }_{v,2}^m$…${\alpha }_{v,r}^m$) (1 ≤ v ≤ n_size), each pair of real-valued genes can be used to generate two new genes with crossover probability Pr_c.

$$\begin{gathered} w_{u,i}^m\prime = h_i{w}_{u,i}^m + (1 - h_i)w_{v,i}^m, w_{v,i}^m\prime = (1 - h_i)w_{u,i}^m + h_i{w}_{v,i}^m, i = 1, 2, \dots , 6 \\ {\theta }_u^m\prime = h_7{\theta }_u^m + (1 - h_7){\theta }_v^m, {\theta }_v^m\prime = (1 - h_7) {\theta }_u^m + h_7{\theta }_v^m \\ {r}_u^m\prime = h_8{r}_u^m + (1 - h_8)r_v^m, r_v^m\prime = (1 - h_8) r_u^m + h_8{r}_v^m \\ {p}_{u,i}^m\prime = h_{8+j}{p}_{u,i}^m + (1 - h_{8+j})p_{v,i}^m, p_{v,i}^m\prime = (1 - h_{8+j})p_{u,i}^m + h_{8+j}{p}_{v,i}^m, j = 1, 2, \dots , r - 1 \\ {\alpha }_{u,i}^m\prime = h_{7+r+j}{\alpha }_{u,i}^m + (1 - h_{7+r+j}){\alpha }_{v,i}^m, p_{v,i}^m\prime = (1 - h_{7+r+j}){\alpha }_{u,i}^m + h_{7+r+j}{\alpha }_{v,i}^m, j = 1, 2, \dots , r \end{gathered}$$

where h₁, h₂, …, h_7+2r are all random numbers in the interval [0, 1]. It is noted that Pr_c should be specified as a large value because it controls the exploratory range in the solution space.

3.2.3. Mutation

Mutation was performed with probability Pr_m for each real valued parameter in a new chromosome generated by crossover. To avoid excessive perturbation, a low mutation rate was taken into account. When a mutation happened with a real valued gene, that gene was changed by adding a randomly selected number from a specified interval. After crossover and mutation, n_del (0 ≤ n_del ≤ n_size) chromosomes in P_m+1 were removed randomly from the set of new chromosomes to create space for the chromosome with maximum fitness value in P_m.

4. Empirical Study

4.1. Background

The global tourism industry plays a significant role in the economic development of a country. To boost the tourism industry, devising tourism development and marketing strategies by estimating the number of the foreign tourists has become increasingly important for governments and industries in the private sector such as airlines, hospitality services, and travel agencies. Effective tourism demand forecasting can significantly affect the amount of resources that governments and private sectors invest [6]. In Taiwan, tourism statistics show that foreign tourists mainly came from Japan, Hong Kong, Macao, Korea, China, and USA for 2014–2016. It is noteworthy that the number of tourist arrivals from Southeast Asia increased by 15% in May 2016 compared to May 2015. In face of the growth rate, authorities have actively investigated how to continuously expand the tourism market in the Southeast Asia through new policies. Therefore, foreign tourist forecasting will have a great impact on the outcomes of programs related to the policy.

Real datasets are used to conduct experiments to compare foreign tourist forecasting from the proposed NN-Grey-Markov model against the original GM(1,1), MCGM(1,1), and several models proposed by Sun et al. [25], including segmented GM(1,1) (SGM(1,1)), SGM(1,1) using Markov chain (MCSGM(1,1)), and MCSGM(1,1) using a Cuckoo search algorithm (CMCSGM(1,1)). In contrast to the original GM(1,1) and MCGM(1,1) using all observed data, the SGM model first used a rolling mechanism to determine the set of newly observed data, and then constructed the GM(1,1) model. Thus, the rolling mechanism could select only a few recent data by capturing the developing trend from all observed data. This reflects the premise that as the system develops, the significance of older data reduces [9].

As the system develops further, the significance of the older data reduces [9,48]. Therefore, the training data, retained after rolling, were applied to the SGM(1,1), MCSGM(1,1) and CMCSGM(1,1) models. The rolling mechanism could select only a few recent data by capturing the developing trend from the training data. For $x_{}^{(0)}$ = ($x_1^{(0)}$, $x_2^{(0)}$, …, $x_n^{(0)}$), the l-point rolling (4 ≤ l ≤ n − 1) can be exercised on $x_{}^{(0)}$ to construct a GM(1,1) model. MAPE_l corresponding to the l-point rolling can be computed as

$${\mathrm{MAPE}}_l=\frac{1}{n-l}{\displaystyle \sum _{k=l+1}^n\frac{\left|x_k^{(0)}-{\tilde{x}}_k^{(0)}\right|}{x_k^{(0)}}}\times 100\%$$

(21)

Finally, the best number of point, say v, that can be used to construct a GM(1,1) model, called SGM(1,1), is determined as

$$v=\arg \underset{l}{\min }{\mathrm{MAPE}}_l$$

(22)

For fair comparisons, the proposed NN-Grey-Markov model used the same training data as the SGM(1,1), the MCSGM(1,1), and the CMCSGM(1,1) models. The rest of this section is organized as follows. Section 4.1 presents the parameter specifications for the GA and Section 4.2 presents prediction accuracy for different grey prediction models on real data.

4.2. GA Parameters

It is known that population size and crossover and mutation probabilities can have impacts on GA performance. There are no optimal parameter settings. Therefore, following [42,44], the experiment parameters were chosen to be:

(i)

n_size = 200: It is reasonable to specify population size ranging from 50 to 500 individuals.

(ii)

n_max = 1000: n_max plays a role of stopping condition, and it should take available computing time into account.

(iii)

n_del = 2: A small number of elite chromosomes is considered.

(iv)

Pr_c = 0.8, Pr_m = 0.01.

In the experiment, no matter what the data set is, the same parameters of GA were used to examine the prediction accuracy of the proposed NN-Grey-Markov model.

4.3. Applications to Foreign Tourist Forecasting

4.3.1. Case I

The first experiment was conducted on the yearly statistics reported by Taiwan Tourism Bureau [49].

Table 1. Historical annual foreign tourists from six countries to Taiwan.

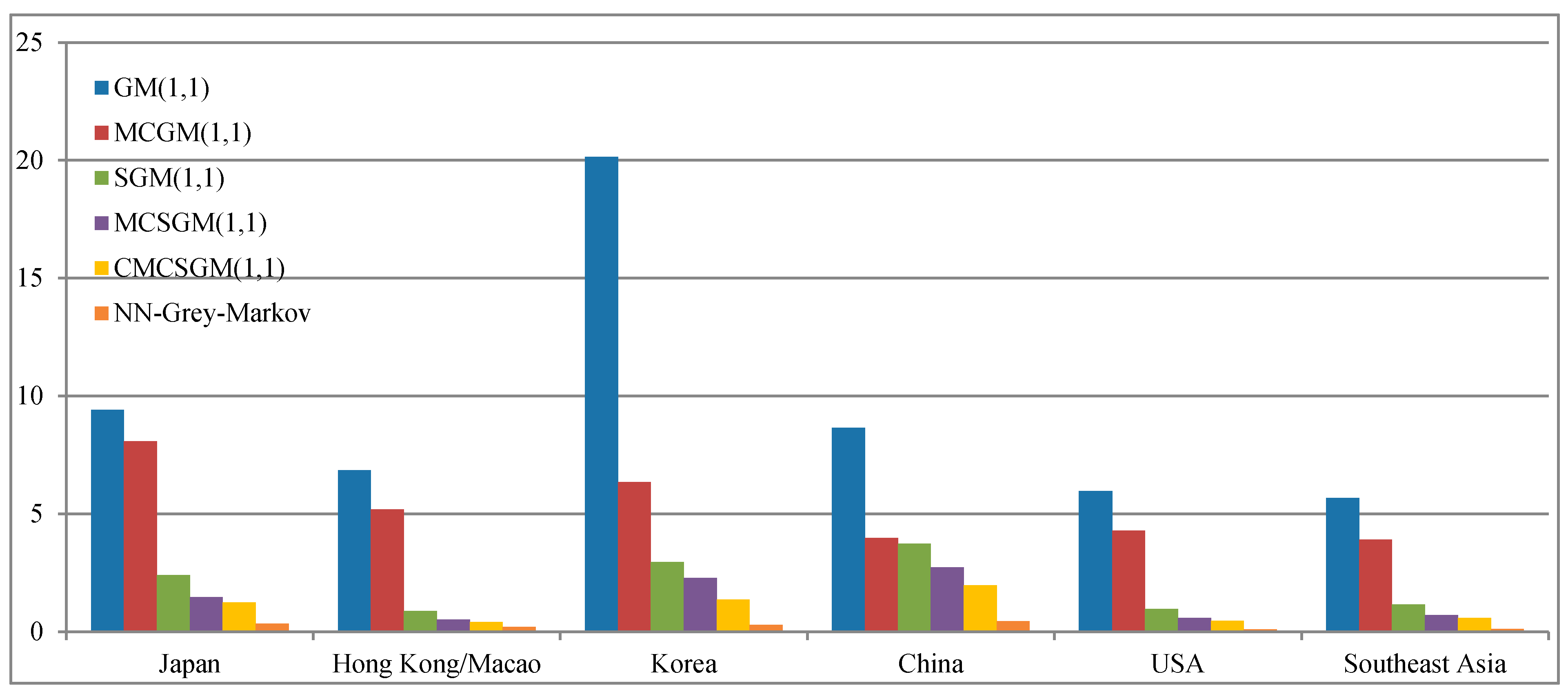
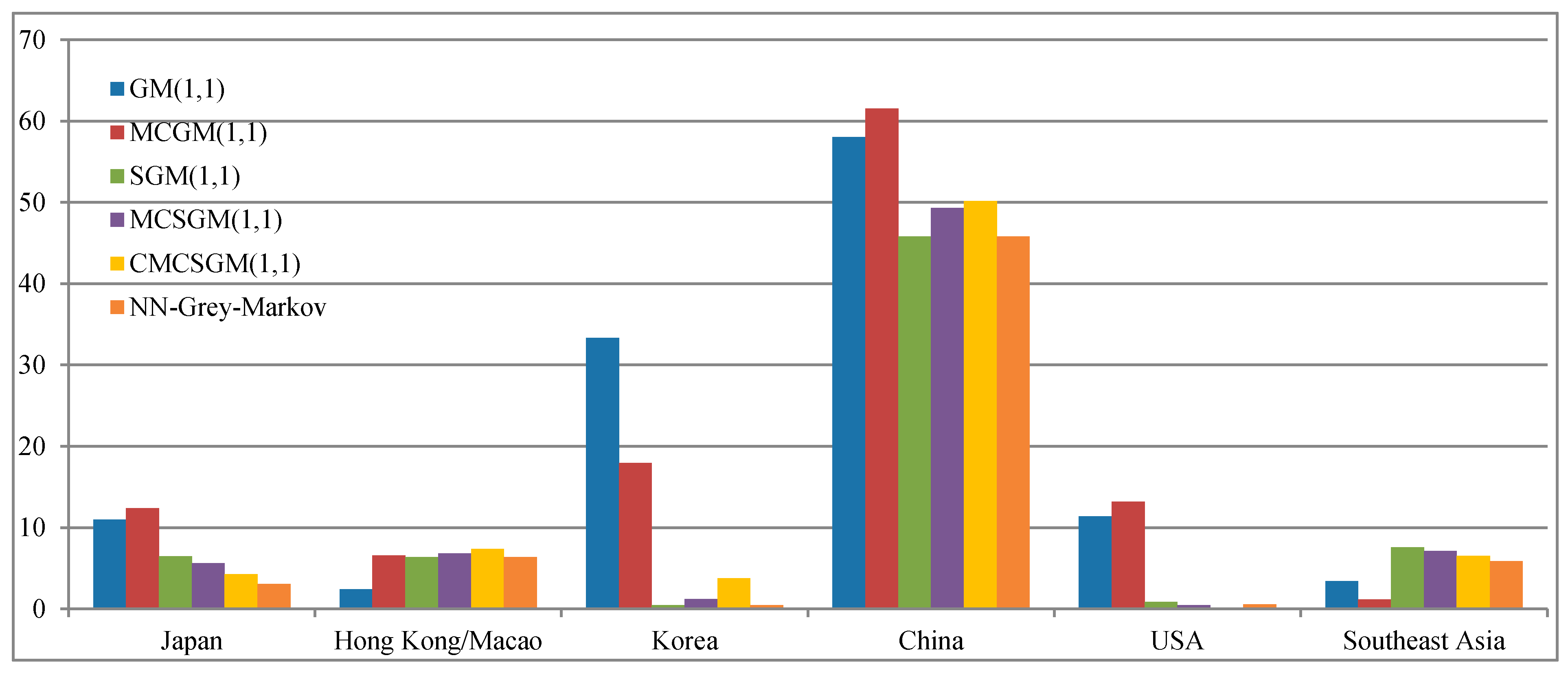
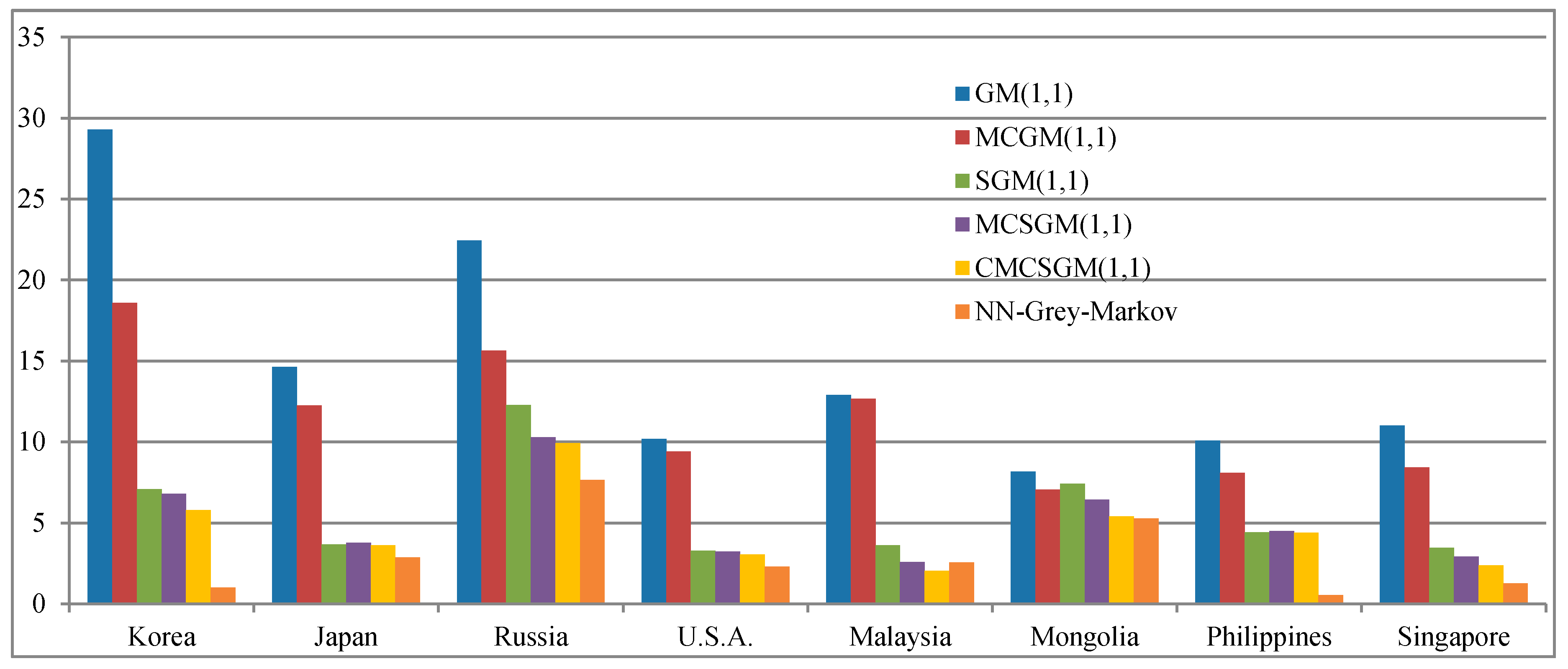
Year	Japan	Hong Kong/Macao	Korea	China	U.S.A.	Southeast Asia
2001	976,750	435,164	85,744		348,808	488,968
2002	998,497	456,554	83,624		377,470	530,319
2003	657,053	323,178	92,893		272,858	457,103
2004	887,311	417,087	148,095		382,822	568,269
2005	1,124,334	432,718	182,517		390,929	636,925
2006	1,161,489	431,884	196,260		394,802	643,338
2007	1,166,380	491,437	225,814		397,965	700,287
2008	1,086,691	618,667	252,266	329,204	387,197	725,751
2009	1,000,661	718,806	167,641	972,123	369,258	689,027
2010	1,080,153	794,362	216,901	1,630,735	395,729	911,174
2011	1,294,758	817,944	242,902	1,784,185	412,617	1,071,975
2012	1,432,315	1,016,356	259,089	2,586,428	411,416	1,132,592
2013	1,421,550	1,183,341	351,301	2,874,702	414,060	1,261,596
2014	1,634,790	1,375,770	527,684	3,987,152	458,691	1,388,305
2015	1,627,229	1,513,597	658,757	4,184,102	479,452	1,425,485
2016	1,895,702	1,614,803	884,397	3,511,734	523,888	1,653,908

shows historical annual foreign tourists to Taiwan from six countries, Japan, Hong Kong/Macao, Korea, China, USA, and Southeast Asia, collected from 2001 to 2016. Year 2016 was used for testing using a one-step transition probability matrix, i.e., m = 1. Therefore, after performing the rolling mechanism, 2011–2015 data from China and 2012–2015 from the other countries can be used for model-fitting for the SGM(1,1), the MCSGM(1,1), the CMCSGM(1,1), and proposed grey prediction models. Whichever the country is, the original GM(1,1) and the MCGM(1,1) were constructed using data from 2001 to 2015.

Figure 1 and Figure 2 show prediction results with respect to model fitting and testing for different models, respectively. Figure 1 shows that the proposed NN-Grey-Markov model outperforms the other prediction models considered for model-fitting. For testing, the proposed NN-Grey-Markov model outperforms the SGM(1,1), the MCSGM(1,1), and the CMCSGM(1,1) models, and it is little inferior to the original GM(1,1) and the MCGM(1,1) models for Hong Kong/Macao and Southeast Asia.

4.3.2. Case II

Historical annual data from 1997 to 2013 published by China National Tourism Administration were used to conduct the second experiment. The data were summarized in Reference [25]. The collected data were associated with foreign tourists from eight main countries, including Japan, Korea, Malaysia, Mongolia, Philippines, Russia, Singapore, and USA. Year 2013 was used for testing by a one-step transition probability matrix. Performing the rolling mechanism, 2005–2012 data from Korea, Japan, USA, and Malaysia; 2006–2012 from Russia, 2003–2012 from Mongolia and Philippines; and 2004–2012 from Singapore from 2004 to 2012 can be used to construct the SGM(1,1), the MCSGM(1,1), the CMCSGM(1,1), and proposed NN-Grey-Markov models. The original GM(1,1) and the MCGM(1,1) were constructed using data from 1997 to 2012 for each economy. Using the same data, Sun et al. [25] demonstrated the effectiveness of the CMCSGM(1,1) model.

Figure 3 and Figure 4 show prediction results with respect to model fitting and testing for different prediction models, respectively. For model-fitting, Figure 3 shows that the proposed NN-Grey-Markov model is comparable or superior to the compared models. It is slightly inferior to the CMCSGM(1,1) model for Malaysia. As for testing results, prediction accuracy of the proposed NN-Grey-Markov model outperforms that of the CMCSGM(1,1) model, except for Malaysia and Singapore. The proposed grey prediction model is superior to the original GM(1,1), the SGM(1,1), and the MCSGM(1,1) models. It is obvious that the proposed NN-Grey-Markov model provides comparable and satisfactory results compared to the other prediction models considered.

5. Discussion and Conclusions

Data fluctuations such as tourism time series data often arise from random factors, which can be effectively reduced by the Grey-Markov model. Based on the Grey-Markov model, this study proposed a novel grey residual modification model, NN-Grey-Markov, for tourism demand prediction. Compared to previous studies based on MCGM(1,1), there are two distinctive features of the proposed NN-Grey-Markov model. First, the proposed grey prediction model incorporates FLN to estimate the sign of each revised residual, and available degree to which a predicted value from the GM(1,1) model can be adjusted. Second, we need not define the number of states and their bounds for the Markov chain in advance, since these can be fully determined by GA. It should be noted that, the FLNGM(1,1) model [45] integrated the original GM(1,1) with the residual GM(1,1) models and then used the functional-link net to estimate the sign and the modification range with respect to a predicted residual obtained from the residual GM(1,1) model. The implementation of the proposed NN-Grey-Markov model is therefore different from that of the FLNGM(1,1) model.

Development of the tourism industry has contributed relatively highly to economic prosperity. In the variable global tourism market, accurate prediction of tourism demand is crucial for governments and private sectors to set up strategies—such as investment and construction—to promote the tourism industry. It is challenging to predict precisely the trend of tourism demand. From the perspective of the grey system, it is reasonable to apply the GM(1,1) model to foreign tourist prediction. Historical annual data for foreign tourists, collected from Taiwan and China official institutions, were used to evaluate prediction performance of the proposed NN-Grey-Markov model. The proposed model with pre-specified GA parameters, including population size, number of generations, probabilities for crossover and mutation, performs well. This means that fine parameter tuning is not required for the proposed prediction model, and that parameter specifications introduced in the previous section were acceptable. Real case experiments reveal that the proposed NN-Grey-Markov model outperformed other grey prediction models considered for the majority of data sets. This validated the potential usefulness of the proposed NN-Grey-Markov model for tourism demand prediction.

For future studies, there are two issues that require addressing. First, this study used a one-step transition probability matrix to predict the residual for testing on a predicted time period. The other alternative is to sum the rows of the transition probability matrices corresponding to some near time periods prior to a predicted one to estimate the residual corresponding to a predicted time period [32,33]. It would be interesting to examine the influence on foreign tourist prediction using the proposed NN-Grey-Markov model. Second, FLN used the hyperbolic tangent function as the output neuron’s activation function, computing a weighted sum of a vector of connection weights with an enhanced pattern. This assumes additivity among individual variables in the enhanced pattern [50]. However, these criteria are not always independent [12,51,52], and would be interesting to explore the impact of non-additivity on prediction performance of the proposed NN-Grey-Markov model.