Uncertain Production Scheduling Based on Fuzzy Theory Considering Utility and Production Rate
Abstract
:1. Introduction
2. Problem State
3. Deterministic Scheduling Model Based on USEBCT Modeling Method
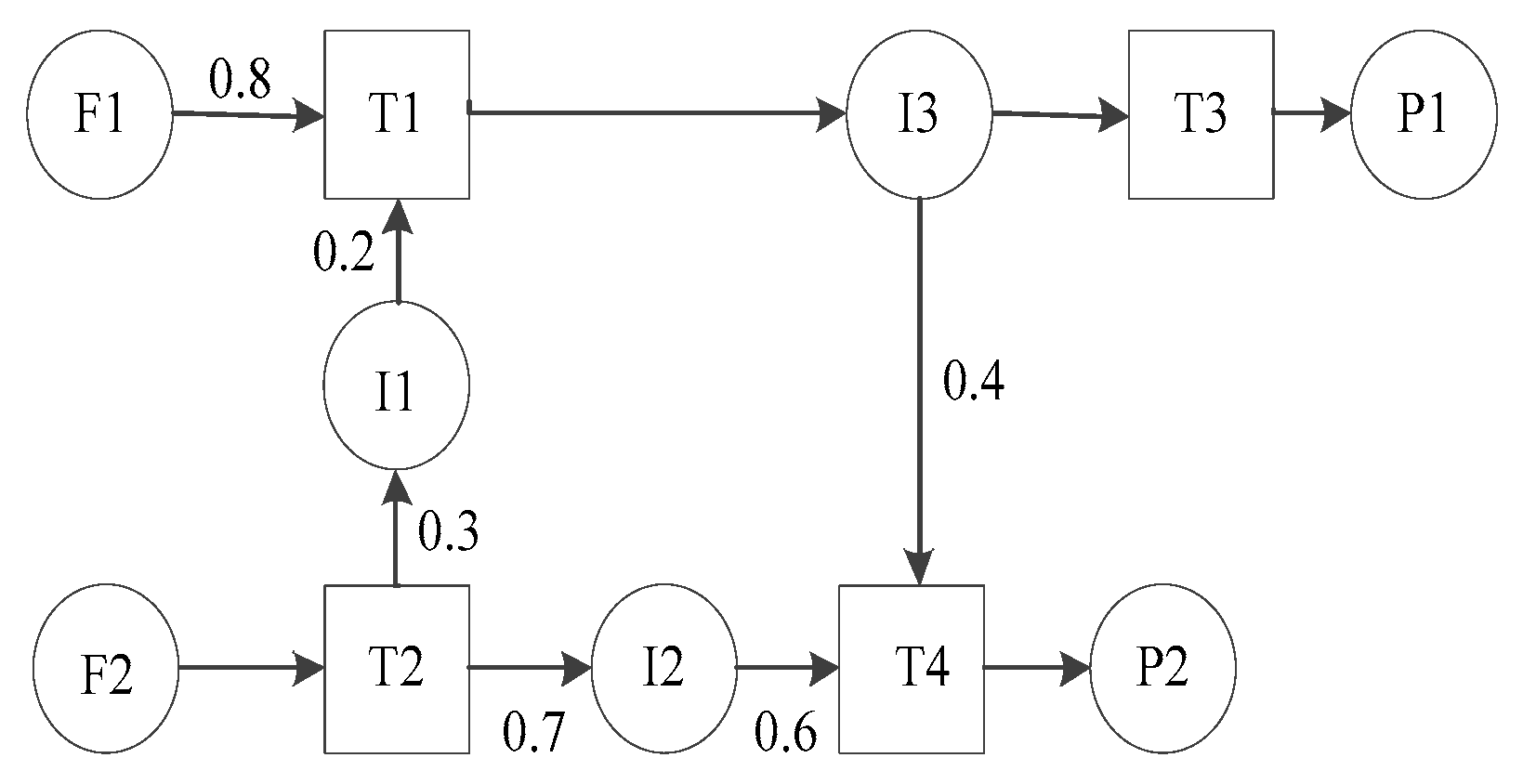
3.1. Basic Concepts of USEBCT Model
- (1)
- Event: time measurement, each event has one start time and finish time;
- (2)
- State: raw materials, intermediates and final products;
- (3)
- Task: action of producing or consuming one state;
- (4)
- Unit: machines in which the task can be performed.
3.2. Deterministic Scheduling Model
4. Fuzzy Scheduling Model and Defuzzification
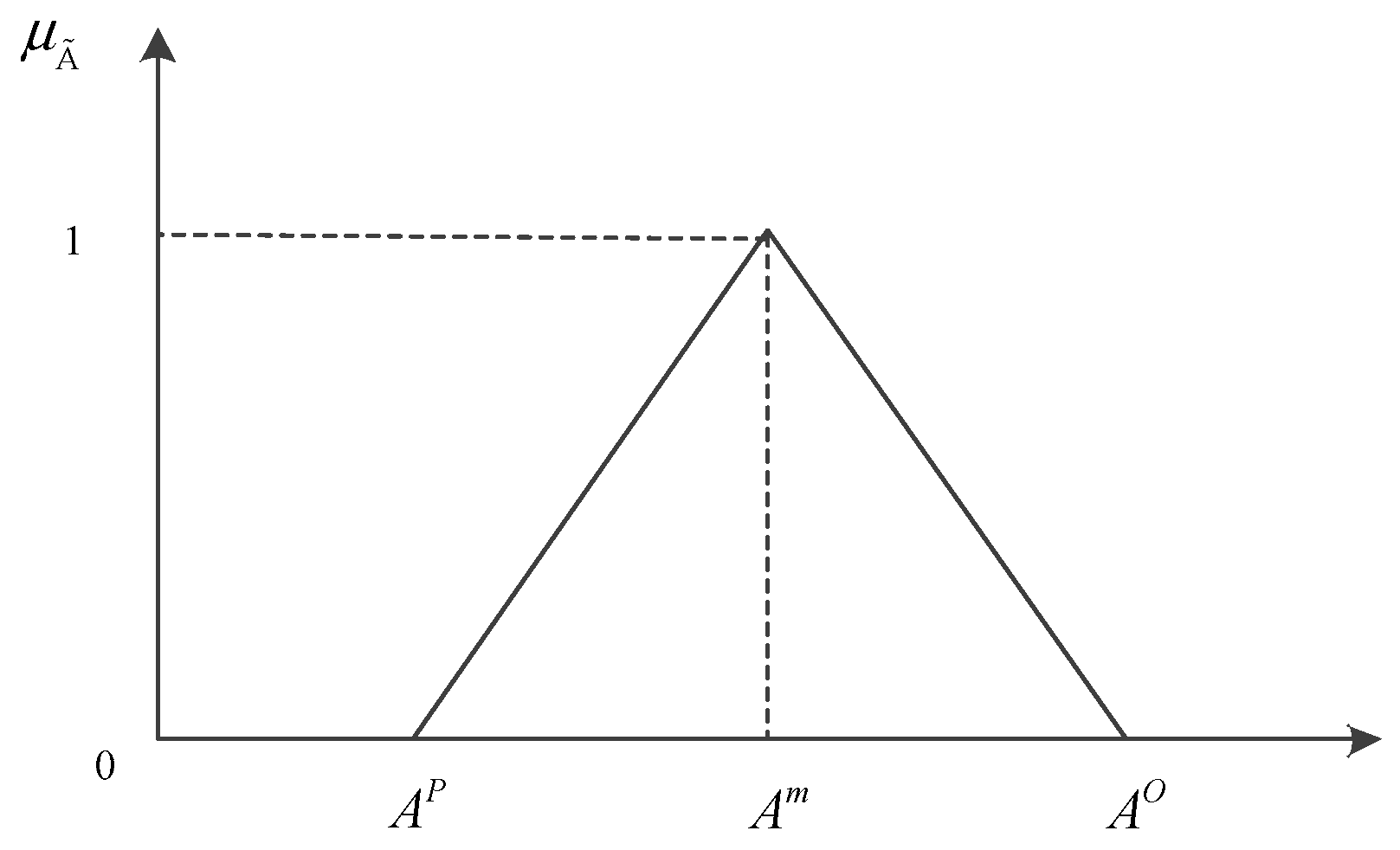
4.1. Uncertainty Description
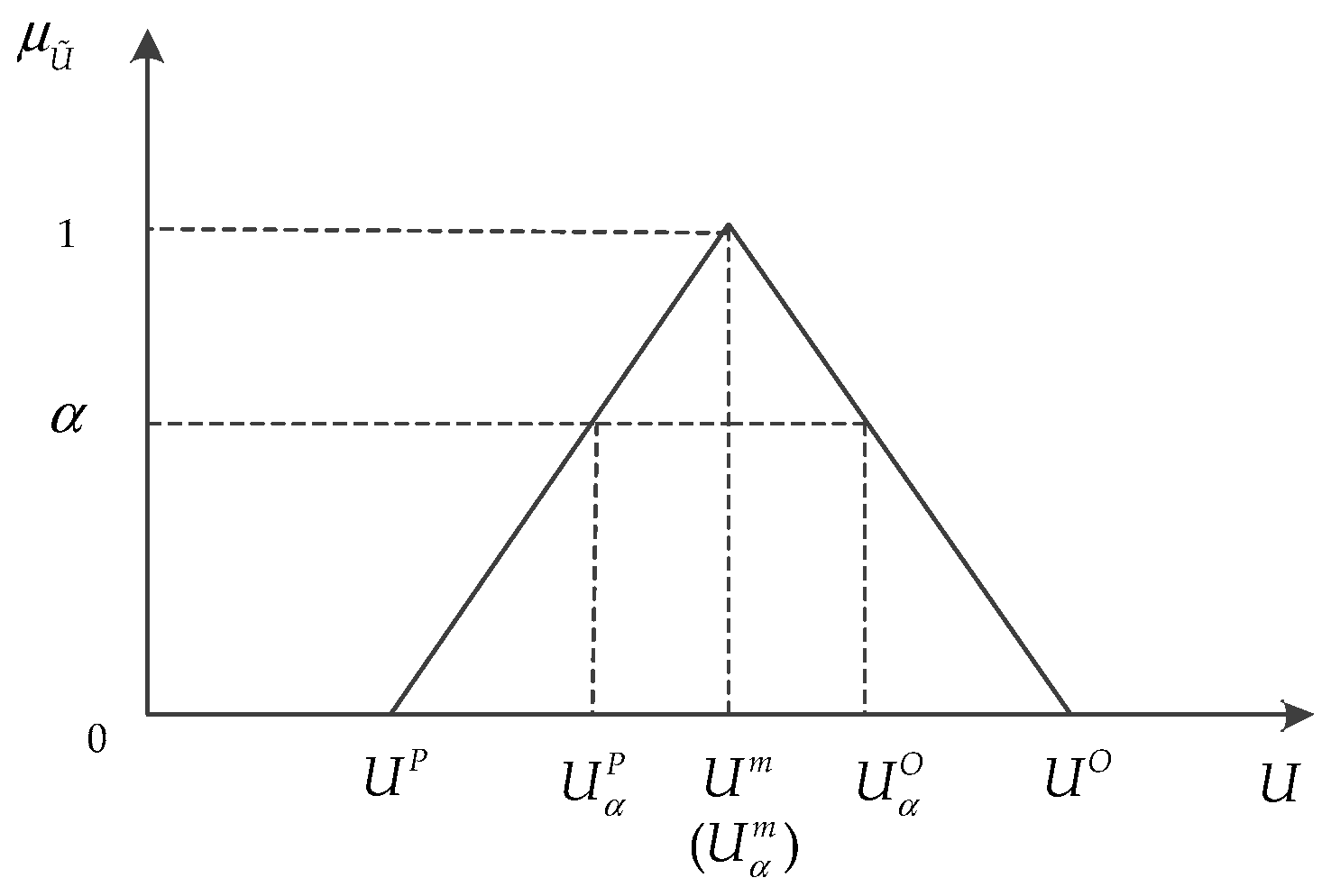
4.2. Defuzzification of Fuzzy Scheduling Model
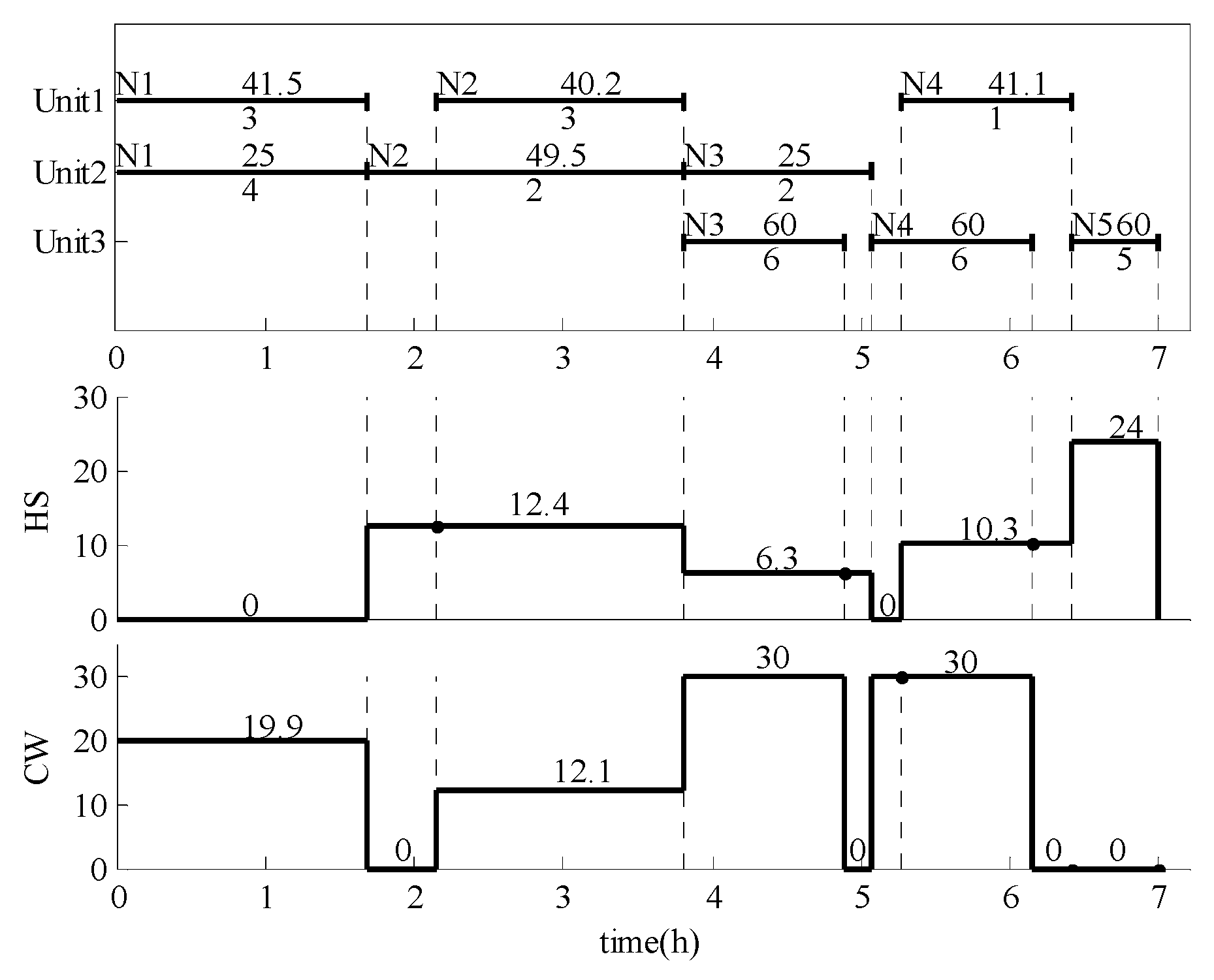
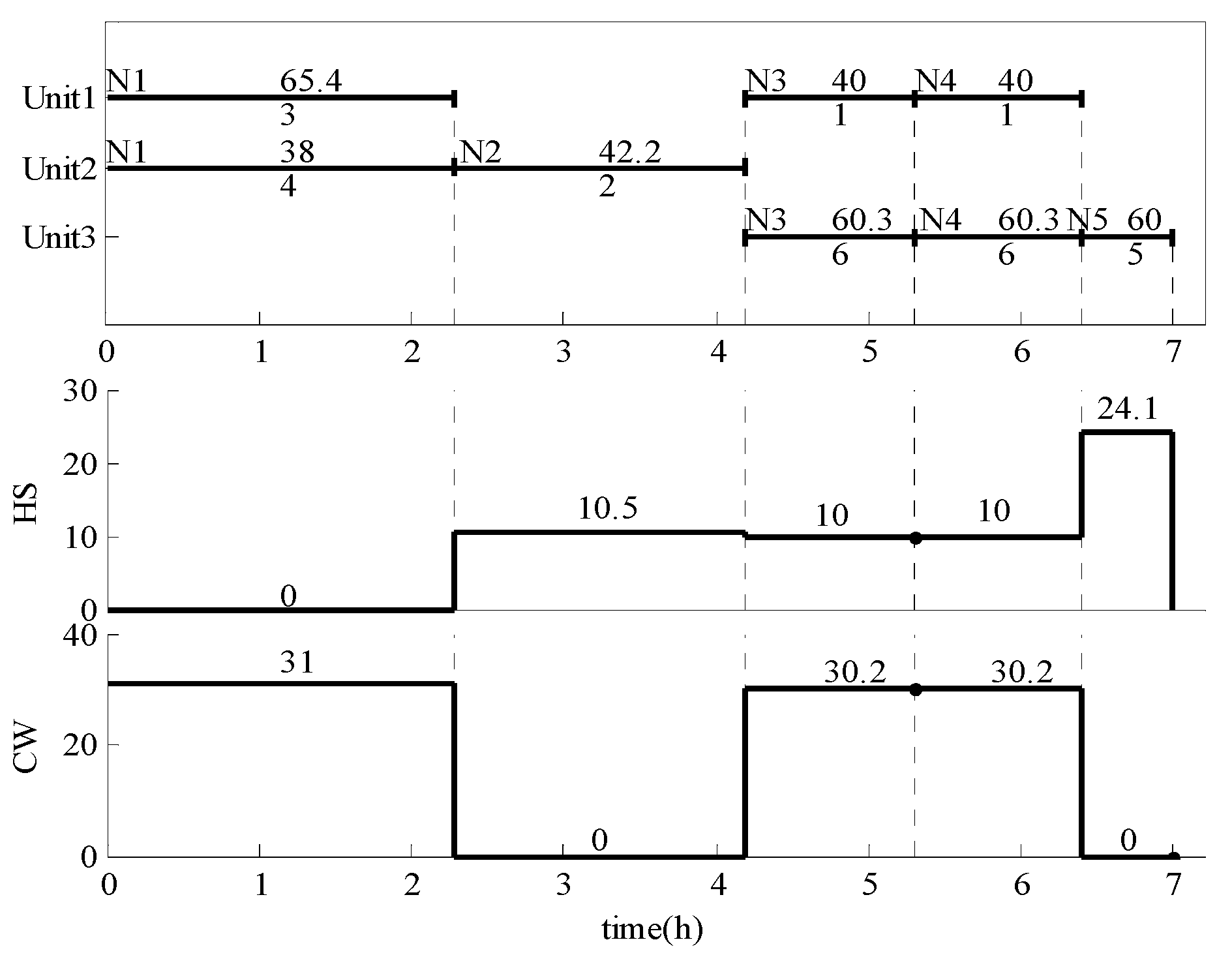
5. Case Study
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Upper layer: | |
| Indices | |
| task | |
| unit | |
| event | |
| state | |
| utility | |
| Sets | |
| tasks | |
| tasks which can be performed in unit j | |
| tasks which produce state | |
| tasks which consume state | |
| tasks which consume utility | |
| units | |
| units which are suitable for performing task | |
| total events postulated in the scheduling horizon | |
| states | |
| states that are raw materials | |
| states that are final products | |
| states that are intermediates | |
| utilities | |
| utilities that are required by task | |
| intermediate states with dedicated finite intermediate storage | |
| Parameters | |
| minimum batch size of task | |
| maximum batch size of task | |
| initial amount available for state | |
| maximum storage capacity for state | |
| proportion of state consumed by task | |
| proportion of state produced by task | |
| coefficient between production rate and consumption of utility consumed by task | |
| minimum production rate of task | |
| price of state | |
| large positive number in big-M constraints | |
| short-term scheduling horizon | |
| coefficient between consumption of utility and amount of material consumed/processed by task at event | |
| maximum availability of utility for task | |
| limit on the maximum number of events over which a task is allowed to continue | |
| Binary variables | |
| binary variable for task active at event | |
| Positive variables | |
| amount of material processed by task at event | |
| production rate of task at event | |
| excess amount of state that needs to be stored at event | |
| start time of a task at event | |
| end time of a task at event | |
| consumption of utility by task at event | |
| start time at which there is a change in the consumption of utility at event |
References
- Wang, J.; Abid, H.; Lee, S.; Shu, L.; Xia, F. A Secured Health Care Application Architecture for Cyber-Physical Systems. J. Control Eng. Appl. Inform. 2011, 13, 101–108. [Google Scholar]
- Satchidanandan, B.; Kumar, P.R. Dynamic Watermarking: Active Defense of Networked Cyber–Physical Systems. Proc. IEEE 2016, 105, 219–240. [Google Scholar] [CrossRef]
- Niu, H.; Jagannathan, S. Optimal Defense and Control for Cyber-Physical Systems. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 634–639. [Google Scholar]
- Moller, D.P.F.; Vakilzadian, H. Cyber-physical systems in smart transportation. In Proceedings of the IEEE International Conference on Electro Information Technology, Grand Forks, ND, USA, 19–21 May 2016; pp. 776–781. [Google Scholar]
- Thramboulidis, K. A cyber-physical system-based approach for industrial automation systems. Comput. Ind. 2015, 72, 92–102. [Google Scholar] [CrossRef]
- Al Faruque, M.A.; Ahourai, F. A model-based design of Cyber-Physical Energy Systems. In Proceedings of the 19th Asia and South Pacific, Design Automation Conference, Singapore, 20–23 January 2014; pp. 97–104. [Google Scholar]
- Ilic, M.D.; Xie, L.; Khan, U.A. Modeling future cyber-physical energy systems. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–9. [Google Scholar]
- Costanzo, A.; Faro, A.; Giordano, D.; Pino, C. Mobile cyber physical systems for health care: Functions, ambient ontology and e-diagnostics. In Proceedings of the IEEE Consumer Communications & Networking Conference, Las Vegas, NV, USA, 9–12 January 2016; pp. 972–975. [Google Scholar]
- Mehdipour, F. Smart Field Monitoring: An Application of Cyber-Physical Systems in Agriculture (Work in Progress). In Proceedings of the IIAI 3rd International Conference on Advanced Applied Informatics, Kitakyushu, Japan, 31 August–4 September 2014; pp. 181–184. [Google Scholar]
- Rad, C.R.; Olteanu, G.; Takacs, I.A.; Olteanu, G. Smart Monitoring of Potato Crop: A Cyber-Physical System Architecture Model in the Field of Precision Agriculture. Agric. Agric. Sci. Procedia 2015, 6, 73–79. [Google Scholar] [CrossRef]
- Haque, S.A.; Aziz, S.M.; Rahman, M. Review of Cyber-Physical System in Healthcare. Int. J. Distrib. Sens. Netw. 2014, 10, 20. [Google Scholar] [CrossRef]
- Zhang, M.; Selic, B.; Ali, S.; Yue, T.; Okariz, O.; Norgren, R. Understanding Uncertainty in Cyber-Physical Systems: A Conceptual Model. In Modelling Foundations and Applications; Springer International Publishing: Cham, The Switzerland, 2016. [Google Scholar]
- Berger, C.; Hees, A.; Braunreuther, S.; Reinhart, G. Characterization of Cyber-Physical Sensor Systems. Procedia CIRP 2016, 41, 638–643. [Google Scholar] [CrossRef]
- Guillén, G.; Mele, F.D.; Antonio Espuña, A.; Puigjaner, L. Addressing the Design of Chemical Supply Chains under Demand Uncertainty. Comput. Aided Chem. Eng. 2006, 21, 1095–1100. [Google Scholar]
- Zhu, J.; Gu, X.; Gu, W. Robust optimization approach for short-term scheduling of batch plants under demand uncertainty. Kybernetes 2011, 40, 860–870. [Google Scholar] [CrossRef]
- And, J.P.V.; Ierapetritou, M.G. Robust Short-Term Scheduling of Multiproduct Batch Plants under Demand Uncertainty. Ind. Eng. Chem. Res. 2001, 40, 4543–4554. [Google Scholar]
- Xu, Z.H.; Gu, X.S.; Jiao, B. Scheduling of Uncertain Multi-product Batch Processes Under Finite Intermediate Storage Policy. IFAC Proc. Vol. 2008, 41, 14864–14869. [Google Scholar]
- Lindholm, A.; Johnsson, C. Plant-wide utility disturbance management in the process industry. Comput. Chem. Eng. 2013, 49, 146–157. [Google Scholar] [CrossRef]
- Lindholm, A.; Giselsson, P. Minimization of economical losses due to utility disturbances in the process industry. J. Process Control 2013, 23, 767–777. [Google Scholar] [CrossRef]
- Lindholm, A.; Johnsson, C.; Quttineh, N.-H.; Lidestam, H.; Henningsson, M.; Wikner, J.; Tang, O.; Nytzen, N.-P.; Forsman, K. Hierarchical Scheduling and Utility Disturbance Management in the Process Industry. IFAC Proc. Vol. 2013, 46, 140–145. [Google Scholar] [CrossRef]
- Wang, K.; Choi, S.H.; Lu, H. A hybrid estimation of distribution algorithm for simulation-based scheduling in a stochastic permutation flowshop. Comput. Ind. Eng. 2015, 90, 186–196. [Google Scholar] [CrossRef]
- Aytug, H.; Lawley, M.A.; Mckay, K.; Mohan, S.; Uzsoy, R. Executing production schedules in the face of uncertainties: A review and some future directions. Eur. J. Oper. Res. 2005, 161, 86–110. [Google Scholar] [CrossRef]
- Sabuncuoglu, I.; Goren, S. Hedging production schedules against uncertainty in manufacturing environment with a review of robustness and stability research. Int. J. Comput. Integr. Manuf. 2009, 22, 138–157. [Google Scholar] [CrossRef]
- Mou, D.; Chang, X. An Uncertain Programming for the Integrated Planning of Production and Transportation. Math. Probl. Eng. 2014, 2014, 135–142. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Chen, X. Multistage scenario-based interval-stochastic programming for planning water resources allocation. Stoch. Environ. Res. Risk Assess. 2009, 23, 781–792. [Google Scholar] [CrossRef]
- Vooradi, R.; Shaik, M.A. Improved three-index unit-specific event-based model for short-term scheduling of batch plants. Comput. Chem. Eng. 2012, 43, 148–172. [Google Scholar] [CrossRef]
- Munawar, A.S.; Christodoulos, A.F. Improved Unit-Specific Event-Based Continuous-Time Model for Short-Term Scheduling of Continuous Processes: Rigorous Treatment of Storage Requirements. Ind. Eng. Chem. Res. 2007, 46, 1764–1779. [Google Scholar]
- Shaik, M.A.; Floudas, C.A. Novel Unified Modeling Approach for Short-Term Scheduling. Ind. Eng. Chem. Res. 2009, 48, 2947–2964. [Google Scholar] [CrossRef]
- Shaik, M.A.; Floudas, C.A. Unit-specific event-based continuous-time approach for short-term scheduling of batch plants using RTN framework. Comput. Chem. Eng. 2008, 32, 260–274. [Google Scholar] [CrossRef]
- Castro, P.; Barbosa-Póvoa, A.P.F.D.; Matos, H. An Improved RTN Continuous-Time Formulation for the Short-term Scheduling of Multipurpose Batch Plants. Ind. Eng. Chem. Res. 2001, 40, 5040–5041. [Google Scholar] [CrossRef]
- Ierapetritou, M.G.; Floudas, C.A. Effective continuous-time formulation for short-term scheduling. 1. Multipurpose batch processes. Ind. Eng. Chem. Res. 1998, 37, 4341–4359. [Google Scholar] [CrossRef]
- Lai, Y.J.; Hwang, C.L. A new approach to some possibilistic linear programming problems. Fuzzy Sets Syst. 1992, 49, 121–133. [Google Scholar] [CrossRef]
- Lai, Y.J.; Hwang, C.L. Possibilistic linear programming for managing interest rate risk. Fuzzy Sets Syst. 1993, 54, 135–146. [Google Scholar] [CrossRef]
- Liang, T.F. Distribution planning decisions using interactive fuzzy multi-objective linear programming. Fuzzy Sets Syst. 2006, 157, 1303–1316. [Google Scholar] [CrossRef]
- Liang, T.F. Integrating production-transportation planning decision with fuzzy multiple goals in supply chains. Int. J. Prod. Res. 2008, 46, 1477–1494. [Google Scholar] [CrossRef]
- Torabi, S.A.; Hassini, E. An interactive possibilistic programming approach for multiple objective supply chain master planning. Fuzzy Sets Syst. 2008, 159, 193–214. [Google Scholar] [CrossRef]
- Torabi, S.A.; Ebadian, M.; Tanha, R. Fuzzy hierarchical production planning (with a case study). Fuzzy Sets Syst. 2010, 161, 1511–1529. [Google Scholar] [CrossRef]
- Torabi, S.A. Multi-site production planning integrating procurement and distribution plans in multi-echelon supply chains: An interactive fuzzy goal programming approach. Int. J. Prod. Res. 2009, 47, 5475–5499. [Google Scholar] [CrossRef]
- Basyigit, A.I.; Ulu, C.; Guzelkaya, M. A New Fuzzy Time Series Model Using Triangular and Trapezoidal Membership Functions. In Proceedings of the International Work-Conference on Time Series, Granada, Spain, 25–27 June 2014. [Google Scholar]
- Noori-Darvish, S.; Mahdavi, I.; Mahdavi-Amiri, N. A bi-objective possibilistic programming model for open shop scheduling problems with sequence-dependent setup times, fuzzy processing times, and fuzzy due dates. Appl. Soft Comput. J. 2012, 12, 1399–1416. [Google Scholar] [CrossRef]
- Wang, R.C.; Liang, T.F. Applying possibilistic linear programming to aggregate production planning. Int. J. Prod. Econ. 2005, 98, 328–341. [Google Scholar] [CrossRef]
- Garciasabater, J.P. Capacity and material requirement planning modelling by comparing deterministic and fuzzy models. Int. J. Prod. Res. 2008, 46, 5589–5606. [Google Scholar]
- Christou, I.T.; Lycopoulou, A.G.L.D. Hierarchical production planning for multi-product lines in the beverage industry. Prod. Plan. Control 2007, 18, 367–376. [Google Scholar] [CrossRef]
- Maravelias, C.T.; Grossmann, I.E. A New General Continuous-Time State Task Network Formulation for Short-Term Scheduling of Multipurpose Batch Plants. Ind. Eng. Chem. Res. 2003, 42, 3056–3074. [Google Scholar] [CrossRef]
- Wang, Y.; Su, H.; Shao, H.; Xie, L. Unit-Specific Event-Based and Slot-Based Hybrid Model Framework with Hierarchical Structure for Short-Term Scheduling. Math. Probl. Eng. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
| Task 1 (R1) | Task 2 (R2) | Task 3 (R3) | Task 4 (R4) | |||
|---|---|---|---|---|---|---|
| RI1 | 40 | 80 | 0.25 | 0.3 | - | - |
| RI2 | 25 | 50 | 0.25 | 0.3 | - | - |
| RII | 40 | 80 | - | - | 0.2 | 0.5 |
| F1 | F2 | I1 | I2 | I3 | P1 | P2 | |
|---|---|---|---|---|---|---|---|
| STsmax | 1000 | 1000 | 200 | 100 | 500 | 1000 | 1000 |
| STs0 | 400 | 400 | 0 | 0 | 0 | 0 | 0 |
| Prices | 0 | 0 | 0 | 0 | 0 | 30 | 40 |
| Task 1 | Task 2 | Task 3 | Task 4 | ||||
|---|---|---|---|---|---|---|---|
| RI1 | RI2 | RI1 | RI2 | RII | RII | ||
| three prominent values | (0.8 1 1.3) | (0.4 0.6 0.7) | (0.55 0.6 0.62) | (0.4 0.5 0.6) | (1.9 2 2.2) | (0.9 1 1.2) | |
| actual data | event 1 | 0.92 | 0.65 | 0.60 | 0.45 | 1.95 | 0.95 |
| event 2 | 0.90 | 0.60 | 0.61 | 0.50 | 2.10 | 1.00 | |
| event 3 | 0.98 | 0.62 | 0.60 | 0.50 | 2.00 | 0.98 | |
| event 4 | 1.00 | 0.58 | 0.59 | 0.51 | 1.98 | 1.10 | |
| event 5 | 1.15 | 0.50 | 0.58 | 0.55 | 2.00 | 1.00 | |
| Task 1 | Task 2 | Task 3 | Task 4 | ||||
|---|---|---|---|---|---|---|---|
| RI1 | RI2 | RI1 | RI2 | RII | RII | ||
| three prominent values | (23 24 25) | (20 24 27) | (27 30 35) | (28 30 31) | (22 24 27) | (29 30 33) | |
| actual data | event 1 | 23.5 | 25.5 | 32.5 | 30.0 | 25.4 | 29.7 |
| event 2 | 24.0 | 23.0 | 31.2 | 30.5 | 23.6 | 31.5 | |
| event 3 | 23.8 | 24.0 | 28.5 | 30.0 | 24.0 | 29.6 | |
| event 4 | 24.5 | 22.0 | 30.0 | 29.4 | 24.0 | 30.0 | |
| event 5 | 24.0 | 24.7 | 29.6 | 29.0 | 23.0 | 30.8 | |
| Results Based on Actual Data | Deterministic Model | Fuzzy Model | ||||
|---|---|---|---|---|---|---|
| Objective Function ($) | Completion Time (h) | Objective Function ($) | Completion Time (h) | Objective Function ($) | Completion Time (h) | |
| 5448 | 11.20 | 5400 | 12.30 | 0.5 | 5426.25 | 11.42 |
| 0.6 | 5421.00 | 12.10 | ||||
| 0.7 | 5415.75 | 12.19 | ||||
| 0.8 | 5410.50 | 11.37 | ||||
| Deterministic Model | Fuzzy Model | |||
|---|---|---|---|---|
| Objective Function ($) | Completion Time (h) | Objective Function ($) | Completion Time (h) | |
| 0.88% | 9.82% | 0.5 | 0.40% | 1.96% |
| 0.6 | 0.50% | 8.04% | ||
| 0.7 | 0.59% | 8.84% | ||
| 0.8 | 0.69% | 1.52% | ||
| average value | 0.545% | 5.09% | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Jin, X.; Xie, L.; Zhang, Y.; Lu, S. Uncertain Production Scheduling Based on Fuzzy Theory Considering Utility and Production Rate. Information 2017, 8, 158. https://doi.org/10.3390/info8040158
Wang Y, Jin X, Xie L, Zhang Y, Lu S. Uncertain Production Scheduling Based on Fuzzy Theory Considering Utility and Production Rate. Information. 2017; 8(4):158. https://doi.org/10.3390/info8040158
Chicago/Turabian StyleWang, Yue, Xin Jin, Lei Xie, Yanhui Zhang, and Shan Lu. 2017. "Uncertain Production Scheduling Based on Fuzzy Theory Considering Utility and Production Rate" Information 8, no. 4: 158. https://doi.org/10.3390/info8040158
APA StyleWang, Y., Jin, X., Xie, L., Zhang, Y., & Lu, S. (2017). Uncertain Production Scheduling Based on Fuzzy Theory Considering Utility and Production Rate. Information, 8(4), 158. https://doi.org/10.3390/info8040158






