Abstract
The article is devoted to a matrix method of comparative analysis of long nucleotide sequences by means of presenting each sequence in the form of three digital binary sequences. This method uses a set of symmetries of biochemical attributes of nucleotides. It also uses the possibility of presentation of every whole set of N-mers as one of the members of a Kronecker family of genetic matrices. With this method, a long nucleotide sequence can be visually represented as an individual fractal-like mosaic or another regular mosaic of binary type. In contrast to natural nucleotide sequences, artificial random sequences give non-regular patterns. Examples of binary mosaics of long nucleotide sequences are shown, including cases of human chromosomes and penicillins. The obtained results are then discussed.
1. Introduction
Long nucleotide sequences are studied by many authors because of their importance for bioinformatics and theoretical biology. For example, some of works relate to the famous second rule of Chargaff [1,2,3,4,5,6,7,8,9,10,11]. Other publications discuss the application of the method of Chaos Game Representation to study long genetic sequences. The latter was originally proposed in the work [12] and used by many other authors later [13,14,15,16,17,18,19]. The notion of “a long nucleotide sequence” usually means a sequence with more than 50,000 nucleotides [9].
Our article is devoted to searching for new approaches for visualization of structural peculiarities of long nucleotide sequences in connection with the bio-mathematical conception of geno-logical coding [20,21,22,23]. This concept or biological hypothesis supposes that—besides the known genetic code of amino acid sequences of proteins—an additional coding system exists in biological organisms addressing the inheritance of processes and bio-informational algorithms along the chains of generations. Mathematical modeling of this geno-logical coding system is connected with dyadic groups of binary numbers, the logical operation of modulo-2 addition, Walsh functions, Hadamard matrices and the Kronecker product of matrices. These mathematical notions are well known in the theory of digital signal processing, but are relatively new in bioinformatics, where they help in developing algebraic biology [24,25,26,27,28,29,30], a wide modern branch of theoretical and mathematical biology. Possibilities of applying the above mentioned mathematical notions to study genetic structures were revealed in the so called “matrix genetics” [31,32,33,34,35,36,37]. Some of these mathematical tools are used in our article for visualization of long genetic sequences on the basis of a special matrix method for their visualization proposed by I. Stepanyan.
Matrix genetics studies matrix representations of natural ensembles of molecular genetic elements to reveal hidden regularities in cooperative genetic structures and to model inherited biological phenomena, whose features should be accommodated within the structural organization of the genetic code to be transferred along a chain of generations. Genetic information is encoded in DNA by means of a set of four nitrogenous bases: adenine A, cytosine C, guanine G, thymine T (in RNA, uracil U replaces thymine T). Our findings discussed in this article reveal and argue for the development of novel mathematical tools for modeling inheritable algorithmic processes to advance algebraic biology.
Known scientific methods for studying nucleotide sequences usually concentrate their attention on those fragments (or N-mers, or N-plets), which exist inside the sequences. Contrary to these, our method concentrates on studying those fragments of nucleotide sequences, which are missing in them. In other words, the described method investigates a deficit of different types of N-plets in nucleotide sequences. We suppose that this method can be useful for comparative analysis and classification of long genetic sequences. It could also help in understanding deeper genetic phenomena.
One should also emphasize that our method introduces an important notion in the field of molecular genetics and bioinformatics: binary fractals. They have been known in mathematics, physics, informatics and the engineering disciplines for a long time. The subject of binary fractals can be used as a new useful concept to bridge the biological and non-biological disciplines. Let us recall some approaches to matrix representations of molecular-genetic alphabets as discussed in [32,33,34,35,36,37].
2. Matrix Representations of Whole Sets of N-Plets (or N-Mers)
The genetic code system is based on sets or alphabets of N-plets (or N-mers) such as:
- the set of 41 monoplets (in DNA: A, C, G, T) (in RNA, uracil U replaces thymine T);
- the set of 42 = 16 duplets (AA, AC, AG, AT, ….);
- the set of 43 = 64 triplets (AAA, AAC, ACA, ACG, ACT, ….);
- etc.
Each whole set of 4N N-plets coincides with the whole set of 4N entries in a (2N × 2N)-matrix, which belongs to the Kronecker family of genetic matrices [A G; C T](N), where (N) means Kronecker (or tensor) power. Figure 1 shows the first three members of this Kronecker family for n = 1, 2, 3. It also shows that—inside such matrix [A G; C T](N)—each N-plet has its individual binary coordinates (or appropriate coordinates in decimal notation) due to biochemical attributes of N-plets. This is explained in detail below.
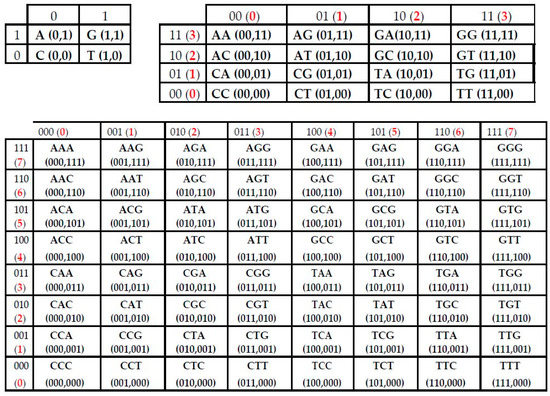
Figure 1.
The first members of the Kronecker family of symbolic genomatrices [A G; C T](N) for n = 1, 2, 3. Inside each genomatrix [A G; C T](N), each row and each column has its individual binary numeration due to genetic sub-alphabets (see explanation in text below). Correspondingly each N-plet, which is located on a row-column crossing, has two digital binary coordinates in such matrix. The decimal equivalents of these binary numbers are shown in red.
The four nitrogenous bases—adenine A, guanine G, cytosine C, thymine T (or uracil U in RNA)—represent specific poly-nuclear constructions with special bio-chemical properties. The set of these four constructions is not absolutely heterogeneous, but it bears the substantial symmetric system of distinctive-uniting attributes (or, more precisely, pairs of an “attribute–antiattribute”). This system of pairs of opposite attributes divides the genetic four-letter alphabet into three pairs of letters in all possible ways; letters of each such pair are equivalent to each other in accordance with one of these attributes or with its absence.
The system of such attributes divides the genetic four-letter alphabet into three pairs of letters, which are equivalent from a viewpoint of one of these attributes or its absence: (1) С = T and A = G (according to the binary-opposite attributes: “pyrimidine” or “non-pyrimidine”, that is purine); (2) А = С and G = T (according to the binary-opposite attributes “keto” or “amino” [38]); (3) С = G and А = T (according to the attributes: three or two hydrogen bonds (or strong–weak divisions) are materialized in these complementary pairs). The possibility of such division of the genetic alphabet into three binary sub-alphabets is known from the work [38]. We will utilize these known sub-alphabets by means of the following approach in the field of matrix genetics. We will attach appropriate binary symbols, “0” or “1”, to each of the genetic letters from the viewpoint of each of these sub-alphabets. Then we will use these binary symbols for binary numbering of the columns and the rows of the genetic matrices of the Kronecker family.
Let us mark the abovethree kinds of binary-opposite attributes with the numbers N = 1, 2, 3 and let us ascribe to each of the four genetic letters the symbol “0N” (the symbol “1N”) in case of presence (or of absence, correspondingly) of the attribute under number “N” at this letter. In result we receive the following representation of the genetic four-letter alphabet in the system of its three “binary sub-alphabets to attributes” (Figure 2).
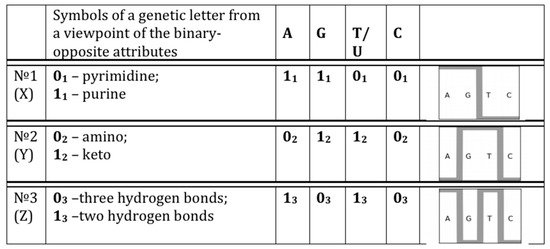
Figure 2.
Three binary sub-alphabets according to three kinds of binary-opposite attributes in the set of nitrogenous bases C, A, G, T/U. Symbols X, Y, Z in the left column mean names of axes of Cartesian systems of coordinates. Schemes in the right column graphically symbolize each sub-alphabet, which is characterized by a set of numbers 0 and 1.
The table on Figure 2 shows that, on the basis of each kind of the attributes, each of the letters A, C, G, T/U possesses three “faces” or meanings in the three binary sub-alphabets. On the basis of each kind of attribute, the genetic four-letter alphabet is reduced to the two-letter alphabet. For example, on the basis of the first kind of binary-opposite attributes we have (instead of the four-letter alphabet) the alphabet from two letters 01 and 11, which one can name “the binary sub-alphabet to the first kind of the binary attributes”.
Accordingly, any genetic message as a sequence of the four letters C, A, G, T consists of three parallel and various binary texts or three different sequences of zero and unit (such binary sequences are used at storage and transfer of the information in computers). Each from these parallel binary texts, based on objective biochemical attributes, can provide its own genetic function in organisms.
In view of these three binary sub-alphabets, any nucleotide sequence can be represented as three different binary sequences. For example, the sequence ATGGC... is represented as:
- 10110... (in accordance with the first sub-alphabet; its decimal equivalent can be located on the “X” axis of a Cartesian system of coordinates);
- 01110... (in accordance with the second sub-alphabet; its decimal equivalent can be located on the “Y” axis of a Cartesian system of coordinates);
- 11000... (in accordance with the third sub-alphabet; its decimal equivalent can be located on the “Z” axis of a Cartesian system of coordinates).
For an unambiguous determination of the nucleotide sequence is sufficient to know its binary representations in any two of the three sub-alphabets [31,32,37]. In particularly, in this example of the sequence ATGGC..., to get its third binary representation 11000... (in accordance with the third sub-alphabet) it is enough to summarize its other two representations 10110... and 01110... (received in accordance with the first two sub-alphabets) by means of modulo-2 addition.
In genetic matrices of the Kronecker family (see Figure 1), each row has its individual binary number, which is connected with the fact that all N-plets inside this row have identical binary representation from the point of view of the first sub-alphabets on Figure 2. For example, in the (8 × 8)-matrix [A G; C T](3) on Figure 1, the second row has its binary numeration 110 because each of its triplets (AAC, AAT, AGC, AGT, GAC, GAT, GGC, GGT) is a sequence “purine-purine-pyrimidine” that corresponds to binary number 110 from the point of view of the first sub-alphabet on Figure 2. Analogically in genetic matrices of the Kronecker family (see Figure 1), each column has its individual binary number, which is connected with the fact that all N-plets inside this column have identical binary representation from the point of view of the second sub-alphabet on Figure 2. For example, in the (8 × 8)-matrix [A G; C T](3) on Figure 1, the third column has its binary numeration 010 because each of its triplets (AGA, AGC, ATA, ATC, CGA, CGC, CTA, CTC) is a “amino–keto–amino” sequence that corresponds to binary number 010 from the point of view of the second sub-alphabet on Figure 2. Respectively, each N-plet, which is located in an appropriate genetic matrix on crossing “column–row”, obtains its individual 2-dimensional coordinates on the base of binary numeration of its column and row. For example, the triplet AGC, which is located on crossing of the mentioned column and row (Figure 1), obtains its individual binary coordinates (010, 110), or in decimal notation (2, 6).
Any long nucleotide sequence can be divided into equal pieces of arbitrary length, and a binary record of these fragments can be read in decimal notation. Then, any long nucleotide sequence is represented in the form of three different sequences of decimal numbers, and its unique identification is sufficient to know its decimal representation in any two sub-alphabets.
If one divides a long nucleotide sequence into equal fragments, whose lengths are equal to “n” (N-mers or N-plets), then each of these fragments is defined by means of its two binary representations (from points of view of the two sub-alphabets) or by means of their equivalents in decimal notations. For example the 5-mer ATGGC is represented as 10110 (in accordance with the first sub-alphabet) and 01110 (in accordance with the second sub-alphabet). Its appropriate decimal meanings are 22 and 14. In such way, this 5-mer ATGGC can be represented not only as the appropriate cell with coordinates (22, 14) inside the genomatrix [A G; C T](5) but also as the point with decimal coordinates (22, 14) in the orthogonal Cartesian system of coordinates (x, y). Taking into account the chosen connection (Figure 2) between each sub-alphabet and one of the X, Y, Z axes of the Cartesian system of coordinates, the following correspondence exists between Kronecker families of genomatrices and 2-dimensional planes (x, y), (x, z) and (y, z) of the Cartesian system:
- the plane (x, y) corresponds to matrices [A G; C T](N), whose rows and columns are binary numerated from the point of view of the first sub-alphabet and the second sub-alphabet respectively;
- the plane (x, z) corresponds to matrices [G A; C T](N), whose rows and columns are binary numerated from the point of view of the first sub-alphabet and the third sub-alphabet respectively;
- the plane (y, z) corresponds to matrices [G T; C A](N), whose rows and columns are binary numerated from the point of view of the second sub-alphabet and the third sub-alphabet respectively.
Taking into account this 2-dimensional representation of each N-plet, one can introduce a notion of Euclidean distance R between any pair of N-plets V(a1, b1) and W(a2, b2):
R = [(a2 − a1)2 + (b2 − b1)2]0.5
One can also introduce notions of distance of other types.
The method, which is described below, uses many variants of a division of a nucleotide sequence into fragments of equal lengths (N-plets). Each whole set of N-plets, which contains 4N members, is located inside one of the matrices of the Kronecker family of matrices such as [A G; C T](N). Correspondingly this method is closely connected with Kronecker multiplication of matrices, which is widely used in mathematics, informatics, physics, etc. and which is one of the main mathematical operations in the field of matrix genetics [32,33,34,35,36,37]. Kronecker multiplication of matrices is used when one needs to go from spaces of smaller dimension into associated spaces of higher dimension. If one uses the mathematical language of vector spaces for modeling the ontogenetic complication of a living organism, it is natural to apply the ideology of a gradual transition from the spaces of low dimensions into spaces of higher dimensions. Such gradual transition is described by means of a series of Kronecker multiplication of matrices.
3. The Description of the Matrix Method for Long Nucleotide Sequences
In a general case, the proposed method includes the following algorithmic steps:
- Any long nucleotide sequence, which contains K nucleotides, is divided into equal fragments of length “N” (N-plets or N-mers), where “N” takes different values: n = 1, 2, 3, …, K; in the result, an appropriate set of different symbolic representations of this sequence as a chain of N-plets appears;
- Each N-plet in every of these representations of the sequence is transformed into three kinds of n-bit binary numbers by means of its reading from the point of view of the three sub-alphabets (Figure 2). Each of these binary numbers is transformed into its decimal equivalent. In the result, an appropriate set of different decimal representations of the initial symbolic sequence appears in a form of three kinds of sequences of decimal numbers respectively for positive integer coordinates on Cartesian axes X, Y, Z (or for numeration of rows and columns of appropriate genetic matrices).
- Any two of the received numeric sequences define an appropriate sequence of pairs of positive integer coordinates of points on the 2-dimensional Cartesian plane (or coordinates of cells inside an appropriate genetic matrix of a Kronecker family). On the base of these pairs of coordinates, a set of corresponding points is built on the 2-dimensional Cartesian plane (or a set of corresponding cells in black inside a respective genetic matrix of a Kronecker family in contrast to other cells, which remain in white).
As a result of these algorithmic steps, different black-and-white mosaics arise as representations of any long nucleotide sequence in different cases of its division into N-plets. Figure 3 shows examples of fractal-like and other visual patterns, which have been received on the basis of the described method for some long nucleotide sequences.

Figure 3.
Examples of visual patterns, which have been received on the base of the described method for different nucleotide sequences (see explanation in the text). Two symbols are shown at the right side of each pattern to indicate what kinds of the sub-alphabets from Figure 2 were used to construct the pattern.
The numbered patterns on Figure 3 correspond to the following sequences:
- Homo sapiens contactin associated protein-like 2 (CNTNAP2), RefSeqGene on chromosome 7 (N = 63).
- Homo sapiens contactin associated protein-like 2 (CNTNAP2), RefSeqGene on chromosome 7 (N = 63).
- Sorangium cellulosum So0157-2, complete genome (N = 63).
- Burkholderia multivorans ATCC 17616 genomic DNA, complete genome, chromosome 2 (N = 63).
- Thermofilum sp. 1910b, complete genome (N = 63).
- Thermofilum sp. 1910b, complete genome (N = 63).
- Dinoroseobacter shibae DFL 12, complete genome (N = 8).
- Escherichia coli LY180, complete genome (N = 24).
- Francisella tularensis subsp. tularensis SCHU S4 complete genome (N = 24).
- Halomonas elongata DSM 2581, complete genome (N = 24).
- Helicobacter mustelae 12198 complete genome (N = 24).
- Helicobacter mustelae 12198 complete genome (N = 12).
- Invertebrate iridovirus 22 complete genome (N = 8).
- Methanosalsum zhilinae DSM 4017, complete genome (N = 12).
- Methanosalsum zhilinae DSM 4017, complete genome (N = 12).
- Mycobacterium abscessus subsp. bolletii INCQS 00594 INCQS00594_scaffold1, whole genome shotgun sequence (N = 12).
- Penicillium chrysogenum Wisconsin 54-1255 complete genome, contig Pc00c12 (N = 32).
- Riemerella anatipestifer DSM 15868, complete genome (N = 12).
- Riemerella anatipestifer DSM 15868, complete genome (N = 12).
- Burkholderia multivorans ATCC 17616 genomic DNA, complete genome, chromosome 2 (N = 8).
Thismosaic pattern shows the phenomenology of “presence and absence” of different N-plets. Note that a division of a long nucleotide sequence into only a single possible variant of its equal fragmentation (for example, a division into 16-plets) does not provide an unambiguous definition of this sequence; such a separate case of a division represents this sequence as a set of fragments but without a reflection of their order in the sequence (any permutation of these fragments gives a new sequence with the same set of N-plets). To get an unambiguous definition of the sequence, one should take into consideration all (or many) possible variants of its equal partitions (N = 1, 2, 3, …). In practice for many tasks of a comparison analysis and classification of different long nucleotide sequences it is enough to consider some chosen variants of fragmentations of these sequences, for example, variants with N = 16, 32, 64.
Another possible way to get an unambiguous representation of a long nucleotide sequence in the case of its division with a certain value n (for example, with N = 8) is connected with construction of additional visual patterns, which reflect an order of N-plets in the sequence.
Figure 4 shows two examples of such mosaic patterns for Homo sapiens chromosome 22 genomic scaffold and for Arabidopsis thaliana mitochondrion in the case of their representations as sets of 16-mers. On these mosaics, white places correspond to dispositions of those 16-mers on a corresponding 2-dimensional plane, which are missing in such representations of the sequences. The mosaic pattern depends on a concrete choice of two kinds of sub-alphabets from Figure 2. Figure 4 shows two mosaic patterns on 2-dimensional Cartesian planes (x, y) and (y, z), which are identical to black-and-white mosaics of the genetic matrices [A G; C T](16) and [G T; C A](16) respectively, where cells with existing 16-plets of the sequence are shown in black and cells with missing 16-plets are shown in white.

Figure 4.
Two examples of patterns which are constructed on the base of the described method. Left side: the visual pattern of the nucleotide sequence Homo sapiens chromosome 22 genomic scaffold, which has 648,059 nucleotides and which is divided into a sequence of 16-mers; these 16-mers are transformed into 16-bit binary numbers on the basis of the first sub-alphabet and of the second sub-alphabet (Figure 2); then their decimal equivalents are plotted on the x and y axes respectively. Right side: the visual pattern of the nucleotide sequence Arabidopsis thaliana mitochondrion, which has 366,924 nucleotides and which is divided into a sequence of 16-mers; these 16-mers are transformed into 16-bit binary numbers on the basis of the second sub-alphabet and of the third sub-alphabet (Figure 2); then their decimal equivalents are plotted on the axes “y” and “z” respectively.
Figure 5 shows one of interesting patterns received by the described method.
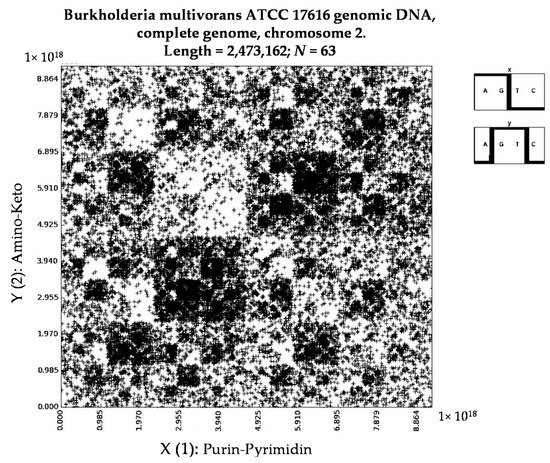
Figure 5.
The pattern of the sequence “Burkholderia multivorans ATCC 17616 genomic DNA, complete genome, chromosome 2” with 2,473,162 nucleotides in the case of its division into 63-plets.
Binary representations of N-mers are expressed in a form of n-bit binary numbers, the quantity of kinds of which is equal to 2n. For example, the set of 3-bit binary numbers contains 23 = 8 members: 000, 001, 010, 011, 100, 101, 110, 111 (their equivalents in decimal notation are 0, 1, 2, 3, 4, 5, 6, 7). Decimal equivalent of the biggest n-bit binary member in a set of n-bit binary numbers is equal to 2n − 1. Such sets of N-bit binary numbers are named “dyadic groups” (see details in [6]).
The most interesting application of this matrix method is realized in the case of long nucleotide sequences, which are divided into relative long N-mers (N = 8, 9, 10, …). The reasons for this are the following (see Figure 6):
- a long nucleotide sequence, which is divided into relative short N-mers (N = 1, 2, 3, 4), usually contains all possible kinds of such short N-mers; correspondingly, its visual pattern is trivial because it contains all possible points with positive integer coordinates (x, y) inside an appropriate numeric range;
- a long nucleotide sequence, which is divided into relative long N-mers (N = 8, 9, 10, …), usually generates a regular non-trivial mosaic of a fractal-like or other character. This was detected using a special computer program in the course of initial investigations of different long nucleotide sequences by means of the described method.
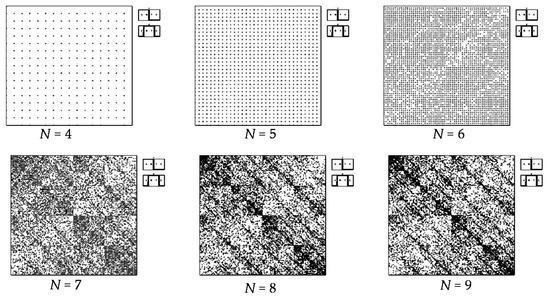
Figure 6.
Examples of patterns for the sequence Fistulifera sp. JPCC DA0580 chloroplast, complete genome in cases of its divisions into N-plets with N= 4, 5, 6, 7, 8, 9.
Figure 6 (lower level) also illustrates that—in a certain range of changing values “N”—visual fractal mosaics for different “N” approximately repeat each other (see Section 5 about this “stability” of the fractal-like mosaics).
Fractal patterns, which are obtained by means of the described matrix method, sometimes resemble fractal patterns of long nucleotide sequences and amino acid sequences, which were previously obtained by means of the known method “Chaos Game Representation” (CGR-method) in work [12], though both methods are quite different in their algorithmic essence. In particularly, CGR-method deals with representations of nucleotide sequences or other long sequences by means of four numbers 0, 1, 2, 3 but not by means of binary numbers 0, 1. In addition our new method seems to be simpler to understand and be used by biologists.
4. Long Random Sequences
What kinds of visual patterns are produced by the described method in cases of long random sequences of nucleotides? To answer on this question, different random sequences were generated by a computer program. Their study is revealed that appropriate visual patterns have non-regular characters in contrast to cases of real genomes. Figure 7 shows examples of visual patterns for a case of the random sequence with 100,000 nucleotides in cases of its division into N-plets with N = 8, 16, 28 (this sequence is available at website pentagramon.com for its possible additional testing). Each of visual patterns of this random sequence for two other 2-dimensional planes (x, z) and (y, z) has a similar non-regular character.

Figure 7.
Examples of visual patterns of a random nucleotide sequence with 100,000 nucleotides (pentagramon.com) in cases of its division with N = 8, 16, 28.
5. Kronecker Multiplication, Fractal Lattices and the Problem of Coding an Organism on Different Stages of Its Ontogenesis
Previous sections have shown that the described method gives very different types of visual patterns for random nucleotide sequences (where non-regular patterns arise as on Figure 7) and for real nucleotide sequences (where fractal-like patterns have been revealed as on Figure 3, Figure 4, Figure 5 and Figure 6). The authors note that in many cases these fractal-like patterns of long nucleotide sequences resemble fractal lattices, which are automatically generated for matrices of Kronecker families. We should explain this in more detail.
Let us take a square (k × k)-matrix M, whose entries are equal only to 0 or 1. Any integer Kronecker power (N) of this matrix generates a new (kn × kn)-matrix M(N) with a fractal location of entries 0 and 1 inside it (Figure 8 and Figure 9). These fractal mosaics inside such matrices of Kronecker families are called “fractal lattices.” The theme of “Kronecker multiplication and fractal lattices” is accurately described in a previous book [39]. Such fractal lattices (Figure 8) are generated due to a general definition of Kronecker multiplication of matrices as a special mathematical operation.
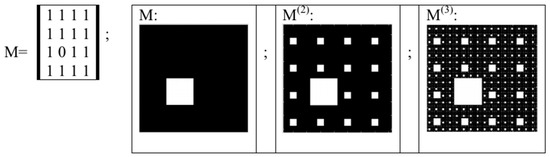
Figure 8.
An example of generating fractal lattices by means of Kronecker exponentiation of matrices. Left side: the (4 × 4)-matrix M with entries 0 and 1. Right side: visual patterns of the matrix M and its Kronecker powers M(2) and M(3), which are (16 × 16)-matrix and (64 × 64)-matrix respectively. Here, black corresponds to matrix cells with entries of 1 and white corresponds to cells with entries of 0.
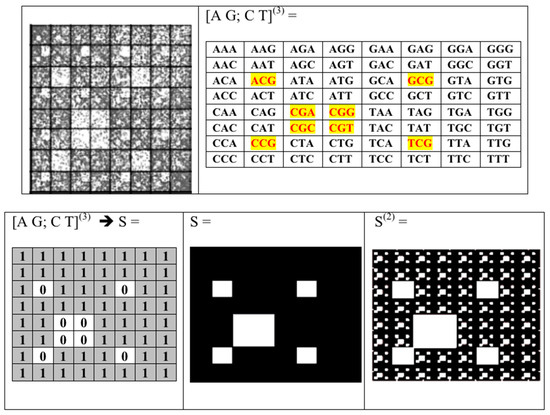
Figure 9.
Illustration of relations among Kronecker multiplication, fractal lattices and fractal-like patterns of long nucleotide sequences (explanations in text).
One should note that, in many cases, significant features of fractal-like patterns of real nucleotide sequences can be simulated by means of fractal lattices of matrices of a Kronecker family, if a matrix kernel of the Kronecker family is adequately chosen. For example let us take the pattern (from Figure 4) of the nucleotide sequence Homo sapiens chromosome 22 genomic scaffold, which has 648,059 nucleotides [40,41] and which is divided into a sequence of 16-mers. If this pattern is covered by the uniform (8 × 8)-grid, 8 cells of this grid will be almost white color in contrast to the remaining 56 cells (Figure 9, upper level, left side). In such case this (8 × 8)-mosaic of black-and-white type is similar to mosaic of the genetic (8 × 8)-matrix [A G; C T](3) of 64 triplets where those 8 triplets are missing, which are located in this matrix on the same places and which are marked by red color on Figure 9 (upper level, right side). Let us replace these 8 missing triplets by number 0, and all other 56 triplets by number 1. It leads to a transformation of this variant of symbolic matrix [A G; C T](3) into a numeric matrix S (Figure 9, bottom level, left side).
Kronecker exponentiation of the matrix S generates matrices S(2), S(3), …, whose visual patterns illustrate appropriate fractal lattices, one of which for the matrix S (2) is shown on Figure 9 (bottom level, right side). The numeric matrix S(16) contains the whole set of 16-plets with an appropriate fractal lattice, which resembles the visual pattern of the real nucleotide sequence Homo sapiens chromosome 22 genomic scaffold on Figure 4. One should note that the visual pattern of this real sequence contains more white places (than in the matrix S(16)) because many additional 16-plets are absent since the sequence has a finite length in 648,059 nucleotides.
Fractal-like lattices in visual patterns of long nucleotide sequences testify in favor of significance of Kronecker multiplication for structuration of these genetic sequences. This is not an isolated fact about a genetic significance of Kronecker multiplication. Previously we have provided other evidence for the biological significance of Kronecker multiplication of matrices in phenomenology of natural ensembles of molecular-genetic alphabets [32,33,34,35,36,37] and also in a structure of Punnet squares in the field of Mendelian genetics in connection with the Mendelian laws of independent inheritance of traits [33].
6. Patterns of Human Chromosomes
What kinds of binary mosaics are generated by means of the described method for all 23 pairs of human chromosomes, the data for which can be taken from [41,42]. Our results of their testing show that they are represented by binary mosaics of analogical types. Figure 10 shows mosaics of the first 15,000,000 nucleotides of the following sequences in the case of their division into 63-plets: Homo sapiens chromosomes X and Y together with Homo sapiens chromosome 1 (they have 152,634,166, 50,961,097 and 245,203,898 nucleotides respectively).
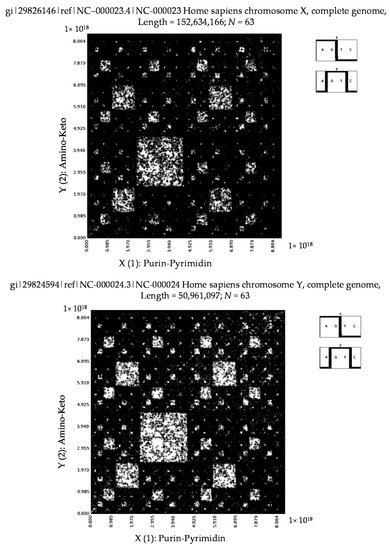
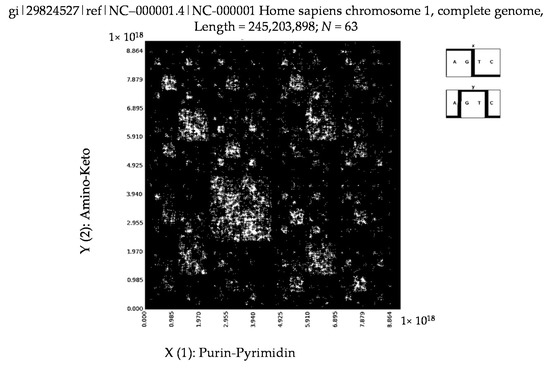
Figure 10.
The binary mosaics of the first 15,000,000 nucleotides of the sequences of Homo sapiens chromosomes X and Y (two upper levels) and Homo sapiens chromosome 1 in the case of their division into 63-plets. Two symbols are shown at the right side of each pattern to indicate what kinds of the sub-alphabets from Figure 2 were used to construct the pattern. Initial data were taken from [41,42].
Also, we tested the first 15,000,000 nucleotides of every human chromosome from the mentioned website. Structures of 2-dimensional mosaics of these tested sequences externally resembled each other, but the quantitative evaluation of the degree of their similarity is still to be developed.
Then we took different parts of the same sequence Homo sapiens chromosome 1; each part comprised 15,000,000 nucleotides. Again our results of their testing testify that these parts generate very similar mosaics by the described method. Figure 11 shows examples of two parts of this long sequences: one part corresponds to interval of this sequence from 45,000,000 to 60,000,000 nucleotides, and the second part corresponds to the interval from 135,000,000 to 150,000,000 nucleotides.
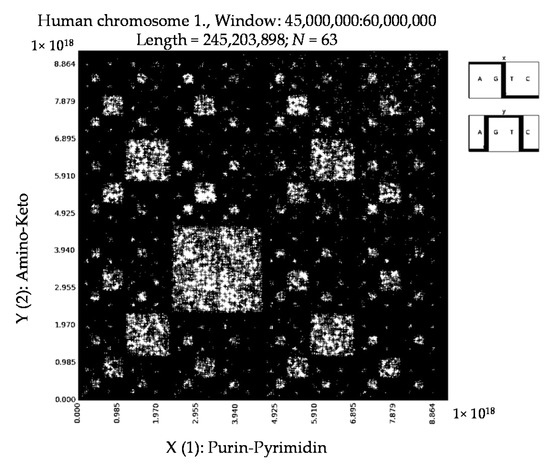
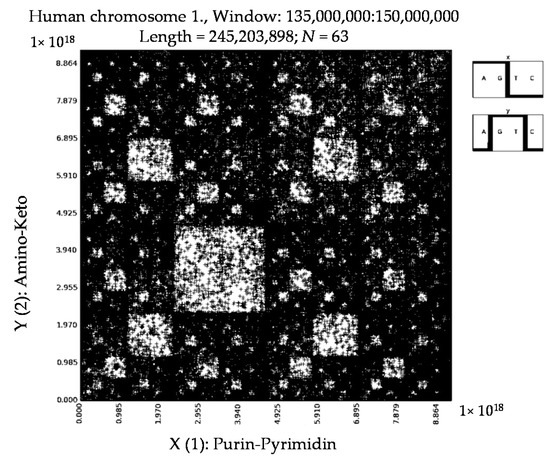
Figure 11.
Examples of binary mosaics for two parts of Homo sapiens chromosome 1 [41,42], which has 245,203,898 nucleotides: one part corresponds to interval of this sequence from 45,000,000 to 60,000,000 nucleotides, and the second part corresponds to the interval from 135,000,000 to 150,000,000 nucleotides.
7. Patterns of Penicillin
Additionally, we have tested different kinds of penicillin by the described method to identify their binary patterns. The results show that in this group of antibiotics their long nucleotide sequences usually generate non-regular mosaics, which resemble mosaics of random nucleotide sequences (Figure 12). Why does penicillin have non-regular mosaics? Does this feature of penicillin have hidden links with its medicinal properties? It is currently an open question.
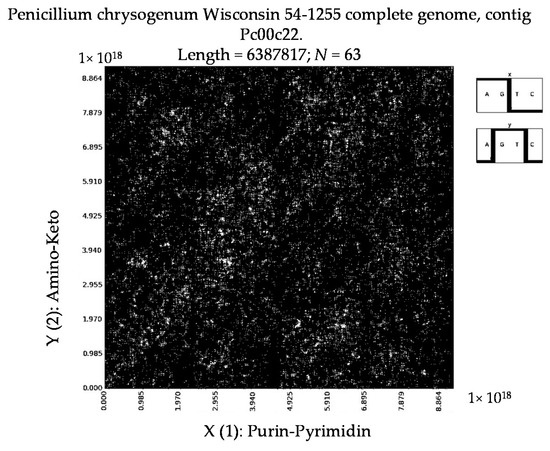
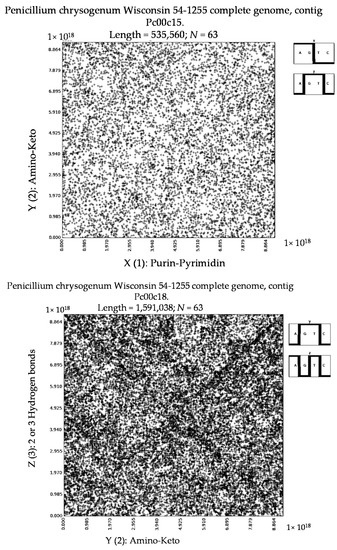
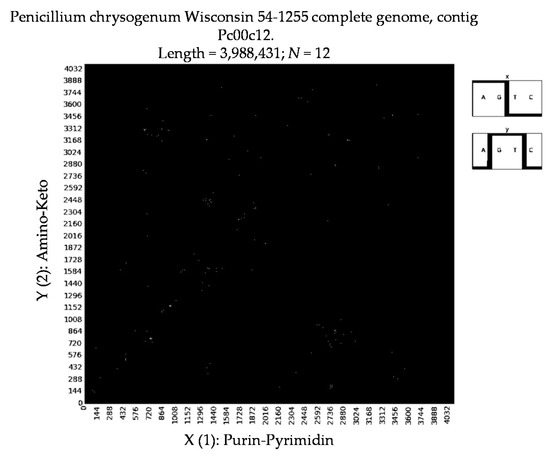
Figure 12.
Examples of binary mosaics for long nucleotide sequences of different contigs of Penicillium chrysogenum Wisconsin 54-1255 complete genome. Upper level: the mosaic for the contig 22, which contains 6,387,817 nucleotides, for the case of 63-plets. The second level: the mosaic for the contig 15, which contains 535,560 nucleotides, for the case of 63-plets. The third level: the mosaic for the contig 18, which contains 1,591,038 nucleotides, for the case of 63-plets. Lower level: the mosaic for the contig 12, which contains 3,988,431 nucleotides, for the case of 12-plets. Symbols from the right side of each mosaic indicate the pair of the sub-alphabets that were used for a transformation of these N-plets into binary numbers.
8. About 3D-Representations
Until now we have talked about 2-dimensional representations of long nucleotide sequences by means of the described method. But it is obvious that 3d patterns can be also constructed in a similar way on the basis of all three binary (and decimal) representations of any nucleotide sequence by means of the three sub-alphabets from Figure 2.
One can initially consider a special case when on a 2-dimensional Cartesian plane (x, y) all points with positive integer coordinates exist in the range of coordinate decimal values from (0, 0) up to (100, 100) or in the range of their binary values from (0, 0) up to (1,100,100, 1,100,100). Above in the Section 2, it was noted that the binary representation of any nucleotide N-plet from the point of view of the third sub-alphabet (Figure 2) can be received by means of modulo-2 addition of its two binary representations from the points of view of the first and second sub-alphabets. Correspondingly we suppose that a value of coordinate “z” of every considered point (x, y) is defined as a sum of its binary coordinates “x” and “y” on basis of modulo-2 addition. A set of points (x, y, z) of an “ideal” 3-dimensional configuration arises in this case. This ideal 3d configuration has a non-simple character and contains all possible points of the considered range (or all corresponding N-plets).
Figure 13 (upper level) shows two 2-dimensional images of this ideal 3d-configuration in its examination from two oblique foreshortening. Also Figure 13 (lower level) shows a real 3d configuration, which was constructed for a real nucleotide sequence by means of the same definition of its third coordinate “z” (as a sum of binary values of coordinates “x” and “y” of N-plets of the sequence). This real 3d configuration differs from the ideal 3d-configuration due to the many additional “white” areas in its structure because of the absence of appropriate number of N-plets. Projections of the real 3d configuration of a nucleotide sequence into 2-dimensional planes (x, y), (x, z) or (y, z) give the corresponding 2d patterns of the sequence.
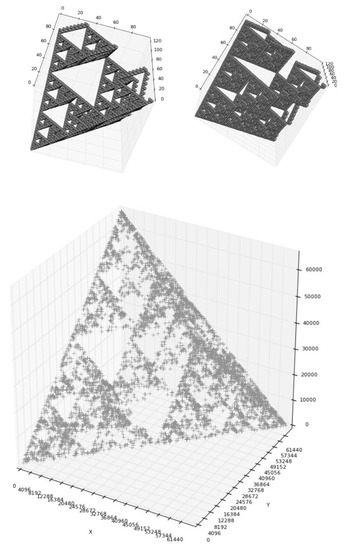
Figure 13.
Upper level: two 2-dimensional images of an “ideal” 3d configuration in its examination from two oblique foreshortening; Lower level: a real 3d configuration for a real nucleotide sequence (see explanation in text).
According to our additional research, use of our visualization method for the binary representation of long nucleotide sequences from the point of view of Gray code gives much less expressive symmetric patterns in the mosaic in comparison with the case of conventional binary code described above. Some questions about a possible connection between genetic matrices and Gray code were described in other work [43].
9. Conclusions
We have obtained the first results of the application of this new method of analysis of long nucleotide sequences. The preliminary results include, for example, the stability of resulting fractal-like and other patterns in the case of shifts of reading frame of such sequences, of reversing of sequences, of the permutation of fragments of a sequence, or of a removal of certain parts of sequences; these results are mainly similar to the results of studies of fractal genetic networks for long nucleotide sequences [44]. In particular, we saw a stability of mosaic patterns in cases of transformations of examined nucleotide sequences by means of removal of the every second nucleotide in sequences, or removal of the every third nucleotide in sequences, etc. Many adjacent variants can be added to the described method for deeper research of long genetic sequences by means of their binary presentation (for example, quantities of elements 0 and 1, which are met in N-plets of two kinds of the n-bit binary presentation of a long nucleotide sequence, can be used to construct a new type of a visual pattern of the sequence).
Different types of genetic sequences (for example amino acid sequences) can be also represented in the form of pairs of binary sequences through the use of various sets of their binary-oppositional attributes; in these cases, this method of analysis of their content can also be applied.
The described method of analysis of long nucleotide sequences seems to be useful for the study of hidden regularities in genetic sequences and also for classification and comparative analysis of different genetic sequences with possible applications in biotechnology and medicine. This article adds new material to the field of algebraic biology, where matrix methods seem to be extremely useful [32,33,34,35,36,37]. The discovery of new binary fractal-like patterns, which are revealed from long genetic sequences by means of this method, provokes many questions about relationship between the genetic system and those fields of science and technology where digital binary fractals are used, for example the fields of fractals in radiophysics, technology of fractal antenna, and fractal codes. In our opinion, the described results are useful for the bio-mathematical concept of geno-logical coding [20,21,22,23].
Computer software for the application of this method was created by I. Stepanyan. Many of the described results were received by means of using the supercomputer of the “Joint Supercomputer Center of the Russian Academy of Sciences”.
Acknowledgments
The authors are grateful to the administration of the Mechanical Engineering Research Institute of the Russian Academy of Sciences for its support.
Author Contributions
Ivan V. Stepanyan developed the used method of visualization of long nucleotide sequences, created also a special computer program and applied the method for analyzing of such sequences taken from http://www.ncbi.nlm.nih.gov. Sergey V. Petoukhov participated in a creation of bases of this method, in interpretation of the results of such visualization and he wrote the paper. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bell, S.J.; Forsdyke, D.R. Deviations from Chargaff’s second parity rule correlate with direction of transcription. J. Theor. Biol. 1999, 197, 63–76. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, H. Negative correlation between compositional symmetries and local recombination rates. Bioinformatics 2005, 21, 3951–3958. [Google Scholar] [CrossRef] [PubMed]
- Dong, Q.; Cuticchia, A.J. Compositional symmetries in complete genomes. Bioinformatics 2001, 17, 557–559. [Google Scholar]
- Forsdyke, D.R. A stem-loop “kissing” model for the initiation of recombination and the origin of introns. Mol. Biol. Evol. 1995, 12, 949–958. [Google Scholar] [PubMed]
- Forsdyke, D.R. Symmetry observations in long nucleotide sequences: A commentary on the discovery of Qi and Cuticchia. Bioinform. Lett. 2002, 18, 215–217. [Google Scholar] [CrossRef]
- Forsdyke, D.R.; Bell, S.J. A discussion of the application of elementary principles to early chemical observations. Appl. Bioinform. 2004, 3, 3–8. [Google Scholar] [CrossRef]
- Mitchell, D.; Bride, R. A test of Chargaff’s second rule. BBRC 2006, 340, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Perez, J.-C. Codon populations in single-stranded whole human genome DNA are fractal and fine-tuned by the golden ratio 1.618. Interdiscip. Sci. Comput. Life Sci. 2010, 2, 1–13. [Google Scholar]
- Prabhu, V.V. Symmetry observation in long nucleotide sequences. Nucleic Acids Res. 1993, 21, 2797–2800. [Google Scholar] [CrossRef] [PubMed]
- Grebnev, Y.V.; Sadovsky, M.G. Second Chargaff's rules and symmetry genomes. Fundam. Res. 2014, 12, 965–968. (In Russian) [Google Scholar]
- Yamagishi, M.; Herai, R. Chargaff’s “Grammar of Biology”: New Fractal-like Rules. Available online: https://arxiv.org/pdf/1112.1528.pdf (accessed on 7 December 2011).
- Jeffrey, H.J. Chaos game representation of gene structure. Nucleic Acids Res. 1990, 18, 2163–2170. [Google Scholar] [CrossRef] [PubMed]
- Goldman, N. Nucleotide, dinucleotide and trinucleotide frequencies explain patterns observed in chaos game representations of DNA sequences. Nucleic Acid Res. 1993, 21, 2487–2491. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, J.M.; Rodriguez, M.A.; Abramson, G. Multifractal analysis of DNA sequences using novel chaos-game representation. Physica A 2001, 300, 271–284. [Google Scholar] [CrossRef]
- Joseph, J.; Sasikumar, R. Chaos game representation for comparison of whole genomes. BMC Bioinform. 2006, 7, 243–246. [Google Scholar] [CrossRef] [PubMed]
- Oliver, J.L.; Bernaola-Galvan, P.; Guerrero-Garcia, J.; Roman-Roldan, R. Entropic profiles of DNA sequences through chaos-game-derived images. J. Theor. Biol. 1993, 160, 457–470. [Google Scholar] [CrossRef] [PubMed]
- Tavassoly, I.; Tavassoly, O.; Rad, M.; Dastjerdi, N. Multifractal analysis of Chaos Game Representation images of mitochondrial DNA. In Proceedings of the IEEE Conference: Frontiers in the Convergence of Bioscience and Information Technologies, Jeju City, Korea, 11–13 October 2007; Howard, D., Ed.; IEEE Press: Jeju City, Korea, 2007; pp. 224–229. [Google Scholar]
- Tavassoly, I.; Tavassoly, O.; Rad, M.; Dastjerdi, N. Three dimensional Chaos Game Representation of genomic sequences. In Proceedings of the IEEE Conference: Frontiers in the Convergence of Bioscience and Information Technologies, Jeju City, Korea, 11–13 October 2007; Howard, D., Ed.; IEEE Press: Jeju City, Korea, 2007; pp. 219–223. [Google Scholar]
- Wang, Y.; Hill, K.; Singh, S.; Kari, L. The spectrum of genomic signatures: From dinucleotides to chaos game representation. Gene 2005, 346, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Petoukhov, S.V. The genetic code, 8-dimensional hypercomplex numbers and dyadic shifts. Available online: https://arxiv.org/pdf/1102.3596v11.pdf (accessed on 15 July 2016).
- Petoukhov, S.V. Symmetries of the genetic code, Walsh functions and the theory of genetic logical holography. Symmetry Cult. Sci. 2016, 27, 95–98. [Google Scholar]
- Petoukhov, S.V.; Petukhova, E.S. Symmetries in genetics, Walsh functions and the geno-logical code. In Periodic Collection of Articles: “Symmetry: Theoretical and Methodological Aspects”, Issue 21; Ammosova, N.V., Ed.; Publishing House LLC “Triad”: Astrakhan, Russia, 2016; pp. 79–87. (In Russian) [Google Scholar]
- Petoukhov, S.V.; Petukhova, E.S. Resonances, Walsh functions and logical holography in genetics and musicology. Symmetry Cult. Sci. 2017, 28, 21–40. [Google Scholar]
- Horimoto, K.; Nakatsui, M.; Popov, N. (Eds.) Algebraic and Numeric Biology, 2012 ed.; In Proceedings of the 4th International Conference, ANB 2010, Hagenberg, Austria, 31 July–2 August 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 6479.
- Hornos, J.E.M.; Hornos, Y.M.M. Algebraic model for the evolution of the genetic code. Phys. Rev. Lett. 1993, 71, 4401–4404. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, D.L. The mathematical structure of the genetic code. In The Codes of Life: The Rules of Macroevolution, Biosemiotics; Barbieri, M., Hoffmeyer, J., Eds.; Springer: Dordrecht, The Netherlands, 2008; Volume 1, Chapter 8; pp. 111–152. [Google Scholar]
- Gonzalez, D.L.; Giannerini, S.; Rosa, R. On the origin of the mitochondrial genetic code: Towards a unified mathematical framework for the management of genetic information. Nat. Proc. 2012. [Google Scholar] [CrossRef]
- Dragovich, B. p-Adic structure of the genetic code. NeuroQuantology 2011, 9, 716–727. [Google Scholar] [CrossRef]
- Fimmel, E.; Giannerini, S.; Gonzalez, D.; Strüngmann, L. Dinucleotide circular codes and bijective transformations. J. Theor. Biol. 2015, 386, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Fimmel, E.; Giannerini, S.; Gonzalez, D.; Strüngmann, L. Circular codes, symmetries and transformations. J. Math. Biol. 2014, 70, 1623–1644. [Google Scholar] [CrossRef] [PubMed]
- Petoukhov, S.V. Biperiodic Table of the Genetic Code and Number of Protons; MKC: Moscow, Russia, 2001; p. 258. (In Russian) [Google Scholar]
- Petoukhov, S.V. Matrix Genetics, Algebras of the Genetic Code, Noise-Immunity; Regular and Chaotic Dynamics: Moscow, Russia, 2008; p. 316. (In Russian) [Google Scholar]
- Petoukhov, S.V. Matrix genetics and algebraic properties of the multi-level system of genetic alphabets. Neuroquantology 2011, 9, 60–81. [Google Scholar] [CrossRef]
- Petoukhov, S.V. Symmetries of the genetic code, hypercomplex numbers and genetic matrices with internal complementarities. Symmetry Cult. Sci. 2012, 23, 275–301. [Google Scholar]
- Petoukhov, S.V. Dyadic Groups, Dyadic Trees and Symmetries in Long Nucleotide Sequences. Available online: http://arxiv.org/abs/1204.6247v2 (accessed on 17 January 2013).
- Petoukhov, S.V. The Genetic Code, Algebra of Projection Operators and Problems of Inherited Biological Ensembles. Available online: http://arxiv.org/abs/1307.7882 (accessed on 31 December 2014).
- Petoukhov, S.V.; He, M. Symmetrical Analysis Techniques for Genetic Systems and Bioinformatics: Advanced Patterns and Applications; IGI Global: Hershey, PA, USA, 2010; p. 271. [Google Scholar]
- Karlin, S.; Ost, F.; Blaisdell, B.E. Patterns in DNA and Amino Acid Sequences and Their Statistical Significance; Waterman, M.S., Ed.; Mathematical Methods for DNA Sequences; CRC Press: Raton, FL, USA, 1989. [Google Scholar]
- Gazalé, M.J. Gnomon: From Pharaons to Fractals; Princeton University Press: Princeton, NJ, USA, 1999; p. 280. [Google Scholar]
- Homo Sapiens Chromosome 22 Genomic Scaffold, Alternate Assembly CHM1_1.0, Whole Genome Shotgun Sequence. NCBI Reference Sequence: NW_004078110.1. Available online: http://www.ncbi.nlm.nih.gov/nuccore/NW_004078110.1?report=genbank (accessed on 31 October 2013).
- Stepanyan, I.V.; Petoukhov, S.V. The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences. Available online: https://arxiv.org/abs/1310.8469v1 (accessed on 31 October 2013).
- Human Chromosomes. Available online: ftp://ftp.ncbi.nih.gov//genomes/H_sapiens/April_14_2003/ (accessed on 14 April 2003).
- Kappraff, J.; Petoukhov, S.V. Symmetries, generalized numbers and harmonic laws in matrix genetics. Symmetry Cult. Sci. 2009, 20, 23–50. [Google Scholar]
- Petoukhov, S.V.; Svirin, V.I. Fractal genetic nets and symmetry principles in long nucleotide sequences. Symmetry Cult. Sci. 2012, 23, 303–322. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).