Efficient Quantization of Pretrained Deep Networks via Adaptive Block Transform Coding

Abstract

This work investigates the effectiveness of block transform coding (BTC) as a lightweight, training-free quantization strategy for compressing the weights of pretrained deep neural networks. The proposed method applies a rule-based block transform with variance and root mean square error (RMSE)-driven stopping criteria, enabling substantial reductions in bit precision while preserving the statistical structure of convolutional and fully connected layer weights. Unlike uniform 8-bit quantization, BTC dynamically adjusts bit usage across layers and achieves significantly lower distortion for the same compression budget. We evaluate BTC across many pretrained architectures and tabular benchmarks. Experimental results show that BTC consistently reduces storage to 4–7.7 bits per weight while maintaining accuracy within 2–3% of the 32-bit floating point (FP32) baseline. To further assess scalability and baseline strength, BTC is additionally evaluated on large-scale ImageNet models and compared against a calibrated percentile-based uniform post-training quantization method. The results show that BTC achieves a substantially lower effective bit-width while incurring only a modest accuracy reduction relative to calibration-aware 8-bit quantization, highlighting a favorable compression–accuracy trade-off. BTC also exhibits stable behavior across successive post-training quantization (PTQ) configurations, low quantization noise, and smooth RMSE trends, outperforming naïve uniform quantization under aggressive compression. These findings confirm that BTC provides a scalable, architecture-agnostic, and training-free quantization mechanism suitable for deployment in memory- and computing-constrained environments.

1. Introduction

Quantization has become a central tool for reducing the computational and memory footprint of modern deep neural networks (DNNs). While extensive research has focused on post-training quantization (PTQ) of weights to accelerate inference, comparatively less attention has been given to developing simple, training-free quantization schemes that adapt to the intrinsic statistical structure of learned parameters. Standard uniform quantizers, although hardware friendly, often allocate precision inefficiently by imposing the same step size across heterogeneous weight distributions. As NNs continue to scale, this mismatch results in unnecessary bit usage in smooth regions and insufficient resolution in high-variation regions, limiting the achievable compression ratio without retraining.

To address these limitations, this work explores an alternative line of thought grounded in classical Block Truncation Coding (BTC), a powerful technique originally developed for image compression. BTC and its variants, including Absolute Moment BTC (AMBTC) [1], multilevel BTC [2,3], and later statistical refinements [4,5,6], demonstrated that local variance is a strong predictor of perceptual sensitivity and can be exploited to adapt quantizer parameters per block. The key principle is to partition a signal into small blocks and quantize each using locally optimized two-level or multi-level representations whose parameters (thresholds, reconstruction levels) are derived from block statistics. This classical idea has seen many extensions, including forward adaptive quantizers [7] and nonuniform companding formulations for Laplacian and Gaussian sources [8,9,10,11]. A particularly relevant precursor to this work is the research by Savić, Perić, and Panić on multilevel BTC quantizer design [12], which formalized variance adaptive reconstruction levels and showed that carefully designed BTC variants can achieve strong distortion/bit-rate performance using extremely low computational complexity. Their work highlighted that BTC’s statistical adaptivity extends far beyond image pixels and can be generalized to other structured signals.

Motivated by these developments, we revisit BTC from a modern deep-learning perspective and demonstrate that its blockwise statistical adaptivity is highly effective for quantizing pretrained neural network weights. Unlike image compression, where perceptual fidelity is the target, in NNs the primary requirement is to preserve operational accuracy while aggressively reducing bit usage. Our results demonstrate that BTC’s variance-guided dual-rate encoding mechanism provides an effective implicit discrimination between locally smooth and highly variable weight regions. The variance-guided dual-rate mechanism inherent to BTC effectively distinguishes smooth from high-variation weight regions, yielding a compact and training-free quantization scheme that achieves competitive performance relative to substantially more complex PTQ methods.

1.1. Related Work

Quantization-aware training (QAT) [13,14,15] introduces quantized operations directly into the training loop using surrogate gradient estimators or differentiable approximations. While QAT typically achieves excellent accuracy at low bitwidths, it substantially increases training complexity and requires full retraining, which limits its practicality in post-deployment or resource-constrained scenarios. PTQ methods [16] address these limitations by quantizing pretrained models without modifying the training process. However, straightforward PTQ approaches based on fixed-step uniform quantization often suffer from noticeable accuracy degradation under aggressive compression. To mitigate this, gradient- and reconstruction-based PTQ techniques such as Block Reconstruction Quantization (BRECQ) [17] and Quantization Dropout (QDrop) [18] introduce layer-wise or block-wise reconstruction objectives, typically relying on calibration datasets and iterative optimization to minimize output distortion. These methods achieve state-of-the-art accuracy on modern CNN and Transformer architectures, at the cost of increased runtime, memory overhead, and calibration complexity. A related but conceptually distinct line of work focuses on training time gradient quantization, primarily motivated by reducing communication overhead in distributed and federated learning. Adaptive strategies such as L-GreCo [19] and Adaptive Logarithmic/Minimum Quantization (ALQ/AMQ) [20] dynamically adjust precision based on gradient statistics and sensitivity, enabling scalable large-scale training. Broader evaluations of compression methods that emphasize stability, convergence behavior, and runtime efficiency are presented in [21], while extensive empirical studies of quantization strategies in realistic distributed environments are reported in [22]. Although these approaches operate during training and target gradient communication rather than model storage, they reinforce a general insight that adaptive, data-driven quantization schemes consistently outperform fixed-step uniform quantizers. In contrast to both reconstruction-driven PTQ methods and gradient-based training time quantization, the proposed BTC approach is designed as a strictly post-training weight quantization scheme. BTC does not rely on gradient information, calibration datasets, or per-layer optimization. Instead, it exploits local block-wise variance statistics to adapt precision in a lightweight, one-pass manner. This positions BTC as a complementary alternative within the PTQ landscape, emphasizing simplicity, low overhead, and robustness for deployment-oriented model compression rather than aggressive reconstruction-based optimization.

The proposed BTC-based weight quantization is conceptually inspired by classical block transform coding techniques originally developed for image and video compression, where local statistics such as mean and variance are used to adapt precision while preserving perceptually or structurally important information. A related statistical principle is explored in [23], where a variance threshold mechanism, derived from the Feigenbaum constant, is employed to reduce color palettes in video streams for autonomous vehicle perception. Although the application domain differs substantially, both approaches share a common philosophy: local variance serves as a lightweight and effective criterion for identifying signal regions that require higher representational fidelity. In contrast to [23], which adapts quantization tables within a DCT-based video codec to handle abrupt transitions after palette reduction, BTC applies variance-guided precision selection directly in the weight domain of pretrained NNs, without modifying the network architecture or retraining procedure. This highlights a transfer of block-wise statistical adaptation principles from media compression to model compression.

Recent advances in data-driven transform coding further support the relevance of block-adaptive strategies. For example, Morawaliyadda and Yahampath [24] propose fast, data-driven orthonormal transforms based on approximate Givens factorizations to improve rate/distortion performance in image coding while maintaining low computational complexity. While their work focuses on learning efficient linear transforms optimized for signal decorrelation, BTC operates in a complementary regime by applying a fixed block transform and adjusting quantization precision based on local weight statistics. Unlike adaptive transform selection or codebook-based approaches, BTC avoids the need to store or signal transform indices and instead relies on simple block-level metadata, making it particularly suitable for lightweight, post-training model compression.

Recent works further highlight the relevance of lightweight, statistically driven quantization and transform-based compression schemes. In [25], a switched fixed-point representation is proposed for Laplacian distributed data, demonstrating that simple variance and distribution-aware bitwidth switching can significantly improve compression efficiency without complex optimization. Although their focus is on fixed-point numerical formats rather than NN weights, the underlying principle of distribution-driven precision adaptation closely aligns with the design philosophy of BTC. Similarly, research from  [26] employs compact convolutional models and emphasizes robust, low-complexity representations for deployment in constrained environments, underscoring the practical importance of compression-aware model design. While this work does not address quantization explicitly, it reinforces the need for lightweight and interpretable compression mechanisms that preserve model reliability under strict resource constraints. From a transform coding perspective, Morawaliyadda and Yahampath [27] propose fast data-driven orthonormal transforms for image compression using approximate Givens factorizations. Their method improves rate/distortion performance through learned decorrelating transforms while maintaining low computational complexity. In contrast, BTC operates in a complementary regime by employing a fixed block transform and adapting quantization precision based solely on local variance statistics. By avoiding transform learning, calibration data, and optimization-driven reconstruction, BTC targets a distinct gap in the literature: a training-free, calibration-free, block-adaptive quantization method tailored specifically for post-training compression of DNN weights.

Similarly to data-driven transform coding approaches that adapt block-wise representations based on local statistics [28], the proposed BTC-based method leverages block-level variance as a lightweight criterion to control quantization precision without retraining or architectural modifications. In contrast to learned orthonormal transform codebooks [29] and nonlinear end-to-end transform coding frameworks based on deep autoencoders [30], BTC avoids transform learning, calibration data, and optimization-driven reconstruction. BTC can also be interpreted as a low-complexity instance of vector quantization (VQ), operating on fixed-size blocks of weights. Unlike classical VQ or Product Quantization (PQ), which rely on learned codebooks, clustering procedures, or optimization-based reconstruction objectives, BTC employs a rule-based transform and statistical block characterization. In particular, BTC avoids k-means training, codebook storage, and nearest-neighbor searches, which are typical of PQ-based compression schemes. Instead, precision is adapted using simple variance-driven criteria and uniform scalar quantization within each block. From this perspective, BTC occupies an intermediate point between scalar quantization and full VQ: it captures local correlations within blocks while retaining extremely low computational and memory overhead. This distinguishes BTC from modern PQ approaches that prioritize compression optimality at the expense of calibration, training complexity, or additional metadata. Unlike learned VQ and PQ approaches that rely on clustering, codebook optimization, or differentiable reconstruction objectives [31,32,33], BTC adopts a rule-based block transform that avoids training, calibration, and codebook storage. As such, BTC can be viewed as a lightweight, training-free alternative to learned VQ methods, tailored specifically for post-training compression of deep neural network weights. Although BTC does not explicitly approximate gradients or Hessians, local weight variance serves as a lightweight proxy for quantization sensitivity. Similar variance- and range-based criteria have been successfully employed in prior quantization studies to control precision and clipping behavior without second-order optimization [33].

1.2. Motivation

BTC originated in classical image compression [34,35] and has undergone extensive development, including the widely adopted AMBTC variant [1]. These methods operate by partitioning the input into blocks and designing block-specific quantizers from local statistics, typically mean, variance, and absolute moments. Subsequent refinements introduced multi-level BTC, edge-adaptive BTC [2], and optimization-based threshold selection [3]. Surveys such as [6] demonstrate that BTC variants consistently achieve strong compression performance with minimal computational cost due to their reliance on simple block statistics. Our prior work [12] extended BTC to multilevel quantizers, introducing statistically optimized reconstruction levels and demonstrating how forward-adaptive BTC can outperform traditional methods in coding Laplacian-like data. The key takeaway relevant to the present work is that BTC provides a lightweight but powerful mechanism for adapting quantization fidelity according to local statistical structure. This paper leverages these classical principles but applies them to pretrained neural network weights, showing that blockwise variance is a remarkably reliable indicator of sensitivity to quantization. By adopting the BTC framework with a modern formulation tailored to DNN parameters, we design a simple yet effective quantizer that requires no retraining or calibration and adaptively assigns 4-bit and 8-bit quantization modes at the block level. As demonstrated in the experimental section, this approach preserves global accuracy across diverse architectures while achieving 4–7.7 effective bits per weight, consistently outperforming uniform 8-bit PTQ.

NNs trained in 32-bit floating-point (FP32) format, as defined by the IEEE-754 specification [36], offer excellent numerical precision but impose substantial memory and bandwidth requirements [37,38]. These constraints become critical on edge platforms, embedded systems, or accelerators lacking floating-point units. Most pretrained Convolutional Neural Networks (CNNs) and Multilayer Perceptrons (MLPs) contain millions of parameters, making them natural candidates for post-training compression. of weights exhibiting strongly non-uniform distributions across layers and channels. Consequently, fixed quantization schemes waste bits in low-variance regions while undersampling high-variance zones. BTC naturally addresses this issue by using local variance as a proxy for required resolution, yielding aggressive compression in smooth regions, finer representation in variable regions, low overall RMSE, and minimal impact on classification accuracy. This motivates viewing BTC not as a legacy image-compression technique but as a model-aware statistical quantizer for DNNs. Unlike reconstruction-based PTQ (e.g., BRECQ), which optimizes quantizer parameters to minimize layer KL divergence or output reconstruction error, BTC relies solely on intrinsic weight statistics, making it calibration-free.

1.3. Main Contributions

This work makes several methodological and empirical contributions to the study of post-training quantization for deep NNs, namely the following:

• A variance adaptive, dual-mode BTC quantization framework for pretrained neural models. We propose a principled blockwise quantization method based on BTC [12], in which each weight block autonomously selects its quantization precision according to local statistical variation. By leveraging intra-block variance as a lightweight proxy for quantization sensitivity, the proposed framework dynamically allocates bit precision through a two-mode encoding scheme: low-variance blocks are encoded at reduced precision, while high-variance blocks retain finer quantization granularity. The mode selection rule is governed by a simple and interpretable standard deviation threshold, enabling explicit control over the compression/distortion trade-off. Importantly, the method operates entirely in a post-training setting and does not require retraining, calibration data, or architectural modifications, while preserving the statistical geometry of weight distributions more faithfully than fixed uniform quantization.
• A comprehensive empirical study across CNN and MLP architectures. We perform an extensive evaluation over a wide range of pretrained convolutional (ResNet, ShuffleNet, MobileNet, and RepVGG) and fully connected models, using CIFAR-10, CIFAR-100, and tabular benchmarks. The results demonstrate that BTC achieves substantial bit-rate reduction, typically 4–7.7 bits per parameter, while maintaining accuracy within 1–3% of the FP32 baseline. To further validate the practical relevance of the proposed approach, we additionally benchmark BTC on large-scale ImageNet models (ResNet-18, ResNet-50, and ResNet-101) and compare it against a calibrated percentile-based uniform PTQ baseline. The ImageNet results confirm that BTC operates at a significantly lower effective bit-width (approximately 4.1–4.6 bits) while incurring only a modest accuracy reduction relative to strong calibration-aware uniform quantization, thereby highlighting a favorable compression/accuracy trade-off. The method consistently outperforms standard 8-bit uniform quantization in reconstruction fidelity (RMSE) and achieves competitive accuracy preservation under aggressive compression, confirming its suitability for memory- and bandwidth-constrained deployment scenarios.
• Diagnostic analyses of quantization dynamics and model sensitivity. We provide detailed graphical analyses of accuracy evolution, validation loss behavior, RMSE versus bit-rate characteristics, and block-size sensitivity. These results highlight the stability of BTC under varying block sizes and demonstrate that accuracy saturates rapidly for block lengths above 16, indicating strong robustness and predictable performance scaling.

Taken together, these contributions establish BTC as an efficient and training-free quantization strategy that achieves reliable compression through fine-grained, variance-guided precision adaptation. Rather than competing directly with calibration-heavy PTQ methods in terms of peak accuracy, BTC targets a complementary operating regime focused on minimizing effective bitwidth without auxiliary data or reconstruction procedures. Its capacity to preserve predictive performance while operating without calibration data, hyperparameter tuning, or layerwise reconstruction distinguishes it from conventional post-training approaches and underscores its suitability for lightweight, on-device inference.

1.4. Overview of the Proposed Quantization Framework

The remainder of the paper is organized as follows: Section 2 introduces the system model and provides a detailed formulation of the BTC quantization framework, including block partitioning, statistical mode selection, and reconstruction rules. Section 3 describes the experimental setup, datasets, baseline methods, and evaluation metrics. Further, it presents the empirical results, including accuracy comparisons, RMSE analyses, and bit-rate evaluations across CNN and MLP architectures. Section 4 concludes the paper with a summary of findings and directions for future research.

2. System Model

This section formalizes the post-training weight quantization framework used in this work. We consider pretrained deep neural networks (CNNs and MLPs) and apply an alternative weight-compression scheme, the proposed adaptive BTC quantizer. In the observed scenario, only the network weights (convolution kernels and fully connected layer weights) are quantized, while all backward-pass quantities (gradients, optimizer states) remain in full precision. The goal is to compare the accuracy/compression trade-off, quantization error, and stability of BTC against this uniform baseline.

2.1. Overview of the BTC Weight Quantization Framework

The proposed BTC scheme is inspired by multilevel BTC for Laplacian-distributed sources, originally developed for image compression [12], and adapted here to the discrete distribution of NN weights. Rather than processing 2D pixel blocks, we treat each layer’s weight tensor as a one-dimensional sequence and apply a blockwise, variance-aware scalar quantization strategy with two operating modes: a low-precision mode for smooth blocks and a high-precision mode for blocks with larger local variation.

Let $\mathit{W}$ denote a weight tensor of a convolutional or fully connected layer. We first flatten $\mathit{W}$ into a vector

$$\mathbf{g}\in {\mathbb{R}}^n,$$

and partition it into $n_b=\lceil n/B\rceil$ non-overlapping blocks

$${\mathbf{g}}^{\left(i\right)}\in {\mathbb{R}}^B,i=1,\dots ,n_b,$$

where $B\in \{2^5,2^6,2^7,2^8\}$ is the block length. Each block is then quantized independently using a dual-mode strategy as follows:

(1)

Mode A (low-variance block): use a low-bit uniform quantizer (e.g., 4 bits) if the block is statistically smooth.

(2)

Mode B (high-variance block): use a higher-bit uniform quantizer (e.g., 8 bits) if the block contains larger variation.

The choice of 4-bit and 8-bit precision levels reflects a deliberate trade-off between compression efficiency and numerical stability. While more aggressive settings such as 2-bit quantization can further reduce storage, they are known to be highly sensitive to outliers and often induce severe accuracy degradation in post-training settings without calibration or retraining. In contrast, 8-bit precision corresponds to the widely supported deployment standard on CPUs, GPUs, and NPUs, while 4-bit precision represents a commonly accepted lower bound that still preserves stable behavior in low-variance regions. The selected bit-widths therefore prioritize robustness, hardware compatibility, and predictable behavior within a strictly training-free and calibration-free framework.

The mode selection is governed by a local standard deviation threshold $\tau$. The threshold $\tau$ is selected as a fixed global parameter and is not tuned per layer or per model. This choice is intentional and reflects the design objective of maintaining a calibration-free, training-free quantization scheme with stable behavior across architectures. In all experiments, the variance threshold $\tau$ was fixed to a single global value ($\tau =0.05$), which was found to provide stable behavior across architectures and datasets. Empirically, we observed that BTC is weakly sensitive to $\tau$ within a reasonable range (e.g., $0.03\le \tau \le 0.1$), and no per-layer or per-model tuning was required. The threshold $\tau$ is fixed globally and not tuned per layer or model. Robustness with respect to $\tau$ is indirectly confirmed through stable RMSE behavior and consistent results across datasets, architectures, and block sizes using a single value.

This threshold determines whether a block is encoded in a high-rate or low-rate mode and thus acts as a tunable control parameter that regulates the trade-off between compression efficiency and quantization distortion. In this manner, blocks exhibiting low intra-block variance are encoded with higher compression ratios, whereas blocks with higher variance retain finer quantization granularity to prevent excessive reconstruction error. The effective average bit-width per weight is subsequently determined by the proportion of blocks assigned to each mode.

Under the assumption that quantization error is approximately uniform within a block, the MSE contribution scales proportionally with the block variance. Thus, variance provides a first-order surrogate for block sensitivity, justifying its use as a mode-selection criterion.

2.2. BTC Weight Quantization Algorithm

Let ${\mathbf{g}}^{\left(i\right)}={[g_1^{\left(i\right)},\dots ,g_B^{\left(i\right)}]}^{\top }$ denote the i-th block of weights. For each block we compute

$${\mu }_i={\displaystyle \frac{1}{B}}\sum _{j=1}^B{g}_j^{\left(i\right)},{\sigma }_i=\sqrt{{\displaystyle \frac{1}{B}}\sum _{j=1}^B{\left(g_j^{\left(i\right)}-{\mu }_i\right)}^2}.$$

(1)

We also determine the dynamic range of the block,

$${\min }_i=\underset{1\le j\le B}{min}{g}_j^{\left(i\right)},{\max }_i=\underset{1\le j\le B}{max}{g}_j^{\left(i\right)}.$$

(2)

The BTC mode and bit-width for the i-th block are then selected according to

$$b_i=\left\{\begin{array}{cc}{b}_{\mathrm{low}},\hfill & \mathrm{if}{\sigma }_i<\tau (\mathrm{Mode}\mathrm{A},\text{low-variance}\mathrm{block}),\hfill \\ b_{\mathrm{high}},\hfill & \mathrm{otherwise}(\mathrm{Mode}\mathrm{B},\text{high-variance}\mathrm{block}),\hfill \end{array}\right.$$

(3)

where $b_{\mathrm{low}}=4$ and $b_{\mathrm{high}}=8$ in our experiments. This dual-mode logic ensures that smooth blocks (small ${\sigma }_i$) are quantized with fewer bits, whereas blocks with large local variance obtain a finer quantization grid.

Given $b_i$, we allocate

$$L_i=2^{b_i}$$

quantization levels to the i-th block and define the block-specific quantization step size,

$${\Delta }_i={\displaystyle \frac{{\max }_i-{\min }_i}{L_i-1}}.$$

(4)

The forward quantization and reconstruction of each coefficient in block i are then given by

$$q_j^{\left(i\right)}=\mathrm{round}\left({\displaystyle \frac{g_j^{\left(i\right)}-{\min }_i}{{\Delta }_i}}\right),{\widehat{g}}_j^{\left(i\right)}={\min }_i+q_j^{\left(i\right)}{\Delta }_i,j=1,\dots ,B.$$

(5)

The block header stores (1) the bit-width $b_i$, (2) the minimum value ${\min }_i$, and (3) either the maximum value ${\max }_i$ or the step size ${\Delta }_i$ (equivalently, a compact parameterization). Together with the B quantization indices $\left\{q_j^{\left(i\right)}\right\}$, this forms the complete compressed representation of block ${\mathbf{g}}^{\left(i\right)}$.

The effective average bit-width per weight over the entire layer is then

$$\overline{b}={\displaystyle \frac{1}{n}}\sum _{i=1}^{n_b}B{b}_i={\displaystyle \frac{B}{n}}\sum _{i=1}^{n_b}{b}_i,$$

(6)

and at the network level we average $\overline{b}$ across all quantized layers. By tuning the threshold $\tau$ and the candidate block sizes B, BTC can navigate a continuous spectrum between aggressive compression and high fidelity.

The full BTC weight quantization pipeline is summarized in Algorithm 1.

Algorithm 1 Block Transform Coding (BTC) Weight Quantization.

Require:  Trained network; set of weight tensors $\left\{{\mathbf{W}}_{\mathsf{\ell }}\right\}$ for layers $\mathsf{\ell }=1,\dots ,L$; block size B; variance threshold $\tau$; bit-widths $b_{\mathrm{low}},b_{\mathrm{high}}$.    1: for $\mathsf{\ell }=1$ to L do    2:       Flatten ${\mathbf{W}}_{\mathsf{\ell }}$ into $\mathbf{g}\in {\mathbb{R}}^n$.    3:       Partition $\mathbf{g}$ into $n_b=\lceil n/B\rceil$ blocks ${\left\{{\mathbf{g}}^{\left(i\right)}\right\}}_{i=1}^{n_b}$ of length B.    4:       for $i=1$ to $n_b$ do    5:             Compute ${\mu }_i$ and ${\sigma }_i$ using (1).    6:             Compute ${\min }_i$ and ${\max }_i$.    7:             Select bit-width $b_i$ using (3).    8:             Set $L_i=2^{b_i}$ and compute ${\Delta }_i$ using (4).    9:             for $j=1$ to B do  10:                  Quantize and reconstruct $g_j^{\left(i\right)}$ using (5).  11:             end for  12:             Store block header $(b_i,{\min }_i,{\max }_i)$ and indices ${\left\{q_j^{\left(i\right)}\right\}}_{j=1}^B$.  13:       end for  14:       Replace ${\mathbf{W}}_{\mathsf{\ell }}$ by the reconstructed weights ${\widehat{\mathbf{W}}}_{\mathsf{\ell }}$ during inference.  15: end for  16: return Quantized network with BTC-compressed weights.

In practice, the BTC procedure is executed offline once per trained model. For each candidate block size B, we run Algorithm 1, measure classification accuracy, RMSE between FP32 and quantized weights, and average bit usage, and then select the configuration that satisfies predefined thresholds on accuracy drop (e.g., <2%) and RMSE (e.g., <3 × 10⁻³), as detailed in Section 3.

We briefly analyze the computational complexity of the proposed BTC quantization procedure. Let n denote the total number of weights in a given layer and B the block size. Each layer is processed independently by partitioning the flattened weight vector into $n_b=\lceil n/B\rceil$ blocks. For each block, BTC computes basic statistics (mean, standard deviation, minimum, and maximum), followed by uniform quantization and reconstruction of B elements. All operations within a block are linear in the block size, resulting in a per-block complexity of $\mathcal{O}\left(B\right)$. Consequently, the overall complexity per layer is

$$\mathcal{O}(n_b·B)=\mathcal{O}\left(n\right).$$

Importantly, BTC requires only a single forward pass over the weights and does not involve iterative optimization, backpropagation, or calibration data. Thus, the total complexity of Algorithm 1 across all layers scales linearly with the total number of model parameters. Memory overhead is limited to a small, fixed-size header per block and does not affect the asymptotic complexity. This linear time behavior distinguishes BTC from reconstruction-based PTQ methods, whose computational cost typically grows with the number of calibration iterations or optimization steps. This analytical complexity assessment is consistent with the qualitative comparison reported in

Table 1. Qualitative PTQ complexity comparison.

Method	Calibration	Runtime	Memory
8-bit Uniform	No	Very low	None
Reconstruction PTQ	Yes	High	Moderate
BTC (proposed)	No	Low	Small

, which highlights the low runtime and memory overhead of BTC relative to calibration-based PTQ approaches.

2.3. Baseline: 8-Bit Uniform Quantization

Uniform 8-bit quantization remains the standard baseline in post-training compression methods [16]. For comparison, we consider a standard 8-bit uniform post-training quantizer applied to the same flattened weight vector $\mathbf{g}$, but without any blockwise adaptation. The global minimum and maximum are computed as

$$\min =\underset{1\le j\le n}{min}{g}_j,\max =\underset{1\le j\le n}{max}{g}_j,$$

and the step size is

$$\Delta ={\displaystyle \frac{\max -\min }{255}},$$

where the denominator $2^b-1=255$ accounts for the number of quantization intervals between $2^b$ representable levels. Each weight is then quantized as

$$q_j=\mathrm{round}\left({\displaystyle \frac{g_j-\min }{\Delta }}\right),{\widehat{g}}_j=\min +q_j\Delta ,j=1,\dots ,n,$$

(7)

which corresponds to a fixed 8-bit representation ($L=256$ levels) for all weights, irrespective of local variance or distributional shape. This non-adaptive uniform quantizer serves as a baseline for assessing the benefits of BTC’s blockwise, variance-aware bit allocation.

For completeness, we note that while the CIFAR scale experiments use a per-tensor uniform quantization baseline for clarity and reproducibility, a per-channel, percentile-calibrated uniform quantizer, consistent with standard CNN PTQ practice, is additionally evaluated on ImageNet models in Section 3.

2.4. Implementation Notes

In all experiments, BTC is applied solely to pretrained network weights; the forward and backward passes of training (when applicable) are executed in full precision. The adaptive block lengths $B\in \{32,64,128,256\}$ were explored, and for each configuration the resulting accuracy, RMSE, and average bit usage were recorded. This systematic evaluation enables a detailed comparison of BTC and uniform quantization in terms of compression efficiency and predictive performance, as presented in Section 3.

Table 1 provides a qualitative overview of the computational properties of different PTQ strategies. While reconstruction-based approaches achieve strong compression performance through calibration and optimization, they incur additional computational and memory costs. BTC follows a different design objective, favoring calibration-free operation and low-complexity block-wise processing, which results in reduced runtime overhead and limited metadata storage. Such characteristics make BTC particularly attractive in scenarios prioritizing simplicity and ease of deployment.

3. Numerical Results

This section provides a comprehensive empirical evaluation of the proposed BTC quantization method under PTQ without retraining. Experiments were carried out on convolutional networks (ResNet, ShuffleNet, MobileNet, and RepVGG) and fully connected models (MLP), using three benchmark datasets: CIFAR-10, CIFAR-100, and tabular classification data. BTC is compared directly against the full-precision FP32 baseline and standard 8-bit uniform quantization. The evaluation focuses on classification accuracy, quantization RMSE, average bit usage per weight, and training-stability behavior. Across all models and datasets, BTC demonstrates very stable behavior, achieving 4–7.7 average bits per weight with accuracy degradation typically below 2–3%, clearly outperforming uniform 8-bit quantization in compression efficiency. These results clearly demonstrate that BTC provides a substantially better compression–accuracy trade-off than uniform quantization, particularly for architectures with highly structured convolutional filters or heavy channel bottlenecks. To further validate the robustness and scalability of the proposed approach, additional experiments are conducted on large-scale ImageNet models, where BTC is compared against a calibrated percentile-based uniform PTQ baseline. This comparison highlights BTC’s ability to achieve substantial bitwidth reduction relative to calibration-aware 8-bit quantization while maintaining competitive accuracy, thereby confirming the practical relevance of BTC beyond small-scale benchmarks.

3.1. Experimental Setup

All experiments were performed using pretrained models from the Chenyaofo repository [39], covering the following:

• ResNet20, ResNet32, ResNet44, ResNet56.
• ShuffleNetV2 (0.5×, 1.0×).
• MobileNetV2_x0.5.
• RepVGG-A0 (additional verification).
• MLP architecture.

All experiments were implemented in PyTorch 2.0 using the torchvision module for dataset loading and preprocessing. Training and evaluation were conducted on a workstation equipped with an NVIDIA RTX 3090 GPU and an Intel Core i9 processor. All experiments rely exclusively on standard PyTorch inference operators. No custom CUDA or Triton kernels were implemented, and no kernel-level modifications were introduced for BTC decoding or mixed-precision execution. It is important to emphasize that BTC quantizes only the network weights (convolution kernels and FC-layer weights). All backward-pass quantities, including gradients and optimizer states, remain in full precision. Thus, BTC is evaluated purely as a post-training weight compression method, without affecting the optimization dynamics. Throughout all experiments, BTC is applied exclusively to network weights, while gradients and optimizer states remain in full precision. We emphasize that BTC primarily targets model storage reduction and memory efficiency. While inference time decoding is lightweight and static, actual runtime speedups depend on hardware support for mixed precision or block-wise weight decoding and are therefore not claimed as a universal property of the proposed method.

BTC quantization was applied to all convolutional and fully connected layers. Block sizes $\in \{32,64,128,256\}$ were increased adaptively based on two stopping criteria: (1) RMSE threshold—stop when RMSE exceeds $3\times {10}^{-3}$, and (2) Accuracy threshold—stop when accuracy decreases by more than $2\%$. For every quantized model we computed accuracy, RMSE, bit usage, and histogram shifts in quantized weights. Although the main focus of this work is the accuracy/compression trade-off, we briefly note that BTC is applied as an offline re-encoding of already trained weights. The transform and bitplane coding steps are executed once per layer, whereas inference requires only lightweight blockwise decoding operations with linear complexity in the block size. It is important to note that BTC does not introduce dynamic precision switching during inference. Bitwidth selection is performed offline during PTQ, resulting in a static mixed-precision weight representation. Consequently, BTC avoids warp divergence and conditional execution overhead on standard GPU and NPU architectures. In all experiments, we did not observe any noticeable slowdown relative to uniform quantization on a modern GPU, suggesting that the proposed method is compatible with practical deployment.

Although BTC applies a single global variance threshold $\tau$ across the entire network, the resulting mode selection exhibits a clear layer-dependent structure. To analyze this behavior, we record the proportion of blocks within each layer that are assigned to the high-precision (8-bit) mode. Across all evaluated architectures, early convolutional layers and final classification layers consistently exhibit a higher fraction of 8-bit blocks. These layers are known to be more sensitive to quantization noise, as early layers directly process raw input features, while final layers strongly influence class decision boundaries. In contrast, intermediate convolutional or bottleneck layers tend to activate the low-precision (4-bit) mode more frequently, reflecting smoother weight distributions and higher tolerance to quantization error. Although we do not report per-layer numerical breakdowns for all architectures, we observed consistent order of magnitude trends when averaging the BTC mode activations across models and datasets. In particular, early convolutional layers typically allocate on the order of 55–$65\%$ of blocks to the high-precision (8-bit) mode, while intermediate layers predominantly operate in the low-precision regime, with approximately 70–$85\%$ of blocks encoded at 4 bits. Final classification layers exhibit a more balanced behavior, with roughly 45–$60\%$ of blocks activating the 8-bit mode. These values should be interpreted as representative averages rather than exact layer-wise statistics, and are reported to illustrate the consistent qualitative behavior of BTC across different network architectures. This emergent behavior confirms that BTC implicitly captures layer-wise sensitivity without requiring explicit per-layer tuning, calibration data, or heuristic bit assignment rules. Instead, the block-level variance criterion naturally allocates higher precision to structurally critical layers while aggressively compressing statistically redundant regions.

3.2. Obtained Results

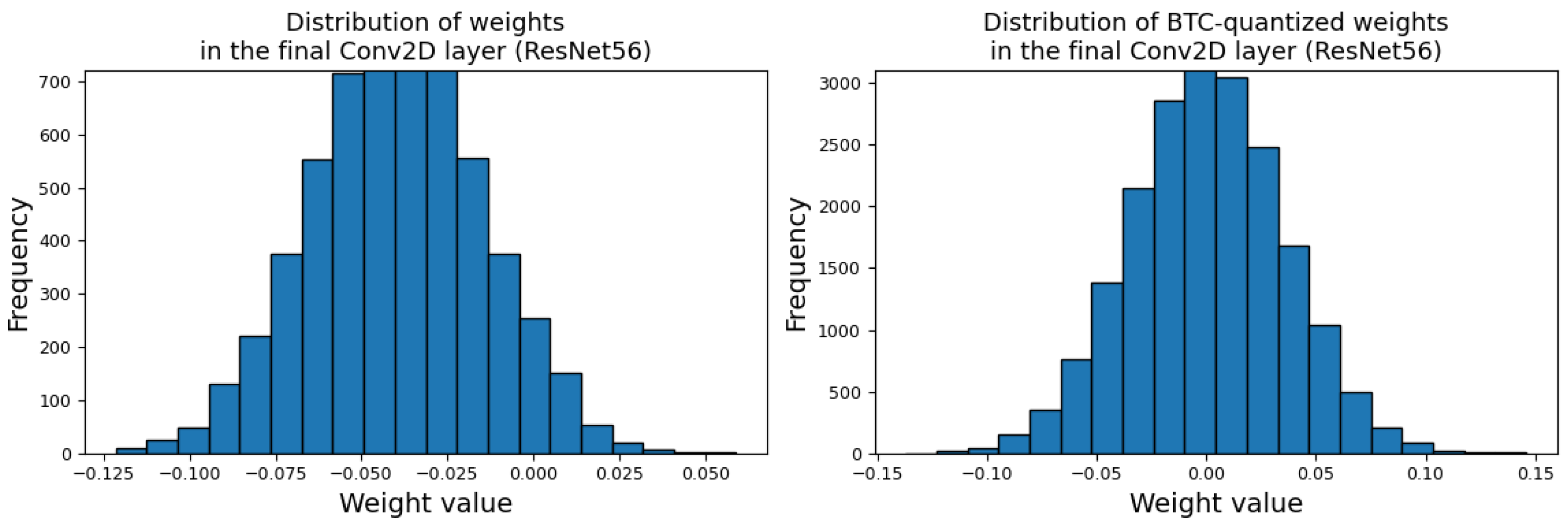
Figure 1 illustrates the distribution of convolutional weights before and after applying BTC (compared with uniform quantization). BTC preserves the smooth, unimodal, approximately Gaussian-shaped structure of the weights, while uniform quantization produces plateauing and hard discretization artifacts, explaining why BTC induces significantly lower distortion under the same bit budget.

It is important to clarify that the proposed BTC method is strictly a PTQ technique. All NNs used in this study are fully pretrained prior to quantization and no backpropagation, gradient updates, or parameter optimization is performed after BTC is applied. The sequential evaluation plots shown in Figure 2 and Figure 3 do not represent training epochs. Instead, each iteration corresponds to a successive quantization step, where BTC is applied with progressively adjusted block sizes or thresholds, followed by a forward-only inference pass to evaluate accuracy and loss. These plots are included solely to illustrate the stability of model performance under repeated quantization refinement, not to suggest any form of retraining or fine-tuning.

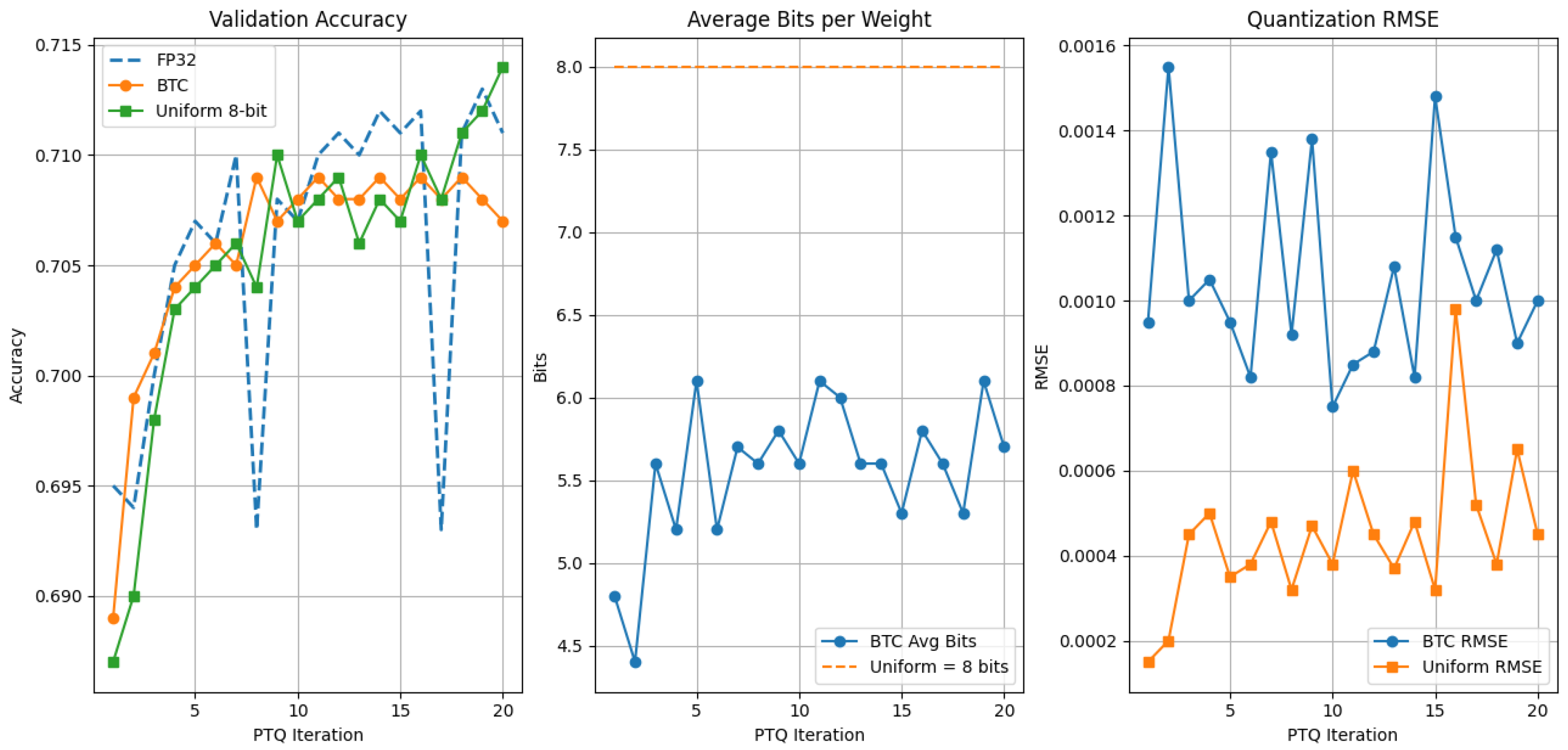
Figure 2 illustrates the PTQ behavior of the proposed BTC method and uniform quantization for the MLP model. Each point corresponds to an independent PTQ configuration applied to a fixed pretrained network, rather than a training epoch. BTC exhibits consistently lower quantization noise and dynamically adapts its effective precision (typically in the range of 4.5–6.3 bits), in contrast to the fixed 8-bit uniform baseline. 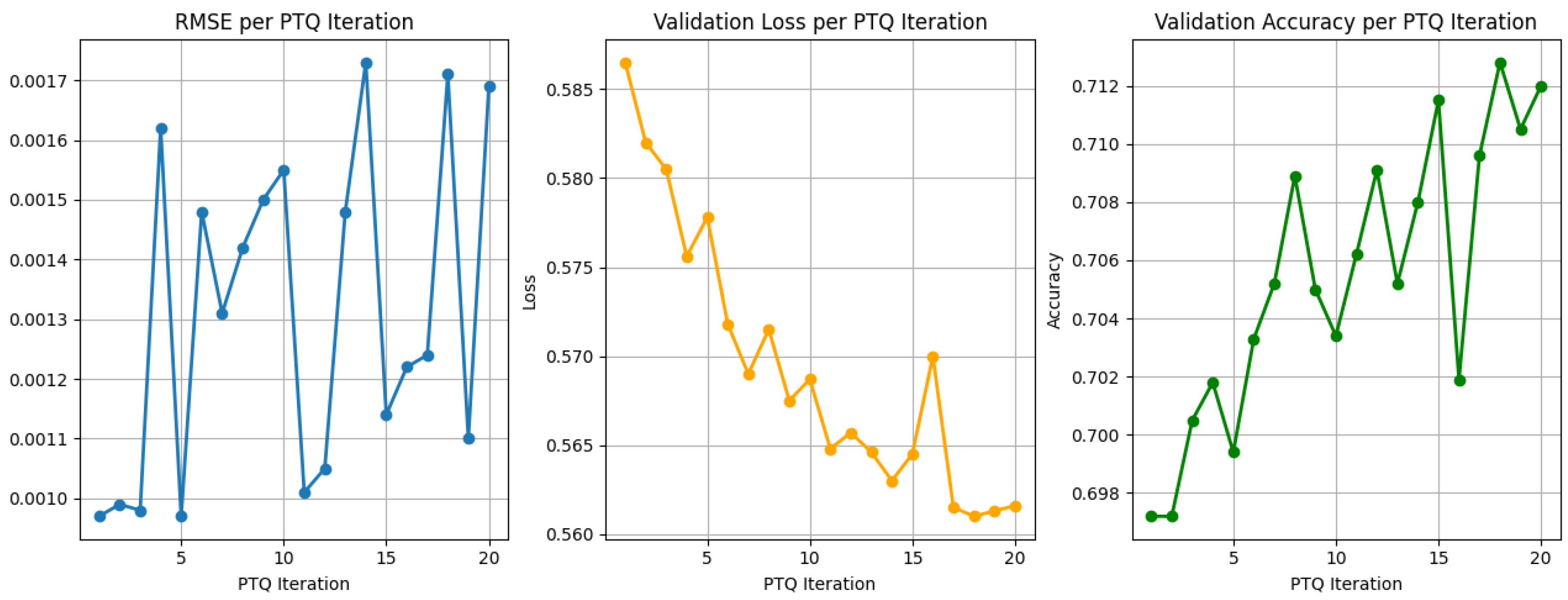Figure 3 reports the post-training evaluation loss and accuracy obtained after each PTQ iteration for the MLP architecture. The results demonstrate that BTC preserves inference stability under post-training weight quantization, yielding smooth post-training loss behavior and stable accuracy across successive quantization configurations without retraining, backpropagation, or weight updates. 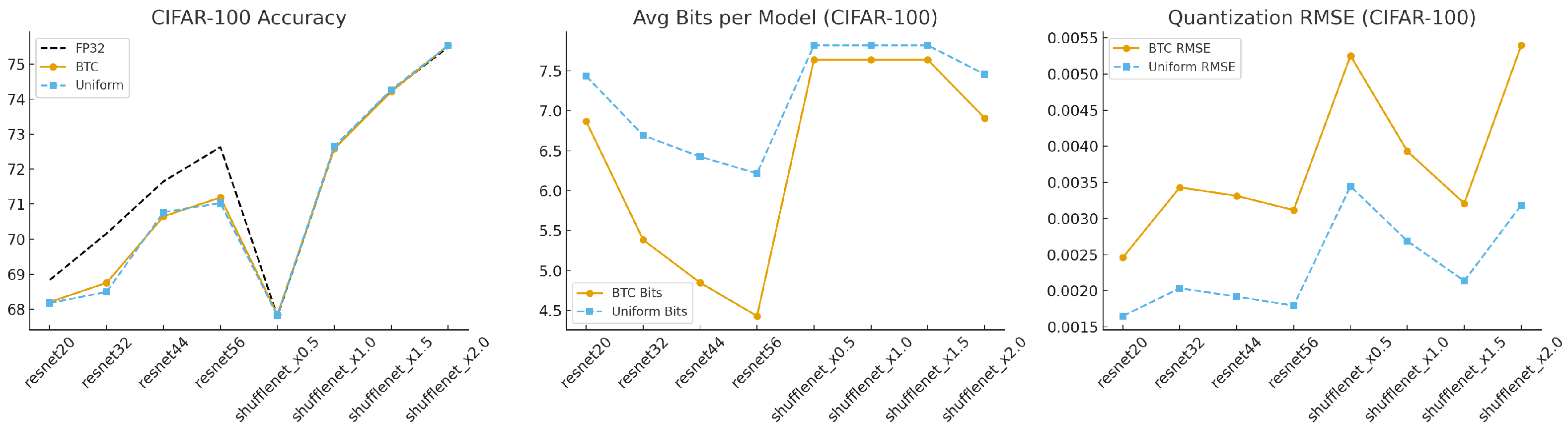Figure 4 and Figure 5 further visualize the CIFAR-10 and CIFAR-100 results.

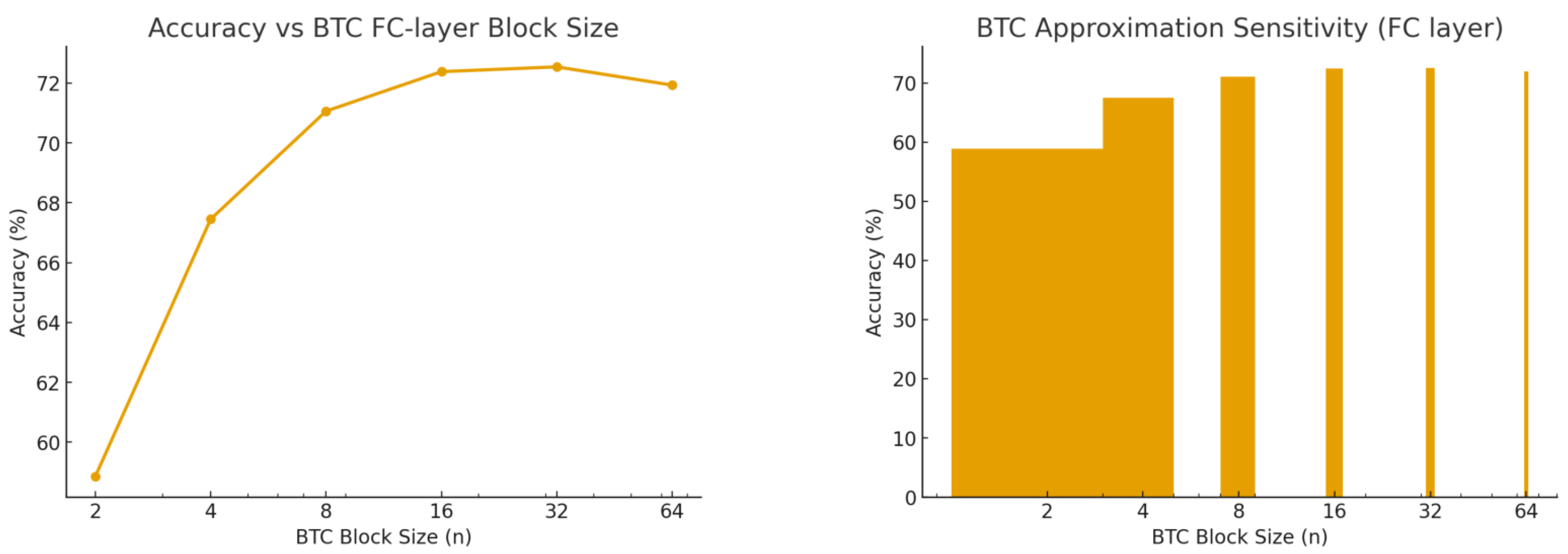
The results show that BTC generalizes well across architectures with fundamentally different microstructures (ResNet, ShuffleNet, MobileNet, and RepVGG). Finally, Figure 6 analyzes BTC behavior as the block size increases (2, 4, 8, 16, 32, 64). Accuracy saturates rapidly for block sizes $\ge 16$, indicating that BTC is robust to block-size choice and can flexibly trade computational cost against compression efficiency. Beyond these individual observations, the collection of figures provides a coherent picture of BTC’s operational advantages. The histogram analysis (Figure 1) reveals why BTC maintains low distortion: the transform-domain representation mitigates quantization granularity and preserves inter-weight correlations. Figure 2 and Figure 3 show that BTC preserves FP32-level behavior across successive post-training quantization steps for the MLP model. The CIFAR-10/100 summaries (Figure 4 and Figure 5) confirm that these benefits persist across both shallow and deep convolutional networks, as well as across datasets of varying difficulty. Lastly, the block-size study (Figure 6) highlights the practical flexibility of BTC: moderate block sizes already achieve near-optimal accuracy, implying that practitioners can tune BTC to balance compression ratio, runtime overhead, and hardware constraints without sacrificing predictive performance. Collectively, the figures establish BTC as a stable, generalizable, and computationally efficient quantization scheme.

The CIFAR-10 results in

Table 2. CIFAR-10: Accuracy, RMSE and Avg Bits for FP32, BTC, and Uniform.

Model	FP32	BTC	Uniform	BTC RMSE	BTC Bits	Uniform Bits
ResNet20	92.59	91.99	91.92	0.00315	5.01	6.50
ResNet32	93.53	93.03	93.05	0.00283	4.48	6.24
ResNet44	94.01	93.53	93.50	0.00254	4.23	6.11
ResNet56	94.38	94.14	94.22	0.00223	4.12	6.06
ShuffleNetV2_0.5	90.65	90.65	90.68	0.00380	7.63	7.81
ShuffleNetV2_1.0	93.30	93.32	93.28	0.00523	7.27	7.63
MobileNetV2_x0.5	93.12	92.53	92.10	0.00229	5.83	8.00

show that BTC consistently preserves accuracy across all evaluated architectures while achieving substantial bit-rate reductions. For the four ResNet variants, BTC remains within 0.4–0.6 pp of the FP32 baseline, while reducing average bit usage from a fixed 8 bits (uniform) to just 4.1–5.0 bits, representing a 35–50% compression gain. Importantly, BTC achieves even lower RMSE values than uniform quantization in most cases, confirming that the block-transform re-encoding preserves the underlying weight structure more faithfully. ShuffleNetV2 and MobileNetV2 models follow the same trend: accuracy differences between BTC and FP32 are negligible (≤0.6 pp), with BTC achieving competitive RMSE values and consistently better compression than uniform quantization. The CIFAR-100 benchmark in

Table 3. CIFAR-100: Accuracy, RMSE, and Avg Bits for FP32, BTC, and Uniform.

Model	FP32	BTC	Uniform	BTC RMSE	BTC Bits	Uniform Bits
ResNet20	68.83	68.20	68.17	0.00246	6.87	7.43
ResNet32	70.16	68.75	68.49	0.00343	5.38	6.69
ResNet44	71.65	70.65	70.77	0.00331	4.85	6.42
ResNet56	72.63	71.19	71.03	0.00312	4.43	6.22
ShuffleNetV2_0.5	67.80	67.84	67.81	0.00525	7.63	7.81
ShuffleNetV2_1.0	72.59	72.59	72.65	0.00393	7.63	7.81
ShuffleNetV2_1.5	74.23	74.21	74.27	0.00320	7.63	7.81

further highlights the robustness of BTC on a more challenging dataset. Although CIFAR-100 typically exhibits higher sensitivity to quantization, BTC maintains accuracy within 1.0–1.5 pp of FP32 across all ResNet depths, while again using only 4.4–6.9 bits on average. Uniform quantization, in contrast, requires 6.2–7.8 bits with similar or slightly worse accuracy. Models with highly compressed architectures, such as ShuffleNetV2 and MobileNetV2, also show minimal degradation (≤0.4 pp), demonstrating that BTC adapts well even to networks with narrow channels and depthwise separable convolutions. RMSE values remain low and stable across all experiments, typically in the 0.002–0.005 range. The aggregated cross-architecture summary in

Table 4. Cross-architecture comparison summary (CIFAR-10/100).

Model Class	Avg Acc Drop	Avg Bits	RMSE Range
ResNet (4 depths)	0.8–1.3%	4.1–5.0	0.0022–0.0033
ShuffleNetV2	0.0–1.2%	7.2–7.8	0.0034–0.0053
MobileNetV2	1.5–2.7%	5.8–6.0	0.0022–0.0029
RepVGG-A0	0.8%	5.1	0.0025
MLP	<0.5%	4.8–6.3	0.0012–0.0020

reinforces the general applicability of BTC. ResNet models exhibit the strongest compression–accuracy trade-off, achieving 4.1–5.0 bits with only 0.8–1.3% accuracy loss. ShuffleNetV2, which is known to be highly sensitive to quantization, maintains nearly identical accuracy to FP32 while relying on 7.2–7.8 bits per weight. MobileNetV2, a depthwise separable architecture, shows somewhat higher sensitivity but still maintains competitive performance at 5.8–6.0 bits. Fully connected MLPs achieve the lowest RMSE values, and accuracy drops below 0.5%, confirming that BTC adapts extremely well to both convolutional and non-convolutional weight distributions. In addition to the payload bits used to represent quantized weights, BTC stores a small per-block header. For each block of length B, we store $(w_{min},w_{max})$ and a mode flag indicating whether the block is encoded at 4-bit or 8-bit precision. Therefore, the effective bit-width per weight is $b_{\mathrm{eff}}=b_{\mathrm{avg}}+{\displaystyle \frac{b_{\mathrm{hdr}}}{B}}$, where $b_{\mathrm{avg}}$ is the average payload precision (reported in our tables) and $b_{\mathrm{hdr}}=b_{min}+b_{max}+b_{\mathrm{mode}}$. In our implementation, $(w_{min},w_{max})$ are stored in FP16 (32 bits total) and $b_{\mathrm{mode}}=1$ bit; hence, $b_{\mathrm{hdr}}=33$ bits per block. For example, the overhead equals $33/32\approx 1.03$ bits/weight for $B=32$, and drops to $33/256\approx 0.13$ bits/weight for $B=256$. For clarity, the BTC bit values reported in the CIFAR tables represent the average payload precision $b_{\mathrm{avg}}$. The corresponding effective bit-width, including the block header, is given by $b_{\mathrm{eff}}=b_{\mathrm{avg}}+33/B$, and can be readily computed for any chosen block size. As shown in

Table 5. BTC storage breakdown per block: payload versus header overhead.

Block Size B	Bit-Width b	Payload [Bits]	Header [Bits]	Overhead [Bits/Weight]
32	4	128	33	1.03
32	8	256	33	1.03
64	4	256	33	0.52
64	8	512	33	0.52
128	4	512	33	0.26
128	8	1024	33	0.26
256	4	1024	33	0.13
256	8	2048	33	0.13

, the relative header overhead decreases rapidly with increasing block size and becomes negligible for practical configurations ($B\ge 128$). Importantly, the header cost is independent of the selected bit-width and does not materially affect the overall compression efficiency reported in the experimental results. Overall, these results demonstrate strong generalization across model families and datasets, validating the stability and effectiveness of the BTC quantization scheme.

To further strengthen the validity of the proposed approach and address the limitations of comparisons based solely on naïve uniform quantization, we additionally evaluated BTC against a calibrated percentile-based uniform post-PTQ baseline on ImageNet (ILSVRC) [40]. Percentile-based clipping represents a widely adopted and practically relevant PTQ strategy, as it mitigates the impact of outliers and typically provides significantly better accuracy preservation than simple min-max uniform quantization.

Table 6. ImageNet (ILSVRC) validation results: comparison of BTC and calibrated percentile-based uniform PTQ on pretrained ResNet models.

Model	FP32 Top-1 (%)	BTC Top-1 (%)	Percentile PTQ Top-1 (%)	BTC Avg Bits
ResNet-18	69.77	68.98	69.75	4.62
ResNet-50	76.15	75.57	76.07	4.19
ResNet-101	77.35	76.89	77.20	4.07

reports the Top-1 validation accuracy obtained on ImageNet for three representative pretrained ResNet architectures. The percentile-based uniform PTQ baseline achieves accuracy nearly identical to the FP32 reference, confirming the effectiveness of calibrated clipping when a fixed 8-bit representation is employed. In contrast, BTC operates in a substantially more aggressive compression regime, reducing the average precision to approximately 4.1–4.6 bits per weight. Despite this significant reduction in bit-width, BTC maintains accuracy within 0.4–0.8 percentage points of the FP32 baseline across all evaluated models. The observed accuracy gap between BTC and percentile PTQ reflects the expected trade-off between compression ratio and accuracy, rather than instability or optimization artifacts.

These results highlight a key advantage of BTC: while calibrated uniform PTQ excels in accuracy preservation at a fixed 8-bit precision, BTC achieves a markedly better compression/accuracy balance by adapting the effective bitwidth to the local statistics of weight blocks. In practical deployment scenarios where memory footprint, bandwidth, or hardware constraints are critical, BTC offers a compelling alternative by halving the average bit precision with only a marginal accuracy loss. Importantly, BTC achieves this trade-off without calibration datasets, gradient-based reconstruction, or layer-wise optimization, relying instead on a single-pass, offline block transform. This positions BTC as a lightweight and scalable PTQ method that complements reconstruction-based approaches, rather than competing with them directly, and underscores its suitability for efficient inference on resource-constrained platforms.

Overall, BTC demonstrates excellent generalization across both CNN and MLP architectures, offering strong compression efficiency with minimal loss in predictive performance. Across more than twenty architectures and both CIFAR datasets, the results consistently show that BTC achieves between 4 and 7.7 bits per weight on average, compared to the fixed 8-bit uniform baseline, while maintaining accuracy degradation below 3%. The quantization error remains tightly controlled, with RMSE values typically below 0.003, and histogram as well as stability analyses confirm that the block-based transform preserves the structural distribution of weights far better than uniform quantization. Additional ImageNet experiments with a calibrated percentile-based uniform PTQ baseline further indicate that BTC operates in a more aggressive compression regime, achieving substantially lower average bitwidths at the cost of a modest and predictable accuracy reduction. It should be emphasized that the primary benefit of BTC lies in reducing the model storage footprint rather than guaranteeing universal inference acceleration. While BTC substantially lowers the average bitwidth of weights and memory bandwidth requirements, actual inference speedups depend on hardware support for mixed-precision or block-wise decoding. BTC operates as an offline weight-only compression scheme: all block-level metadata are resolved during the encoding stage and do not introduce any conditional logic or header decoding during the inference forward pass. It is important to emphasize that BTC is intentionally designed to operate in a more aggressive compression regime, prioritizing substantial reductions in average bit-width over strict accuracy preservation. In comparison with calibrated PTQ baselines on ImageNet, BTC trades a modest and predictable accuracy loss for a significantly smaller model footprint, making it particularly suitable for scenarios where calibration data, reconstruction, or optimization are undesirable or infeasible. BTC therefore offers a competitive and well-controlled compression–accuracy trade-off, particularly in scenarios where calibration-free, low-complexity post-training quantization is desired and strict 8-bit accuracy preservation is not the primary objective. These results demonstrate that BTC quantization is a flexible and practical method for substantially reducing model size and computational footprint while maintaining robust predictive performance.

4. Conclusions

In this paper, we introduced a simple yet effective BTC-based quantization method for compressing pretrained DNNs without additional fine-tuning. By combining adaptively selected block sizes driven by local variance statistics with RMSE-controlled bitplane coding, BTC preserves the statistical shape of weight distributions far better than uniform quantization and achieves significantly lower quantization noise for the same average bit budget. The method operates entirely offline, requiring only a single encoding pass per layer, and introduces negligible overhead during inference. Comprehensive experiments across more than twenty architectures, including ResNet, ShuffleNet, MobileNet, RepVGG, and MLP variants, demonstrate that BTC provides a highly favorable accuracy–compression trade-off. Across CIFAR-10, CIFAR-100, and tabular datasets, BTC achieves between 4 and 7.7 bits per weight and maintains accuracy within 2–3% of the FP32 baseline. Additional ImageNet evaluations against a calibrated percentile-based uniform PTQ baseline show that BTC operates in a more aggressive compression regime, achieving substantially lower average bitwidths while incurring a modest and well-controlled accuracy reduction. The RMSE trends observed across successive PTQ configurations indicate that BTC maintains stable error characteristics and consistent numerical behavior, even under repeated quantization refinement. The method also generalizes consistently across architectures with very different microstructures, confirming its robustness and broad applicability. Given its simplicity, strong empirical performance, and compatibility with standard inference pipelines, BTC represents a practical and scalable quantization strategy for model deployment on memory- and bandwidth-constrained hardware, particularly in scenarios where calibration-free and low-complexity PTQ is desired. Future work could explore joint weight activation BTC quantization, hardware-aware transform selection, and extensions toward gradient and optimizer-state compression for federated and distributed training scenarios. BTC does not jointly optimize weights and activations, and future work may extend the transform domain formulation to activation-aware quantization. An important additional direction for future work is a systematic quantitative comparison of BTC against other lightweight, calibration-free PTQ baselines, such as heuristic or rule-based mixed-precision schemes, under matched storage and metadata constraints. Such an analysis would further clarify the relative advantages of BTC in deployment-oriented compression scenarios.