1. Introduction
Wind energy has experienced significant growth in recent decades, particularly in the development of small-scale wind turbines for decentralized energy generation. However, the efficiency and operational lifespan of these turbines are directly influenced by structural integrity issues, notably blade fissures [
1,
2]. Aerodynamic stresses, environmental conditions, and cyclic loads can lead to the formation and propagation of cracks, compromising performance and safety [
3]. Traditional damage detection techniques rely on periodic inspections and vibration-based monitoring, utilizing time-domain and frequency-domain analyses. While traditional damage detection methods are effective, they often require expert interpretation and are sensitive to noise and operational variations. Recent advancements in computational techniques, particularly machine learning and signal transformation methods, have opened new possibilities for more robust and automated damage detection systems [
4,
5,
6].
Several studies have explored advanced signal processing and machine learning techniques for damage detection in wind turbine blades. Among signal processing approaches, Aranizadeh et al. [
7] introduced a method based on frequency domain analysis using power spectral density (PSD) to detect faults in small-scale wind turbine blades. Their approach includes digital filtering and classification of structural conditions by comparing frequency components, emphasizing the superior performance of strain sensors over accelerometers, particularly for identifying torsional mode faults. Similarly, Chandrasekhar et al. [
4] investigated the application of machine learning algorithms for detecting damage in operational wind turbine blades, demonstrating improved detection accuracy compared to traditional techniques. Raju et al. [
8] presented a machine learning-based strategy to enhance wind turbine efficiency through intelligent fault detection and optimized turbine placement. Chenchen et al. [
9] developed a precise and non-invasive approach for damage detection by analyzing acoustic signals using deep neural networks combined with advanced noise reduction techniques. Ogaili et al. [
10] addressed the detection of multiple blade faults using classifiers such as k-nearest neighbors (KNNs), support vector machines (SVMs), and random forests, trained on vibration signal data. To improve model performance, they applied feature selection techniques including ReliefF, chi-square tests, and information gain. Catedra et al. [
11] proposed a methodology combining fault trees and binary decision diagrams (FT–BDD) to evaluate the dynamic reliability of wind turbines and prioritize maintenance actions. While traditional machine learning approaches require manual feature selection, deep learning methods can automatically extract features directly from raw data, such as images. For example, Xiao et al. [
12] employed UAV-acquired imagery to detect blade cracks using a deep learning-based image recognition model called Multivariate Information You Only Look Once (MI-YOLO). Gou et al. [
13] advanced this further by combining deep convolutional neural networks (CNNs) with an AdaBoost cascade classifier, improving detection through hierarchical decision-making. Additionally, Memari et al. [
14] conducted a comprehensive review on the integration of deep learning and UAV technologies for wind turbine blade inspection, highlighting the growing trend toward autonomous, data-driven monitoring systems. In addition to the aforementioned approaches, several studies, beyond the field of wind turbines, have proposed alternative strategies for transforming temporal signals into images to facilitate pattern recognition with neural networks. For instance, Short-Time Fourier Transform (STFT) has been successfully applied in fault detection tasks for electric motors, including prior work by the authors involving motor current signal analysis during transient states [
15].
While these methods have shown promising results, the image generation process can be computationally intensive and often requires complex preprocessing steps to achieve meaningful representations. This complexity poses challenges for real-time monitoring systems or low-resource environments. Consequently, there is a growing interest in signal transformation techniques that can efficiently produce informative image representations while preserving essential temporal characteristics. One such method is the Gramian Angular Field (GAF), which enables the visualization of time-series data as structured images well-suited for deep learning-based classification. In the generation of images from time-series signals, various transformation methods have been proposed, for instance the STFT [
15]. However, GAF stands out for its ability to move beyond classical frequency-based analysis, offering better results when dealing with cyclic data. This method preserves the temporal structure of signals, enabling more effective feature extraction for classification tasks. Zhang et al. [
16] applied GAF-based imaging techniques combined with an improved convolutional neural network for fault detection in transmission lines. Similarly, Zhou et al. [
17] performed bearing failure diagnosis using GAF and DenseNet through transfer learning. While these approaches have shown promise, there remains a need for a comprehensive methodology that effectively integrates GAF imaging with neural networks for fine-grained. The application of GAF to transform vibration signals into images presents a promising approach for detecting fissures in wind turbine blades. This method also facilitates the use of CNNs for effective classification [
18].
This study presents a novel approach for wind turbine blade damage detection by leveraging vibration signals transformed into images through the GAF technique and analyzed using a single-layer hidden CNN. Unlike previous works focused on binary classification or conventional time-frequency methods, our approach enables multi-class classification across four damage severity levels: healthy, light, intermediate, and severe. The model is trained and tested using GAF images derived from all the vibration axes (x, y, and z) captured at two representative rotational speeds, i.e., 3 rps (start-up speed) and 12 rps (maximum operating speed), which allows the system to account for dynamic variations in turbine behavior. GAF plays a critical role by preserving the temporal dependencies and amplifying structural patterns within the signal, thus enabling the CNN to extract more meaningful spatial features for damage characterization. The proposed method achieved a classification accuracy of 99.9%, offering a robust and scalable solution for condition monitoring in wind turbines. This performance highlights its potential to outperform traditional approaches by minimizing reliance on expert interpretation and enhancing early detection capabilities.
5. Discussion
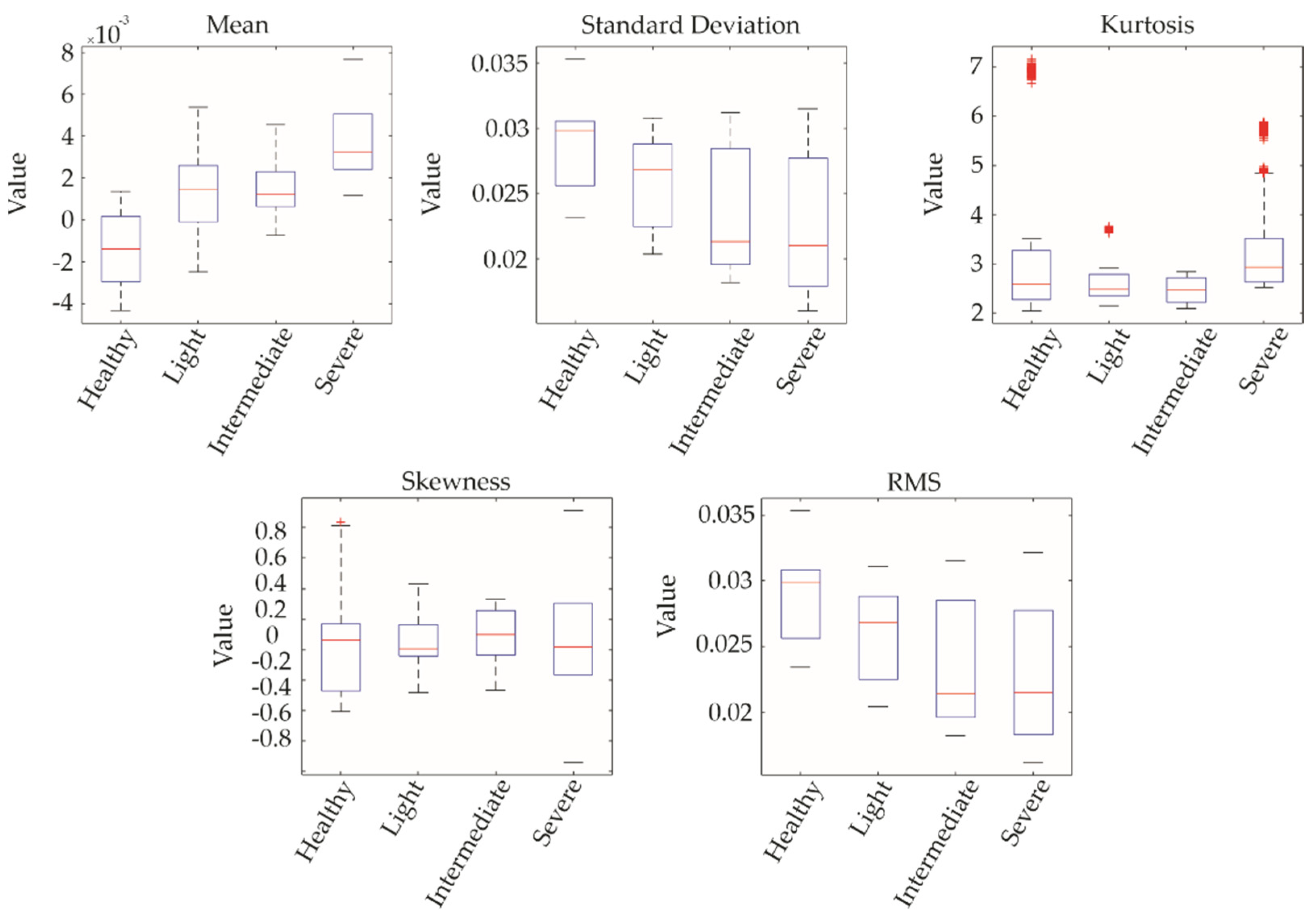
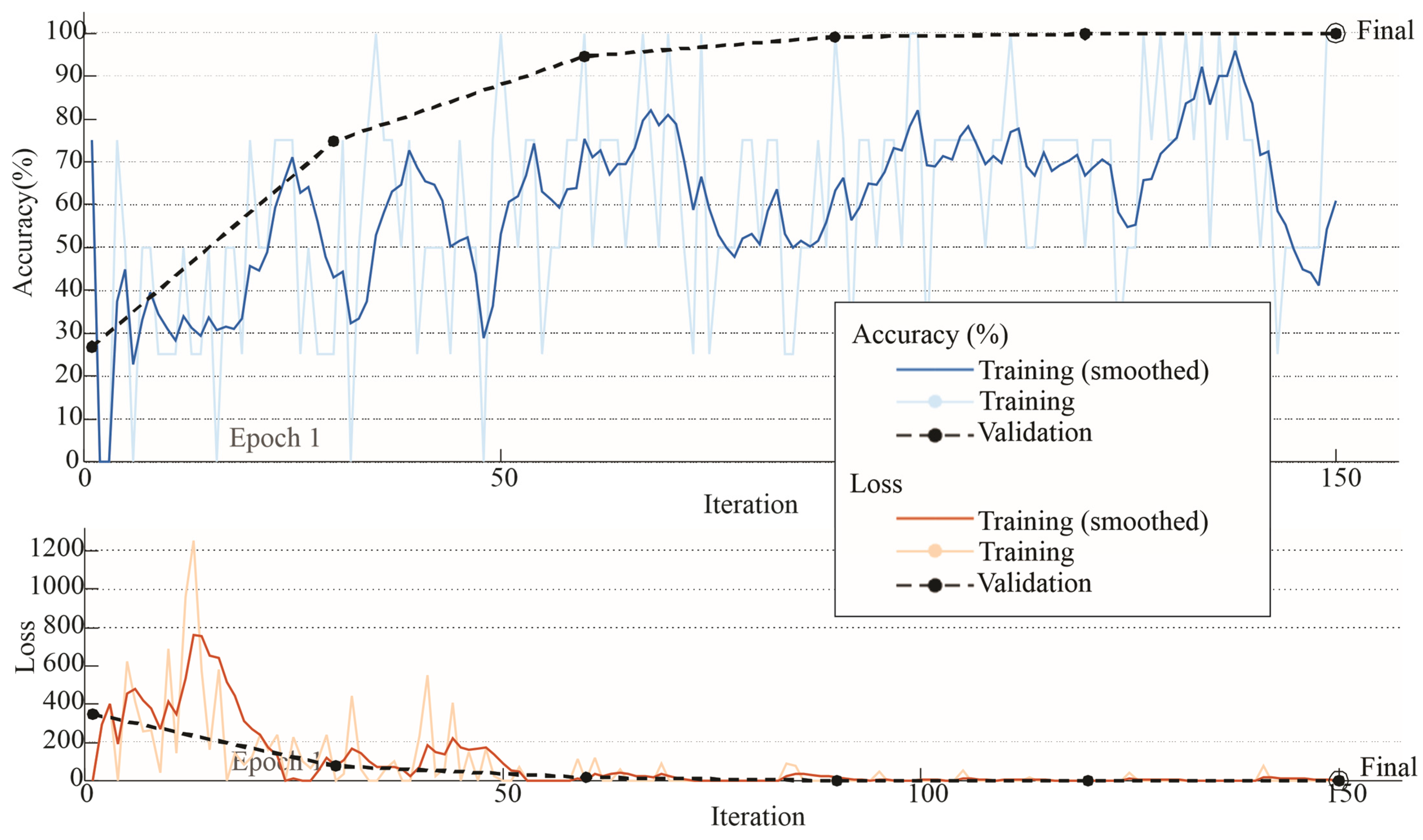
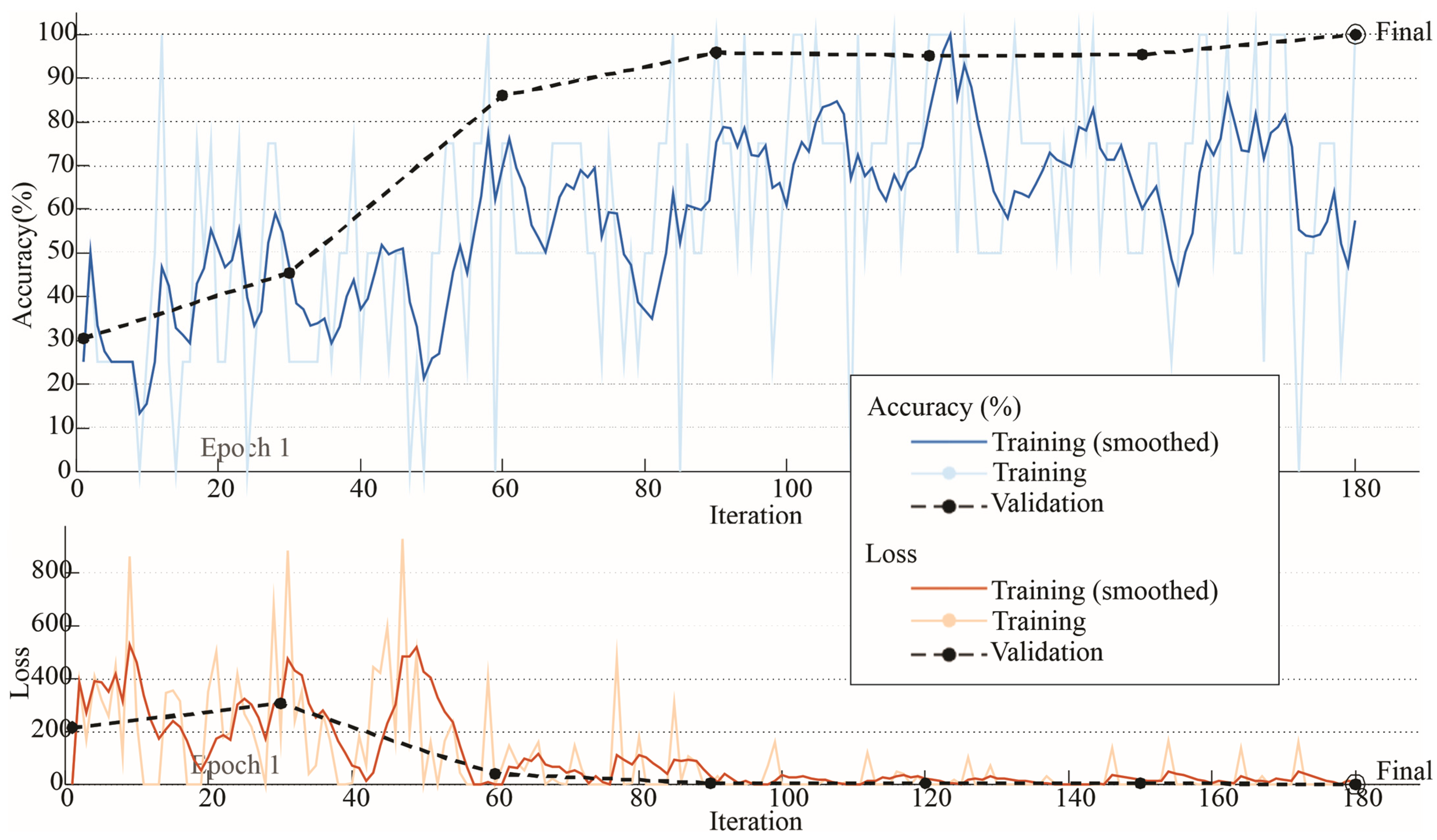
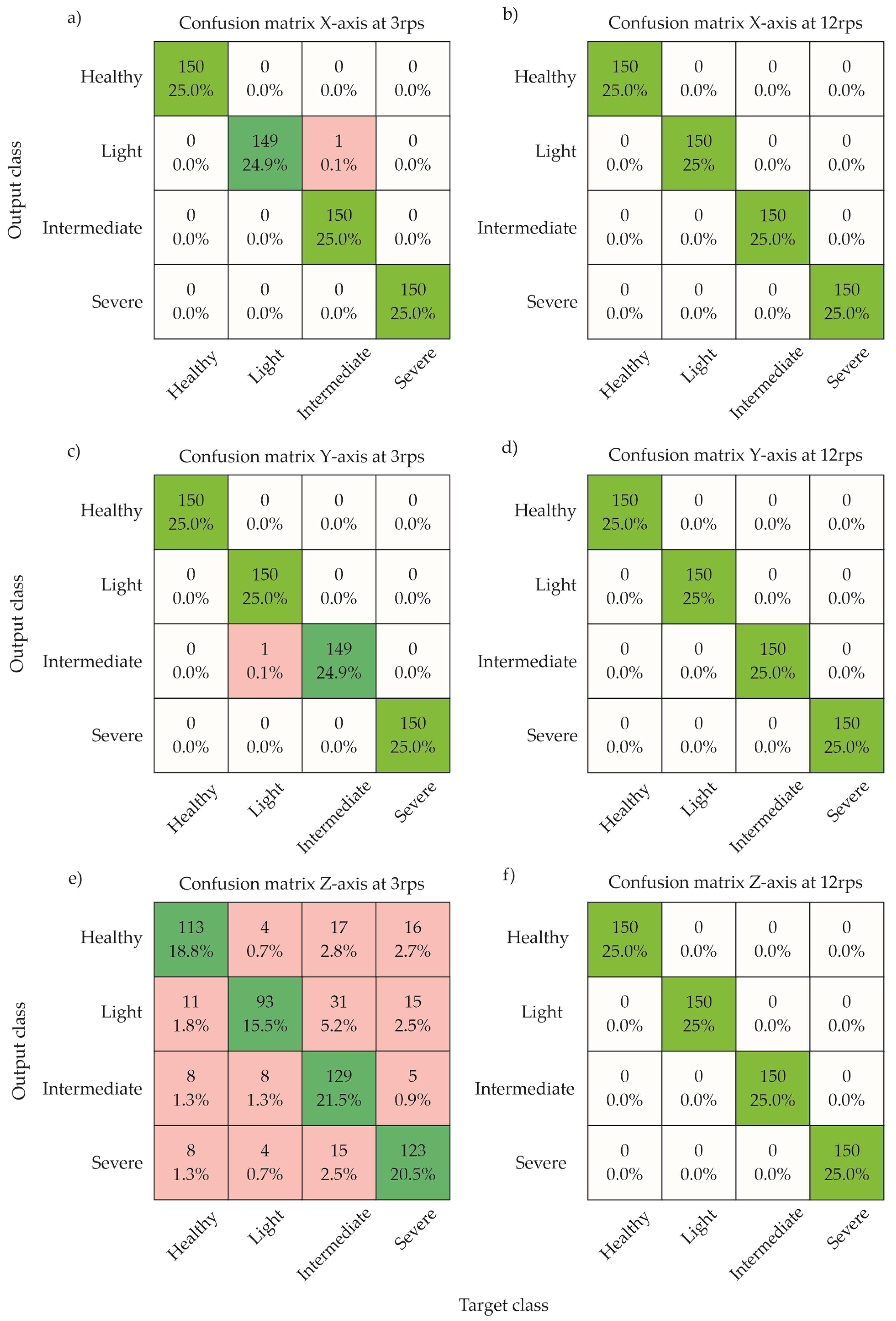
The results obtained in this study demonstrate the high potential of GAF-transformed vibration signals combined with CNNs for accurate damage detection in wind turbine blades. The model achieved a classification accuracy over 99.9% for two axes (X and Y), highlighting the effectiveness of this approach in identifying and distinguishing between different damage severity levels, including intermediate conditions that are often more challenging to characterize.
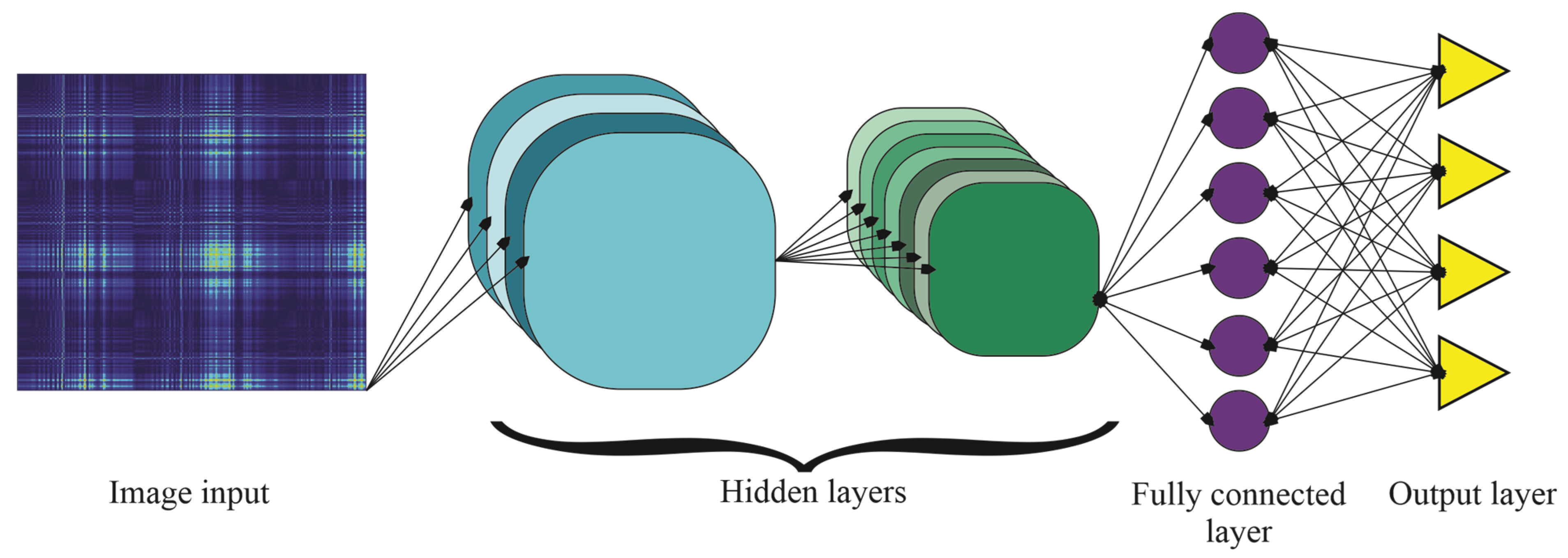
The success of the proposed model can be largely attributed to the GAF transformation, which converts raw vibration signals into structured 879×600-pixel images, enabling the CNN to automatically extract relevant features without manual feature engineering. By employing a compact and low-complexity CNN, consisting of a single hidden layer with only three filters, the approach achieves high classification accuracy while maintaining computational efficiency. This combination makes the model particularly suitable for online monitoring applications and deployment in systems with limited processing resources. Unlike conventional methods that depend heavily on expert interpretation and complex preprocessing, this methodology facilitates automated, robust, and efficient damage detection. The present study focused on controlled artificial damage to ensure repeatability; however, future research will include datasets involving naturally occurring cracks, which often exhibit more complex geometries, different locations, and propagation paths, allowing for the assessment of the model’s performance under more realistic and diverse operational conditions. Although a modal analysis of each damage scenario was not performed, the vibration measurements were obtained from the nacelle of the fully assembled wind turbine, enabling the capture of integrated structural responses. This configuration allowed for the detection of crack-related vibration signatures without requiring direct instrumentation of the blade surface; however, in future works, detailed modal analysis will be carried out.
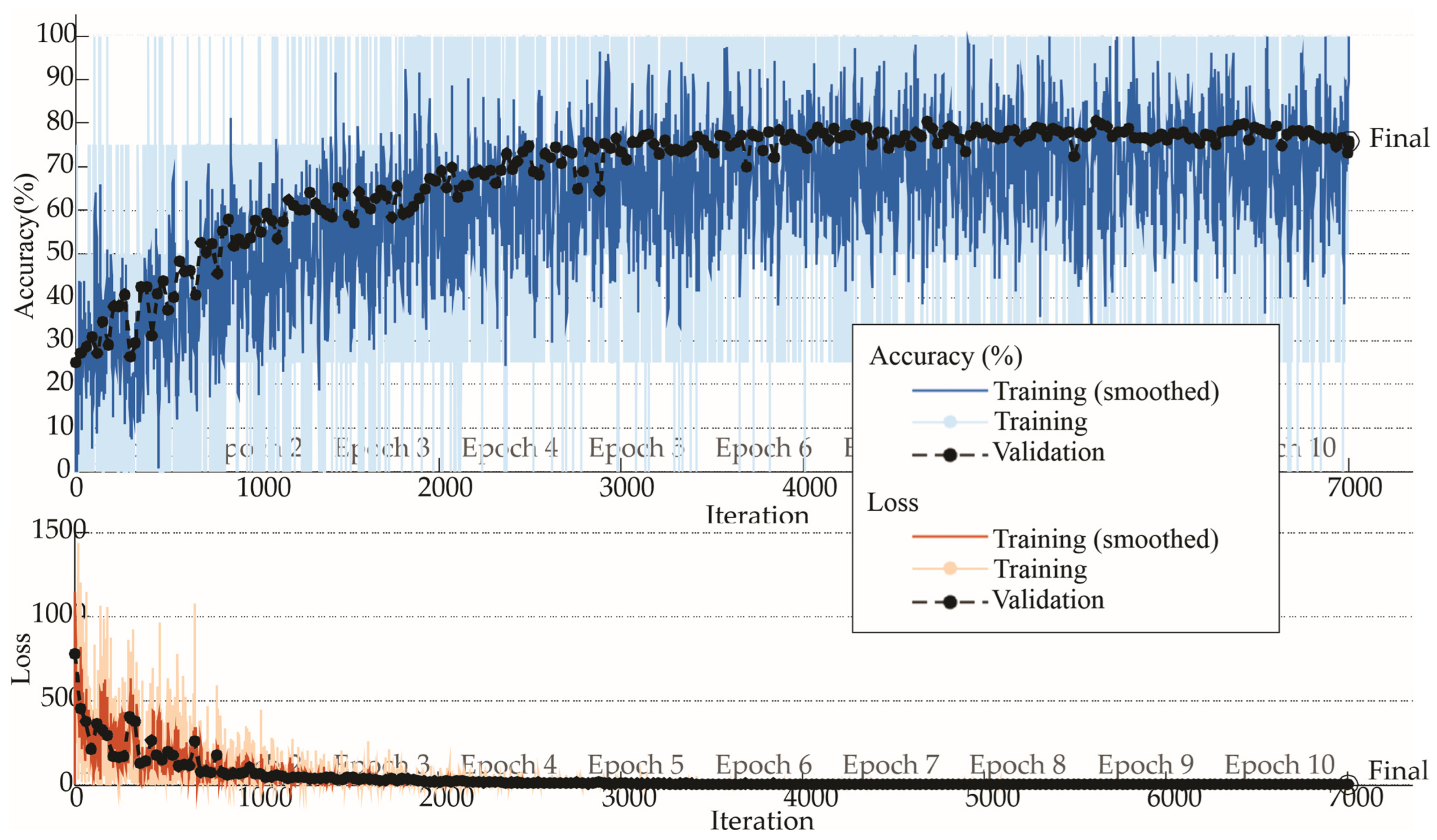
Throughout the study, vibration signals from all three axes (X, Y, and Z) were analyzed to ensure a comprehensive assessment of the wind turbine’s dynamic behavior under different operational conditions. The results showed consistently high classification accuracies for the X and Y axes at both steady-state (12 rps) and startup (3 rps) speeds. However, the Z-axis exhibited a noticeable drop in performance during startup, likely due to lower amplitude responses at reduced speeds. These findings highlight the importance of multi-axis data acquisition and suggest that leveraging information from multiple directions can contribute to the development of more resilient and adaptable diagnostic models.
It is also noteworthy that no signal filtering techniques were applied prior to the GAF transformation. Future studies should investigate the potential benefits of advanced preprocessing methods, such as noise filtering and signal enhancement, to further improve classification performance, mainly for the Z-axis. Also, it is important to test a wider range of speed values. Future work will also explore the inclusion of intermediate rotational speeds to capture transitional dynamics, which may enhance fault detection, particularly for axes such as Z that exhibit reduced sensitivity at low speeds.
The high classification accuracy achieved in this research confirms that CNN-based models, such as the proposed GAF–CNN approach, can be highly effective for crack detection in wind turbines, including the classification of intermediate and severe damage levels. While this work did not include a direct experimental comparison with alternative methods on the same dataset, the results obtained provided a strong basis for future studies aimed at benchmarking the approach against other state-of-the-art techniques. This advancement represents a valuable contribution toward the development of fully automated and intelligent condition monitoring systems for wind turbines. Although the proposal is tested on small-scale wind turbines, the obtained results prove promising to scale its application to larger wind turbines. However, some limitations remain. The approach requires a large number of labeled images for effective training, which may not always be readily available in real-world scenarios. Additionally, while the model is computationally lightweight, the image generation process via GAF can be time-consuming when dealing with large-scale datasets or real-time processing. Future work could explore data augmentation strategies and optimization techniques to address these challenges, including both the GAF-based image size and the CNN-based classification model. These insights lay the groundwork for implementing low-cost, high-accuracy diagnostic systems in real-world wind energy applications. In addition to the current analysis, future research could benefit from statistical evaluations of vibration data, as well as exploration data analysis techniques such as cluster analysis and principal component analysis (PCA). These methods would allow for assessing the intrinsic structure and separability of the dataset prior to CNN training, providing complementary evidence of class distinctiveness.
6. Conclusions
This work presents a robust approach for the classification of structural damage in wind turbine blades by combining GAF representations of vibration signals with CNNs. The proposed method achieved a classification accuracy over 99.9% for two axes, effectively distinguishing between four severity levels: healthy, light, intermediate, and severe. These results confirm the model’s potential for deployment in automated structural health monitoring systems, particularly in small-scale wind turbines where manual inspections are often impractical or costly. Moreover, due to its scalability and low computational requirements, the methodology also shows promise for adaptation to larger wind turbine systems, expanding its applicability in real-world industrial settings.
In particular, the evaluation across different axes and operating speeds revealed important insights into the model’s robustness. Transforming raw vibration signals into image representations using GAF enhanced the CNN’s ability to automatically extract relevant features, eliminating the need for manual signal processing or complex descriptors. The proposed method demonstrated consistent performance across the three vibration axes (X, Y, and Z) at a steady-state operating speed of 12 rps, achieving an accuracy of 100% in all cases. However, at the startup speed of 3 rps, a drop in classification accuracy was observed for the Z-axis, decreasing to approximately 78%, while the X and Y axes maintained high performance. These results highlight the resilience of the method under varying operational conditions and the importance of axis selection in low-speed scenarios.
Future research should aim to expand the model’s generalization capabilities by incorporating vibration data from all three accelerometer axes. Although the Y-axis provided highly informative signals, a multi-axis fusion strategy may improve robustness, especially under varying operational conditions. Additionally, the exploration of advanced preprocessing methods, such as signal filtering and noise reduction, could further enhance the quality of the GAF images and the performance of the classification model, mainly for the Z-axis.
Finally, real-world validation in operational wind turbines is recommended to assess the model’s adaptability to real environmental conditions, including variable rotational speeds, blade aging effects, and different turbine configurations. Overall, the integration of GAF and CNNs offers a promising pathway toward intelligent, cost-effective, and reliable early fault detection in wind turbine systems.
Author Contributions
Conceptualization, A.H.R.-R. and M.V.-R.; methodology, A.H.R.-R., J.P.A.-S. and M.V.-R.; software, formal analysis, resources, and data curation, A.H.R.-R., D.G.-L., M.V.-R.; writing—review and editing, all authors; supervision, project administration, and funding acquisition, J.P.A.-S., D.C.-M., M.B.-L., and M.V.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the “Fondo para el Fortalecimiento de la Investigación, Vinculación y Extensión (FONFIVE-UAQ 2025)” project.
Data Availability Statement
The data presented in this study are not publicly available.
Acknowledgments
We would like to thank the “Secretaria de Ciencia, Humanidades, Tecnología e Innovación (SECIHTI)—México” which partially financed this research under the scholarship 826907 given to A.H. Rangel-Rodriguez, and the scholarships 253732, 253652, 329800, and 296574, given to D. Granados-Lieberman, J. P. Amezquita-Sanchez, D. Camarena-Martinez, and M. Valtierra-Rodriguez, respectively, through the “Sistema Nacional de Investigadoras e Investigadores (SNII)–SECIHTI–México”.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mishnaevsky, L., Jr. Root causes and mechanisms of failure of wind turbine blades: Overview. Materials 2022, 15, 2959. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Zhou, S.; Jing, X.; Peng, Y.; Wu, H.; Kwok, N. Damage detection techniques for wind turbine blades: A review. Mech. Syst. Signal Process. 2020, 141, 106445. [Google Scholar] [CrossRef]
- Yang, W.; Peng, Z.; Wei, K.; Tian, W. Structural health monitoring of composite wind turbine blades: Challenges, issues and potential solutions. IET Renew. Power Gener. 2017, 11, 411–416. [Google Scholar] [CrossRef]
- Chandrasekhar, K.; Stevanovic, N.; Cross, E.J.; Dervilis, N.; Worden, K. Damage detection in operational wind turbine blades using a new approach based on machine learning. Renew. Energy 2021, 168, 1249–1264. [Google Scholar] [CrossRef]
- Ding, S.; Yang, C.; Zhang, S. Acoustic-signal-based damage detection of wind turbine blades—A review. Sensors 2023, 23, 4987. [Google Scholar] [CrossRef]
- Korolis, J.S.; Bourdalos, D.M.; Sakellariou, J.S. Machine Learning-Based Damage Diagnosis in Floating Wind Turbines Using Vibration Signals: A Lab-Scale Study Under Different Wind Speeds and Directions. Sensors 2025, 25, 1170. [Google Scholar] [CrossRef]
- Aranizadeh, A.; Shad, H.; Vahidi, B.; Khorsandi, A. A novel small-scale wind-turbine blade failure detection according to monitored-data. Results Eng. 2025, 25, 103809. [Google Scholar] [CrossRef]
- Raju, S.K.; Periyasamy, M.; Alhussan, A.A.; Kannan, S.; Raghavendran, S.; El-Kenawy, E.S.M. Machine learning boosts wind turbine efficiency with smart failure detection and strategic placement. Sci. Rep. 2025, 15, 1485. [Google Scholar] [CrossRef]
- Yang, C.; Ding, S.; Zhou, G. Wind turbine blade damage detection based on acoustic signals. Sci. Rep. 2025, 15, 3930. [Google Scholar] [CrossRef] [PubMed]
- Ogaili, A.A.F.; Jaber, A.A.; Hamzah, M.N. A methodological approach for detecting multiple faults in wind turbine blades based on vibration signals and machine learning. Curved Layer. Struct. 2023, 10, 20220214. [Google Scholar] [CrossRef]
- García Márquez, F.P.; Segovia Ramírez, I.; Mohammadi-Ivatloo, B.; Marugán, A.P. Reliability Dynamic Analysis by Fault Trees and Binary Decision Diagrams. Information 2020, 11, 324. [Google Scholar] [CrossRef]
- Xiaoxun, Z.; Xinyu, H.; Xiaoxia, G.; Xing, Y.; Zixu, X.; Yu, W.; Huaxin, L. Research on crack detection method of wind turbine blade based on a deep learning method. Appl. Energy 2022, 328, 120241. [Google Scholar] [CrossRef]
- Guo, J.; Liu, C.; Cao, J.; Jiang, D. Damage identification of wind turbine blades with deep convolutional neural networks. Renew. Energy 2021, 174, 122–133. [Google Scholar] [CrossRef]
- Memari, M.; Shakya, P.; Shekaramiz, M.; Seibi, A.C.; Masoum, M.A. Review on the advancements in wind turbine blade inspection: Integrating drone and deep learning technologies for enhanced defect detection. IEEE Access 2024, 12, 33236–33282. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; Rivera-Guillen, J.R.; Basurto-Hurtado, J.A.; De-Santiago-Perez, J.J.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P. Convolutional neural network and motor current signature analysis during the transient state for detection of broken rotor bars in induction motors. Sensors 2020, 20, 3721. [Google Scholar] [CrossRef]
- Zhang, Q.; Qi, Z.; Cui, P.; Xie, M.; Din, J. Detection of single-phase-to-ground faults in distribution networks based on Gramian Angular Field and Improved Convolutional Neural Networks. Electr. Power Syst. Res. 2023, 221, 109501. [Google Scholar] [CrossRef]
- Zhou, Y.; Long, X.; Sun, M.; Chen, Z. Bearing fault diagnosis based on Gramian angular field and DenseNet. Math. Biosci. Eng. 2022, 19, 14086–14101. [Google Scholar] [CrossRef] [PubMed]
- Spajić, M.; Talajić, M.; Pejić Bach, M. Harnessing Convolutional Neural Networks for Automated Wind Turbine Blade Defect Detection. Designs 2024, 9, 2. [Google Scholar] [CrossRef]
- Hau, E.; Von Renouard, H. Wind turbines: Fundamentals, technologies, application, economics. In Wind Turbines; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rangel-Rodriguez, A.H.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P.; Bueno-Lopez, M.; Valtierra-Rodriguez, M. Analysis of vibration signals based on machine learning for crack detection in a low-power wind turbine. Entropy 2023, 25, 1188. [Google Scholar] [CrossRef]
- Xu, J.; Ding, X.; Gong, Y.; Wu, N.; Yan, H. Rotor imbalance detection and quantification in wind turbines via vibration analysis. Wind. Eng. 2021, 46, 3–11. [Google Scholar] [CrossRef]
- Han, Y.; Li, B.; Huang, Y.; Li, L. Bearing fault diagnosis method based on Gramian angular field and ensemble deep learning. J. Vibroeng. 2023, 25, 42–52. [Google Scholar] [CrossRef]
- Li, Y.D.; Hao, Z.B.; Lei, H. Survey of convolutional neural network. J. Comput. Appl. 2016, 36, 2508–2515. [Google Scholar]
- Zhang, J.; Li, H.; Song, W.; Zhang, J.; Shi, M. STCYOLO: Subway Tunnel Crack Detection Model with Complex Scenarios. Information 2025, 16, 507. [Google Scholar] [CrossRef]
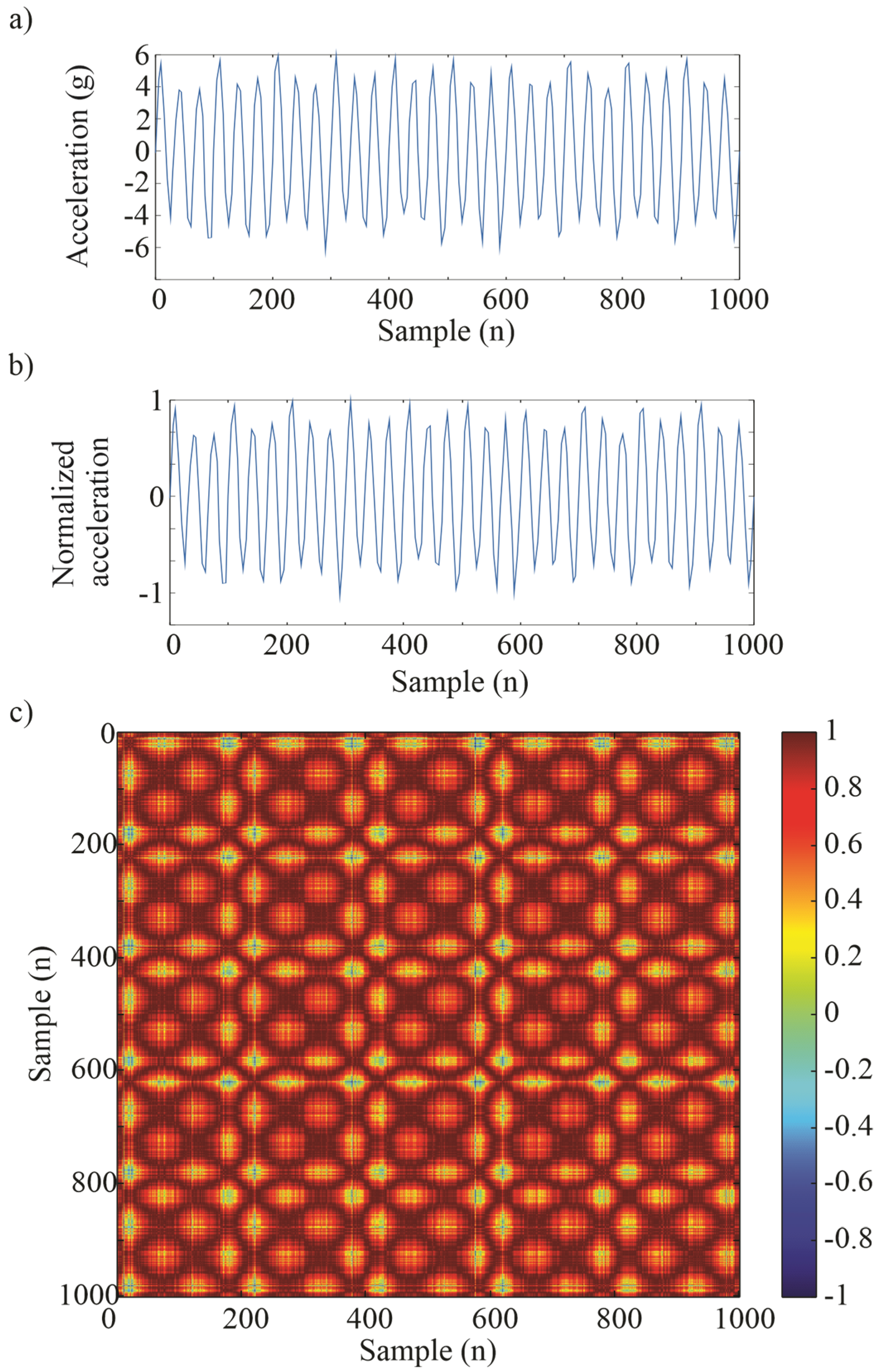
Figure 1.
GAF image representation: (a) original vibration signal, (b) normalized signal, and (c) resulting GAF image.
Figure 2.
Convolutional Neural Network.
Figure 3.
Proposed methodology.
Figure 4.
Experimental setup.
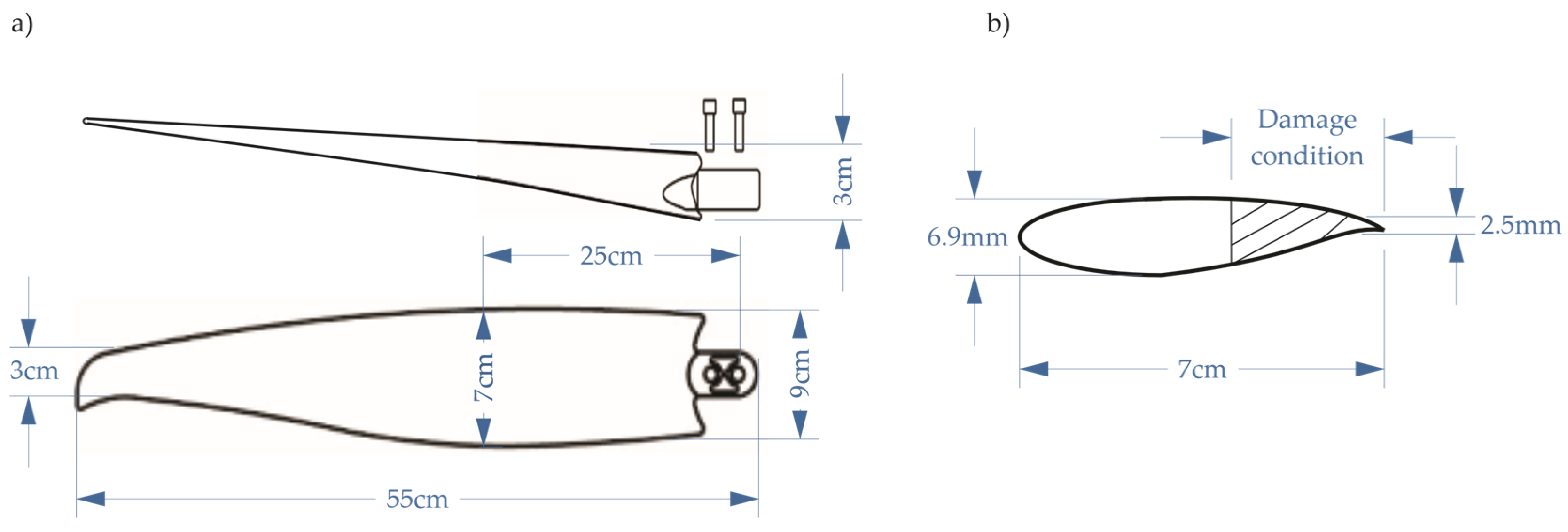
Figure 5.
Dimensioned drawing of the blade showing (a) the blade plane and (b) the cross-section of the blade at the location of the damage.
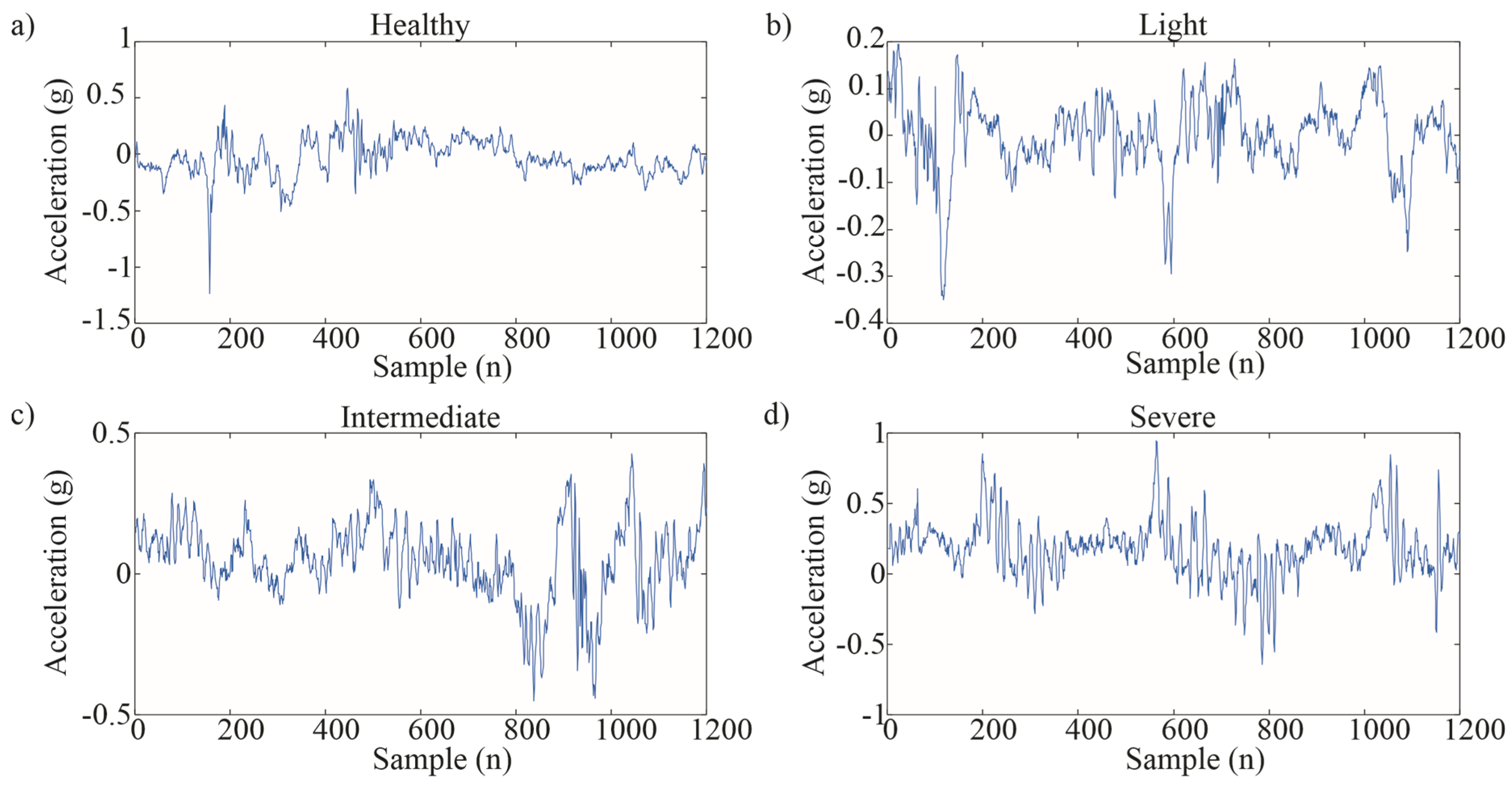
Figure 6.
Vibrations of each condition from Y-axis: (a) healthy, (b) light, (c) Intermediate, and (d) severe.
Figure 7.
Comparative boxplot.
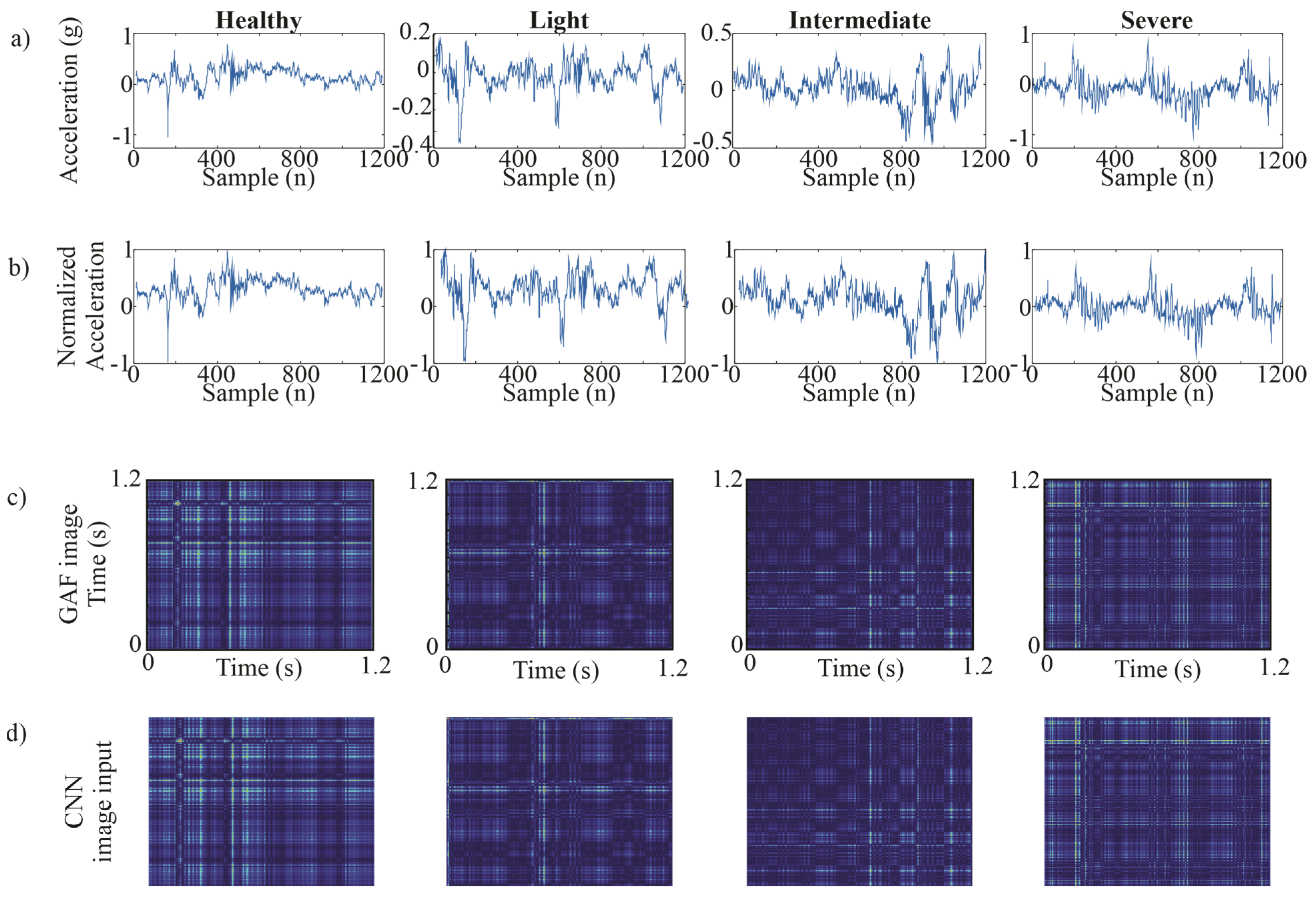
Figure 8.
X-axis GAF image process (a) vibration signal, (b) the normalized signal, (c) the GAF-generated image, and (d) image input to CNN.
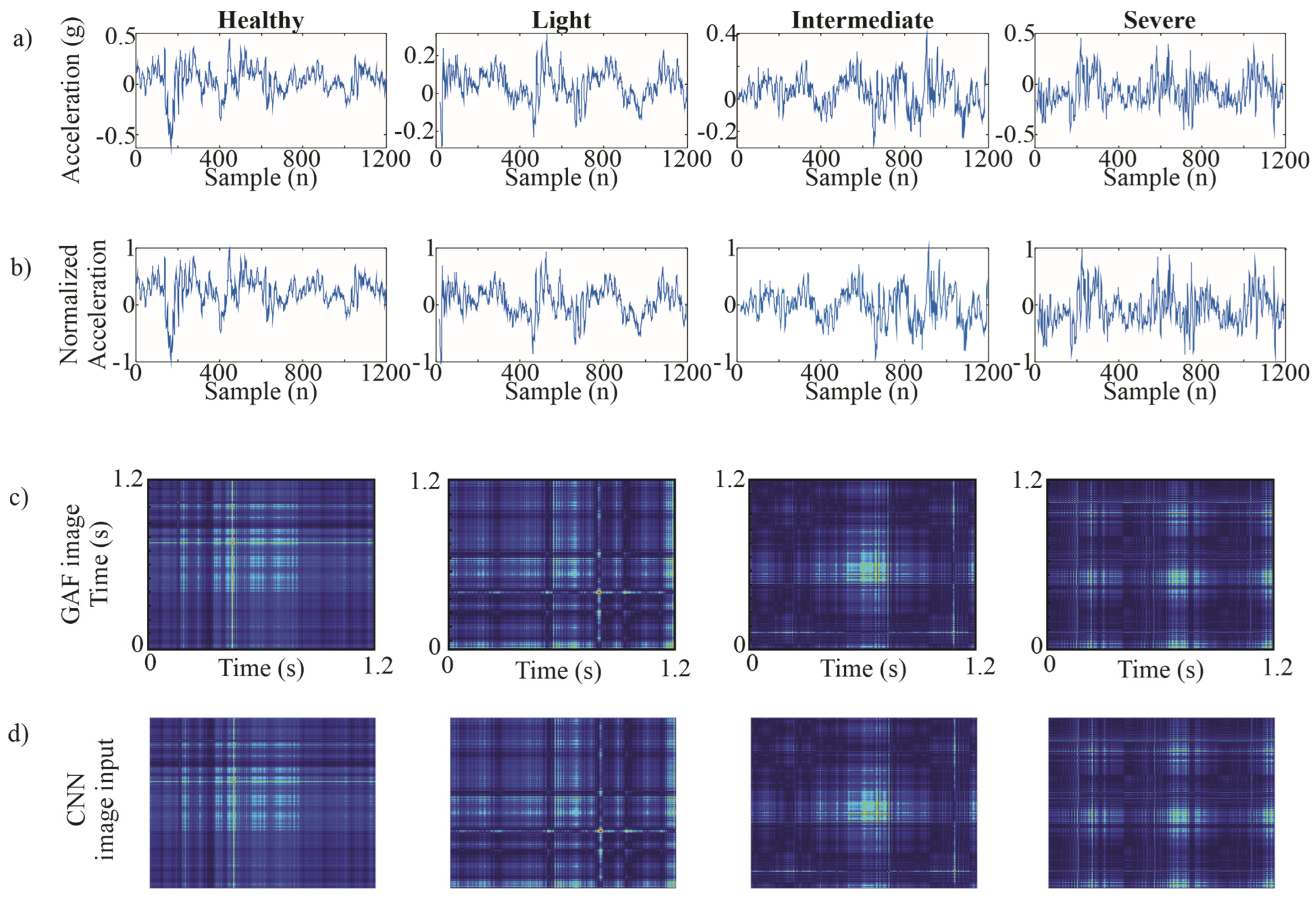
Figure 9.
Y-axis GAF image process (a) vibration signal, (b) the normalized signal, (c) the GAF-generated image, and (d) image input to CNN.
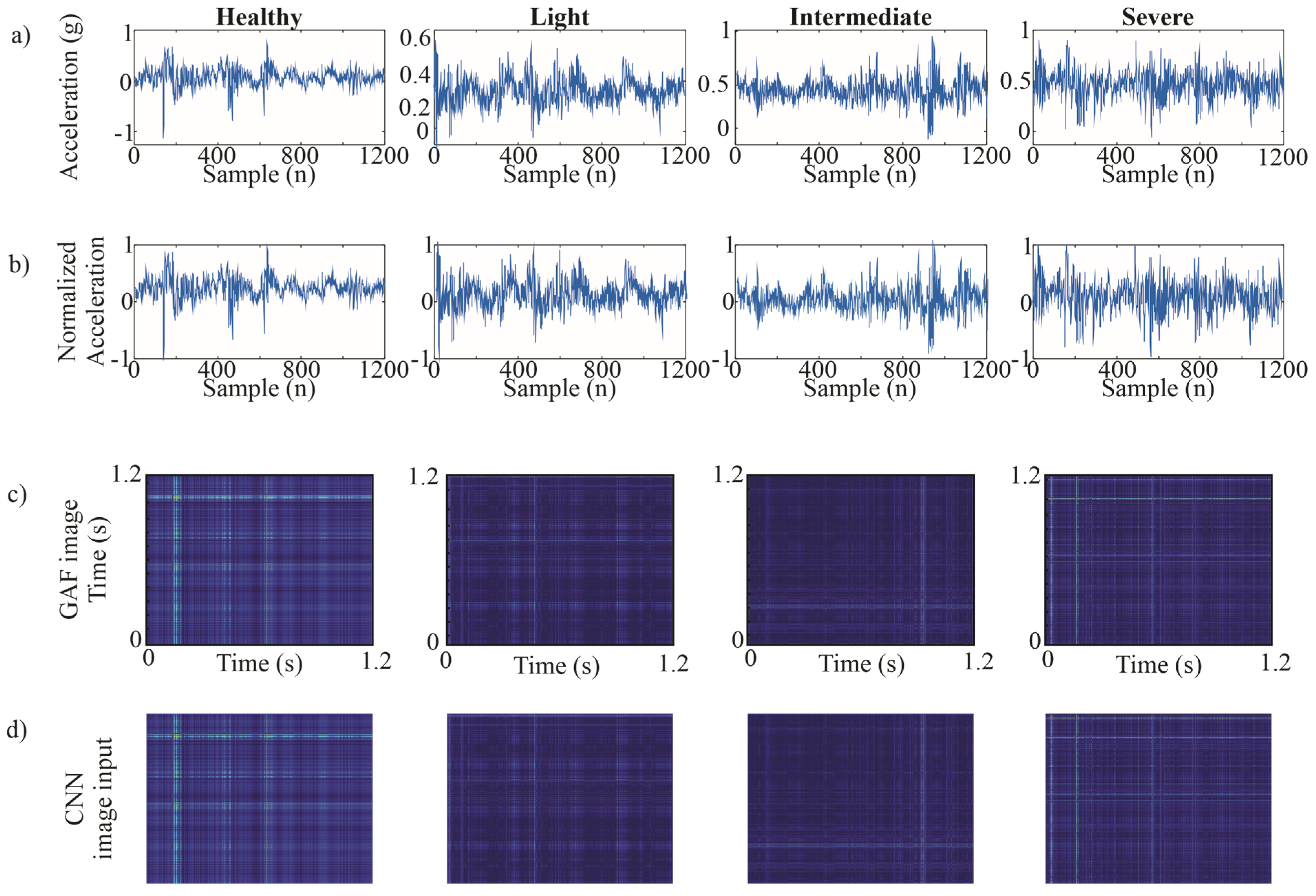
Figure 10.
Z-axis GAF image process (a) vibration signal, (b) the normalized signal, (c) the GAF-generated image, and (d) image input to CNN.
Figure 11.
Accuracy and Loss Graph Y-axis.
Figure 12.
Accuracy and Loss Graph X-axis.
Figure 13.
Accuracy and Loss Graph Z-axis.
Figure 14.
Confusion matrices by axis and speed: (a) X-3 rps, (b) X-12 rps, (c) Y-3 rps, (d) Y-12 rps, (e) Z-3 rps, (f) Z-12 rps.
Table 1.
Number of vibration signal tests from each speed.
| Damage Condition | Number of Tests from X-Axis | Number of Tests from Y-Axis | Number of Tests from Z-Axis |
|---|
| Healthy | 1000 | 1000 | 1000 |
| Light | 1000 | 1000 | 1000 |
| Intermediate | 1000 | 1000 | 1000 |
| Severe | 1000 | 1000 | 1000 |
Table 2.
Accuracy per speed.
| Speed | X-Axis Accuracy | Y-Axis Accuracy | Z-Axis Accuracy |
|---|
| 3 rps | 99.9% | 99.9% | 78% |
| 12 rps | 100% | 100% | 100% |
Table 3.
Comparison between CNN trained with raw vibration signals and CNN with GAF transformation.
| Axis | Raw Signal | With GAF |
|---|
| X | 91.50% | 98.67% |
| Y | 85.33% | 100% |
| Z | 25.83% | 33.17% |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).