Controlling Heterogeneous Multi-Agent Systems Under Uncertainty Using Fuzzy Inference and Evolutionary Search

Abstract

Real-time coordination of heterogeneous multi-agent systems in dynamic and partially observable environments poses significant challenges. To address this, we propose a framework that integrates fuzzy inference systems with real-valued genetic algorithms to optimize decision-making under strict time constraints and sensory uncertainty. We evaluate the proposed method in the RoboCup Soccer Simulation 2D League, where 22 autonomous agents coordinate through a fuzzy-evaluated action sequence search. Spatial heuristics are encoded as fuzzy rules, and optimization based on genetic algorithms refines evaluation function parameters according to performance metrics such as number of shots, goal area entries, and scoring rates. The resulting control strategy remains interpretable; spatial heat maps reveal emergent behaviors such as coordinated positioning and ridgeline passing patterns near the penalty area. The experiments against established RoboCup teams, serving as benchmarks, demonstrate the competitive performance of our trained agents while enabling analyses of evolving decision structures and agent behaviors. Our method provides a transparent and adaptable framework for controlling heterogeneous agents in uncertain real-time environments, with broad applicability to robotics, autonomous systems, and distributed control systems.

1. Introduction

The control of heterogeneous multi-agent systems (MAS) in uncertain and dynamic environments has become a central challenge in the field of artificial intelligence (AI). In such settings, agents must act autonomously, assume varying roles, and operate in real time, often under conditions of partial observability or information noise. Conventional approaches based on rule-based systems or probabilistic models frequently encounter scalability issues and lack the flexibility or interpretability required for complex cooperative behavior [1]. Recent developments in agent coordination have explored the integration of AI into IoT systems and distributed environments, emphasizing the need for interpretable and adaptive control mechanisms in real-time applications [1,2]. While deep reinforcement learning has shown promise in dynamic decision-making, it often suffers from high computational overhead and lack of transparency in reasoning [3,4]. To address these limitations, researchers have explored fuzzy inference systems (FISs) due to their ability to model expert knowledge in a linguistically transparent manner and handle uncertainty effectively [5]. However, the manual design of fuzzy rule bases and membership functions presents a significant challenge, particularly in large-scale multi-agent systems with high-dimensional state spaces. This issue has been addressed by incorporating evolutionary computation methods such as genetic algorithms (GAs) [6], which are well suited for optimizing fuzzy systems in real-time and distributed settings [7]. The combination of fuzzy inference systems and genetic algorithms has proven to be effective in various domains, such as traffic management [8] and distributed computing [7], offering an interpretable yet adaptive alternative to black box models. Recent advances have extended single-layer FIS into cascaded ANFIS structures, stacking multiple fuzzy neural modules to capture highly nonlinear relationships in real-world data [9].

Building upon these foundations, this study investigates a genetic algorithm-optimized fuzzy evaluation framework to train our own agents, which are then evaluated against heterogeneous benchmark opponents in the RoboCup Soccer Simulation 2D League. This environment simulates highly complex competitive scenarios involving 22 autonomous agents, requiring both fast decision-making and team coordination. The proposed approach constructs an evaluation function based on spatial fuzzy rules, for which their parameters are optimized using real-valued genetic algorithms under performance-based fitness criteria. The goal is to enhance real-time adaptability while preserving the interpretability of agent behavior, which is an increasingly important quality in applications that demand safety and explainability [8,10].

The contributions of this paper are threefold: (1) the development of a fuzzy inference-based evaluation function specifically designed for action decision trees in real-time multi-agent systems; (2) the implementation of a genetic algorithm to optimize fuzzy rule parameters using fitness measures derived from actual game performance; and (3) a demonstration of how this method enhances agent coordination, scoring efficiency, and interpretability within a competitive and partially observable environment.

2. Related Work

The control of heterogeneous multi-agent systems (MASs) under uncertainty and real-time constraints has been a central challenge in recent research. Luzolo et al. [1] highlighted the need for scalable agent coordination and the integration of AI models into edge-level IoT devices, emphasizing the importance of real-time response in multi-agent collaboration. Fuzzy inference systems (FISs), known for their interpretability and rule-based structure, have been applied across a wide range of decision-making contexts. For instance, Saini et al. [11] proposed a fuzzy inference system optimized by both Particle Swarm Optimization (PSO) [12] and genetic algorithms (GAs) for real-time PM10 air quality forecasting. Their work demonstrated how hybrid metaheuristics can significantly improve FIS performance for predictions that require timely responses. Similarly, De Santis et al. [13] employed a hierarchical fuzzy logic controller optimized using a genetic algorithm to manage energy flows in microgrids, highlighting the adaptability of FISs in complex and distributed systems. Furthermore, Li et al. [14] developed an adaptive real-time energy management system for hybrid electric vehicles using a neuro-fuzzy inference system, showcasing the practical effectiveness of FIS in embedded systems that require decisions to be made in real time. Tynchenko et al. [7] addressed the challenge of optimization in high-dimensional distributed systems using multi-criteria genetic algorithms, stressing the importance of maintaining interpretability and efficiency. Kalusivalingam et al. [8] also emphasized the need for interpretable reinforcement learning and optimization based on genetic algorithms in complex real-time systems. Furthermore, Chen and Heydari [10] proposed interpretable deep reinforcement learning techniques for resource allocation in system-of-systems contexts, identifying the trade-offs between transparency and learning flexibility. In contrast to black box models, the present study proposes a fuzzy inference framework with genetic algorithm optimization that enables decision transparency through interpretable evaluation surfaces $U(x,y)$. This contributes to a growing body of work focused on robust and explainable decision-making in real-time multi-agent environments.

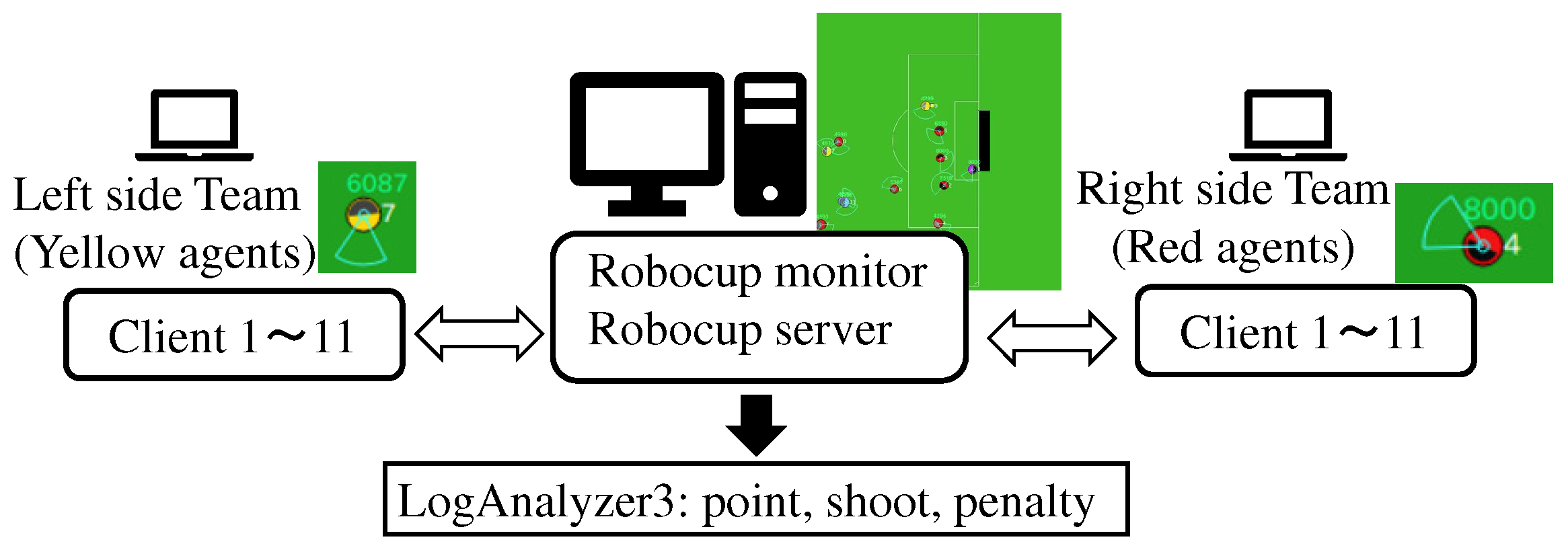
3. RoboCup 2D as an Experimental Platform

The RoboCup Soccer Simulation 2D League (RoboCup2D) provides a well-established testbed for evaluating multi-agent systems and artificial intelligence (AI) algorithms under dynamic, partially observable, and adversarial conditions. This study utilizes RoboCup2D to investigate control strategies for autonomous agents, with a specific focus on optimizing action evaluation through fuzzy inference and evolutionary computation. The RoboCup2D environment is built on a “matchup system” that enables fully autonomous soccer matches in a simulated two-dimensional space. This system comprises two principal components. The first is the soccer server, a centralized simulation engine responsible for maintaining the game state, updating player and ball positions, and enforcing rules. It functions as both the referee and game manager. The second component consists of multiple agent clients, each of which independently controls a single virtual player. These clients connect to the server via network interfaces, perceive the game state through simulated sensors, and issue commands such as movement, passing, or shooting [15]. This client server architecture enables the development and evaluation of decentralized decision-making strategies in competitive environments with limited time. Each agent operates under conditions of partial observability, delayed communication, and limited control authority, making RoboCup2D a compelling benchmark for research in distributed AI, behavioral learning, and multi-agent cooperation. A schematic overview of the RoboCup2D matchup system is presented in Figure 1.

4. Agent2D as a Benchmark in Multi-Agent Systems

Multi-agent systems (MASs) require real-time decision-making in dynamic environments where agents must act autonomously, respond to environmental changes, and coordinate with teammates. The RoboCup Soccer Simulation 2D League (RoboCup2D) provides a rich experimental platform for evaluating MAS performance under such conditions. In this study, the RoboCup2D environment is utilized to investigate learning-based optimization of behavior in autonomous agents, focusing on designing and tuning an evaluation function that governs both individual-level and team-level decision-making.

Agent2D, a widely used open-source base team in RoboCup2D, serves as the benchmark for this research. Originally derived from the championship-winning Team HELIOS of RoboCup 2010 [16,17,18], Agent2D integrates advanced tactical artificial intelligence features and forms the foundation for many competitive team implementations [19,20]. Its modularity, reproducibility, and representative performance make it suitable for evaluating improvements in action selection logic and team coordination algorithms.

4.1. Characteristics of Agent2D in Multi-Agent Contexts

Agent2D operates in a decentralized manner, with each agent executing actions based on partial observations and limited communication. Agent decisions are made autonomously within strict real-time constraints, typically within 0.1 s per decision cycle. This constraint requires lightweight and efficient reasoning mechanisms. The system includes key capabilities fundamental to MAS research: Autonomous Operation: Agents make decisions independently, without external control.

Sensor-Based Perception: Agents estimate the environment through virtual sensors (for example, vision and audio).

Reactive and Strategic Behavior: Decision-making is influenced by internal tactics, role assignments, and the evolving state of the game. Limited Inter-Agent Communication: Coordination is possible only through constrained message passing (for example, the “talk” command), reflecting communication limits found in real-world situations. Adaptability: Agent2D includes infrastructure for evaluating team formations and strategies using the Matchup System [21].

These features reflect the challenges common in general multi-agent systems: asynchronous control, uncertain state information, coordination under limited communication, and computationally bounded action selection.

4.2. Action Sequence Search Algorithm

Central to Agent2D’s decision-making architecture is the action sequence search algorithm, which governs the player’s action selection when they possess the ball. This algorithm constructs a search tree of potential actions (e.g., dribble, pass, shoot) and evaluates resulting game states using a scoring function $U(x,y)$ that reflects the positional advantage of the predicted ball location [22,23].

Given the dynamic and partially observable nature of the environment, this search process must be both efficient and robust. At each decision cycle, the agent generates action sequences, simulates outcomes over a short-term horizon, and evaluates them using $U(x,y)$. The action sequence with the highest score is selected for execution. The evaluation function, therefore, plays a critical role in shaping the agent’s offensive and cooperative behavior [24].

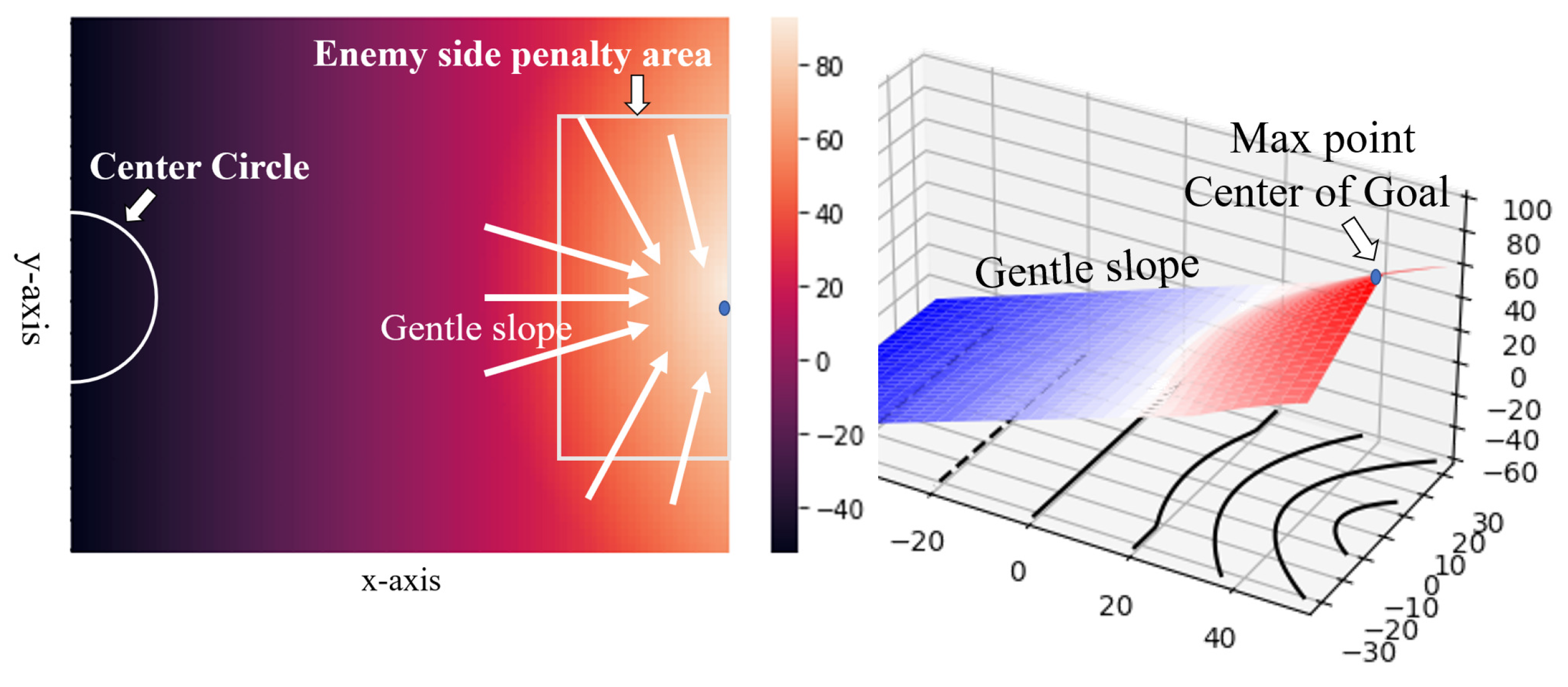
4.3. Motivation for Optimization of Evaluation Function

The default $U(x,y)$ used in Agent2D is a hand-crafted heuristic function that favors movement toward the center of the goal, as shown in Figure 2. While this encourages direct attacks, it often leads to repetitive and suboptimal behaviors, particularly in complex situations requiring strategic passes or coordinated plays. The simplicity of the slope-based function yields smooth and undifferentiated action preferences, thereby limiting the potential for emergent cooperative behavior.

To enhance decision-making, this study proposes an improved evaluation function utilizing fuzzy inference systems to express positional heuristics and genetic algorithms for automatically optimizing parameters. The fuzzy rules encode human-like decision reasoning (for example, prefer near-goal corners with fewer defenders). At the same time, the genetic algorithm tunes the rule weights and output grades based on game performance metrics.

• The evaluation focuses on task-specific indicators, including the following:

• Number of shots taken;
• Frequency of ball penetration into the penalty area;
• Scoring success rate.

These metrics are chosen for their relevance to offensive effectiveness in multi-agent coordination. The learning system is trained through repeated simulations, enabling it to adapt to emergent team behavior and opponent dynamics.

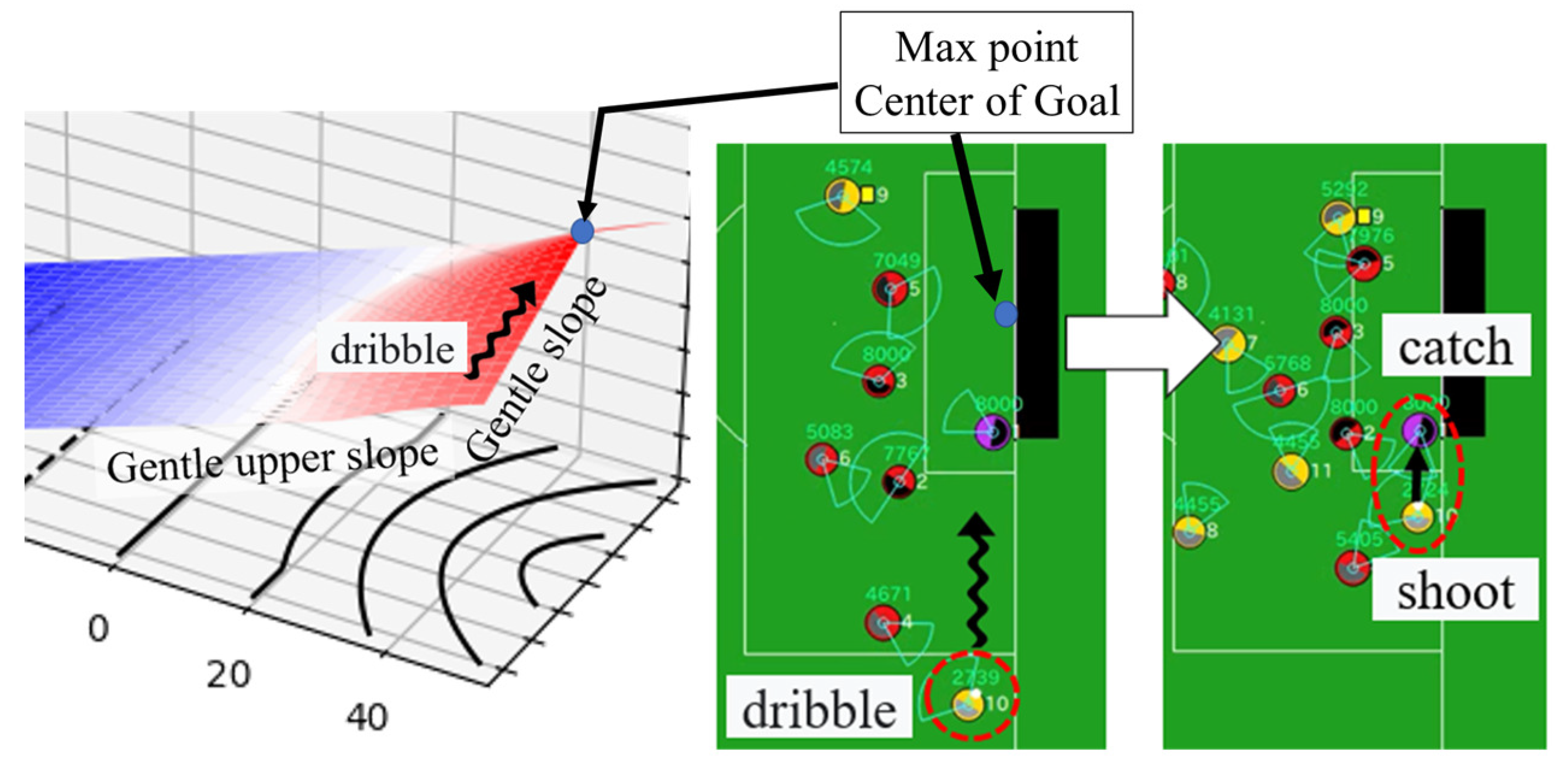
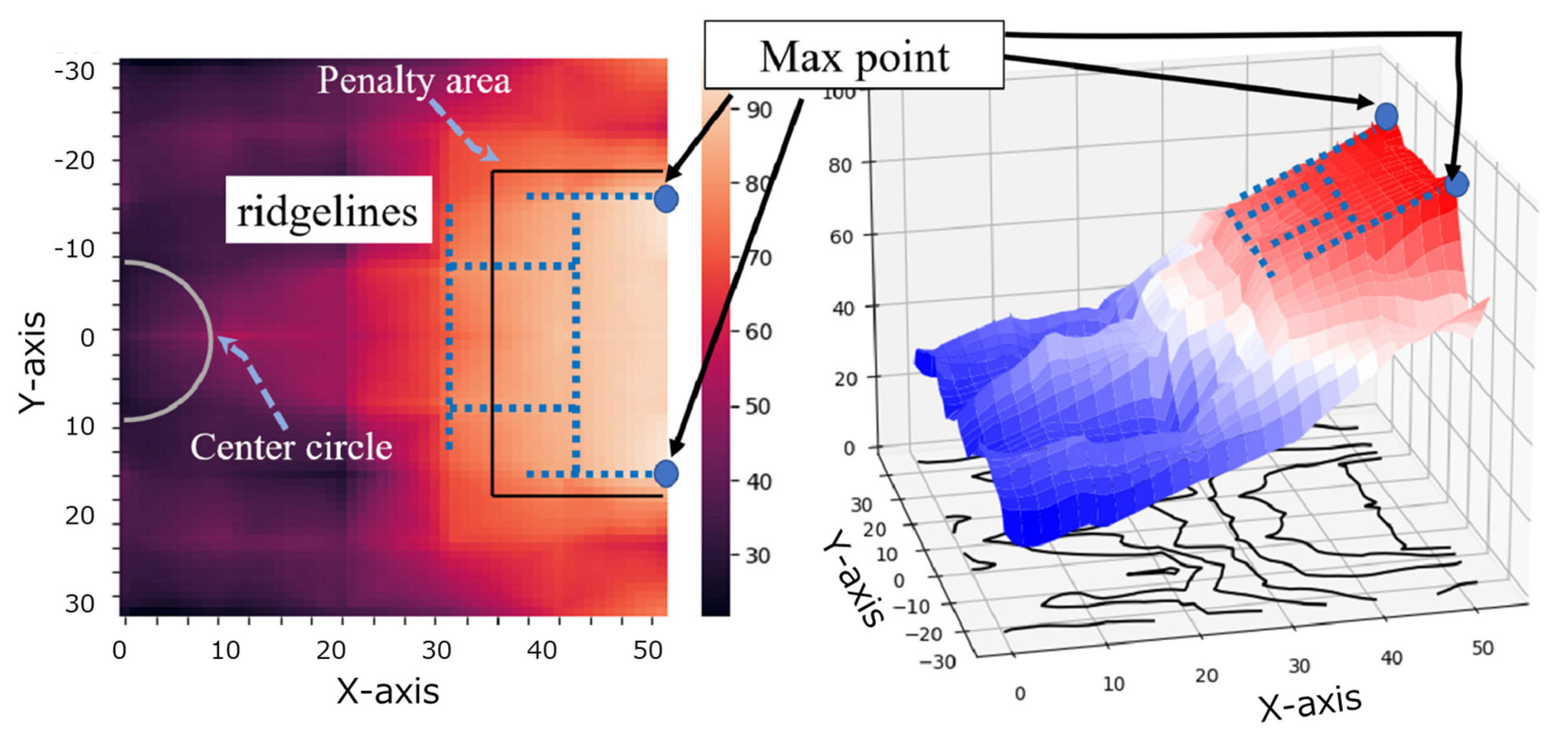
4.4. Illustration of the Default Evaluation Function

Figure 2 shows a heat map of the default $U(x,y)$ used in Agent2D. The brightness represents higher evaluation scores, which increase near the center of the opponent’s goal. As shown in the example behavior (Figure 3), agents often attempt direct dribbling toward the center without considering side attacks or pass options, which the goalkeeper can easily block [25]. This reinforces the need for an evaluation function that is more expressive and sensitive to context.

$$U(x,y)=x+max\left\{0,40-\sqrt{{(x-x_{\mathrm{goal}})}^2+{(y-y_{\mathrm{goal}})}^2}\right\}$$

(1)

This formulation encourages agents to carry the ball toward the center of the goal, which may be effective in isolated scenarios but is insufficient for coordinated team strategies. The proposed enhancements aim to overcome this limitation by enabling the learning of diverse and situation-aware action evaluations that reflect the multi-agent nature of the game.

5. Methodology

This section outlines the proposed methodology for optimizing an evaluation function in a multi-agent system using fuzzy inference and genetic algorithms (GAs). The objective is to improve real-time action selection in Agent2D soccer agents by enhancing the evaluation function $U(x,y)$ within the action sequence search algorithm. The genetic algorithm configuration used for optimizing the fuzzy rule parameters is summarized in

Table 1. Genetic algorithm setup.

Parameter	Value/Description
Generations	3600
Population size	30
Gene structure	60-dimensional real vector: ${\omega }_k^{*}$, $r_k^{*}$ for $k=1\dots 30$
Selection method	Tournament selection (size = 4)
Crossover method	BLX-$\alpha$ crossover ($\alpha =0.2$)
Crossover probability	0.5
Mutation method	Gaussian mutation (mean = 0; std. dev = 10)
Mutation probability	0.2
Fitness evaluation	Average over 3 games (3000 cycles each)

. These settings were determined empirically to strike a balance between computational cost and convergence stability.

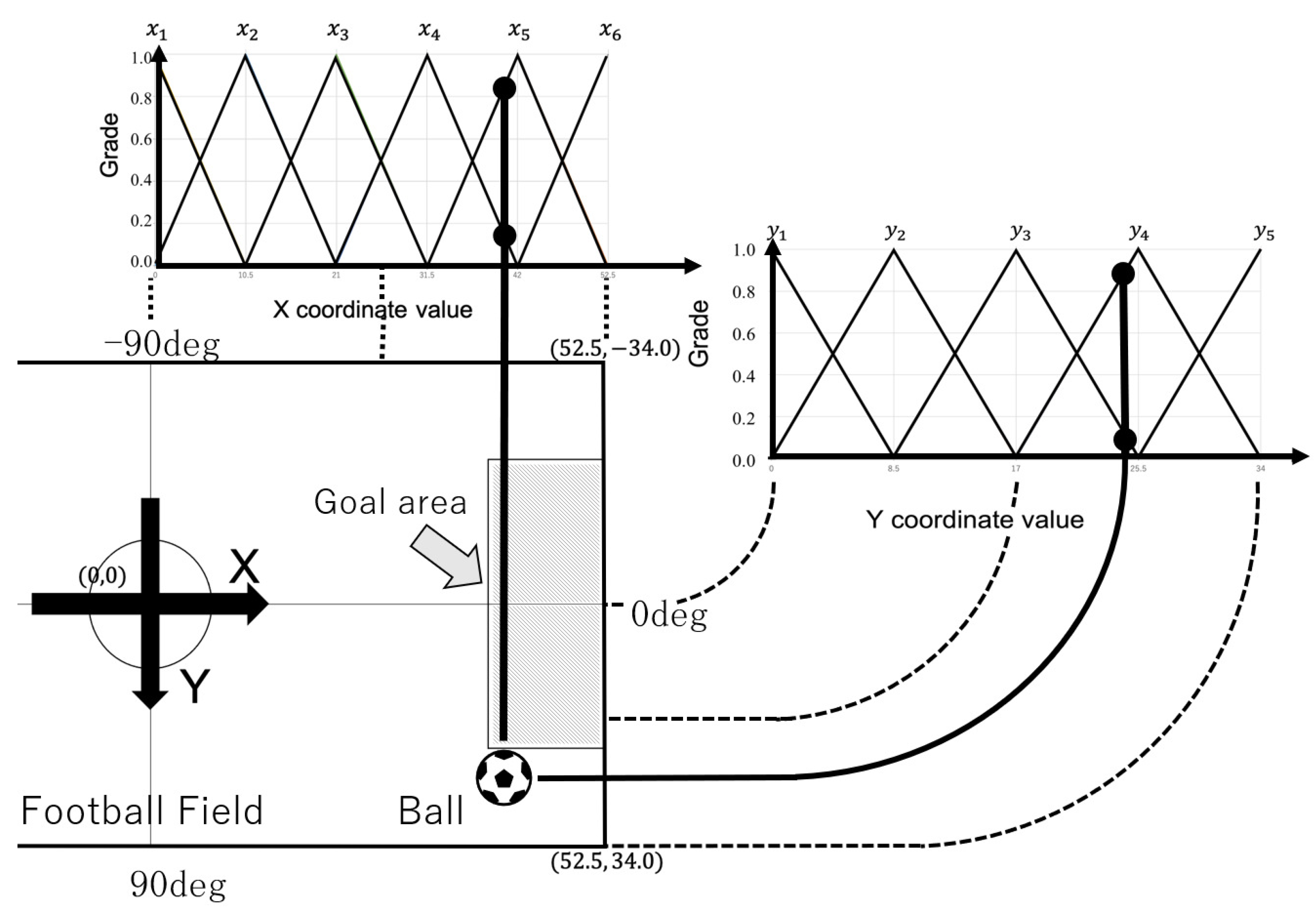
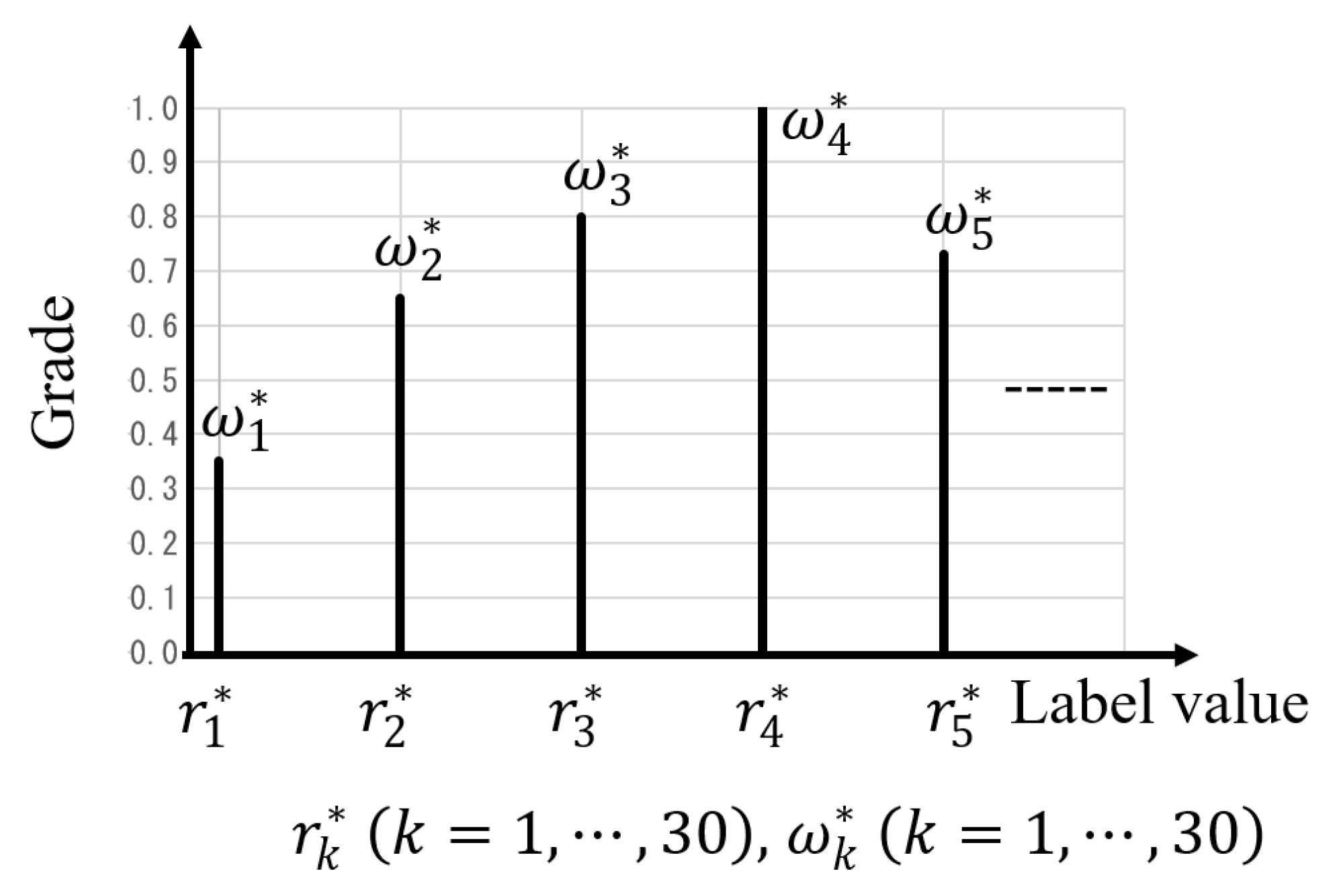
5.1. Fuzzy Inference-Based Evaluation Function

To support decision-making under uncertainty, we employ a fuzzy inference system that defines the evaluation function, $U(x,y)$, which assesses the desirability of placing the ball at position (x, y) on the field (Figure 4 and Figure 5). This system encodes positional heuristics through a set of fuzzy rules based on the ball’s spatial coordinates [26].

Let v denote a generic spatial coordinate ($v=x$ or $v=y$). We employ a family of N triangular membership functions ${\left\{{\mu }_i\left(v\right)\right\}}_{i=1}^N$, each parameterized by the triple $(a_i,b_i,c_i)$, where $a_i$ and $c_i$ are the “feet” and $b_i$ the “peak” of the ith triangle:

$${\mu }_i\left(v\right)=\left\{\begin{array}{cc}0\hfill & (v\le a_i)\hfill \\ {\displaystyle \frac{v-a_i}{b_i-a_i}}\hfill & (a_i<v\le b_i)\hfill \\ {\displaystyle \frac{c_i-v}{c_i-b_i}}\hfill & (b_i<v<c_i)\hfill \\ 0\hfill & (v\ge c_i)\hfill \end{array}\right.$$

For the x-axis we set $N=6$ (functions ${\mu }_{x,1}\dots {\mu }_{x,6}$), and for the y-axis, $N=5$ (functions ${\mu }_{y,1}\dots {\mu }_{y,5}$). The specific $(a_i,b_i,c_i)$ values are depicted in Figure 5.

In this study, the evaluate function $U(x,y)$ represents the desirability of placing the ball at position $(x,y)$ on the field. Rather than directly determining the agent’s action, this function serves as a heuristic guide for a search algorithm that selects the actual ball movement. The evaluation function is constructed using a simplified fuzzy inference system consisting of $k=1\dots 30$ rules.

The fuzzy rule base includes 30 rules of the following form:

$$R_k:\mathrm{If}\left(x\mathrm{is}{x}_k\right)\mathrm{and}\left(y\mathrm{is}{y}_j\right)\mathrm{Then}\left(R\mathrm{is}{r}_k^{*}\right)\mathrm{with}{\omega }_k^{*}(k=1\dots 30)$$

(2)

Each ${\mu }_k$ is defined as a product of the membership degrees along the x and y axes, computed via membership functions ${\mu }_x$ and ${\mu }_y$, respectively. The firing strength ${\mu }_k$ of the k-th rule is calculated as follows:

$${\mu }_k(x,y)=min(x_k\left(x\right),y_k\left(y\right))$$

(3)

As illustrated in Figure 6, the singleton output value ${\mu }_k$ is clipped by the firing strength ${\omega }_k^{*}$, which serves as the grade (or importance weight) assigned to the rule’s output. The inferred result r is then computed through a weighted average over all rules:

$$r={\displaystyle \frac{{\sum }_{k=1}^n\left(min({\omega }_k^{*},{\mu }_k(x,y))\right)r_k^{*}}{{\sum }_{k=1}^n\left({\mu }_k(x,y)\right)}}$$

(4)

This simplified inference mechanism avoids the need for fuzzy set aggregation and continuous defuzzification, providing a computationally efficient approach suited for real-time decision-making in dynamic environments.

The final evaluation value is given by the following:

$$U(x,y)=x+r$$

(5)

Figure 4, Figure 5 and Figure 6 illustrate the field coordinate system, membership function distribution, and singleton consequent structure, respectively. This fuzzy evaluation is designed to run within a 1 ms constraint per decision cycle. A simplified inference approach, based on Maeda et al. [27], is used for efficient computation.

To apply this evaluation in actual decision making, the fuzzy inference output is embedded into an action sequence search framework that determines the agent’s next move in real time. As outlined in Algorithm 1, the action sequence search is evaluated using the fuzzy inference-based utility function $U(x,y)$. The optimization of fuzzy parameters is then performed using the genetic algorithm, as shown in Algorithm 2.

Algorithm 1 Fuzzy-Evaluated Action Sequence Search
Require:  current state $s_0$, depth D Ensure: best action sequence ${\pi }^{*}$
1: ${\pi }^{*}\leftarrow \left[\right]$, $V^{*}\leftarrow -\infty$   2: for all action sequences $\pi$ of length $\le D$ do   3:     $V\leftarrow 0$   4:     $s\leftarrow s_0$   5:     for a in $\pi$ do
6:         $s\leftarrow$ simulate_action($s,a$)	▹ predict next ball pos.$(x,y)$
7:         $V+=U(x,y)$	▹ via fuzzy inference (Equation (4))
8:     end for   9:     if $V>V^{*}$ then ${\pi }^{*}\leftarrow \pi ,V^{*}\leftarrow V$ 10:     end if 11: end for 12: return ${\pi }^{*}$

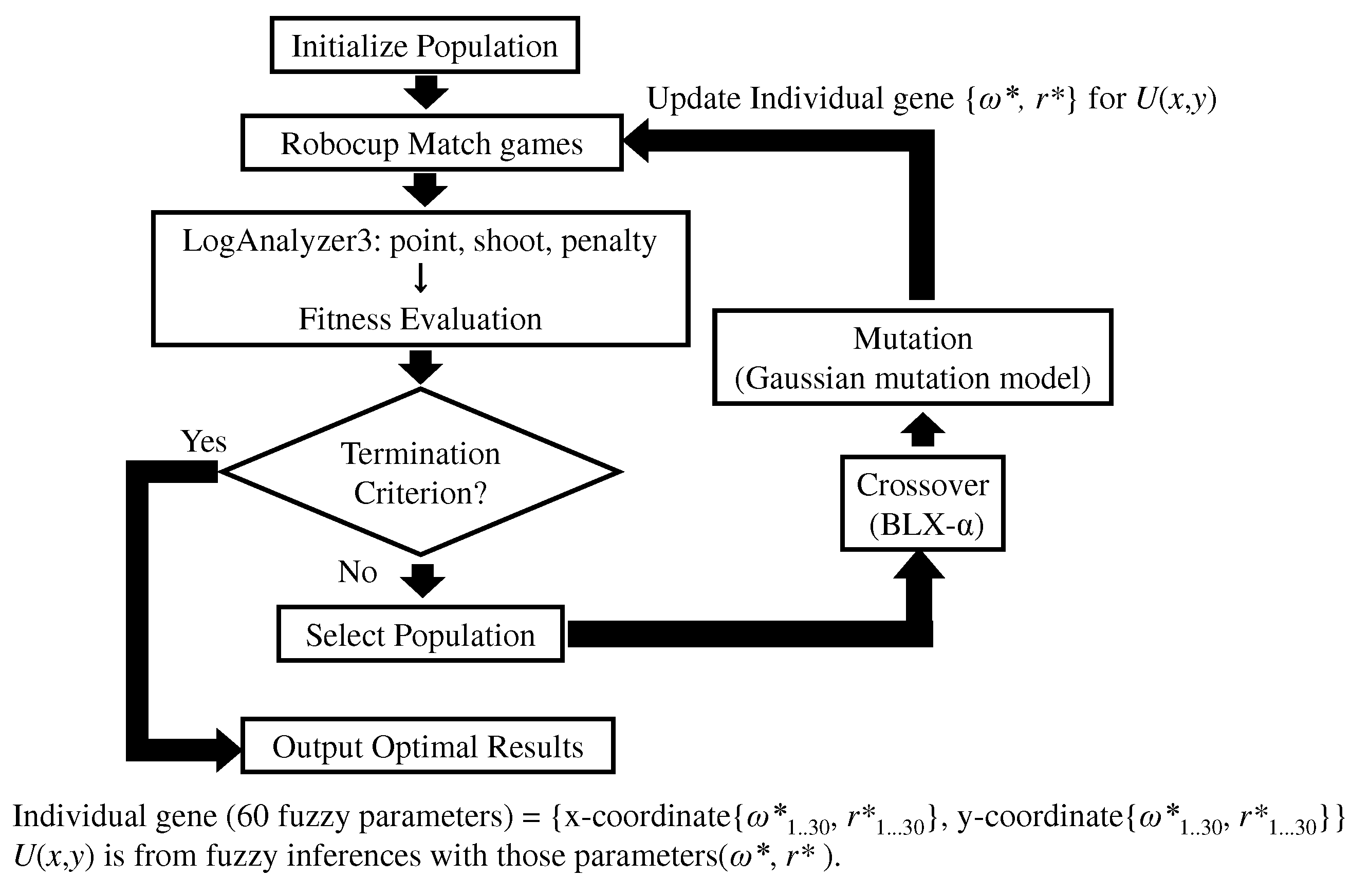
5.2. Genetic Algorithm for Fuzzy Parameter Optimization

A real-valued genetic algorithm is utilized to optimize the fuzzy parameters ${\omega }_k^{*}$ and $r_k^{*}$ for each rule. The fitness of an individual is evaluated using match performance statistics extracted via LogAnalyzer3, which aggregates data from three simulated games.

The evaluation metrics are as follows:

• Number of goals scored (point);
• Number of shots taken (shoot);
• Number of penalty area penetrations (penalty).

The fitness function is defined as follows:

$$fitness=2.0\times point+1.0\times shoot+0.3\times penalty$$

(6)

The genetic algorithm setup is shown in Table 1.

Figure 7 illustrates the training process using genetic algorithms. The optimization aims to enhance $U(x,y)$, enabling Agent2D to exhibit improved decision-making in dynamic game environments. The training of our agent’s utility function $U(x,y)$ was conducted separately against each opponent team to maximize adaptation to their distinct behaviors. This type of learning, specific to opponents, was adopted to maximize adaptation to distinct team behaviors and formation strategies. However, this approach implies that the learned utility function is not guaranteed to generalize across different opponents. Future extensions may involve training with a diverse group of teams or leveraging meta-learning techniques for generalization across different opponents.

Algorithm 2 Genetic Algorithm-Based Fuzzy Parameter Optimization

1: Initialize population P of size N with $\{{\omega }_k^{*},r_k^{*}\}$   2: for $g=1$ to G do                                                             ▹$G=3600$ generations   3:     for all $ind\in P$ do   4:         set_fuzzy_params(ind)   5:         play 3 matches, within each use Algorithm 1   6:         compute_fitness(ind)$\leftarrow 2\mathit{point}+1\mathit{shoot}+0.3\mathit{penalty}$   7:     end for   8:     $P\leftarrow$ select_and_reproduce(P) ▹ tournament, BLX-$\alpha$ crossover, Gaussian mutation   9: end for 10: return best individual in P

5.3. Experimental Setup

The experiments were conducted in the RoboCup2D simulation environment using two benchmark opponent teams: Jyo_sen and Persepolis. Each game consisted of 3000 cycles, representing one half of a match, and the experimental setting included a specialized free kick mode, in which 15 free kicks were randomly triggered per match [28]. These conditions ensured consistent opportunities to assess and address offensive behaviors.

The learning process involved 160 generations of a genetic algorithm, with a population of 30 individuals. Each generation performed evaluations over 3 games per individual, resulting in a total of 90 games per generation. The final model was evaluated based on performance averaged over the last 100 games. Jyo_sen is a team composed of programming school participants from Akihabara, with demonstrated performance at a mid-level in RoboCup2021, ranking ninth out of sixteen. Persepolis, formerly known as Razi, is an Iranian team that placed 12th at the same competition, having achieved notable success in prior years [29,30,31].

To evaluate the learning capacity and adaptability of our proposed system under varying levels of strategic complexity, we selected three benchmark opponents: Agent2D, Persepolis, and jyo_sen. These teams were selected to represent a range of tactical difficulties within the RoboCup Soccer Simulation 2D League. Agent2D, a widely used open source base team derived from the championship winning HELIOS team, provides a stable and reproducible baseline. Its action selection is governed by simple hand-coded heuristics, and it lacks strategic diversity or dynamic adaptation. As such, it offers a relatively low complexity environment where learning-based systems can easily outperform static behavior baselines. Persepolis, formerly known as Razi, represents a moderate challenge. While it demonstrates coordinated offensive and defensive patterns and exhibits a higher level of tactical sophistication than Agent2D, its strategies tend to follow identifiable patterns. Once its play style is recognized, it becomes more predictable and vulnerable to counter strategies, making it a good test bed for evaluating adaptability and pattern exploitation. jyo_sen, developed by a Japanese programming school team, is significantly more challenging. It employs well-structured formations and a strong defensive architecture, suggesting a higher level of programming effort and tactical depth. In our experiments, the learning algorithm showed clear signs of stagnation against jyo_sen, implying that its robust, modular decision-making system is difficult to surpass using the current fuzzy rule framework. These distinctions justify their selection as targets for evaluation. Agent2D serves as a stable and easily learnable baseline, Persepolis offers a tactically structured but exploitable opponent, and jyo_sen acts as a stress test for the generalization capacity of the learned evaluation function under competitive and resilient conditions.

6. Results and Discussion

The proposed method, which trains our agent’s fuzzy evaluation function using genetic algorithms, showed significant performance improvements when evaluated against the baseline Agent2D, as well as the established benchmark teams Jyo_sen and Persepolis.

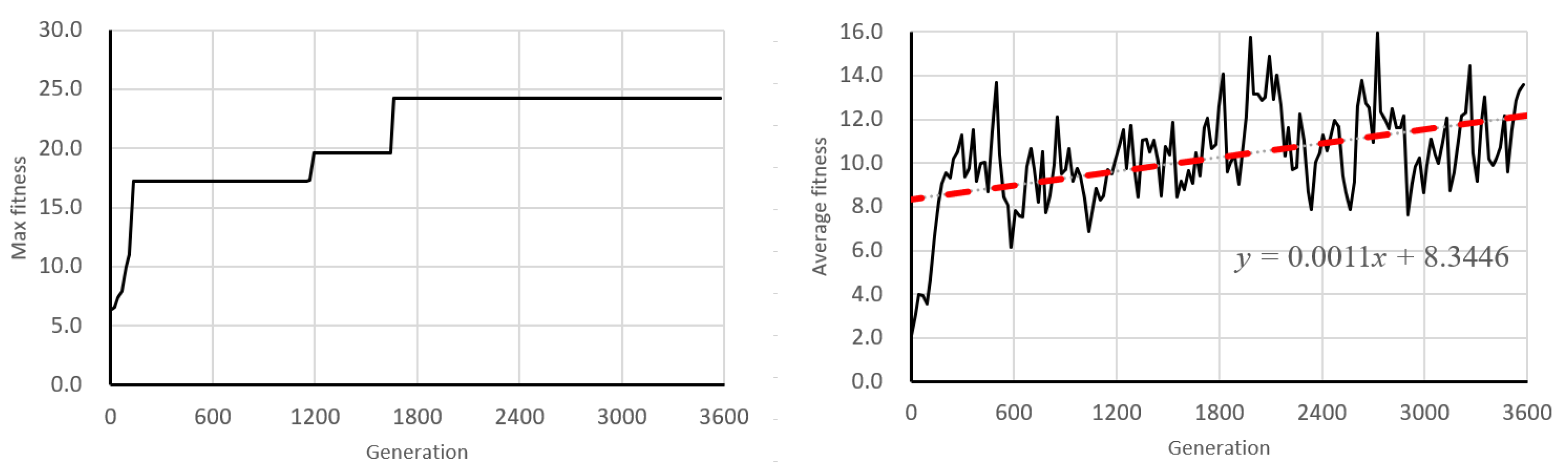
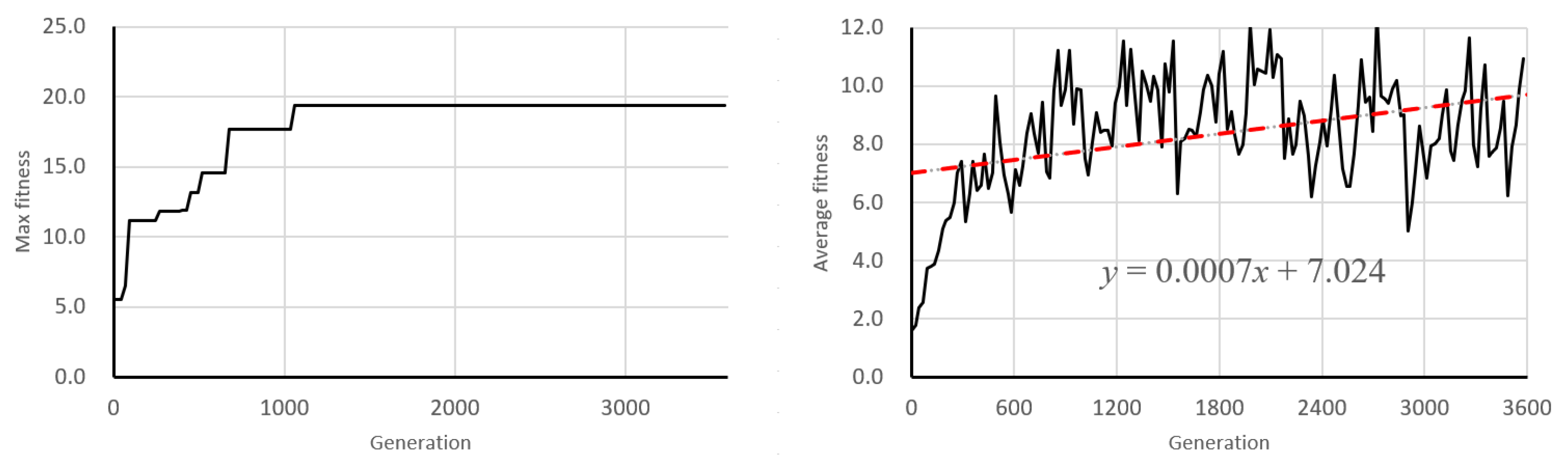
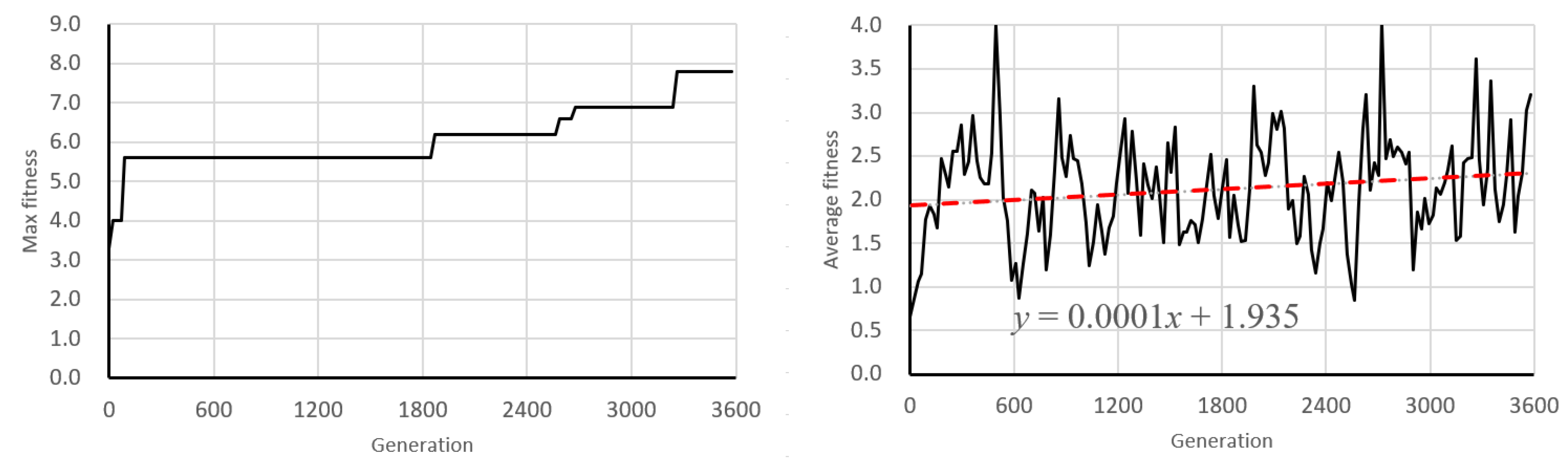
6.1. Learning Behavior of Genetic Algorithm

The evolution of fitness across generations is visualized in Figure 8, Figure 9 and Figure 10. The results indicate progressive improvement for Agent2D and Persepolis, with both mean and maximum fitness values increasing steadily. In contrast, fitness values for Jyo_sen showed more fluctuation, suggesting the presence of untuned parameters or unmodeled complexities. Each figure corresponds to one of the target teams: Figure 8 for Agent2D, Figure 9 for Persepolis, and Figure 10 for Jyo_sen. In each figure, the left curve represents the maximum fitness value observed in a generation, while the right curve shows the average fitness value. These dual axes were adopted to better visualize the dynamic range of both metrics over generations, especially given their differing scales. Curves and labeled legends have been added to make the correspondence clear: average fitness and maximum fitness. All values are derived from matches against the designated target team, and the performance curves reflect how well the proposed method adapts to each specific opponent over time. To enhance readability, we have improved the visual resolution of these plots and clarified the axis annotations and legends accordingly. In addition, a linear approximation (trend line) from generation 600 to 3600 is included in each figure. Although the slope is modest, it consistently shows a gradual upward trend. This suggests that the genetic algorithm (GA) is functioning as intended. Furthermore, the consistent increase in maximum fitness values within the population also supports the interpretation that the agent team is still improving its performance over time.

The final evaluation over 100 matches at 3600 generations is summarized in

Table 2. Average results of 100 evaluation matches of Agent2D against Agent2D, Persepolis, and Jyo_sen. Metrics include goals, shots, and penalty area (PA) entries.

Agent2D	Goals Scored	Shot Attempts	Penalty Area Entries
Agent2D	$1.64\pm 1.26$	$4.16\pm 1.80$	$9.90\pm 2.35$
Persepolis	$0.63\pm 0.82$	$1.31\pm 1.16$	$3.82\pm 1.73$
Jyo_sen	$0.33\pm 0.60$	$1.03\pm 1.15$	$2.99\pm 1.98$

and

Table 3. Average results of 100 evaluation matches of proposed method against Agent2D, Persepolis, and Jyo_sen. Metrics include goals, shots, and penalty area (PA) entries.

Proposed Method	Goals Scored	Shot Attempts	Penalty Area Entries
Agent2D	$2.10\pm 1.36$	$3.77\pm 1.99$	$10.91\pm 2.71$
Persepolis	$0.69\pm 0.71$	$1.31\pm 1.23$	$4.78\pm 2.22$
Jyo_sen	$0.31\pm 0.52$	$0.67\pm 0.89$	$2.51\pm 1.94$

. The proposed method outperformed Agent2D across several metrics and achieved goal-scoring and attacking behavior on par with competitive RoboCup teams. The results presented in Table 2 and Table 3 provide a nuanced view of the performance comparison between our proposed method and the baseline strategy, Agent2D. The performance varied significantly depending on the opponent team. Against Agent2D and Persepolis, the proposed method generally shows a consistent advantage over the baseline. Our approach resulted in clear improvements in key offensive metrics, such as scoring and attacks into the penalty area, against both opponents. This suggests that the proposed method is effective against teams with less complex tactical patterns. However, the performance against Jyo_sen presents a different outcome. In this challenging scenario, the proposed method’s performance was consistently lower than that of the baseline across all evaluation metrics. This indicates that while our method is effective in a general context, it struggles to overcome the sophisticated and robust defensive strategies employed by a top-tier team like Jyo_sen. The current fuzzy rule framework appears to be insufficient to generate actions complex enough to surpass such an advanced modular decision-making system. In conclusion, the proposed method’s effectiveness is contingent on the opponent’s strategy, with further research needed to improve its robustness against high-tier teams.

Beyond this performance analysis, it is also important to examine the qualitative changes in the agent’s behavior. The results confirm that the evolved evaluation function $U(x,y)$ mitigates the side-attack bias present in standard Agent2D by forming ridgeline strategies and context-aware passing behavior. These improvements are achieved using a compact rule-based fuzzy inference system, optimized through GAs to adjust both the output grade value $r_k^{*}$ and rule weight ${\omega }_k^{*}$. Additional plots (Figure 11, Figure 12 and Figure 13) depict the breakdown of scoring performance across generations, offering insight into the GA’s convergence behavior. These findings suggest potential future enhancements through expanded input dimensions or adaptive fuzzy systems. Overall, the methodology demonstrates the feasibility of interpretable, learnable evaluation functions for real-time control in multi-agent environments.

6.2. Discussion of Learning Dynamics and Convergence Trends

To further interpret the impact of genetic algorithm (GA) optimization, a focused analysis was conducted on three specific generation ranges:

• 100–130 generations (early training phase);
• 2000–2030 generations (middle-to-late phase);
• 3570–3600 generations (final convergence phase).

These ranges were selected to examine both the evolution of agent behavior over time and the degree of convergence in performance metrics. The key indicators examined are as follows:

• Goals Scored (Points)—indicating final task success;
• Shoot Attempts (Time)—reflecting offensive activity and aggressiveness;
• Penalty Area Entries (Time)—representing spatial penetration and strategic advancement.

Figure 8, Figure 9 and Figure 10 depict the overall fitness evolution across generations when evaluated against Agent2D, Persepolis, and Jyo_sen, respectively. These curves illustrate the comparison between the proposed method and established benchmarks in terms of cumulative performance. However, due to their aggregate nature, these plots alone may obscure the finer details of how and when meaningful improvements occurred during the genetic optimization process. These fitness trends also indirectly reflect the relative performance of the proposed method against each opponent. Against Agent2D and Persepolis, both average and maximum fitness values steadily increase, indicating that the genetic algorithm successfully adapted to their strategies. In contrast, learning progress against Jyo_sen was less consistent, with greater fluctuations and a lower final fitness, suggesting that Jyo_sen presents a stronger defensive structure and more complex behavior patterns. This disparity highlights the system’s ability to adapt well to mid-tier teams while still struggling against more sophisticated opponents.

Figure 11, Figure 12 and Figure 13 provide additional clarity on how agent performance evolved across the selected generational intervals. Statistical comparisons between these periods reveal important dynamics: Significant differences (p < 0.05) between early and middle or late phases suggest effective optimization and progress in learning. Conversely, a lack of significance (n.s.) between the middle and final phases indicates convergence or stagnation. Notably, while Agent2D and Persepolis showed meaningful improvements in early phases, performance gains flattened by the end, indicating that the GA had reached a local optimum. Against Jyo_sen, no significant changes were observed across any interval, implying that the evolutionary search failed to escape local optima or lacked sufficient discriminatory power in the fuzzy evaluation function. This target-specific divergence highlights both the robustness of Jyo_sen and the need for enhanced representations or input features in future work.

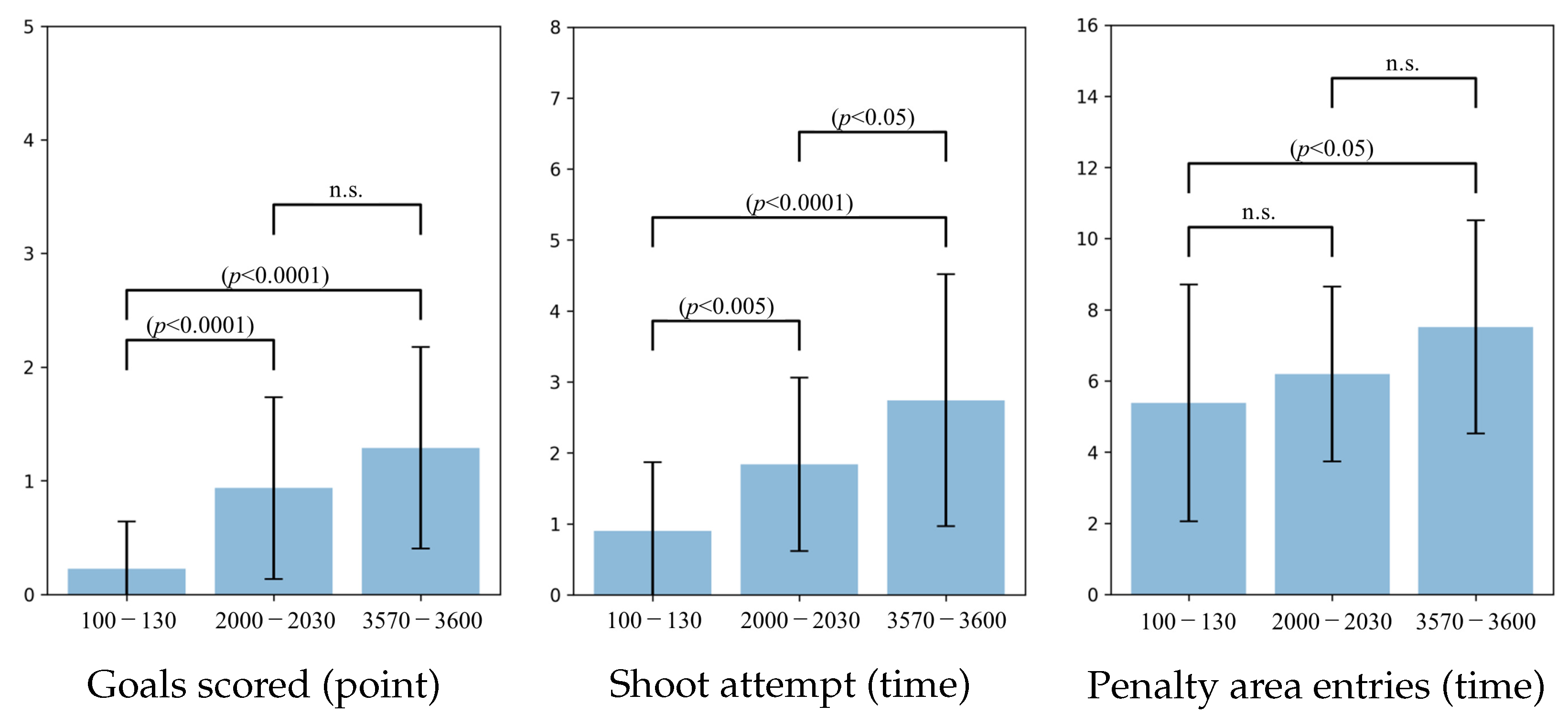
6.3. Agent2D

In the case of Agent2D, the number of shoot attempts increased significantly between the early and later phases. This trend highlights the learnability of aggressive behaviors such as shooting frequency. However, no statistically significant changes were observed in the number of goals scored or penalty area entries between the latter two ranges (2000–2030 vs. 3570–3600 generations). This suggests that GA optimization reached a plateau in improving deeper strategic coordination or finishing efficiency, indicating convergence. See Figure 11.

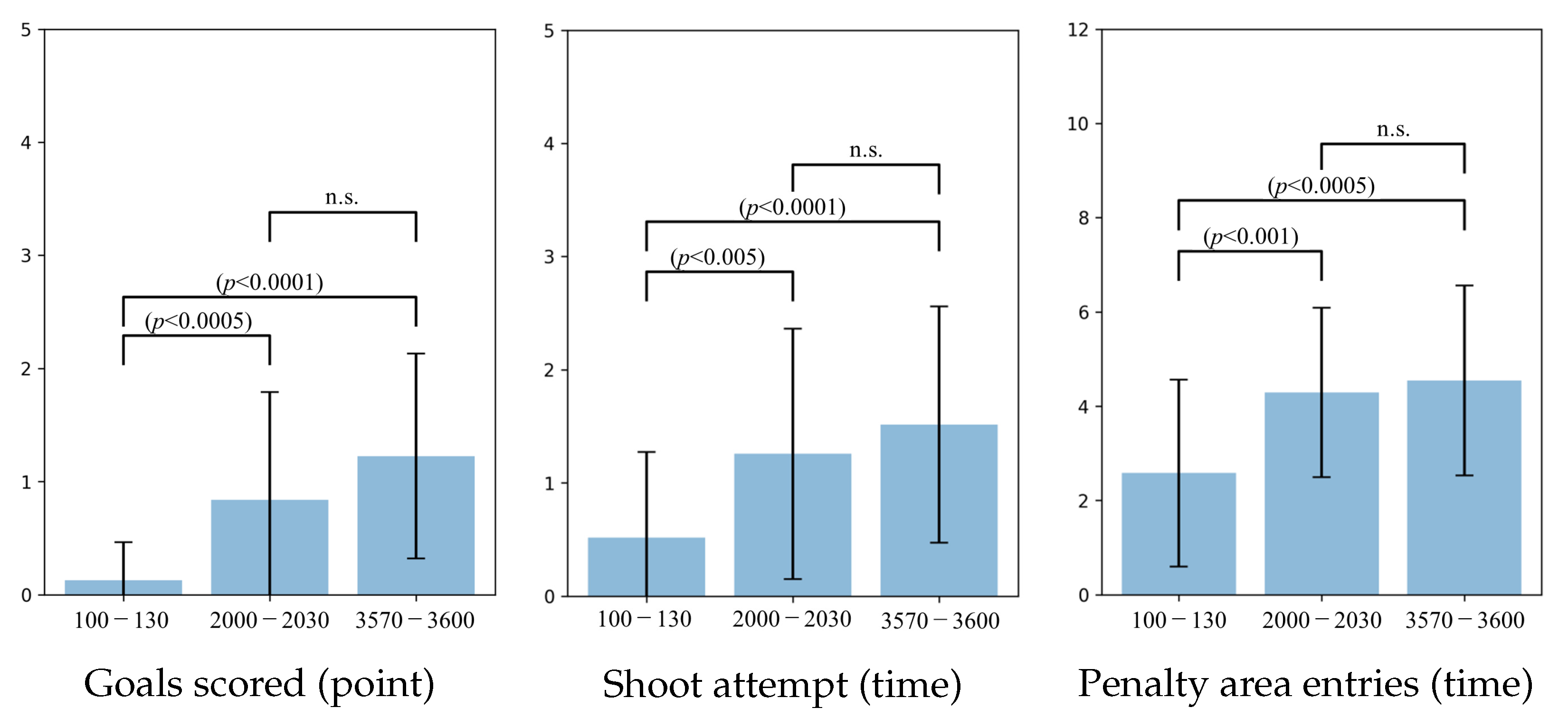
6.4. Persepolis

For Persepolis, the GA demonstrated strong learning behavior. Significant improvements were observed across all three generation ranges for all metrics, including goals scored. The continuous upward trend indicates that the GA was effective in both exploration and exploitation phases. Moreover, the similarity between performance in the 2000–2030 and 3570–3600 ranges suggests that the algorithm had successfully converged to a near-optimal fuzzy parameter set. Refer to Figure 12.

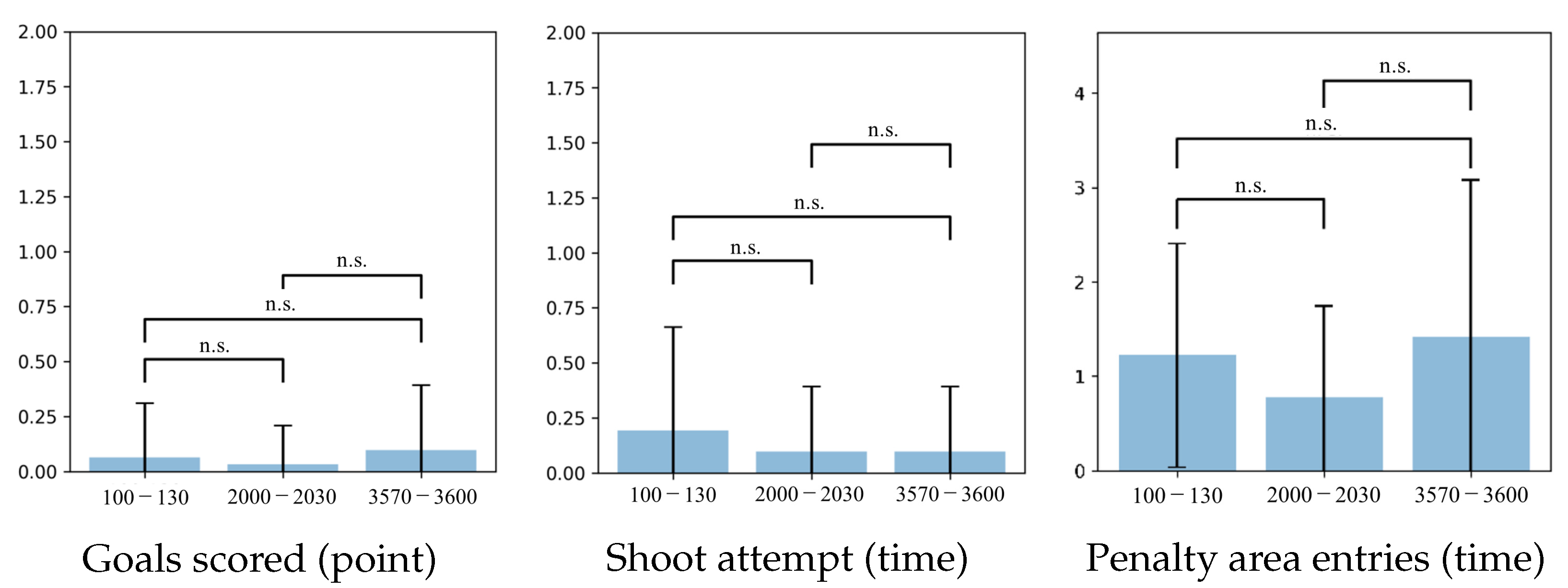
6.5. Jyo_sen

In contrast, experiments against Jyo_sen did not show statistically significant changes across generations in any of the evaluated metrics. However, a closer examination reveals moderate shifts in the number of goals and penalty area entries, implying that the GA was still navigating the search space. These results suggest two possibilities: (1) The current fuzzy rule set and fitness function may not sufficiently capture the discriminative features necessary for defeating stronger opponents, or (2) the local optima discovered are insufficient for generalizing to Jyo_sen’s specific strategies. This points to a need for either redesigning the fuzzy logic structure or incorporating additional state variables into the input feature space. See Figure 13.

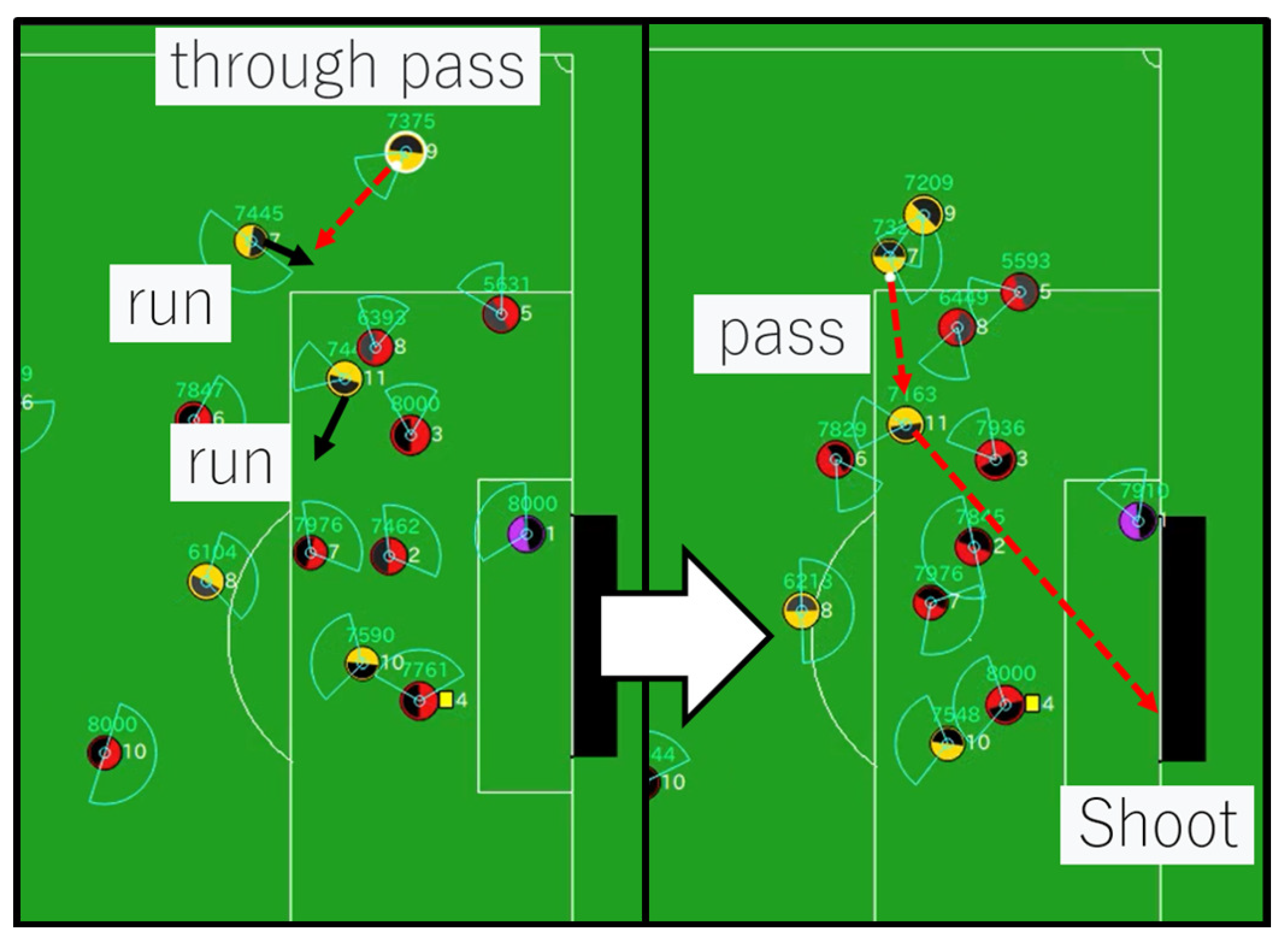
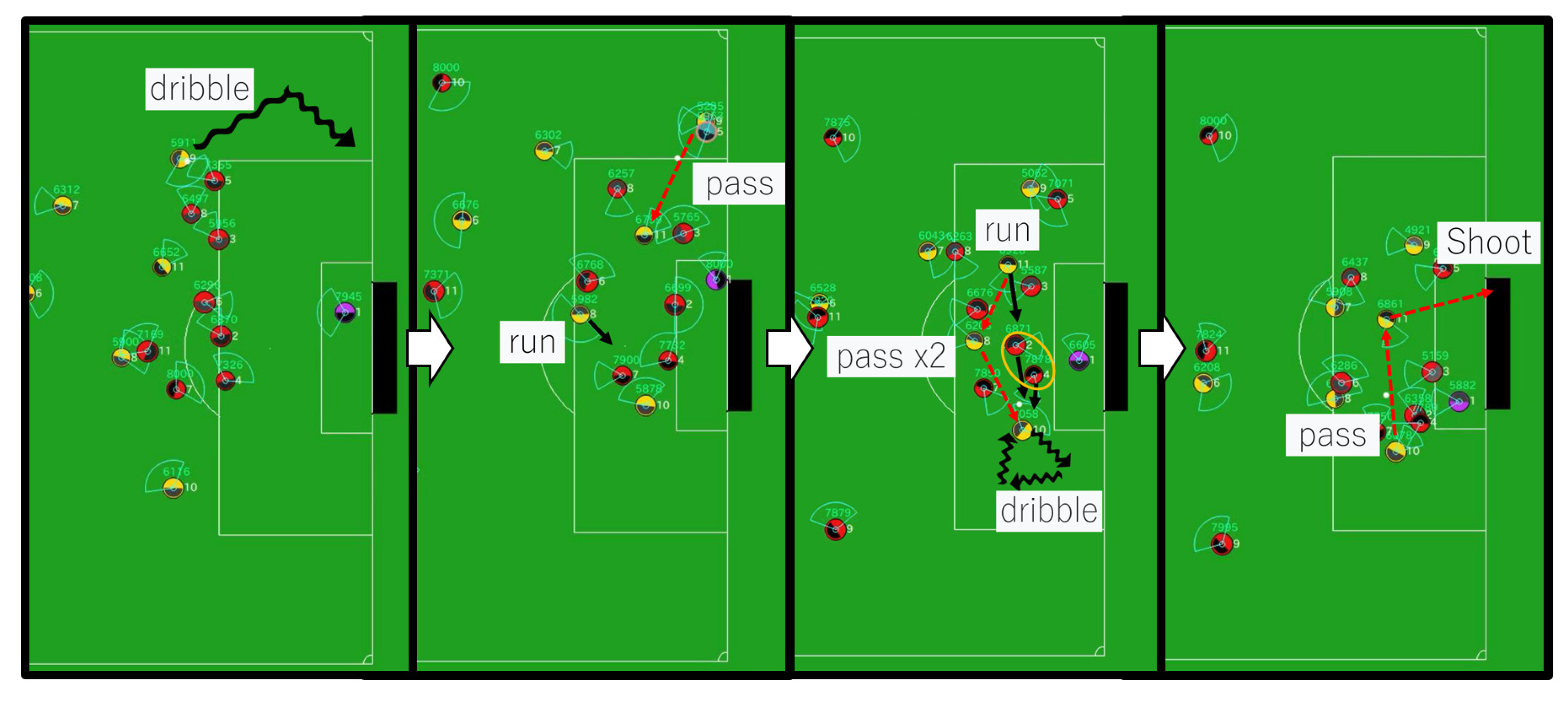
6.6. Behavioral Analysis of Soccer Agent Team

Figure 14 and Figure 15 refer to the search ratings for the soccer field in this experiment compared to Prespolice and illustrate the corresponding goal scoring behaviors, respectively. Figure 16 and Figure 17 refer to the search ratings for the soccer field in this experiment compared to Jyo_sen and illustrate the corresponding goal scoring behaviors, respectively.

Figure 15 illustrates one example of the action of scoring a goal in a match against Persepolis. In this experiment, the observation involves employing runs and through passes by the agent. Additionally, there are connections between running, passing, and ultimately scoring the goal. These actions unfold near the penalty area. GA realizes this strategy by exerting control over the action sequence search algorithm. Finally, the agent completed a shot into the corner of the goal. Areas with high evaluation values are concentrated near the goal area. A similarity between the two experiments is that they both exhibit high evaluation values for the corners of the penalty area. By examining the highly evaluated positions and edges of the contour lines in Figure 14, it is clear that these movements are influenced by the effect of $U(x,y)$ due to GA and fuzzy inference. The proposed system performed admirably. The agents exhibited intelligent running and passing behaviors, including through passes into open space. This outcome aligns with the expectations that resulted when the action sequence search algorithm was implemented with this specific behavior. However, the complexity of the design of $U(x,y)$ prevented it from being translated directly into an algorithm for a long time. The proposed method utilized fuzzy inference to realize significant differences among multiple ridgelines, enabling the creation of valley structures and multiple summit areas. Consequently, the action sequence search algorithm successfully discovered the through-pass movement. Figure 17 illustrates the four-step shoot case against Jyo_sen. The agent began dribbling and breaking through towards the left side, progressing towards the goal line. In the second step, a pass is made to another agent positioned on the ridgeline while another agent simultaneously runs towards the ridgeline. The third step involves precise passing and drawing the attention of opponents. The agent passes the ball to a nearby teammate and simultaneously makes a run towards the goal. The receiving agent then passes on to another teammate on the opposite side. The agent on the receiving end of the pass engages in dribbling to draw the attention of the enemy agent and the goalkeeper in front of the goal. Finally, the ball is passed back to the previous agent, who immediately takes a shot at the goal. The action sequence search algorithm demonstrates efficient performance in this case. Utilizing dribbling and running to create a path on a high ridgeline, the $U(x,y)$ function effectively controls the enemy agent and the goalkeeper. This suggests that the GA search successfully fine-tuned the evaluation function $U(x,y)$ for efficient searching.

Therefore, the following can be considered: The combination of all agents in the attack is designed to move the ball like a ridgeline. Passes, dribbles, and agent positions are determined by a search algorithm that considers an action sequence. Upon analyzing these behaviors, it became evident that fuzzy inference holds significant potential as an evaluation function for exploration.

Furthermore, the agent’s actions carried out in this experiment resulted in detailed play combinations near the goal, as depicted in Figure 15 and Figure 17. This suggests that focusing ball circulation more aggressively near the goal area leads to more shots and points, as evidenced by the value function’s contours after the GA exploration evaluation; refer to Figure 14 and Figure 16.

By comparing these scenarios, we observed that areas with high evaluation values in both cases were located near the corners of the penalty area. Utilizing the ball’s position coordinates as input values for optimization may increase the probability of scoring because this concentrates the balls near the corners of the penalty area.

The high-level edge line combinations depicted in the diagram represent points of interest. The search algorithm identifies these paths and selects shorter, more accurate, and more durable paths as the agent dribbles along that edge line or the ball moves to a higher edge line. If the search algorithm detects a higher-level point or edge line, the agent chooses a long pass or a shot on goal.

7. Conclusions

This research introduces a novel methodology that combines fuzzy inference systems with real-valued genetic algorithms to optimize decision-making in a multi-agent control environment. The proposed approach is applied to the RoboCup Soccer Simulation 2D League, offering a concrete example of how interpretable AI and evolutionary computation can be integrated in real-time strategic planning.

A key contribution of this work is the design of an evaluation function that enables autonomous agents to adaptively assess their positional advantage using fuzzy rules. This function is not manually tuned but learned through evolutionary processes, allowing the agents to self-organize around goal-scoring strategies without the need for handcrafted reward shaping. The ability of the agents to learn high-value regions—such as the corners of the penalty area and edge lines near the opponent’s goal—demonstrates the emergence of coordinated team behavior from simple fuzzy rules and fitness-guided optimization.

Another novel aspect lies in the interpretability of the learned behavior. Unlike black-box reinforcement learning approaches, this method allows researchers and system designers to visualize and understand the logic behind agent decisions, providing transparency and the potential for manual adjustment or domain-specific constraints. In particular, the evaluation function $U(x,y)$ can be visualized as a 3D contour or surface plot, enabling direct interpretation of how the agent prioritizes field positions. This visualization provides an intuitive map of the agent’s spatial preferences, showing, for example, how high-evaluation areas emerge near the goal edge lines or penalty corners. Such representations bridge the gap between quantitative optimization and qualitative reasoning, supporting safer deployment in broader robotics applications where explainability is crucial. Furthermore, this study is among the first to systematically explore how fuzzy logic can be accelerated for real-time multi-agent systems through GA-based parameter tuning. Previous approaches often relied on static or manually calibrated evaluation functions. In contrast, the proposed system dynamically evolves its evaluation criteria based on competitive performance, resulting in measurable improvements in both individual and team-level behavior.

Collectively, these contributions provide a practical and interpretable approach to enhancing decision-making in cooperative, uncertain, and dynamic multi-agent systems. The proposed method is computationally lightweight, behaviorally rich, and scalable to more complex agent environments.

Despite the promising results, several limitations remain. First, the current fuzzy rule base relies solely on spatial coordinates (x, y) as inputs, limiting its capacity to represent more nuanced game contexts such as opponent proximity, game phase, or agent roles. Second, although emergent coordination behavior was observed, the scalability of this framework to more heterogeneous agent systems or larger decision spaces remains untested. Third, the performance plateau observed against strong teams like Jyo_sen suggests that richer input features or more expressive fuzzy structures may be required to escape local optima. Another critical limitation lies in the computational cost of training. A full-scale experiment involving 3600 generations for a single opponent team requires approximately two full days to complete, even when using fast-match simulation modes. This makes extensive experimentation prohibitively time-consuming. To overcome this bottleneck, future work must consider algorithmic and architectural enhancements, particularly the parallelization of genetic algorithm evaluations across multiple processors or machines. Distributed optimization strategies or surrogate-based evaluations could also be explored to reduce computational overhead without sacrificing performance. Future research directions include incorporating additional state features (e.g., agent roles, ball dynamics, opponent positions), adopting adaptive or hierarchical fuzzy rule structures, and exploring hybrid models that combine fuzzy inference with deep learning for richer representation and decision-making. The framework’s applicability beyond RoboCup, such as in swarm robotics, autonomous driving, or decentralized logistics, also warrants further investigation to validate its generalizability.

8. Highlights and Contributions

This research explores a forward-looking approach to real-time multi-agent collaboration under uncertainty by integrating fuzzy inference systems with evolutionary optimization. The experimental platform is RoboCup Soccer Simulation 2D, where 22 autonomous agents compete in dynamic soccer scenarios. The core challenge addressed is not merely individual agent competence but the emergence of coordinated and adaptive team behavior in partially observable and time-constrained environments. Nevertheless, the current approach relies on a fixed fuzzy rule structure, where the set of linguistic rules is predefined. While the rule parameters are optimized, the lack of structural adaptivity may limit the system’s flexibility in highly dynamic or high dimensional domains. To broaden applicability, future research should investigate methods for automated rule induction or structural learning in fuzzy systems. Building on automated rule induction in cascaded ANFIS, where both the rule base and architecture adapt over time, could further enhance flexibility in high-dimensional or evolving multi-agent scenarios [32].

Moreover, the evaluation of our method remains confined to the RoboCup Soccer Simulation 2D environment. Although this platform offers a rigorous and controlled benchmark for agent coordination, the transferability of the proposed framework to real-world domains such as heterogeneous robotic teams, swarm intelligence, or autonomous traffic control has yet to be demonstrated. Further validation under diverse operational constraints and richer behavioral contexts will be necessary to confirm its generalizability.

8.1. NovelEvaluation Function Based on Fuzzy Inference and Evolutionary Search

A key contribution of this study is the design and implementation of a new evaluation function, $U(x,y)$, which utilizes fuzzy inference rules to represent domain knowledge in a manner that closely resembles human intuition. Instead of relying on rigid rules or predefined scoring heuristics, this method allows agents to dynamically evaluate field positions based on flexible linguistic conditions (e.g., proximity to the goal, number of nearby defenders). The parameters of the fuzzy evaluation rules, including their weights and singleton outputs, are optimized using a genetic algorithm with real-valued representation. The genetic algorithm leverages game outcomes, such as the number of shots, goals, and penalty area entries, to guide learning over generations. As a result, the system autonomously discovers effective tactical regions on the field without prior human instruction, improving both shot frequency and goal scoring ability.

8.2. Emergence of Ridgeline Strategies and Adaptive Team Behavior

Through evolutionary learning, agents began to exploit tactical structures such as “ridgelines,” which are high-value zones near the flanks and penalty corners. These were not manually encoded; instead, they emerged organically from the optimization process. The agents learned to navigate these areas and coordinate movements that mimic human-like strategies, such as drawing defenders away, setting up through passes, and attacking from advantageous angles. This emergent behavior stands in stark contrast to the original baseline (Agent2D), which followed a naive hill-climbing policy toward the goal center. The optimized agents exhibited more complex, unpredictable, and effective team play, representing a qualitative leap in multi-agent coordination.

8.3. Interpretability via Visualization of $U(x,y)$

Unlike black-box reinforcement learning systems, the proposed method provides interpretability. The evaluation function $U(x,y)$ can be visualized as a three-dimensional surface or contour map over the soccer field, allowing for direct inspection of the agent’s decision-making logic. This makes it possible to understand why agents prefer certain positions or paths, which in turn enhances trust, transparency, and the ease of debugging.

8.4. Broader Implications for Real-World Multi-Agent Systems

The implications of this study extend beyond simulated soccer. The combination of intuitive rule-based reasoning with evolutionary tuning presents a generalizable framework for real-time multi-agent control. Applications include autonomous vehicle coordination, warehouse logistics, disaster response robotics, and swarm navigation, which are domains where explainable, adaptive, and collaborative behavior is critical. Furthermore, the interpretable nature of the learned policies supports safe deployment in environments with high stakes, addressing an increasingly important demand for explainable artificial intelligence (XAI).

8.5. Toward Human AI Co-Design and Learning

Finally, this research offers a compelling case for human AI co design. While fuzzy rules encode human insight about tactical reasoning, genetic algorithms enable machines to autonomously optimize these insights based on environmental feedback. This combination fosters a learning system where artificial intelligence not only supports human decisions but also inspires new strategies that surpass those that are manually designed. The success of this approach in RoboCup2D highlights its potential as a blueprint for future artificial intelligence systems that are both capable and understandable, laying the foundation for more trustworthy and collaborative interactions between humans and intelligent agents.