Abstract
Adversarial machine learning exploits the vulnerabilities of artificial intelligence (AI) models by inducing malicious distortion in input data. Starting with the effect of adversarial methods on well-known MNIST and CIFAR-10 open datasets, this paper investigates the ability of Uniform Manifold Approximation and Projection (UMAP) in providing useful representations of both legitimate and malicious images and analyzes the attacks’ behavior under various conditions. By enabling the extraction of decision rules and the ranking of important features from classifiers such as decision trees, eXplainable AI (XAI) achieves zero false positives and negatives in detection through very simple if-then rules over UMAP variables. Several examples are reported in order to highlight attacks behaviour. The data availability statement details all code and data which is publicly available to offer support to reproducibility.
1. Introduction
Deep learning has become the most widespread subfield of Artificial Intelligence (AI) for image analytics tasks, concentrating on designing models such as convolutional neural networks (CNNs) [1] and statistical models to empower computers in learning from data and making predictions or decisions without explicit instructions. It has made an immense impact on image classification [2], segmentation [3], and detection [4]. Despite this great advancement and continuous improvement, adversarial attacks pose a serious challenge to these models. Adversarial learning is an emerging threat, affecting machine learning (ML) models, that deals with intentionally crafting adversarial inputs to ML models that induce model errors, even though these inputs may appear normal to humans [5,6]. FGSM, PGD, and CW, among others, are techniques used to generate adversarial examples [7].
These techniques are particularly relevant in the context of image datasets, as they can be used to design imperceptible perturbations to images that cause deep learning models to misclassify them [8]. Adversarial learning has implications for the robustness and security of AI systems, as understanding and defending against adversarial attacks is crucial for deploying AI models in real-world applications where security and reliability are paramount [5,9]. Nevertheless, the reliable detection of adversarial attacks remains very challenging [10].
In this context, data dimensionality reduction allows the translation of the high-dimensional, complex, information of pixel-level space into a lower-dimensional (simpler) embedding domain. Among several techniques, UMAP is well suitable, being a nonlinear transformation that preserves the local data structure.
The paper investigates the detection of the attacks by exploiting their representation in the UMAP space, through XAI-based techniques such as feature extraction and rules generation. This was made possible through the following steps:
- I.
- Leveraging state-of-the-art attack techniques such as CW and FGSM on image datasets of MNIST and CIFAR in UMAP space.
- II.
- Assessment of Carlini–Wagner, FGSM, and PGD for malicious datasets via UMAP embeddings.
- III.
- UMAP visualization of legitimate and malicious MNIST and CIFAR datasets.
- IV.
- Interpretable insights of vulnerabilities.
- V.
- Detection of adversarial images by employing XAI techniques.
The rest of the paper is structured as follows: in Section 2, we review related work of the paper. Section 3 contains the methodology. Section 4 presents and discusses the obtained results and covers XAI-based analysis. Finally, Section 5 concludes the paper and discusses possible future work on the topic.
2. Related Work
2.1. Image Dimensionality Reduction
Beyond deep learning, another important aspect of image dataset analysis is UMAP [11], which is a dimensionality reduction technique that has gained popularity for visualizing high-dimensional data in lower-dimensional spaces, including image datasets while preserving the underlying structure of the data [12,13]. Unlike traditional dimensionality reduction techniques such as PCA [14,15,16,17] or t-SNE [18], UMAP offers several advantages, including scalability to large datasets, faster computation, and better preservation of global structure. UMAP achieves dimensionality reduction by modeling the manifold structure of the data and optimizing a low-dimensional representation that retains local and global relationships between data points [19]. This makes UMAP particularly useful for exploratory data analysis, clustering, and visualization tasks in machine learning and data science applications. UMAP is applied in practical scenarios, such as refining the dimensions of fingerprint portraits in radio maps [20]. We argue that UMAP’s ability to capture data structures robustly makes it a valuable tool in detecting and filtering out adversarial samples, thereby fortifying machine learning systems against attacks [21]. Integrating UMAP embedding into adversarial training processes could enhance the resilience of machine learning models by exposing them to adversarial instances during training, thus improving their ability to withstand attacks.
2.2. Adversarial ML Attacks
Adversarial attacks [5,22] pose severe security threats in the fields of machine learning, deep learning, and other artificial intelligence domains. These attacks are often targeted against AI-based computer vision systems, which are mainly based on deep neural models trained on raw data. These systems can be easily fooled either as targeted [23] or untargeted [24,25] by modifying input images in a way that is not visible to the average system user. This can be achieved through the generation of an adversarial example that introduces small perturbations to the original image while maintaining its visual similarity to the human eye [25]. Adversarial machine learning includes a range of attack methods, such as adversarial examples, poisoning attacks [26], extraction attacks [27], inference attacks [28], and evasion attacks [23]. In the context of autonomous vehicles where image detection is pivotal concern, researchers [29,30] have presented an instance of adversarial attack, which represents a notable hazard to the functionality of deep neural networks within such vehicles. The CW, FGSM, and PGD are adversarial machine learning attacks that have been used in the distortion of image datasets as in [31,32,33] by attackers. Generally, previous studies in different domain and image classification have acknowledged the effectiveness of these attacks against adversarial defense strategies, especially the Carlini– Wagner method.
2.3. Explainable AI
Explainable artificial intelligence is fundamental in ensuring transparency and trustworthiness in machine learning models, particularly in adversarial contexts. To this end, we employ interpretable classification strategies, including first-level classifiers such as decision trees [34], which naturally support feature importance ranking and rule extraction. XAI techniques, such as feature importance rankings and rule extraction, enhance the usability of models in critical domains by making decisions understandable to human experts. In this study, we evaluate the ability of XAI techniques to detect adversarial perturbations in the MNIST and CIFAR-10 datasets, following dimensionality reduction using UMAP.
2.4. Benchmarks
Studies that report detection of Carlini–Wagner on traditional datasets, such as MNIST, generally show above 90% true positive detection rates. For example, [35] reports that feature squeezing reduces the adversary’s success rate dramatically on MNIST, while detecting Carlini examples with accuracy around 99%. Under the same setting of [35], the FPR is 20%. The more recent approach by [36] demonstrated very good performance on CIFAR-10, though going beyond canonical machine learning through an iterative counter attack process. There are also noise-based detection methods like [37] that have been evaluated on CIFAR-10; while their performance can depend on the exact settings and attack parameters, they report good detection rates.
3. Methodology
This section covers the methodological framework adopted to detect adversarial behavior and explainability, starting from datasets description, preprocessing, CNN model building, UMAP data (dimensionality reduction and visualization), and implementation of adversarial attacking techniques. Detection is studied across two complementary settings: (i) single and multiple image detection directly in the original input space, and (ii) detection in a reduced-dimensionality space obtained via UMAP. The proposed workflow, illustrated in Figure 1, begins with the training of CNN models on MNIST and CIFAR datasets. Subsequently, adversarial examples are generated using attacking techniques to detect adversarial perturbations. Both legitimate and adversarial samples are then embedded into a lower-dimensional space using UMAP for further analysis. Machine learning techniques, such as decision trees and explainable artificial intelligence techniques, like importance feature extraction and rules generation, are applied, enabling the detection of adversarial samples and susceptibility of the models.
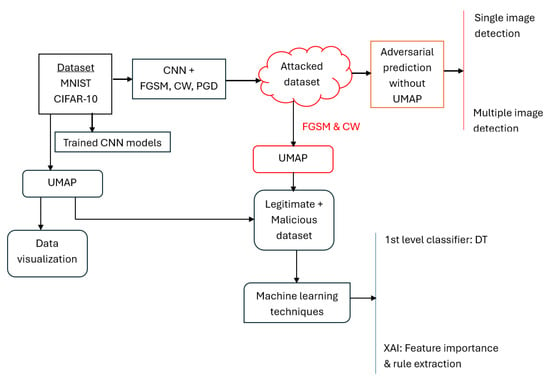
Figure 1.
Methodological workflow diagram outlining the sequential steps of CNN model training, adversarial attack generation, data visualization via UMAP, ligitimate and malicious data generation and analysis of generated UMAP data via XAI, and decision trees classifier.
3.1. Dataset
The MNIST [38] and CIFAR-10 [39] image datasets are used because of their renown and versatility in the field of computer vision and widespread use in training of machine learning and deep learning models. The MNIST handwritten digit image dataset ranges from 0 to 9 (0, 1, 2, 3, 4,5, 7, 8, 9), making a total of 10 classes, with each image having a pixel value of 28 × 28 grayscale dimensions. This dataset is divided into a training set size consisting of 60,000 images and a test set size consisting of 10,000 images [38]. The test set size of 10,000 images is used to evaluate the detection rate of the CNN model and when embedded via UMAP. CIFAR-10 comprises 60,000 32 × 32 color images divided into 10 categories (airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck), with each category containing 6000 images. The dataset includes a training set of 50,000 images and a test set of 10,000 images. The dataset consists of five sets for training and one set for testing, with each set containing 10,000 images. The test set precisely includes 1000 randomly chosen images from each category. CIFAR-10 is widely employed as a standard to assess the performance of image classification models. It is more challenging than MNIST due to the higher resolution and the inclusion of color images [39].
3.2. Adversarial Attacking Techniques
This section presents the adversarial machine learning techniques considered in this paper without the use of UMAP, such as FGSM, PGD, and CW used to evaluate the robustness of classification models. The attacks were applied to the MNIST and CIFAR-10 test sets, while the train sets were used to train the CNN model. All adversarial attacks were generated using the Adversarial Robustness Toolbox (ART) [40] The images of the MNIST dataset were then preprocessed by flattening each 28 × 28 grayscale image into a 784 dimensional vector and normalized pixel values to the [0, 1] range before a pretrained CNN model wrapped with ART’s KerasClassifier. FGSM was then applied with varying values. The same method of preprocessing of the MNIST dataset was applied for the Carlini–Wagner method, configured with parameters controlling confidence = 0.8, maximum iteration = 20, initial distortion constraint , and largest distortion constraint . A similar preprocessing and attack configuration was applied to the CIFAR-10 dataset.
3.2.1. Deep Learning for Single Image Detection
During the process of image detection and classification, an image is fed to the trained model, allowing the model to assign a class label to the input image. Given that the dataset encompasses multiple classes with 10 labels, the input image label was detected with the value “1” along with its corresponding position (index). A class prediction was generated, resulting in an output corresponding to the input image. Following adversarial manipulation, the prediction for the input image was misclassified.
The analysis of Figure 2 suggests that the model’s prediction was altered by the adversarial attack, resulting in a misclassification of the image from its true label of ‘3’ to a wrongly predicted label ‘8’. This highlights the susceptibility of machine learning models to adversarial perturbations.
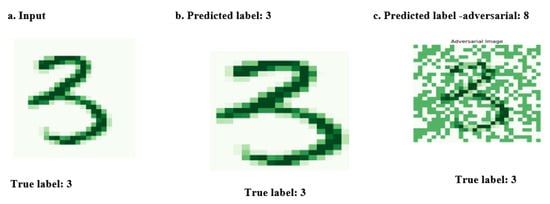
Figure 2.
The figure illustrates how adversarial attacks can lead to misclassification in the MNIST digit dataset, with some perturbations being visibly detectable.
Despite certain adversarial perturbations being visually detectable, many remain imperceptible to the human eye while still misleading the classification model. Figure 3 illustrates these vulnerability cases, emphasizing the deceptive effectiveness of such attacks.

Figure 3.
Clean vs. adversarial examples from CIFAR-10 and MNIST demonstrate imperceptible perturbations generated by Carlini–Wagner, FGSM, and DeepFool attacks. Despite visual similarity to original inputs, all adversarial samples lead to model misclassification. (a) Clean vs. adversarial images of CIFAR10 dataset for Carlini–Wagner attack. (b) Clean versus adversarial images of CIFAR10 dataset for FGSM attack. (c) Clean vs. adversarial images of CIFAR10 dataset for DeepFool attack. (d) Clean versus adversarial images of MNIST dataset for DeepFool attack.
3.2.2. Deep Learning for Multiple Image Detection
The same pretrained CNN model for single-image detection is used in parallel with a random iteration across the entire 10,000-test set executed simultaneously for a chosen value. This process aims to identify misclassified images and document their corresponding indices. Random target labels are assigned for misclassification in testing set images, and adversarial attacks are performed by varying epsilon values using the FGSM method. The results of each attack, including image index, value, original label, true label output, and predicted label post-attack, are stored for further examination—offering comprehensive insights into the susceptibility of the model to adversarial attacks and its response under perturbation conditions while revealing both its strengths as well as potential weaknesses beyond standard classification accuracy metrics. The predictions obtained for the 10,000 input images across different values are presented in Section 4.2, under the performance of FGSM adversarial attack detection on MNIST dataset without applying UMAP dimensionality reduction.
3.3. Uniform Manifold Approximation and Projection for Dimensionality Reduction
UMAP is a novel topological learning technique which is constructed from an algebraic topology-based framework and Riemannian geometry [11]. Its preservation of the global structures is higher along with relatively better computation and faster runtime performance [12,41]. These properties make UMAP suitable to study the characteristics, at different degrees of reduction, of MNIST and CIFAR images, both legitimate and when injected with adversarial attacking techniques. First, we visualize the entire legitimate and malicious test datasets separately to detect any physical characteristic or decision boundary across different dimensions, followed by further detection analysis using XAI techniques.
3.3.1. Data Visualization
MNIST, CIFAR-10, and CIFAR-100 images were each transformed through the UMAP method using the umap–learn library [42]. The visualization of the obtained embeddings allowed a clear understanding of the separation of the features of each class especially in the case of the MNIST dataset, as shown in Figure 4. In the case of the CIFAR datasets, Figure 5, the clustering and separation of same classes were not detectable. The purpose of these datasets’ visualization was to gain insights into the characteristics and distribution of each class within the datasets. It was possible to observe any patterns or clusters that exist within the datasets.

Figure 4.
UMAP 2D representations of the entire MNIST dataset. Digit classes form well-defined, identifiable clusters that are clearly separable from one another.
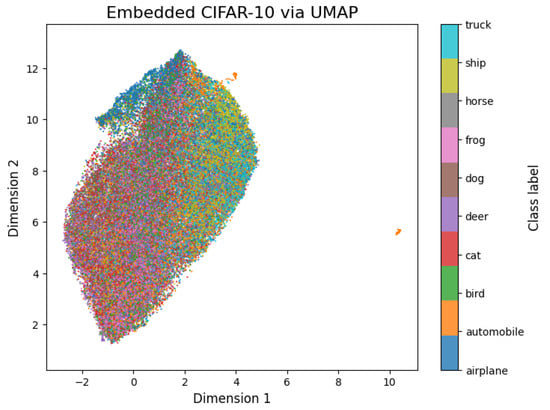
Figure 5.
UMAP 2D projection of the CIFAR-10 dataset. Different classes exhibit overlapping clusters, resulting in poor distinguishability and limited separability.
Figure 4 and Figure 5 provide insights into how the different classes are separated or clustered in the UMAP embedding space. In the case of the MNIST dataset, we can observe clusters of similar classes, indicating that UMAP has successfully captured the inherent similarities between images belonging to the same fine-grained categories. For the CIFAR datasets, UMAP was not able to capture classes and separate them like the MNIST dataset.
During comparison of Figure 4 and Figure 6a of the 2D visualization for the entire MNIST dataset and 2D representation of the test set, respectively, a clear difference in orientation and positions is observed when the entire dataset (70,000 images), Figure 4, is embedded via UMAP and when only the test set (10,000 images) is embedded. For instance, class one with the orange color in the entire dataset is positioned at the bottom left with a dense elongated shape, while the embeddings of the split test set positioned class one in the bottom right of Figure 6a with a sparse linear shape. We also noticed a flip towards the positive horizontal direction. This phenomenon illustrates UMAP’s ability to capture intricate patterns and position them based on the quantity of data be fed.
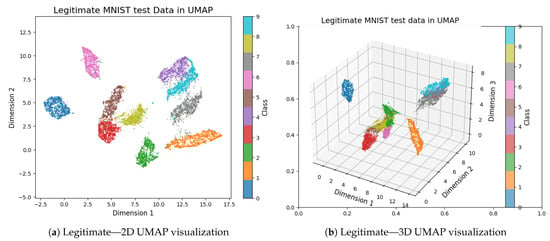
Figure 6.
UMAP projections of the legitimate MNIST test dataset in 2D (a) and 3D (b). These visualizations reveal the structure and clustering of digit classes in lower-dimensional space, enabling intuitive inspection of class separability and overlap.
In Figure 7a and Figure 8a, 2D and 3D distortion, respectively, it can be observed that the FGSM attack method is successful in distorting the MNIST dataset by clustering different classes to a specific position in UMAP space.
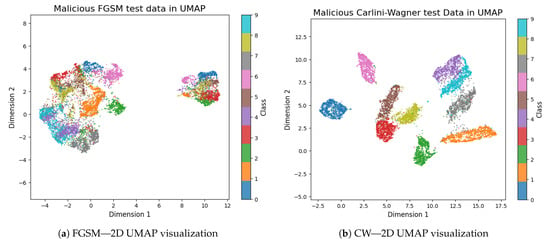
Figure 7.
UMAP 2D projections of adversarial MNIST test samples: (a) FGSM attack and (b) CW attack. These visualizations illustrate how FGSM and CW attacks reduce class separability and increase overlap in the embedded space, compared to legitimate samples.
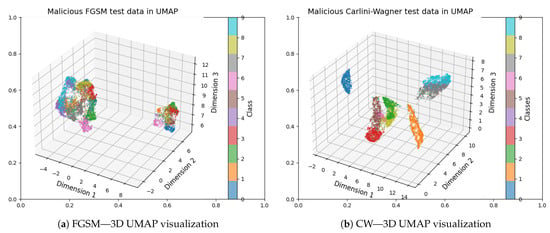
Figure 8.
UMAP 3D projections of adversarial MNIST test samples: (a) FGSM attack and (b) CW attack. The 3D visualizations reveal how adversarial perturbations reshape the spatial distribution of digit classes, leading to less distinct clustering and greater class overlap compared to legitimate data.
From Figure 7b and Figure 8b, unlike the former in the FGSM attack, the CW distortion is physically observable by compressing the lengths and broadening the width of some of the individual classes, such as 1 and 5, while the other classes are being stretched and narrowed in shape for the 2D case. A similar situation is seen for the 3D, though not with the same classes as those of 2D.
3.3.2. Feature and Label Extraction
Legitimate MNIST and CIFAR-10 dataset was transformed via UMAP by adopting different numbers of components (in UMAP space): . Next, the legitimate MNIST dataset was manipulated by the adversarial (FGSM and Carlini–Wagner techniques) with the help of a trained CNN model of the dataset. This altered dataset was then embedded via UMAP. A dataset encompassing both legitimate and malicious features is created in a single CSV file with “0” for legitimate and “1” for malicious images. Another similar phase was conducted for both the legitimate and manipulated datasets, capturing legitimate and adversarial features, along with corresponding labels and attack success indicators. In both phases, the procedure was repeated for the CIFAR-10 dataset with dimensions of .
4. Results
In this section, we present the results obtained and analyses made on the impact of adversarial machine learning attacking techniques, starting with the parameters used in building the CNN models for both the MNIST and CIFAR-10 datasets. Again, a comparison on the datasets not embedded via UMAP is made to determine the robustness of the attacking techniques by visualization through graphs of the accuracy and time taken to execute an attack. This helps in identifying trends of vulnerabilities in the datasets of the trained CNN models. Also, we tested the ability of UMAP in detecting malicious images of the test datasets injected by the FGSM and CW attacks for 2D–10D dimensions. The analyzed results obtained via XAI techniques and first-level classifiers are also reported, as they prove to be robust in detecting distorted datasets of UMAP embeddings. Code and data are publicly available in GitHub (https://github.com/AchmedSamuel/UMAP-adversarial-image-detection, accessed on 29 April 2025), and more details are described in Appendix B.
4.1. Adversarial Attack Success Rate on MNIST and CIFAR10
Before evaluating the robustness of our decision tree rule-based model, we constructed test datasets composed of both clean and adversarial samples. Adversarial samples are generated using FGSM, Carlini-Wagner and DeepFool on the MNIST and CIFAR-10 datasets. Table 1 summarizes the attack success rate, measured as the percentage of adversarial examples that successfully fooled the base CNN model. These success rates highlight the varying robustness of different adversarial methods on the benchmark datasets. The success rate reveals CIFAR-10 to be more susceptible, particularly to the Carlini-Wagner attack and followed by DeepFool attack which near-perfect always succeeded in misleading the entire configuration of the CNN model. On the CIFAR-10 dataset, the Carlini-Wagner attack achieved a 99.5% success rate and 2.4% on MNIST. These results confirm the difficulty of the adversarial detection task and reflect the increasing vulnerability of complex, high-resolution datasets to advanced attack techniques and highlight the challenge for any robust classifier.

Table 1.
The table shows the success rates (%) of three adversarial attack techniques—FGSM, Carlini-Wagner, and DeepFool—on MNIST and CIFAR-10 datasets. Higher values indicate greater vulnerability of the models to adversarial perturbations.
4.2. CNN Model Training Results
Two convolutional neural network (CNN) models were trained for classification tasks on the MNIST and CIFAR-10 datasets. For MNIST, 60,000 training images were used in building the model architecture, which included four convolutional layers with ReLU activations, each followed by max-pooling, and a dense layer with 100 units before the softmax output layer. Training was performed over 50 epochs using the Adam optimizer and sparse categorical cross-entropy loss, with a batch size of 64, achieving an accuracy of 99.2%. Similarly, the CNN architecture of the CIFAR-10 dataset consisted of three convolutional layers (with 64, 128, and 256 filters), each followed by max-pooling, and two fully connected layers with dropout for regularization. Images were normalized, and labels one-hot encoded for multiclass classification. The model was trained for 50 epochs with the Adam optimizer (learning rate = 0.001), a batch size of 512, and a validation split of 0.1. The final model achieved an accuracy of 74.8%. Table 2 outlines a summary of the parameters utilized in training CNN models for the MNIST and CIFAR-10 datasets.

Table 2.
Training parameters and accuracy for the MNIST and CIFAR-10 datasets.
Impact of Attacking Techniques on MNIST and CIFAR-10 Datasets
In assessing the robustness of adversarial attacks on the MNIST handwritten digit image dataset and CIFAR image dataset, we considered the time taken to execute the attack and the weight of . The time defines how long the attacker can penetrate the model before achieving his desired goal. The controls the perturbation magnitude for FGSM and defines the maximum perturbation budgets for PGD. In each case, if has a smaller value, the attack is effective but not visible to the human eye. While a larger makes the attack very robust, it will noticeably be making it very different from the original input. Table 3 and Table 4 show the result obtained, while Figure 9a,b illustrate the model’s performance in terms of accuracy before (original trained CNN model) and after attacks as well as the time taken to perform an attack. A similar situation is demonstrated, as seen in Figure 10a,b, for the CIFAR10 dataset.

Table 3.
Model accuracy and attack time comparison for MNIST: FGSM vs. PGD.

Table 4.
Model accuracy and attack time comparison for CIFAR10: FGSM vs. PGD.
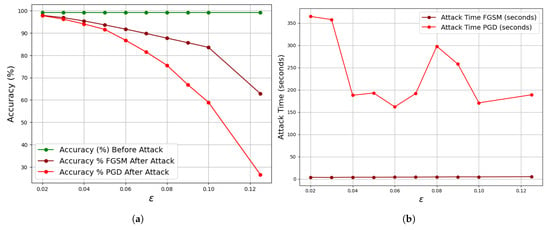
Figure 9.
Accuracy and execution time for FGSM and PGD attacks at varying epsilon values on the MNIST dataset. The figure illustrates how increasing perturbation strength leads to a decline in model accuracy, highlighting increased susceptibility to adversarial attacks. PGD typically results in lower accuracy and greater computational cost compared to FGSM. (a) Accuracy vs. epsilon for FGSM and PGD attacks. (b) Computation time vs. epsilon for FGSM and PGD attacks.
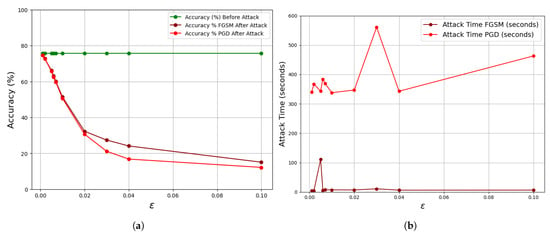
Figure 10.
Comparison of accuracy and execution time for FGSM and PGD attacks on the CIFAR-10 dataset across varying epsilon values. As perturbation strength increases, classification accuracy declines, indicating higher model vulnerability. PGD consistently results in lower accuracy and longer execution times compared to FGSM. (a) Accuracy vs. epsilon for FGSM and PGD attacks. (b) Computation time vs. epsilon for FGSM and PGD attacks.
Table 3 and Table 4 record the output of the result obtained from the FGSM and PGD attacking methods when applied to the MNIST and CIFAR datasets, respectively. The graph of Figure 9a illustrates the perturbation effect of the on the MNIST dataset for both FGSM and PGD. The CNN model is trained with an accuracy of 99.2% before attack. It can be noticed that when a perturbed image of the FGSM or PGD is applied to the trained CNN model, the accuracy differs from its original value. The decrease in the original accuracy of the CNN model signifies the attacker hitting his target on the image, which is not detectable by the physical human eyes. For instance, with = 0.02, the accuracy dropped from 99.2% to 97.88% and to 97.74% for the FGSM and PGD, respectively. It could be noticed that the larger the perturbation, the more robust the attacking technique on the trained model. The MNIST dataset is vulnerable to the FGSM attack compared to PGD, as detected when the attacker increased the value. A linear pattern of time showed up for the FGSM, while a nonlinear pattern was observed for the PGD with varying . These findings provide valuable insights into the model’s susceptibility to adversarial perturbations and the associated computational costs of different attack methods. Table 4 records the results obtained for the FGSM and PGD when the CNN model is trained with the CIFAR-10 dataset, with performance being illustrated in Figure 10a. At very small perturbation, the attacker succeeded in deceiving the model, for example, with = 0.001, the CNN accuracy dropped from 75.68% to 74.66% and 74.64% of the FGSM and PGD, respectively. Unlike the MNIST dataset, the CIFAR-10 dataset is very vulnerable to PGD attack while resistive to the FGSM attack. As seen from the MNIST dataset, with varying , the time taken to complete an attack is linear with minor inconsistency, while the PGD exhibited a nonlinear pattern. Generally, MNIST, with its simpler digital images, demonstrates higher accuracy before attacks compared to the more complex CIFAR-10 dataset. While both datasets experience decreasing accuracy with increasing , CIFAR-10 shows a more significant decline, suggesting higher susceptibility to adversarial perturbations. Furthermore, the attack times for generating adversarial examples are generally lower for MNIST compared to CIFAR-10, indicating a difference in computational requirements between the datasets.
We further investigate the effectiveness of FGSM adversarial attacks on the MNIST dataset across different values of the perturbation parameter in Table 5. It can be seen that as increases, the magnitude of perturbation applied to the original images grows, making adversarial examples more detectable. For example, the attack success count increases from 6727 at = 0.3 to 8796 at = 1.0. These results highlight the vulnerability of image datasets to adversarial examples even without the application of dimensionality reduction techniques such as UMAP.

Table 5.
Performance of FGSM adversarial attack detection on MNIST dataset without applying UMAP dimensionality reduction.
4.3. Image Dimensionality Reduction: UMAP vs. PCA
Previous results have shown how the considered adversarial attacks downgrade the performance of the trained CNN. The next step consists of reducing data dimensionalities, transforming images into numerical representations (embeddings). Among possible techniques [43], we decided to adopt UMAP.
The rationale for choosing UMAP over other dimensionality reduction techniques such as PCA in this study is that UMAP has a better ability in managing the nonlinearity and complexity of data and preserves both local and global data structures better than principal component analysis (PCA). To validate this statement, we conducted experiments on the CIFAR-10 dataset (legitimate and malicious) for various dimensions as shown in Table 6. The results obtained demonstrate that UMAP achieves significantly lower FPR and FNR than PCA. For example, from Table 6, in 5D, UMAP recorded 1% FPR and 2% FNR, while PCA showed 16% FPR and 87% FNR. Also, as the dimensions increase, UMAP keeps on performing better, as seen for the 10D case. These findings underscore UMAP’s superior ability to enhance the separability between legitimate and adversarial instances, making it a more effective tool for adversarial detection in complex, high-dimensional data.

Table 6.
The table shows the results of the Carlini technique on the CIFAR-10 dataset across different dimensions for a comparison of UMAP and PCA. The FPR and FNR measure the error detection rate. All metrics are expressed in percentage.
4.4. Performance Evaluation
Canonical machine learning techniques such as decision tree are explored in detecting the presence of adversarial attacks on MNIST and CIFAR10 distorted datasets from UMAP embeddings. In achieving this investigation, the first-level classifiers are employed. The first level of classification is carried out via the decision tree model (DT).
4.5. Decision Tree
A canonical machine learning algorithm, i.e., the decision tree, was applied in detecting possible adversarial attacks from the UMAP environment. The distorted datasets contain features and labels of 50% legitimate and 50% malicious in each row. In implementing the first-level classifiers, the vectors (distorted datasets)—2D, 3D, 5D, and 10D were split into 70% training set and 30% testing set. For the successful implementation of these classifiers, the Python programming language and the SKlearn library [44,45] were used. The results are presented using metrics derived from confusion matrices. Key metrics considered for the analysis are true positive rate (TPR), true negative rate (TNR), false positive rate (FPR), false negative rate (FNR), accuracy (ACC), PPV, and F1-score for the chosen classifier. The TPR, TNR, PPV, and F1-score are important metrics for evaluating the model’s ability to correctly classify instances, while the FPR, FNR, and accuracy specifically quantify the model’s error rates in terms of distortion detection.
To evaluate the robustness and generalizability of the models, we conducted 10-fold cross-validation using the same classifier (decision trees classifier) and a fixed random state for reproducibility, with optimized hyperparameters obtained from the grid search algorithm. This technique randomly divides the dataset into k subsets, training the model on k − 1 folds and validating it on the remaining fold in each iteration, thereby ensuring that every data point is used for both training and validation. The metrics are computed and stored for each fold and then the average score across the ten folds is computed. This provides a more reliable estimate of the model’s predictive detection capabilities. The metrics consistency results across these runs provide evidence of the model’s stability and effectiveness in detecting malicious samples.
The results of the classifier for train–test split and cross-validation score are displayed in Table 7 for various dimensions of the dataset of the FGSM and Carlini–Wagner attacks. All metrics are expressed in percentages.

Table 7.
Performance metrics for MNIST dataset: FGSM vs. Carlini–Wagner across dimensions 2D–10D with train–test split (TTS) and cross-validation score (CVS). The cross-validation score metrics validate the stability and generalizability detection of the model.
From Table 7, it can be observed that across different dimensions (2D, 3D, and 5D), the error rates, for instance, the FPR of Carlini–Wagner attack, is high for 2D, 3D, and 5D. This error gradually continues to decrease as the reduction dimensionality continues. This signifies that as dimension reduction continues, the detection rate of adversarial examples increases. For example, let us consider the MNIST result for 2D–5D dimensions. The error (FPR) 85%, 50%, and 20%, and accuracy (ACC) of detection 56%, 67%, and 86%, respectively, satisfies the above claim. The FNR and related accuracy display a similar character. In Table 8, the CIFAR10 dataset shows similar characteristics to those metrics of the MNIST dataset as explained above. From the analysis of the metrics of the MNIST and CIFAR-10 datasets, it shows that images have a similar vulnerability to adversarial machine learning. These results of the FPR, FNR, and other metrics prompted the possibility to further assess the robustness of the FGSM and Carlini–Wagner attack.

Table 8.
Performance metrics for CIFAR-10: FGSM vs. Carlini–Wagner across dimensions 2D–10D with train–test split (TTS) and cross-validation score (CVS). The cross-validation score metrics validate the stability and generalizability detection of the model.
4.6. Feature Ranking and Rule Extraction
To further assess the detection of adversarial attacks on the MNIST image dataset via UMAP embeddings, we considered exploiting the explainability of the features by important feature rankings for 2D, 3D, and 5D and rules extraction for 5D and 10D. We also show the visualization of the 2D and 3D of both legitimate and malicious detection of the FGSM attack.
In enhancing XAI, a canonical machine learning classifier, decision trees, is trained on UMAP-compressed features, yielding feature importance rankings and interpretable decision rules. The decision tree model computes feature importance rankings of UMAP-transformed features based on the total reduction in Gini impurity achieved across all tree splits, identifying higher importance to features most frequently used for classification. In rules extraction, the trained tree is recursively traversed to identify all root-to-leaf paths, where each path consists of a sequence of UMAP-based thresholds generating transparent “if–then” rules. In addition, each rule is quantitatively evaluated based on its coverage and error metrics, indicating the transparency of each rule in detecting adversarial inputs. This approach ensures that global structure and local decisions of the DT model are transparent, verifiable, and meet XAI objectives.
4.6.1. Feature Rankings and Visualization
To understand which features mostly contribute to adversarial detection, we conducted analysis and visualization of the feature importance scores across different UMAP-reduced dimensions. This technique uncovers how the contribution of individual features shifts in higher-dimensional latent spaces. Also, we visualize the 2D and 3D UMAP-generated datasets of the FGSM attack to physically observe the patterns and separability between legitimate and adversarial examples.
Figure 11 shows the relevance of the changes in features in the detection of FGSM attacks as more dimensions show important classifications of the characteristics of FGSM attacks. In Figure 11a, the feature UMAP0 will greatly influence the detection of the FGSM attack as it registers a feature importance score of 0.7, which is more than double that of the UMAP1 feature importance score. Also, in Figure 11b, it is depicted that UMAP0 still shows a stronger effect as the most important feature, with a score of 0.6, while UMAP1 and UMAP2 registered a score of approximately 0.2, in detecting the attack in 3D. In Figure 11c for the 5D, UMAP1 emerges as the most importance feature, followed by UMAP3 and UMAP0. As we further investigate the detection of adversarial attacks on the most important features in reduced dimensions, we generally conclude that image datasets for 2D and 3D dimensions may likely have a consistent feature ranking of a single feature showing as the most importance feature. Also, ee can generally conclude that as more dimensions are reduced there is an instability of consistency of the most important feature in influencing the success of the attack, as seen in Figure 11c. This pattern suggests that FGSM attacks influence multiple dimensions of the data, and the importance of features shifts as the data representation becomes more complex.
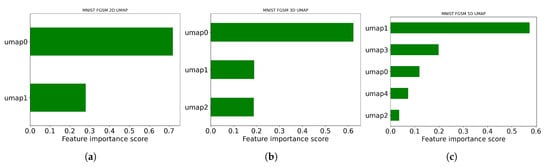
Figure 11.
MNIST UMAP FGSM feature extraction. This figure shows the ranking order in 2D, 3D, and 5D, respectively, of the most important features of the MNIST dataset when FGSM attack is implemented. (a) Features—2D UMAP visualization. (b) Features—3D UMAP visualization. (c) Features—5D UMAP visualization.
In Figure 12, we visualize the 2D and 3D detection of the FGSM attacks to understand the interaction and physical characteristics between the legitimate (green color) and malicious (red color) datasets. As seen in Figure 12a, the malicious dataset overlaps the legitimate dataset on the left, and a few points overlap in the middle. When set to 3D visualization, Figure 12b shows a pattern similar to 2D visualization but more clustered to the top left with few overlap points. It can be observed that in both the 2D and 3D visualization, more than 90% separability was possible between the legitimate and malicious datasets. In the 2D, legitimate datasets are internally separable (that is, individual classes), unlike the 3D case. This explainability gives an overall intuition of the vulnerability of image datasets when embedded via UMAP after being exposed to the FGSM attack.
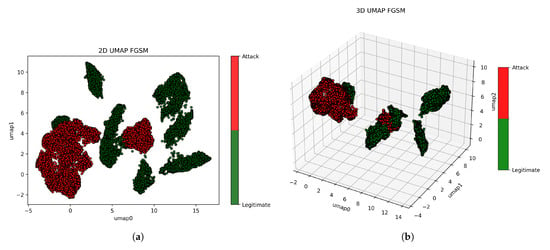
Figure 12.
2D and 3D UMAP visualizations of MNIST under FGSM attack to physically observe the patterns and separability between legitimate (green) and adversarial (red) examples. (a) 2D UMAP plot of legitimate and adversarial examples. (b) 3D UMAP projection of legitimate and adversarial examples.
4.6.2. Rules Extraction
Rules are generated using the DT classifier from the UMAP embedded datasets of 5D and 10D for the Carlini–Wagner attack. Table 9 shows the top three rules with their covering and error sorted by covering of the Carlini–Wagner attacks. It is observed that of the three most important rules, two rules show the detection of the attack (i.e., attack = True) with the highest covering.

Table 9.
Carlini–Wagner: Top 3 rules for MNIST 5D UMAP.
Shown in Table 10 are the rules for the 10D Carlini–Wagner attack, with umap9 as the only feature showing a covering of 100% and 0% error. This means that the attacker will be successful in accurately deceiving the model for the 10D when umap9 .

Table 10.
Carlini–Wagner: Rules for MNIST 10D UMAP.
We conclude that for 5D and 10D extracted rules, 10D effectively captures the attack patterns of the UMAP embedded dataset, with the importance of the feature slightly shifting as the dimension increases. This will provide feature selection strategies for adversarial defense and guide the development of robust classifiers against adversarial attacks of UMAP embedded image datasets.
The rules in Table 10 and Table 11 of the Carlini–Wagner and FGSM attacks achieved the aim of this paper by reaching both extreme simplicity in explainability and zero FPRs and FNRs. It is also worth noting that the rules exploit two different variables for the two attacks. They can, therefore, be used together for a perfect detection of the two attacks in parallel over time (sometimes FGSM, sometimes Carlini). This would not be true if the two models would experience overlapping thresholds over the same variable.

Table 11.
FGSM: Rules for MNIST 10D UMAP.
4.6.3. DeepFool Case Study
Our detection framework was evaluated beyond the adversarial attacks considered so far (e.g., FGSM, Carlini-Wagner), by extending our analysis to also include DeepFool attack [46]. Its core mechanism consists in treating the classifier as a locally linear function and iteratively perturbing the inputs until they cross the decision boundary and make the classifier’s decision change.
We adopted decision tree classifiers on UMAP-transformed legitimate versus DeepFool dataset, by considering several UMAP dimensionalities. The obtained performance, in line with the other attacks (FGSM and Carlini-Wagner), is shown in Table 12, while Table 13 reports an example of the obtained rules.

Table 12.
Detection performance metrics for the DeepFool attack on the MNIST dataset using a decision tree classifier across UMAP dimensions (2D–10D). Metrics are reported using train–test split (TTS) and cross-validation score (CVS) and are all reported in percentages. Attack parameters: , , , , .

Table 13.
DeepFool: Rules for MNIST 10D UMAP.
5. Conclusions and Future Work
In this paper, we investigate the integration of UMAP and explainable AI for the detection of adversarial machine learning in image classification tasks. At the best of authors’ knowledge, this is the first time the Carlini attack is fully detected (without false positives) on the presented datasets. In line with the squeezing idea of [35], the main issue is to find the most proper level of compression of raw input data. The adoption of UMAP on eXplainable AI provides the right way to balance the minimum level of compression, still achieving zero error in detection. The semantic simplicity of the detector, i.e., just a single if-then rule, would open the door to future investigations of more complex scenarios with image and logitudinal data. Future work therefore explores the structure of adversarial clusters in higher dimensional UMAP embeddings, extends the approach to more complex datasets and integrates rule-based detection into real-time defensive pipelines.
Author Contributions
Conceptualization, M.M.; methodology, S.N. and M.M.; software, A.S.K. and E.C.; validation, A.S.K. and S.N.; investigation, all; resources, S.N. and E.C.; data curation, A.S.K.; writing—original draft preparation, A.S.K.; writing—review and editing, all; visualization, A.S.K.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
The manuscript is part of research carried out by the authors within the following projects, funded in part by the European Union–NextGeneration EU and by the Italian Ministry of University and Research (MUR), National Recovery and Resilience Plan (PNRR): Future Artificial Intelligence Research (FAIR), Spoke 3 and Robotics and AI for Socio-economic Empowerment (RAISE), Spoke 2, Mission 4, Component 2, Investment 1.5.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets and codes used to support the findings in this study are publicly available: the MNIST dataset at http://yann.lecun.com/exdb/mnist/ (accessed on 21 July 2025) and the CIFAR-10 dataset at https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 21 July 2025). The legitimate and adversarial UMAP samples generated, along with relevant source code and trained models, are available in the GitHub public repository at https://github.com/AchmedSamuel/UMAP-adversarial-image-detection (accessed on 24 July 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Abbreviation | Full Term |
| AI | Artificial Intelligence |
| XAI | Explainable AI |
| UMAP | Uniform Manifold Approximation and Projection |
| FGSM | Fast Gradient Sign Method |
| CW | Carlini–Wagner |
| PGD | Projected Gradient Descent |
| CNN | Convolutional Neural Network |
| MNIST | Modified National Institute of Standards and Technology |
| CIFAR | Canadian Institute for Advanced Research |
| DT | Decision Tree |
| PCA | Principal Component Analysis |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
| PPV | Positive Predictive Value |
| TPR | True Positive Rate |
| FPR | False Positive Rate |
Appendix A
To tackle concerns about the perceptibility of adversarial perturbations, we provide 2D and 3D visualizations of adversarial instances generated by the Carlini–Wagner and DeepFool attacks on the MNIST dataset. These UMAP-reduced projections give qualitative information on the separability and structural distortions generated by each attack. The visualizations corroborate the idea that the perturbations are subtle and may be imperceptible in pixel space but cause considerable alterations in feature space representations. This is illustrated in the figures below.
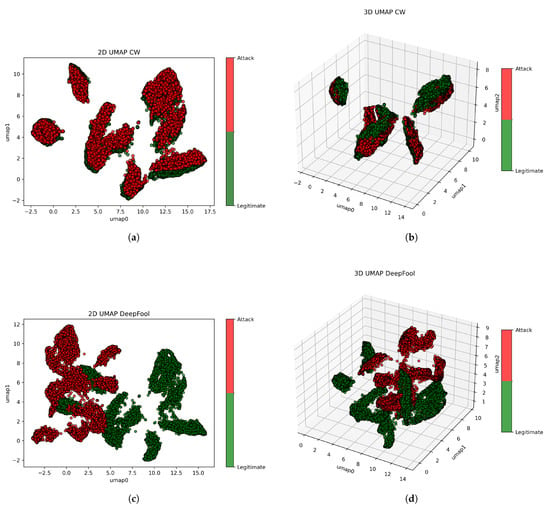
Figure A1.
2D and 3D UMAP visualizations of MNIST dataset samples under Carlini–Wagner (CW) and DeepFool adversarial attacks. (a) 2D UMAP projection showing MNIST samples with Carlini–Wagner perturbations. (b) 3D UMAP embedding of MNIST under Carlini–Wagner attack perturbation. (c) 2D UMAP visualization of MNIST samples affected by DeepFool attack. (d) 3D UMAP embedding showing DeepFool-perturbed MNIST data.
Appendix B
Table A1 and Table A2 below summarize the structure of the datasets associated to the experiments of the paper. It enables rapid prototyping of attacks and detectability, providing clear comparison for adversarial robustness.

Table A1.
Data before UMAP: MNIST datasets prior to dimensionality reduction for legitimate and adversarial.
Table A1.
Data before UMAP: MNIST datasets prior to dimensionality reduction for legitimate and adversarial.
| Dataset | Data Type | Shape | No. Samples | Label |
|---|---|---|---|---|
| MNIST | Clean | (10,000, 784) | 10,000 | 0 |
| MNIST-FGSM | Adversarial | (10,000, 784) | 10,000 | 1 |
| MNIST-CW | Adversarial | (10,000, 784) | 10,000 | 1 |
| MNIST-DeepFool | Adversarial | (7000, 784) | 7000 | 1 |

Table A2.
Data after UMAP: UMAP-transformed datasets used for detection. Each dataset combines clean and adversarial samples and is reduced to n-dimensions 2D space. The CSV files are used for training and evaluating decision tree classifiers and extracting rules.
Table A2.
Data after UMAP: UMAP-transformed datasets used for detection. Each dataset combines clean and adversarial samples and is reduced to n-dimensions 2D space. The CSV files are used for training and evaluating decision tree classifiers and extracting rules.
| Dataset | UMAP | Shape | No. Samples | Label | csv File |
|---|---|---|---|---|---|
| Clean+FGSM | 2D | (20,000, 3) | 20,000 | 0/1 | |
| Clean+CW | 2D | (20,000, 3) | 20,000 | 0/1 | |
| Clean+DeepFool | 2D | (14,000, 3) | 14,000 | 0/1 |
The code structure, also available in the repository, follows the organization reported in the following.
- Trained CNN Models
- —
- Files:
- *
- mnist_CNN_model.h5
- *
- cifar10_CNN_models.h5
- —
- Purpose: Target models to the adversarial attacks, to be wrapped with kerasClassifier.
- Before Detection
- —
- generate_UMAP_adversarial_fgsm_CW.ipynb
- *
- Load pre-trained CNN models.
- *
- Generate adversarial examples using FGSM and CW attacks.
- *
- Evaluate attack success rates.
- —
- generate_UMAP_adversarial_DeepFool.ipynb
- *
- Generate adversarial examples using the DeepFool attack.
- *
- Evaluate the attack success rate.
- After Detection
- —
- umap_detection_metrics_feat_rules_cv.ipynb
- *
- Train decision tree classifiers on UMAP-reduced datasets.
- *
- Compute detection metrics: TPR, FPR, FNR, ACC, PPV, F1-score.
- *
- Extract feature importance and if-then rules.
- —
- fgsm_cw_DeepFool_UMAP_2D_3D_viz.ipynb
- *
- Visualize 2D and 3D UMAP representations of legitimate vs. adversarial samples.
Before the adoption of any adversarial machine learning, CNN models for image classification are built from scratch with accuracies above 99.0% and 74% for MNIST and CIFAR datasets, respectively. The code is based upon Python scikit-learn and tensorflow.
Data management is as follows. The dataset of both legitimate and malicious are separately embedded via UMAP and later vertically combined to generate a single CSV file detailing the features (e.g., umap1, umap2 and attack for 2D case). Each dataset, legitimate and malicious, has 10,000 rows with the first 10,000 rows representing legitimate where attack column is ‘0’ and from 10,000 row to the 20,000 row are malicious with ‘1’ representing attack. The same structure is followed for different UMAP dimensions (3D, 5D, 10D) with a variability in the number of features as the number of dimensions increases while the attack column remains constant. The datasets generated are with respect to 2D, 3D, 5D and 10D for the implemented attacks (FGSM, Carlini and DeepFool).
Typical workflow is as follows. With all the required python libraries and dependencies in place, the MNIST dataset is loaded and preprocessed. The UMAP components (2D, 3D) are then trained and fit with legitimate dataset (X_test) containing 10,000 images, then the pretrained CNN model (MNIST - mnist_CNN_model.h5), trained with 60,000 images is loaded. To generate the adversarial attacks (FGSM and Carlini-Wagner), a classifier is created with the loaded pretrained model. For example, an instance of the FGSM attack (FGSM) is generated by passing the CNN and . This instance is applied to the legitimate dataset to give x_test_adv_fgsm which is embedded via UMAP to create the dataset of UMAP embeddings. The UMAP legitimate and UMAP adversarial are concatenated to produce a file containing both sets. This is given in input to the Decision Tree to learn how to detect the attack. A similar implementation is done for the other attacks.
References
- Pimenidis, E.; Angelov, P.; Jayne, C.; Papaleonidas, A.; Aydin, M. Artificial Neural Networks and Machine Learning. In Proceedings of the 31st International Conference on Artificial Neural Networks (ICANN 2022), Part I, Bristol, UK, 6–9 September 2022. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Ma, Y.; Liu, H.C. Adversarial Attacks and Defenses in Images, Graphs and Text: A Review. Int. J. Autom. Comput. 2019, 17, 151–178. [Google Scholar] [CrossRef]
- Lukas, B.; Kathrin, G.; Michael, B.; Battista, B.; Katharina, K. Mental Models of Adversarial Machine Learning. arXiv 2021, arXiv:2105.03726. [Google Scholar]
- Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 35–57. [Google Scholar] [CrossRef]
- Mortezapour, F.; Perumal, S.T.; Mustapha, N.; Mohamed, R.C. A Comprehensive Overview and Comparative Analysis on Deep Learning Models. J. Artif. Intell. 2024, 6, 302–346. [Google Scholar] [CrossRef]
- Katzir, Z.; Elovici, Y. Who’s Afraid of Adversarial Transferability? arXiv 2021, arXiv:2105.00433. [Google Scholar]
- Vaccari, I.; Carlevaro, A.; Narteni, S.; Cambiaso, E.; Mongelli, M. eXplainable and Reliable Against Adversarial Machine Learning in Data Analytics. IEEE Access 2022, 10, 83949–83970. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar]
- Pal, K.; Sharma, M. Performance evaluation of non-linear techniques UMAP and t-SNE for data in higher dimensional topological space. In Proceedings of the Fourth International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Palladam, India, 7–9 October 2020. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Siddique, A.; Hamid, I.; Li, W.; Nawaz, Q.; Gilani, S.M.M. Image Representation Using Variants of Principal Component Analysis: A Comparative Study. In Proceedings of the 2019 IEEE 11th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 12–15 June 2019. [Google Scholar]
- Nakouri, H.; Limam, M. An Incremental Two-Dimensional Principal Component Analysis for Image Compression and Recognition. In Proceedings of the 2016 12th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Naples, Italy, 28 November–1 December 2016. [Google Scholar]
- Imani, M.; Ghassemian, H. Principal Component Discriminant Analysis for Feature Extraction and Classification of Hyperspectral Images. In Proceedings of the 2014 Iranian Conference on Intelligent Systems (ICIS), Bam, Iran, 4–6 February 2014. [Google Scholar]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality Reduction for Visualizing Single-Cell Data Using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Zu, X.; Wang, Y.; Lelieveldt, B.P.F.; Tao, Q. Deep Recursive Embedding for High-Dimensional Data. IEEE Trans. Neural Netw. Learn. Syst. 2022, 28, 1237–1248. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Huang, B.; Jia, B.; Li, W.; Lü, H. A Boundary Aware WiFi Localization Scheme Based on UMAP and KNN. IEEE Commun. Lett. 2022, 26, 1789–1793. [Google Scholar] [CrossRef]
- Tan, J.W.; Goh, P.Y.; Tan, S.C.; Chong, L.Y. Projecting the Pattern of Adversarial Attack in Low Dimensional Space. In Proceedings of the 2024 12th International Conference on Information and Communication Technology (ICoICT), Bandung, Indonesia, 7–8 August 2024. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing Properties of Neural Networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Sciforce. Adversarial Attacks Explained (And How to Defend ML Models Against Them). 2022. Available online: https://medium.com/sciforce/adversarial-attacks-explained-and-how-to-defend-ml-models-against-them-d76f7d013b18 (accessed on 21 July 2025).
- Biggio, B.; Nelson, B.; Laskov, P. Poisoning Attacks against Support Vector Machines. arXiv 2012, arXiv:1206.6389. [Google Scholar]
- Tramèr, F.; Zhang, F.; Juels, A.; Reiter, M.K.; Ristenpart, T. Stealing Machine Learning Models via Prediction APIs. arXiv 2016, arXiv:1609.02943. [Google Scholar]
- Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership Inference Attacks against Machine Learning Models. arXiv 2016, arXiv:1610.05820. [Google Scholar]
- Kumar, K.N.; Vishnu, C.; Mitra, R.; Mohan, C.K. Black-box Adversarial Attacks in Autonomous Vehicle Technology. In Proceedings of the 2020 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 13–15 October 2020; pp. 1–7. [Google Scholar]
- Xu, L.; Zhai, J. DCVAE-adv: A Universal Adversarial Example Generation Method for White and Black Box Attacks. Tsinghua Sci. Technol. 2024, 29, 430–446. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y. Adversarial Attacks on Image Classification Models – FGSM and Patch Attacks and their Impact. arXiv 2023, arXiv:2307.02055. [Google Scholar]
- Li, H.; Zhou, X.; Liu, M. Adversarial Attacks and Defenses in Image Classification: A Practical Perspective. IEEE Access 2022, 10, 100815–100841. [Google Scholar] [CrossRef]
- Zhao, Q.; Huang, L. Adversarial Attacks on Image Classification Models: Analysis and Defense. arXiv 2023, arXiv:2312.16880. [Google Scholar]
- MachineLearningModels.org. Using Decision Trees for Accurate Fraud Detection in Finance. 2025. Available online: https://machinelearningmodels.org/using-decision-trees-for-accurate-fraud-detection-in-finance/ (accessed on 21 November 2024).
- Xu, W.; Evans, D.; Qi, Y. Feature Squeezing Mitigates and Detects Carlini/Wagner Adversarial Examples. arXiv 2017, arXiv:1705.10686. [Google Scholar]
- Rottmann, M.; Maag, K.; Peyron, M.; Gottschalk, H.; Krejić, N. Detection of Iterative Adversarial Attacks via Counter Attack. J. Optim. Theory Appl. 2023, 198, 892–929. [Google Scholar] [CrossRef]
- Kloster, M.A.; Hernán Cúñale, A.; Mato, G. Noise Based Approach for the Detection of Adversarial Examples. In Proceedings of the VI Simposio Argentino de Ciencia de Datos y GRANdes DAtos (AGRANDA 2020)—JAIIO 49, Virtual, 25–27 November 2020. [Google Scholar]
- THE MNIST DATABASE of Handwritten Digits. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 14 February 2024).
- CIFAR Dataset. Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 10 February 2024).
- Nicolae, M.I.; Sinn, M.; Tran, M.N.; Buesser, B.; Rawat, A.; Wistuba, M.; Zantedeschi, V.; Baracaldo, N.; Chen, B.; Ludwig, H.; et al. Adversarial Robustness Toolbox v1.2.0. 2018. Available online: https://github.com/Trusted-AI/adversarial-robustness-toolbox (accessed on 1 November 2024).
- Myasnikov, E. Using UMAP for Dimensionality Reduction of Hyperspectral Data. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; pp. 1–5. [Google Scholar]
- McInnes, L.; Healy, J.; Saul, N.; Grossberger, L. UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Espadoto, M.; Martins, R.M.; Kerren, A.; Hirata, N.S.; Telea, A.C. Toward a quantitative survey of dimension reduction techniques. IEEE Trans. Vis. Comput. Graph. 2019, 27, 2153–2173. [Google Scholar] [CrossRef]
- Scikit-Learn. Available online: https://en.wikipedia.org/wiki/Scikit-learn (accessed on 29 February 2024).
- Scikit-Learn: Machine Learning in Python. Available online: https://scikit-learn.org/stable/supervised_learning.html#supervised-learning (accessed on 29 February 2024).
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).