Adaptive Multi-Gradient Guidance with Conflict Resolution for Limited-Sample Regression
Abstract
1. Introduction
- Different reference models contribute gradients that emphasize distinct characteristics of the objective.
- Combining these gradients can retain useful directions from each model and offset individual biases.
- An effective fusion rule should consider both directional agreement and the relative importance of each source.
2. Related Works
3. Multi-Gradient Guided Network for Limited-Sample Regression
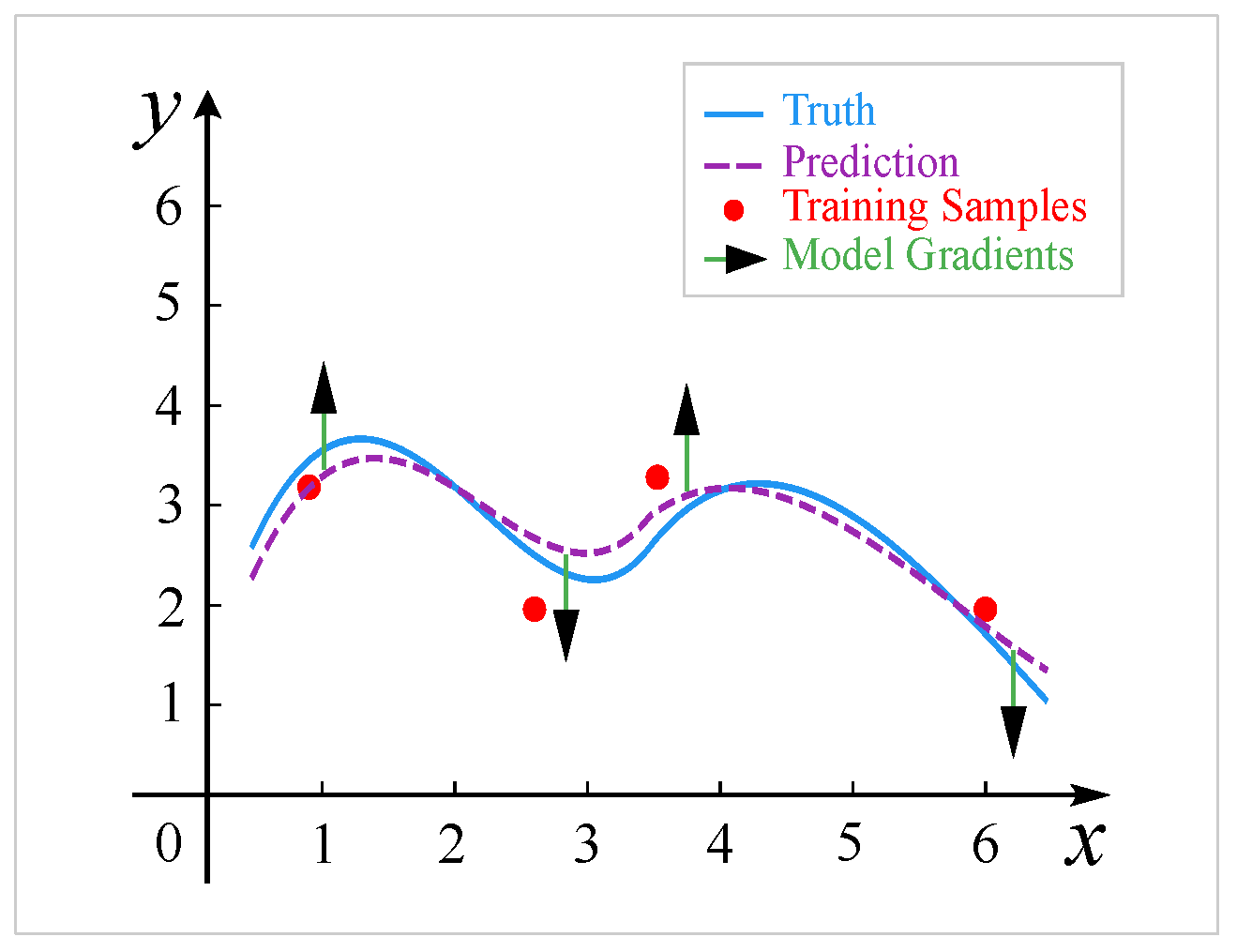
3.1. Gradient-Guided Limited-Sample Regression
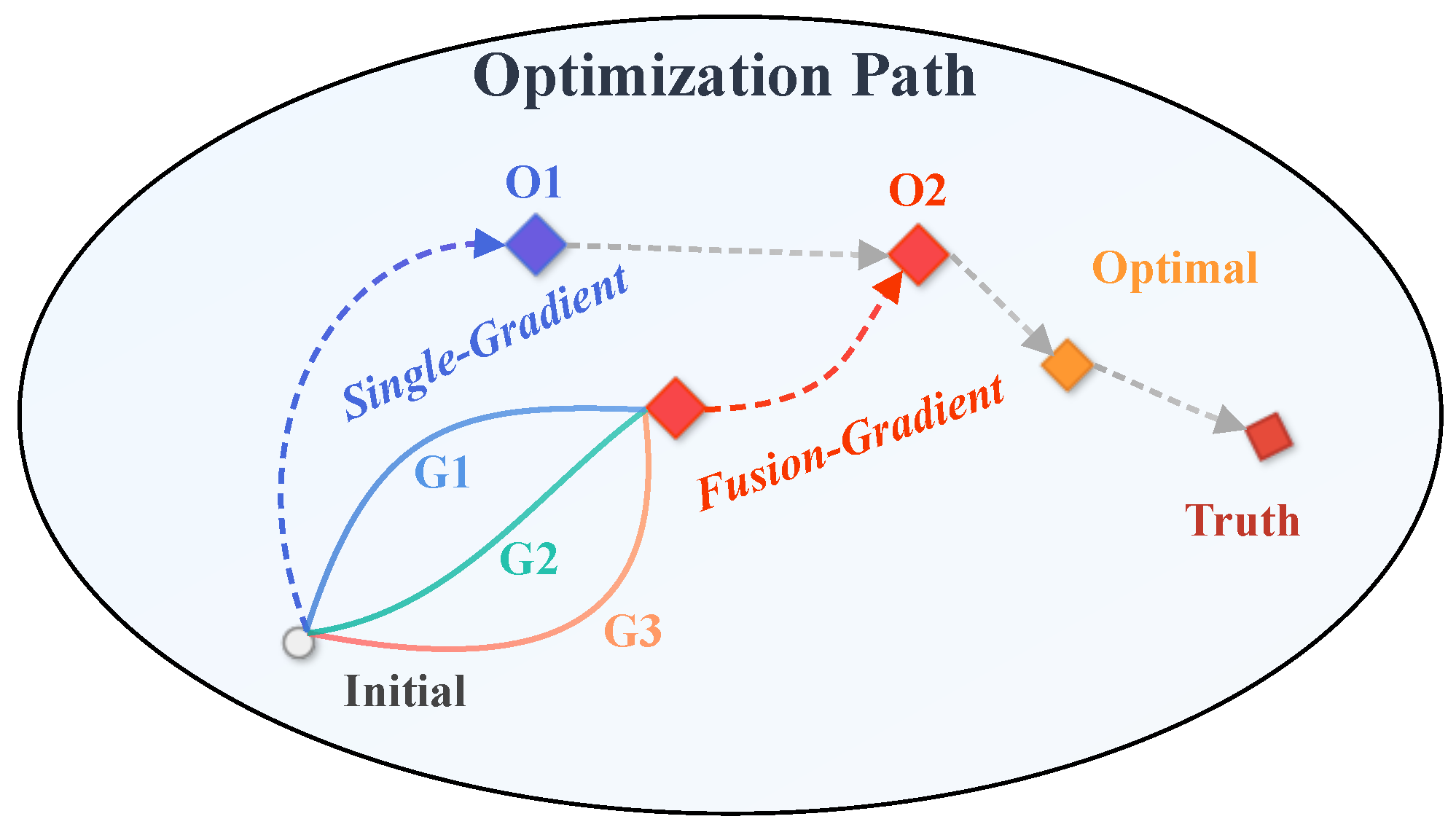
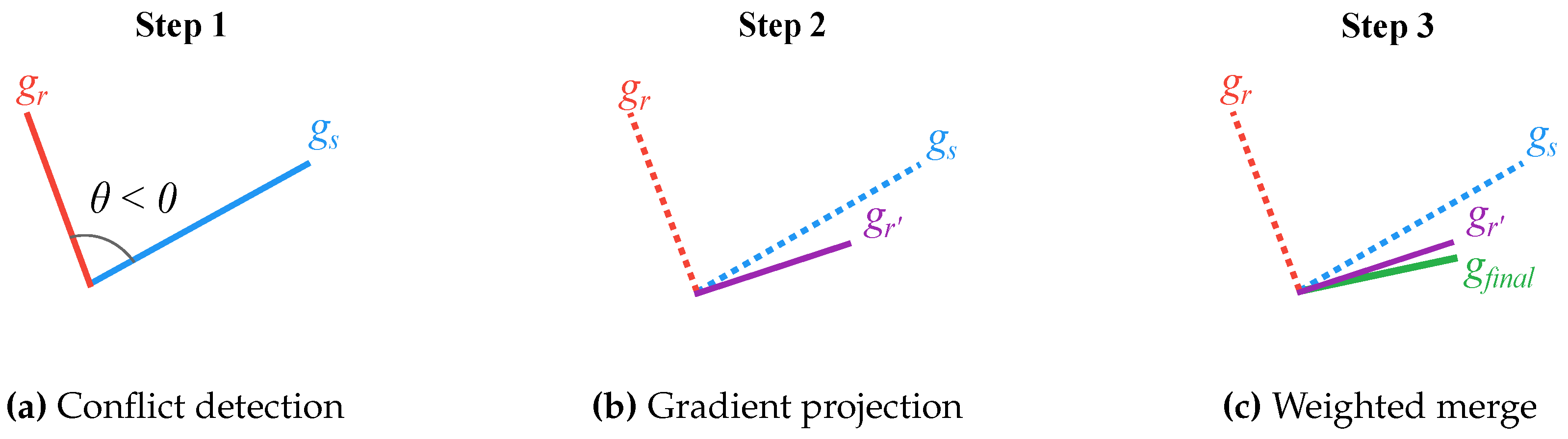
3.2. Multi-Gradient Fusion
3.3. Multi-Gradient Guided Neural Network
| Algorithm 1 Multi-Gradient Guided Neural Network (MGGN) |
|
4. Experiment
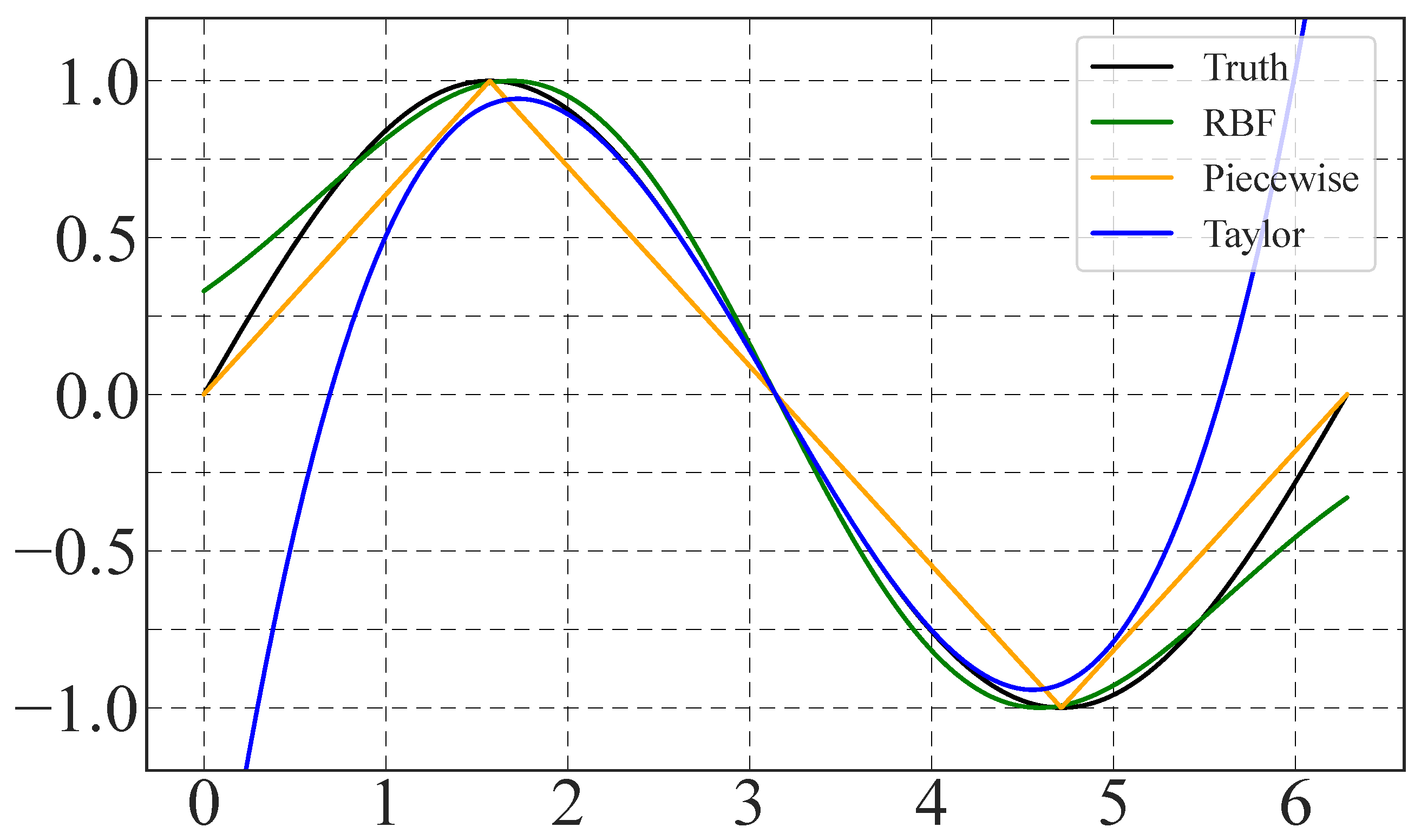
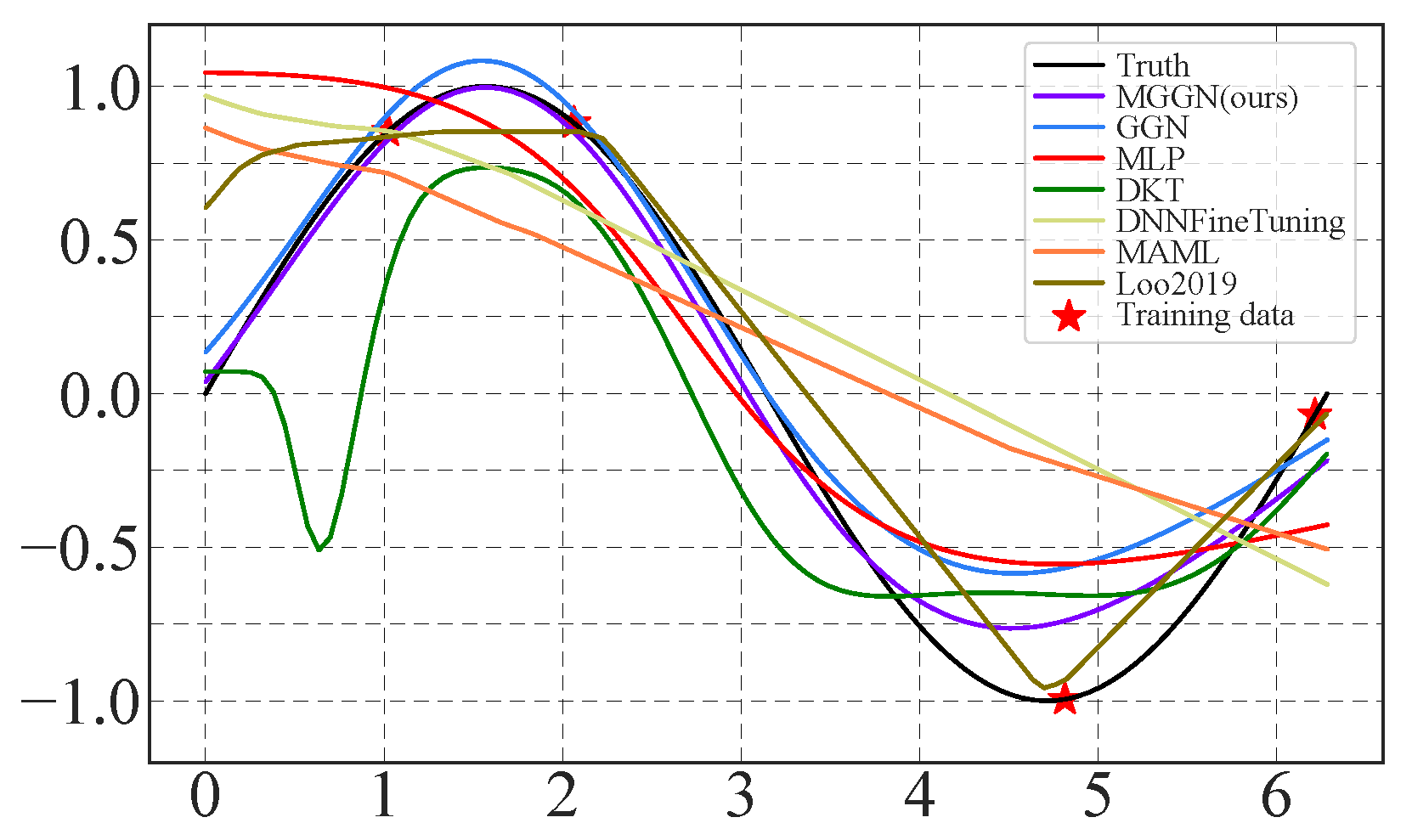
4.1. Sine Regression
4.2. Results Comparison
4.3. Reference Model Combination Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, D.; Liu, Z.; Jia, W.; Liu, H.; Tan, J. Contrastive Decoder Generator for Few-Shot Learning in Product Quality Prediction. IEEE Trans. Ind. Inform. 2022, 19, 11367–11379. [Google Scholar] [CrossRef]
- Ahuja, C.; Sethia, D. Harnessing Few-Shot Learning for EEG signal classification: A survey of state-of-the-art techniques and future directions. Front. Hum. Neurosci. 2024, 18, 1421922. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Yang, Q.; Shao, J.; Wang, G. Runoff Prediction in a Data Scarce Region Based on Few-Shot Learning. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 6304–6307. [Google Scholar]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Qi, H.; Brown, M.; Lowe, D.G. Low-shot learning with imprinted weights. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5822–5830. [Google Scholar]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-sgd: Learning to learn quickly for few-shot learning. arXiv 2017, arXiv:1707.09835. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.S.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Tipton, E. Small sample adjustments for robust variance estimation with meta-regression. Psychol. Methods 2015, 20, 375. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, Z.; Xu, H.; Darrell, T.; Wang, X. Meta-baseline: Exploring simple meta-learning for few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 9062–9071. [Google Scholar]
- Chao, X.; Zhang, L. Few-shot imbalanced classification based on data augmentation. Multimed. Syst. 2023, 29, 2843–2851. [Google Scholar] [CrossRef]
- Shi, P.; Huang, G.; He, H.; Zhao, G.; Hao, X.; Huang, Y. Few-shot regression with differentiable reference model. Inf. Sci. 2024, 658, 120010. [Google Scholar] [CrossRef]
- Yu, T.; Kumar, S.; Gupta, A.; Levine, S.; Hausman, K.; Finn, C. Gradient surgery for multi-task learning. Adv. Neural Inf. Process. Syst. 2020, 33, 5824–5836. [Google Scholar]
- Tang, M.; Jin, Z.; Zou, L.; Shiuan-Ni, L. Learning to Resolve Conflicts in Multi-Task Learning. In Proceedings of the International Conference on Artificial Neural Networks, Crete, Greece, 26–29 September 2023; pp. 477–489. [Google Scholar]
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Patacchiola, M.; Turner, J.; Crowley, E.J.; O’Boyle, M.; Storkey, A.J. Bayesian meta-learning for the few-shot setting via deep kernels. Adv. Neural Inf. Process. Syst. 2020, 33, 16108–16118. [Google Scholar]
- Loo, Y.; Lim, S.K.; Roig, G.; Cheung, N.M. Few-shot regression via learned basis functions. Int. Conf. Learn. Represent. 2019. Available online: https://openreview.net/forum?id=r1ldYi9rOV (accessed on 15 June 2025).
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Zeng, W.; Xiao, Z.Y. Few-shot learning based on deep learning: A survey. Math. Biosci. Eng. 2024, 21, 679–711. [Google Scholar] [CrossRef] [PubMed]
- Baik, S.; Choi, M.; Choi, J.; Kim, H.; Lee, K.M. Learning to learn task-adaptive hyperparameters for few-shot learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 46, 1441–1454. [Google Scholar] [CrossRef] [PubMed]
- Savaşlı, Ç.; Tütüncü, D.; Ndigande, A.P.; Özer, S. Performance analysis of meta-learning based bayesian deep kernel transfer methods for regression tasks. In Proceedings of the 2023 31st Signal Processing and Communications Applications Conference (SIU), Istanbul, Turkey, 5–8 July 2023; pp. 1–4. [Google Scholar]
- Oreshkin, B.; Rodríguez López, P.; Lacoste, A. Tadam: Task dependent adaptive metric for improved few-shot learning. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Sui, X.; He, S.; Zheng, Y.; Che, Y.; Teodorescu, R. Early Prediction of Lithium-Ion Batteries Lifetime via Few-Shot Learning. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Xu, J.; Li, K.; Li, D. An Automated Few-Shot Learning for Time Series Forecasting in Smart Grid Under Data Scarcity. IEEE Trans. Artif. Intell. 2024, 6, 2482–2492. [Google Scholar] [CrossRef]
- Hou, H.; Bi, S.; Zheng, L.; Lin, X.; Quan, Z. Sample-efficient cross-domain WiFi indoor crowd counting via few-shot learning. In Proceedings of the 2022 31st Wireless and Optical Communications Conference (WOCC), Shenzhen, China, 11–12 August 2022; pp. 132–137. [Google Scholar]
- Chen, X.; Yi, J.; Wang, A.; Deng, X. Wi-Fi Fingerprint Based Indoor Localization Using Few Shot Regression. EasyChair Preprint 2024. [Google Scholar] [CrossRef]
- Tian, P.; Xie, S. An adversarial meta-training framework for cross-domain few-shot learning. IEEE Trans. Multimed. 2022, 25, 6881–6891. [Google Scholar] [CrossRef]
- Lim, J.Y.; Lim, K.M.; Lee, C.P.; Tan, Y.X. SSL-ProtoNet: Self-supervised Learning Prototypical Networks for few-shot learning. Expert Syst. Appl. 2024, 238, 122173. [Google Scholar] [CrossRef]

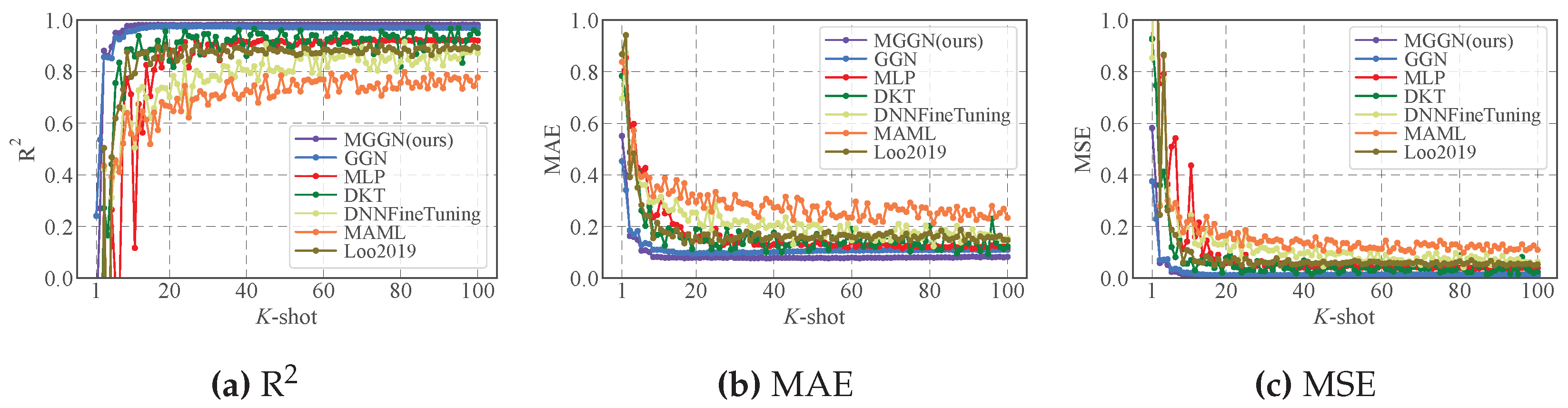
| K | MGGN (Ours) | GGN | MLP | DKT | DNNFineTuning | MAML | Loo2019 |
|---|---|---|---|---|---|---|---|
| 1 | 0.551 ± 0.253 | 0.454 ± 0.194 | 0.784 ± 0.121 | 0.784 ± 0.123 | 0.696 ± 0.274 | 0.838 ± 0.610 | 0.868 ± 0.311 |
| 2 | 0.406 ± 0.233 | 0.342 ± 0.150 | 0.854 ± 0.302 | 0.699 ± 0.106 | 0.873 ± 0.489 | 0.798 ± 0.562 | 0.942 ± 0.587 |
| 3 | 0.163 ± 0.040 | 0.185 ± 0.038 | 0.590 ± 0.162 | 0.488 ± 0.082 | 0.419 ± 0.062 | 0.445 ± 0.059 | 0.392 ± 0.074 |
| 4 | 0.160 ± 0.051 | 0.170 ± 0.041 | 0.598 ± 0.263 | 0.479 ± 0.187 | 0.533 ± 0.362 | 0.572 ± 0.446 | 0.484 ± 0.505 |
| 5 | 0.149 ± 0.045 | 0.183 ± 0.053 | 0.428 ± 0.116 | 0.414 ± 0.145 | 0.395 ± 0.063 | 0.405 ± 0.078 | 0.351 ± 0.108 |
| 6 | 0.107 ± 0.019 | 0.129 ± 0.020 | 0.416 ± 0.238 | 0.262 ± 0.081 | 0.361 ± 0.039 | 0.393 ± 0.056 | 0.283 ± 0.074 |
| 7 | 0.108 ± 0.025 | 0.136 ± 0.022 | 0.427 ± 0.207 | 0.203 ± 0.043 | 0.362 ± 0.073 | 0.400 ± 0.049 | 0.243 ± 0.071 |
| 8 | 0.102 ± 0.041 | 0.132 ± 0.037 | 0.291 ± 0.114 | 0.277 ± 0.131 | 0.296 ± 0.092 | 0.389 ± 0.084 | 0.241 ± 0.113 |
| 9 | 0.082 ± 0.008 | 0.111 ± 0.019 | 0.236 ± 0.082 | 0.174 ± 0.053 | 0.295 ± 0.057 | 0.317 ± 0.049 | 0.156 ± 0.057 |
| 10 | 0.083 ± 0.007 | 0.110 ± 0.013 | 0.245 ± 0.093 | 0.167 ± 0.048 | 0.301 ± 0.078 | 0.355 ± 0.068 | 0.215 ± 0.037 |
| K | MGGN (Ours) | GGN | |||||
|---|---|---|---|---|---|---|---|
| PRT | PR | PT | RT | P | R | T | |
| 1 | 0.551 ± 0.253 | 0.477 ± 0.193 | 0.533 ± 0.224 | 0.800 ± 0.236 | 0.454 ± 0.194 | 0.388 ± 0.144 | 1.237 ± 0.156 |
| 2 | 0.406 ± 0.233 | 0.267 ± 0.059 | 0.344 ± 0.297 | 0.356 ± 0.338 | 0.342 ± 0.150 | 0.269 ± 0.103 | 0.853 ± 0.444 |
| 3 | 0.163 ± 0.040 | 0.282 ± 0.159 | 0.235 ± 0.103 | 0.379 ± 0.352 | 0.185 ± 0.038 | 0.204 ± 0.037 | 0.370 ± 0.110 |
| 4 | 0.160 ± 0.051 | 0.217 ± 0.066 | 0.171 ± 0.057 | 0.168 ± 0.057 | 0.170 ± 0.041 | 0.167 ± 0.027 | 0.326 ± 0.211 |
| 5 | 0.149 ± 0.045 | 0.162 ± 0.031 | 0.116 ± 0.036 | 0.153 ± 0.043 | 0.183 ± 0.053 | 0.164 ± 0.033 | 0.266 ± 0.060 |
| 6 | 0.107 ± 0.019 | 0.134 ± 0.023 | 0.102 ± 0.027 | 0.160 ± 0.030 | 0.129 ± 0.020 | 0.132 ± 0.018 | 0.283 ± 0.066 |
| 7 | 0.108 ± 0.025 | 0.140 ± 0.023 | 0.100 ± 0.023 | 0.138 ± 0.024 | 0.136 ± 0.022 | 0.130 ± 0.024 | 0.282 ± 0.062 |
| 8 | 0.102 ± 0.041 | 0.132 ± 0.015 | 0.103 ± 0.016 | 0.154 ± 0.021 | 0.132 ± 0.037 | 0.128 ± 0.015 | 0.299 ± 0.065 |
| 9 | 0.082 ± 0.008 | 0.118 ± 0.017 | 0.097 ± 0.007 | 0.170 ± 0.065 | 0.111 ± 0.019 | 0.115 ± 0.016 | 0.275 ± 0.044 |
| 10 | 0.083 ± 0.007 | 0.111 ± 0.017 | 0.106 ± 0.015 | 0.149 ± 0.014 | 0.110 ± 0.013 | 0.121 ± 0.017 | 0.308 ± 0.059 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Lin, J.; Zhang, K.; Zheng, Q.; Lin, L.; Chen, Q. Adaptive Multi-Gradient Guidance with Conflict Resolution for Limited-Sample Regression. Information 2025, 16, 619. https://doi.org/10.3390/info16070619
Lin Y, Lin J, Zhang K, Zheng Q, Lin L, Chen Q. Adaptive Multi-Gradient Guidance with Conflict Resolution for Limited-Sample Regression. Information. 2025; 16(7):619. https://doi.org/10.3390/info16070619
Chicago/Turabian StyleLin, Yu, Jiaxiang Lin, Keju Zhang, Qin Zheng, Liqiang Lin, and Qianqian Chen. 2025. "Adaptive Multi-Gradient Guidance with Conflict Resolution for Limited-Sample Regression" Information 16, no. 7: 619. https://doi.org/10.3390/info16070619
APA StyleLin, Y., Lin, J., Zhang, K., Zheng, Q., Lin, L., & Chen, Q. (2025). Adaptive Multi-Gradient Guidance with Conflict Resolution for Limited-Sample Regression. Information, 16(7), 619. https://doi.org/10.3390/info16070619





