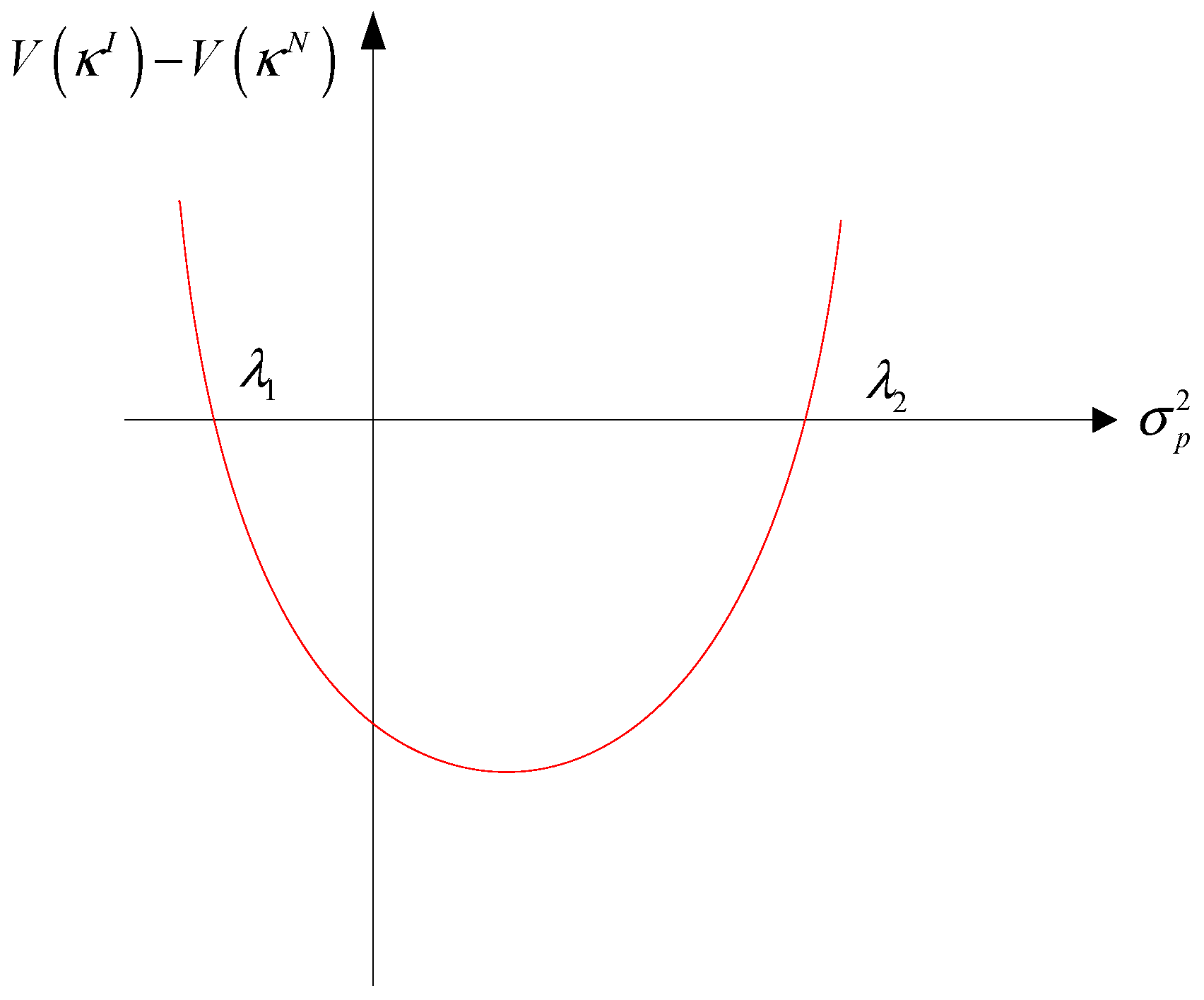Blockchain Adoption or Not? Analysis of Demand Information Sharing in Maritime Supply Chain

Abstract

This study examines whether adopting blockchain technology can enhance maritime supply chain performance by improving information sharing in the presence of mismatches between service capacity and demand. We analyze a maritime supply chain with one port and one carrier. Depending on whether the port and the carrier adopt blockchain technology to share forecast information, we consider two scenarios: neither party adopts the technology, or both the port and the carrier adopt it. We find that when the port’s ex ante expected demand is relatively low, the adoption of blockchain technology not only incentivizes the port to expand its service capacity but also increases the actual demand from the carrier. In addition, when the port has a high forecasting accuracy, it prompts both the port and the carrier to make more stable decisions on the service capacity and freight rates under demand uncertainty. Finally, while the port and the carrier exhibit conflicting incentives to adopt blockchain technology, these tensions can nonetheless be reconciled. This alignment becomes possible due to blockchain’s spillover effect: by enabling information sharing, it facilitates a closer match between the port’s service capacity and the carrier’s realized demand.

1. Introduction

In recent years, the maritime supply chain has faced unprecedented demand uncertainty due to unpredictable events such as public health events and geopolitical tensions [1]. In response, some carriers, such as Maersk [2] and CMA CGM [3], adopt big data technology or information systems to forecast market demand and mitigate the impact of demand uncertainty [4]. At the same time, some carriers start to share their forecasting demand information with upstream ports. For example, DexFreight collaborates with the Port of Antwerp-Bruges on information sharing and commits to improving the operational efficiency and service transparency of ports and carriers [5,6]. Sharing forecast information among supply chain members can mitigate the impact of demand uncertainty [7] and facilitate supply and demand coordination [8]. In addition, information sharing can effectively reduce decision volatility among supply chain members. In the absence of information sharing, demand surges or port congestion often lead to sharp volatility in freight rates, which in turn disrupts the stability of the entire supply chain [9]. By improving information consistency among supply chain participants, information sharing mitigates decision-making volatility [10], the effect of which has already been observed in other industries [11].

Blockchain technology, as a decentralized digital ledger system, has been increasingly applied in supply chain management in recent years to support trustworthy and efficient information sharing. Compared with traditional information sharing methods, the low cost and high reliability of blockchain create new opportunities and advantages for its adoption [12]. Blockchain technology has also begun to be applied in maritime supply chains, with well-known platforms such as TradeLens and Ethereum [13]. However, despite the potential benefits, many members of the maritime supply chain are unwilling to adopt blockchain technology. A notable example is TradeLens, a blockchain technology platform launched by Maersk to foster information sharing across industry players, including direct competitors [14]. However, due to limited cooperation from participants, the initiative was terminated in 2022 [15]. Such reluctance is rational, because adopting blockchain may create a dilemma: on one hand, increased information availability can improve operational decisions; on the other hand, participants in the blockchain can exploit the information shared by others, which reduces the value of their private information. In addition, inaccurate forecast information further complicates the decision for members of the maritime supply chain to participate in the blockchain platform to share their forecast information. Inaccurate information not only reduces the value of shared information but also undermines the overall supply chain performance [16].

The above discussion indicates that although adopting blockchain technology in the maritime supply chain enhances the transparency of demand information and mitigates demand uncertainty, it may nonetheless be detrimental to the participants. Thus, we aim to answer the following research questions:

(1)

What impact does blockchain technology have on the decision-making of supply chain members? Can it help supply chain members reduce decision-making fluctuations?

(2)

Under what conditions do the port and the carrier agree to adopt blockchain technology?

To answer the above questions, we construct a shipping supply chain model consisting of a port and a carrier, where the port operates an information sharing platform developed based on blockchain technology [5,6]. Both the port and the carrier forecast demand information and consider whether to adopt blockchain technology to share their private forecasts. It is important to note that if only the port or carrier adopts blockchain technology, information sharing cannot be realized. In other words, blockchain-based information sharing is feasible only when both the port and the carrier adopt the technology. Accordingly, we develop two scenarios based on whether blockchain technology is adopted: (i) neither the port nor the carrier adopts blockchain technology; (ii) both the port and the carrier adopt blockchain technology. We compare the static equilibrium solutions under the two scenarios, identify the conditions under which blockchain adoption occurs, and examine how information sharing affects the decisions of supply chain members.

Our key findings are as follows. We find that when the port’s ex ante expected demand is relatively low, the adoption of blockchain technology not only incentivizes the port to expand its service capacity but also increases the actual demand from the carrier. In addition, when the port has a high forecasting accuracy, it prompts both the port and the carrier to make more stable decisions on service capacity and freight rates under demand uncertainty. Finally, while the port and the carrier exhibit conflicting incentives to adopt blockchain technology, these tensions can nonetheless be reconciled. This alignment becomes possible due to blockchain’s spillover effect: by enabling information sharing, it facilitates a closer match between the port’s service capacity and the carrier’s realized demand.

The remaining part of our work will unfold in the following order. In Section 2, we will review the relevant literature and explore the uniqueness of this study. In Section 3, we will introduce the model we constructed and explain the relevant symbols. The model solution will be arranged in Section 4. We will analyze the impact of the motivation behind the port and the carrier sharing information in Section 5. We will expand our model in Section 6. Section 7 summarizes our research. All proofs are included in the Appendix A.

2. Literature Review

Our work is closely relevant to demand uncertainty in the maritime supply chain. Traditional research in this area has focused on exploring the impact of market demand uncertainty on the decision-making of maritime supply chain members. Wang and Meng [17] used an algorithm to try to determine the optimal freight decision of the carrier in the spot market under uncertain demand. Their algorithm addressed the real-world pricing problem of spot container shipping, where both the spot demand and the vessel’s available capacity are subject to uncertainty. Zheng et al. [18] considered the pricing strategies of two competing ocean shipping companies facing uncertain demand. Their findings provided the necessary and sufficient conditions for determining whether the optimal prices of the two carriers are positively or negatively affected by the intensity of competition. Nomikos and Tsouknidis [19] sorted out the demand and supply shocks driving the shipping and freight market and evaluated their impact on net contracting activities. Their findings constructed a new shipping demand index and quantified policy-relevant issues by illustrating scenario forecasts of actual freight rate responses to unexpected demand and supply shocks. Song and Wang [20] studied a model of slot allocation and exchange within a shipping alliance under profit-sharing agreements and demand uncertainty. They subsequently developed a customized pattern search-based algorithm to solve the model, ensuring that it could simultaneously enhance the profits of shipping companies within the alliance and maintain fairness among alliance members. To our knowledge, certain unforeseen events, such as the outbreak of COVID-19, had the potential to cause significant disruptions to the maritime supply chain. Depellegrin et al. [21] conducted an empirical study on the impact of unforeseen events on the marine environment. Their findings indicated that such events could lead to severe fluctuations in the shipping demand, with market demand even experiencing temporary termination. Currently, demand interruptions in maritime supply chain are a focal point for many researchers. Jeong and Kim [22] considered and solved the problem of finding a reliable facility location for foldable container disruptions. Siswanto et al. [23] examined supply and transportation disruptions and developed several scenarios for recovery from the disruptions. They found that the best scenario was selected by finding trade-offs or compromises between key performance indicators. Xiao and Bai [24] took the scenario of demand interruption pressures in several Chinese ports as an example, investigating the potential impacts of demand interruption pressures on container trade routes. Their results indicated that interruptions in Chinese ports could have significant implications for major global trade routes. However, the abovementioned literature aimed to analyze the qualitative impacts of demand uncertainty/disruption and does not describe market demand uncertainty from a forecasting perspective. Zhao et al. [25] investigated from the perspective of investment in forecasting information channels. They built a three-tier maritime supply chain model based on the assumption that demand interruptions are a primary cause of asymmetric information. Their study explored the impacts of stochastic demand disruptions and channel competition, suggesting that the decision to invest in predictive information channels depended on the chain members’ attitudes towards interruption risks. In contrast, we examine a maritime supply chain consisting of a port and a carrier, where both the port and the carrier can forecast information related to market demand uncertainty. Our focus is on the incentives for both parties to adopt blockchain technology to share information, particularly in the context of demand mismatches.

Our work is related to information asymmetry in a (maritime) supply chain. Information asymmetry in the existing literature mainly focuses on cost information asymmetry and demand information asymmetry. Several studies have addressed cost information asymmetry. Wu and Yu [26] investigated the impact of blockchain technology on platform supply chains from the perspective of information transparency and transaction costs. They found that blockchain technology can become a powerful weapon for platforms to adjust prices and control the market. Cheng et al. [27] developed a cost data model that includes the required confidential cost information. They found that project members can have reliable and confidential cost data for dispute resolution and cost analysis, as well as efficient cost data access and transmission. We focus on demand information asymmetry in the supply chain. Kumar et al. [28] emphasized the information asymmetry in supplier evaluation and used signaling theory to analyze information asymmetric behavior. They pointed out that for focal buyers, the instability of the supplier’s downstream self-network can serve as a signal of supplier unreliability, thereby reducing the price buyers pay to suppliers in service exchanges. Li et al. [29] used satellite-based Automatic Information System (AIS) data to identify liner shipping companies’ services in each market. They found that both HHI and CR at the alliance level were negatively correlated with freight rates, meaning that shipping alliances may help lower prices. Li et al. [30] used a novel asymmetric multifractal detrended fluctuation analysis method. They found that the main shipping freight rates in Xi’an are multifractal, and their multifractal properties tend to increase with the increase in the fractal scale. Li et al. [16] explored the factors that affect the value of supply disruption information and how the accuracy of information affects its value. Their results suggested that information accuracy, particularly information bias and information variance, play an important role in determining the value of the disruption of information. Most of them focus on the value of private information, and our work mainly discusses the incentives for carriers to adopt blockchain technology and share information with the port, as well as the impact of blockchain technology on the decision-making stability.

Our work is also closely related to maritime information sharing (by blockchain technology). Researchers have explored various aspects. For example, Parthibaraj et al. [31] developed a sustainable decision-making model for allocating vessel capacity to meet the shipping demand and generate route planning. Their proposed model and approach help liner shipping managers better achieve their desired economic and social sustainability goals through the sharing of information, costs, and benefits. Based on this conclusion, more and more literature has shown that maritime supply chain members are motivated to build blockchain technology platforms to promote information sharing. Lind et al. [32] suggested that future shipping will involve collaboration through digitization. Their conclusions suggested that the amount of data shared through digital data flows will grow significantly, new opportunities for enhanced transparency will continue to emerge, and new avenues for collaboration will continue to emerge. Ivanov et al. [33] have designed a blockchain technology platform in the cloud, utilizing third-party physical or digital assets to redesign and manage supply chain networks for improved collaboration among maritime supply chain members. Their results summarized several aspects related to the main generic characteristics of cloud supply chains. Based on these aspects, future research directions were discussed, including the new context of Industry 5.0. Xiao et al. [34] provided an understanding of information-sharing incentives for blockchain technology platform participants from the perspectives of supporters and contributors and proposed strategies based on varying privacy costs. They found that when platform firms take the lead, key players with high privacy costs should be subsidized to compensate for the negative externalities of data. Another study evaluated the potential impact of digital trade processes on the international shipping ecosystem [35]. Their results highlighted the motivations and opportunities for digitalization of shipping processes and point to its impact on business models and operations. While blockchain technology platforms can simplify the complexity of day-to-day transactions among chain members and enhance operational efficiency, participants are not always willing to share data. Yang and Lin [36] developed a model encompassing digitalization, the adoption of digital logistics platforms, organizational digital transformation, and organizational performance, and tested the relationships among these factors through six research hypotheses. Their findings indicated that, at the current stage, the adoption of digital logistics platforms does not have a significant impact on organizational performance. Other related studies also indicate that the adoption of digital technologies is subject to conditional limitations. Huang et al. [37] considered a duopoly market structure, exploring information-sharing strategies in scenarios of price competition and quality competition. Their study indicated that the decision of liner companies to invest in demand forecasting information and the decision to share information depends on the accuracy of demand forecasting information. Liu et al. [38] analyzed the optimal carbon reduction technology adoption strategies for enterprises in turbulent environments under quota and trading systems. Their results indicated that the impact of information sharing on profits varies under different technological conditions, and the optimal adoption of technology will change with changes in carbon prices. Differing from the studies mentioned above, our research investigates the incentives for both the port and the carrier to adopt blockchain technology and share information, particularly in the presence of mismatches between port service capacity and carrier demand.

3. Model Framework

We consider a maritime supply chain consisting of a port and a carrier. The port offers service capacity, and the carrier is responsible for providing maritime transportation services. All members are risk-neutral and aim to maximize their profits. We use game theory models to describe the decisions of supply chain participants because the mathematical formulation of game theory models allows us to precisely define real-life concepts, such as coordination, demand volatility, and capacity alignment, and better understand the motivations behind the actions and decisions of supply chain participants [39]. By using game theory models, we can simulate important features of real-world situations and derive optimal decisions for the participants, thereby gaining a deeper understanding of these situations [40]. The demand functions are as follows:

$$Q=a+\xi -p+\gamma \left(\kappa -Q\right),$$

(1)

where $a+\xi$ is the demand intercept and represents the market potential, and $\xi$ is used to represent the market uncertainty, which is a normally distributed random variable with mean zero and variance ${\sigma }^2$. $\gamma$ represents the punishment parameters. $\gamma \left(\kappa -Q\right)$ indicates the effect of port congestion on the demand, where $\kappa$ is the port’s service capacity and is the decision-making variable for the port. Clearly, $\gamma \left(\kappa -Q\right)$ shows that when a port’s service capacity exceeds demand, cargo can be handled promptly, which positively impacts port demand. Conversely, if the port’s service capacity falls short of demand, congestion occurs, negatively affecting port demand. Demand functions have been widely adopted in the marketing science and operations management literature (e.g., [41,42]). The carrier uses the market-information-gathering techniques to forecast about $\xi$; then, carrier $i$ obtains a forecast $Y_i$ regarding random part $\xi$ of the demand function:

$$Y_i=\xi +{\epsilon }_i, \mathrm{for} i=c,p.$$

(2)

where $Y_i$ represents carrier $i$’s forecast about $\xi$, and ${\epsilon }_i$ is the carrier $i$’s error in the forecast. ${\epsilon }_i$ is independent of the market uncertainty $\xi$ and carrier $j$’s forecast error ${\epsilon }_j$. ${\epsilon }_i$ is normally distributed with mean zero and variance ${\sigma }_i^2$, so $Y_i$ is an unbiased estimator of $\xi$. According to Vives [43], Raju and Roy [44], and Mishra et al. [45], we have some assumptions regarding the conditional expectations and variances, as follows:

$$E[\xi \left|Y_i\right.]=E[Y_j\left|Y_i\right.]={\displaystyle \frac{{\sigma }^2{Y}_i}{{\sigma }^2+{\sigma }_i^2}}, \mathrm{for} i=c,p, j\ne i,$$

(3)

$$V[\xi \left|Y_i\right.]={\displaystyle \frac{{\sigma }^2{\sigma }_i^2}{{\sigma }^2+{\sigma }_i^2}}, \mathrm{for} i=c,p,$$

(4)

$$E[\left.\xi \right|Y_c,Y_p]={\displaystyle \frac{{\sigma }^2{\sigma }_p^2{Y}_c+{\sigma }^2{\sigma }_c^2{Y}_p}{{\sigma }^2{\sigma }_p^2+{\sigma }^2{\sigma }_c^2+{\sigma }_p^2{\sigma }_c^2}},$$

(5)

$$V[\xi \left|Y_c\right.,Y_p]={\displaystyle \frac{{\sigma }^2{\sigma }_c^2{\sigma }_p^2}{{\sigma }^2{\sigma }_c^2+{\sigma }^2{\sigma }_p^2+{\sigma }_c^2{\sigma }_p^2}}.$$

(6)

Please see

Table 1. Summary of notations.

Parameters	Title 2
$a$	Constant portion of potential market size
$c$	Adjustment cost of service capability
$\xi$	Variable portion of potential market size
${\sigma }^2$	Variance of the variable $\xi$
$\gamma$	Cross-price sensitivity parameter
$Y_i$	Signal regarding $\xi$ received by carrier $i$
${\epsilon }_i$	Carrier $i$’s error in the forecast regarding $\xi$
${\sigma }_i^2$	Variance of the variable ${\epsilon }_i$
$\mu$	Port’s service fee
$Q_i$	Carrier $i$’s transport demand
Decision variables
$\kappa$	Port’s service capability
$p_i$	Carrier $i$’s freight rate
Objective functions
$\mathrm{\Pi }$	Profit of the port
$\pi$	Profit of the carrier

for a summary of parameters and notations which will be used in our model formulation:

The sequence of events in this game are illustrated in Figure 1. The game unfolds in four stages. In the first stage, the port and the carrier simultaneously decide whether to adopt blockchain technology to share forecast information. In the second stage, the port determines its service capacity based on the information available. In the third stage, the carrier sets the freight rate according to its own information. In the final stage, market demand uncertainty is realized. We assume that the carrier must truly share its information with the port, if the carrier adopts blockchain technology.

4. Model Analysis

In this section, depending on whether the port and the carrier adopt blockchain technology to share forecast information, we consider two scenarios: neither party adopts the technology, or both the port and the carrier adopt it. We use backward induction to solve these two models. For clarity and consistency, we use superscripts N and I to denote scenarios N and I, respectively.

4.1. Scenario N

We first examine scenario N, in which neither the port nor the carrier adopts blockchain technology. In this case, the carrier does not share its information with the port. In this scenario, the parties’ expected profits are as follows:

$$E[\mathrm{\Pi }\left|Y_p\right.]=E[\left(\mu -c{\kappa }^N\right)Q^N\left|Y_p\right.],$$

(7)

$$E[\pi \left|Y_c\right.]=E[{\displaystyle \frac{\left(p^N-\mu \right)\left(a+\xi -p^N+\gamma {\kappa }^N\right)}{1+\gamma }}\left|Y_c\right.],$$

(8)

where ${\kappa }^N$ is the port’s service capacity. In the first stage, as the leader, the port decides the service capacity. In the second stage, as the followers, the carrier determines the freight rates after observing the port’s decision, respectively. We use backward induction to solve the two-stage game. Therefore, given the port’s service capacity ${\kappa }^N$, the carrier simultaneously selects the freight rates $p$ to maximize its profits, as follows:

$$\underset{p}{\max }E[\pi \left|Y_c\right.]=E[{\displaystyle \frac{\left(p-\mu \right)\left(a+\xi -p+\gamma {\kappa }^N\right)}{1+\gamma }}\left|Y_c\right.]$$

(9)

Similarly to Gal-Or et al. [46], we assume that the carrier uses the decision rule $p_i=A_0+A_1\mu +A_2{Y}_i$ to select the freight rate. From the two first-order conditions, we have

$$2p^N=a+E[\xi \left|Y_c\right.]+\gamma {\kappa }^N+\mu .$$

(10)

Substituting $p_i=A_0+A_1\mu +A_2{Y}_i$ into the right side of (10), the carrier $i$’s optimal freight rates are given by

$$p^N={\displaystyle \frac{a+E[\xi \left|Y_c\right.]+\gamma {\kappa }^N+\mu }{2}}.$$

(11)

We proceed to analyze the port’s service capacity decision in the first stage. The port’s decision problem is given by the following function:

$$\underset{\kappa }{\max }E[{\mathrm{\Pi }}^N]=E[\mathrm{\Pi }\left|Y_p\right.]=E[\left(\mu -c\kappa \right)Q\left|Y_p\right.].$$

(12)

Before making decisions on service capabilities, the port needs to predict pricing and anticipate actual demand. Therefore, port enterprises predict that the freight rate and demand of carrier will be

$$E[p^N\left|Y_p\right.]={\displaystyle \frac{a+E[E[\xi \left|Y_c\right.]\left|Y_p\right.]+\gamma \kappa +\mu }{2}},$$

$$E[Q^N\left|Y_p\right.]={\displaystyle \frac{a+2E[\xi \left|Y_p\right.]-E[E[\xi \left|Y_c\right.]\left|Y_p\right.]-\mu +\gamma {\kappa }^N}{2\left(1+\gamma \right)}}.$$

Substituting this into Equation (12), we can rewrite the port’s decision problem as follows:

$$E[{\mathrm{\Pi }}^N\left|Y_p\right.]=\left(\mu -c{\kappa }^N\right){\displaystyle \frac{a+\frac{{\sigma }^2\left({\sigma }^2+2{\sigma }_c^2\right)Y_p}{\left({\sigma }^2+{\sigma }_c^2\right)\left({\sigma }^2+{\sigma }_p^2\right)}-\mu +\gamma {\kappa }^N}{2\left(1+\gamma \right)}}.$$

(13)

Based on the first-order condition for the port’s decision problem, we can obtain the optimal service capacity, as follows:

$${\kappa }^N={\displaystyle \frac{c\mu +\gamma \mu -ca}{2\gamma c}}-{\displaystyle \frac{2E[\xi \left|Y_p\right.]-E[E[\xi \left|Y_c\right.]\left|Y_p\right.]}{2\gamma }}.$$

(14)

Substituting (14) into (11), the carrier’s optimal freight rate is obtained as

$$p^N={\displaystyle \frac{ca+3c\mu +\gamma \mu }{4c}}-{\displaystyle \frac{{\sigma }^2\left({\sigma }^2+2{\sigma }_c^2\right)Y_p}{4\left({\sigma }^2+{\sigma }_c^2\right)\left({\sigma }^2+{\sigma }_p^2\right)}}+{\displaystyle \frac{E[\xi \left|Y_c\right.]}{2}}.$$

(15)

Substituting (15) into (1), the corresponding conditional demand quantities in scenario NN are obtained:

$$Q^N={\displaystyle \frac{\frac{ca-c\mu +\gamma \mu }{2c}-\frac{{\sigma }^2\left({\sigma }^2+2{\sigma }_c^2\right)Y_p}{2\left({\sigma }^2+{\sigma }_c^2\right)\left({\sigma }^2+{\sigma }_p^2\right)}+2\xi -\frac{{\sigma }^2{Y}_c}{{\sigma }^2+{\sigma }_c^2}}{2\left(1+\gamma \right)}}.$$

(16)

Then, substituting (14) and (15) into (7) and (8), the carrier’s and the port’s ex ante expected profits are obtained as

$$E[{\mathrm{\Pi }}^N]={\displaystyle \frac{{\left(\gamma \mu -c\mu +ca\right)}^2}{8\gamma c\left(1+\gamma \right)}}+{\displaystyle \frac{c{\sigma }^4{\left({\sigma }^2+2{\sigma }_c^2\right)}^2}{8\gamma \left(1+\gamma \right){\left({\sigma }^2+{\sigma }_c^2\right)}^2\left({\sigma }^2+{\sigma }_p^2\right)}},$$

(17)

$$E[{\pi }^N]={\displaystyle \frac{{\left(ca-c\mu +\gamma \mu \right)}^2}{16c^2\left(1+\gamma \right)}}+{\displaystyle \frac{{\sigma }^4\left({\sigma }^4-4{\sigma }_c^4-8{\sigma }^2{\sigma }_c^2+4{\sigma }^2{\sigma }_p^2+4{\sigma }_p^2{\sigma }_c^2\right)}{16\left(1+\gamma \right){\left({\sigma }^2+{\sigma }_c^2\right)}^2\left({\sigma }^2+{\sigma }_p^2\right)}}.$$

(18)

4.2. Scenario I

Next, we investigate scenario I, in which both the port and the carrier adopt blockchain technology, meaning they share the information. Under this scenario, the expected profits of the parties are as follows:

$$E[{\mathrm{\Pi }}^I\left|Y_c,Y_p\right.]=E[\left(\mu -c\kappa \right)Q\left|Y_c,Y_p\right.],$$

(19)

$$E[{\pi }^I\left|Y_c,Y_p\right.]=E[{\displaystyle \frac{\left(p-\mu \right)\left(a+\xi -p+\gamma \kappa \right)}{1+\gamma }}\left|Y_c,Y_p\right.],$$

(20)

where ${\kappa }^I$ is the port’s service capacity. In the first stage, as the leader, the port decides the service capacity. In the second stage, as the follower, the carrier determines the freight rates after observing the port’s decision, respectively. We use backward induction to solve the two-stage game. Therefore, given the port’s service capacity ${\kappa }^I$, the carrier simultaneously selects the freight rates $p$ to maximize its profits as follows:

$$\underset{p}{\max }E[{\pi }^I\left|Y_c,Y_p\right.]=E[{\displaystyle \frac{\left(p-\mu \right)\left(a+\xi -p+\gamma {\kappa }^I\right)}{1+\gamma }}\left|Y_c,Y_p\right.],$$

(21)

Carrier sets its freight rates $p$ according to the port’s service capacity ${\kappa }^I$ and the sharing forecast information. Following to Gal-Or et al. [46], we have

$$p^I={\displaystyle \frac{a+E[\xi \left|Y_c,Y_p\right.]+\gamma \kappa +\mu }{2}}.$$

(22)

Then, we have

$$p^I={\displaystyle \frac{a+\frac{{\sigma }^2{\sigma }_p^2{Y}_c+{\sigma }^2{\sigma }_c^2{Y}_p}{{\sigma }^2{\sigma }_p^2+{\sigma }^2{\sigma }_c^2+{\sigma }_p^2{\sigma }_c^2}+\gamma \kappa +\mu }{2}}.$$

(23)

We proceed to analyze the port’s service capacity decision in the first stage. The port’s decision problem is given by the following function:

$$\underset{\kappa }{\max }E[{\mathrm{\Pi }}^I\left|Y_c,Y_p\right.]=E[\left(\mu -c\kappa \right)Q\left|Y_c,Y_p\right.].$$

(24)

Before making decisions on service capabilities, the port needs to predict pricing and anticipate actual demand. Therefore, port enterprises predict that the demand of the carrier will be

$$E[Q^I\left|Y_c,Y_p\right.]={\displaystyle \frac{a+E[\xi \left|Y_c,Y_p\right.]+\gamma \kappa -\mu }{2\left(1+\gamma \right)}}.$$

(25)

We proceed to analyze the port’s service capacity decision in the first stage. Substituting Equations (24) and (25) into Equation (19), the port’s decision problem is given by the following function:

$$\underset{p}{\max }E[{\mathrm{\Pi }}^I\left|Y_c,Y_p\right.]={\displaystyle \frac{\left(\mu -c\kappa \right)\left(a+E[\xi \left|Y_c,Y_p\right.]+\gamma \kappa -\mu \right)}{2\left(1+\gamma \right)}}$$

(26)

Based on the first-order condition for the port’s decision problem, we can obtain the optimal service fee as follows:

$${\kappa }^I={\displaystyle \frac{\gamma \mu +c\mu -ca-cE[\xi \left|Y_c,Y_p\right.]}{2\gamma c}}.$$

(27)

Substituting (27) into (26), the carrier’s optimal freight rates are obtained as

$$p^I={\displaystyle \frac{ca+3c\mu +\gamma \mu +cE[\xi \left|Y_c,Y_p\right.]}{4c}}.$$

(28)

Substituting (27) and (28) into (25), the corresponding conditional demand quantities for carrier in scenario I are obtained:

$$Q^I={\displaystyle \frac{\gamma \mu -c\mu +ca+4c\xi -3cE[\xi \left|Y_c,Y_p\right.]}{4c\left(1+\gamma \right)}}.$$

(29)

Substituting (27), (28), and (29) into (19) and (20), the carrier and the port’s ex ante expected profits are obtained as

$$E[{\mathrm{\Pi }}^I]={\displaystyle \frac{{\left(\gamma \mu -c\mu +ca\right)}^2}{8\gamma c\left(1+\gamma \right)}}+{\displaystyle \frac{{\sigma }^4\left({\sigma }_p^2+{\sigma }_c^2\right)c}{8\gamma \left(1+\gamma \right)\left({\sigma }^2{\sigma }_c^2+{\sigma }_c^2{\sigma }_p^2+{\sigma }^2{\sigma }_p^2\right)}},$$

(30)

$$E[{\pi }^I]={\displaystyle \frac{{\left(ca+\gamma \mu -c\mu \right)}^2}{16c^2\left(1+\gamma \right)}}+{\displaystyle \frac{{\sigma }^4\left({\sigma }_p^2+{\sigma }_c^2\right)}{16\left(1+\gamma \right)\left({\sigma }^2{\sigma }_c^2+{\sigma }_c^2{\sigma }_p^2+{\sigma }^2{\sigma }_p^2\right)}}.$$

(31)

5. Incentive Analysis

In this section, we compare the equilibrium results in the two scenarios, in order to analyze the value of adopting blockchain technology and parties’ willingness to share forecast information.

Proposition 1. 

${\kappa }^I>{\kappa }^N$ always holds if $E[\xi \left|Y_c,Y_p\right.]<2E[\xi \left|Y_p\right.]-E[E[\xi \left|Y_c\right.]\left|Y_p\right.]$ is satisfied.

Proposition 1 shows that blockchain technology promotes the expansion of port service capacity if and only if the port’s ex ante expected demand is low enough. When blockchain technology is not adopted, the port must form expectations about the carrier’s pricing decision strategy based on its private information and decide its service capacity accordingly. In contrast, when blockchain technology is adopted, the port can access the carrier’s private demand information to make more accurate demand forecasts and optimize capacity decision. In this case, even with complete information, if the port’s ex ante expected demand is high, the marginal benefit of capacity expansion will decrease due to increased costs and the indirect effect of higher freight rates set by the carrier. In contrast, when the ex ante expected demand is low enough, the port has an incentive to expand capacity to stimulate market demand. Therefore, when the port’s ex ante expected demand is low, blockchain technology will promote capacity expansion.

Proposition 2. 

$Q^N<Q^I$ always holds if $3E[\xi \left|Y_c,Y_p\right.]<2E[\xi \left|Y_p\right.]-E[E[\xi \left|Y_c\right.]\left|Y_p\right.]+2E[\xi \left|Y_c\right.]$ is satisfied.

Proposition 2 indicates that when blockchain technology is adopted in the supply chain, the carrier’s actual demand will increase if and only if the port’s ex ante expected demand is sufficiently low. In other words, blockchain adoption only enhances the actual demand under low expected demand conditions; conversely, when expected demand is already high, it may even suppress the carrier’s realized demand. This is because, when the blockchain is adopted, the port can more accurately assess market demand and adjust its service capacity decisions accordingly. If the ex ante expected demand is low, the port is incentivized to expand its service capacity to stimulate demand. In response, the carrier is likely to reduce its freight rate to attract more demand, leading to an increase in the actual demand. However, when the port’s ex ante expected demand are already high, the associated increase in freight rates may suppress the carrier’s realized demand.

Next, we compare the variance of supply chain members’ decisions under different scenarios to assess how carrier participation in blockchain affects decision volatility. We use $Var[X^Y]$ to denote the volatility of decision $X$ under scenario $Y$. For example, $Var[{\kappa }^N]$ represents the volatility of the port’s service capacity when blockchain technology is not adopted.

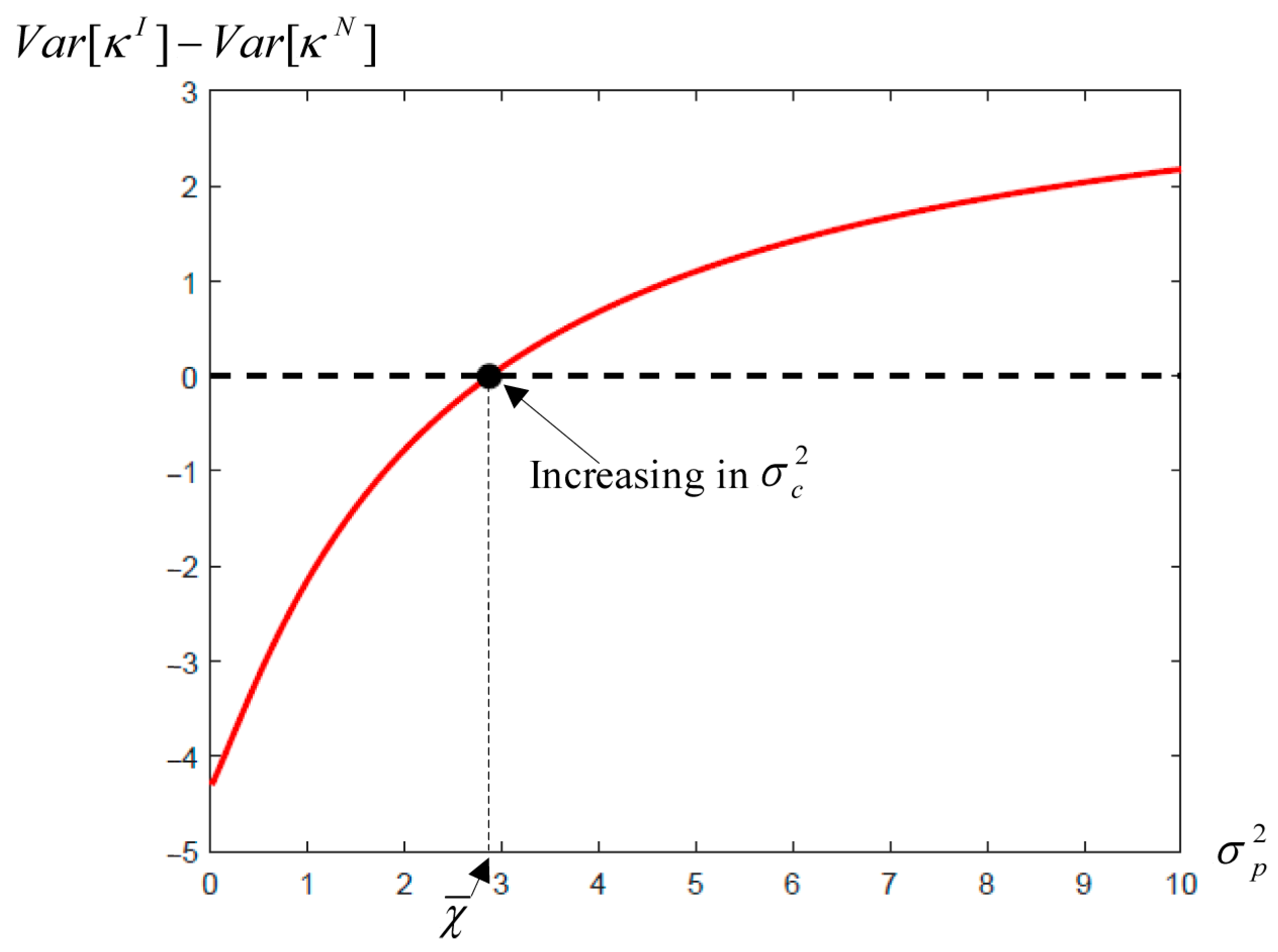
Proposition 3. 

If ${\sigma }_p^2<\overline{\chi }$ is satisfied, then $Var[{\kappa }^I]<Var[{\kappa }^N]$ always holds, where ${\displaystyle \frac{\partial \overline{\chi }}{\partial {\sigma }_c^2}}>0$. Here, $\overline{\chi }={\sigma }_c^2+{\displaystyle \frac{{\sigma }_c^4}{2\left({\sigma }^2+{\sigma }_c^2\right)}}+{\displaystyle \frac{\sqrt{3}\sqrt{{\sigma }_c^4{\left({\sigma }^2+{\sigma }_c^2\right)}^2\left(4{\sigma }^4+8{\sigma }^2{\sigma }_c^2+3{\sigma }_c^4\right)}}{2{\left({\sigma }^2+{\sigma }_c^2\right)}^2}}$.

Proposition 3 indicates that when the port has a high level of forecasting accuracy, i.e., ${\sigma }_p^2<\overline{\chi }$, blockchain technology reduces the variance of the port’s service capacity decisions under demand uncertainty, as shown in Figure 2. In other words, the information-sharing mechanism enabled by blockchain helps stabilize the port’s service capacity decisions in the context of high forecast accuracy. Note that when blockchain technology is adopted, both the port and the carrier have access to the full set of forecast information. Under this condition, if the port possesses a higher forecasting accuracy, i.e., ${\sigma }_p^2<\overline{\chi }$, the carrier can rely on the port’s accurate forecasts to make more stable pricing decisions, which in turn reduces demand-side volatility. Anticipating this, the port is also incentivized to set a more stable service capacity in its earlier stage decisions. Therefore, accurate forecast information, facilitated by blockchain adoption, weakens the transmission of demand uncertainty into service capacity volatility. Conversely, if the port has low forecasting accuracy, i.e., ${\sigma }_p^2>\overline{\chi }$, its private information may act as noise under the blockchain mechanism, disrupting the carrier’s decision. Upon receiving lower accuracy information, the carrier may increase the volatility of its pricing strategy, thereby amplifying uncertainty in the port’s own service capacity decisions. Upon receiving low-accuracy information, the carrier cannot determine an accurate freight rate and is more affected by demand uncertainty. This increases the carrier’s decision volatility and amplifies uncertainty in the port’s service capacity decision.

Proposition 3 further reveals that the threshold $\overline{\chi }$ increases with the variance of the carrier’s forecast error. In other words, even when the port’s own forecast is imprecise, its service capacity decisions can remain robust—provided the carrier’s information is sufficiently noisy. The intuition lies in the asymmetry of informational reliance: as the carrier’s forecast accuracy declines, its dependence on the port’s signal intensifies. Consequently, the value of the port’s information rises.

Proposition 4. 

(a) For $0<{\sigma }_c^2<{\displaystyle \frac{2{\sigma }^2}{3}}$, $Var\left(p^I\right)>Var\left(p^N\right)$ always holds. (b) For ${\sigma }_c^2>{\displaystyle \frac{2{\sigma }^2}{3}}$, $Var\left(p^I\right)<Var\left(p^N\right)$ always holds if $0<{\sigma }_p^2<\stackrel{⌢}{\chi }$ is satisfied. Here, $\stackrel{⌢}{\chi }={\displaystyle \frac{{\sigma }_c^2\left(-2{\sigma }^2-3{\sigma }_c^2+\sqrt{28{\sigma }^4-24{\sigma }^2{\sigma }_c^2+9{\sigma }_c^4}\right)}{6\left({\sigma }^2+{\sigma }_c^2\right)}}$.

Proposition 4 suggests that the impact of blockchain technology on freight rate volatility is contingent upon the forecast accuracy of both the port and the carrier. When the carrier’s forecast accuracy is high, i.e., ${\sigma }_c^2<{\displaystyle \frac{2{\sigma }^2}{3}}$, the introduction of shared information through blockchain may exacerbate volatility rather than mitigate it. In this case, the benefit of additional signals diminishes, while the risk of introducing informational noise increases—ultimately destabilizing the carrier’s pricing decision. By contrast, when the carrier has a low forecast accuracy, i.e., ${\sigma }_c^2>{\displaystyle \frac{2{\sigma }^2}{3}}$, and the port possesses more precise information, i.e., $0<{\sigma }_p^2<\stackrel{⌢}{\chi }$, blockchain technology acts as an effective signaling device. The carrier updates its information using the port’s credible forecast, thereby smoothing its freight rate decisions. However, in scenarios where both parties hold imprecise forecasts, the value of the exchange of information deteriorates. Rather than reducing volatility, blockchain technology may transmit low-accuracy signals, further amplifying pricing volatility.

Proposition 5. 

$E[{\mathrm{\Pi }}^I]>E[{\mathrm{\Pi }}^N]$ always holds if ${\sigma }_p^2>\tilde{\chi }$ is satisfied, where ${\displaystyle \frac{\partial \tilde{\chi }}{\partial {\sigma }_c^2}}>0$. Here, $\tilde{\chi }={\displaystyle \frac{\sqrt{3}\sqrt{{\sigma }_c^4{\left({\sigma }^2+{\sigma }_c^2\right)}^2\left(2{\sigma }^2+{\sigma }_c^2\right)\left(2{\sigma }^2+3{\sigma }_c^2\right)}}{2{\left({\sigma }^2+{\sigma }_c^2\right)}^2}}+{\displaystyle \frac{{\sigma }_c^4+2{\sigma }_c^2\left(a+{\sigma }_c^2\right)}{2\left(a+{\sigma }_c^2\right)}}$.

Proposition 5 shows that the port is motivated to adopt blockchain technology only when its own forecast accuracy is large enough. This result is not difficult to understand. When both parties participate in blockchain technology, forecast information is exchanged transparently on the platform, triggering a twofold informational effect for the port. On the one hand, if the port’s forecast accuracy is low, access to the carrier’s more reliable signal enables corrective adjustments in service capacity, thereby improving its profits. On the other hand, when the port already possesses a superior forecasting accuracy, incorporating a noisier signal from the carrier yields limited value—and may even degrade decision quality. Therefore, it can be found that the port will adopt blockchain technology only when its own forecast accuracy is not high, because it may hope to obtain some information value from the carrier. Proposition 5 also shows that the threshold $\tilde{\chi }$ increases as the variance of the carrier’s prediction accuracy increases. This is because when the carrier’s forecast accuracy is low enough, the port is more reluctant to adopt blockchain technology.

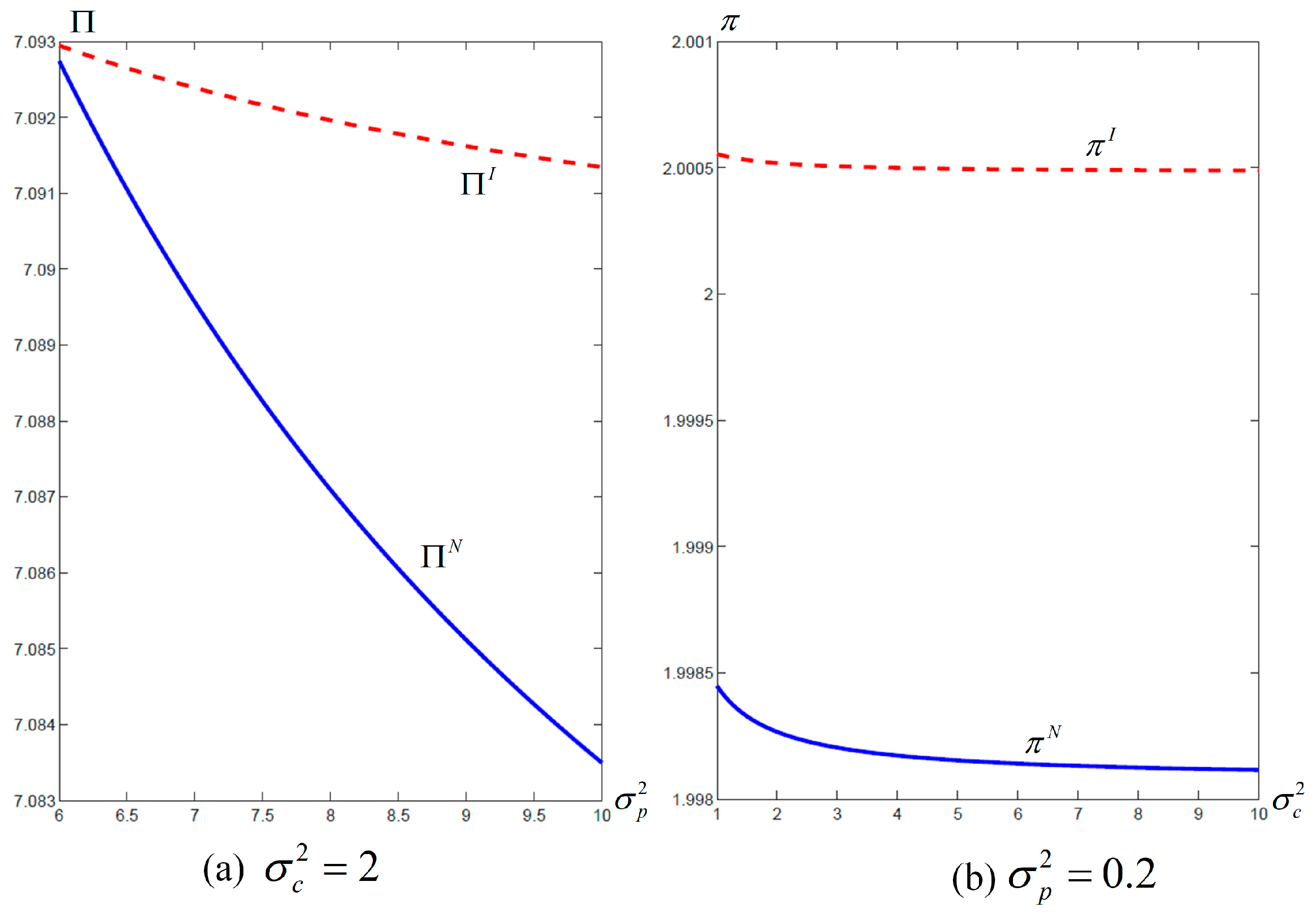
Proposition 6. 

If ${\sigma }_p^2<\widehat{\chi }$ is satisfied, then $E[{\pi }^I]>E[{\pi }^N]$ always holds, where ${\displaystyle \frac{\partial \widehat{\chi }}{\partial {\sigma }_c^2}}>0$. Here, $\widehat{\chi }={\displaystyle \frac{{\sigma }_c^2\left(6{\sigma }^2+5{\sigma }_c^2+\sqrt{156{\sigma }^4+120{\sigma }^2{\sigma }_c^2+25{\sigma }_c^4}\right)}{6\left({\sigma }^2+{\sigma }_c^2\right)}}$.

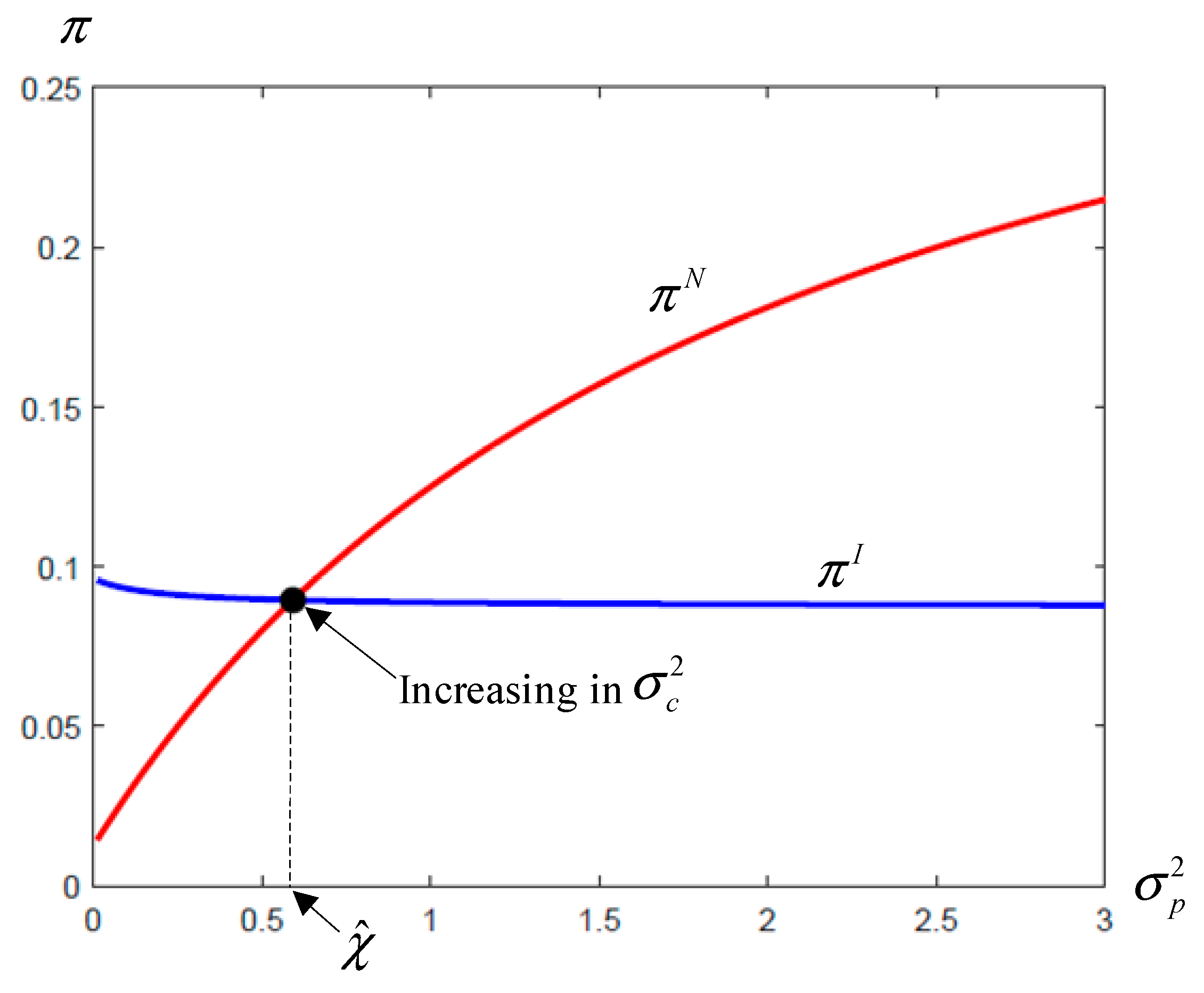
Proposition 6 shows that the carrier benefits from adopting blockchain technology only when the port’s forecast accuracy is sufficiently high, as shown in Figure 3. Once both adopt blockchain, private forecasts become fully observable, leading to a symmetric information environment. Under such conditions, highly accurate information from the port can be strategically exploited by the carrier to better anticipate market demand, optimize its pricing decision, and improve profitability. In this case, the shared signal enhances the carrier’s information value. However, the informational advantage reverses when the port’s forecast is imprecise while the carrier already holds accurate predictions. The incorporation of noisy signals not only adds negligible value but may also mislead the carrier’s decision-making. In this case, the port’s information acts as a distortion rather than a refinement. As a result, blockchain—rather than offering a strategic benefit—can reduce the carrier’s profits by degrading its original advantage in informational precision. Without sufficiently accurate signals from the port, blockchain technology may become a liability for the carrier, not a benefit.

Proposition 7. 

$\tilde{\chi }>\widehat{\chi }$ always holds if $\left\{\begin{array}{l}0<{\sigma }^2<{\displaystyle \frac{6}{5}}\\ {\sigma }_c^2>{\sigma }_c^{2*}\end{array}\right.$. Here, ${\sigma }_c^{2*}$ can be found in Appendix A.

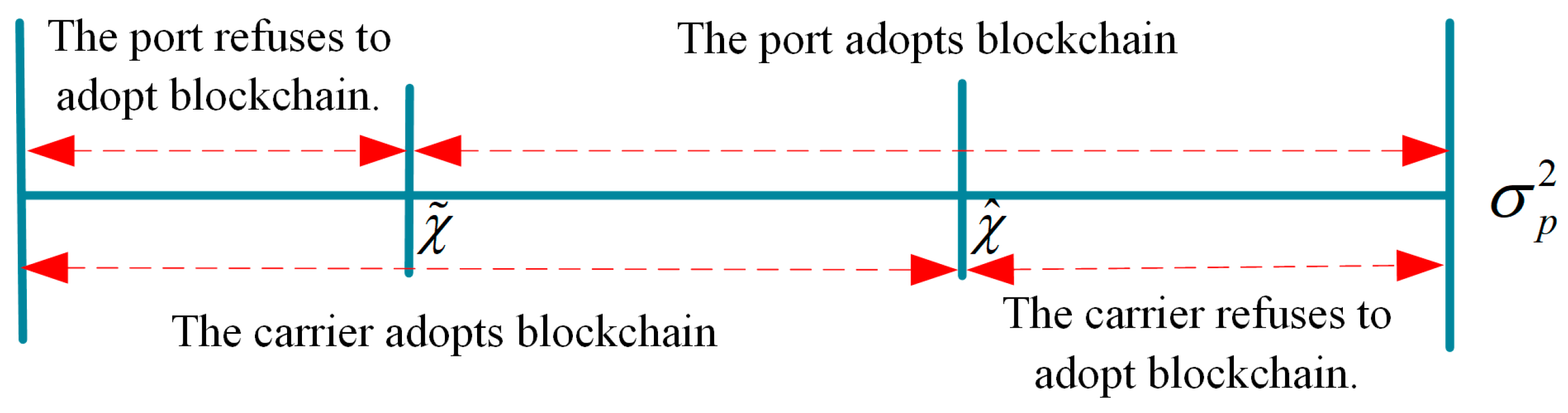
Proposition 7 reveals an interesting fact: when market volatility is low and the carrier’s forecast is less accurate, the port and the carrier are motivated to adopt blockchain technology, as shown in Figure 4. Recalling Propositions 5 and 6, we find that the motivations of the port and the carrier to adopt blockchain seem to be conflicting. Because the port expects that adopting blockchain technology will not lead to a large loss of information value, the carrier hopes to gain more information value through blockchain technology. This seems to be irreconcilable. However, Proposition 7 proposes an interval that makes this conflict reconcilable. Specifically, when the carrier’s forecast accuracy is low enough, i.e., ${\sigma }_c^2>{\sigma }_c^{2*}$, the blockchain becomes attractive from its perspective, as the shared forecast from the port can enable the carrier to obtain additional information value, making it efficient to update its own information. In this case, if market demand volatility becomes smooth, the port is also motivated to adopt blockchain technology. When the market volatility is smooth, i.e., ${\sigma }^2<{\displaystyle \frac{6}{5}}$, if the carrier’s forecast accuracy is low, this will drive the carrier to set a more aggressive pricing strategy, resulting in greater volatility on the demand side. This is obviously not good for the port because it leads to an increase in the misalignment between service capacity and demand. As demonstrated in Propositions 3 and 4, the carrier utilize the port’s high accuracy forecast to stabilize their own pricing strategies. The resulting reduction in market volatility enables the port to better align capacity with realized demand, mitigating mismatch losses. In this case, the port’s gain in profit may not stem directly from informational enhancement, but rather from strategic coordination effects induced by blockchain-facilitated information alignment.

Proposition 8. 

(a) For any ${\sigma }^2$, ${\sigma }_c^2$, ${\sigma }_p^2$, ${\displaystyle \frac{\partial {\pi }^i}{\partial {\sigma }_c^2}}<0$ and ${\displaystyle \frac{\partial \left({\pi }^I-{\pi }^N\right)}{\partial {\sigma }_c^2}}>0$ always holds; (b) for any ${\sigma }^2$, ${\sigma }_c^2$, ${\sigma }_p^2$, ${\displaystyle \frac{\partial {\mathrm{\Pi }}^i}{\partial {\sigma }_p^2}}<0$ and ${\displaystyle \frac{\partial \left({\mathrm{\Pi }}^I-{\mathrm{\Pi }}^N\right)}{\partial {\sigma }_p^2}}>0$ always holds.

Proposition 8 shows that while improving the forecasting accuracy unambiguously increases the profit of both the port and the carrier, it simultaneously diminishes their incentive to adopt blockchain technology. This result arises from two factors: although enhanced accuracy yields direct returns by refining decision quality, it reduces the value of shared information under a symmetric information structure. As forecast precision improves, the informational advantage becomes obvious; once blockchain is adopted, the improved signal of one party is partially appropriated by the other. Consequently, the benefit from sharing declines with accuracy. This result is summarized in Figure 5.

6. Extension

In the main model, we assume that the forecasting accuracy is exogenous, and in this section, we relaxed this assumption. That is to say, supply chain members can determine the accuracy of their forecasting information. When supply chain members need to improve the predictive accuracy, they need to incur certain costs. Improving the forecast accuracy can include investing in data processing capabilities or improving data availability and quality. In this case, we follow the assumption of diminishing marginal utility in economics: when other inputs remain constant, continuously increasing investment in blockchain technology will eventually yield smaller improvements in the forecasting accuracy. Therefore, we assume that the cost of technological advancement is inversely proportional to the accuracy of the technology. Both the port and the carrier have a cost–benefit coefficient ${\eta }_c$ and ${\eta }_p$, where a larger ${\eta }_c$/${\eta }_p$ represents a smaller cost–benefit ratio, meaning that the cost of improving one unit of accuracy is higher. For ease of analysis, referring to previous literature [47,48], we will consider ${\eta }_c={\eta }_p=\eta$. Under this setting, we believe that investing in big data prediction technology for prediction accuracy comes before all decisions, as it is a significant strategic decision. Therefore, we have referred to previous literature on technology investment and provided the profit functions for the port and the carrier below [47,48].

Without blockchain technology, the profit functions of the port and the carrier are as follows:

$$E[\mathrm{\Pi }\left|Y_p\right.]=E[\left(\mu -c\kappa \right)Q-\eta {\left({\displaystyle \frac{1}{{\sigma }_p^2}}\right)}^2\left|Y_p\right.]$$

$$E[\pi \left|Y_c\right.]=E[{\displaystyle \frac{\left(p-\mu \right)\left(a+\xi -p+\gamma \kappa \right)}{1+\gamma }}-\eta {\left({\displaystyle \frac{1}{{\sigma }_c^2}}\right)}^2\left|Y_c\right.]$$

With blockchain technology, the profit functions of the port and the carrier are as follows:

$$E[{\mathrm{\Pi }}^I\left|Y_c,Y_p\right.]=E[\left(\mu -c\kappa \right)Q-\eta {\left({\displaystyle \frac{1}{{\sigma }_p^2}}\right)}^2\left|Y_c,Y_p\right.]$$

$$E[{\pi }^I\left|Y_c,Y_p\right.]=E[{\displaystyle \frac{\left(p-\mu \right)\left(a+\xi -p+\gamma \kappa \right)}{1+\gamma }}-\eta {\left({\displaystyle \frac{1}{{\sigma }_c^2}}\right)}^2\left|Y_c,Y_p\right.]$$

We also solve this problem using backward induction, following the same procedure as in the main model. Due to the complexity of the expressions and the difficulty of obtaining closed-form solutions, we conduct numerical experiments to investigate the decisions of the port and the carrier. All procedures can be found in Appendix A.

Table 2. Typical subgame refined Nash equilibrium.

	$\mathit{\eta }=0.1$	$\mathit{\eta }=0.3$	$\mathit{\eta }=0.5$	$\mathit{\eta }=0.7$	$\mathit{\eta }=0.9$
$\left({({\sigma }_c^2)}^{N*},{({\sigma }_p^2)}^{N*}\right)$	(1.35, 3.73)	(2.48, 6.59)	(3.35, 8.86)	(4.13, 10.92)	(4.85, 12.86)
$\left({\pi }^{N*},{\mathrm{\Pi }}^{N*}\right)$	(0.120, 0.315)	(0.116, 0.311)	(0.114, 0.309)	(0.113, 0.308)	(0.112, 0.307)
$\left({({\sigma }_c^2)}^{I*},{({\sigma }_p^2)}^{I*}\right)$	(3.72, 5.59)	(3.72, 5.59)	(9.49, 14.24)	(11.92, 17.88)	(14.25, 21.37)
$\left({\pi }^{I*},{\mathrm{\Pi }}^{I*}\right)$	(0.138, 0.327)	(0.125, 0.319)	(0.120, 0.314)	(0.116, 0.312)	(0.114, 0.311)
${\pi }^{I*}-{\pi }^{N*}$	>0	>0	>0	>0	>0
${\mathrm{\Pi }}^{I*}-{\mathrm{\Pi }}^{N*}$	>0	>0	>0	>0	>0

($a=1,c=0.05,\mu =0.3,\gamma =0.3,{\sigma }^2=2$).

presents several representative subgame perfect Nash equilibria from our numerical experiments.

Observation 1. 

$\left({({\sigma }_c^2)}^{I*},{({\sigma }_p^2)}^{I*}\right)>\left({({\sigma }_c^2)}^{N*},{({\sigma }_p^2)}^{N*}\right)$ and ${({\sigma }_c^2)}^{i*}>{({\sigma }_p^2)}^{i*},i\in \{N,I\}$ always holds.

Observation 1 reveals a strategic tension arising when both the port and the carrier adopt blockchain technology and treat forecasting accuracy as a decision variable. While a higher forecast accuracy enhances individual informational value (as shown in Proposition 8), mutual information sharing under blockchain reshapes incentives. The equilibrium result may exhibit reduced accuracy levels. This strategic inefficiency stems from two factors. First, forecast improvements involve input costs, leading each player to weigh marginal benefits against escalating investment. Second, and more importantly, blockchain transforms private forecasts into common signals, thereby generating informational spillovers. Any improvement in one party’s forecast becomes partially appropriated by the other, reducing its private return. Anticipating such free riding, each party internalizes a disincentive to invest beyond a certain level, causing a lower accuracy level than would be optimal without blockchain.

Observation 1 further reveals that, regardless of blockchain’s presence, the carrier tends to maintain a higher forecast accuracy than the port. This asymmetry arises from the carrier’s dual pressure in uncertainty demand and in capacity signals from the port, necessitating more responsive and accurate forecasting technology.

Observation 2. 

${\pi }^{I*}>{\pi }^{N*}$ and ${\mathrm{\Pi }}^{I*}>{\mathrm{\Pi }}^{N*}$ always holds.

Observation 2 shows that blockchain enhances profits for both the port and the carrier. The port’s benefits from information sharing are well established (see Proposition 5). This is because the port’s forecast accuracy is always lower, which means that the loss of information value is less. Importantly, the carrier also gains consistently from blockchain technology. Although Proposition 7 indicates reluctance by the carrier to adopt blockchain when the port’s forecast accuracy falls below a critical level, observation 2 reveals the port’s capacity to strategically maintain forecast accuracy above this threshold. Such a strategic adjustment ensures that information sharing generates mutual gains, thereby incentivizing the carrier’s participation. Through this mechanism, the port effectively induces blockchain adoption by the carrier, establishing a cooperative equilibrium favorable to both parties.

7. Discussion

7.1. Backgroud and Key Results

In recent years, the maritime supply chain has become increasingly exposed to demand volatility, largely due to frequent and unpredictable disruptions. A central challenge under such uncertainty lies in the strategic alignment of the port’s service capacity with the carrier’s anticipated demand. Blockchain technology, by enabling verifiable information exchange without central authority, offers a potential resolution. To explore the strategic motives underpinning its adoption, we construct a game-theoretic model of a two-tier supply chain involving one port and one carrier. Two benchmark settings are considered: one without blockchain adoption and another in which both parties adopt and share forecasts via the blockchain. Within this framework, we investigate the potential motivations for the port and the carrier to adopt blockchain to share information.

Our key findings highlight the strategic role of blockchain adoption in the maritime supply chain. We find that when the port’s ex ante expected demand is relatively low, the adoption of blockchain technology not only incentivizes the port to expand its service capacity but also increases the actual demand from the carrier. In addition, when the port has a high forecasting accuracy, it prompts both the port and the carrier to make more stable decisions on service capacity and freight rates under demand uncertainty. Finally, while the port and the carrier exhibit conflicting incentives to adopt blockchain technology, these tensions can nonetheless be reconciled. This alignment becomes possible due to blockchain’s spillover effect: by enabling information sharing, it facilitates a closer match between the port’s service capacity and the carrier’s realized demand.

7.2. Contributions

Theoretical Contributions: This paper makes a unique contribution to the promotion of blockchain technology for information sharing in the maritime supply chain. To the best of our knowledge, this is the first study that examines whether adopting blockchain technology can enhance maritime supply chain performance by improving information sharing in the presence of mismatches between service capacity and demand. For example, Xiao et al. [34] only explored the information-sharing game between the platform and the main players but did not consider scenarios involving service capacity adjustment. Huang et al. [37] examined the information-sharing decisions of downstream liner companies but did not include ports. Therefore, we believe this work is unique. At the same time, it also provides a useful reference for research on information sharing, although the computational analysis is relatively complex.

Practical Implications: This work is based on real-world collaboration cases such as DexFreight and ports’ adoption of blockchain technology [5,6]. While the port and the carrier exhibit conflicting incentives to adopt blockchain technology, these tensions can nonetheless be reconciled. This alignment becomes possible due to blockchain’s spillover effect: by enabling information sharing, it facilitates a closer match between the port’s service capacity and the carrier’s realized demand. Ports should increase investment in big data technologies to enhance forecasting accuracy, which can incentivize carriers to participate in blockchain-based information sharing, leading to win–win outcomes. Otherwise, carriers may be reluctant to adopt blockchain technology, potentially resulting in failures similar to that of the TradeLens platform [14].

7.3. Limitations and Future Work

We acknowledge some limitations of our study and suggest promising directions for future research. First, extending the model to a three-party information-sharing framework involving the port and two carriers would be both meaningful and complex. Second, considering port capacity constraints and developing a competitive model in which information sharing prompts carriers to compete for prioritized slots would also be of interest. Finally, applying empirical methods to validate the value of blockchain adoption for carriers represents another important future direction.