Limited Data Availability in Building Energy Consumption Prediction: A Low-Rank Transfer Learning with Attention-Enhanced Temporal Convolution Network
Abstract
1. Introduction
- We propose integrating the attention mechanism with TCN, named AtTCN. AtTCN enhances the model’s ability to dynamically capture global dependencies with the attention mechanism, addressing the limitations of TCN’s local receptive field, and capturing both local and global hidden features more effectively.
- By introducing low-rank decomposition, we propose a novel transfer learning-based AtTCN method, named LRTL-AtTCN, which significantly reduces the number of parameters during the transfer learning process and achieves better prediction performance in conditions of limited data, demonstrating great adaptability across different building types.
- We evaluate LRTL-AtTCN, focusing on its performance in BECP in the source domain and the target domain with limited data, and specifically investigate the impact of the experimental results of the attention mechanism and low-rank decomposition. The code in this paper is available at https://github.com/Fechos/LRTL-AtTCN (accessed on 21 May 2025).
2. Related Works
2.1. Physics-Based Modeling Methods
2.2. Data-Driven Methods
2.3. Methods for Handling Limited Data Availability
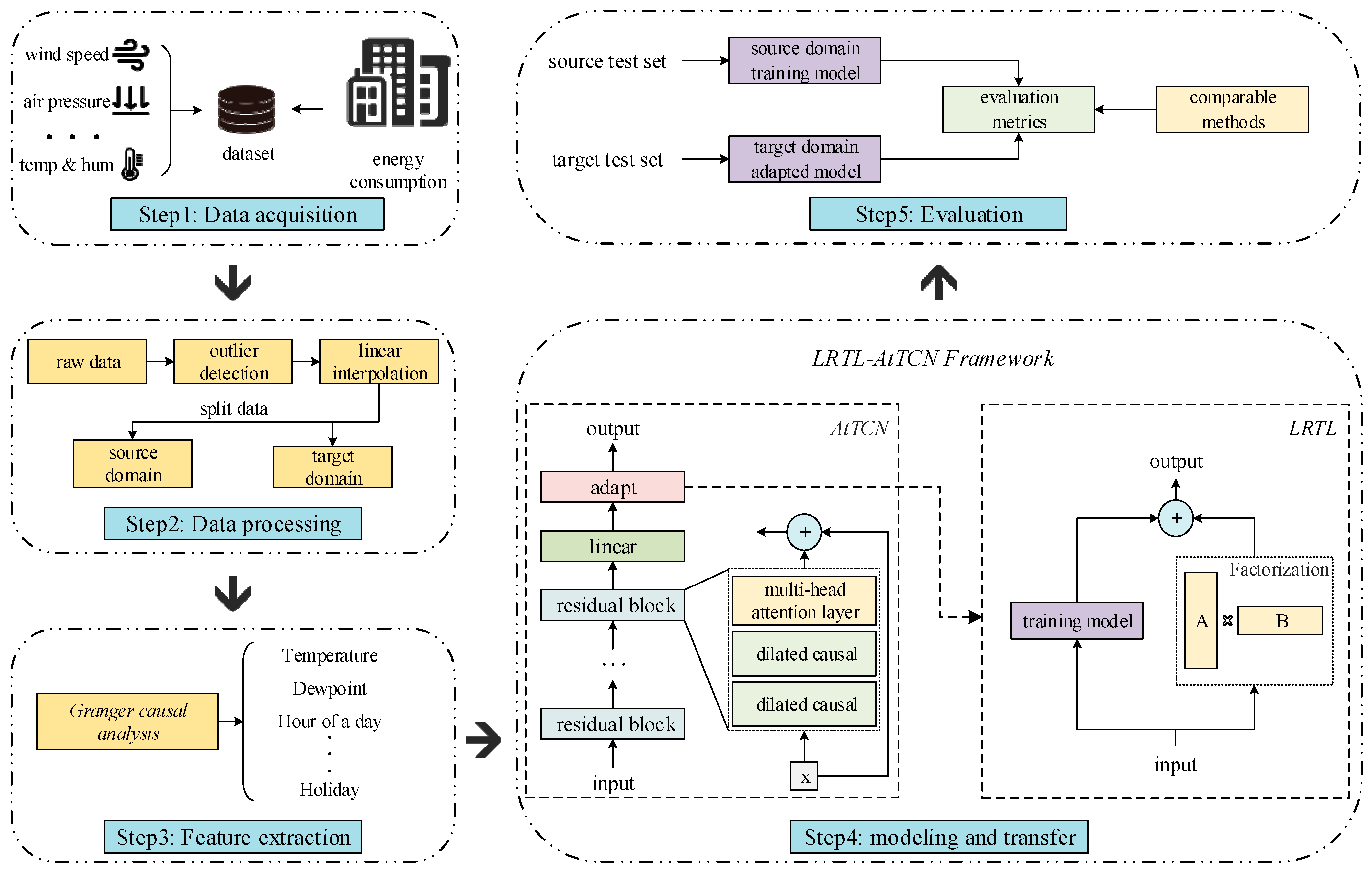
3. Methodology
3.1. Problem Statement
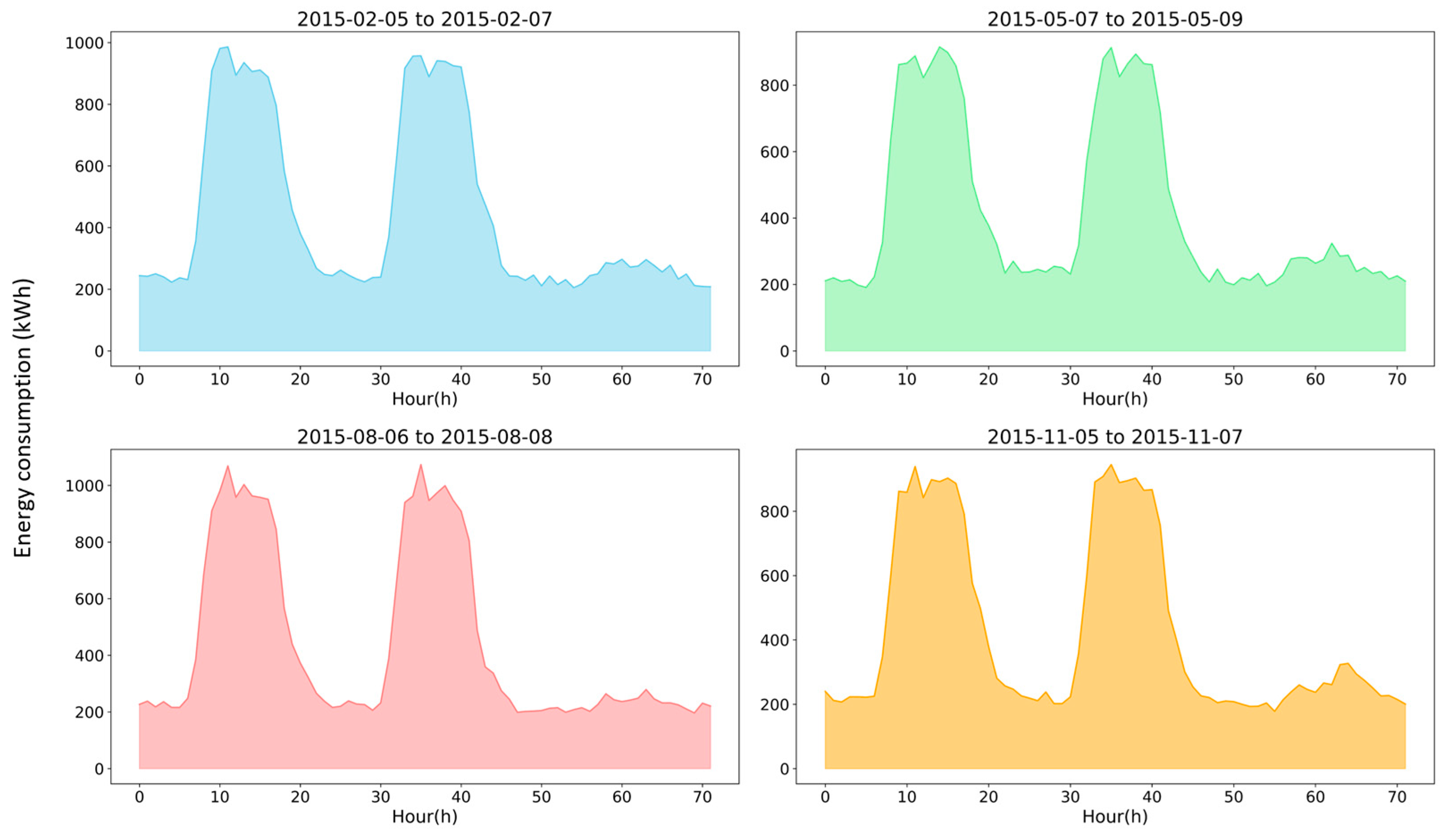
3.2. Data Processing
3.3. Feature Engineering
- When , we reject the null hypothesis, indicating that has a Granger causal influence on .
- When , we accept the null hypothesis, indicating that has no Granger causal influence on .
3.4. Low-Rank Attention-Enhanced Temporal Convolutional Transfer Learning (LRTL-AtTCN)
3.4.1. Attention-Enhanced Temporal Convolution Network(AtTCN)
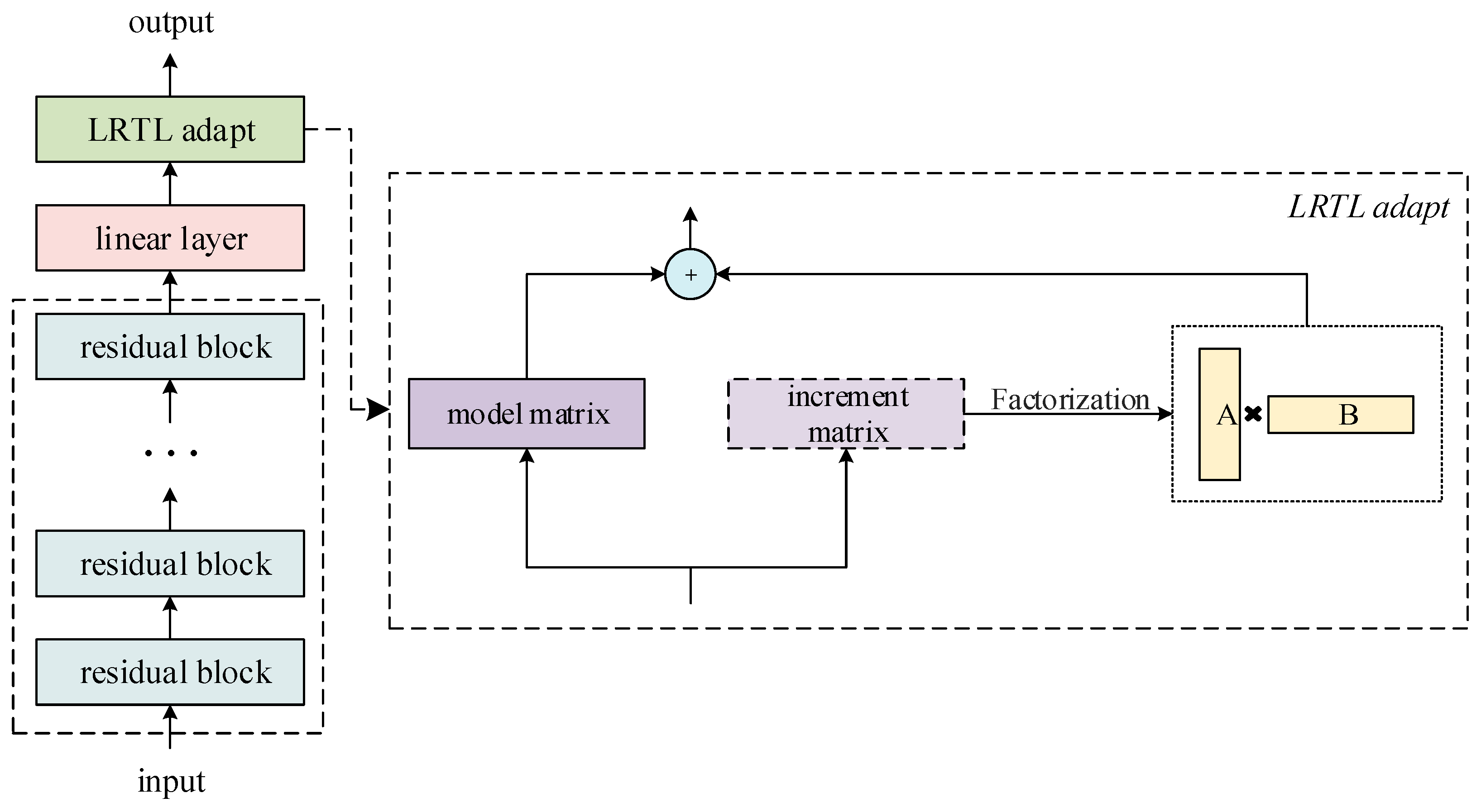
3.4.2. Low-Rank Transfer Learning (LRTL)
3.4.3. Algorithm
| Algorithm 1 LRTL-AtTCN method for energy consumption prediction | |
| Input: Source building energy consumption data and target energy consumption data , where is external features, y is building energy consumption data, is the number of the time steps, and is the number of features, the last column is the target variable; | |
| Output: predicted values for the target variable. | |
| 1: | Source Domain Training Stage |
| 2: | Initialize AtTCN model; |
| 3: | for episode = 1 to EPISODES do |
| 4: | for each layer do |
| 5: | |
| 6: | ; |
| 7: | end for |
| 8: | ; |
| 9: | Loss computation: ; |
| 10: | Update AtTCN using: ; |
| 11: | end for |
| 12: | Save AtTCN model; |
| 13: | |
| 14: | Transfer Learning Stage |
| 15: | Initialize LRTL model and load AtTCN model; |
| 16: | for episode = 1 to EPISODES do |
| 17: | compute the forward pass using the model weights (); |
| 18: | loss computation: ; |
| 19: | Update using: ; |
| 20: | Update using: ; |
| 21: | end for |
| 22: | Save transferred model |
4. Results
4.1. Experiments Setting
4.2. Evaluation Metrics
4.3. Results and Analysis
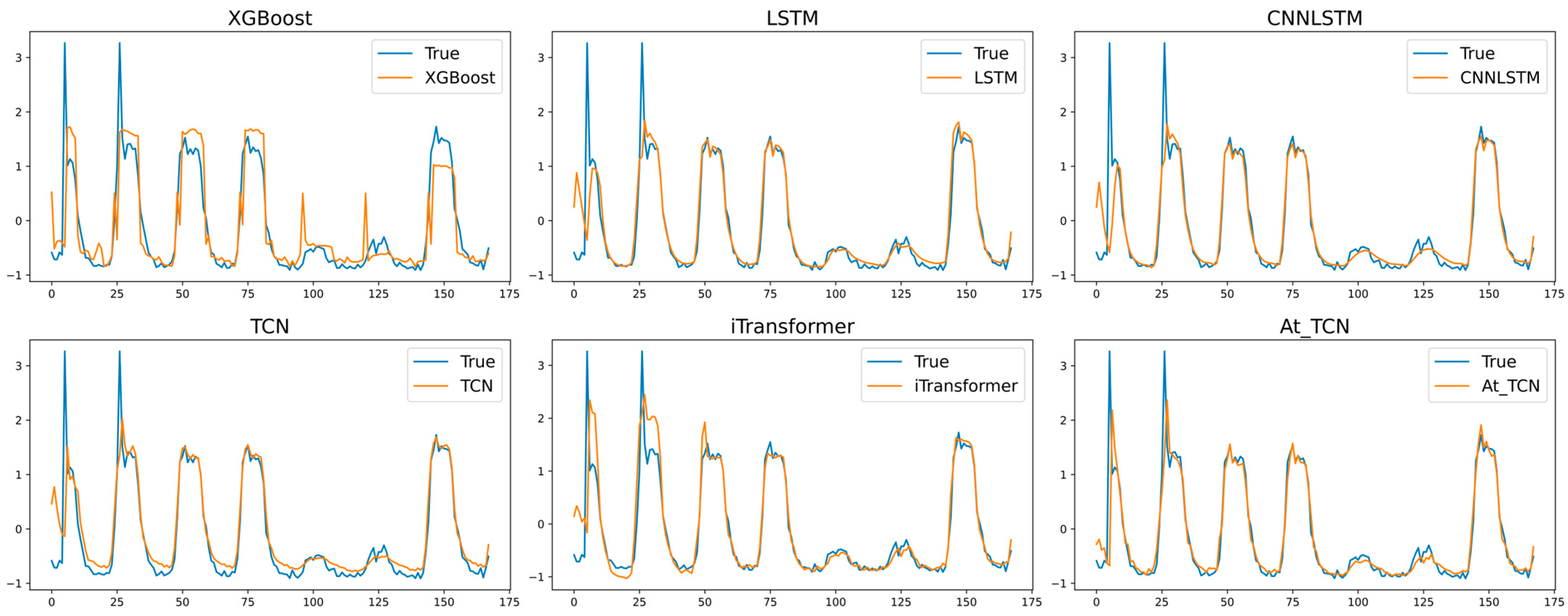
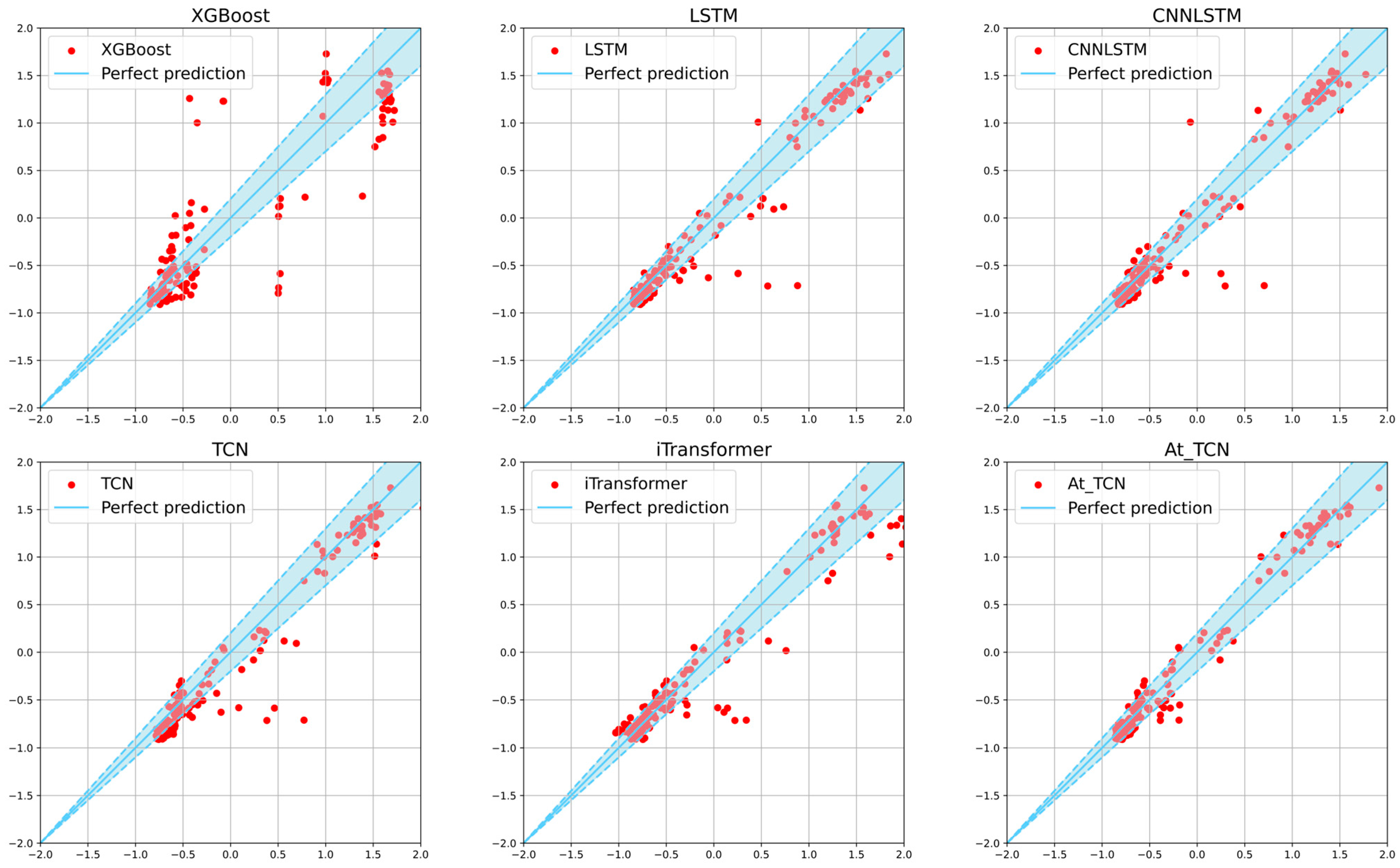
4.3.1. Method Performance Comparison
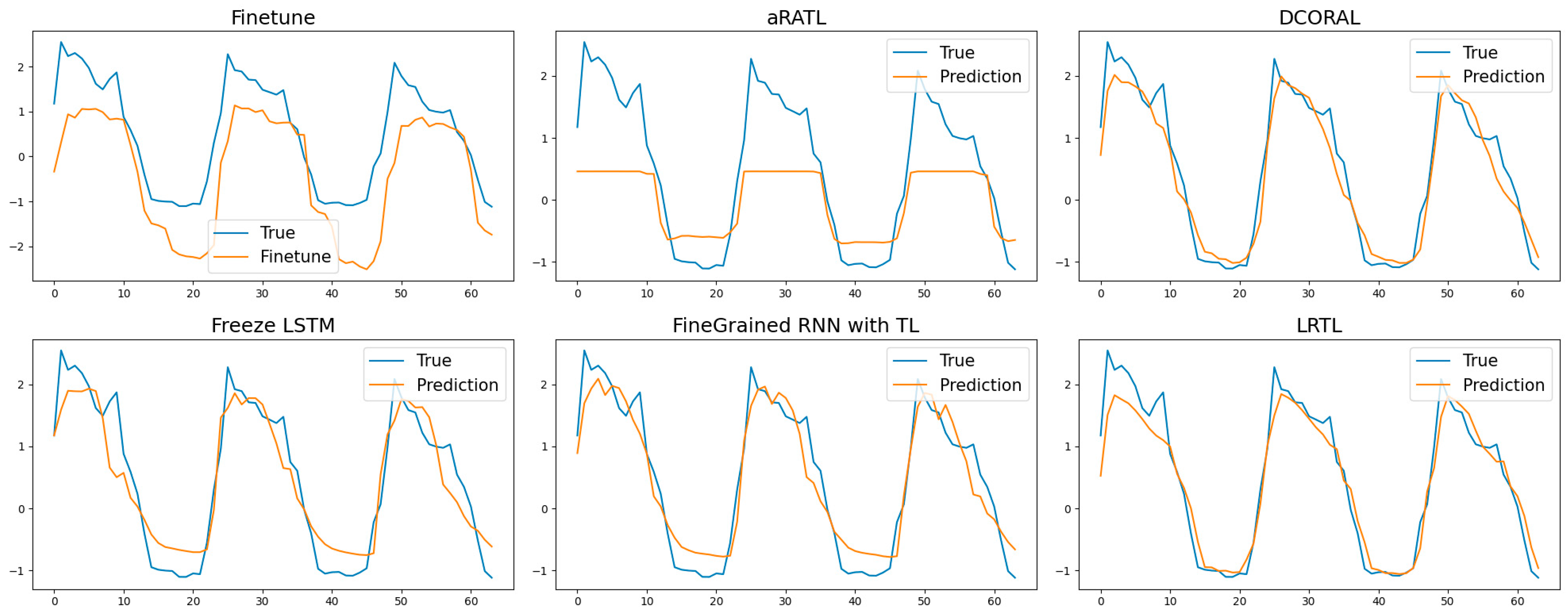
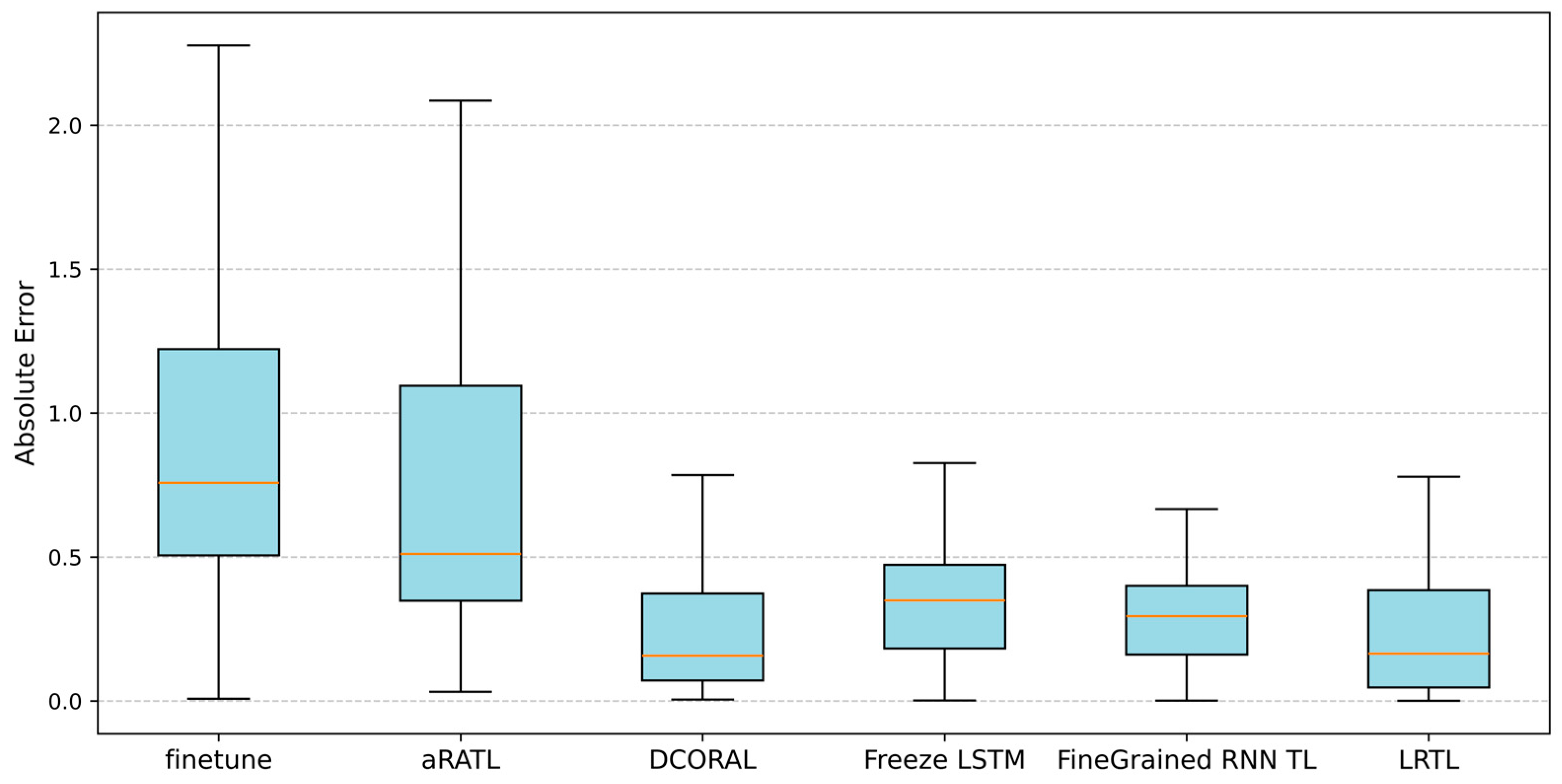
4.3.2. Method Details Exploration
4.3.3. Ablation Analysis
4.3.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variables | Meaning |
| Dataset | |
| External features series of building energy consumption series | |
| An external feature column of the building energy consumption series | |
| The normalized eigenvalue | |
| The mean of data, the standard deviation of data | |
| Building energy consumption series | |
| The length of time series | |
| Number of external features | |
| The length of the predict length | |
| Source domain | |
| Target domain | |
| The hyperparameter that balances the losses between the source building domain and the target building domain | |
| Constant term | |
| to recur at the same value | |
| The maximum lag coefficient | |
| The error term | |
| The corresponding p-value | |
| Significance level | |
| The size of the convolution kernel | |
| Layer index | |
| Model parameters | |
| Model weight matrix | |
| Low-rank matrices for adaption | |
| Matrix rank |
References
- Sulkowska, M.S.N.; Nugent, A.; Nugent, A.; Vega, L.A.; Carrazco, C. Global Status Report for Global Status Report for Buildings and Construction; UN Environment Programme: Nairobi, Kenya, 2024. [Google Scholar]
- Chen, Y.; Guo, M.; Chen, Z.; Chen, Z.; Ji, Y. Physical Energy and Data-Driven Models in Building Energy Prediction: A Review. Energy Rep. 2022, 8, 2656–2671. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A Review of Data-Driven Building Energy Consumption Prediction Studies. Renew. Sust. Energ. Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Owolabi, H.; Akanbi, L.; Ganiyu, S. Data-Driven Tools for Building Energy Consumption Prediction: A Review. Energies 2023, 16, 2574. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Zhang, Y.; Wang, Z.; Li, J. A Review of Data Mining Technologies in Building Energy Systems: Load Prediction, Pattern Identification, Fault Detection and Diagnosis. Energy Build. 2020, 1, 149–164. [Google Scholar] [CrossRef]
- Darwazeh, D.; Duquette, J.; Gunay, B.; Wilton, I.; Shillinglaw, S. Review of Peak Load Management Strategies in Commercial Buildings. Sustain. Cities Soc. 2022, 77, 103493. [Google Scholar] [CrossRef]
- Qiu, S.; Li, Z.; Pang, Z.; Zhang, W.; Li, Z. A Quick Auto-Calibration Method Based on Normative Energy Models. Energy Build. 2018, 172, 35–46. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, J.; Jia, H.; Mu, Y.; Lv, S. Vector Field-Based Support Vector Regression for Building Energy Consumption Prediction. Appl. Energy 2019, 242, 403–414. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, X.; Zhou, G.; Fan, C.; Ding, P.; Chen, Q. An Online Physical-Based Multiple Linear Regression Model for Building’s Hourly Cooling Load Prediction. Energy Build. 2022, 254, 111574. [Google Scholar] [CrossRef]
- Rana, M.; Sethuvenkatraman, S.; Goldsworthy, M. A Data-Driven Method Based on Quantile Regression Forest to Forecast Cooling Load for Commercial Buildings. Sustain. Cities Soc. 2022, 76, 103511. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Association for Computing Machinery, New York, NY, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Chalapathy, R.; Khoa, N.L.D.; Sethuvenkatraman, S. Comparing Multi-step Ahead Building Cooling Load Prediction Using Shallow Machine Learning and Deep Learning Models. Sustain. Energy Grids. 2021, 28, 100543. [Google Scholar] [CrossRef]
- Chen, X.; Qiu, X.; Zhu, C.; Liu, P.; Huang, X. Long Short-Term Memory Neural Networks for Chinese Word Segmentation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1197–1206. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of Gated Recurrent Unit (GRU) Neural Networks. In Proceedings of the IEEE 60th International Midwest Symposium on Circuits and Systems, Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J.C. Temporal Convolutional Networks Applied to Energy-Related Time Series Forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks for Action Segmentation and Detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Dong, H.; Zhu, J.; Li, S.; Wu, W.; Zhu, H.; Fan, J. Short-Term Residential Household Reactive Power Forecasting Considering Active Power Demand via Deep Transformer Sequence-to-Sequence Networks. Appl. Energy 2023, 329, 120281. [Google Scholar] [CrossRef]
- Fan, C.; Chen, M.; Tang, R.; Wang, J. A Novel Deep Generative Modeling-Based Data Augmentation Strategy for Improving Short-Term Building Energy Predictions. Build. Simul. 2022, 15, 197–211. [Google Scholar] [CrossRef]
- Roth, J.; Martin, A.; Miller, C.; Jain, R.K. SynCity: Using Open Data to Create a Synthetic City of Hourly Building Energy Estimates by Integrating Data-Driven and Physics-Based Methods. Appl. Energy 2020, 280, 115981. [Google Scholar] [CrossRef]
- Fang, X.; Gong, G.; Li, G.; Chun, L.; Li, W.; Peng, P. A Hybrid Deep Transfer Learning Strategy for Short-Term Cross-Building Energy Prediction. Energy 2021, 215, 119208. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Al-Hyari, L.; Kassai, M. Development and Experimental Validation of TRNSYS Simulation Model for Heat Wheel Operated in Air Handling Unit. Energies 2020, 13, 4957. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a New-Generation Building Energy Simulation Program. Energ. Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Im, P.; Joe, J.; Bae, Y.; New, J.R. Empirical Validation of Building Energy Modeling for Multi-Zones Commercial Buildings in Cooling Season. Appl. Energy 2020, 261, 114374. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Z.; Xu, P.; Li, W.; Sha, H.; Yang, Z.; Li, G.; Hu, C. Quantification of Electricity Flexibility in Demand Response: Office Building Case Study. Energy 2019, 157, 1–259. [Google Scholar] [CrossRef]
- Soleimani-Mohseni, M.; Nair, G.; Hasselrot, R. Energy Simulation for a High-Rise Building Using IDA ICE: Investigations in Different Climates. Build. Simul. -China 2016, 9, 629–640. [Google Scholar] [CrossRef]
- Zhou, Y.; Su, Y.; Xu, Z.; Wang, X.; Wu, J.; Guan, X. A Hybrid Physics-Based/Data-Driven Model for Personalized Dynamic Thermal Comfort in Ordinary Office Environment. Energ. Build. 2021, 238, 110790. [Google Scholar] [CrossRef]
- Ngo, N.; Truong, T.T.H.; Truong, N.; Pham, A.; Huynh, N.; Pham, T.M.; Pham, V.H.S. Proposing a Hybrid Metaheuristic Optimization Algorithm and Machine Learning Model for Energy Use Forecast in Non-Residential Buildings. Sci. Rep. 2022, 12, 1065. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Y. Cooling Load Prediction and Optimal Operation of HVAC Systems Using a Multiple Nonlinear Regression Model. Energ. Build. 2019, 197, 7–17. [Google Scholar] [CrossRef]
- He, N.; Liu, L.; Qian, C.; Zhang, L.; Yang, Z.; Li, S. A Closed-Loop Data-Fusion Framework for Air Conditioning Load Prediction Based on LBF. Energy Rep. 2022, 8, 7724–7734. [Google Scholar] [CrossRef]
- Le, T.; Vo, M.; Vo, B.; Hwang, E.; Rho, S.; Baik, S. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Appl. Sci. 2019, 9, 4237. [Google Scholar] [CrossRef]
- Cen, S.; Lim, C.G. Multi-Task Learning of the PatchTCN-TST Model for Short-Term Multi-Load Energy Forecasting Considering Indoor Environments in a Smart Building. IEEE Access 2024, 12, 19553–19568. [Google Scholar] [CrossRef]
- Li, L.; Su, X.; Bi, X.; Lu, Y.; Sun, X. A Novel Transformer-Based Network Forecasting Method for Building Cooling Loads. Energ. Build. 2023, 296, 113409. [Google Scholar] [CrossRef]
- Alsmadi, L.; Lei, G.; Li, L. Forecasting Day-Ahead Electricity Demand in Australia Using a CNN-LSTM Model with an Attention Mechanism. Appl. Sci. 2025, 15, 3829. [Google Scholar] [CrossRef]
- Cheng, J.; Jin, S.; Zheng, Z.; Hu, K.; Yin, L.; Wang, Y. Energy consumption prediction for water-based thermal energy storage systems using an attention-based TCN-LSTM model. Sustain. Cities Soc. 2025, 126, 106383. [Google Scholar] [CrossRef]
- Liu, S.; Xu, T.; Du, X.; Zhang, Y.; Wu, J. A hybrid deep learning model based on parallel architecture TCN-LSTM with Savitzky-Golay filter for wind power prediction. Energy Convers. Manag. 2024, 302, 118122. [Google Scholar] [CrossRef]
- Bandara, K.; Hewamalage, H.; Liu, Y.; Kang, Y.; Bergmeir, C. Improving the Accuracy of Global Forecasting Models Using Time Series Data Augmentation. Pattern Recogn. 2021, 120, 108148. [Google Scholar] [CrossRef]
- Fekri, M.N.; Ghosh, A.M.; Grolinger, K. Generating Energy Data for Machine Learning with Recurrent Generative Adversarial Networks. Energies 2020, 13, 130. [Google Scholar] [CrossRef]
- Gao, Y.; Ruan, Y.; Fang, C.; Yin, S. Deep Learning and Transfer Learning Models of Energy Consumption Forecasting for a Building with Poor Information Data. Energ. Build. 2023, 292, 113164. [Google Scholar] [CrossRef]
- Ye, R.; Dai, Q. A Relationship-Aligned Transfer Learning Algorithm for Time Series Forecasting. Inform. Sci. 2022, 593, 17–34. [Google Scholar] [CrossRef]
- Zang, L.; Wang, T.; Zhang, B.; Li, C. Transfer Learning-Based Nonstationary Traffic Flow Prediction Using AdaRNN and DCORAL. Expert Syst. Appl. 2024, 258, 125143. [Google Scholar] [CrossRef]
- Hua, Y.; Sevegnani, M.; Yi, D.; Birnie, A.; McAslan, S. Fine-Grained RNN with Transfer Learning for Energy Consumption Estimation on EVs. IEEE Trans. Ind. Inform. 2022, 18, 8182–8190. [Google Scholar] [CrossRef]
- Xing, Z.; Pan, Y.; Yang, Y.; Yuan, X.; Liang, Y.; Huang, Z. Transfer Learning Integrating Similarity Analysis for Short-Term and Long-Term Building Energy Consumption Prediction. Appl. Energy 2024, 365, 123276. [Google Scholar] [CrossRef]
- Li, G.; Wu, Y.; Yan, C.; Fang, X.; Li, T.; Gao, J.; Xu, C.; Wang, Z. An improved transfer learning strategy for short-term cross-building energy prediction using data incremental. Build. Simul. 2024, 17, 165–183. [Google Scholar] [CrossRef]
- Kamalov, F.; Sulieman, H.; Moussa, S.; Avante Reyes, J.; Safaraliev, M. Powering Electricity Forecasting with Transfer Learning. Energies 2024, 17, 626. [Google Scholar] [CrossRef]
- Cheng, X.; Cao, Y.; Song, Z.; Zhang, C. Wind power prediction using stacking and transfer learning. Sci. Rep. 2025, 15, 11566. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K.; Barrett, A.B.; Barnett, L. Granger Causality Analysis in Neuroscience and Neuroimaging. J. Neurosci. 2015, 35, 3293–3297. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Liao, S.; Fu, S.; Li, Y.; Han, H. Image Inpainting Using Non-Convex Low Rank Decomposition and Multidirectional Search. Appl. Math. Comput. 2023, 452, 128048. [Google Scholar] [CrossRef]
- Kim, T.; Cho, S. Predicting Residential Energy Consumption Using CNN-LSTM Neural Networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Li, T.; Liu, T.; Sawyer, A.O.; Tang, P.; Loftness, V.; Lu, Y.; Xie, J. Generalized Building Energy and Carbon Emissions Benchmarking with Post-Prediction Analysis. Dev. Built Environ. 2024, 17, 100320. [Google Scholar] [CrossRef]


| Category | Tools/Methods | Key Features | Limitations |
|---|---|---|---|
| Physics-based Modeling | TRNSYS [22], EnergyPlus [23], DOE-2 [24], Dymola [25], IDA-ICE [26] | Based on energy balance principles; precise and detailed building energy consumption modeling | Requires large number of input parameters; complex setup; difficult data collection |
| Statistical Learning | WIO-SVR [28], MNR [29] | Optimizes feature engineering; uses algorithms for improved accuracy | Limited capability for high-dimensional and complex data; insufficient adaptability |
| Deep Learning | PF+LSTM+BP [30], EECP-CBL [31], TCN [15], PatchTCN-TST [32], Transformer-based [33], CNN-LSTM-Attention [34], Attention-TCN-LSTM [35], TCN-LSTM hybrid [36] | Captures complex temporal features; integrates multiple network architectures and attention mechanisms | Heavy reliance on large historical datasets; limited performance with scarce data |
| Data Augmentation | GFM + Transfer Learning [37], GAN-based augmentation [38] | Augments data by generating synthetic samples; merges datasets to enrich training data | Synthetic data quality may affect model generalization; still needs domain alignment |
| Transfer Learning | Seq2seq + 2D CNN [39], aRATL [40], AdaRNN-DCORAL [41], LSTM-DANN-CDI [44], Zero-shot NBEATS [45], Stacking + Transfer Learning [46] et al. | Applies knowledge transfer, incremental learning, domain adaptation to leverage related tasks | Domain discrepancies between buildings, especially HVAC and occupant behavior, reduce transfer efficiency; need better transfer strategies |
| Feature | Type | Range | Unit |
|---|---|---|---|
| building energy consumption | continuous | kWh | |
| temperature | continuous | °C | |
| dew point | continuous | °C | |
| relative humidity | continuous | % | |
| air pressure | continuous | Pa | |
| wind speed | continuous | m/s | |
| month of the year | categorical | - | |
| day of the year | categorical | - | |
| day of the month | categorical | - | |
| day of the week | categorical | - | |
| hour of the day | categorical | - | |
| season | categorical | - | |
| holiday status | categorical | - |
| Method | ||||
|---|---|---|---|---|
| Xgboost [11] | 0.2092 ± 0.0164 | 0.1161 ± 0.0234 | 111.93% ± 21.45% | 0.8497 ± 0.0303 |
| LSTM [13] | 0.1072 ± 0.0041 | 0.0348 ± 0.0013 | 36.26% ± 1.29% | 0.9459 ± 0.0017 |
| CNNLSTM [50] | 0.1010 ± 0.0065 | 0.0321 ± 0.0020 | 41.72% ± 3.88% | 0.9509 ± 0.0026 |
| TCN [16] | 0.1046 ± 0.0190 | 0.0278 ± 0.0044 | 51.46% ± 5.96% | 0.9611 ± 0.0056 |
| iTransformer [51] | 0.0887 ± 0.0023 | 0.0248 ± 0.0007 | 35.83% ± 2.65% | 0.9674 ± 0.0009 |
| AtTCN (Ours) | 0.0830 ± 0.0026 | 0.0234 ± 0.0005 | 35.21% ± 2.01% | 0.9696 ± 0.0007 |
| Time Series | Method | ||||
|---|---|---|---|---|---|
| 1 Week | AtTCN(baseline) | 1.2116 ± 0.2805 | 1.7144 ± 0.6034 | 2673% ± 2474% | - |
| fine-tuned AtTCN | 0.9848 ± 0.2535 | 1.2330 ± 0.4055 | 2077% ± 2040% | - | |
| aRATL [40] | 0.8342 ± 0.2992 | 0.8556 ± 0.4419 | 449.40% ± 276.39% | - | |
| DCORAL [41] | 0.5852 ± 0.3015 | 0.5060 ± 0.3513 | 63.54% ± 32.54% | - | |
| Fine-Grained RNN&TL [42] | 0.2345 ± 0.0010 | 0.0551 ± 0.0005 | 25.49% ± 0.11% | - | |
| Freeze-LSTM [43] | 0.0618 ± 0.0004 | 0.0618 ± 0.0004 | 27.01% ± 0.10% | - | |
| LRTL-AtTCN(Ours) | 0.1064 ± 0.0280 | 0.0150 ± 0.0168 | 16.10% ± 0.86% | - | |
| 2 Weeks | AtTCN(baseline) | 0.3619 ± 0.1830 | 0.3236 ± 0.2086 | 702.31% ± 980.99% | - |
| fine-tuned AtTCN | 0.2529 ± 0.1565 | 0.1306 ± 0.1915 | 392.01% ± 401.24% | 0.6642 ± 0.2570 | |
| aRATL [40] | 0.2860 ± 0.0292 | 0.0898 ± 0.0157 | 293.13% ± 160.11% | 0.5435 ± 0.0698 | |
| DCORAL [41] | 0.4146 ± 0.1220 | 0.2989 ± 0.1393 | 277.04% ± 117.03% | 0.3557 ± 0.4040 | |
| Fine-Grained RNN&TL [42] | 0.3114 ± 0.0001 | 0.1337 ± 0.0001 | 275.87% ± 0.24% | 0.3924 ± 0.0005 | |
| Freeze-LSTM [43] | 0.2994 ± 0.0001 | 0.1146 ± 0.0001 | 284.04% ± 0.24% | 0.0813 ± 0.0002 | |
| LRTL-AtTCN(Ours) | 0.1859 ± 0.0113 | 0.0533 ± 0.0035 | 155.10% ± 4.95% | 0.8628 ± 0.0155 | |
| 1 Month | AtTCN(baseline) | 0.3059 ± 0.2190 | 0.1810 ± 0.4073 | 132.95% ± 132.85% | 0.8188 ± 0.2058 |
| fine-tuned AtTCN | 0.2742 ± 0.2075 | 0.1353 ± 0.2033 | 86.85% ± 75.27% | 0.8763 ± 0.2101 | |
| aRATL [40] | 0.2408 ± 0.0294 | 0.1062 ± 0.026 | 67.51% ± 29.06% | 0.9038 ± 0.0316 | |
| DCORAL [41] | 0.2401 ± 0.0073 | 0.1030 ± 0.0041 | 66.53% ± 5.95% | 0.9018 ± 0.0029 | |
| Fine-Grained RNN&TL [42] | 0.3041 ± 0.0001 | 0.1332 ± 0.0001 | 50.57% ± 0.01% | 0.8769 ± 0.0001 | |
| Freeze-LSTM [43] | 0.3594 ± 0.0001 | 0.1956 ± 0.0001 | 66.13% ± 0.01% | 0.7983 ± 0.0002 | |
| LRTL-AtTCN(Ours) | 0.2251 ± 0.0124 | 0.0911 ± 0.085 | 50.57% ± 3.75% | 0.9286 ± 0.0157 |
| ID | Feature Combination | ||||
|---|---|---|---|---|---|
| F1 | energy features | 0.3737 ± 0.0050 | 0.2696 ± 0.0056 | 183.25% ± 8.20% | 0.7805 ± 0.0059 |
| F2 | energy features + weather feature | 0.3059 ± 0.0076 | 0.1263 ± 0.0079 | 161.22% ± 5.21% | 0.8783 ± 0.0145 |
| F3 | energy features + timestamp features | 0.3402 ± 0.0009 | 0.2150 ± 0.0008 | 102.88% ± 1.82% | 0.8227 ± 0.0053 |
| F4 | energy features + weather feature + timestamp features | 0.2770 ± 0.0031 | 0.1012 ± 0.0027 | 54.81% ± 1.30% | 0.9111 ± 0.0050 |
| F5 | Granger-selected feature | 0.2251 ± 0.0124 | 0.0911 ± 0.085 | 50.57% ± 3.75% | 0.9286 ± 0.0157 |
| Rank | |||
|---|---|---|---|
| 4 | 16,681 | 260 | 0.9844 |
| 8 | 16,689 | 520 | 0.9688 |
| 16 | 16,705 | 1040 | 0.9377 |
| 32 | 16,737 | 2080 | 0.8757 |
| 64 | 16,801 | 4160 | 0.7524 |
| Rank Setting | ||||
|---|---|---|---|---|
| 4 | 0.2251 ± 0.0124 | 0.0911 ± 0.085 | 50.57% ± 3.75% | 0.9286 ± 0.0157 |
| 8 | 0.2919 ± 0.0058 | 0.1432 ± 0.0040 | 103.39% ± 2.34% | 0.8638 ± 0.0069 |
| 16 | 0.2934 ± 0.0111 | 0.1439 ± 0.0078 | 123.57% ± 4.71% | 0.8624 ± 0.0135 |
| 32 | 0.2955 ± 0.0283 | 0.1459 ± 0.0210 | 154.81% ± 5.30% | 0.8576 ± 0.0399 |
| 64 | 0.3064 ± 0.0158 | 0.1587 ± 0.0113 | 168.20% ± 9.50% | 0.8333 ± 0.0218 |
| Time Series | Transfer Strategies | ||||
|---|---|---|---|---|---|
| 1 Week | direct training | 1.2116 ± 0.2805 | 1.7144 ± 0.6034 | 2673% ± 2474% | - |
| unadapted | 0.1668 | 0.0278 | - | ||
| fine-tuned | 0.9848 ± 0.2535 | 1.2330 ± 0.4055 | 2077% ± 2040% | - | |
| unifying training | 0.2941 ± 0.0145 | 0.0869 ± 0.0085 | 47.07% ± 3.45% | - | |
| LRTL | 0.1064 ± 0.0280 | 0.0150 ± 0.0168 | 16.10% ± 0.86% | - | |
| 2 Weeks | direct training | 0.3619 ± 0.1830 | 0.3236 ± 0.2086 | 702.31% ± 980.99% | - |
| unadapted | 0.3043 | 0.1193 | 0.5912 | ||
| fine-tuned | 0.2529 ± 0.1565 | 0.1306 ± 0.1915 | 392.01% ± 401.24% | 0.6642 ± 0.2570 | |
| unifying training | 0.2505 ± 0.0220 | 0.0851 ± 0.0154 | 172.04% ± 60.20% | 0.4594 ± 0.1512 | |
| LRTL | 0.1859 ± 0.0113 | 0.0533 ± 0.0035 | 155.10% ± 4.95% | 0.8628 ± 0.0155 | |
| 1 Month | direct training | 0.3059 ± 0.2190 | 0.1810 ± 0.4073 | 132.95% ± 132.85% | 0.8188 ± 0.2058 |
| unadapted | 0.2903 | 0.1285 | 0.8772 | ||
| fine-tuned | 0.2742 ± 0.2075 | 0.1353± 0.2033 | 86.85% ± 75.27% | 0.8763 ± 0.2101 | |
| unifying training | 0.3487 ± 0.0143 | 0.1656 ± 0.0143 | 143.78% ± 31.13% | 0.8600 ± 0.0110 | |
| LRTL | 0.2251 ± 0.0124 | 0.0911 ± 0.085 | 50.57% ± 3.75% | 0.9286 ± 0.0157 |
| Source Domain Combination | ||||
|---|---|---|---|---|
| LRTL-LSTM | 0.3888 ± 0.0022 | 0.2063 ± 0.0026 | 121.40% ± 2.16% | 0.8060 ± 0.0078 |
| LRTL-CNNLSTM | 0.3342 ± 0.0002 | 0.1581 ± 0.0005 | 109.08% ± 0.78% | 0.8645 ± 0.0021 |
| LRTL-TCN | 0.2923 ± 0.0005 | 0.1120 ± 0.0010 | 374.04% ± 4.34% | 0.9000 ± 0.0030 |
| LRTL-iTransformer | 0.2746 ± 0.0020 | 0.1171 ± 0.0015 | 80.36% ± 0.77% | 0.9018 ± 0.0028 |
| LRTL-AtTCN | 0.2251 ± 0.0124 | 0.0911 ± 0.085 | 50.57% ± 3.75% | 0.9286 ± 0.0157 |
| Layer Arrangements | ||||
|---|---|---|---|---|
| attention + conv1 + conv2 | 0.2779 ± 0.0001 | 0.1076 ± 0.0002 | 45.25% ± 0.19% | 0.9117 ± 0.0007 |
| conv1 + attention + conv2 | 0.2690 ± 0.0004 | 0.1028 ± 0.0005 | 293.30% ± 1.51% | 0.9167 ± 0.0012 |
| conv1 + conv2 + attention | 0.2251 ± 0.0124 | 0.0911 ± 0.085 | 50.57% ± 3.75% | 0.9286 ± 0.0157 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Fu, Q.; Lu, Y.; Liu, K. Limited Data Availability in Building Energy Consumption Prediction: A Low-Rank Transfer Learning with Attention-Enhanced Temporal Convolution Network. Information 2025, 16, 575. https://doi.org/10.3390/info16070575
Wang B, Fu Q, Lu Y, Liu K. Limited Data Availability in Building Energy Consumption Prediction: A Low-Rank Transfer Learning with Attention-Enhanced Temporal Convolution Network. Information. 2025; 16(7):575. https://doi.org/10.3390/info16070575
Chicago/Turabian StyleWang, Bo, Qiming Fu, You Lu, and Ke Liu. 2025. "Limited Data Availability in Building Energy Consumption Prediction: A Low-Rank Transfer Learning with Attention-Enhanced Temporal Convolution Network" Information 16, no. 7: 575. https://doi.org/10.3390/info16070575
APA StyleWang, B., Fu, Q., Lu, Y., & Liu, K. (2025). Limited Data Availability in Building Energy Consumption Prediction: A Low-Rank Transfer Learning with Attention-Enhanced Temporal Convolution Network. Information, 16(7), 575. https://doi.org/10.3390/info16070575






