Abstract
Sparse matrix–vector multiplication (SpMV) plays a significant role in the computational costs of many scientific applications such as 2D/3D robotics, power network problems, and computer vision. Numerous implementations using different sparse matrix formats have been introduced to optimize this kernel on CPUs and GPUs. However, due to the sparsity patterns of matrices and the diverse configurations of hardware, accurately modeling the performance of SpMV remains a complex challenge. SpMV computation is often a time-consuming process because of its sparse matrix structure. To address this, we propose a machine learning-based tool, namely Elegante+, that predicts optimal scheduling policies by analyzing matrix structures. This approach eliminates the need for repetitive trial and error, minimizes errors, and finds the best solution of the SpMV kernel, which enables users to make informed decisions about scheduling policies that maximize computational efficiency. For this purpose, we collected 1000+ sparse matrices from the SuiteSparse matrix market collection and converted them into the compressed sparse row (CSR) format, and SpMV computation was performed by extracting 14 key sparse matrix features. After creating a comprehensive dataset, we trained various machine learning models to predict the optimal scheduling policy, significantly enhancing the computational efficiency and reducing the overhead in high-performance computing environments. Our proposed tool, Elegante+ (XGB with all SpMV features), achieved the highest cross-validation score of 79% and performed five times faster than the default scheduling policy during SpMV in a high-performance computing (HPC) environment.
1. Introduction
Sparse matrix–vector multiplication (SpMV), as a key kernel for iterative solutions of sparse linear systems in scientific and engineering computations, is widely used in fields such as graph computation [1,2], machine learning [3], and linear algebra [4]. It plays a critical role in high-performance computing (HPC) by significantly influencing computational efficiency, memory access patterns, and scalability. SpMV is particularly important in applications like natural language processing, recommender systems, and graph analytics, as well as in computational physics, finite element analysis, and biomedical simulations, where large-scale sparse matrices are commonly encountered. By optimizing SpMV, researchers can reduce computational time and resource usage, allowing for the management of complex models and larger datasets. Furthermore, efficient SpMV execution enhances parallel processing, enabling shared-memory multicore architectures to perform large-scale matrix operations with reduced latency. This is especially crucial for scientific simulations and engineering problems, where the computational costs of sparse matrix operations directly impact real-time performance and decision-making. Advancements in SpMV techniques lead to more efficient algorithms, driving innovation in data-intensive fields. Overall, optimizing SpMV is crucial for improving the scalability and performance of modern computational tasks, particularly in shared-memory multicore systems, where architectural complexity poses significant challenges due to shared memory and multiple levels of memory hierarchy, leading to non-uniform memory access (NUMA) latencies [5,6].
Over the years, performance optimization of SpMV on general-purpose multicore processors (CPUs) and many-core processors (GPUs) has received extensive attention from researchers [7,8,9,10,11,12,13]; however, achieving optimal performance remains a challenge due to irregular memory access patterns and the inherent sparsity of the matrices, which can significantly affect data locality and computational efficiency. Addressing these challenges requires a structured approach that integrates machine learning models to predict execution behaviors and adapt scheduling policies accordingly.
Sparse matrices typically contain a large number of zero elements, with non-zero elements constituting only a small proportion. Therefore, they cannot be stored using simple two-dimensional arrays like dense matrices. To reduce storage overhead, transmission costs to devices, and memory access overhead on devices, sparse matrices are generally stored in compressed formats. Common sparse matrix storage formats include Coordinate Format (COO), compressed sparse row (CSR), ELLPACK (ELL), and Diagonal Format (DIA). Other encoding formats proposed over the years have built upon these four fundamental formats, aiming to further optimize memory efficiency and computational performance for specific sparse matrix structures. SpMV can be expressed using Formula (1), where A is an M × N sparse matrix, and x and y are dense vectors measuring N × 1 and M × 1, respectively.
Recently, researchers have proposed various effective optimization techniques to address the main challenges of SpMV, including designing specialized sparse matrix storage formats [14], optimizing vector storage [15,16], and addressing data dependency issues during computation [17,18]. The goal is to reduce these overheads while enhancing computational efficiency and maximizing performance across the system. The sparsity pattern of the matrix is often unknown until runtime, making manual mapping of processes and data through trial and error a tedious and inefficient process. Moreover, the lack of a standardized approach for dynamically selecting optimal scheduling strategies further complicates SpMV execution in real-world applications. Furthermore, the irregular nature of matrices means that this process must be repeated for each matrix, further complicating optimization efforts [19].
Over time, scheduling policies have evolved to address the increasing complexity of modern high-performance computing (HPC) architectures and diverse workload characteristics. Initially, static scheduling was widely used due to its simplicity and low overhead, but it struggled with load imbalance in irregular computations. To overcome these limitations, dynamic and guided scheduling strategies were introduced, allowing for better adaptability and resource utilization, particularly in scenarios with varying computational loads. Scheduling policies play a crucial role in optimizing SpMV computations by managing workload distribution and improving execution efficiency. Policies such as guided, runtime, dynamic, and static scheduling determine how tasks are assigned to threads, directly impacting performance. Guided scheduling enables adaptive workload distribution, while runtime scheduling dynamically adjusts based on real-time system conditions. Dynamic and static scheduling strategies also offer distinct benefits in balancing load and minimizing overhead, leading to enhanced efficiency in HPC environments.
Random selection and trial and error approaches to choosing a scheduling policy are both time-consuming and prone to errors. Owing to the irregular structures of sparse matrices, determining a suitable scheduling policy often requires multiple iterations. To overcome these inefficiencies, this study introduced an automated, data-driven approach to predict optimal scheduling strategies based on matrix characteristics. Our proposed solution addresses these issues by predicting an optimal scheduling policy based on the matrix structure. This approach eliminates the need for repetitive random selection and minimizes errors.
To tackle this issue, this study introduced a machine learning-driven tool called Elegante+, which was designed to optimize the performance of SpMV on shared-memory architectures. Our approach worked directly on the standard CSR data format. To achieve this objective, this study employed various machine learning algorithms, such as decision tree (DT), Random Forest (RF), Extreme Gradient Boosting (XGB), and K-Nearest Neighbor (K-NN), to predict near-optimal scheduling policies by leveraging the structural properties of matrices to enhance the efficiency of SpMV computations. The reason for selecting these algorithms was their ability to effectively handle structured data and their superior predictive performance in our experimental evaluation.
The method comprised five key phases: (1) collection of sparse matrices, (2) conversion of the sparse matrices to the CSR format and execution of SpMV computations for dataset preparation, (3) feature extraction, (4) model training and testing, and (5) evaluation of the models using k-fold cross-validation. Initially, over 1000 real-world sparse matrices were sourced from diverse domains, ensuring the robustness and generalizability of the model. These matrices were obtained from the SuiteSparse matrix market collection [20] on the University of Florida website. Subsequently, various scheduling policies such as static, dynamic, guided, and runtime scheduling were applied to execute SpMV computation [21] across 48 threads, repeating each execution 2000 times to account for performance fluctuations, minimize measurement noise, and ensure statistically reliable execution time analysis. For each scheduling policy, the minimum, maximum, and average execution times were recorded. Additionally, the execution time when using the default OpenMP configuration was also noted, resulting in labeled data that included execution times across different scheduling strategies. We extracted 14 key features from each matrix, focusing on computationally significant attributes that influenced scheduling decisions. These comprehensive data enabled the compilation of a detailed corpus of 14 sparse matrix features that corresponded to each scheduling policy. Once the dataset was fully assembled, we proceeded to the training phase. To the best of our knowledge, this is a relatively new approach that leverages CSR matrix characteristics to predict optimal scheduling policies for SpMV computations in a shared-memory architecture. By focusing on key CSR characteristics like row pointers, column indices, and non-zero values, we aimed to optimize scheduling policies and enhance performance in high-performance computing environments.
This study makes the following key contributions:
- ✓
- Building on our previous research, where we introduced Elegante, a machine learning tool that predicts a near-optimal number of threads for SpMV computations on shared-memory architectures, we now present Elegante+, an enhanced machine learning-based approach that predicts the best scheduling policies to further optimize SpMV execution. Unlike manual trial-and-error approaches, Elegante+ was evaluated against OpenMP’s default scheduling policy, demonstrating improved performance under multiple threads.
- ✓
- Elegante+ was trained and tested on a diverse dataset of nearly 100 real-world matrices sourced from 44 different applications domains such as linear programming, 2D/3D modeling, computer graphics, computer vision, and computational fluid dynamics (CFD).
- ✓
- Elegante+ evaluates and optimizes SpMV execution, empowering users to make informed decisions regarding scheduling policies, thereby maximizing computational efficiency across various architectures.
- ✓
- Through extensive benchmarking, Elegante+ provides actionable insights for HPC practitioners, facilitating improved workflow optimization and enhanced computational performance in fields ranging from machine learning to large-scale scientific simulations.
The remainder of this paper is organized as follows: Section 2 explores related work. Section 3 describes the methodology of the proposed approach. Detailed experimental results and an analysis of different scheduling policies for SpMV are presented in Section 4. Finally, Section 5 presents the limitations of the proposed methodology, and Section 6 concludes this study and outlines potential future research directions.
2. Related Survey
Usman et al. [22] introduced ZAKI+, which focuses on optimizing process mapping for parallel SpMV computations on distributed-memory systems using machine learning. While ZAKI+ improves data distribution and process mapping efficiency, our proposed tool, Elegante+, takes a different approach by predicting optimal scheduling policies specifically for shared-memory high-performance computing (HPC) environments. Unlike ZAKI+, which optimizes process mapping for distributed systems, Elegante+ analyzes sparse matrix structures and predicts the best scheduling strategy to maximize computational efficiency in a shared-memory setting.
Ahmad et al. [23] presented AAQAL, a machine learning-based tool designed to optimize the sparse matrix–vector product (SpMV) by automating data distribution and selecting near-optimal block sizes using the block compressed sparse row (BCSR) format. Trained on nearly 700 real-world matrices from 43 application domains, AAQAL achieved 93.47% of the maximum attainable performance, significantly outperforming manual or random block size selection. This work was the first to exploit the matrix structure with BCSR for optimal block size selection in SpMV computations using machine learning techniques.
Usman et al. [24] explored the convergence of high-performance computing (HPC), big data, and artificial intelligence in optimizing sparse matrix–vector product (SpMV) computations for smart cities. The authors proposed the tool ZAKI, a machine learning approach used to predict optimal process configurations and parallelization strategies for sparse matrix–vector product (SpMV) computations on distributed-memory machines. They evaluated four machine learning algorithms using 1838 real-world sparse matrices, addressing challenges related to data locality and energy efficiency for exascale computing.
Xiao et al. [25] proposed a machine learning-based adaptive framework for SpMV, DTSpMV. This framework uses a decision tree to automatically select optimal SpMV kernels based on input data changes during graph computations. Experimental results showed a 152× performance improvement compared to cuSPARSE on an NVIDIA Tesla T4 GPU.
Yesil et al. [26] developed a machine learning framework called WISE to predict the best SpMV method for a given sparse matrix based on its size, skew, and locality traits. Using WISE, they predicted the acceleration magnitudes of different methods over a baseline, achieving a 2.4× acceleration over Intel’s MKL. Their framework accurately selected the optimal SpMV methods for a wide range of matrices, demonstrating improved performance.
Gao et al. [27] proposed a machine learning-based thread assignment strategy for optimizing sparse SpMV on GPUs. They predicted near-optimal thread configurations by partitioning irregular matrices into blocks and designing a new kernel to accelerate execution. Experimental results showed improved performance after machine learning-based thread prediction and matrix partitioning.
Shi et al. [28] proposed a machine learning-based thread assignment tool for optimizing sparse SpMV on GPUs, addressing the issues of irregular memory access and unbalanced workloads. They partitioned irregular sparse matrices into blocks based on the non-zero element distribution and predicted the optimal thread configurations for each block. A new SpMV kernel was designed to enhance execution efficiency. Experimental results showed improved performance for irregular matrices using this approach.
Dufrechou et al. [29] reviewed various GPU routines for SpMV and applied machine learning to predict the best method for each sparse matrix. They showed that machine learning can predict optimal SpMV methods with over 80% accuracy. This approach leads to significant reductions in execution time and energy consumption.
Ahmad et al. [30] introduced Elegante, which focuses on optimizing SpMV performance by automating data distribution and selecting an optimal number of threads. However, our work extended beyond thread selection and introduced Elegante+, which predicts optimal scheduling policies based on sparse matrix structures. Unlike Elegante, which primarily focuses on thread optimization, our approach leveraged 14 key sparse matrix features to train machine learning models, allowing us to predict the best scheduling strategy rather than just the number of threads. Additionally, our model achieved a higher cross-validation score of 79% and demonstrated 5× acceleration compared to the default scheduling policies in high-performance computing (HPC) environments. By moving beyond thread selection to comprehensive scheduling optimization, our work provides a more generalized and efficient solution for SpMV performance enhancement.
3. Methodology and Design
3.1. Construction of Dataset
We manually collected over 1000 sparse matrices from the SuiteSparse matrix collection, covering diverse application domains such as 2D/3D robotics, computational fluid dynamics (CFD), power networks, and computer vision. We selected multiple matrices from each domain to ensure comprehensive representation of real-world scenarios. As a representative sample, one matrix from each application domain was chosen to be presented in Table 1. These matrices were selected based on their structural variety, computational complexity, and sparsity levels, capturing different row/column distributions and numerical patterns, to enable the model to learn from a diverse dataset.

Table 1.
Sample sparse matrices from various application domains.
After collecting the sparse matrices, we converted the SuiteSparse format to the well-known CSR format, and SpMV computations were performed under various scheduling policies with different numbers of threads. We extracted 14 key sparse matrix features to determine the specific scheduling policy that yielded the minimum execution time, which is referred to as the label or target variable, to make a comprehensive dataset.
The inclusion of matrices from different domains enhanced the generalizability of the model by exposing it to a wide range of structural characteristics and computational behaviors. This ensured that the model can effectively predict scheduling policies for unseen matrices from various applications, rather than being biased toward a specific domain. The extracted features serve as domain-agnostic indicators of matrix behavior, making the trained model adaptable to new problem sets.
To identify the optimal scheduling policy for each matrix, various machine learning models were trained using sparse matrix features along with their corresponding labels, as seen in Figure 1. This approach allowed for the prediction of the best scheduling policy and thread configuration for efficient execution of sparse matrix operations. Table 1 outlines various application domains and their associated matrices, providing key information on matrix dimensions and types. Each matrix is listed with its name; type; and numbers of rows, columns, and non-zero elements (NNZ).
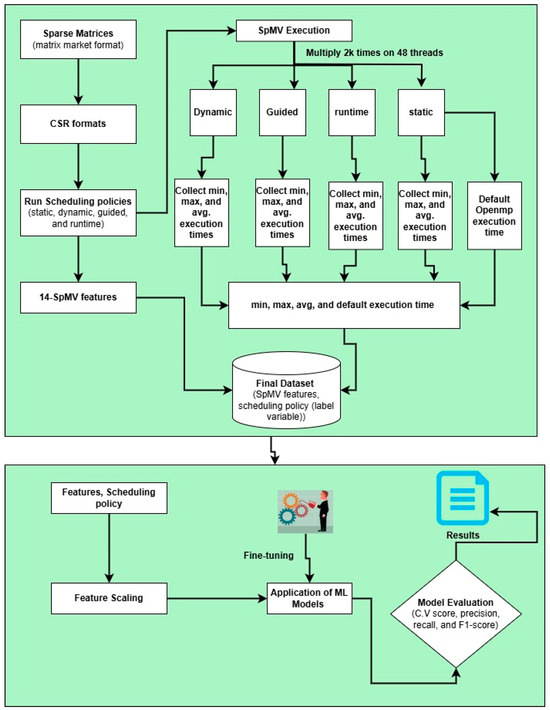
Figure 1.
Architecture of proposed methodology.
3.2. Data Labeling, Training, and Testing
SpMV computations were performed 2 k times using 48 threads, starting with the runtime scheduling policy. Subsequently computations were executed for the static, dynamic, and guided policies. After conducting these computations, we recorded the minimum, maximum, and average execution times, as well as that obtained when using the default OpenMP configuration, for each scheduling policy across the 48 threads. Once we obtained these statistics for all policies, we calculated the minimum, maximum, and average execution times for each scheduling policy while also noting the policy with the minimum execution time. This process resulted in a dataset containing the minimum, maximum, and average execution times along with their corresponding scheduling policies. Finally, we combined these data with the 14 sparse matrix features (Table 2) in a separate CSV file, establishing the scheduling policy as our target variable for further training and testing procedures. These 14 extracted features were carefully chosen, as they capture essential properties of sparse matrices, such as the sparsity pattern, non-zero distribution, and computational complexity, which directly impact scheduling efficiency. For instance, matrices with irregular sparsity patterns may benefit from dynamic scheduling, while structured matrices with uniform non-zero distributions might perform better with static scheduling. The final dataset was imbalanced owing to disproportionate representations of different scheduling policies, resulting in policies with significantly more samples than others, which could adversely affect model performance. Because of the imbalanced nature of the data, we used a random oversampling technique to balance the dataset. We employed cross-validation to evaluate the model using five folds, where a portion of the dataset was used for training and a different portion was used for testing in each iteration.

Table 2.
SpMV features.
3.3. Feature Scaling
Feature scaling is a widely used technique in machine learning and statistics that involves standardizing the ranges of independent variables or data features to ensure that all features are equally important in a model. This is crucial because many algorithms can be affected by the magnitudes of their features, leading to poor performance. In our study, we used min–max scaling, which transforms the features to a range from 0 to 1, as shown in Formula (2):
3.4. Model Evaluation Phase
After constructing the proposed model, various evaluation metrics were applied to assess its performance. The model training phase involved four machine learning models: DT, KNN, XGB, and RF. The proposed models were evaluated using metrics such as accuracy, recall, precision, and the F1-score to measure their performance. The following formulas were used to compute these metrics:
Cross-validation: cross-validation is a technique that divides a dataset into multiple subsets (folds) to train and test a model iteratively, ensuring better performance evaluation and reducing over-fitting risk, as seen in Figure 2.
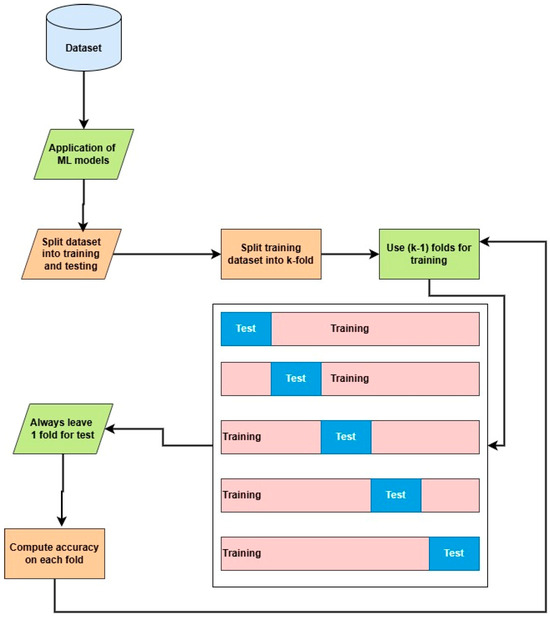
Figure 2.
Illustration of k-fold cross-validation.
Precision: the total number of correct predictions in our model was retrieved during document retrieval.
Recall: recall indicates the classifier’s ability to identify all relevant instances in the dataset.
F1-score: the F1-score is a metric that combines precision and recall.
Formula (3) was used for the cross-validation score, while Formulas (4)–(6) were used for precision, recall, and the F1-score, respectively.
where M is the overall mean, Mi is the ith value (e.g., the performance from the cross-validation fold), k is the total number of folds, TP is true positives, FP is false positives, and FN is false negatives.
4. Results and Analysis
4.1. Software and Hardware
Table 3 provides an overview of the hardware and software setup used in this study. On the hardware side, the system was powered by an AMD EPYC 7401P CPU (Advanced Micro Devices (AMD), a multinational semiconductor company headquartered in Santa Clara, CA, USA), featuring 24 physical cores with 2 threads per core, allowing for a total of 48 threads to handle computational tasks efficiently. The software environment included Windows 10 Pro (version 18363.904) as the operating system, paired with OpenMP 5.1 for parallel processing capabilities. Development work was supported by Visual Studio Professional 2019 (version 16.5) as the primary compiler. For Python-based workflows, Google Colab (Python 3.6.7) provided a cloud-based platform, and Scikit-Learn 0.23.1 was employed for machine learning tasks. Together, this setup offered a robust and efficient environment for computational and AI-driven projects.

Table 3.
Hardware and software details.
4.2. Execution Time Analysis of SpMV Computation
The SpMV computations using the CSR storage format were executed across various numbers of threads. For each matrix, the maximum, default OpenMP, and minimum execution times were determined in seconds.
The SpMV computations started with the runtime scheduling policy. Subsequently, the computations were executed for the static, dynamic, and guided policies. After conducting these tests, we recorded the minimum, maximum, and average execution times for each scheduling policy across the 48 threads. Once we obtained these statistics for all policies, we calculated the minimum, maximum, and average execution times for each scheduling policy while also noting the default OpenMP configuration. This process resulted in a dataset containing the minimum, maximum, default OpenMP, and average execution times, along with their corresponding scheduling policies. Finally, we combined these data with the 14 previously extracted sparse matrix features in a separate CSV file, establishing the scheduling policy as our target variable for further procedures.
Figure 3 and Figure 4 illustrate the execution times for SpMV computations using datasets sorted in ascending order by the numbers of rows and non-zero elements (nnz), respectively. In both figures, the X-axis categorizes different matrices from the 46 application domains according to the minimum to maximum sorting of rows and nnz, whereas the Y-axis represents the execution times (in seconds) on a logarithmic scale.
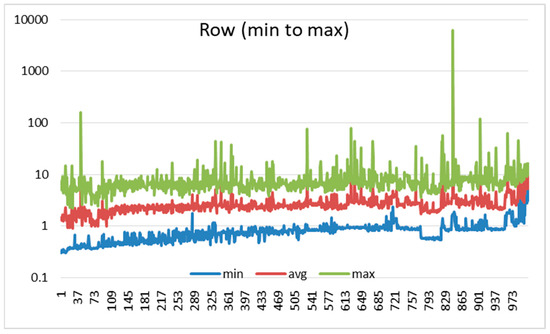
Figure 3.
Execution time comparison for data sorted by row.
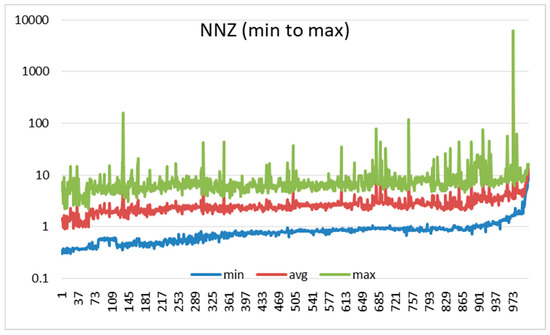
Figure 4.
Execution time comparison for data sorted by NNZ.
4.3. Acceleration
In this section, we will discuss the acceleration achieved in sparse matrix–vector multiplication (SpMV) operations. Adaptive scheduling techniques were applied to the CPU with the goal of minimizing idle-time scenarios across threads and optimizing load balancing, resulting in significant acceleration and improved performance in SpMV computations.
Figure 5 and Figure 6 show the acceleration sorted by row (min to max) and NNZ (min to max), while Figure 7 and Figure 8 show the domain-wise execution time and Figure 9 and Figure 10 show the domain-wise reduction in the execution time of SpMV multiplication for different matrices across 44 application domains. The acceleration was calculated using Formulas (7) and (8). The x-axis represents the total number of matrices, whereas the y-axis (log scale) represents the execution time in seconds. The graph compares the average acceleration (blue) with the maximum acceleration (red). As observed, the maximum acceleration was generally higher than the average, indicating that there were cases in which certain matrices achieved significantly better optimization.
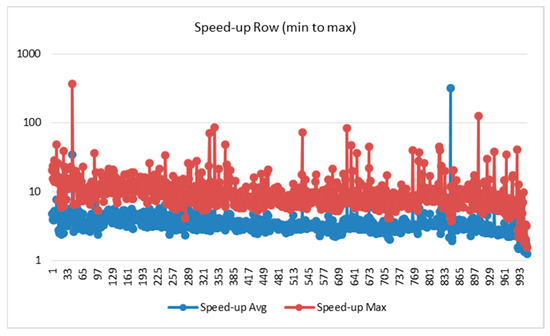
Figure 5.
Speed-up row sorted data.
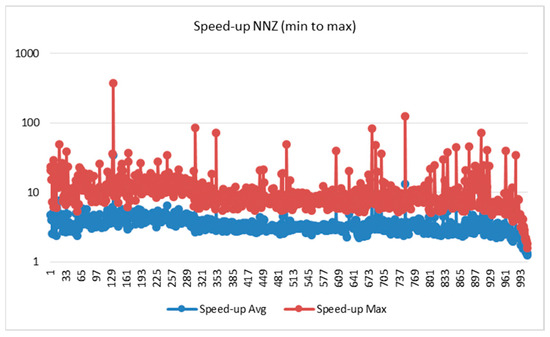
Figure 6.
Speed-up NNZ sorted data.
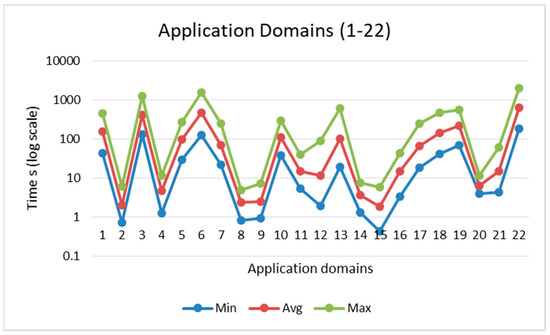
Figure 7.
Domain-wise execution time (application domains 1 to 22).
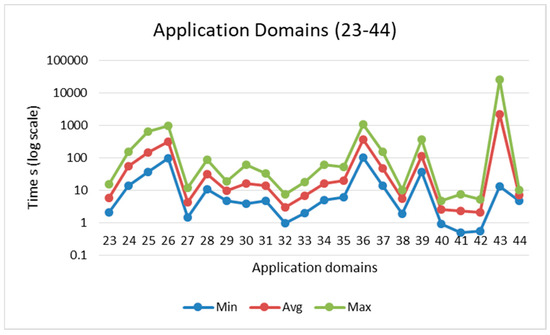
Figure 8.
Domain-wise execution time (application domains 23 to 44).
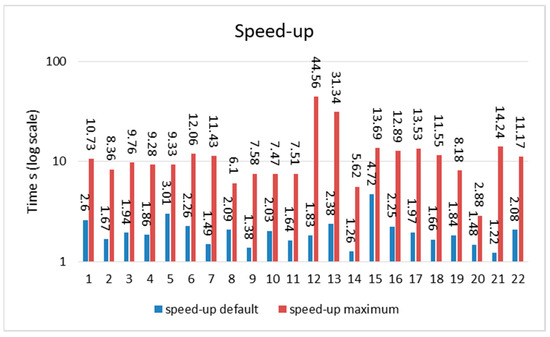
Figure 9.
Domain-wise acceleration time (application domains 1 to 22).
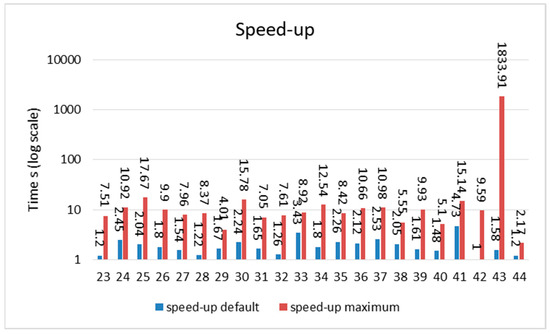
Figure 10.
Domain-wise acceleration time (application domains 23 to 44).
In the above formulas, Timax is the maximum time for each matrix, Timin is the minimum execution time, and Tidef is the default execution time.
4.4. Predictive Analysis
In this section we will discuss how our proposed methodology concentrates on predicting a near-optimal scheduling policy through analysis of the sparse matrix structure. For this purpose, we used four machine learning models to predict the best solution to enable users to make informed decisions about scheduling policies that maximize the computational efficiency of SpMV computation. The prominent features, identified by the highest feature importance scores, were selected as significant contributors within the dataset, as illustrated in Figure 11, and features that did not require a full scan of the matrix were identified as basic features.
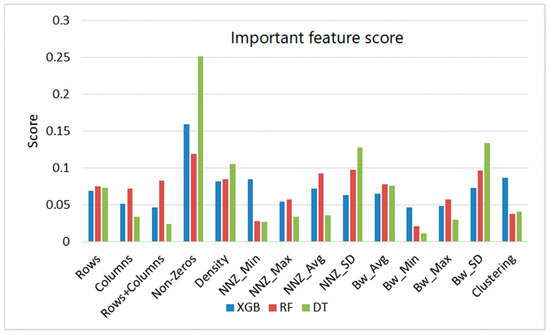
Figure 11.
Comparison of important features.
Table 4 shows the performance evaluations of different machine learning models for SpMV using all, important, or basic features and highlights notable trends. RF and XGB emerged as the top performers across all feature sets, with RF achieving a CV score of 0.792 and an F1-score of 0.9213, while XGB scored a slightly higher CV of 0.793 with an F1-score of 0.9206. Decision Tree (DT) also demonstrated strong results, especially in precision and recall, with an F1-score of 0.9213 for all features. However, KNN consistently lagged behind, exhibiting the lowest performance metrics across all categories, with a CV score of only 0.639 and an F1-score of 0.7698. When examining the important features, RF maintained a solid performance, but both RF and DT excelled compared to XGB and KNN with regard to precision and recall. For the basic features, all models saw a decline in performance, with RF still leading but significantly lower than with all features. Overall, RF and XGB are the most effective models for SpMV feature classification, while KNN may require reconsideration for optimal results. Figure 12, Figure 13 and Figure 14 show the confusion matrices of the top-performing models with respect to the cross-validation score for each feature set (all, important, and basic features, respectively).

Table 4.
Model evaluations with basic, important, and all features.
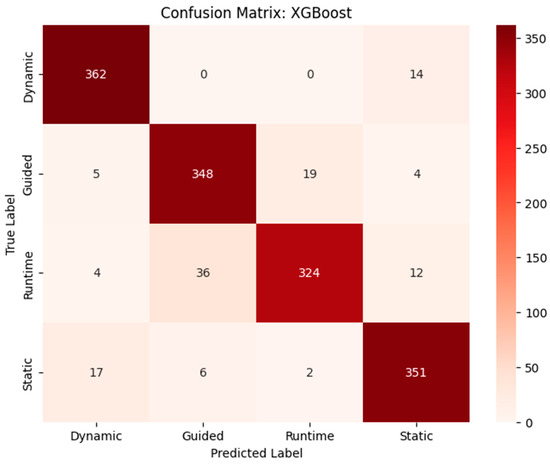
Figure 12.
Confusion matrix of XGB with all features.
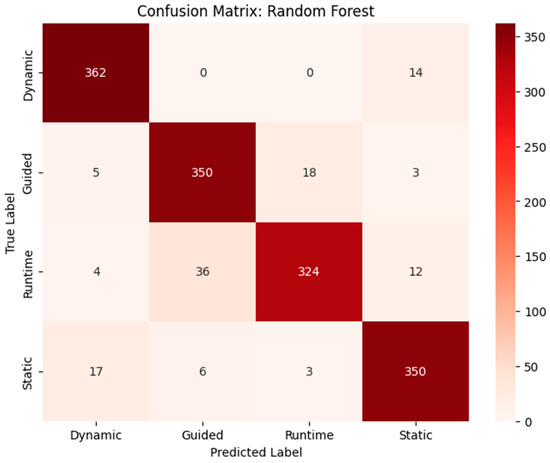
Figure 13.
Confusion matrix of RF with important features.
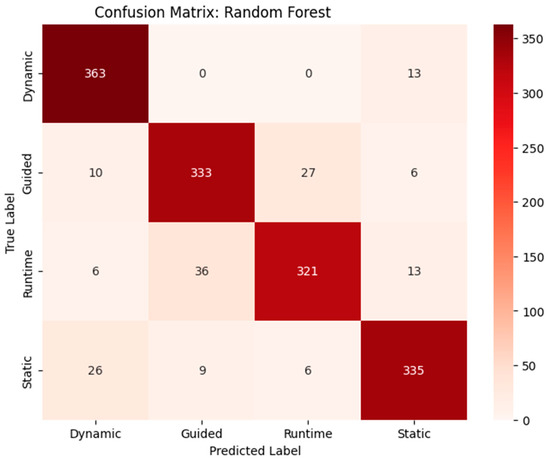
Figure 14.
Confusion matrix of RF with basic features.
Table 5 presents the classification reports of the top-performing models (Random Forest (RF) and XGBoost (XGB)) using different feature sets (important features, all features, and basic features) across four classes: dynamic, runtime, guided, and static scheduling. Each row contains the precision, recall, F1-score, and support (376 instances per class) for the respective model–feature combination. When using important features with RF, the model achieved strong performance, particularly for the dynamic class (F1-score: 0.95), but a slightly lower recall was observed for runtime scheduling (0.86). With all features and XGBoost, performance improved slightly across all classes, with the highest F1-score of 0.94 observed for static scheduling. The basic features and the RF setup demonstrated slightly lower precision and recall, particularly for the runtime (F1-score: 0.88) and guided (F1-score: 0.88) classes. Overall, the XGBoost setup with all features provided the best balance of precision and recall, suggesting that a more comprehensive feature set enhances model performance, particularly for structured classification tasks.

Table 5.
Class-wise scores of basic, important, and all features.
4.5. Performance Gain
Figure 15 illustrates a performance comparison, highlighting that the proposed methodology (predicted) achieved a significant improvement over the default scheduling policy. As OpenMP’s default thread scheduling is a standard baseline in parallel computing research, we evaluated our model’s performance against it. The results clearly demonstrate that our approach consistently outperformed the default scheduling across various sparse matrices, achieving superior computational efficiency and load balancing. However, the predicted method took 1190.66 s, while the default scheduling policy required 2256.518 s, meaning our approach reduced the execution time by nearly 47%. Additionally, compared to the average execution time (5914.266191 s), our method offered a substantial performance boost, cutting the time by approximately 80%. This demonstrated that if a user were to select scheduling randomly, the time could range anywhere between the average (5914.266191 s) and maximum (37,089.022 s), often leading to much longer execution times. By using our proposed methodology, users can avoid the unpredictability of random selection and achieve consistently near-optimal performance, significantly improving efficiency over the default scheduling policy.
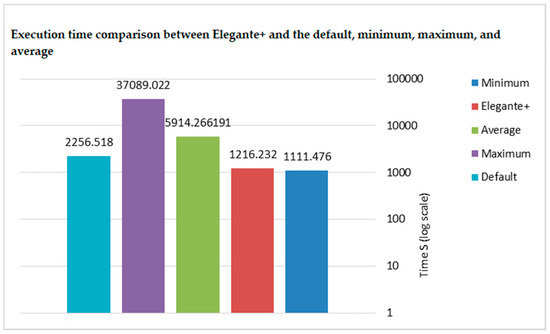
Figure 15.
Execution time comparison between Elegante+ and the default, minimum, maximum, and average values.
Figure 16 illustrates the performance gains of various execution times compared to the best (minimum) time, which is set as the baseline at 100%, using the geometric mean of normalized performance (GMNP). The predicted time closely approached the best, achieving a performance of 99.34%, indicating only a minor difference. The maximum time performed significantly worse, with only 3% of the best performance, showcasing its inefficiency. The default OpenMP time reached 49.27% of the best time, indicating it was approximately half as efficient as the best and predicted times. Meanwhile, the average time performed at 18.79% of the best, indicating that it was considerably slower than the best and predicted times but still significantly better than the maximum time. This comparison highlights that the proposed system, as represented by the predicted time, significantly outperformed the default OpenMP execution, with about 2.015 times as much performance improvement.
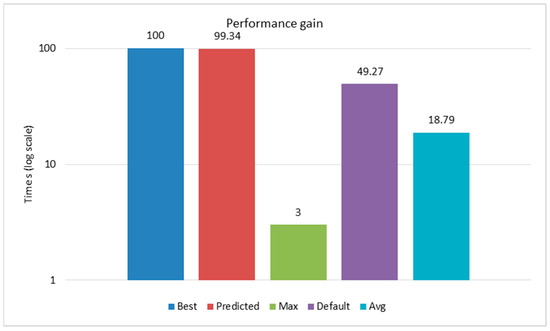
Figure 16.
GMNP of proposed methodology.
5. Limitations of the Proposed Solution
Our proposed methodology predicts a near-optimal scheduling policy based on the sparse matrix structure and shows considerable performance gain. Limitations associated with the proposed solution are highlighted in this section. Firstly, the selection of 14 sparse matrix features might not capture all the relevant factors that influence SpMV computation, potentially omitting important characteristics. Secondly, while the machine learning model aims to predict the optimal number of threads for SpMV computation, the actual optimal number may be affected by various factors not considered in this study, such as hardware architecture, memory bandwidth, and specific SpMV algorithm implementations. Thirdly, a machine learning model trained on a specific dataset may not generalize well to different types of matrices or various hardware configurations. Lastly, performing feature extraction and SpMV computations with different numbers of threads could introduce additional computational overhead that is not reflective of real-world scenarios.
6. Conclusions
Sparse matrix–vector multiplication (SpMV) is a critical operation in many scientific and engineering applications, and its optimization plays a key role in enhancing the performance of high-performance computing (HPC) systems. Over the years, SpMV optimization has evolved from manual heuristics and hardware-specific tuning to machine learning-driven automation, reflecting the increasing complexity of modern computing architectures.
In this study, we proposed Elegante+, a machine learning-based tool designed to predict near-optimal scheduling policies for SpMV computations in shared-memory architectures. Unlike conventional approaches that rely on trial and error, our method analyzes sparse matrix structures and optimizes workload distribution, enabling users to make informed decisions that maximize computational efficiency. To achieve this, we sourced 1000+ sparse matrices from the SuiteSparse matrix collection across various domains and extracted 14 key sparse matrix features. Our results demonstrate a substantial performance improvement in SpMV execution using the CSR format, with Elegante+ achieving a 79% cross-validation score and delivering 5× acceleration compared to the default scheduling policies.
Future work will focus on refining our machine learning models by incorporating additional matrix features and exploring deep learning techniques for even more accurate predictions. Additionally, we aim to extend Elegante+ to support dynamic scheduling for real-time applications and to integrate it with other HPC frameworks to broaden its applicability across diverse computational environments and hardware configurations.
Author Contributions
Conceptualization, S.U., M.A. and A.H.; methodology, M.A. and A.H.; software, M.A. and M.M.; validation, I.B. and M.A.; formal analysis, I.B. and S.U.; investigation, I.B. and U.S; resources, S.U. and I.B.; data curation, M.A.; writing—original draft preparation, M.A., A.H. and M.M.; writing—review and editing, M.A. and A.H.; visualization, M.M. and A.H.; supervision, I.B.; project administration, I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available upon request.
Acknowledgments
This work was performed with partial support from the Mexican Government through grant A1-S-47854 of CONACYT, Mexico, and grants 20241816, 20241819, and 20240951 of the Secretaría de Investigación y Posgrado of the Instituto Politécnico Nacional, Mexico. The authors thank CONACYT for the computing resources provided through the Plataforma de Aprendizaje Profundo para Tecnologías del Lenguaje of the Laboratorio de Supercómputo of the INAOE, Mexico, and acknowledge support from Microsoft through the Microsoft Latin America PhD.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hu, Y.; Du, Y.; Ustun, E.; Zhang, Z. GraphLily: Accelerating graph linear algebra on HBM-equipped FPGAs. In Proceedings of the 2021 IEEE/ACM International Conference on Computer Aided Design (ICCAD), Munich, Germany, 1–4 November 2021. [Google Scholar]
- Yesil, S.; Heidarshenas, A.; Morrison, A.; Torrellas, J. Speeding up SpMV for power-law graph analytics by enhancing locality & vectorization. In Proceedings of the SC20: IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020. [Google Scholar]
- Sun, M.; Li, Z.; Lu, A.; Li, Y.; Chang, S.E.; Ma, X.; Lin, X.; Fang, Z. FILM-QNN: Efficient FPGA acceleration of deep neural networks with intra-layer, mixed-precision quantization. In Proceedings of the 2022 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, New York, NY, USA, 27 February–1 March 2022. [Google Scholar]
- Nathan, B.; Garland, M. Implementing sparse matrix-vector multiplication on throughput-oriented processors. In Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, Portland, OR, USA, 14–20 November 2009. [Google Scholar]
- Feng, X.; Jin, H.; Zheng, R.; Hu, K.; Zeng, J.; Shao, Z. Optimization of sparse matrix-vector multiplication with variant CSR on GPUs. In Proceedings of the 2011 IEEE 17th International Conference on Parallel and Distributed Systems, Tainan, Taiwan, 7–9 December 2011; pp. 165–172. [Google Scholar]
- Kislal, O.; Ding, M.; Kandemir, I.; Demirkiran, M. Optimizing Sparse Matrix-Vector Multiplication on Emerging Multicores. In Proceedings of the IEEE 6th International Workshop on Multi-/Many-Core Computing Systems (MuCoCoS), Paris, France, 22–23 September 2013; pp. 1–10. [Google Scholar]
- Nickolls, J.; Buck, I.; Garland, M.; Skadron, K. Scalable parallel programming with CUDA: Is CUDA the parallel programming model that application developers have been waiting for? Queue 2008, 6, 40–53. [Google Scholar] [CrossRef]
- Baskaran, M.; Bordawekar, R. Optimizing Sparse Matrix-Vector Multiplication on GPUs; RC24704 W0812–047; IBM Research Reports: Yorktown Heights, NY, USA, 2009. [Google Scholar]
- Mike, G. Efficient sparse matrix-vector multiplication on cache-based GPUs. In Proceedings of the IEEE 2012 Innovative Parallel Computing (InPar), Jeju Island, Republic of Korea, 9–11 July 2012. [Google Scholar]
- Greathouse, J.L.; Daga, M. Efficient sparse matrix-vector multiplication on GPUs using the CSR storage format. In Proceedings of the SC’14 IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014. [Google Scholar]
- Weifeng, L.; Vinter, B. CSR5: An efficient storage format for cross-platform sparse matrix-vector multiplication. In Proceedings of the 29th ACM on International Conference on Supercomputing, Newport Beach, CA, USA, 8–11 June 2015. [Google Scholar]
- Daga, M.; Greathouse, J.L. Structural agnostic SpMV: Adapting CSR-adaptive for irregular matrices. In Proceedings of the 2015 IEEE 22nd International Conference on High Performance Computing (HiPC), Bengaluru, India, 16–19 December 2015. [Google Scholar]
- Yang, W.; Li, K.; Mo, Z.; Li, K. Performance optimization using partitioned SpMV on GPUs and multicore CPUs. IEEE Trans. Comput. 2014, 64, 2623–2636. [Google Scholar] [CrossRef]
- Hosseinabady, M.; Nunez-Yanez, J.L. A streaming dataflow engine for sparse matrix-vector multiplication using high-level synthesis. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 39, 1272–1285. [Google Scholar] [CrossRef]
- Bowen, L.; Liu, D. Towards high-bandwidth-utilization SpMV on FPGA via partial vector duplication. In Proceedings of the 28th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 6–19 January 2023. [Google Scholar]
- Kourtis, K.; Karakasis, V.; Goumas, G.; Koziris, N. CSX: An extended compression format for SpMV on shared memory systems. ACM SIGPLAN Not. 2011, 46, 247–256. [Google Scholar] [CrossRef]
- Geng, T.; Wang, T.; Sanaullah, A.; Yang, C.; Patel, R.; Herbordt, M. A framework for acceleration of CNN training on deeply-pipelined FPGA clusters with work and weight load balancing. In Proceedings of the IEEE 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 3–6 September 2018. [Google Scholar]
- Du, Y.; Hu, Y.; Zhou, Z.; Zhang, Z. High-performance sparse linear algebra on HBM-equipped FPGA using HLS: A case study on SpMV. In Proceedings of the 2022 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 27 February–1 March 2022. [Google Scholar]
- Muhammed, T.; Mehmood, R.; Albeshri, A.; Katib, I. SURAA: A novel method and tool for Loadbalanced and coalesced SpMV computations on GPUs. Appl. Sci. 2019, 9, 947. [Google Scholar] [CrossRef]
- Davis, T.A.; Hu, Y. The University of Florida sparse matrix collection, ACM Trans. Math. Softw. 2011, 38, 1–25. [Google Scholar]
- Pinar, A.; Heath, M.T. Improving performance of sparse matrix-vector multiplication. In Proceedings of the 1999 ACM/IEEE Conference on Supercomputing, Portland, OR, USA, 14–19 November 1999; p. 30. [Google Scholar]
- Usman, S.; Mehmood, R.; Katib, I.; Albeshri, A. ZAKI+: A Machine Learning Based Process Mapping Tool for SpMV Computations on Distributed Memory Architectures. IEEE Access 2019, 7, 81279–81296. [Google Scholar] [CrossRef]
- Ahmed, M.; Usman, S.; Shah, N.A.; Ashraf, M.U.; Alghamdi, A.M.; Bahadded, A.A.; Almarhabi, K.A. AAQAL: A machine learning-based tool for performance optimization of parallel SPMV computations using block CSR. Appl. Sci. 2022, 12, 7073. [Google Scholar] [CrossRef]
- Usman, S.; Mehmood, R.; Katib, I.; Albeshri, A.; Altowaijri, S.M. ZAKI: A smart method and tool for automatic performance optimization of parallel SpMV computations on distributed memory machines. Mob. Netw. Appl. 2023, 28, 744–763. [Google Scholar] [CrossRef]
- Xiao, G.; Zhou, T.; Chen, Y.; Hu, Y.; Li, K. Machine Learning-Based Kernel Selector for SpMV Optimization in Graph Analysis. ACM Trans. Parallel Comput. 2024, 11, 1–25. [Google Scholar] [CrossRef]
- Yesil, S.; Heidarshenas, A.; Morrison, A.; Torrellas, J. Wise: Predicting the performance of sparse matrix vector multiplication with machine learning. In Proceedings of the 28th ACM SIGPLAN Annual Symposium on Principles and Practice of Parallel Programming, Montreal, QC, Canada, 25 February–1 March 2023; pp. 329–341. [Google Scholar]
- Gao, J.; Ji, W.; Liu, J.; Wang, Y.; Shi, F. Revisiting thread configuration of SpMV kernels on GPU: A machine learning based approach. J. Parallel Distrib. Comput. 2024, 185, 104799. [Google Scholar] [CrossRef]
- Shi, Y.; Dong, P.; Zhang, L.J. An irregular sparse matrix SpMV method. Comput. Eng. Sci. 2024, 46, 1175. [Google Scholar]
- Dufrechou, E.; Ezzatti, P.; Quintana-Orti, E.S. Selecting optimal SpMV realizations for GPUs via machine learning. Int. J. High-Perform. Comput. Appl. 2021, 35, 254–267. [Google Scholar] [CrossRef]
- Ahmad, M.; Sardar, U.; Batyrshin, I.; Hasnain, M.; Sajid, K.; Sidorov, G. Elegante: A Machine Learning-Based Threads Configuration Tool for SpMV Computations on Shared Memory Architecture. Information 2024, 15, 685. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).