Robust and Scalable Quantum Repeaters Using Machine Learning

Abstract

Quantum repeaters are integral systems to quantum computing and quantum communication as they allow the transfer of information between qubits, particularly over long distances. Because of the “no-cloning theorem,” which says that general quantum states cannot be directly copied, one cannot perform signal amplification in the usual way. The standard approach uses entanglement swapping, in which quantum states are teleported from one (short) segment to the next, using at each step a shared entangled pair. This is the job of the repeater. In general, this requires reliable quantum memories and shared entanglement resources, which are vulnerable to noise and decoherence. It is also difficult to manually create and implement the quantum algorithm for the swap circuit as the size of the system increases. Here, we propose a different approach: to use machine learning to train a repeater node. To demonstrate the feasibility of this method, the system is simulated in MATLAB 2022a. Training is conducted for a system of 2 qubits. It is then scaled up, with no additional training, to systems of 4, 6, and 8 qubits using transfer learning. Finally, the systems are tested in noisy conditions. The results show that the scale-up is very effective and relatively easy, and the effects of noise and decoherence are $reduced$ as the size of the system increases.

1. Introduction and Literature Review

Large-scale quantum communication networks face a unique (quantum) problem: the standard (classical) amplification of a signal is impossible because a quantum state cannot be copied [1,2]. Thus, the attenuation of a signal from the scattering or absorption of the photons as they travel through optical fibers (or air) needs to be addressed in a different way. Quantum repeaters provide one solution for dealing with this. The standard approach uses entanglement swapping, in which quantum states are teleported from one (short) segment to the next, using at each step a shared entangled pair [3,4,5]. The usual approach also necessitates a reliable set of quantum memories at each node to store the entangled pairs used to perform the teleportation. There is the alternative of “all-photonic” quantum repeaters [6], but these require instead a very large overhead of photons and entangled resources [7]. Great progress has been made in all of the contributing components to this protocol: researchers have demonstrated entanglement swapping operations, quantum memories, and, even on a small scale, full quantum networks. But the field is still in flux in the sense that no one technology or physical implementation has been settled on [8,9,10] and many difficulties remain. A major issue is noise and decoherence effects. To deal with these, one can use some form of error correction, such as entanglement purification [3,11]. Substantial progress still needs to be made, and new approaches [12,13,14] need to be tried. For example, Liu et al. [12] propose returning to the old idea of vacuum beam guides in place of optical fibers, as they offer orders of magnitude lower loss. Mastriani [14] presents a simplified version of entanglement swapping that is less expensive for quantum repeaters. Another avenue being explored is quantum zero repeaters [15], which offer high-fidelity entanglement swapping and which require fewer computational resources. Azuma et al. [7] have a good comprehensive recent review of the various approaches.

In our research presented here, building on our prior quantum machine learning work, we propose a different kind of simplification: to use quantum machine learning [16] to perform all the necessary operations. In this way, we bypass the quantum memory and its attendant measurements. Scale-up is easy, as we use a quantum version of the well-known technique of transfer learning [17] to leverage knowledge of the larger system from the smaller system. Transfer learning is now in widespread use in classical machine learning; according to a survey paper from 2016 [18], over 700 papers in the previous 5 years had used the method and in a vast array of (classical) contexts. We applied this in earlier work on entanglement [19]. This transfer learning could be called “bootstrapping”, a term we coined when we first applied this to quantum computing [20] when thinking about how a classical computer uses a small “boot sector” program to launch a much larger OS. Most important, because of the parallel and distributed nature of the trained quantum neural network architecture, the resultant operation is robust to both noise and decoherence [21], analogously to the way classical neural networks have long been successfully used to deal with incomplete or damaged data. In fact, the network becomes more robust as the system size increases [22], which is a major result of our work presented here.

In general, using this kind of approach for a number of problems, we have found that the tedious complexity of developing quantum algorithms by hand can be forgone, handing the task over to a machine learning system. It also frequently shortens [23] and/or simplifies [24] a sequence from one found by the so-called “lego” method, using gates as building blocks. This is because instead of a sequence of steps, the problem is considered as a whole: to find the desired output from a given input. This kind of approach may have important and far reaching applications, for example, in quantum secure direct communication [25] or quantum key distribution (QKD) [26].

2. Methodology

2.1. System Description

We use a standard qubit Hamiltonian [27]. We label the amplitude for a qubit to flip between the states $|0\rangle$ and $|1\rangle$ as K (also called [27] the “tunneling” amplitude), $ϵ$ for bias or relative energy of the two states, and $\zeta$ for coupling between pairs of qubits. The Hamiltonian for n qubits is then

$${\displaystyle H=\sum _{i=1}^n{K}_i{\sigma }_{x,i}+\sum _{i=1}^n{ϵ}_i{\sigma }_{z,i}+\frac{1}{2}\sum _{i\ne j}^n{\zeta }_{i,j}{\sigma }_{z,i}{\sigma }_{z,j}}$$

where $K_i$ is the tunneling amplitude for qubit i, ${ϵ}_i$ is the bias for qubit i, ${\zeta }_{i,j}$ is the coupling coefficient between the i j pair of qubits in the system, and ${\sigma }_x$ and ${\sigma }_z$ are the Pauli spin matrices.

The parameters K, $ϵ$, and $\zeta$ of the Hamiltonian are time-dependent, as then so is H. The quantum system state variable is the density matrix, $\rho$, which evolves from an initial ${\rho }_0$ at t = 0 to a ${\rho }^f$ at the final time $t_f$ according to the Schrodinger equation

$${\displaystyle \frac{d\rho }{dt}}={\displaystyle \frac{1}{ih}}[H,\rho ]$$

(1)

The quantum parameters are trained using machine learning to achieve a final target density matrix at the final time ${\rho }^f=T$. So, an initial ${\rho }_0$ paired with a target ${\rho }^f=T$ represents the required quantum state change. More details about this are given later. The time dependence of each parameter is represented as a finite Fourier series, and the Fourier coefficients are trained using an adjoint Levenberg–Marquardt machine learning method also described below.

2.2. Cost Function with Frobenius Output Measure

The quantum system evolves in time according to the Schrodinger equation, from an initial density matrix ${\rho }_0$ to a final density matrix ${\rho }^f$ at the final time $t_f$. Recall that the Hamiltonian, H, is time varying. A cost function, L, is defined as a positive definite error based on the Frobenius norm of a matrix. T is the target output density matrix for the quantum system and $\rho$ at $t^f$ is the actual quantum system output density matrix. The system dynamics are enforced as a constraint with Lagrange multiplier matrix $\gamma$ where ⊙ is the element-by-element dot product of two matrices.

$$\begin{array}{c}\hfill L=\sum {(T_{ij}-{\rho }_{ij})}^{†}(T_{ij}-{\rho }_{ij}){|}_{t_f}+{\int }_0^{t_f}{\gamma }^{†}\odot \left[{\displaystyle \frac{d\rho }{dt}}-{\displaystyle \frac{1}{ih}}[H,\rho ]\right]dt\\ \hfill +\int {\left[{\displaystyle \frac{d\rho }{dt}}-{\displaystyle \frac{1}{ih}}[H,\rho ]\right]}^{†}\odot \gamma dt\end{array}$$

(2)

Taking the variation with respect to $\gamma$ and setting it equal to zero enforces the Schrodinger equation dynamics. Integrating the first term in each integral by parts and taking the variation with respect to $\rho$ and setting that equal to zero at any time $t<t_f$ gives

$${\displaystyle \frac{d\gamma }{dt}}=-{\displaystyle \frac{1}{ih}}[H,\gamma ]$$

(3)

and its complex conjugate equation. Note that since $\rho$ is specified at t = 0, its variation at that initial time is zero, and that initial condition term vanishes. At $t_f$, we have (and its conjugate):

$${\gamma }_{ij}=(T_{ij}-{\rho }_{ij})$$

(4)

The Hamiltonian, H, contains parameters mentioned above, which describe how H varies with time. Let w be one of these parameters. Taking the variation in L with respect to w gives a gradient of L that can be used in various gradient-based adaptation methods to determine the parameter.

$${\displaystyle \frac{\delta L}{\delta w}}={\int }_0^{t_f}2Re\left[{\displaystyle \frac{1}{ih}}{\gamma }^t\left[{\displaystyle \frac{dH}{dw}},\rho \right]\right]$$

(5)

Following mainly [28], which is based on the Levenberg–Marquardt method of nonlinear optimization presented in [29,30,31], we derive a quasi-second order method for learning the quantum parameters in H. Levenberg–Marquardt outperforms gradient descent and conjugate gradient methods for medium-sized problems.

Let $\mathbf{W}$ be a vector of the quantum parameters. L is a function of $\mathbf{W}$, so we define $\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]$ as a vector of partials of L with respect to each element of W and then define $\widehat{L}$ as a quadratic (2nd-order) local approximation to L about ${\mathbf{W}}_{\mathbf{0}}$ (the current value of the quantum parameter vector) as

$$\begin{array}{c}\hfill \widehat{L}\left(\mathbf{W}\right)=L\left({\mathbf{W}}_{\mathbf{0}}\right)+{\left[{\displaystyle \frac{\partial L}{\partial \mathbf{w}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T(\mathbf{W}-{\mathbf{W}}_{\mathbf{0}})\\ \hfill +{\displaystyle \frac{1}{4L\left({\mathbf{W}}_{\mathbf{0}}\right)}}(\mathbf{W}-{\mathbf{W}}_{\mathbf{0}}){\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T{\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}{(\mathbf{W}-{\mathbf{W}}_{\mathbf{0}})}^T\end{array}$$

(6)

notice that

$$\widehat{L}\left({\mathbf{W}}_{\mathbf{0}}\right)=L\left({\mathbf{W}}_{\mathbf{0}}\right)$$

(7)

and

$${\left[{\displaystyle \frac{\partial \widehat{L}}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}={\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}$$

(8)

and

$$L\left({\mathbf{W}}_{\mathbf{0}}\right)=\sum {(T_{ij}-{\rho }_{ij})}^t(T_{ij}-{\rho }_{ij}){|}_{t_f}$$

(9)

as the forward dynamics equation constraint being enforced means the other terms in L are zero. This means $L\left({\mathbf{W}}_{\mathbf{0}}\right)$ is the squared “output” error at the final time with the current parameters ${\mathbf{W}}_{\mathbf{0}}$. Then, setting the variation of L with respect to $\mathbf{W}$ equal to 0 gives

$$0={\left[{\displaystyle \frac{\partial \widehat{L}}{\partial \mathbf{W}}}\right]}_{\mathbf{W}}={\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}+{\displaystyle \frac{1}{L\left({\mathbf{W}}_{\mathbf{0}}\right)}}(\mathbf{W}-{\mathbf{W}}_{\mathbf{0}}){\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T{\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}.$$

(10)

Then define a Hessian by

$${\mathbf{H}}_{ess}={\displaystyle \frac{1}{\sqrt{L\left({\mathbf{W}}_{\mathbf{0}}\right)}}}{\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}{\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T{\displaystyle \frac{1}{\sqrt{L\left({\mathbf{W}}_{\mathbf{0}}\right)}}}$$

(11)

giving

$$\mathbf{W}={\mathbf{W}}_{\mathbf{0}}-{\mathbf{H}}_{ess}^{-1}{\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T$$

(12)

The Levenberg–Marquardt algorithm modifies this by combining this Hessian update rule with a gradient descent update rule that is weighted by parameter $\lambda$ that is updated dynamically during the learning process. Also, the Hessian and the gradient of L become averages over all training pairs in the training set, or in a mini-batch subset, and $L\left({\mathbf{W}}_{\mathbf{0}}\right)$ becomes the average squared error over the entire set, by necessity, since it could be zero for any single training data point. For details on the LM process, including updating $\lambda$, see [32].

The combined weight update rule is

$$\mathbf{W}={\mathbf{W}}_{\mathbf{0}}-\eta {[{\mathbf{H}}_{ess}+\lambda \mathbf{I}]}^{-1}{\left[{\displaystyle \frac{\partial L}{\partial w}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T$$

(13)

where $\mathbf{I}$ is the identity matrix and $\eta$ is a constant that controls the rate of the update “learning” of the quantum parameters. The standard LM algorithm is

$$\mathbf{W}={\mathbf{W}}_{\mathbf{0}}-\eta {[{\widehat{\mathbf{H}}}_{ess}+\lambda \mathbf{I}]}^{-1}E{\left[{\displaystyle \frac{\partial O}{\partial w}}\right]}_{{\mathbf{W}}_{\mathbf{0}}}^T$$

(14)

If we absorb $L\left({\mathbf{W}}_{\mathbf{0}}\right)$ into $\eta$ and $\lambda$ and define the output O in the standard LM algorithm above as the squared error L, and have its target value as zero, our update using L looks much like the standard LM formulation. Because the error at the final time

$${\gamma }_{ij}=(T_{ij}-{\rho }_{ij})$$

(15)

is propagated backward through the quantum system dynamics in Equation (3), the error is contained in the gradient calculated via Equation (5). Therefore, “error” E, which multiplies the gradient in the standard LM algorithm, is set to a vector of ones in our LM formulation.

The motivation for the approximation $\widehat{L}$ is as follows. Let a function of one variable, f(x), be approximated close to x = 0 by the form

$$\widehat{f\left(x\right)}={\displaystyle \frac{1}{2}}a{(1+bx)}^2$$

(16)

Note this form matches the form of the first term of L above. Then, choose a = 2f(0) to make f(0) = $\widehat{f}\left(0\right)$ and choose ab = ${\left[{\displaystyle \frac{\partial f}{\partial x}}\right]}_0$ to make ${\left[{\displaystyle \frac{\partial f}{\partial x}}\right]}_0={\left[{\displaystyle \frac{\partial \widehat{f}}{\partial x}}\right]}_0$. Then,

$$\widehat{f}\left(x\right)=f\left(0\right)+{\left[{\displaystyle \frac{\partial f}{\partial x}}\right]}_{0}x+{\displaystyle \frac{1}{4f\left(0\right)}}{x}^2{\left[{\displaystyle \frac{\partial L}{\partial x}}\right]}_0^T{\left[{\displaystyle \frac{\partial f}{\partial x}}\right]}_0$$

(17)

Quoting from our previous paper [32], the following description of the LM procedure we use is as follows: “For small $\lambda$, the update rule is similar to the Gauss-Newton algorithm, allowing larger steps when the error is decreasing rapidly. For larger $\lambda$, the algorithm pivots to be closer to gradient descent and makes smaller updates to the weights. This flexibility is the key to L.M.’s efficacy, changing $\lambda$ to adapt the step size to respond to the needs of convergence: moving quickly through the parameter space where the error function is steep and slowly when near an error plateau and thereby finding small improvements. Our implementation is a modified L.M. algorithm following several suggestions in [33]. One epoch of training consists of the following: (1) Compute the Jacobian $\left[{\displaystyle \frac{\partial L}{\partial \mathbf{W}}}\right]$ and then the Hessian (11) with current weights w (2) Update the damping parameter $\lambda$ (3) Calculate a potential parameter update (4) Find if RMS error has decreased with new parameters, or if an acceptable uphill step is found (5) If neither condition in step 3 is satisfied, reject the update, increase $\lambda$, and return to step 2 (6) For an accepted parameter change, keep the new parameters and decrease $\lambda$, ending the epoch. The identity matrix I that multiplies $\lambda$ can be replaced by a scaling matrix $D^{T}D$ which serves the primary purpose of combating parameter evaporation [34], which is the tendency of the algorithm to push values to infinity while somewhat lost in the parameter space. Following [33], we can choose $D^{T}D$ to be a diagonal matrix with entries equal to the largest diagonal entries of ${\mathbf{H}}_{ess}$ yet encountered in the algorithm, with a minimum value of ${10}^{-6}$. Updates to the damping factor may be done directly or indirectly; our results here use a direct method.”

2.3. System Training and Training Pairs

A list of valid quantum states and the resulting paired swap must be produced to create a set of input/target output pairs to train the network. Each input, with the exception of the charge basis inputs, results from creating a ket of random, uniformly distributed probability amplitude values via a random number generator and subsequently normalizing the ket. The output is then found by applying the appropriate swap operation matrix to the input. An example for the 2 qubit system is as follows: if the (random) input ket is $|\psi \rangle \otimes |\zeta \rangle$, then the target output ket is $|\zeta \rangle \otimes |\psi \rangle$, where ⊗ represents the tensor product. In other words, the receiving state is prepared in a random state $|\zeta \rangle$; after the operation, the incoming state $|\psi \rangle$ is “transmitted” to the receiver. In total, 74 training pairs are generated, with 70 being generated via a random number generation and the remaining 4 training pairs are the standard charge basis [27], which, for a single qubit, is the set $\left\{\right|0\rangle ,|1\rangle \}$. For an n qubit (4, 6 and 8) system, the incoming states $|\psi \rangle$ and $|\zeta \rangle$ are ${\displaystyle \frac{n}{2}}$ qubit states (and can be entangled); the input state for all the qubits would then be $|\psi \rangle \otimes |\zeta \rangle$ and the output or target state would be $|\zeta \rangle \otimes |\psi \rangle$. For testing the transfer learning scaled up from 2 qubits, we use 70 randomly generated inputs and the $2^n$ charge basis.

The input/target output for each training pair can then be represented in their density matrix forms $T={\rho }_f=|{\Psi }_f\rangle \langle {\Psi }_f|$ and ${\rho }_o=|{\Psi }_o\rangle \langle {\Psi }_o|$ where $|{\Psi }_0\rangle$ and $|{\Psi }_f\rangle$ are the kets of the initial “input” and target final “output”. The system Hamiltonian parameters are then trained by presenting it with an initial “input” state from the training set, the system is evolved to the final time according to the Schrodinger equation, $i\hslash {\displaystyle \frac{\partial \rho }{\partial t}}=[H,\rho ]$, the co-state $\gamma \lambda$ is calculated backward in time according to Equation (3) and the associated element of the gradient vector is calculated according to (5). Averaging over all training pairs, the Hessian is then calculated using (11) and the parameters updated with (13). After the completion of the training of the 2-qubit system, the system is then scaled up to 4, 6, and 8 qubits through transfer learning [19,20]. This was carried out by copying the tunneling, K, and bias, $ϵ$, from the original 2 qubits, respectively, to the added 2 qubits. The coupling, $\zeta$, between the first 2 qubits is copied, respectively, to the coupling between the added 2 qubits. There is no coupling between the old 2 and the added 2 qubits. The results of the scale-up are obtained by testing on 70 randomly generated states and $2^n$ charge basis corresponding to the system’s size.

2.4. Noise Simulation

Once the system is trained, the task turns to proving the system’s resilience to noise. Noise is perhaps the most important obstacle to building large-scale quantum computers and networks, and a great deal of research has been devoted to this problem. One approach is error correction [35], but to be most effective, one needs to know ahead of time what the most likely sources of error will be [36]. These will vary from platform to platform. A full treatment would include both unital and non-unital interactions of the quantum system with its environment, which cause not only errors but also decoherence [37]. Here, in this initial work, we do not assume any particular physical implementation of the quantum repeater or model for the environmental effects, but confine ourselves to a simple model of random noise: physically, that there are (small) factors in the time evolution of the system that we do not know. Following [38], we imagine that the Hamiltonian for the noisy system consists of two parts: $H_{total}=H+H_n$, where H is the ideal Hamiltonian and $H_n$ the noise term, equal to some random Hermitian matrix. We do, however, split our random perturbations into real and imaginary parts in order to see, in the simulations, what specifically the resilience is to unitary errors and to dephasing. In line with our previous published work [22], we refer to “pure noise”, which is the addition of random magnitudes to the system, and to “decoherence”, which is the addition of random phases to the system. We performed simulations in which each was present alone and then when both were present (which we called “complex noise”). All three of these were used to test the system.

To add noise to the system, a noise matrix of small random values, that is, Hermitian, positive semi-definite, and possessing a trace of 1 (the required properties of a valid density matrix), is produced at each timestep for each training pair. This noise matrix is then added to the input state’s density matrix and normalized to produce a valid density matrix containing the desired type of noise. The trained system is then tested on specific swap tasks, that is, swap qubit A with qubit B and qubit C with qubit D, etc., depending on the size of the system. The inputs to which the noise is added for the 2-qubit system is identical to the inputs of the training set. For the 4-, 6-, and 8-qubit systems, the inputs to which the noise is added is the same as the ones used to test the system after scale-up.

In the Results Section below, we report an RMS error for the training and testing datasets as well as a measure of the average amount of noise introduced for the testing results. These are calculated as follows. The RMS error for the entire testing dataset is calculated by

$$RMS=\sqrt{{\displaystyle \frac{{\sum }_{ipair}{\left(\frac{\left|\right|T-{\rho }_f{\left|\right|}_{FR}}{Nsiz{e}^2}\right)}^2}{Npairs}}}$$

(18)

The noise level reported below is an average over the elements of the noise matrix, all the timesteps, and all the training pairs calculated by

$$AverageNoise={\displaystyle \frac{{\sum }_{ipair}\sqrt{\frac{{\sum }_{itime}{\left(\frac{\left|\right|{\rho }_{noise}{\left|\right|}_{FR}}{Nsiz{e}^2}\right)}^2}{ntimesteps}}}{Npairs}}$$

(19)

For both equations above, ${\left|\right|A\left|\right|}_{FR}$ is the Frobenius norm of the matrix A. The system is tested with varying levels of average noise and the results are presented in the following section.

3. Results

To first establish a baseline for training effectiveness, a two-qubit system was trained on the dataset described above to sufficiently lower errors, and those parameters were then transferred [19,20] to the four-, six-, and eight-qubit cases with no additional training following the procedure described above. The baseline results are summarized in

Table 1. RMS values from testing WITHOUT noise.

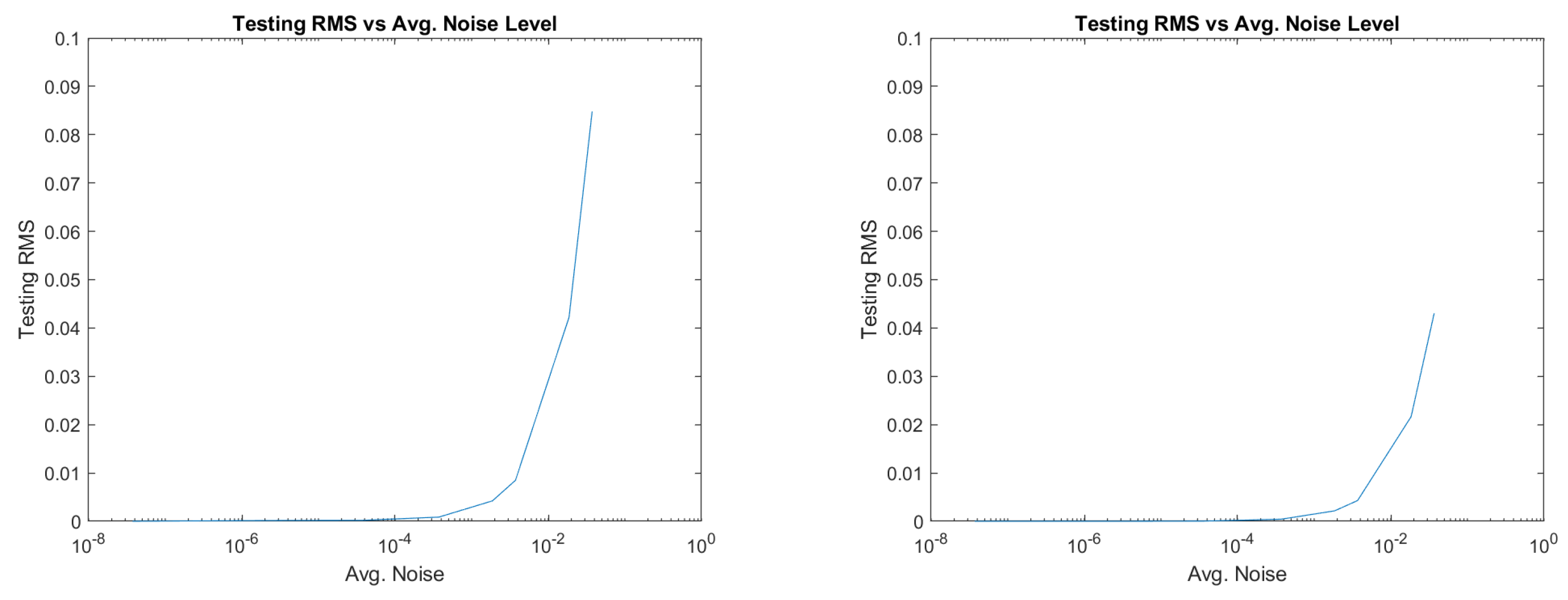
${\mathit{n}}_{\mathit{qubits}}$	Testing RMS
2	$5.38\times {10}^{-8}$
4	$9.02\times {10}^{-6}$
6	$9.62\times {10}^{-7}$
8	$7.32\times {10}^{-8}$

for a $\mathit{testing}$ set consisting of the charge basis states and 70 randomly generated quantum states for each system size. A jump is seen in the RMS error when scaling up from 2 to 4 qubits, but stabilizes from 4 to 6 and 6 to 8 qubits.

Next, noise was added to the system to test the network’s resiliency. Tests were conducted with pure noise and decoherence separately, as well as together, all at various levels, and the errors in the presence of noise are reported in the

Table 2. Error induced by noise for 2 qubits.

RNP	Pure Noise RMS	Decoherence RMS	Complex Noise RMS
$1\times {10}^{-6}$	$1.97\times {10}^{-5}$	$4.91\times {10}^{-5}$	$9.44\times {10}^{-5}$
$1\times {10}^{-5}$	$2.01\times {10}^{-4}$	$4.94\times {10}^{-4}$	$9.44\times {10}^{-4}$
$1\times {10}^{-4}$	0.0019	0.0047	0.0085

,

Table 3. Error induced by noise for 4 qubits.

RNP	Pure Noise RMS	Decoherence RMS	Complex Noise RMS
$1\times {10}^{-6}$	$1.42\times {10}^{-5}$	$2.28\times {10}^{-5}$	$8.30\times {10}^{-5}$
$1\times {10}^{-5}$	$1.07\times {10}^{-4}$	$1.98\times {10}^{-4}$	$6.66\times {10}^{-4}$
$1\times {10}^{-4}$	$8.30\times {10}^{-4}$	0.0012	0.0021

,

Table 4. Error induced by noise for 6 qubits.

RNP	Pure Noise RMS	Decoherence RMS	Complex Noise RMS
$1\times {10}^{-6}$	$1.03\times {10}^{-5}$	$1.94\times {10}^{-5}$	$9.73\times {10}^{-5}$
$1\times {10}^{-5}$	$7.24\times {10}^{-5}$	$1.06\times {10}^{-4}$	$1.74\times {10}^{-4}$
$1\times {10}^{-4}$	$1.72\times {10}^{-4}$	$1.75\times {10}^{-4}$	$1.99\times {10}^{-4}$

and

Table 5. Error induced by noise for 8 qubits.

RNP	Pure Noise RMS	Decoherence RMS	Complex Noise RMS
$1\times {10}^{-6}$	$6.56\times {10}^{-6}$	$9.26\times {10}^{-6}$	$1.36\times {10}^{-5}$
$1\times {10}^{-5}$	$1.34\times {10}^{-5}$	$1.36\times {10}^{-5}$	$1.43\times {10}^{-5}$
$1\times {10}^{-4}$	$2.45\times {10}^{-5}$	$1.39\times {10}^{-5}$	$4.53\times {10}^{-5}$

. RNP is a parameter that we use to generate the level of random noise numbers. The testing RMS is reported for each noise type at each RNP level. We find that the network’s noise tolerance improves as the system’s size increases, as demonstrated by the figures. Therefore, larger systems have the potential to be more noise-tolerant without the need for additional training.

Plots of testing RMS vs. increasing amounts of the average $\mathit{complex}$ noise level are shown in the plots in Figure 1 for 2, 4, 6, and 8 qubits. These plots show the same scale for the vertical axis in order to clearly show the decrease in testing RMS with increasing numbers of qubits. Since 6 and 8 qubits shower lower effect of noise on the testing RMS, the maximum noise level tested was extended to better show the trend. Plots of testing RMS vs. increasing amounts of average $\mathit{complex}$ noise level are shown in the plots in Figure 2 for 6 and 8 qubits.

4. Conclusions and Future Research

Machine learning can be enormously helpful in both quantum computing and quantum communication for several reasons: (1) it bypasses the difficult tasks of both algorithm construction and breaking down a desired unitary into a sequence of gates; (2) scale-up is relatively easy; and (3) the multiple inter-connectivity of the architecture leads to robustness to both noise and decoherence. In the present study, we see both of those advantages: we obtain low-error swap results in the presence of noise and decoherence, and the tolerance to that noise increases as the system size increases.

Robustness to incomplete and/or damaged data, and to environmental noise, is well known in classical neural networks [39]. The fact that this translates to the quantum regime is not only interesting but of great possible practical importance in quantum computing [21] as well as quantum communications. In an upcoming paper [40], we provide a mathematical justification for this in the 2-qubit case.

Since full quantum simulation goes up exponentially with the size of the system, given our computational resources, we were only able to do this exploratory study up to eight qubits. But we hope, in the near future, to be able to perform direct measurements using quantum hardware, which will not suffer from this limitation.

In the meantime, tolerance to all the different specific types of noise tolerance could be explored in simulations. Cheng et al. showed that noise can be modeled by using matrix product density operators, which can produce effective noise models while reducing the computational power required for a simulation on classical computers [41]. Noise might be added during training in addition to or instead of after training. And in the future, it will be interesting to see what kinds of improvements could be made were the training to be carried out online, on an actual quantum hardware system: we might expect to see robustness to actual physical noise and decoherence as the network could learn to take into account the physical flaws, crosstalk, or environment actually present.