Learning-Assisted Multi-IMU Proprioceptive State Estimation for Quadruped Robots
Abstract
1. Introduction
2. Problem Formulation and Related Preliminaries
2.1. Measurements and System Model
2.2. Right-Invariant EKF
2.2.1. Prediction Step
2.2.2. Update Step
2.3. Multi-IMU Proprioceptive Odometry
3. RI-EKF Using Multi-IMU Measurements
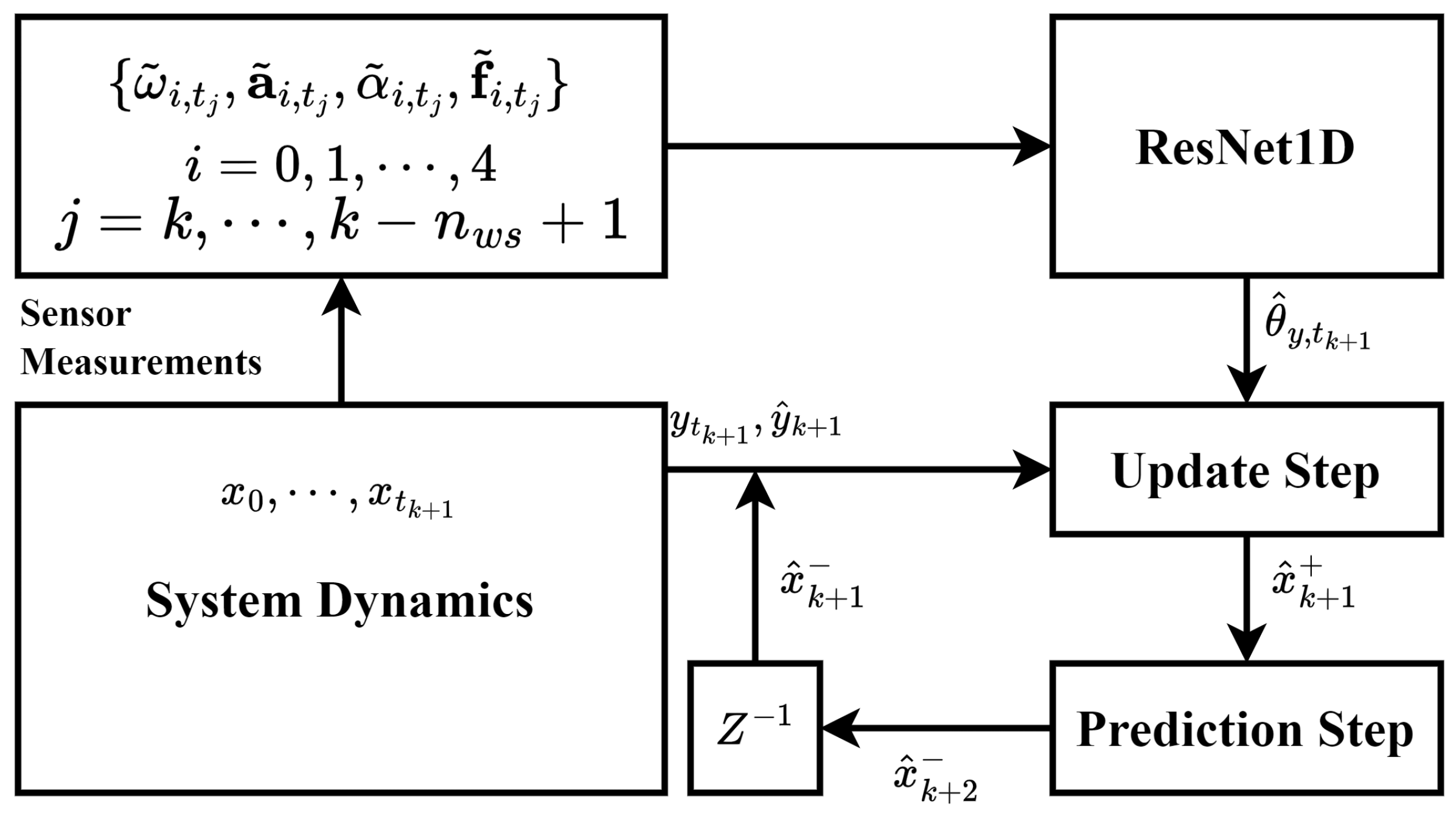
4. Learning-Assisted Multi-IMU Proprioceptive State Estimation
5. Experiments and Validation
5.1. Dataset Description
5.2. Experimental Setup
Impacts of NN Design
5.3. Results and Discussions
5.3.1. Yaw Prediction Model
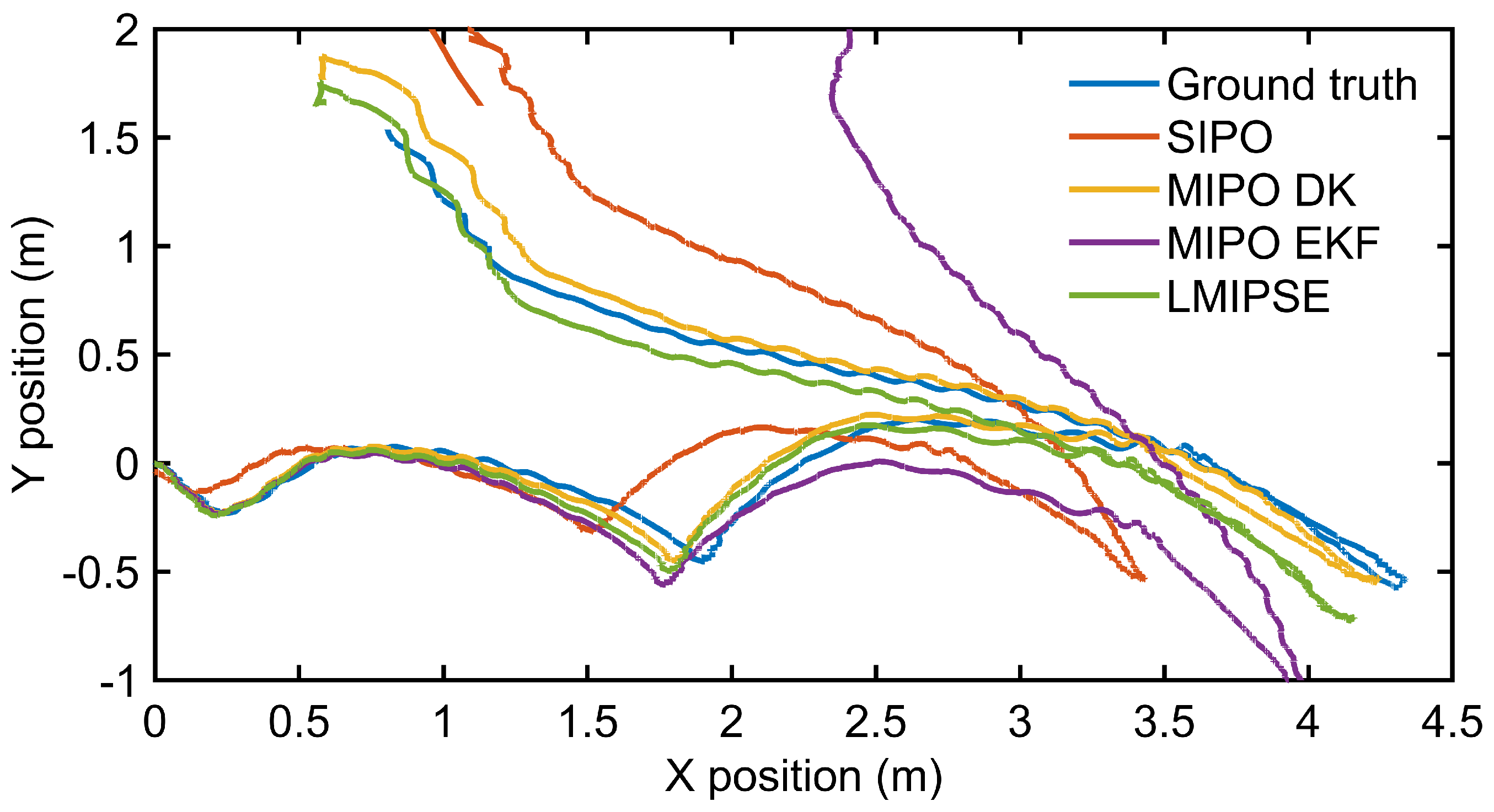
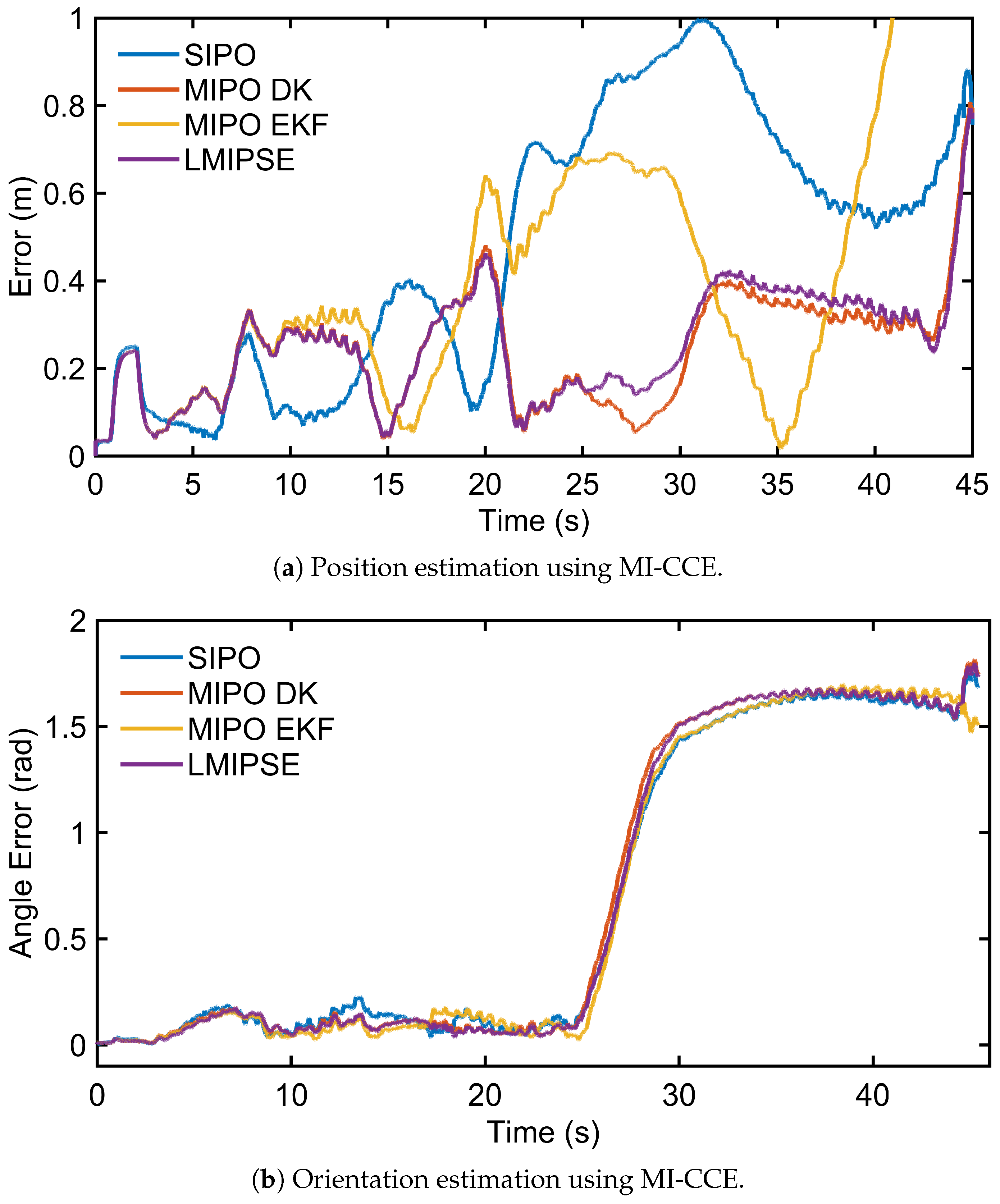
5.3.2. Proprioceptive State Estimation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IMUs | Inertial measurement units |
| KF | Kalman filter |
| EKF | Extended Kalman filter |
| IEKF | Invariant extended Kalman filter |
| RI-EKF | Right-invariant extended Kalman filter |
| mocap | Motion capture |
| CNN | Convolutional neural networks |
| PO | Proprioceptive odometry |
| SIPO | Single-IMU proprioceptive odometry |
| MIPO | Multi-IMU proprioceptive odometry |
| NMN | Neural measurement network |
| MIPSE | Multi-IMU proprioceptive state estimation |
| LMIPSE | Learning-assisted multi-IMU proprioceptive state estimation |
| DK | Dead reckoning |
| MI-CAE | Multi-IMU CNN angle estimator |
| MI-CCE | Multi-IMU CNN angle correction enhancer |
References
- Mastalli, C.; Havoutis, I.; Focchi, M.; Caldwell, D.G.; Semini, C. Motion planning for quadrupedal locomotion: Coupled planning, terrain mapping, and whole-body control. IEEE Trans. Robot. 2020, 36, 1635–1648. [Google Scholar] [CrossRef]
- Bloesch, M. State Estimation for Legged Robots-Kinematics, Inertial Sensing, and Computer Vision. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2017. [Google Scholar]
- He, J.; Gao, F. Mechanism, actuation, perception, and control of highly dynamic multilegged robots: A review. Chin. J. Mech. Eng. 2020, 33, 1–30. [Google Scholar] [CrossRef]
- Nobili, S.; Camurri, M.; Barasuol, V.; Focchi, M.; Caldwell, D.; Semini, C.; Fallon, M. Heterogeneous sensor fusion for accurate state estimation of dynamic legged robots. In Proceedings of the Robotics: Science and System XIII, Cambridge, MA, USA, 12–16 July 2017. [Google Scholar]
- Bloesch, M.; Burri, M.; Omari, S.; Hutter, M.; Siegwart, R. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback. Int. J. Robot. Res. 2017, 36, 1053–1072. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, H.; Wang, P.; Nogueira, L.; Scherer, S. Super odometry: Imu-centric lidar-visual-inertial estimator for challenging environments. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8729–8736. [Google Scholar]
- Fink, G.; Semini, C. Proprioceptive Sensor Fusion for Quadruped Robot State Estimation. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 10914–10920. [Google Scholar] [CrossRef]
- Lin, T.Y.; Li, T.; Tong, W.; Ghaffari, M. Proprioceptive invariant robot state estimation. arXiv 2023, arXiv:2311.04320. [Google Scholar]
- Reinstein, M.; Hoffmann, M. Dead Reckoning in a Dynamic Quadruped Robot Based on Multimodal Proprioceptive Sensory Information. IEEE Trans. Robot. 2013, 29, 563–571. [Google Scholar] [CrossRef]
- Ribeiro, M.I. Kalman and extended kalman filters: Concept, derivation and properties. Inst. Syst. Robot. 2004, 43, 3736–3741. [Google Scholar]
- Camurri, M.; Ramezani, M.; Nobili, S.; Fallon, M. Pronto: A multi-sensor state estimator for legged robots in real-world scenarios. Front. Robot. AI 2020, 7, 68. [Google Scholar] [CrossRef] [PubMed]
- Bloesch, M.; Hutter, M.; Hoepflinger, M.A.; Leutenegger, S.; Gehring, C.; Remy, C.D.; Siegwart, R. State estimation for legged robots-consistent fusion of leg kinematics and IMU. Robotics 2013, 17, 17–24. [Google Scholar]
- Yang, S.; Choset, H.; Manchester, Z. Online kinematic calibration for legged robots. IEEE Robot. Autom. Lett. 2022, 7, 8178–8185. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Z.; Bokser, B.; Manchester, Z. Multi-IMU Proprioceptive Odometry for Legged Robots. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 774–779. [Google Scholar]
- Barrau, A.; Bonnabel, S. The invariant extended Kalman filter as a stable observer. IEEE Trans. Autom. Control 2016, 62, 1797–1812. [Google Scholar] [CrossRef]
- Hartley, R.; Jadidi, M.G.; Grizzle, J.W.; Eustice, R.M. Contact-aided invariant extended Kalman filtering for legged robot state estimation. arXiv 2018, arXiv:1805.10410. [Google Scholar]
- Xavier, F.E.; Burger, G.; Pétriaux, M.; Deschaud, J.E.; Goulette, F. Multi-IMU Proprioceptive State Estimator for Humanoid Robots. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 10880–10887. [Google Scholar]
- Lin, T.Y.; Zhang, R.; Yu, J.; Ghaffari, M. Legged Robot State Estimation using Invariant Kalman Filtering and Learned Contact Events. In Proceedings of the Conference on Robot Learning, PMLR, Auckland, New Zealand, 14–18 December 2022; pp. 1057–1066. [Google Scholar]
- Buchanan, R.; Camurri, M.; Dellaert, F.; Fallon, M. Learning inertial odometry for dynamic legged robot state estimation. In Proceedings of the Conference on Robot Learning, PMLR, Auckland, New Zealand, 14–18 December 2022; pp. 1575–1584. [Google Scholar]
- Youm, D.; Oh, H.; Choi, S.; Kim, H.; Hwangbo, J. Legged Robot State Estimation With Invariant Extended Kalman Filter Using Neural Measurement Network. arXiv 2024, arXiv:2402.00366. [Google Scholar]
- Liu, Y.; Bao, Y.; Cheng, P.; Shen, D.; Chen, G.; Xu, H. Enhanced robot state estimation using physics-informed neural networks and multimodal proprioceptive data. In Proceedings of the Sensors and Systems for Space Applications XVII, SPIE, National Harbor, MD, USA, 21–25 April 2024; Volume 13062, pp. 144–160. [Google Scholar]
- Yang, S.; Zhang, Z.; Fu, Z.; Manchester, Z. Cerberus: Low-drift visual-inertial-leg odometry for agile locomotion. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 4193–4199. [Google Scholar]
- Teng, S.; Mueller, M.W.; Sreenath, K. Legged robot state estimation in slippery environments using invariant extended kalman filter with velocity update. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 3104–3110. [Google Scholar]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Fan, Z.; Cheng, P.; Chen, H.; Bao, Y.; Pham, K.; Blasch, E.; Xu, H.; Chen, G. STAN: Spatial-Temporal Attention Based Inertial Navigation Transformer. In Proceedings of the 37th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2024), Baltimore, MD, USA, 16–20 September 2024; pp. 2825–2836. [Google Scholar]
- Liu, W.; Caruso, D.; Ilg, E.; Dong, J.; Mourikis, A.I.; Daniilidis, K.; Kumar, V.; Engel, J. TLIO: Tight Learned Inertial Odometry. IEEE Robot. Autom. Lett. 2020, 5, 5653–5660. [Google Scholar] [CrossRef]
- Chen, C.; Pan, X. Deep learning for inertial positioning: A survey. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10506–10523. [Google Scholar] [CrossRef]
- Hong, S.; Xu, Y.; Khare, A.; Priambada, S.; Maher, K.; Aljiffry, A.; Sun, J.; Tumanov, A. HOLMES: Health OnLine Model Ensemble Serving for Deep Learning Models in Intensive Care Units. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1614–1624. [Google Scholar]

| Layer (Type) | Output Shape | Param # |
|---|---|---|
| Conv1d-1 | [32, 256, 8691] | 75,776 |
| MyConv1dPadSame-2 | [32, 256, 8691] | 0 |
| BatchNorm1d-3 | [32, 256, 8691] | 512 |
| ReLU-4 | [32, 256, 8691] | 0 |
| Conv1d-5 | [32, 256, 8691] | 327,936 |
| MyConv1dPadSame-6 | [32, 256, 8691] | 0 |
| BatchNorm1d-7 | [32, 256, 8691] | 512 |
| ReLU-8 | [32, 256, 8691] | 0 |
| Dropout-9 | [32, 256, 8691] | 0 |
| Conv1d-10 | [32, 256, 8691] | 327,936 |
| MyConv1dPadSame-11 | [32, 256, 8691] | 0 |
| BasicBlock-12 | [32, 256, 8691] | 0 |
| … | … | … |
| Conv1d-106 | [32, 1024, 544] | 5,243,904 |
| MyConv1dPadSame-107 | [32, 1024, 544] | 0 |
| BasicBlock-108 | [32, 1024, 544] | 0 |
| BatchNorm1d-109 | [32, 1024, 544] | 2048 |
| ReLU-110 | [32, 1024, 544] | 0 |
| Linear-111 | [32, 1] | 1025 |
| Size | 1k | 2k | 3k | 4k | |
|---|---|---|---|---|---|
| Method | |||||
| MI-CAE | 0.0826 | 0.0526 | 0.0464 | 0.0361 | |
| MI-CCE | 0.0445 | 0.0332 | 0.0239 | 0.0236 | |
| Method | Yaw | Filter | Median Drift % | RMSE | Max RSE |
|---|---|---|---|---|---|
| SIPO | Mocap | EKF | 31.52 | 0.57 | 1.00 |
| SIPO | EKF | EKF | 45.19 | 0.95 | 2.12 |
| MIPO | Mocap | EKF | 14.89 | 0.29 | 0.79 |
| MIPO | DK | EKF | 15.12 | 0.28 | 0.81 |
| MIPO | EKF | EKF | 17.83 | 0.62 | 2.11 |
| MIPSE | RI-EKF | RI-EKF | 16.59 | 0.41 | 1.29 |
| LMIPSE | CAE | EKF | 15.23 | 0.30 | 0.87 |
| LMIPSE | CCE | EKF | 14.84 | 0.29 | 0.80 |
| Method | Yaw | Filter | Median Drift % | RMSE | Max RSE |
|---|---|---|---|---|---|
| SIPO | EKF | EKF | 45.90 | 0.96 | 2.13 |
| MIPO | EKF | EKF | 18.30 | 0.66 | 2.22 |
| MIPO | DK | EKF | 15.37 | 0.31 | 0.98 |
| LMIPSE | CCE | EKF | 14.87 | 0.29 | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Bao, Y.; Cheng, P.; Shen, D.; Fan, Z.; Xu, H.; Chen, G. Learning-Assisted Multi-IMU Proprioceptive State Estimation for Quadruped Robots. Information 2025, 16, 479. https://doi.org/10.3390/info16060479
Liu X, Bao Y, Cheng P, Shen D, Fan Z, Xu H, Chen G. Learning-Assisted Multi-IMU Proprioceptive State Estimation for Quadruped Robots. Information. 2025; 16(6):479. https://doi.org/10.3390/info16060479
Chicago/Turabian StyleLiu, Xuanning, Yajie Bao, Peng Cheng, Dan Shen, Zhengyang Fan, Hao Xu, and Genshe Chen. 2025. "Learning-Assisted Multi-IMU Proprioceptive State Estimation for Quadruped Robots" Information 16, no. 6: 479. https://doi.org/10.3390/info16060479
APA StyleLiu, X., Bao, Y., Cheng, P., Shen, D., Fan, Z., Xu, H., & Chen, G. (2025). Learning-Assisted Multi-IMU Proprioceptive State Estimation for Quadruped Robots. Information, 16(6), 479. https://doi.org/10.3390/info16060479






