Automated Crack Width Measurement in 3D Models: A Photogrammetric Approach with Image Selection
Abstract
1. Introduction
2. Preliminary Procedures
2.1. Image Acquisition on Site
2.2. Manual Crack Measurements on Site
2.3. 3D Scene Reconstruction in Metashape
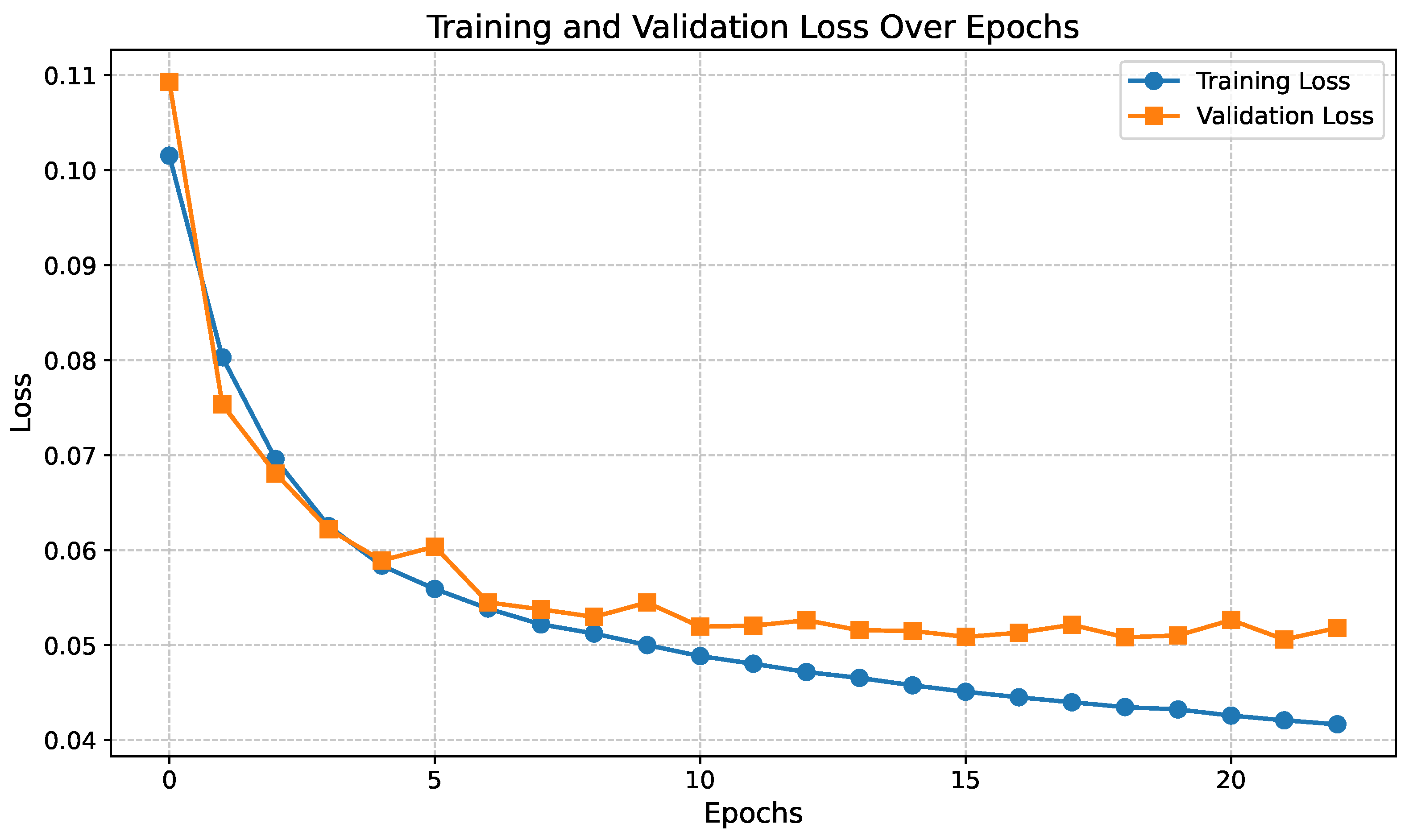
3. Automated Crack Detection and Measurement
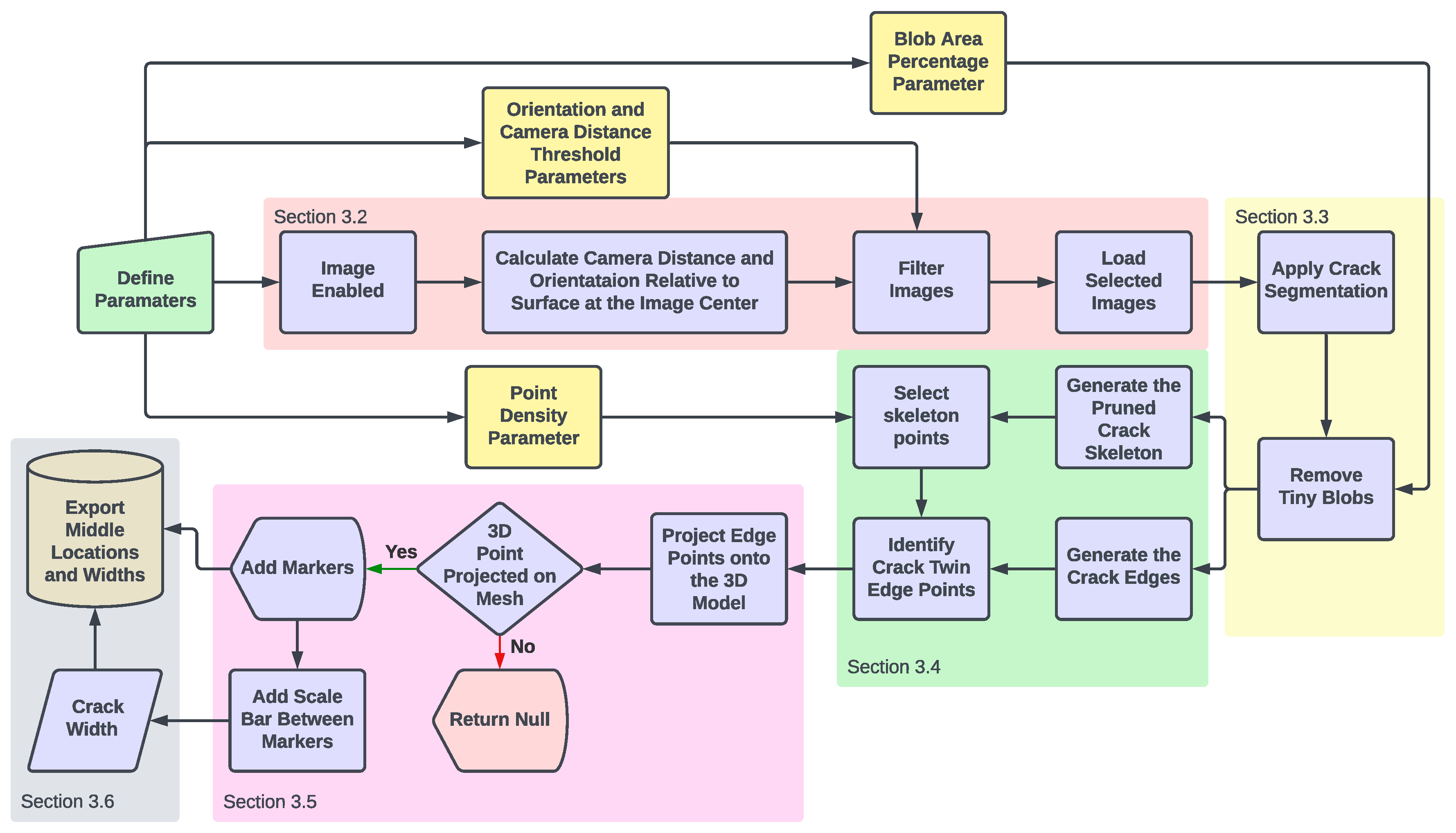
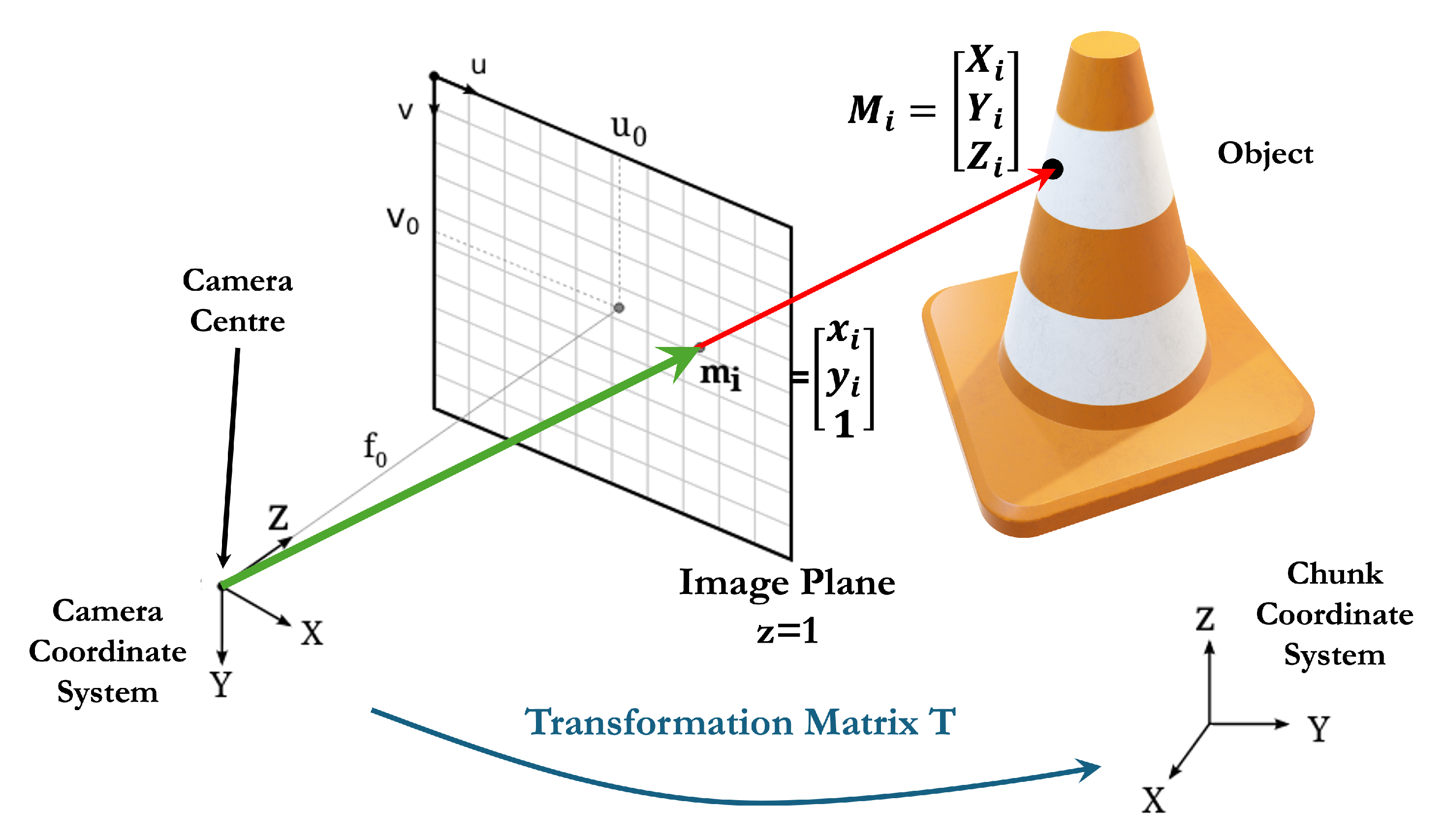
3.1. Crack Detection and Projection Algorithm
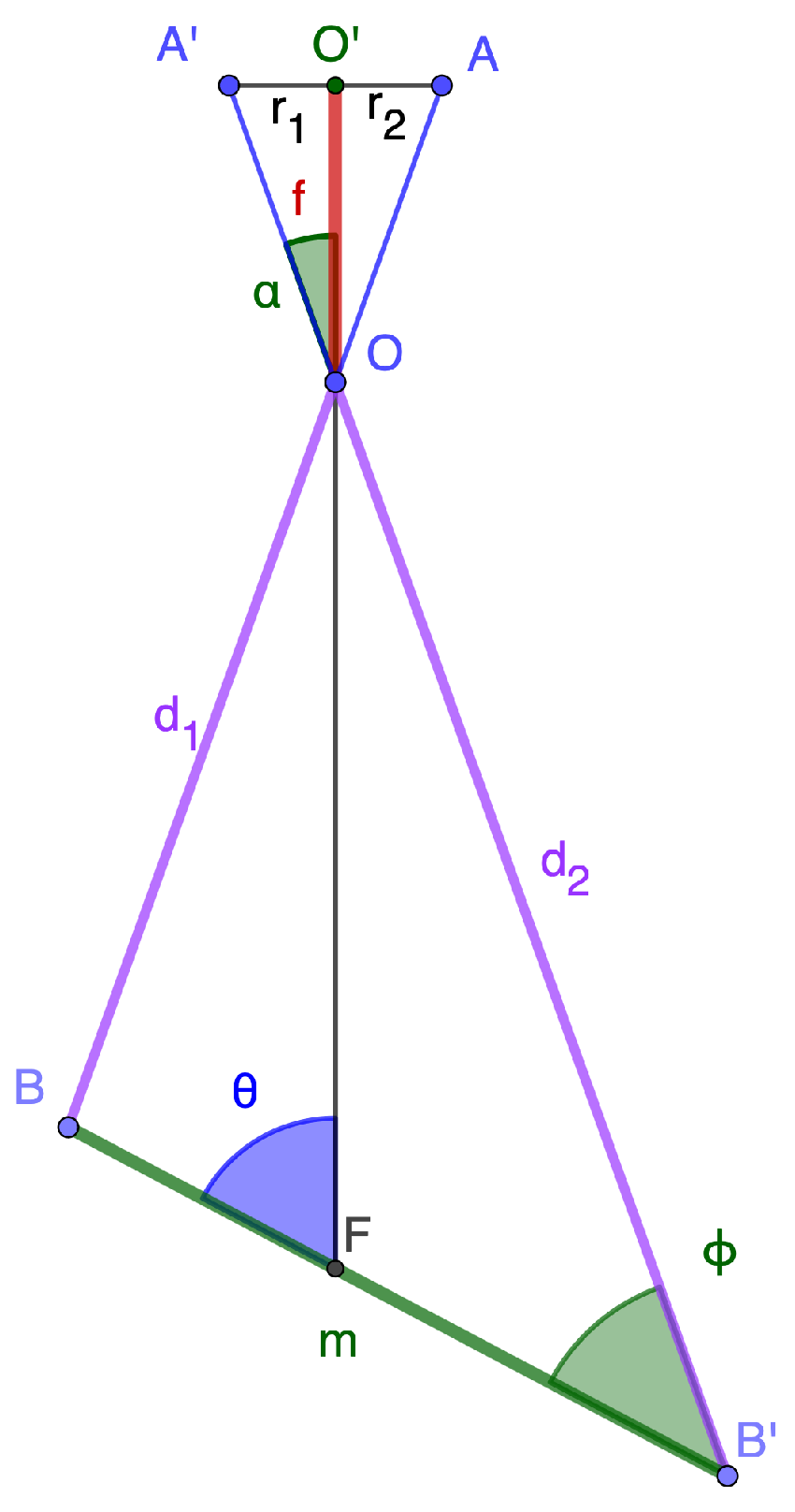
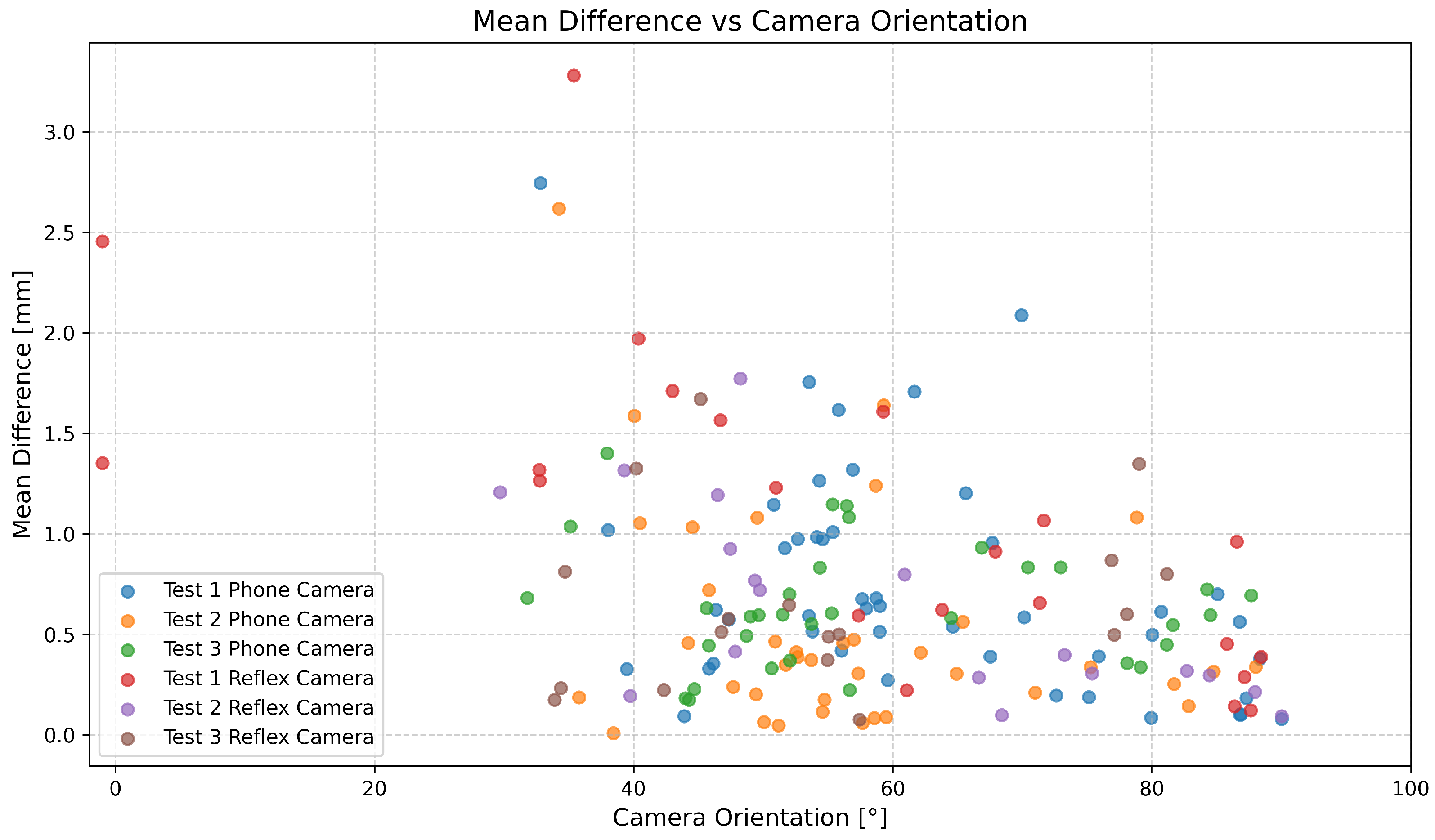
3.2. Camera Selection
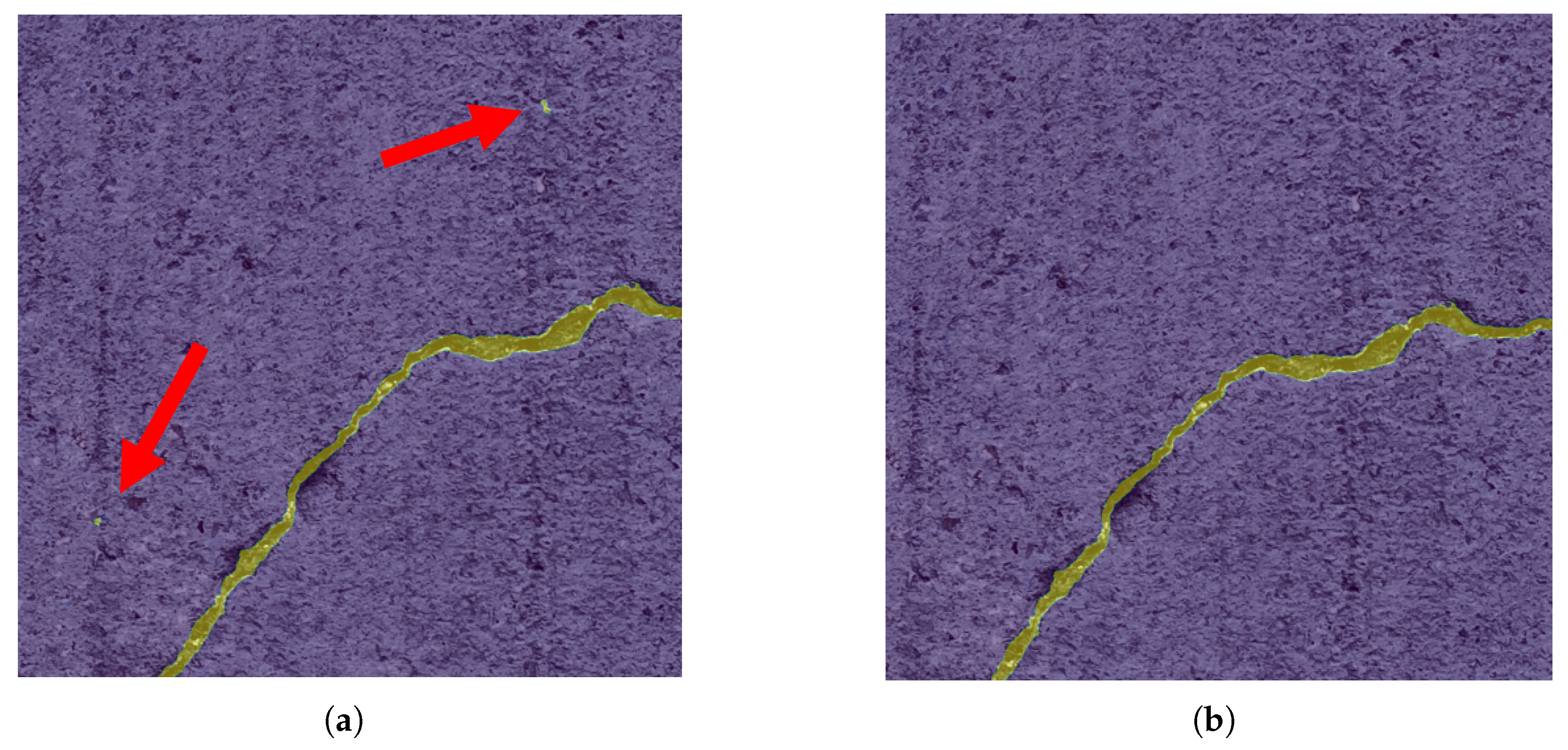
3.3. Binary Crack Segmentation
3.4. Selecting Crack Edge Twins
3.5. Projection of Crack Edges on 3D Mesh Model
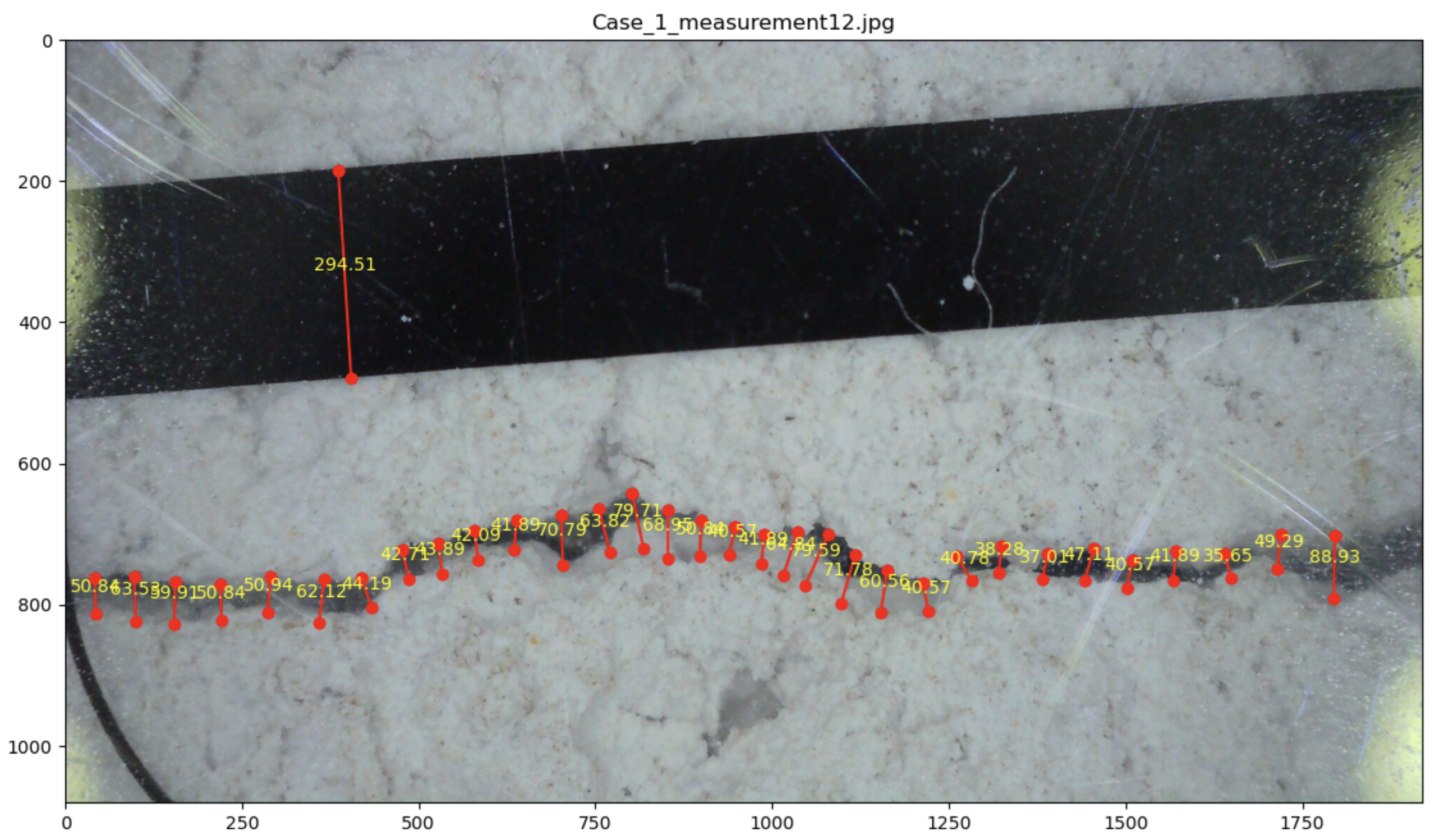
3.6. Exporting Results
4. Laboratory Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adhikari, R.S.; Moselhi, O.; Bagchi, A. Image-Based Retrieval of Concrete Crack Properties. Autom. Constr. 2014, 39, 180–194. [Google Scholar] [CrossRef]
- Yeum, C.M.; Dyke, S.J. Vision-Based Automated Crack Detection for Bridge Inspection. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 759–770. [Google Scholar] [CrossRef]
- Li, G.; He, S.; Ju, Y.; Du, K. Long-distance precision inspection method for bridge cracks with image processing. Autom. Constr. 2013, 41, 83–95. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature Pyramid and Hierarchical Boosting Network for Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2019, 99, 1–11. [Google Scholar] [CrossRef]
- Shi, Z.; Jin, N.; Chen, D.; Ai, D. A comparison study of semantic segmentation networks for crack detection in construction materials. Constr. Build. Mater. 2024, 414, 134950. [Google Scholar] [CrossRef]
- Liu, Y.-F.; Nie, X.; Fan, J.-S.; Liu, X.-G. Image-based crack assessment of bridge piers using unmanned aerial vehicles and three-dimensional scene reconstruction. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 511–529. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, Y.; Jia, H.; Zhang, L.; Xu, F.; Tian, Y.; Ma, Z.; Liu, X.; Guo, S.; Wu, Y.; et al. UAV vision-based crack quantification and visualization of bridges: System design and engineering application. Struct. Health Monit. 2024, 24, 1083–1100. [Google Scholar] [CrossRef]
- Ioli, F.; Pinto, A.; Pinto, L. UAV Photogrammetry for Metric Evaluation of Concrete Bridge Cracks. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 1025–1032. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Hao, X.; Fan, J. Crack Detection of Bridge Concrete Components Based on Large-Scene Images Using an Unmanned Aerial Vehicle. Sensors 2023, 23, 6271. [Google Scholar] [CrossRef]
- Dung, C.V.; Anh, L.D. Autonomous concrete crack detection using deep fully convolutional neural network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, Y.; Wang, Y.; Wang, W. Computer Vision-Based Concrete Crack Detection Using U-Net Fully Convolutional Networks. Autom. Constr. 2019, 104, 129–139. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerlan, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Yu, C.; Du, J.; Li, M.; Li, Y.; Li, W. An improved U-Net model for concrete crack detection. Mach. Learn. Appl. 2022, 10, 100436. [Google Scholar]
- Chen, Y.-C.; Wu, R.-T.; Puranam, A. Multi-task deep learning for crack segmentation and quantification in RC structures. Autom. Constr. 2024, 166, 105599. [Google Scholar] [CrossRef]
- Taheri, S. A review on five key sensors for monitoring of concrete structures. Constr. Build. Mater. 2019, 204, 492–509. [Google Scholar] [CrossRef]
- Son, T.T.; Nguyen, S.D.; Lee, H.J.; Phuc, T.V. Advanced crack detection and segmentation on bridge decks using deep learning. Constr. Build. Mater. 2023, 400, 132839. [Google Scholar]
- Golding, V.P.; Gharineiat, Z.; Suliman, H.; Ullah, F. Crack Detection in Concrete Structures Using Deep Learning. Sustainability 2022, 14, 13. [Google Scholar] [CrossRef]
- Dorafshan, S.; Thomas, R.; Maguire, M. Comparison of deep convolutional neural networks and edge detectors for image-based crack detection in concrete. Constr. Build. Mater. 2018, 186, 1031–1045. [Google Scholar] [CrossRef]
- Agisoft LLC. Agisoft Metashape User Manual Professional Edition, Version 2.2. Available online: https://www.agisoft.com/pdf/metashape-pro_2_2_en.pdf (accessed on 2 January 2025).
- Zhou, S.; Canchila, C.; Song, W. Deep learning-based crack segmentation for civil infrastructure: Data types, architectures, and benchmarked performance. Autom. Constr. 2023, 146, 104678. [Google Scholar] [CrossRef]
- Yang, G.; Liu, K.; Zhang, J.; Zhao, B.; Zhao, Z.; Chen, X.; Chen, B.M. Datasets and processing methods for boosting visual inspection of civil infrastructure: A comprehensive review and algorithm comparison for crack classification, segmentation, and detection. Constr. Build. Mater. 2022, 356, 129226. [Google Scholar] [CrossRef]
- khanhha. Crack Segmentation. Available online: https://github.com/khanhha/crack_segmentation (accessed on 10 December 2024).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Las Vegas, NV, USA, 2016. [Google Scholar]
- Zhang, L.; Yang, F.; Zhang, Y.D.; Zhu, Y.J. Road crack detection using deep convolutional neural network. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3708–3712. [Google Scholar]
- Esenbach, M.; Stricker, R.; Seichter, D.; Amende, K.; Debes, K.; Sesselmann, M.; Ebersbach, D.; Stoeckert, U.; Gross, H.-M. How to get pavement distress detection ready for deep learning? A systematic approach. In Proceedings of the 2017 International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic Road Crack Detection Using Random Structured Forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Amhaz, R.; Chambon, S.; Idier, J.; Baltazart, V. Automatic Crack Detection on Two-Dimensional Pavement Images: An Algorithm Based on Minimal Path Selection. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2718–2729. [Google Scholar] [CrossRef]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Özgenel, Ç.F.; Sorguç, A. Performance Comparison of Pretrained Convolutional Neural Networks on Crack Detection in Buildings. Isarc Proc. Int. Symp. Autom. Robot. Constr. 2018, 35, 1–8. [Google Scholar]
- Ong, J.C. A-Hybrid-Method-for-Pavement-Crack-Width-Measurement. Available online: https://github.com/JeremyOng96/A-Hybrid-Method-for-Pavement-Crack-Width-Measurement (accessed on 15 November 2024).
- Lee, T.; Kashyap, R.; Chu, C. Building Skeleton Models via 3-D Medial Surface Axis Thinning Algorithms. CVGIP Graph. Model. Image Process. 1994, 56, 462–478. [Google Scholar] [CrossRef]
- Bai, X.; Latecki, L.J.; Liu, W. Skeleton Pruning by Contour Partitioning with Discrete Curve Evolution. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 449–462. [Google Scholar] [CrossRef]
- Canny, J.F. A Computational Approach To Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Ong, J.C.; Ismadi, M.-Z.P.; Wang, X. A hybrid method for pavement crack width measurement. Measurement 2022, 197, 111260. [Google Scholar] [CrossRef]



















| Dataset Name | Year | Number of Images | Structure Type | Material Type |
|---|---|---|---|---|
| Crack500 [24] | 2019 | 206 | Pavement | Asphalt |
| Gaps384 [25] | 2019 | 304 | Pavement | Asphalt |
| CFD [26] | 2016 | 118 | Pavement | Asphalt |
| AEL [27] | 2016 | 38 | Pavement | Asphalt |
| CrackTree [28] | 2012 | 68 | Pavement | Asphalt |
| CCIC-600 [29] | 2019 | 30 | Bridge | Concrete |
| GSD [mm/pixels] | Nominal Crack Width [mm] | Crack Width in Pixels | |||
|---|---|---|---|---|---|
| Lowest Value | Highest Value | Max | Min | ||
| Test 1 with Phone Camera | 0.05 | 0.15 | 0.72 | 14 | 5 |
| Test 2 with Phone Camera | 0.05 | 0.17 | 1.62 | 32 | 9 |
| Test 2 with Reflex Camera | 0.05 | 0.27 | 1.62 | 32 | 6 |
| Test 3 with Phone Camera | 0.09 | 0.27 | 2.41 | 26 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozturk, H.Y.; Zappa, E. Automated Crack Width Measurement in 3D Models: A Photogrammetric Approach with Image Selection. Information 2025, 16, 448. https://doi.org/10.3390/info16060448
Ozturk HY, Zappa E. Automated Crack Width Measurement in 3D Models: A Photogrammetric Approach with Image Selection. Information. 2025; 16(6):448. https://doi.org/10.3390/info16060448
Chicago/Turabian StyleOzturk, Huseyin Yasin, and Emanuele Zappa. 2025. "Automated Crack Width Measurement in 3D Models: A Photogrammetric Approach with Image Selection" Information 16, no. 6: 448. https://doi.org/10.3390/info16060448
APA StyleOzturk, H. Y., & Zappa, E. (2025). Automated Crack Width Measurement in 3D Models: A Photogrammetric Approach with Image Selection. Information, 16(6), 448. https://doi.org/10.3390/info16060448






