1. Introduction
The Internet of Things (IoT) refers to a network of interconnected smart objects capable of processing information [
1]. Industry sectors such as transportation [
2] and manufacturing [
3] apply IoT technology to enhance operating efficiency. The ease of access to the accompanying tools has enabled companies to develop smart IoT systems to solve real-life problems, and companies are implementing this technology to solve problems across many areas, including healthcare [
4], manufacturing, and agriculture [
5].
Since IoT-based systems form a vital component of Industry 4.0, the architecture of these systems is of prime importance. Choosing the right hardware for these systems forms a part of their design.
The hardware for IoT-based systems should be selected considering cost and system goals. Selecting proper hardware for computer systems is a complex issue that has been studied from various perspectives using diverse methods. Applying multi-criteria decision-making (MCDM) techniques is an effective way to handle and solve IoT-based system hardware selection problems [
6].
Proper hardware selection is a structured process. First, the right experts are identified to provide data on the decision-making problem. Next, the selection criteria are determined and ranked according to expert opinion using methods such as BWM, SWARA, or ITARA. Subsequently, hardware options are assessed and ranked against these criteria using techniques such as COPRAS, EDAS, TOPSIS, VIKOR, or COBRA. Lastly, the selected hardware should comply with the purpose of the system, given the varied objectives and design specifications of existing products.
It is not possible to select hardware for all IoT systems based on just a single decision-making model. Instead, the system must retain and keep hardware information and expert knowledge current. An expert system is one very useful way of doing that.
Expert systems possess expert knowledge and relevant data that apply to the problem [
7]. The knowledge includes selection criteria, their relative significance, and how far each alternative meets these criteria. The stored data can vary from technical specifications, like processing power, to non-technical data, like cost. MCDM methods have also been used in expert systems in past research [
8].
By interacting with the user, the system can understand certain requirements and needs. To prescribe the requisite hardware, the expert system also needs to figure out what components the user’s system requires. Once one understands the decision-making problem, they should be able to categorize and organize the available hardware options.
The main goal of this research is to address the challenge of selecting proper components for IoT-based systems. This research develops an expert system that integrates user needs and expert knowledge. The criteria are weighted using the indifference threshold-based attribute ratio analysis (ITARA) method, which allows unstructured information to be processed by defining indifference thresholds and considering entropy [
9]. These capabilities make it possible to use both technical specifications and expert opinions in constructing a decision problem. Finally, the comprehensive distance-based ranking (COBRA) [
10] method is utilized to rank alternatives. Furthermore, grey numbers are applied to manage uncertainty by allocating interval values for vague parameters [
11]. This makes it possible to handle uncertainty present in parameters and linguistic terms effectively. The study explores the following issues:
Q1: How can an expert system be designed to select the best hardware from the available alternatives?
Q2: Can the grey number approach be combined with the hybrid ITARA-COBRA method? How can this methodology help decision-makers?
To address these questions, this research discusses the existing literature and then posits the proposed methodology and expert system architecture. It then evaluates the hybrid Grey ITARA-COBRA method through sensitivity analysis. Finally, an example of designing IoT-based systems in agriculture is provided.
1.2. Research Gap and Contributions
In previous sections, the problem and the related literature were investigated. In general, three challenges must be addressed to solve the IoT-based hardware selection problem:
Different alternatives, criteria, and criterion weights for different systems, like agricultural and workplace systems;
Vagueness and impreciseness in the existing data, like the accuracy of sensors;
Unstructured data for decision-making, for example, the presence of linguistic terms from experts alongside technical specifications.
The main goal of this research is to design an expert system covering these challenges. One possible solution to the first challenge is to use an expert system. In this type of system, it is possible to use a database and a knowledge base to store data and expert opinions. Then, the system can structure the decision problem based on the needs of the user and the specifications of the desired system.
For the second challenge, grey sets offer a viable approach to handling uncertainty. Grey sets use grey interval values with no precisely known membership values. Not only can grey intervals be applied to linguistic terms, they also address ambiguity in several attributes such as sensor accuracy, power consumption, and durability.
In different problems that are solved using MCDM techniques, there can be different criteria, and each criterion has its own weight, which must be determined by experts. There are different methods for determining the weight of criteria, such as the analytic hierarchy process (AHP) method and the best–worst method (BWM), which are among the well-known methods. The AHP method performs weighting based on pairwise comparisons. Experts must perform these comparisons verbally. Given the ambiguity in some data, the fuzzy AHP approach has also been developed, and applications have been found in various fields, from power systems to supply chains [
31,
32]. The BWM method has also been used in a variety of contexts, from supply chain management [
33] to evaluating healthcare sectors [
34]. In this method, the most important (Best) criterion is compared in pairs with other criteria, and each criterion is compared in pairs to the least important (Worst) criterion. It is worth noting that fuzzy [
35] and grey [
36] implementations of this method have also been presented to handle ambiguity in data. These methods are subjective, which means that they require experts’ linguistic assessments for weighting, and they cannot calculate weights based on numerical data. In these methods, scores are determined based on subjective ratings of criteria from experts. However, in some decision problems, weighting and decision-making may need to be based on numerical data. A new method for determining the weight of criteria is the ITARA method, which can be useful when the data are unstructured. This means that this method can handle both subjective terms and numerical data. ITARA has been used for various issues in transportation, production, material selection, and risk assessment, and in some cases, its fuzzy implementation has also been used. In this method, the entropy of the data is calculated, and the weight of each criterion is determined based on the criterion’s indifference threshold. Considering these cases, ITARA can be used to cover unstructured data.
None of the articles related to IoT hardware selection have utilized the ITARA technique, but its capability to cover unstructured data can help decision-makers make appropriate decisions based on numerical data, like price and processor speed, and linguistic terms based on expert comments. Also, for the first time, the Grey ITARA technique is utilized here. The Grey ITARA technique gives us the ability to handle uncertain data. In the software selection problem, decision-makers must handle imprecise linguistic terms and engineering data that may not be precise enough. In these conditions, the proposed Grey ITARA technique can handle both uncertain and unstructured data. In addition to weighting, a ranking method must be used to rank the existing alternatives. One of the recently developed methods to rank the alternatives is the COBRA method, in which the Euclidean and the Taxicab distances from the best, worst, and average solutions are measured to rank the alternatives. Generally, the capability of the proposed Grey ITARA–Grey COBRA method to handle imprecise and unstructured data is investigated. The research hypothesis is that the proposed Grey ITARA-COBRA method can be useful for weighting criteria and ranking alternatives when designing engineering systems such as IoT-based systems. In these problems, decision-makers must utilize methods that can cover both expert opinions and the existing vague data.
In this paper, an expert system is introduced to help developers select suitable hardware for IoT-based systems. The provided system uses a database and a knowledge base to achieve its goals. The provided system extracts data from the database and a knowledge base to construct the decision matrix based on the desired IoT-based system specifications and solves the decision-making problem with the Grey ITARA-COBRA method to handle unstructured and vague data.
The contributions of this paper are as follows:
Designing an expert system capable of handling engineering data and expert knowledge to support users.
Utilizing Grey systems theory to enhance the ITARA method.
Using the Grey ITARA-COBRA approach to handle imprecise and unstructured data (expert opinions and imprecise numerical data).
4. Discussion
In this study, we sought to design an expert system to select suitable hardware for IoT-based systems. Both expert opinions and product specifications are important in selecting these systems. Also, this expert system should be designed to automatically construct a decision matrix based on user needs announced from the user interface. In the introduction section, two questions were raised for this research, which are answered in this section.
- Q1
: How can an expert system be designed to select the best hardware from the available alternatives?
There are generally three challenges in designing this system:
Utilizing both expert knowledge and technical information.
Understanding user needs.
Existence of vague, unstructured data.
To overcome the first challenge, a knowledge engineering approach can be useful in designing this system. In this approach, expert knowledge should be stored in addition to technical product information. Therefore, this system has a database and a knowledge base.
For the second challenge, the user, through a user interface, inputs product specifications. These are derived from questions the system asks the user, and, as a result, the hardware components to be used are decided. The questions asked vary with different systems and must be designed by IoT system developers. The current approach, which tries to understand the user’s needs by asking a few questions, is very simplistic, and there is room for improvement. Using user feedback and training machine learning models based on big data can be useful in this regard.
Upon user feedback, the system recognizes relevant components and fetches suitable hardware configurations along with their corresponding data, criteria, and expert ratings from the system database and knowledge base.
To overcome the third challenge, the grey number approach can be used and combined with the ITARA and COBRA methods, which overlap with the second research question and will be addressed in the next section.
- Q2
: Can the grey number approach be combined with the hybrid ITARA-COBRA method? How can this methodology help decision-makers?
In answer to the second question, this paper addresses the selection of hardware for IoT systems by solving several decision problems using a hybrid Grey ITARA-COBRA model. In this regard, the decision matrix is constructed from the database and the knowledge base, and the decision-making module ranks the alternatives based on expert-defined criteria.
In this approach, grey numbers are used to cover data with unknown exact values. For example, parameters such as sensor accuracy may not be known precisely. Also, the expert’s linguistic terms can be converted into grey numbers.
Since this approach allows for the use of both technical specifications and expert opinions, it is a suitable method for the engineering design of products. Using this method, existing engineering characteristics can be evaluated using both technical data and expert ratings.
Finally, the results of this study are comparable to those of other studies. In addition to presenting a grey method based on ITARA and COBRA that has the ability to handle unstructured and vague data that can be useful for engineering decision-making problems, this study proposes an architecture for an expert system that supports users in selecting appropriate hardware and designing hardware for IoT-based systems, which has not been seen in previous studies. Also, references [
6,
12,
15,
24] propose approaches for selecting hardware or IoT-based devices, but none of these presents a comprehensive system for selecting different hardware components from different parts of an IoT-based system. The system proposed in this study handles this task using technical data along with expert knowledge management.
5. Conclusions
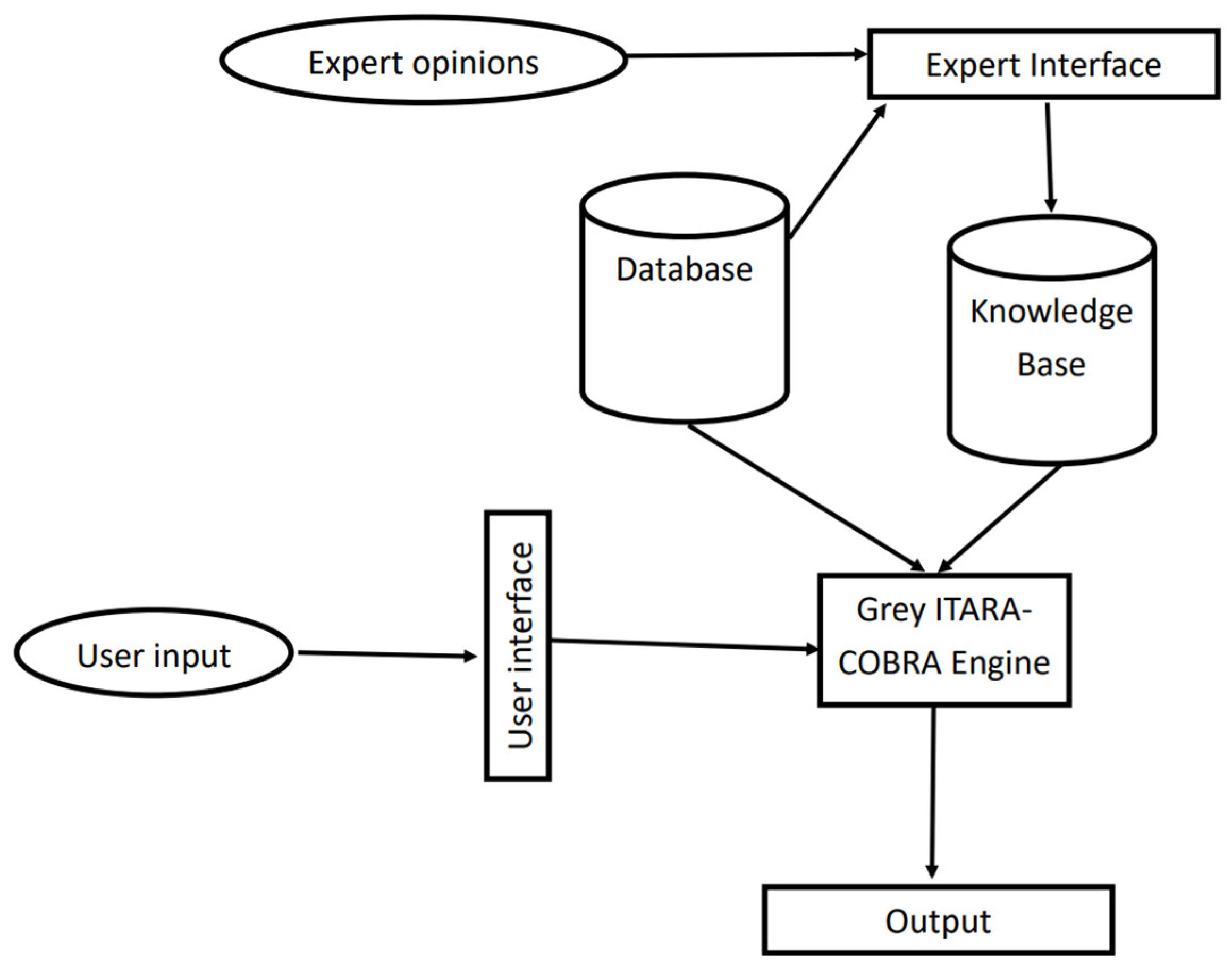
This work presents an expert system architecture for hardware selection in IoT. For this problem, both expert knowledge and hardware specification data are needed. Moreover, the system should communicate with both the user and the expert. The proposed system includes a hardware specifications database, a knowledge base of expert-derived hardware ratings and selection criteria, and an interface to provide expert input and data capture.
In general, the architecture of this system is such that there are two types of interfaces: the user interface and the expert interface. Experts use their interface to enter information, such as their opinions, and users use the user interface and the questions the system asks them to enter their needs. These questions can vary from product to product. Expert ratings are entered into the knowledge base. There is also a database in the system where the technical specifications of the hardware are stored.
Next, the system, which has asked the user about his needs, extracts various hardware options that could be suitable for the user from the database. This hardware information, along with the experts’ scores and decision-making criteria, is given to the system’s decision-making engine to rank the options using the Grey ITARA-COBRA method. In this way, the designed expert system uses both expert ratings and technical specifications to rank the options. If experts have entered their opinions in response to the hardware selection for different systems, the proposed expert system can use the experts’ opinions for all these cases, and there is no need to fill out the questionnaire manually for each user.
The proposed Grey ITARA-COBRA method can be useful in several aspects. First, since grey numbers are utilized, parameters with unknown exact values are covered. Moreover, parameters with exact values can also be converted into grey numbers. It is worth mentioning that the verbal spectra of experts can also be converted into grey numbers.
The second point is that given the possibility of covering unstructured data by the ITARA method, it is possible to use both expert ratings and technical specifications. This makes it possible to use this approach in many engineering fields where both technical specifications and expert scores are used in decision-making.
Finally, it is worth mentioning that the ITARA method, which is used for weighting in the approach of this research, is a method that performs weighting based on both data entropy and the indifference threshold determined based on expert opinion. Considering these cases, both expert opinions and data entropy are effective in determining weights.
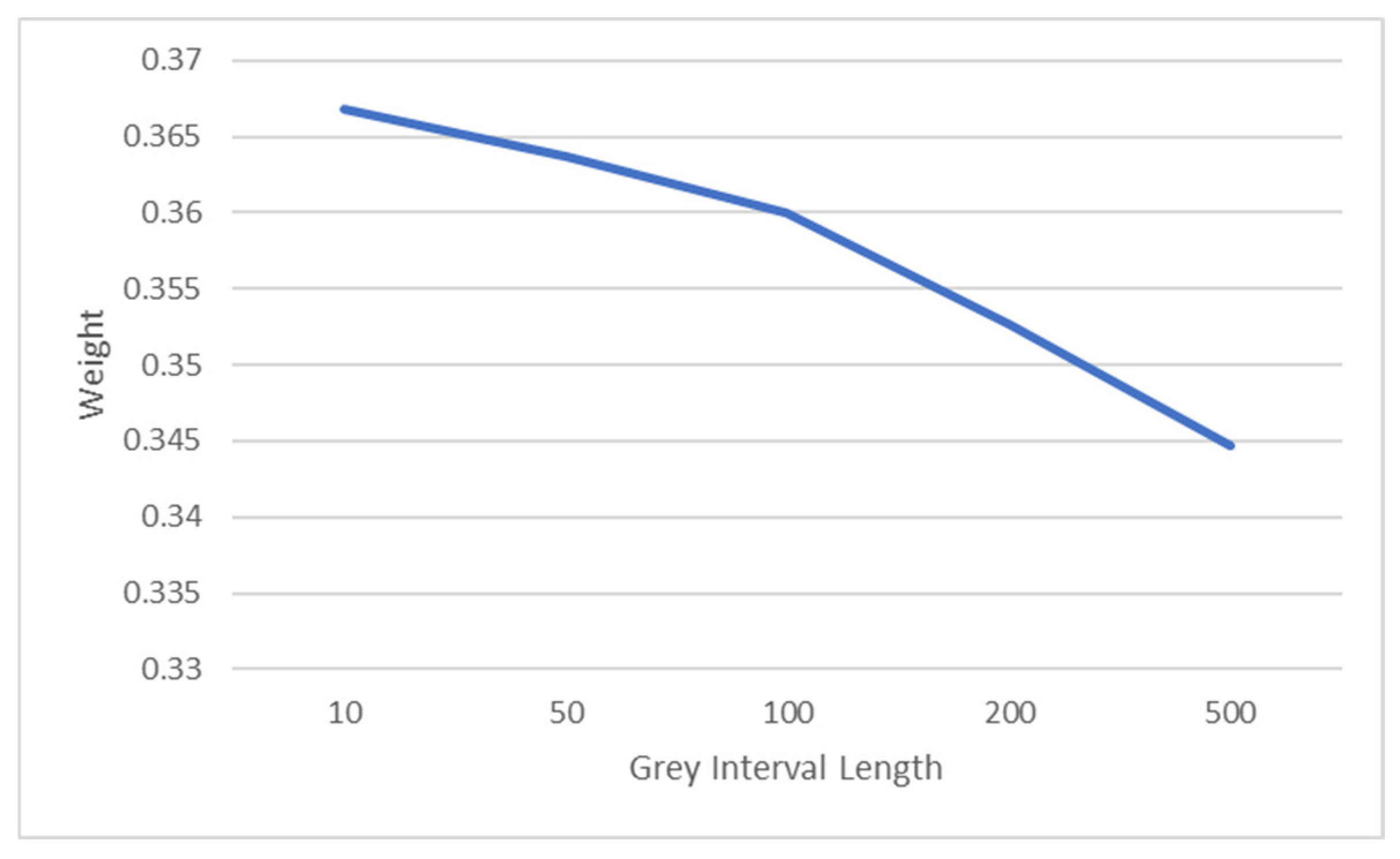
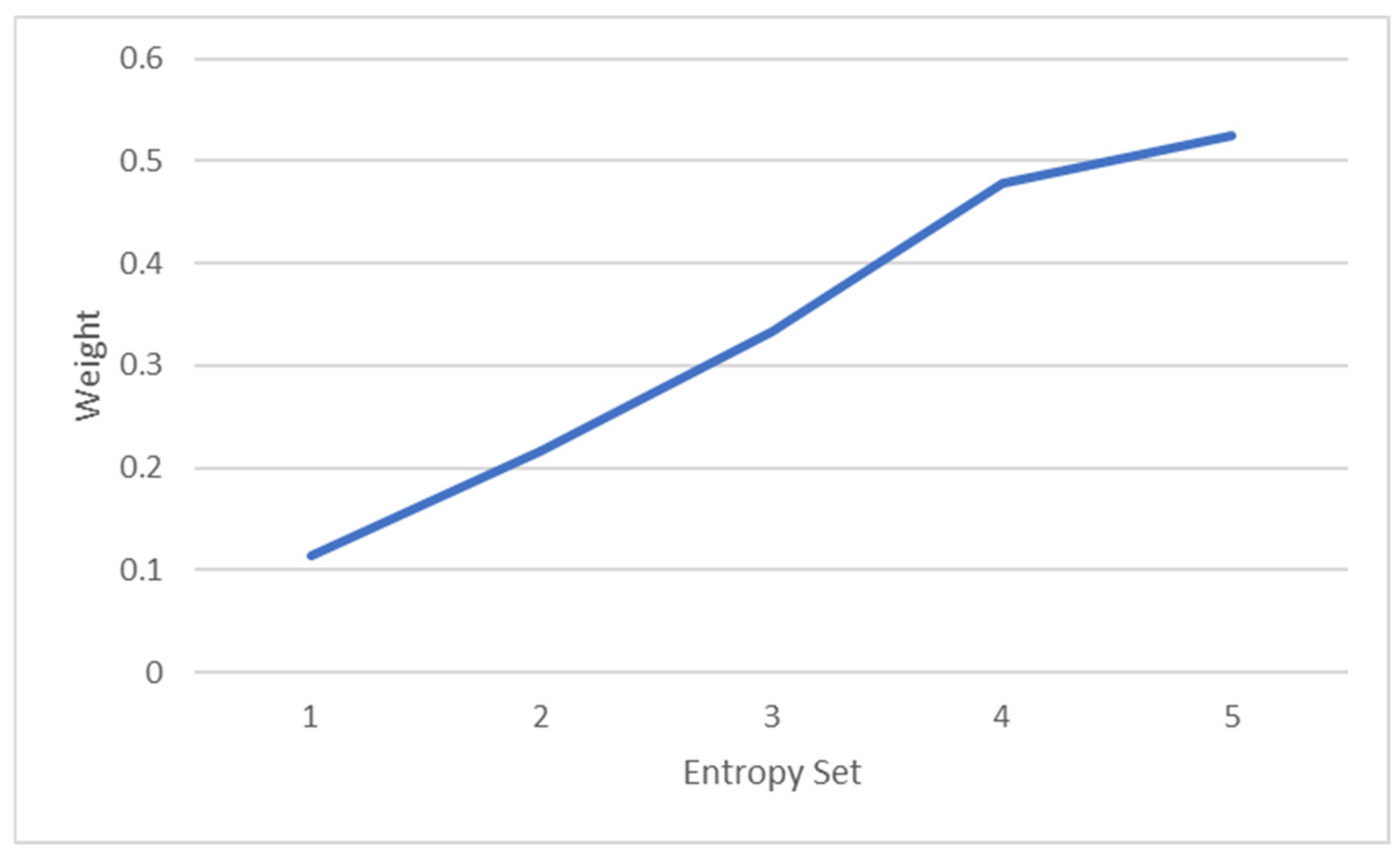
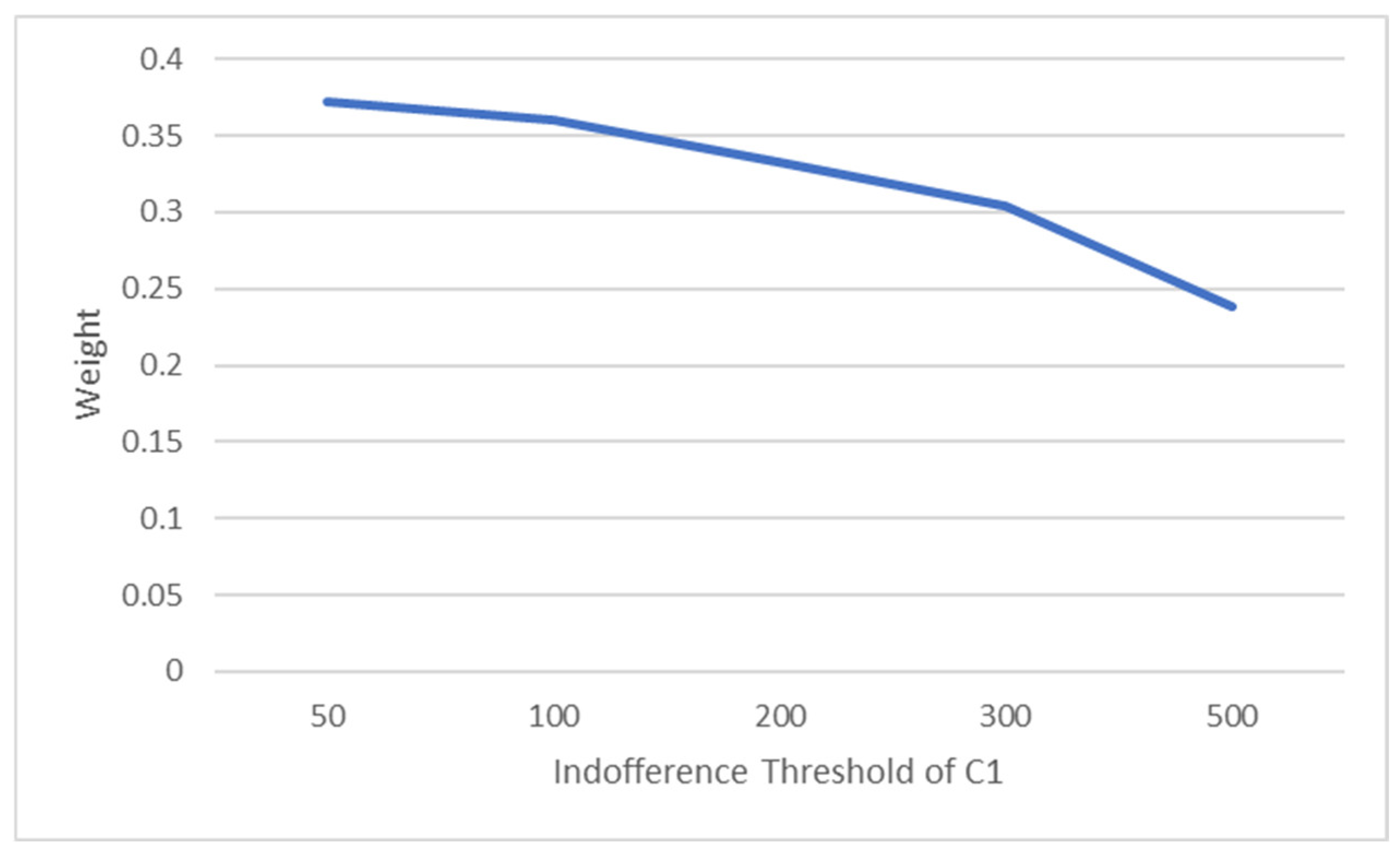
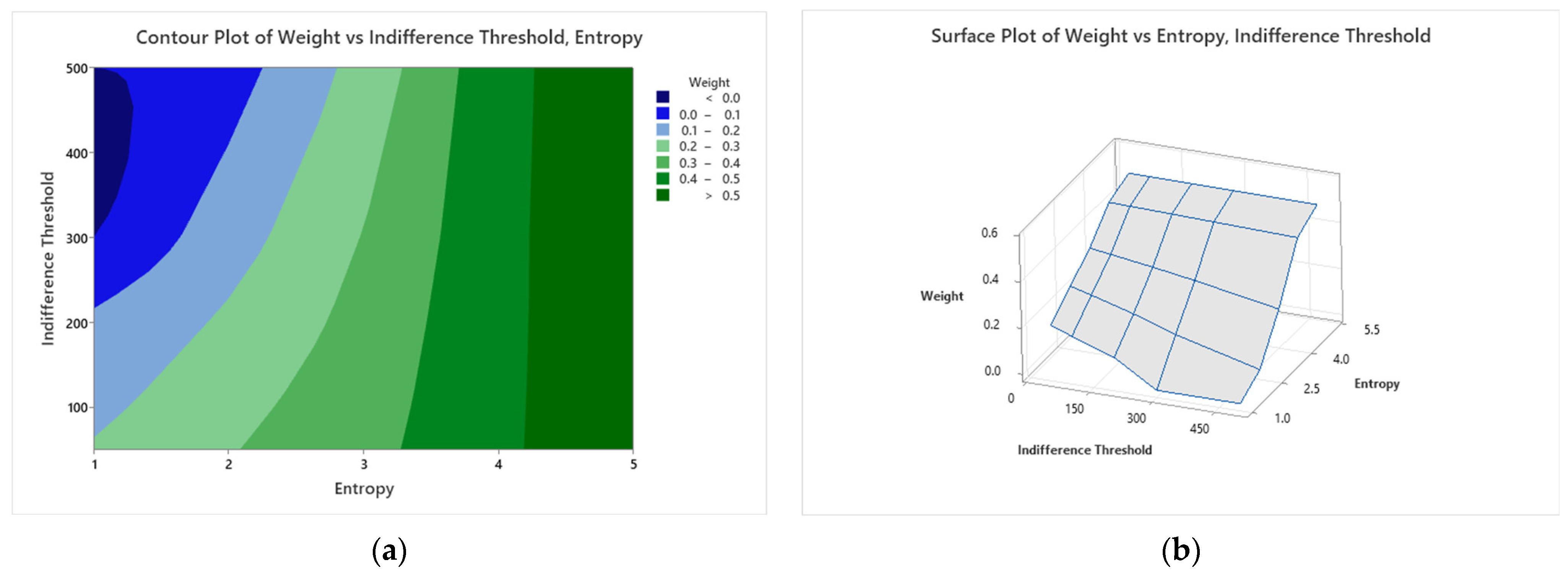
A sensitivity analysis reveals the effectiveness of this approach in dealing with unstructured and imprecise data. The sensitivity of the calculated weights to factors such as grey interval length, entropy, and the indifference threshold is investigated. As the grey interval length increases, the criterion weight decreases. Also, as expected, the criterion weight increases with increasing entropy and decreases with increasing indifference threshold.
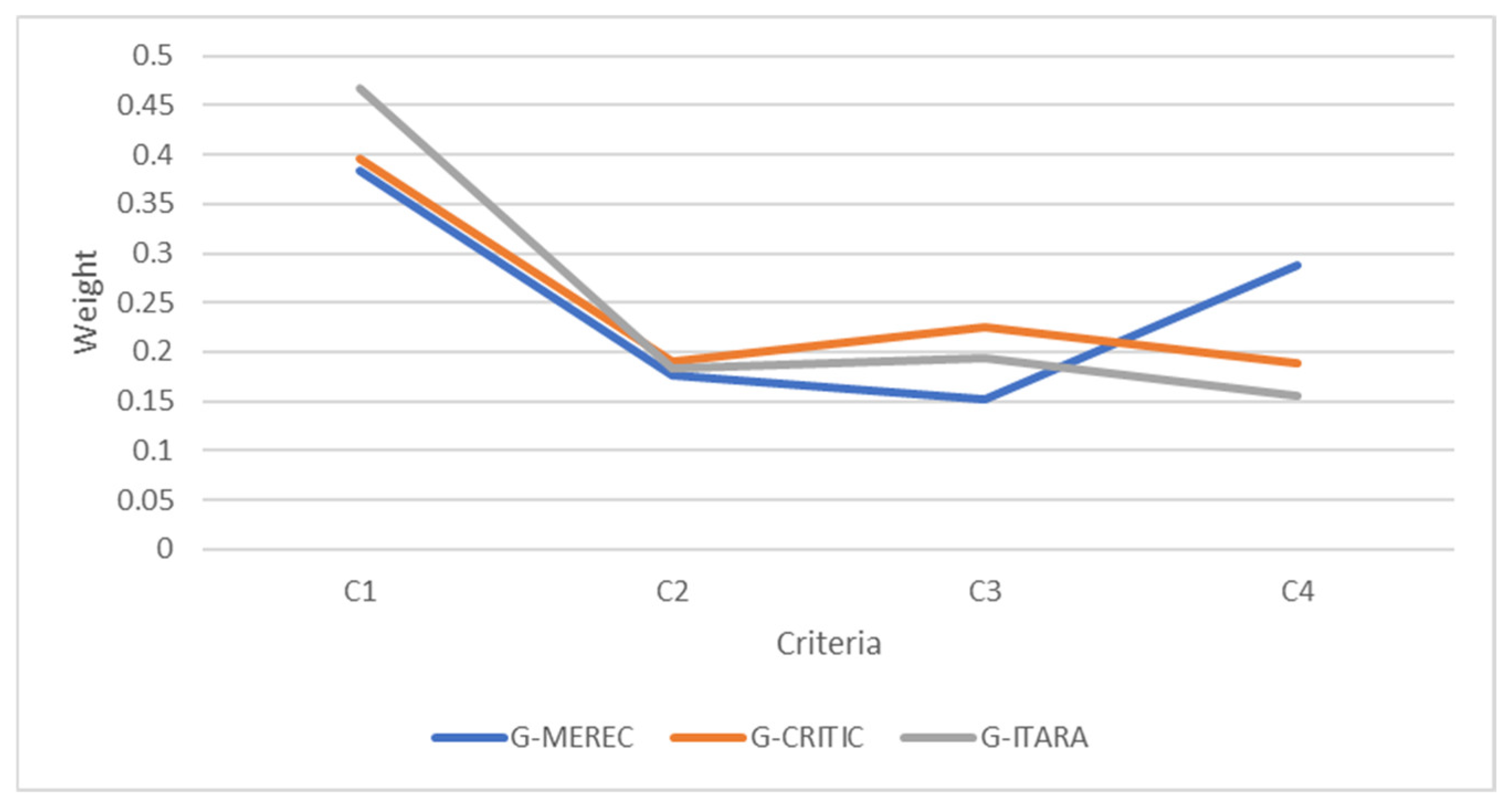
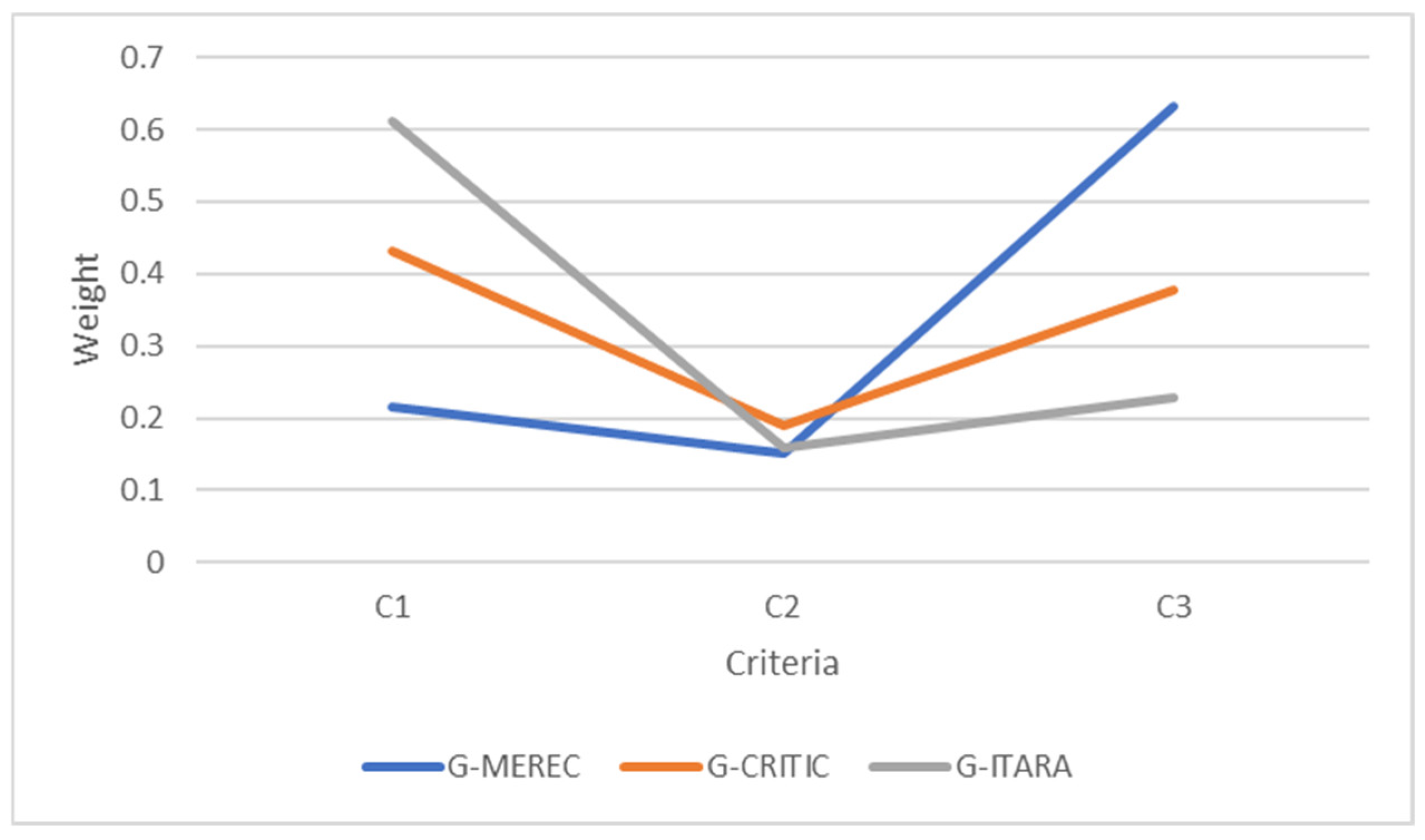
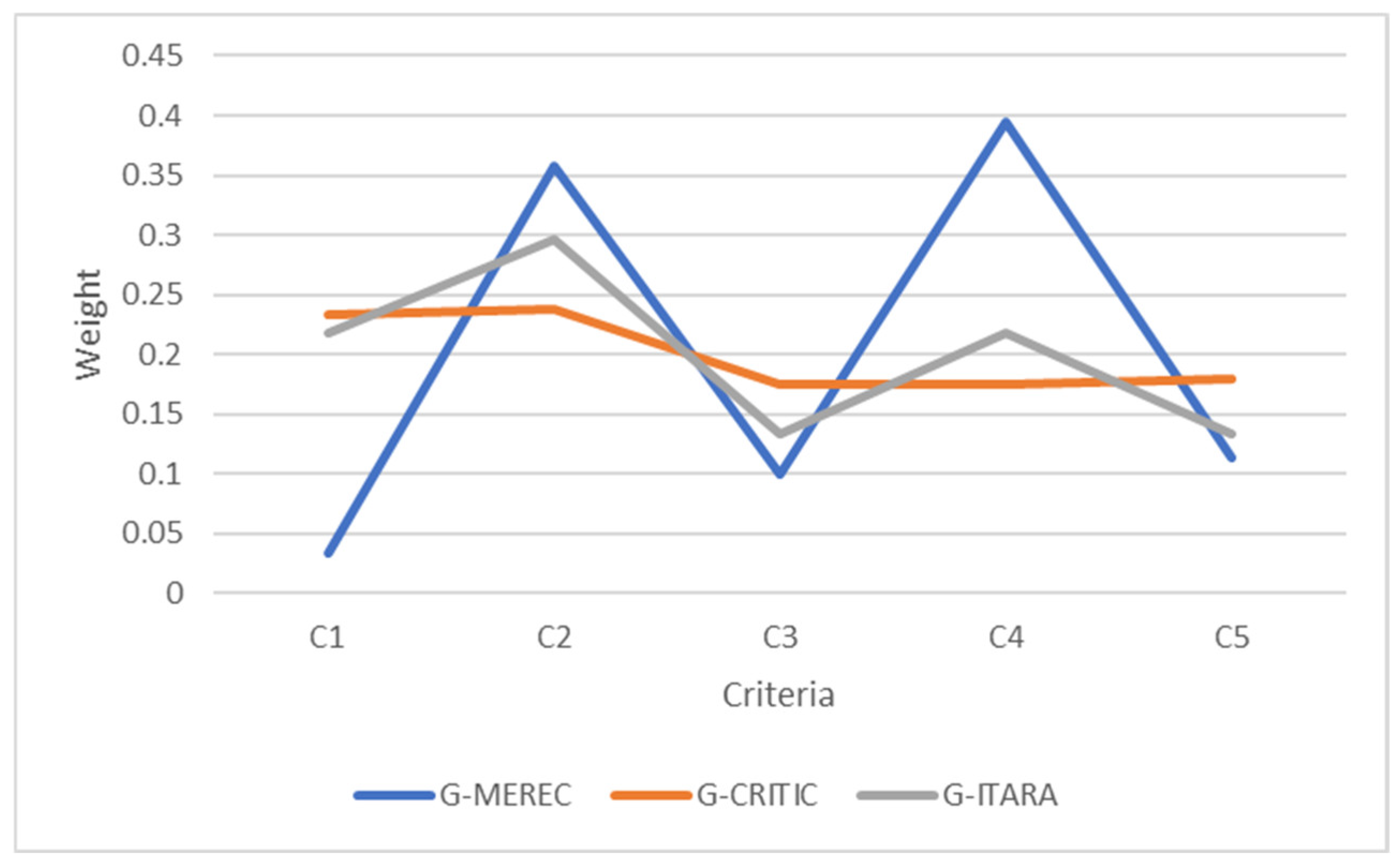
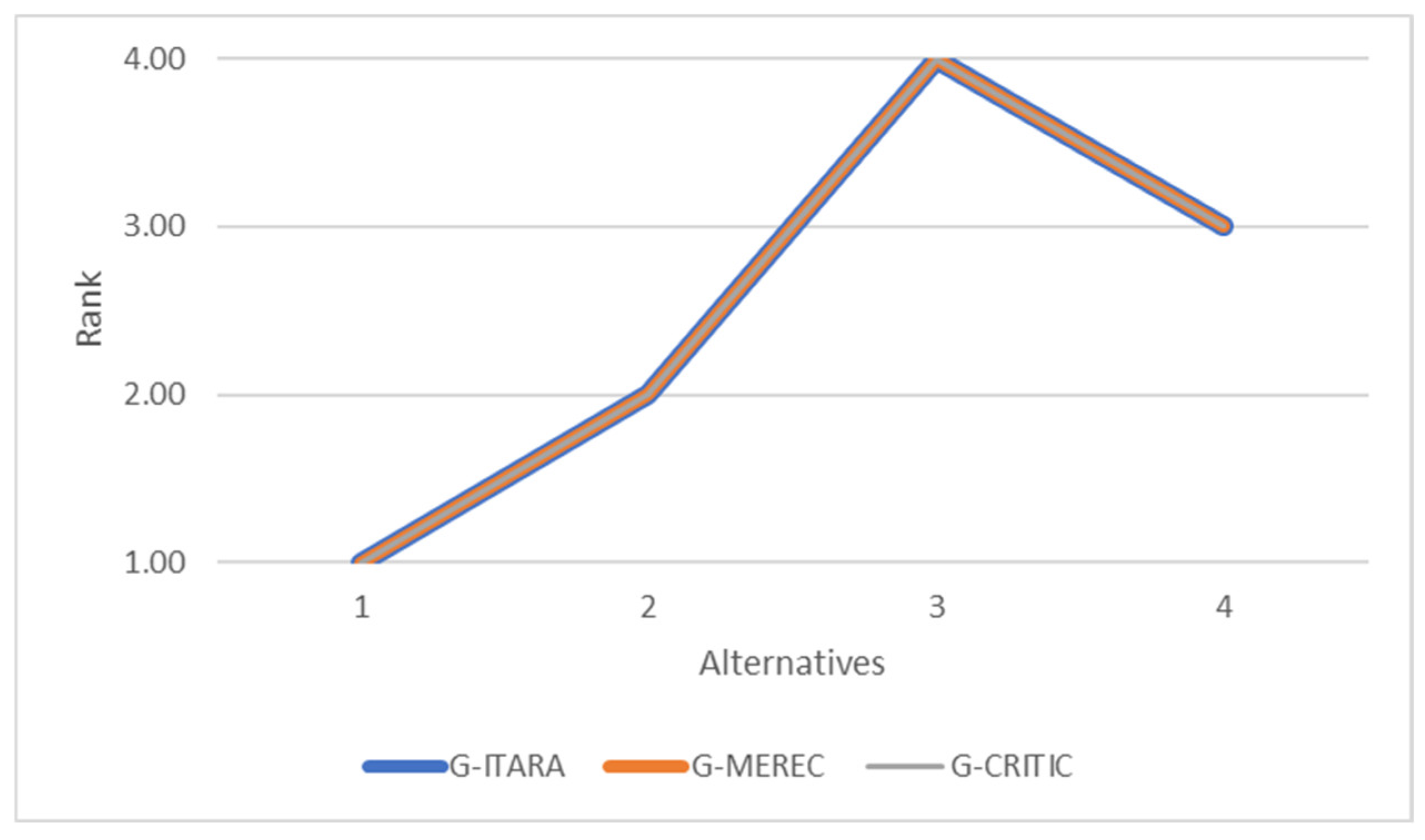
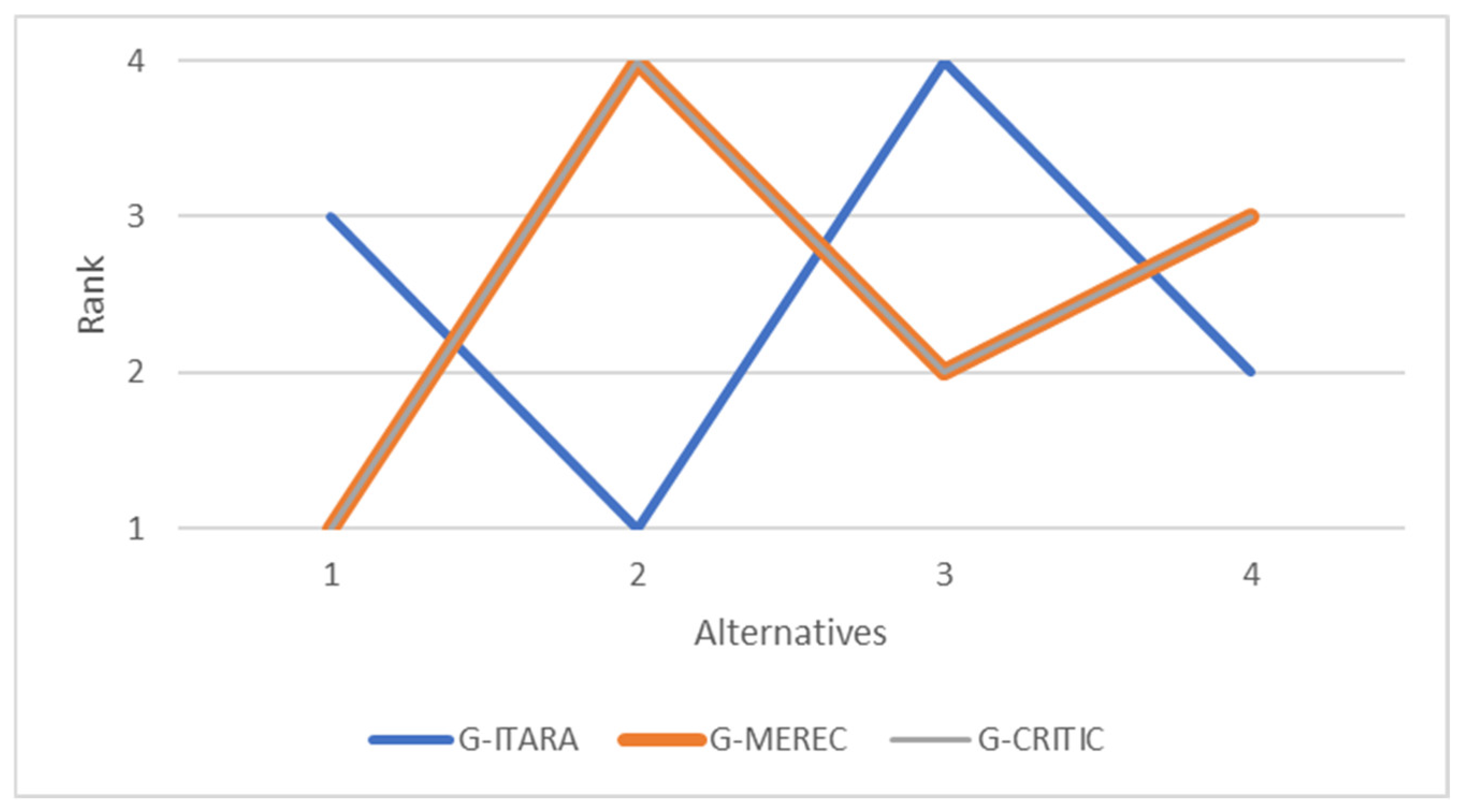
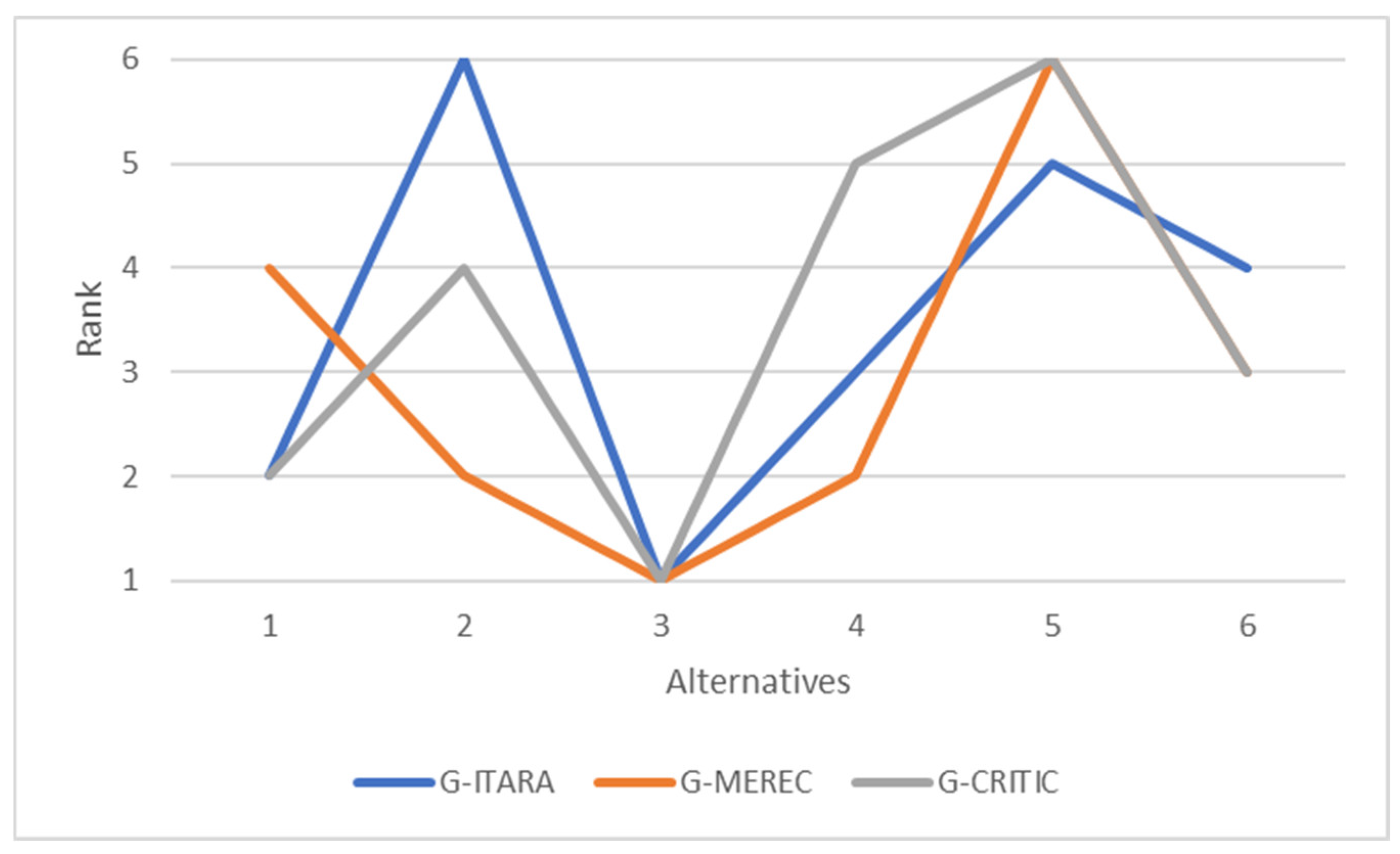
Next, an example scenario was conducted to select the appropriate hardware for designing an IoT-based irrigation system. Initially, it was determined that the system required by the user needs an IoT platform, communication technology, an energy source, and a soil moisture sensor. Then, these alternatives were ranked based on the technical specifications and expert ratings.
In addition to the proposed methodology, weights were calculated using Grey MEREC and Grey CRITIC methods, and the comparisons show the impact of expert-defined indifference thresholds on criterion weights. In addition to these, the final rank of alternatives was calculated based on the Grey MEREC and Grey CRITIC methods and compared to the Grey ITARA method. The comparisons show the effect of utilizing the indifference threshold concept, and due to utilizing both entropy and indifference threshold concepts in addition to grey sets, the Grey ITARA method is preferred. Moreover, the Grey ITARA-COBRA method is proven to be effective and beneficial in the process of hardware selection. These cases confirm the hypothesis of this research, which is to determine the applicability of the Grey ITARA-COBRA method in engineering decision-making problems involving ambiguous unstructured data. The applicability of the Grey COBRA method in handling unstructured data is also confirmed because this approach was used to rank hardware based on ambiguous numerical data and expert opinions in this study. However, the presented approach is not totally perfect. In general, the main restrictions of the designed system are as follows:
The absence of future-oriented scenarios in decision-making.
Using a simplistic algorithm to understand user needs may result in misunderstandings.
The system does not consider user ratings and user experiences when selecting components of IoT-based systems.
In addition, the limitations of this study were as follows:
Lack of access to experts to evaluate a wide range of products, only examining the example of an IoT-based smart irrigation system.
Limited availability of official technical data on hardware.
It is worth noting that with this approach, due to its ability to handle unstructured data, it is possible to use both expert opinions and technical specifications for decision-making. This feature makes the proposed approach a suitable method for evaluating products and selecting them with engineering specifications and expert opinions.
The following are suggested for future research:
Extending the hybrid Grey ITARA-COBRA approach to other decision-making challenges.
Investigating the utilization of fuzzy sets theory for problems with fuzzy datasets.
It is possible to combine the ITARA method with subjective weighting methods to refine the weighting process.
Considering user ratings to rank the alternatives.
Developing a more sophisticated method to determine user needs. Training machine learning models is preferred.
There is a possibility of increasing the efficiency of the IoT-based system that is being designed by considering its architecture in addition to hardware. In this regard, the system can be integrated with existing architectures. For example, Nikkilä et al. proposed an approach for information system management in precision agriculture [
37]. Adopting such an approach can enhance the processes. Additionally, ensuring sustainable services and promoting user awareness and involvement in this domain can be beneficial [
38]. Finally, improving the architecture to better incorporate contextual information can also be valuable [
39].