Improving Physically Unclonable Functions’ Performance Using Second-Order Compensated Measurement

Abstract

In this paper, we study the performance of second-order compensated measurement to generate a multi-bit response in physically unclonable functions (PUFs). The proposed technique is based on a novel second-order compensated measurement generating multiple bits instead of a single bit provided by the conventional compensated measurement. A PUF based on this technique has been proposed and implemented in 40 Artix-7 FPGAs, and its uniqueness and reproducibility have been compared to those of another PUF using the compensated measurement technique. In addition, we demonstrate that the best trade-off between identifiability and computation time performance is obtained when using only two bits. At the same time, the good performance of the technique has been demonstrated, improving the identifiability of a ring oscillator PUF (RO-PUF) between 70 and 90% compared to a RO-PUF that uses conventional compensated measurement. In particular, equal error rates (EER) of the order of EER∼${10}^{-16}$ can be achieved by combining the sign bit with another bit extracted using the proposed technique; and up to EER∼${10}^{-19}$ by using one more extra bit. In addition, the high reliability of the responses generated by this technique against possible temperature and voltage variations has been proved. These results show how this new technique improves the performance of the PUF in terms of identifiability, so it can be effectively used for device identification purposes.

1. Introduction

Nowadays, Internet of Things (IoT) allows the connection of a large number of devices and users leading to a massive exchange of sensitive and even confidential data in many cases [1,2,3]. Therefore, it is necessary to develop technological systems that are present in authentication applications, secure key generation and secure key storage. One of the systems that are increasingly being developed, compared to other cryptographic primitives, are physically unclonable functions (PUFs) [4,5,6]. PUFs use stochastic variations, inherently caused during their manufacture, to generate a device-specific response that is generally digitised in binary format. These systems are often referred to as the “digital fingerprint” of the device. PUFs are great candidates for use in cryptographic, key generation and encryption applications because they are inexpensive to manufacture, simple to implement, and generate a volatile response.

There are numerous PUF architectures depending on the needs and the application in which it is used [7,8]. One of the most widely reported in the literature is the ring oscillator PUF (RO-PUF), as it is simple to implement and does not require a symmetrical configuration to work on most FPGAs [9,10]. Multiple designs operate under the name of RO-PUFs, but all of them are based on measuring the random variations that occur in the frequencies of oscillating digital circuits. The source of this randomness is the manufacturing variations that affect the delay of the digital components, so when these components form a ring oscillator (RO), the oscillation frequencies are also affected.

To obtain the PUF response, usually, the oscillation frequencies of pairs of identical ROs are compared, so that a logical ‘1’ is assigned if the frequency of the first oscillator is higher, or a logical ‘0’ if the frequency is lower than the second oscillator of a pair. In this way, we obtain a binary response through comparison. This technique is called compensated measurement and is one of the most widely used techniques for obtaining a response in RO-PUF [11,12,13]. However, it must be noticed that this method has some limitations, as in most cases an error correction system is required to generate a sufficiently robust and reliable response, as described in [14,15]. It is also limited to obtaining a single bit in each comparison, so the area of the device must be large enough to implement numerous RO chains and generate a response with good enough identifiability.

In order to solve these problems and increase the robustness and security of the generated responses, our proposal is based on using the second-order compensated measurement so that we can obtain several bits from a single comparison in order to improve the identifiability of responses without the need to use correction systems. In this way, using the second-order compensated measurement technique, a greater amount of information can be obtained compared to the conventional compensated measurement technique. Compared to the conventional compensated measurement, the proposed technique allows for a smaller number of oscillators to generate PUF responses of the same length, reducing the PUF consumption in both area and power.

This paper is organised as follows. Section 2 shows related works. Section 3 describes the novel technique developed to obtain different-quality bits; the architecture used and how the RO chains have been implemented is given in Section 4, figures of merit used to check the reliability of the technique as well as the results obtained for the different bits are described in Section 5 and Section 6; finally, the conclusions can be found in Section 7.

2. Related Work

Typically, conventional RO-PUF responses are generated using the compensated measurement technique. However, if we compare this idea with the state of the art, we can find works such as [16], where the authors implement an RO-PUF as a random number generator and extract several bits by comparing the oscillation time of the ROs with the frequency of an RO when it overflows.

Furthermore, in [17], the authors obtain several bits by normalising the frequencies and post-processing the responses. This is different from the procedure that is carried out in [18], in which the authors employ a calibration circuit to select the optimal design parameters to generate multi-bit responses. Finally, a different approach is described in [19], in which the researchers obtain multi-bit responses with a method that is different from conventional compensated measurement and using two error-correcting blocks.

However, in addition to extracting several bits from a single comparison with a simple circuit, without the need to add any additional element to the RO chains or the use of error correction systems, this paper aims to generate multi-bit responses with a better identifiability than that of a conventional RO-PUF in order to reduce the area of the PUF without losing security or robustness.

3. Second-Order Compensated Measurement

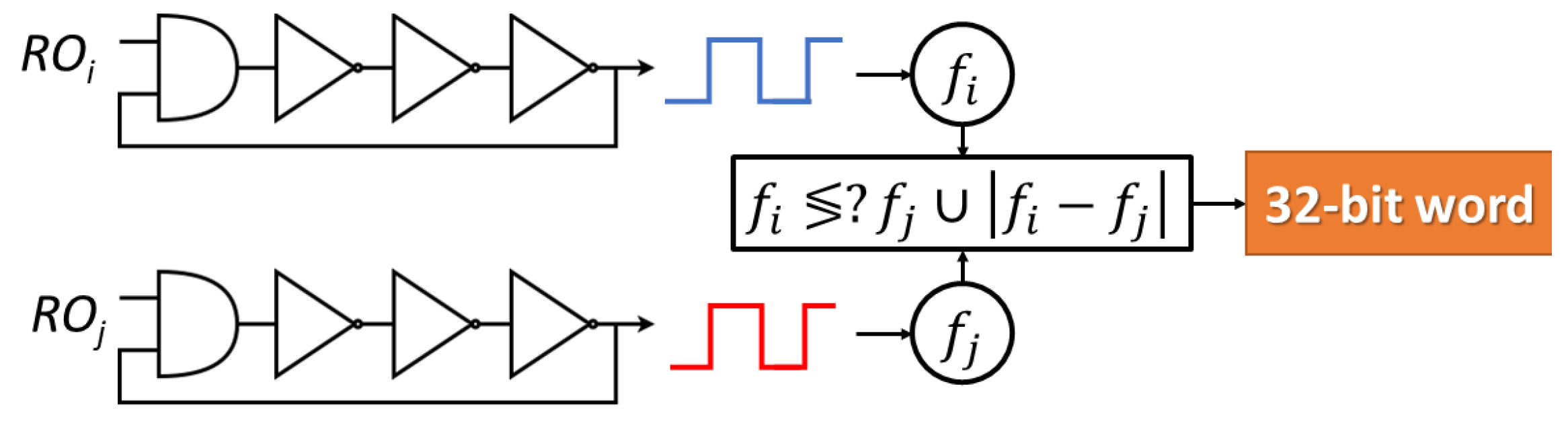
3.1. Description of the Proposal

The main objective of this paper is to use a second-order compensated measurement technique, with the purpose of obtaining several bits from a single comparison between ROs, so that we can generate a multi-bit response, thus improving the performance of the PUF in terms of identifiability per area. This concept was previously introduced in [20,21], where the possibility of obtaining multiple bits from a single comparison was preliminarily suggested. However, the uniqueness and reproducibility of the PUF were only analyzed qualitatively up to two-bits per pair of oscillators. In this paper, we have also tested the performance of the technique, and the possibility of obtaining multi-bit responses from a single comparison is profusely analyzed. In addition, the identifiability of the new responses and their reproducibility under varying environmental conditions has been compared with the responses generated using the conventional compensated measurement technique.

The proposed technique is based on the conventional compensated measurement, where pairs of RO are compared: if the frequency of the first oscillator is higher or lower than the frequency of the second, it is assigned a logical ‘1’ or a logical ‘0’, respectively. In this way, the sign (higher or lower) of the comparison is associated with a bit (1 or 0), which is called the sign bit. To obtain more bits from the comparison between pairs of ROs, we have proposed using the absolute value of the subtraction of the frequencies and then converting it to a binary number using the binary numeral system. This way, the difference between the frequencies is represented in a 32-bit signed integer, where the most significant bit is the sign bit and the rest of the bits correspond to the absolute value of the difference. The length is due to the fact that digitised frequencies in binary format are of the order of 20 bits, so the closest conventional format is a 32-bit word. Figure 1 shows a diagram of the proposed technique, where it is shown how, from a single comparison, we manage to extract several bits that are potential candidates to generate the response of a PUF that uses the compensated measure to generate its characteristic response.

In this work, we analyse the behaviour of the responses generated individually by each of the bits of the 32-bit string, so that we can compare the identifiability with that obtained through the sign bit (which would be obtained by using the conventional compensated measurement). If the results give us new quality bits, the aim of this work is to generate a response that uses the sign bit together with the new quality bits and study if there is an improvement in identifiability.

3.2. Target Application

The main application of a PUF is device identification. In a PUF-based device identification scheme, the PUF response generated by the device is compared to a previously stored response, and if a response with a hamming distance that is less or equal to that of the previous response is found, the device is identified correctly.

A balance must be found between the PUF response length and the security of an identification scheme based on a PUF using the proposed technique. The PUF response should not be too short, as this could reduce the security of the authentication system, but it should not be excessively long either, as this would significantly increase the authentication time. The advantage of the approach proposed in this paper is that it allows multiple bits to be extracted from a single pair of oscillators, reducing the resources required to obtain a PUF response of the same length as that achieved using first-order compensated measurement.

4. Implementation and Methodology

4.1. Experimental Setup

In order to test the performance of the second-order compensated measurement technique, we need to design a PUF architecture whose response is based on comparing physical measurements. In our case, we have chosen to design an array of ROs and implement them on FPGA. Specifically, we have implemented an RO-based PUF using the proposed second-order compensated measurement technique in 40 PYNQ-Z2 boards, each of which includes a System on Chip (SoC) Zynq-7000 manufactured by the company Xilinx (San Jose, CA, USA), which contains an Artix-7 FPGA integrated in 28 $\mathrm{n}$$\mathrm{m}$.

The frequencies of the oscillators were measured and extracted using the UART port of the FPGA. Then, the PUF responses were generated using software tools. The entire process was carried out under nominal conditions of internal temperature and internal power supply voltage of the FPGAs; that is, 37.5 °C and 1.022 V. These values are determined at external ambient temperature (25 °C) and for the default power supply voltage of the FPGAs (1.022 V). In this way, we are able to analyze, in the same measurement, which bits are more suitable for constructing the PUF response and which bits are less suitable.

4.2. PUF Response Generation

To provide accurate results for our technique, we have decided to use a well-understood, fairly simple design, such as that proposed by Suh and Devadas [22], where we have implemented an array formed by 200 identical ROs. Each RO is formed by a logic AND gate and three inverters, so that the output of the last inverter is connected to the input of the AND gate forming an RO. The RO-PUF design has been synthesised and implemented in Vivado 2019.1. To generate the response of the RO-PUFs, we count the oscillations of the ROs during a given clock oscillation time to obtain the characteristic frequency of the ROs. Figure 2 shows a diagram of two ROs whose frequencies are compared to obtain the 32-bit word. The AND gates are placed to select which RO we want to activate in each case and to control the oscillation time. The same structure of 200 ROs has been implemented on 40 different FPGAs in order to study uniqueness using the same bitstream.

To obtain the responses on an FPGA, a set of oscillator pairs is usually selected and their frequencies are compared. With this implementation, we will have a total of $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)$ possible pairs, but these pairs are not independent. If the frequency $f_1$ is higher than $f_2$ and this is higher than $f_3$, it is clear that $f_1$ is higher than $f_3$, and we have a dependency. To solve this problem and to obtain a valid response as a PUF, we use the topology reported in [23] which compares the frequencies using the 2-masking technique. With this technique, all ROs are compared without repetition: the first with the second, the third with the fourth, and so on, up to RO₁₉₉ with RO₂₀₀, thus obtaining ${\displaystyle \frac{n}{2}}$ bit responses. This process is replicated for each of the remaining 39 FPGAs and is repeated for 100 iterations in order to study the reproducibility.

Frequencies will be compared in pairs using the second-order compensated measurement, thus acquiring the different bit strings that will act as the PUF response, as explained in the previous section. With this technique, we will obtain responses that will depend on the bit that we select within the 32-bit string. On the one hand, if we select the sign bit, we will obtain the same response as that obtained using the conventional compensated measurement; this will help us to compare the quality of the responses of the other bits. On the other hand, if we select any of the other 31 bits to generate the response, we will obtain responses that may or may not be useful as PUFs. In case we obtain new quality bits that generate valid responses, we will juxtapose the strings generated by the sign bit and one or several of these new quality bits to generate a multi-bit response whose length will be $2n$, $3n$ or $4n$ bits.

5. Properties and Characteristic Parameters

5.1. Reproducibility, Uniqueness and Identifiability

For an entity to be considered as a PUF, it must fulfil a series of general properties that are defined by different parameters [24]. These factors will serve as figures of merit to evaluate the quality of the proposed technique to generate the response of a PUF. If a PUF is reproducible, it implies that an instance will always have the same, or very similar, response to the same challenge. Reproducibility is characterised using intra-distance, which is defined as a random variable describing the distance between two responses of the same instance to the same challenge. In most cases, intra-distance is measured using the Hamming distance (HD). If the array elements are binary digits, the HD is defined as follows:

$$\mathrm{HD}=\sum _{i=1}^n{x}_i\oplus x_i^{\prime }$$

(1)

where applying the XOR operator, ⊕, on the different positions of the two arrays $x_i,x_i^{\prime }$ we will obtain if both have the same number, or 1 if they are different.

A PUF presents the uniqueness property if, for the same challenge, the responses of different instances are very different. Uniqueness is characterised through the inter-distance, which is a random variable describing the distance between two responses of two different instances to the same challenge. Like intra-distance, inter-distance is measured using HD, and both intra-HD and inter-HD follow a binomial distribution around their mean value. In the case of intra-HD, the ideal mean value is 0%, and in the case of inter-HD, it is 50%.

When a PUF fulfils the properties of reproducibility and uniqueness, it also fulfils the property of identifiability. Through this attribute, it is possible to ensure, with high probability, that the instances of the PUF are unique and reproducible. The identifiability is defined by the intra-HD and inter-HD, so that the necessary condition for a PUF to fulfil this property is that the intra-HD is smaller than the inter-HD with high probability. Finally, it must be noticed that weak PUFs present a single challenge–response pair and resistance to modeling attacks does not have to be analysed.

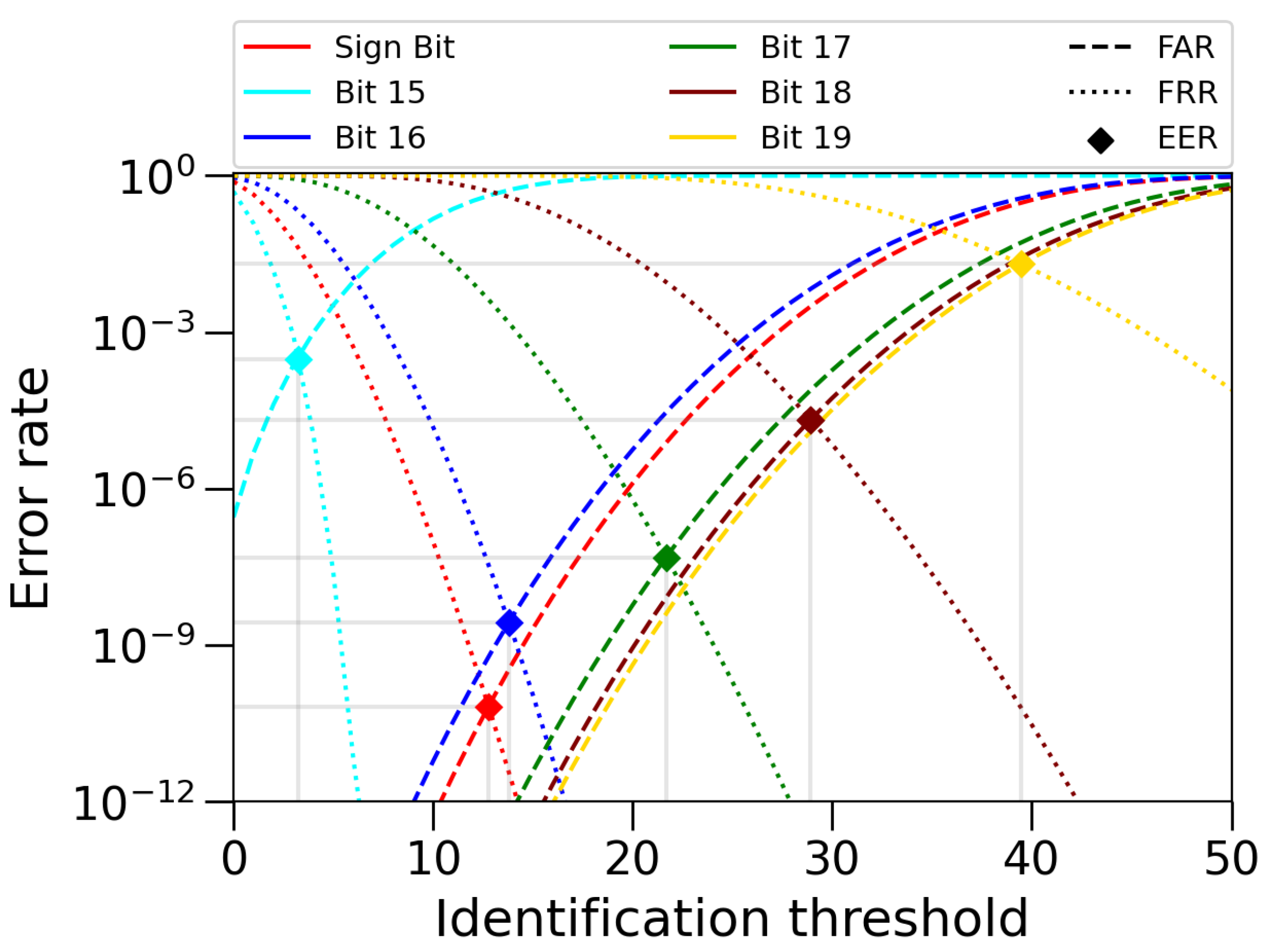
5.2. Identification Threshold: FAR and FRR

In order to assess the extent to which the response of a PUF can be used as an identifier, we must take into account the fuzzy nature of the PUF, in reference to the randomness of its response, as it is not uniformly distributed and is not perfectly reproducible when measured many times. The lack of clarity is reflected in intra-HD and inter-HD distributions where there is a region of overlap between the two distributions. To obtain a more precise measurement, we need to define an identification threshold ($t_{\mathrm{id}}$), so that if the distance between two responses is less than or equal to this threshold, the responses are considered to come from the same instance, while if the distance between responses is greater than the threshold, the responses are considered to come from different instances.

This threshold is not 100% reliable, especially if there is a large overlap between intra-HD and inter-HD, leading to four possible scenarios regarding identifiability [11]. In this paper, we will focus on two of them: false rejection rate (FRR) and false acceptance rate (FAR). The FRR is the probability that the intra-HD is greater than $t_{\mathrm{id}}$ and is equivalent to the complement of the cumulative distribution function of the intra-HD. The FAR is the probability that the inter-HD is less than or equal to $t_{\mathrm{id}}$. This is equivalent to the cumulative distribution function of the inter-HD. We can see the complete expressions for these parameters in (2) and (3), where $F_{\mathrm{bino}}$ is the cumulative binomial distribution and $f_{\mathrm{bino}}$ is the binomial distribution.

$$\begin{array}{cc}\hfill & \mathrm{FAR}\left(t\right)=F_{\mathrm{bino}}(t;n,p)=\sum _{i=0}^t{f}_{\mathrm{bino}}(t;n,p)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \mathrm{FRR}\left(t\right)=1-F_{\mathrm{bino}}(t;n,p)\hfill \end{array}$$

(3)

When we plot the FRR and FAR curves together, the intersection of the two curves indicates an equal error rate (EER). This EER is a good parameter for finding a compromise between security and robustness within a particular identification system. The expression is given as follows:

$$\mathrm{EER}=max\left\{\mathrm{FAR}\left(t_{\mathrm{ERR}}\right),\mathrm{FRR}\left(t_{\mathrm{ERR}}\right)\right\}$$

(4)

Finally, if we want to compare the performance of different systems in terms of identifiability, it is more appropriate to use the Receiver Operating Characteristic (ROC) curve, where the logarithm of the FRR is displayed against the logarithm of the FAR. In this work, we will use both terms to evaluate our results in a more complete way.

6. Results

Using the second-order compensated measurement, we obtain 32 bits: the sign bit, together with 31 new bits, with which we can generate words of ${\displaystyle \frac{n}{2}}$ bits (in this paper, we have used 200 RO, so we will obtain 100-bit words). First, we must check which of these bits are valid to generate the response of a PUF. To achieve this, the responses generated by each of the bits have been evaluated individually, so that depending on the bit we want to generate the response, the same bit is selected in all the 32-bit words obtained in each frequency comparison. In this way, the characteristic responses to each bit are obtained according to the bit’s position within the 32-bit array.

To evaluate the quality of the data obtained, we have compared the intra-HD and inter-HD with their ideal values: 0% for the intra-HD and 50% for the inter-HD.

Table 1. Intra-HD and inter-HD mean distributions of candidate bits. When several bits are analysed (e.g., bit 1 to 14), the standard deviations ($\sigma$) shown refer to the worst-case $\sigma$ of the referred interval of bits.

Property	Sign Bit	Bit 1 to 14	Bit 15	Bit 16	Bit 17	Bit 18	Bit 19	Bit 20 to 31
Intra-HD (%)	$1.474\pm 1.539$	0.0 to $0.096\pm 1.200$	$0.641\pm 1.254$	$2.587\pm 1.578$	$6.217\pm 2.174$	$13.474\pm 2.975$	$28.603\pm 4.397$	45.266 to $50.043\pm 6.103$
Inter-HD (%)	$42.015\pm 5.058$	0.0 to $4.928\pm 2.292$	$14.064\pm 3.359$	$41.664\pm 5.182$	$49.527\pm 5.075$	$50.107\pm 4.921$	$47.961\pm 5.174$	49.919 to $50.038\pm 5.360$

shows the data obtained, where bits 1 to 14 have low uniqueness and bits 20 to 31 have low reproducibility, and this generates a large overlap between the intra-HD and inter-HD distributions, which leads to low identifiability, and therefore these bits are not valid for generating the response of a PUF.

6.1. PUF Analysis Using Single Bits

FRR and FAR curves are shown in Figure 3, where the EER for each of the candidate bits can be seen. As expected, the sign bit used in the conventional compensated measurement gives us the lowest EER, indicating that only 1 error occurs every ${10}^{10}$ evaluations. It is noteworthy that for bits 16 and 17, we also obtain a result close to that obtained for the sign bit, with 1 error every ${10}^8$ evaluations. Good results are also obtained for bit 18, with 1 error every ${10}^5$ evaluations. However, bits 15 and 19 have a very low EER compared to the other bits and should therefore be discarded as possible bits in the generation of the PUF response.

ROC curves for all these bits are shown in Figure 4, which depicts the differences in identifiability and how sign bit, bit 16 and bit 17 have high identifiability. To conclude this first study, we have tested the reliability of identifiability for every quality bit by evaluating variations in mean intra-HD in two scenarios: changing the temperature between −10 °C and 100 °C at nominal internal voltage (Figure 5) and varying the FPGA internal voltage between 0.9 V and 1.1 V at nominal temperature (Figure 6).

In both cases, the mean intra-HD output at nominal FPGA temperature and internal voltage has been used as reference to study changes in the mean intra-HD, resulting in the characteristic V-shape curves. As we can see in Figure 5, there are slight variations in the mean intra-HD for the sign bit and bit 16 (less than 10%). In the case of bit 17, there is a larger deviation in the most extreme FPGA temperature values.

Finally, for bit 18, there is a larger variation of more than 15% as soon as we move more than 20 degrees away from the nominal value. On the other hand, when we study the internal voltage variations, as shown in Figure 6, there is a larger variation in the average intra-HD for all bits. If we move more than 5% from the nominal voltage, the average intra-HD values suffer a larger deviation. For the sign bit, there is no deviation greater than 10% over the whole range studied. For bit 16, there is also some stability, with a maximum deviation of 25%. However, for bit 17 and bit 18, we find deviations of up to 45% and 50%, respectively.

6.2. PUF Analysis Using the Sign Bit Together with Other Quality Bits

These results support the possibility of using these three new bits to generate the response of a PUF and will allow us to generate a joint response with the sign bit and one, two, or three of these bits. If we join the word generated by the sign bit and one of the new bits, we will generate 200-bit responses. To check the quality of these, we evaluate them based on the same nominal conditions as those used previously. Figure 7 shows the ROC curves of the joint response of the sign bit with each of the new bits. As we can see, in each of the cases, we improve the identifiability if we compare it with that generated individually by each of the bits. Moreover, the joint response of the sign bit with bit 16 and the joint response of the sign bit with bit 17 improves the identifiability obtained with the sign bit by several orders of magnitude, with 1 error for each ${10}^{17}$ evaluations.

We have also studied the identifiability of the responses generated with the sign bit and two bits (300-bit words) and responses generated with the sign bit and the three new bits (400-bit words). It should be noted that increasing the size of the responses implies a considerable increase in computation time (defined as the time from obtaining all frequencies until the PUF response is obtained). In Figure 7 we can see that there is a slight improvement in the identifiability compared to that obtained with two bits but the jump is not as large as before. Using the sign bit together with bit 16 and bit 17, we obtain the best identifiability with 1 error every ${10}^{19}$ repetitions; however, using the sign bit together with bit 16 and bit 18, the identifiability obtained is similar to that obtained with two bits. It is worth noting that the identifiability worsens if we use the sign bit together with bits 17 and 18.

Furthermore, if we use the sign bit together with the three new bits, the identifiability is lower than in the best case of three bits, with 1 error every ${10}^{18}$ repetitions. These events may be due to the fact that there may be a correlation between adjacent bits that causes worse uniqueness and reproducibility. Results show that increasing the size of the response does not imply a proportional improvement in identifiability and that, in the case studied, the best option for generating the PUF response in terms of identifiability and computation time is to use the sign bit together with bit 16.

6.3. Entropy Analysis

Below, we have conducted an entropy analysis of the PUF responses. We have evaluated the entropy of three constructed PUFs as follows: (1) using only the sign bit, (2) using only bit 17, and (3) using the sign bit together with bit 17. To achieve this, we have applied the approximate entropy test from NIST SP 800-22 [25]. The block size m of the test has been selected considering the test recommendations shown in [25].

In

Table 2. Approximate entropy NIST test results for three PUFs constructed using (1) only the sign bit, (2) only bit 17, and (3) the sign bit together with bit 17; for two sizes of blocks: $m=1$ and $m=2$.

Selected Bit	$\mathit{m}=1$			$\mathit{m}=2$
	p-Value	Proportion	Pass?	p-Value	Proportion	Pass?
Sign Bit	0.002	38/40	Yes	0.001	39/40	Yes
Bit 17	0.078	40/40	Yes	0.106	40/40	Yes
Sign Bit + 17	0.312	40/40	Yes	0.187	40/40	Yes

, the obtained p-values are shown along with the number of sequences out of a total of 40 sequences (number of FPGAs) that pass the test. In this case, since we have 40 sequences, at least 37/40 sequences must pass the test in order for it to be determined that there are no entropy issues, assuming a significance level of $\alpha =0.01$. However, it is important to note that this $\alpha$ is not the p-value returned by the NIST test shown in the table, as the shown value corresponds to the p-value of the p-values, and sequences are considered to pass the test if this value is equal to or greater than 0.0001. As observed, using the second-order compensated measurement technique with responses constructed using Bit 17 and Sign Bit + Bit 17, the PUF responses successfully pass the NIST approximate entropy test.

6.4. Voltage and Temperature Variations

To complete our study, we have evaluated the possible variations in identifiability associated with temperature and internal voltage variations together, for the response created by the juxtaposition of the sign bit and bit 16 (see Figure 8). The results show an average variation of 2% compared to the average intra-HD obtained at nominal internal temperature and internally, where the worst case occurs at $1.1 \mathrm{V}$ and 80 °C with a deviation of 5%. The high stability for the whole temperature range at $1 \mathrm{V}$ is remarkable.

7. Conclusions

This paper shows how it is possible to obtain new quality bits, in addition to the sign bit, that allow us to generate a valid response for a PUF. Moreover, the results obtained for these bits allow us to generate multi-bit responses with a single comparison. We greatly improve the identifiability using two bits obtained with the second-order compensated measurement versus the identifiability using the sign bit obtained through the conventional compensated measurement.

Specifically, the response of the studied RO-PUF improves its EER by approximately 70%, 90%, and 80% when using two, three, and four bits, respectively; and the best compromise between identifiability and computation time is achieved with a response generated by two bits: the sign bit and the new bit with the lowest EER. In particular, we have shown that by combining the sign bit with one of the bits extracted using the proposed technique, an EER∼${10}^{-16}$ can be achieved, and that by using one more bit, three additional orders of magnitude can be reduced to EER∼${10}^{-19}$. Since the main application of a PUF is device identification, this result is particularly interesting, as very high identifiability values can be achieved with minimal area.

These results can be seen in two complementary ways: with the same resources of a PUF, we can improve its identifiability, or we can reduce the area of the PUF without losing identifiability. All results are obtained with a simple RO-PUF design without using any external circuit or bit error corrections.

Finally, it has been proven that the results obtained, especially for the sign bit and central bit 16 of a 32-bit string, are robust to temperature and voltage variations, showing high reliability in the use of this new compensated measurement technique.