Making Informed Choices: AHP and SAW for Optimal Formwork System Selection

Abstract

The selection of an appropriate formwork system represents a critical decision in the planning of reinforced concrete multi-story buildings. While this decision has traditionally been deferred to the construction phase, increasing evidence of time and cost overruns in construction projects has highlighted the necessity of addressing it during earlier stages, particularly in design and planning. Early identification and selection of the optimal formwork system enhances the likelihood of achieving significant improvements in both time efficiency and cost effectiveness. To facilitate this process, a decision-support framework based on the Analytic Hierarchy Process (AHP) and Simple Additive Weighting (SAW) methods has been developed. This framework provides decision-makers with a structured and systematic approach for evaluating alternatives and selecting the most suitable formwork system for a given project. By offering an analytical foundation for the decision-making process, the framework assists designers and engineers in mitigating risks associated with delays and potential standstills during construction. The findings indicate that the proposed decision-support framework ensures both clarity and consistency in decision-making outcomes, irrespective of the analytical method employed. Consequently, it contributes to more robust planning and execution of construction projects.

1. Introduction

In the construction industry, especially in constructing reinforced concrete multi-story buildings, the cast-in-situ concrete is the most commonly used material as it offers a lot of advantages when compared to other materials [1], such as flexibility, ease of handling, and cost-effective solutions.

The aforementioned is no different in Croatia, where concrete and reinforced concrete (RC) are considered as “the material” [2,3,4,5]. As RC construction consists of three main elements, formwork, rebar, and cast-in-situ concrete [6], it is important to consider both material and processes in pre-construction (initiation, planning, design, and procurement) and construction stages as the key drivers to sustainable usage of the building and post-construction stages. Herein, the focus is on formwork selection, as the formwork is a temporary support for the construction of a concrete structure, which is mainly used to shape and maintain fresh concrete until it reaches adequate strength. Whether it is a traditional or modern system, the final geometry and surface quality of the completed concrete structure are highly dependent on the formwork system (FWS) employed in the construction [7,8]. Thus, the selection criteria and the basic requirements of the formwork system should be thoroughly considered before the commencement of construction [7]. In public investment projects, designers usually highlight the formwork system according to the general design of an RC building, yet shifting the decision to the selected contractor to use the best of his abilities often translates to “what he has.” In such cases, building designs often have a number of details that cannot be constructed by a standard, out-of-the-catalog formwork system, which ultimately slows down the constructor in their work and causes delays.

Therefore, focusing on the future RC building and making informed choices during pre-construction stages is of utmost importance and can significantly influence the later stages, resulting in being within the planned time and budget. Unfortunately, many construction projects result in time and cost overruns [9,10,11,12]. Reasons for such are many, but can be summed up to poor planning, design, and/or execution [13]. As there are many decisions that need to be made in avoiding those overruns, the selection of an appropriate formwork system represents a critical decision in the planning of reinforced concrete multi-story buildings.

While this decision has traditionally been deferred to the construction phase, increasing evidence of time and cost overruns in construction projects has highlighted the necessity of addressing it during earlier stages, particularly in design and planning. Early identification and selection of the optimal FWS enhances the likelihood of achieving significant improvements in both time efficiency and cost effectiveness.

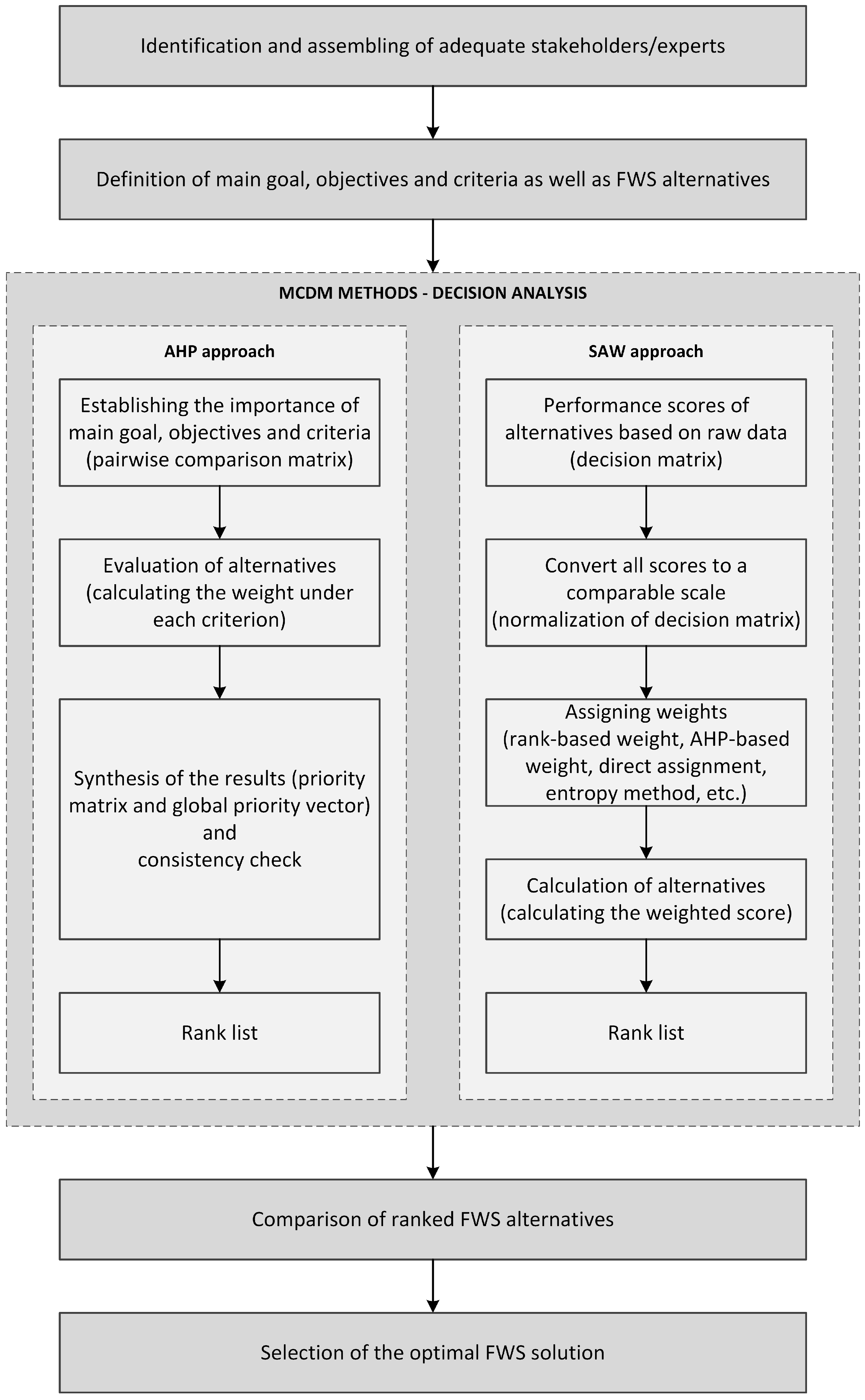
To do so, one of the ways the more clarity and consistency throughout the selection process is the use of adequate multi-criteria decision-making (MCDM) methods such as AHP [14,15,16], SAW [17,18], TOPSIS [19,20], PROMETHEE [21,22,23], VIKOR [24,25], ELECTRE [26], and COPRAS [27]. These methods are based on an analytical approach, whether they are used in single or group decision-making surroundings [28,29,30,31,32,33], and have been extensively explored and applied in many real-world problems. However, comprehending the decision-making process and selecting a satisfactory choice from a large set of alternatives characterized by multiple conflicting attributes imposes a significant cognitive burden on decision-makers.

At first, the optimal FWS selection may be seen as a non-complex problem with meaningless or low impact to construction projects, but knowing that formwork values around 40% to 60% of the whole RC construction project, and in some cases even more [1,4,7], this decision should not be taken lightly. As the choice should be made by an informed decision-maker, in such a demanding multi-criteria and multi-stakeholder environment that is a construction project, making an informed choice of optimal FWS selection is of utmost importance. As the optimal FWS selection problem can be seen as a single or group decision-making problem, the important is to have a such decision-support framework that offers not just a predefined set of criteria to use in making decision, or predefined method to use, but to offer the decision-maker the possibility of building up a set of criteria that will give the best possible result for their RC building problem.

Predominantly, the various authors focus their efforts either to define a finite number of criteria for particular selection or make tremendous efforts in developing new methods to make an appropriate decision. Yet, some focus their efforts on aligning construction processes and the decision process. Antoniou and Tsisoulpa [13] indirectly refer to poor FWS design as one of the identified design errors related to the causes of claims during the construction phase. Their insights show that the driving factors should be made prior to the construction phase. Therefore, to make an optimal FWS selection, the informed choice should be made during the planning and design stage. Such should give advantages in having fewer overruns as the driving decision of FWS selection will have enough checking points to pass, i.e., after each phase, well before construction.

To cope with such a problem, a lot of researchers approach the problem in different ways. Some focused on the parts of the problem, such as the decisive criteria in formwork selection problem [34], or on more broader criteria for FWS, focusing the use of different analytical approaches [35,36,37], while others focused on the particularities of formwork material [38,39], general construction topics and processes [40,41,42,43,44,45,46,47,48], or MCDM methods [40,43,47,48,49,50,51,52,53,54,55,56,57,58,59] that can be used to solve different decision-making problems, such as selecting, sorting, and choosing, that are present in construction project management.

In an FWS selection problem, AHP and SAW methods and their derivatives are predominantly used. The AHP is one of the most world-wide-known outranking methods, with strict mathematical rules seeking consistency [14,15,16], even proved its usability outside consistency [55]. The SAW method lacks stability in such [53], offering more variety in its application. Within similar research, the focus is on setting numerous criteria [35,36,37], which often does more harm than good. Nonetheless, such insights are valuable and well-developed for academic purposes but often lack practical utilization in the professional sector.

Most of the data in a MCDM problem are unstable and changeable, and thus, sensitivity analysis can effectively contribute to making proper decisions. Therefore, Alinezhad et al. [52] offered a new method for sensitivity analysis within SAW so that by changing one element of the decision-making matrix, the changes in the results of a decision-making problem can be determined. On the other hand, Hopfe et al. [51] offer different approaches to normalizing the results of SAW. Both approaches provide more precision to SAW than is usually defined (see Section 2.3). To support the previous statement, Zavadskas et al. [53] concluded that only significant attributes relative to the other attributes have an impact on the results.

Despite the aforementioned, AHP still remained the most used method in such industries [28]. Additionally, Sun et al. [57] even developed a visual analytics approach that integrates visual representations of alternatives with the decision-making analysis process. Such tends to assist decision-makers in gaining a better understanding of the decision-making process and helping them visually identify the best choice. Overall, developing a stable decision-support framework that is transparent and open to adopting changes is proven to be a more efficient and effective way of making informed decisions [41,42,43,48,60].

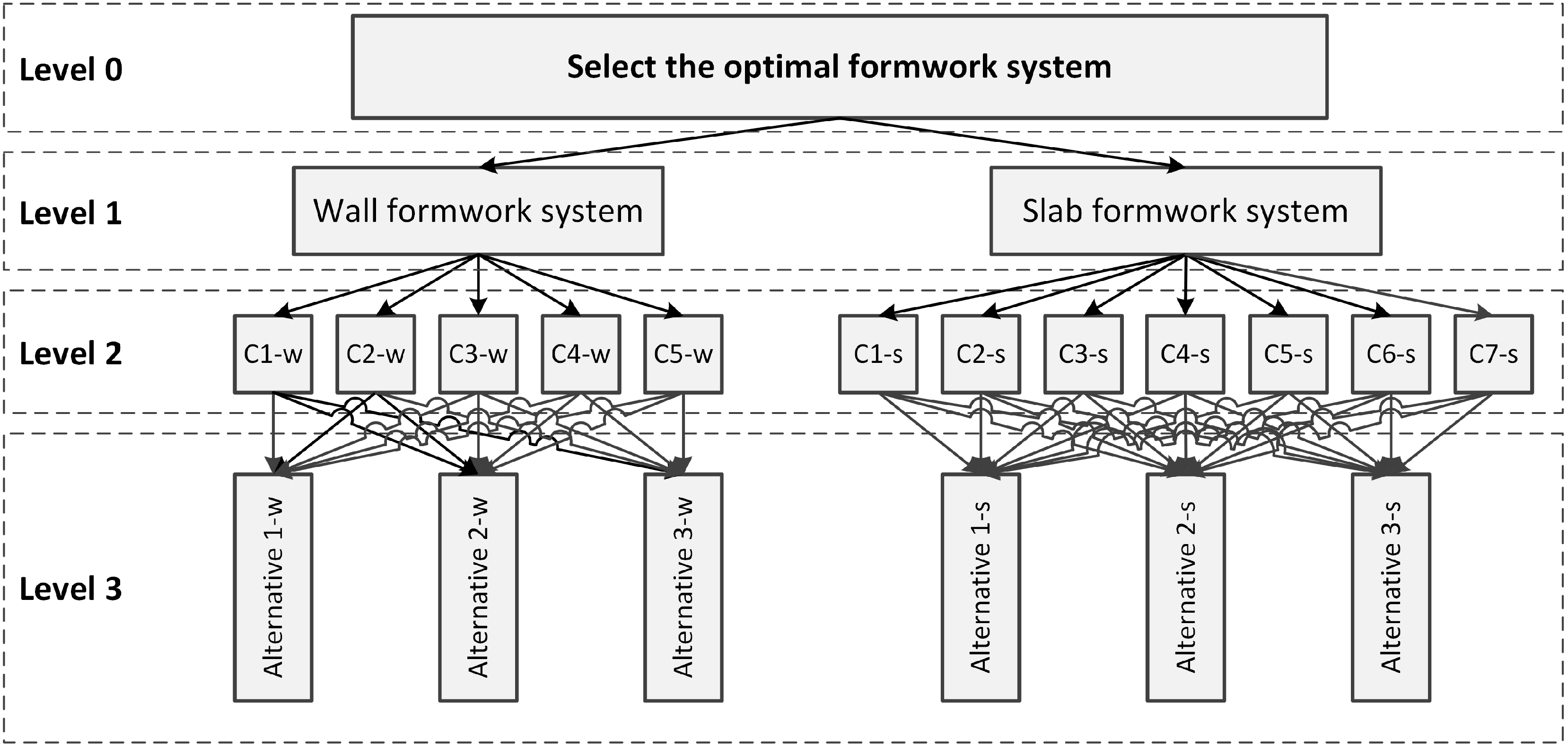
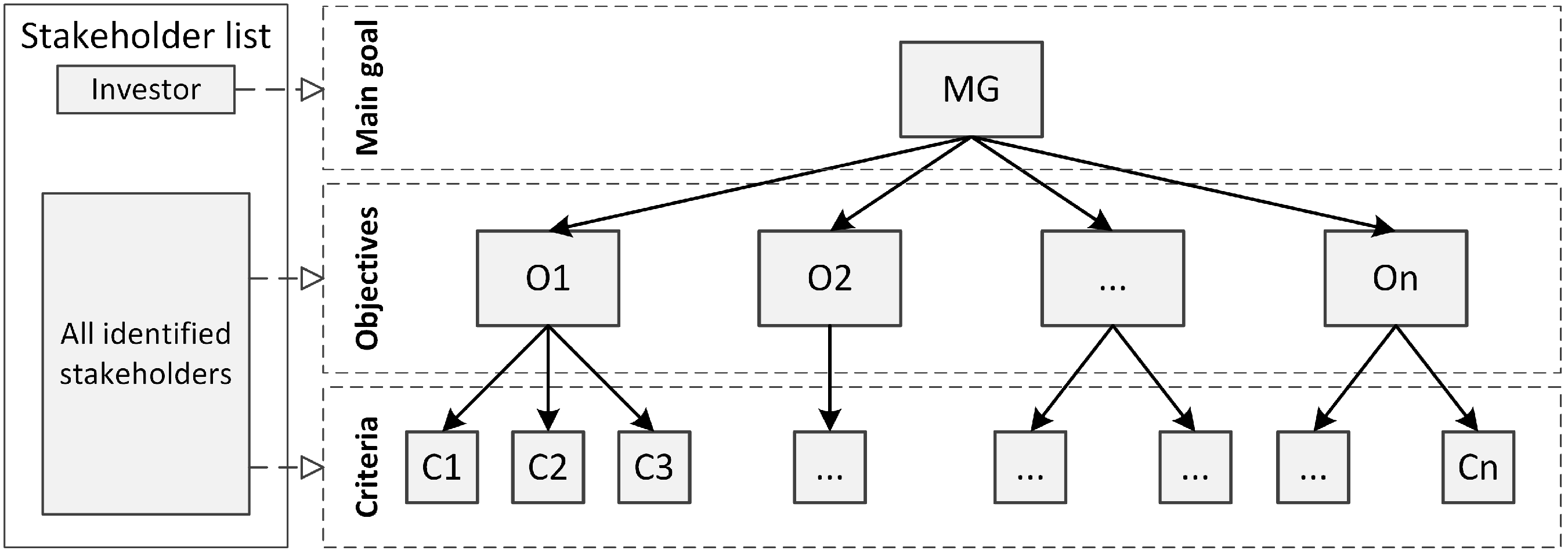
Therefore, the main goal is to develop a decision-support framework based on the Analytic Hierarchy Process (AHP) and Simple Additive Weighting (SAW) methods that will provide decision-makers with a structured and systematic approach for evaluating alternatives and selecting the most suitable formwork system for a given project. The focus is on the following: (1) creating an appropriate framework to build up a hierarchical goal structure that can be applied to any construction project, and (2) showing an analytical approach to decision-making by AHP and SAW methods that will result in a more appropriate approach to use by experts.

By offering an analytical foundation for the decision-making process, ensuring both clarity and consistency in decision-making outcomes, the framework tends to assist designers and engineers during early stages in mitigating risks associated with delays and potential standstills during construction. As such, it is expected that the developed framework will contribute to robust planning and execution of construction projects.

2. Materials and Methods

To ensure that the FWS selection can be completed in the early stages of the construction project by designers and engineers, a decision-support framework for selecting the optimal formwork system has been developed. This includes testing on a real case study, a reinforced concrete multi-story building, while the multi-stakeholder analysis was tested by involving a panel of civil engineering experts throughout the workshops as part of the hierarchical goal structure procedure (shown in Section 2 and Section 3.1). These experts were used in building the hierarchical goal structure for the optimal FWS selection (shown in Section 2.1).

2.1. Framework Development

The proposed decision-support framework for selecting the optimal formwork system consists of several processes, as shown in Figure 1. To achieve the best possible outcome, it is important to focus on identifying and assembling the adequate stakeholders/experts to define a hierarchical goal structure. The pivotal part of this research is on decision analysis and the multi-criteria decision methods (MCDMs), as well as proposed analytical tools for such decisions—Analytical Hierarchy Process (AHP) and Simple Additive Weighting (SAW). As the analysis is finished, it is important to compare the results obtained prior to selecting the optimal solution and making a decision. The proposed framework offers redundancy in selecting the MCDM method by conducting the analysis with one or both, showing the similarities in results. This allows the decision-maker to select either one of the analytical methods to use, and to be sure of the achieved result and that they made an informed choice. With the aforementioned, the decision-support framework for selecting the optimal formwork system is completed.

As previously mentioned, building the hierarchical goal structure (HGS) is of utmost importance. Here, based on investors, i.e., clients, the main goal (MG) or decision problem “to select the optimal FWS,” is set. The systematic literature review was conducted to showcase the most commonly used criteria for such or similar problems in civil engineering, to offer starting boundaries of the problem. To ensure the high quality and novelty of the analyzed criteria knowledge, only papers published in scientific journals between January 2000 and June 2025 were considered. This resulted in a pool of criteria that were further analyzed and discussed by other stakeholders, i.e., experts, during workshops to develop a particular HGS for the MG. As workshops were used as a tool for building the hierarchical goal structure, this general knowledge of criteria can potentially help during workshop discussions to reach a compromise as best they could (see Section 3). As they are focused on achieving a compromise overview of both criteria and their weights, the decision analysis with MCDM methods can be performed, as there is a single decision-maker.

The novelty of the proposed framework lies in its clarity and consistency in decision-making outcomes, as well as its robustness and changes in the decision-making process. This is especially important for using it on different construction projects by different stakeholders and experts, so they can express their attitudes and their demands. One of the pivotal strengths of the approach is that it provides stakeholders to express their attitudes in a clear way (Figure 2) and it is based on previous research [40,45].

Once the HGS is made, it is necessary to determine the importance, i.e., weights, of all objectives and criteria. Such was performed during the decision analysis by means of AHP and SAW separately (shown in Section 3). The same stakeholders/experts were given the opportunity to express their point of view by employing the AHP method (Section 2.2) and the SAW method (Section 2.3). To keep analysis simple and focus on the quality of the solution by employing both methods, both analytical methods used a compromise overview as they reached an agreement, i.e., consensus during the definition of HGS.

Once the weights have been assigned, the rank list was developed by following the steps of each method separately. This offers the possibility to track all aspects of the analyzed problem and offer the most informative choice to make at the end of the process. The key steps are shown below for each method with key mathematical development, while the results are discussed in detail in Section 3.

2.2. AHP Method

The Analytical Hierarchy Process (AHP) requires the decision-maker to perform pairwise comparisons of the criteria using Saaty’s scale [12,13,14]. These judgments are utilized to generate the ranks of listed alternatives in the following three steps.

Step 1: Constructing the pairwise comparison matrix A and computing the priority vector w

For n criteria $C_1, C_2, \dots , C_n$, let $\mathrm{A}=\left[a_{ij}\right]$, $a_{ij}=$ relative importance of the criterion $C_i$ over $C_j$. Matrix A, for all $i,j\in \{1,\dots ,n\}$ has the following properties: $a_{ij}>0, a_{ii}=1, a_{ji}={\displaystyle \frac{1}{a_{ij}}}, \mathrm{i}\ne j$, making it reciprocal and positive.

Next, let $\mathrm{w}={\left[w_1,w_2,\dots ,w_n\right]}^T$, $w_i=$ relative weight of the criterion $C_i, \mathrm{i}=1, \dots , \mathrm{n}$, be the priority vector, which satisfies the eigenvalue problem:

$$\mathrm{A}\mathrm{w}={\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{w},$$

(1)

where ${\mathsf{\lambda }}_{max}$ is the maximum eigenvalue of matrix A. One way of deriving w is the eigenvalue power iteration calculation, which is executed through a multi-step process, as detailed below.

Let $w^{\left(0\right)}$ be an initial positive vector. Vectors $w^{\left(k+1\right)}$ are computed as follows:

$$w^{\left(k+1\right)}=A{w}^{\left(k\right)},$$

(2)

and normalized through dividing it by the sum of its components. The process is repeated until the following condition is met for an arbitrarily small $\mathsf{ϵ}>0$:

$$\left|\left|w^{\left(k+1\right)}-w^{\left(k\right)}\right|\right|<\mathsf{ϵ} .$$

(3)

Finally, ${\mathsf{\lambda }}_{max}$ is derived using the following equation:

$${\mathsf{\lambda }}_{max}={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{a}_{ij}{w}_j.$$

(4)

Step 2: Consistency check

The consistency index (CI) and consistency ratio (CR) are calculated as follows:

$$CI={\displaystyle \frac{{\mathsf{\lambda }}_{max}-n}{n-1}}$$

(5)

$$CR={\displaystyle \frac{CI}{RI}}$$

(6)

where RI is the random index which depends on n [13].

Saaty’s rule [12,13,14] states that if $CI\le 0.10$ the inconsistency is accurate, and if $CI>0.10$ pairwise judgments should be revised.

Step 3: Synthesis and results

Let $P=\left[p_{ij}\right]$, $p_{ij}=$ priority of alternative i under criterion j is the priority matrix. The global priority vector $v={\left[v_1,\dots ,\backslash v_m\right]}^T$, $v_i=$ the final score of the alternative i is obtained as follows:

$$v_i={\displaystyle \sum _{k=1}^n}{p}_{ik}{w}_k.$$

(7)

At the end, the alternative with the highest score $v_i$ is the best, i.e., optimal, option.

2.3. SAW Method

Simple Additive Weighting (SAW) method [15,16] ranks the predefined alternatives in the following three steps.

Step 1: Constructing and normalizing the decision matrix

Let $D=\left[x_{ij}\right]$, $x_{ij}=$ the performance score of the alternative i on criterion j, be the decision matrix. Let $R=\left[r_{ij}\right]$ be a matrix obtained from the matrix D by normalizing it. Therefore, we should look into ascending, i.e., benefit-type (Equation (8)) and descending, i.e., cost-type (Equation (9)) criteria according to the following:

$$r_{ij}={\displaystyle \frac{x_{ij}-min{D}_j}{max{D}_j-min{D}_j}},$$

(8)

$$r_{ij}={\displaystyle \frac{max{D}_j-x_{ij}}{max{D}_j-min{D}_j}}.$$

(9)

where $max{D}_j,min{D}_j$ represent the maximum and minimum value in the j-th column of the matrix D, respectively. If $max{D}_j=min{D}_j$, all the performance scores for criterion j are equal; thus, it should be removed.

Step 2: Assigning weights to criteria

Weight $w_j>0$ is assigned to each criterion j, so the sum of all weights is equal to one. The SAW method does not enforce a specific method for this step (e.g., rank-based weight, AHP-based weight, direct assignment, entropy method), and, among the evaluated approaches, the rank-based weight assignment method demonstrated the highest effectiveness in the context of this study. The core idea is to rank the criteria from most to least important. The weight of criterion j $w_j$ with the rank $r_j$ is obtained using the equation:

$$w_j={\displaystyle \frac{n-r_j+1}{{\sum }_{k=1}^n\left(n-r_k+1\right)}}.$$

(10)

This study adopts rank-based weights in this step because both approaches have been conducted throughout the framework to select the optimal FWS. The differences between the approaches are given in Section 3.2.3. If the AHP-based weight were selected in this step, the approaches would yield the same values in rankings.

Step 3: Ranking the alternatives

For each alternative i, the total weighted score $S_i$ is computed as follows:

$$S_i=\sum _{j=1}^n{w}_j{r}_{ij}$$

(11)

Finally, the alternative with the highest $S_i$ is optimal under the given criteria.

3. Results and Discussion

Once the stakeholders/experts are identified and assembled, and they develop a compromise for the HGS, the MCDM methods are employed. For the purposes of this study, the proposed framework is tested on a case study of a four-story-high reinforced concrete public building. The central issue is to show the possibilities offered by the proposed concept, as well as to show which method gives more clarity to the decision-maker. For such purposes, alternatives were used from the PERI catalog [61] as a well-known, accepted, and used FWS in the construction industry. Additionally, the problem is solved for wall FWS (three alternatives, i.e., DUO, DOMINO, MAXIMO) as well as slab FWS (three alternatives, i.e., DUO, SKYDECK, MULTIFLEX) simultaneously, to show that the framework allows further complexity throughout the process.

At the same time, the procedure for creating HGS is also presented, which is aligned with the project “iron triangle” success imperatives. Additionally, this allows the decision-maker the opportunity to create HGS to the best needs of their project, its specificities, or successful outcomes.

3.1. A Multicriterial Approach for Optimal Formwork System Selection

To develop the HGS procedure for this particular problem, the procedure starts with the investor defining the main goal (on Level 0) and a panel of stakeholders/experts to develop a structure to the last criterion. In this case, the problem is separated into two parts, sub-goals, on Level 1: selection of wall formwork system and selection of slab formwork system. Both sub-goals have particular criteria (Level 2) and particular alternatives (Level 3). During the workshop, they came to a compromise on HGS (Figure 3), that to select the optimal wall FWS, one needs to use five criteria, and to select the optimal slab FWS, one needs to use seven criteria. The list of all criteria with their labels, short descriptions, evaluation techniques, and preferences is presented in

Table 1. Criteria with short description, evaluation technique, and preference.

Criteria Label	Criteria Name	Short Description of Criteria and Evaluation Technique	Min/Max
C1-w	Assembly	This criterion includes standard to assembling particular FWS according to its normative working value. Expressed in h/m2	Min
C2-w	Disassembly	This criterion includes standard to disassembling particular FWS according to its normative working value. Expressed in h/m2	Min
C3-w	Load-carrying capacity	This criterion takes into account load-carrying capacity of particular DWS according to its normative value. Expressed in kN/m2	Max
C4-w	Repeating use (cycles)	This criterion takes into account the number of repeated usages of particular FWS before the need for maintenance or repair. Expressed in numbers	Max
C5-w	Number of needed workers	The number of workers required to do the FWS according to normative values. Expressed in numbers	Min
C1-s	Assembly	This criterion includes standard to assembling particular FWS according to its normative working value. Expressed in h/m2	Min
C2-s	Disassembly	This criterion includes standard to disassembling particular FWS according to its normative working value. Expressed in h/m2	Min
C3-s	Closing of residual areas	This criterion includes the percentage of remaining residual area that is not covered by FWS and demands additional traditional formwork. Expressed in numbers	Min
C4-s	Repeating use (cycles)	This criterion takes into account the number of repeated usages of particular FWS before the need for maintenance or repair. Expressed in numbers	Max
C5-s	Number of needed workers	The number of workers required to do the FWS according to normative values. Expressed in numbers	Min
C6-s	Slab area per slab props	A larger area per support prop under the slab minimizes the number of FWS props. Expressed in m2/props	Max
C7-s	Early disassembly	The number of hours (days) expressing possibility of early disassembly of particular FWS. Expressed in numbers	Min

.

As the main goal and sub-goals have been set by the investor, the panel of experts was used to define particular criteria. As the whole HGS procedure is an iterative process, the workshops were the place for stakeholders/experts to discuss and find the compromise criteria and their weights. This procedure enables having different panels on different RC construction projects and to develop a particular set of the most appropriate criteria for their particular building problem and not use the general ones.

In this particular case, eight experts were selected among project managers and civil engineers with at least 15 years of experience in the construction industry on similar projects. Although the proposed decision-support framework is suited for single decision-making, in interaction with the HGS procedure, it also supports group decision-making. Due to the fact that the compromise should be achieved during workshops, the whole decision analysis works as a single decision-making problem. Therefore, during the first iteration, the workshop’s goal is to reach consensus on a particular set of criteria, while the second iteration serves as a place to reach a compromise weight of those criteria.

Since the HGS procedure is an iterative process that ends in compromise, the decision-maker can be sure that if the procedure is followed, all stakeholders’/experts’ attitudes are embedded in the criteria, objectives, and the main goal. This enables understanding that the process can be repeated anytime, anywhere, for any problem, and gives transparency to the process.

Here, it is important to emphasize that due to the differences in construction projects, the proposed HGS procedure offers the possibility to update this list of criteria, and their data regarding particular RC building projects, or to create a completely new list of criteria that provides the best possible result in terms of projects’ scope, time, cost, and quality.

Once the HGS is made, it is necessary to determine its importance in terms of weights. Such is performed in the following sections by means of AHP and SAW methods. Although the proposed framework can result in adequate selection by a single MCDM method, both methods are used to show the similarity of results in spite of differences in their analytical approach. This enables decision-makers to have additional insights and make a more informed choice, not only to solve a particular problem but also to have an adequate tool to use in that process.

3.2. Comparison of AHP and SAW Results

3.2.1. Results of the AHP Method

As shown in Figure 1, the first step is to establish the importance of the main goal, objectives, and criteria. This is performed through a pairwise comparison matrix. As stakeholders/experts came to a compromise on the criteria weight, the following matrix for selecting the optimal wall FWS (

Table 2. Decision matrix for FWS’s wall criteria.

	C1-w	C2-w	C3-w	C4-w	C5-w
C1-w	1	1	2	3	3
C2-w		1	1/2	3	1/2
C3-w			1	3	1
C4-w				1	1/3
C5-w					1

) and slab FWS (

Table 3. Decision matrix for FWS’s slab criteria.

	C1-s	C2-s	C3-s	C4-s	C5-s	C6-s	C7-s
C1-s	1	3	2	5	3	1	3
C2-s		1	2	3	3	1/2	3
C3-s			1	3	1/2	1/3	1
C4-s				1	1/2	1/3	1/5
C5-s					1	1/2	1/3
C6-s						1	1
C7-s							1

) gives insight into the criteria performance.

This resulted in the following weights for each criterion: C1-w 33,2%, C2-w 17,5%, C3-w 21,6%, C4-w 7,2%, and C5-w 20,5%.

This resulted in the following weights for each criterion: C1-s 27%, C2-s 17,6%, C3-s 9%, C4-s 4,2%, C5-s 8,5%, C6-s 20%, and C7-s 13.7%. After applying Equations (1)–(3), the final decision matrix is created for the FWS slab (

Table 4. Decision matrix for FWS’s wall alternatives with criteria.

	C1-w	C2-w	C3-w	C4-w	C5-w
DUO	0.0348	0.0183	0.0432	0.0522	0.0514
DOMINO	0.0858	0.0452	0.0432	0.0058	0.0514
MAXIMO	0.2115	0.1113	0.1296	0.0135	0.1028

) and FWS wall (

Table 5. Decision matrix for FWS’s slab alternatives with criteria.

	C1-s	C2-s	C3-s	C4-s	C5-s	C6-s	C7-s
DUO	0.0308	0.0200	0.0673	0.0044	0.0203	0.0287	0.0353
SKYDECK	0.1297	0.0845	0.0108	0.0109	0.0465	0.1432	0.0871
MULTIFEX	0.1094	0.0713	0.0120	0.0269	0.0177	0.0287	0.0143

).

The weighting of criteria, as well as alternative ranking, needs to be checked for consistency (Equations (4)–(6)). In this example, the consistency ratio is well below the targeted 0,10; for FWS wall selection (Table 4) is 0.0582, while for FWS slab selection (Table 5) is 0.0601. As is given desired certainty to the decision-maker (CR < 0,10), the process can continue with synthesis and results of the AHP application. Otherwise, pairwise judgements should be revised until the analysis results are in the desired consistency ratio. This is important as the decision-maker can iteratively use experts to give more thought into the problem, as long as the consistency of their opinions is not achieved. This gives additional strength to the “numbers” of analysis, so they can be sure that the random numbers are not taken into the final decision.

Additional in-depth analysis can give insight into stakeholders’ evaluations, showcasing that they did a good job by giving expert pairwise judgements, as well as coming to a good compromise. All in all, an analysis conducted with AHP resulted in the final ranking of both wall and slab alternatives by applying Equation (7). Therefore, the final rank list of FWS wall alternatives (best to worst) is MAXIMO (0.5687), DOMINO (0.2314), and DUO (0.1999), while the final rank list of FWS slab alternatives (best to worst) is SKYDECK (0.5128), MULTIFLEX (0.2803), and DUO (0.2069).

3.2.2. Results of the SAW Method

As part of the construction and normalization of the decision matrix according to the SAW approach, the ascending (benefit-type and seeking maximum) and descending (cost-type seeking minimum) criteria are determined. By focusing on selecting the optimal alternative by employing multiple criteria, the C3-w, C4-w, C4-s, and C6-s are selected as ascending, while the others are selected as descending ones (shown in Table 1). This provides adequate application of Equations (8) and (9) to gain final information for FWS wall selection (

Table 6. Decision matrix for FWS’s wall criteria and alternatives.

	C1-w	C2-w	C3-w	C4-w	C5-w
DUO	0.375	0.340	50	150	5
DOMINO	0.300	0.260	60	45	5
MAXIMO	0.200	0.180	80	75	4

) and FWS slab selection (

Table 7. Decision matrix for FWS’s slab criteria and alternatives.

	C1-s	C2-s	C3-s	C4-s	C5-s	C6-s	C7-s
DUO	0.340	0.270	16	150	5	1.220	3
SKYDECK	0.220	0.190	71	200	4	3.450	2
MULTIFLEX	0.280	0.200	50	250	6	1.220	6

).

In order to proceed with assigning weights to each criterion, the values of the decision matrices shown in Table 6 and Table 7 need normalization. As previously mentioned in Section 2.3, the SAW method enables decision-makers to use different methods to assign weights to criteria. For this case, a rank-based weight method is applied, and by applying Equation (10), it resulted in the following weights (

Table 8. Weights of FWS’s wall and slab criteria.

	1	2	3	4	5	6	7
wj-wall	0.333	0.267	0.200	0.133	0.067	-	-
wj-slab	0.250	0.214	0.179	0.143	0.107	0.071	0.0357

).

The last step of SAW is to rank the alternatives by Equation (10), and the final rank list of FWS wall alternatives (best to worst) is MAXIMO (0.659), DOMINO (0.246), and DUO (0.095), while the final rank list of FWS slab alternatives (best to worst) is SKYDECK (0.489), MULTIFLEX (0.342), and DUO (0.169).

Compared to the previous application of the AHP method, the SAW approach offers no consistency check; therefore, by solely using it, it can bring a certain level of uncertainty into the final decision.

3.2.3. Comparison of Ranked FWS Alternatives

After the decision analysis was carried out, approaches via both methods showed interesting final results (

Table 9. Final rank for FWS’s wall alternatives.

RANK	AHP	SAW
1. MAXIMO	0.5687	0.6590
2. DOMINO	0.2314	0.2460
3. DUO	0.1999	0.0950

and

Table 10. Final rank for FWS’s slab alternatives.

RANK	AHP	SAW
1. SKYDECK	0.5128	0.4890
2. MULTIFLEX	0.2803	0.3420
3. DUO	0.2069	0.1690

). Although the AHP and SAW methods are completely different in clarity, consistency, and certainty (shown in Section 2.2 and Section 2.3), if the decision process is set correctly, they can both be very solid tools and return clear data. In this case, it is visible that the rank of both FWS’s wall and slab alternatives has not changed.

Although there is a small difference between the results of the AHP and SAW approaches, the decision-maker can be sure of the final ranking and outcomes. The main reason why there is a difference between the two lies in the methods themselves. While the AHP approach is structured and seeks consistency of a solution, the approach with SAW is much looser. This is much evident while assigning weights to criteria, as one can freely select what they want, as the SAW method does not enforce a specific method for assigning weights.

Despite the differences in final ranking between the methods, the decision-maker can be sure in both clarity and consistency in decision-making outcomes by using the AHP or SAW method to select the optimal FWS, or both methods to ensure safety in redundancy. This is very important as it is one of the key decisions, i.e., drivers, to be made at the early stages of a construction project.

4. Conclusions

The presented decision-support framework for selecting the optimal formwork system shows a scientific approach for coping with multi-criteria problems in construction project management. To achieve an optimal solution, the framework leverages the synergic effect of using the AHP and SAW methods in selecting the optimal wall and slab formwork system for a given construction project. It also offers insights into the redundancy of using one method over the other. Notably, the AHP proves to be a much more structured and consistent method to use.

The key advantage of the presented framework is its ease of implementation in any construction project team that needs to make informed choices about selecting the optimal formwork system for their particular reinforced concrete building. This framework tends to assist designers and engineers during early stages in mitigating risks associated with delays and potential standstills during the construction phase.

Furthermore, the framework demonstrates resilience and robustness in accommodating changes in projects/problems/criteria/stakeholders due to its open approach to developing a hierarchical goal structure. This ensures clarity and consistency in decision-making outcomes, ultimately contributing to more robust planning and design phases while keeping the project’s future long-term success in focus.