Cross-Attention Enhanced TCN-Informer Model for MOSFET Temperature Prediction in Motor Controllers
Abstract
1. Introduction
- 1.
- A dual-channel modeling framework that integrates a TCN and Informer is proposed, which balances prediction accuracy and computational efficiency by capturing both local temporal patterns and long-range dependencies in MOSFET temperature sequences.
- 2.
- A temporally aligned cross-attention fusion strategy is introduced to dynamically integrate features from the TCN and Informer, enhancing the identification of key driving factors of temperature rise.
2. Analysis and Dataset Construction of Factors Affecting MOSFET Junction Temperature
2.1. Analysis of Influencing Factors
2.2. Dataset Construction
3. TCN–Informer Temperature Prediction with Cross-Attention
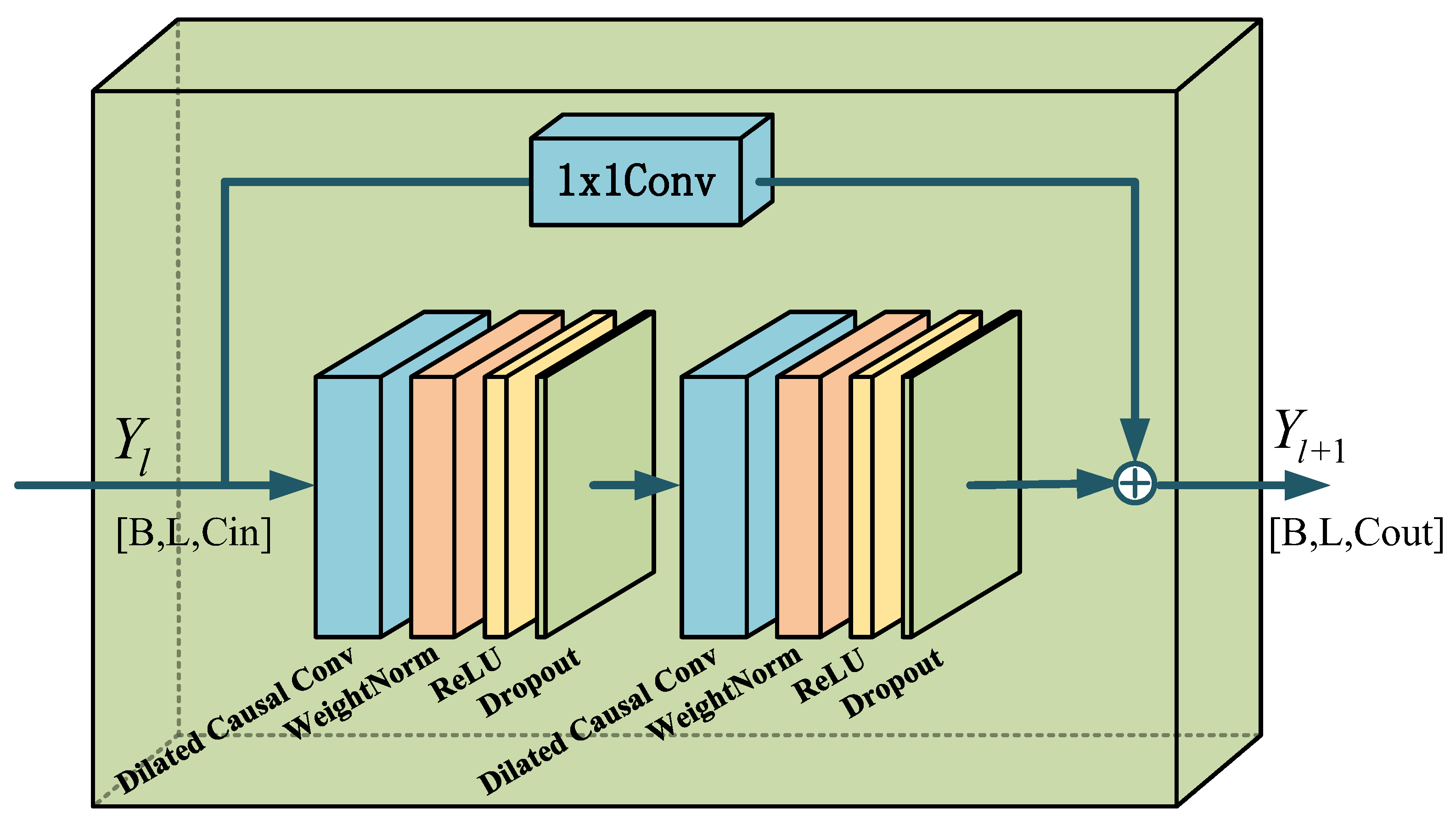
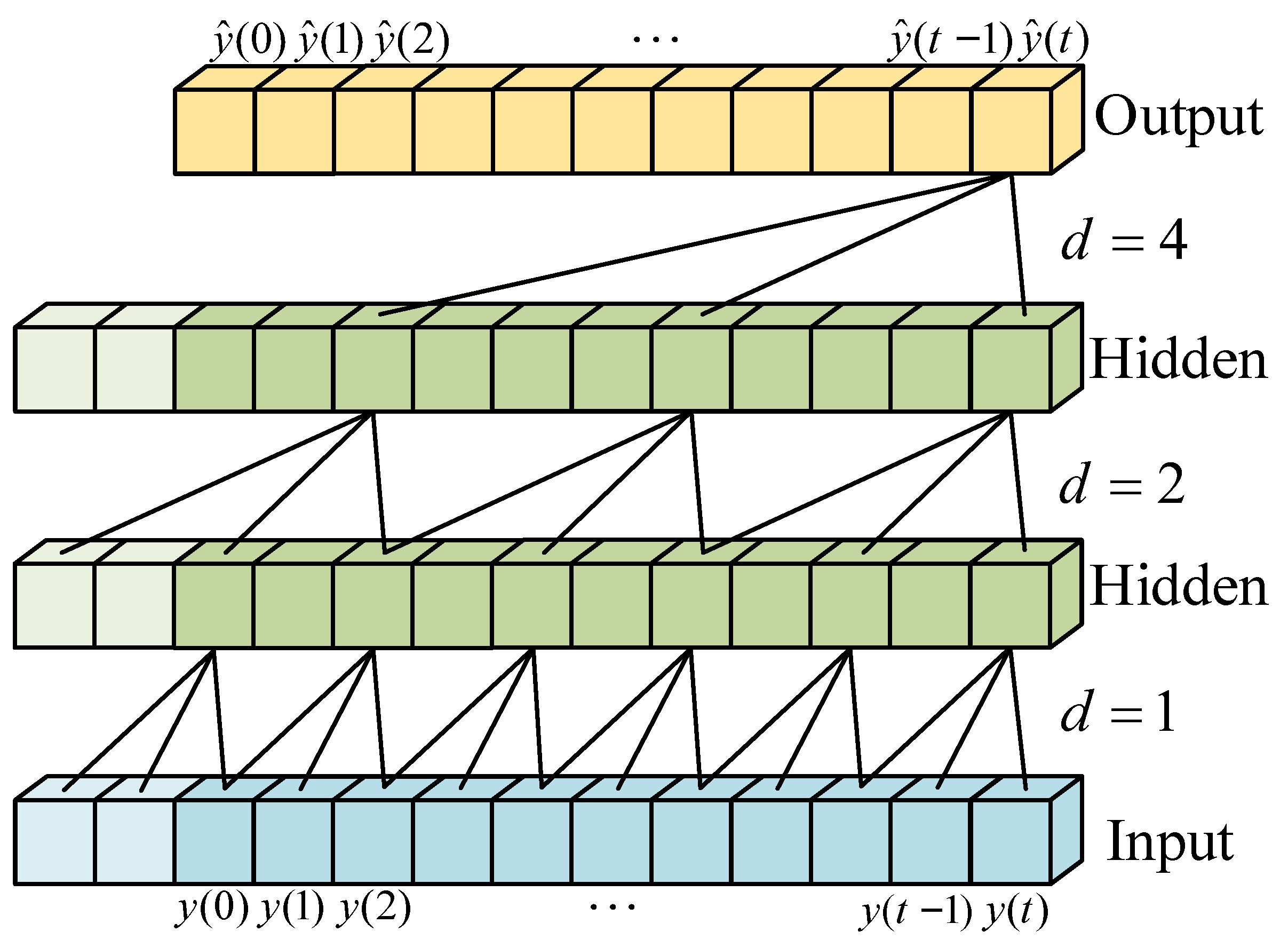
3.1. Temporal Convolutional Network
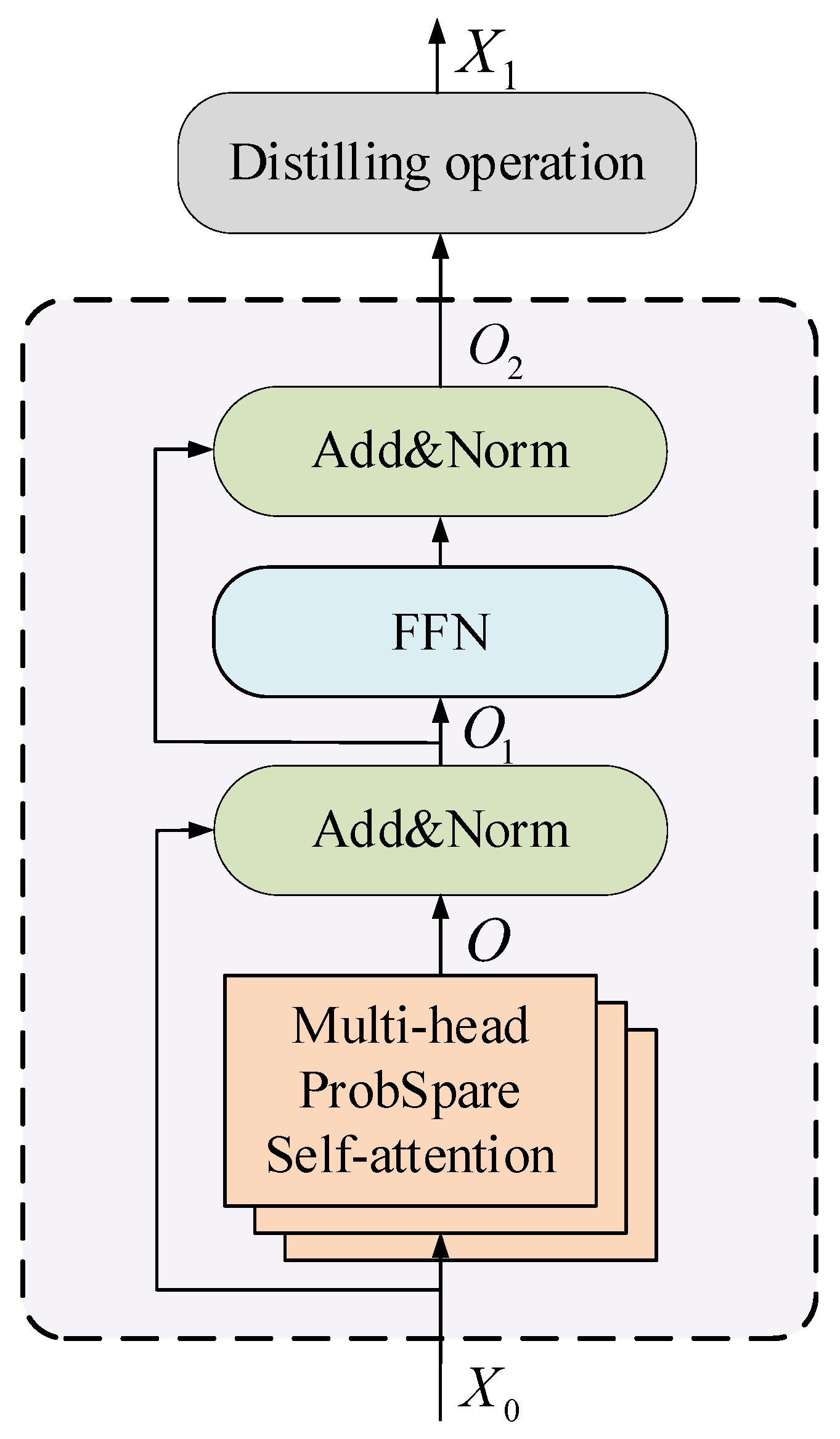
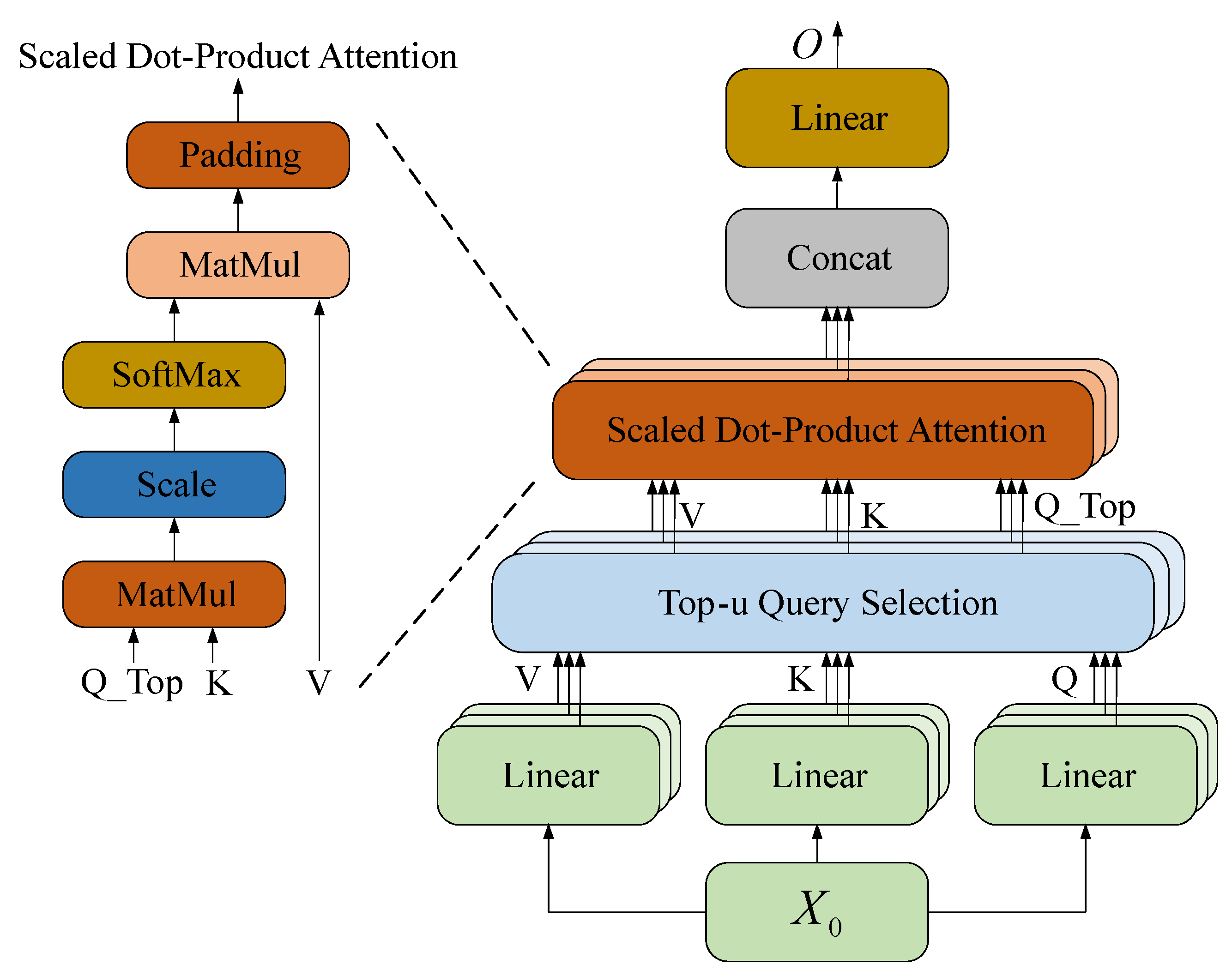
3.2. Informer
3.3. Cross-Attention Mechanism
4. Results
4.1. Experimental Setup and Hyperparameter Settings
4.2. Result Analysis
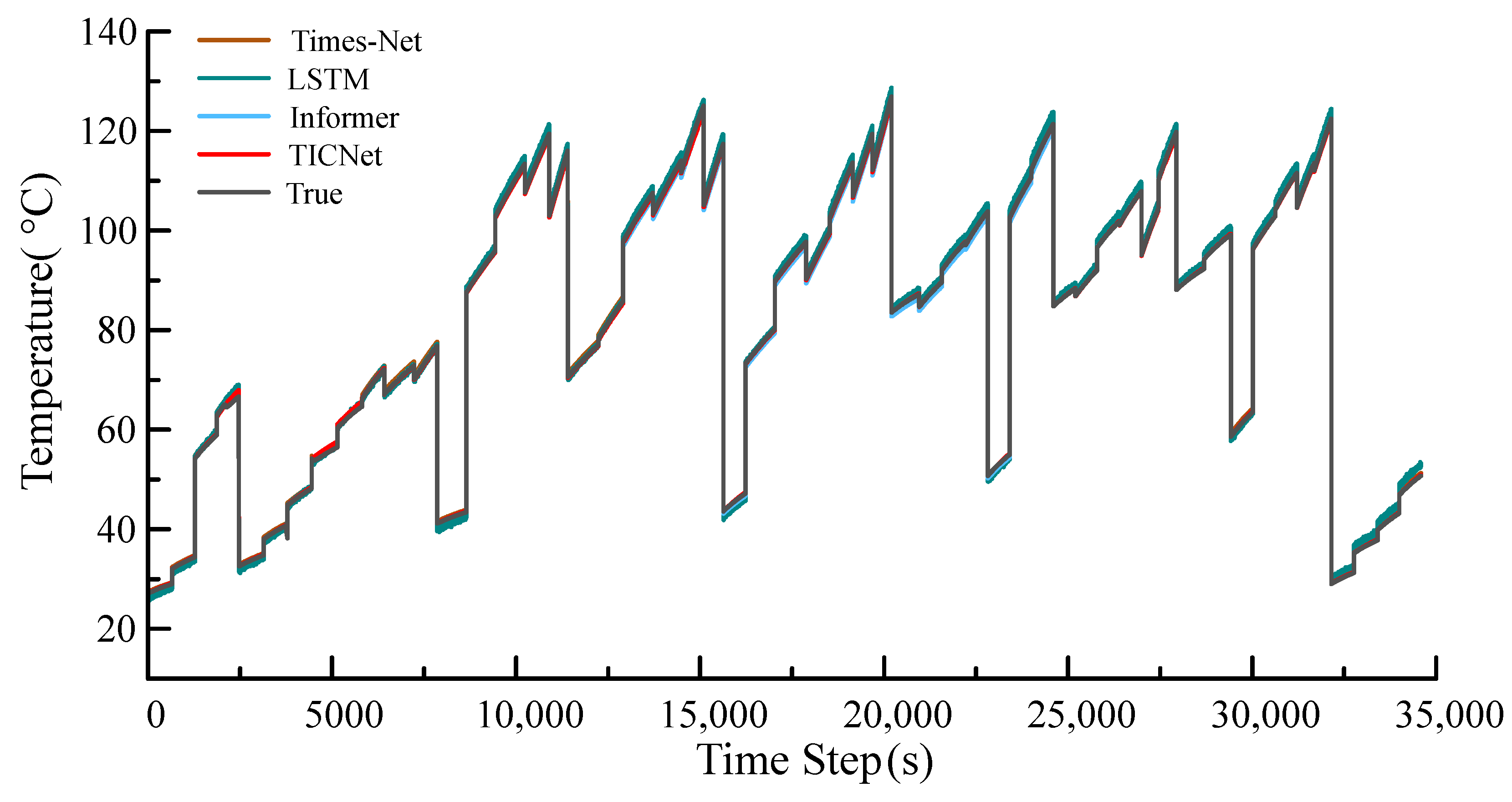
4.2.1. Model Comparison
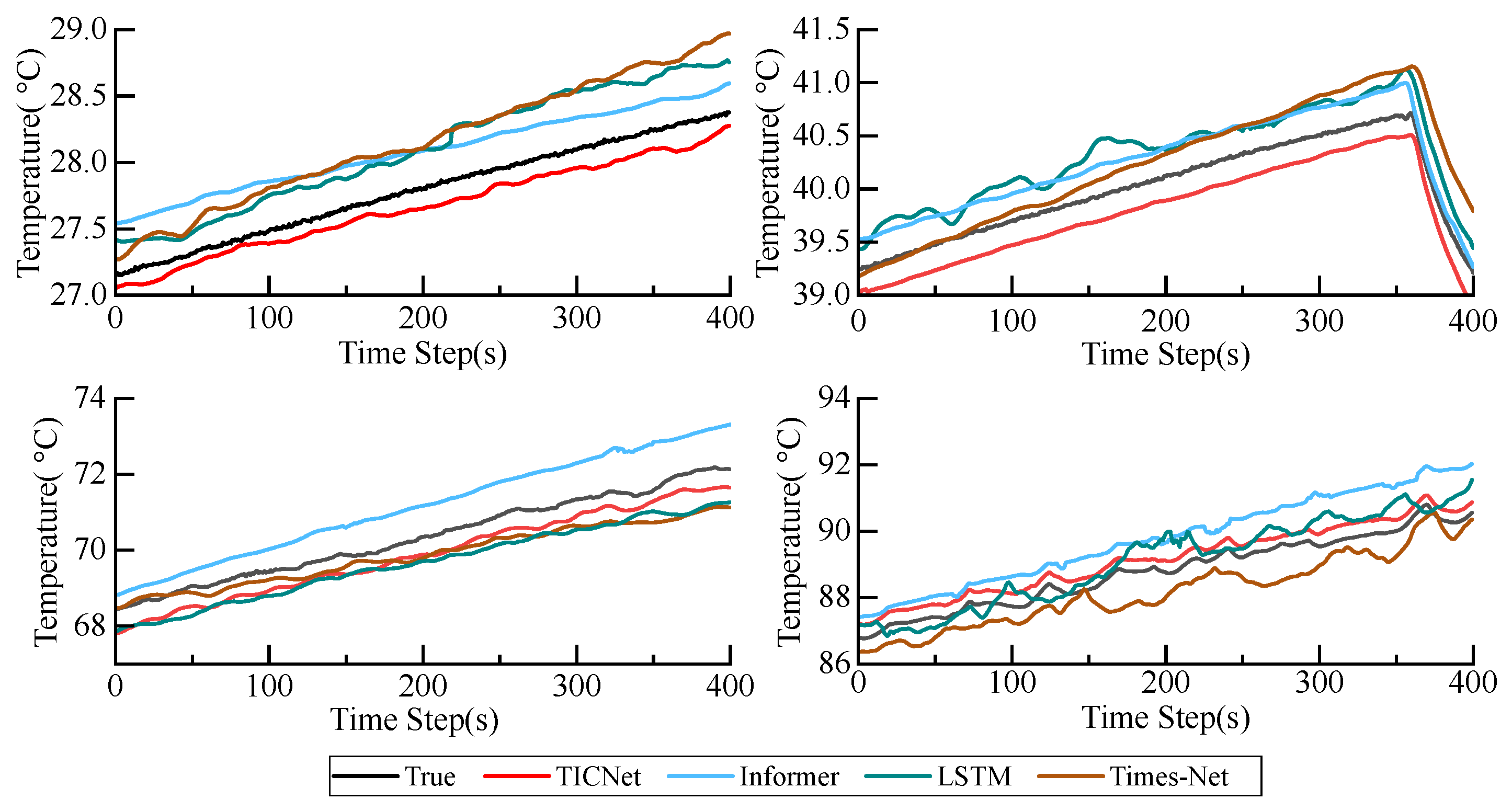
4.2.2. Residual Distribution Analysis
4.2.3. Ablation Study
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Q.; Huang, Q.; Guo, H.; Cao, J. Design and research of permanent magnet synchronous motor controller for electric vehicle. Energy Sci. Eng. 2023, 11, 112–126. [Google Scholar] [CrossRef]
- Shu, X.; Guo, Y.; Yang, H.; Zou, H.; Wei, K. Reliability study of motor controller in electric vehicle by the approach of fault tree analysis. Eng. Fail. Anal. 2021, 121, 105165. [Google Scholar] [CrossRef]
- Vankayalapati, B.T.; Sajadi, R.; Cn, M.A.; Deshmukh, A.V.; Farhadi, M.; Akin, B. Model based junction temperature profile control of SiC MOSFETs in DC power cycling for accurate reliability assessments. IEEE Trans. Ind. Appl. 2024, 60, 7216–7224. [Google Scholar] [CrossRef]
- Lai, W.; Wei, Y.; Chen, M.; Xia, H.; Luo, D.; Li, H. In-situ calibration method of online junction temperature estimation in IGBTs for electric vehicle drives. IEEE Trans. Power Electron. 2022, 38, 1178–1189. [Google Scholar] [CrossRef]
- Ma, M.; Sun, Z.; Wang, Y.; Wang, J.; Wang, R. Method of junction temperature estimation and over temperature protection used for electric vehicle’s IGBT power modules. Microelectron. Reliab. 2018, 88, 1226–1230. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Y.; Ding, X.; Zhang, P. Online junction temperature estimation method for SiC MOSFETs based on the DC bus voltage undershoot. IEEE Trans. Power Electron. 2023, 38, 5422–5431. [Google Scholar] [CrossRef]
- Li, C.; Lu, Z.; Wu, H.; Li, W.; He, X.; Li, S. Junction temperature measurement based on electroluminescence effect in body diode of SiC power MOSFET. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 338–343. [Google Scholar]
- Lee, I.H.; Lee, K.B. Junction temperature estimation of SiC MOSFETs in three-level NPC inverters. J. Electr. Eng. Technol. 2024, 19, 1607–1617. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, M.; Feng, S.; Tang, Y.; Zhang, Y. Online temperature measurement method for SiC MOSFET device based on gate pulse. IEEE Trans. Power Electron. 2024, 39, 4714–4724. [Google Scholar] [CrossRef]
- Teixeira, A.; Cougo, B.; Segond, G.; Morais, L.M.F.; Andrade, M.; Tran, D.H. Precise estimation of dynamic junction temperature of SiC transistors for lifetime prediction of power modules used in three-phase inverters. Microelectron. Reliab. 2023, 150, 115137. [Google Scholar] [CrossRef]
- Matallana, A.; Robles, E.; Ibarra, E.; Andreu, J.; Delmonte, N.; Cova, P. A methodology to determine reliability issues in automotive SiC power modules combining 1D and 3D thermal simulations under driving cycle profiles. Microelectron. Reliab. 2019, 102, 113500. [Google Scholar] [CrossRef]
- Eleffendi, M.A.; Johnson, C.M. Application of Kalman filter to estimate junction temperature in IGBT power modules. IEEE Trans. Power Electron. 2016, 31, 1576–1587. [Google Scholar] [CrossRef]
- Miao, J.; Yin, Q.; Wang, H.; Liu, Y.; Li, H.; Duan, S. IGBT junction temperature estimation based on machine learning method. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Kim, M.K.; Yoon, Y.D.; Yoon, S.W. Actual maximum junction temperature estimation process of multichip SiC MOSFET power modules with new calibration method and deep learning. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5602–5612. [Google Scholar] [CrossRef]
- Shuai, Z.; He, S.; Xue, Y.; Zheng, Y.; Gai, J.; Li, Y.; Li, G.; Li, J. Junction temperature estimation of a SiC MOSFET module for 800 V high-voltage application in electric vehicles. eTransportation 2023, 16, 100241. [Google Scholar] [CrossRef]
- Du, Z.W.; Zhang, Y.; Wang, Y.; Chen, Z.; Wang, Y.-D.; Wu, R.; Zhao, D.; Zhang, X.; Yin, W.-Y. A time series characterization of IGBT junction temperature method based on LSTM network. IEEE Trans. Power Electron. 2025, 40, 2070–2085. [Google Scholar] [CrossRef]
- Bai, S.J.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Chen, Z.L.; Ma, M.B.; Li, T.R.; Wang, H.J.; Li, C.S. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W. Deep time series forecasting models: A comprehensive survey. Mathematics 2024, 12, 1504. [Google Scholar] [CrossRef]
- Lim, H.; Hwang, J.; Kwon, S.; Baek, H.; Uhm, J.; Lee, G. A study on real time IGBT junction temperature estimation using the NTC and calculation of power losses in the automotive inverter system. Sensors 2021, 21, 2454. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.F.; Lu, P.; Shan, Z.Y. A high-accuracy switching loss model of SiC MOSFETs in a motor drive for electric vehicles. Appl. Energy 2021, 291, 116827. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 19–21 May 2021; Volume 35, pp. 11106–11115. [Google Scholar]



| Model Parameters | TCN | Informer Encoder |
|---|---|---|
| Number of layers | 3 | 2 |
| Hidden Channels | [32, 64, 128] | \ |
| Number of Attention Heads | \ | 4 |
| Attention Head Size | \ | 32 |
| Learning Rate | 0.0005 | 0.0005 |
| Optimizer | Adam | Adam |
| Activation Function | ReLU | ReLU |
| Model | MAE (°C) | RMSE (°C) | |
|---|---|---|---|
| TICNet | 0.2521 | 0.3641 | 0.9638 |
| Informer | 0.3294 | 0.4593 | 0.7436 |
| LSTM | 0.9433 | 1.0853 | 0.4985 |
| Times-Net | 0.4989 | 0.5753 | 0.6994 |
| Operating Condition | Load Current (A) | Load Voltage (V) | Ambient Temp °C |
|---|---|---|---|
| Condition 1 | 60 | 60 | 0 |
| Condition 2 | 70 | 80 | 20 |
| Condition 3 | 80 | 60 | 40 |
| Condition 4 | 90 | 80 | 60 |
| Model | TICNet | Informer | LSTM | Times-Net | |
|---|---|---|---|---|---|
| Condition 1 | MAE (°C) | 0.1872 | 0.3114 | 0.4918 | 0.4689 |
| RMSE (°C) | 0.2023 | 0.3257 | 0.4702 | 0.4849 | |
| 0.9208 | 0.6565 | 0.4837 | 0.2776 | ||
| Condition 2 | MAE (°C) | 0.2246 | 0.3119 | 0.4495 | 0.3343 |
| RMSE (°C) | 0.2262 | 0.3211 | 0.4556 | 0.3571 | |
| 0.9353 | 0.7496 | 0.6493 | 0.5262 | ||
| Condition 3 | MAE (°C) | 0.4647 | 0.7862 | 0.9106 | 0.5974 |
| RMSE (°C) | 0.4702 | 0.7922 | 0.9442 | 0.5838 | |
| 0.8998 | 0.6739 | 0.3843 | 0.7055 | ||
| Condition 4 | MAE (°C) | 0.3608 | 0.4288 | 0.9863 | 0.6074 |
| RMSE (°C) | 0.3638 | 0.5119 | 1.0345 | 0.6627 | |
| 0.8822 | 0.7667 | 0.2472 | 0.6109 | ||
| Model | Component Modules | MAE (°C) | RMSE (°C) | |||
|---|---|---|---|---|---|---|
| TCN | Informer | CrossAttention | ||||
| TICNet | √ | √ | √ | 0.2521 | 0.3641 | 0.9638 |
| Structure 1 | √ | √ | × | 0.3652 | 0.3965 | 0.8925 |
| Structure 2 | √ | × | √ | 0.2978 | 0.3885 | 0.9341 |
| Structure 3 | × | √ | × | 0.3791 | 0.4113 | 0.8708 |
| Structure 4 | √ | × | × | 0.4507 | 0.4837 | 0.7644 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, C.; Liu, W.; Xu, D.; Zhang, H.; Fan, D. Cross-Attention Enhanced TCN-Informer Model for MOSFET Temperature Prediction in Motor Controllers. Information 2025, 16, 872. https://doi.org/10.3390/info16100872
Lv C, Liu W, Xu D, Zhang H, Fan D. Cross-Attention Enhanced TCN-Informer Model for MOSFET Temperature Prediction in Motor Controllers. Information. 2025; 16(10):872. https://doi.org/10.3390/info16100872
Chicago/Turabian StyleLv, Changzhi, Wanke Liu, Dongxin Xu, Huaisheng Zhang, and Di Fan. 2025. "Cross-Attention Enhanced TCN-Informer Model for MOSFET Temperature Prediction in Motor Controllers" Information 16, no. 10: 872. https://doi.org/10.3390/info16100872
APA StyleLv, C., Liu, W., Xu, D., Zhang, H., & Fan, D. (2025). Cross-Attention Enhanced TCN-Informer Model for MOSFET Temperature Prediction in Motor Controllers. Information, 16(10), 872. https://doi.org/10.3390/info16100872






