Abstract
Indoor positioning remains a recurrent and significant challenge in research. Unlike outdoor environments, where the Global Positioning System (GPS) provides reliable location information, indoor scenarios lack direct line-of-sight to satellites or cellular towers, rendering GPS inoperative and requiring alternative positioning techniques. Despite numerous approaches, indoor contexts with resource limitations, energy constraints, or physical restrictions continue to suffer from unreliable localization. Many existing methods employ a fixed number of reference anchors, which sets a hard balance between localization accuracy and energy consumption, forcing designers to choose between precise location data and battery life. As a response to this challenge, this paper proposes an energy-aware indoor positioning strategy based on Mobile Ad Hoc Networks (MANETs). The core principle is a self-adaptive control loop that continuously monitors the network’s positioning accuracy. Based on this real-time feedback, the system dynamically adjusts the number of active anchors, increasing them only when accuracy degrades and reducing them to save energy once stability is achieved. The method dynamically estimates relative coordinates by analyzing node encounters and contact durations, from which relative distances are inferred. Generalized Multidimensional Scaling (GMDS) is applied to construct a relative spatial map of the network, which is then transformed into absolute coordinates using reference nodes, known as anchors. The proposal is evaluated in a realistic simulated indoor MANET, assessing positioning accuracy, adaptation dynamics, anchor sensitivity, and energy usage. Results show that the adaptive mechanism achieves higher accuracy than fixed-anchor configurations in most cases, while significantly reducing the average number of required anchors and their associated energy footprint. This makes it suitable for infrastructure-poor, resource-constrained indoor environments where both accuracy and energy efficiency are critical.
1. Introduction
Indoor positioning has emerged as a critical enabler for location-aware services in environments where Global Positioning System (GPS) signals are unavailable or severely degraded [1]. In GPS-denied spaces such as buildings, underground facilities, and industrial plants, signal attenuation and multipath propagation prevent reliable satellite-based localization, creating the need for alternative methods [1]. Accurate indoor localization supports applications ranging from emergency response and industrial asset tracking to human–computer interaction and context-aware computing [2].
Beyond accuracy, energy efficiency is increasingly important in mobile and ad hoc deployments [3]. In battery-powered Mobile Ad Hoc Networks (MANETs), excessive communication and processing for positioning can quickly drain device energy, limiting operational lifetime [3]. This is particularly problematic in scenarios such as temporary event spaces, post-disaster search and rescue, or ad hoc industrial inspections, where recharging or replacing batteries may be impractical [4,5]. Thus, indoor localization strategies must not only be accurate but also minimize energy consumption while adapting to changing network conditions. However, most existing localization schemes use a fixed number of anchor nodes as reference points. This fixed-anchor design imposes a rigid trade-off: maintaining a larger anchor set improves positional accuracy at the cost of higher energy consumption, while reducing the number of anchors conserves energy but sacrifices accuracy. Finding a way to achieve precise indoor positioning in resource-constrained MANETs without incurring prohibitive energy costs is the central problem this paper addresses.
In recent years, a wide spectrum of indoor positioning techniques has been proposed. Range-based approaches such as those using Received Signal Strength Indicator (RSSI) [6], Time of Flight (ToF) [7], or Angle of Arrival (AoA) [8] estimate absolute distances or angles to known anchors, and apply multilateration or triangulation [9]. Fingerprinting methods construct location databases of signal measurements and perform pattern matching at runtime [10]. Connectivity-based schemes, including hop-count or contact graphs, infer relative proximity from network topology [11]. Among these, Multidimensional Scaling (MDS) and its extensions, such as Generalized MDS (GMDS), have proven effective for reconstructing the relative positions of nodes from estimated pairwise distances, particularly in Wireless Sensor Networks (WSNs) [12,13] and MANETs [14,15,16].
However, existing MDS-based localization studies typically rely on stable distance metrics such as RSSI or precise time-based ranging, and assume either dense static deployments or continuous connectivity [17]. These assumptions often do not hold in resource-constrained, opportunistic indoor scenarios, where infrastructure is sparse, measurements are intermittent, devices are mobile, and energy availability is limited. Moreover, traditional methods use a fixed number of anchors, which may result in unnecessary energy expenditure when fewer anchors could maintain the same accuracy.
Considering these remaining challenges, this paper proposes an energy-aware indoor positioning strategy for MANETs based on opportunistic encounters between devices, enhanced with a self-adaptive mechanism for optimizing the number of reference nodes. The method derives pairwise distance estimates from the frequency and duration of contacts. These estimated distances feed a GMDS procedure to construct a relative spatial map of the network, which is transformed into absolute coordinates using a dynamically adjusted set of anchors. By continuously monitoring positioning error, the system increases or decreases the number of anchors to balance accuracy and energy usage. We also address geometric ambiguities by evaluating both direct and reflection corrected transformations, selecting the mapping that minimizes anchor alignment error. Thus, the main contributions of the work are as follows:
- A contact-duration-based distance estimation model for MANET indoor positioning, enabling localization without requiring a dense infrastructure.
- A GMDS-based localization pipeline adapted to opportunistic contact graphs, dynamically incorporating anchors.
- A self-adaptive anchor selection mechanism that dynamically adjusts the number of reference nodes to maintain accuracy while minimizing energy consumption.
- An experimental evaluation in a simulated realistic indoor MANET, showing that the approach can achieve average positioning misalignment of 7 m in high-density scenarios and 12 m in low-density contexts. Meanwhile, the strategy reduces the energy footprint compared to fixed-anchor methods, in more than 25%, achieving the best combined score between accuracy and energy consumption.
The rest of this paper is organized as follows. Section 2 reviews related work in indoor positioning and MDS/GMDS-based localization. Section 3 describes the proposed method in detail. Section 4 presents the experimental setup and results, discussing implications, limitations, and potential extensions. Finally, Section 5 concludes the paper.
2. Related Work
Indoor positioning has been addressed through a wide range of techniques, each with specific trade-offs in accuracy, cost, infrastructure requirements, and energy consumption [1]. Below, we review the main categories most relevant to this work, with emphasis on GMDS-based localization, encounter-driven positioning, and adaptive anchor strategies.
2.1. Range-Based and Fingerprinting Approaches
Range-based methods estimate distances or angles to known anchors, then apply multilateration or triangulation. Typical measurement modalities include RSSI, ToF, AoA, and Time Difference of Arrival (TDoA) [10,18]. Works such as [19] have extensively studied indoor Wi-Fi positioning using RSSI trilateration, facing multipath and fading effects as potential challenges, reducing accuracy in complex indoor environments. Moreover, continuous measurement exchanges and active scanning incur high communication and processing costs, leading to increased energy consumption in battery-powered devices [20]. Due to their reliance on stable anchors and frequent measurements, these schemes are best suited to static or infrastructure-rich settings; their complexity and power demands make them unsuitable for sparse or highly mobile MANETs.
Other works are based on fingerprinting techniques [21], building databases of signal characteristics at known locations and performing pattern matching at runtime. While these methods can achieve high accuracy, they require costly site surveys, frequent recalibration to account for environmental changes, and periodic active probing [22]. These factors contribute to significant energy overhead in mobile deployments. Moreover, fingerprinting methods assume consistent signal signatures, so their applicability to sparse MANETs is limited: the lack of persistent infrastructure and the mobility of nodes erode fingerprint stability, making these approaches suited for opportunistic, infrastructure-poor environments.
2.2. Localization Based on Connectivity and Hop Count
An alternative to precise ranging is connectivity-based localization, where distances are approximated from network topology metrics. Early works [23] estimated pairwise distances based on the number of hops between nodes and an average hop length. While simple, these approaches degrade in accuracy when hop lengths vary significantly or connectivity is sparse. From an energy perspective, these methods can be lightweight when using passive neighbor discovery, but accuracy issues often necessitate additional message exchanges, increasing the energy footprint. These hop-count based methods assume relatively dense and uniformly connected networks; in sparse MANETs, long and variable hop distances lead to large positioning errors, so the techniques offer only low suitability in mobile environments.
2.3. GMDS and MDS Based Localization in WSNs and MANETs
MDS has been widely adopted to reconstruct node positions from pairwise distances. Decades ago, works such as [24] introduced MDS-MAP, which computes a relative coordinate map from estimated distances and aligns it to an absolute frame using a set of anchors. Variants have extended this approach to distributed computation and to adapt to irregular distance error patterns [25]. On the other hand, GMDS extends classical MDS to handle incomplete and noisy distance matrices more effectively, making it suitable for opportunistic and sparse connectivity scenarios [26]. Recently, modern works have adapted these techniques to the latest advances in Artificial Intelligence [27]. Considering this, GMDS becomes a flexible technique extensible with new approaches, including MANETs, where node encounters are intermittent and range measurements are unreliable.
MDS, GMDS, and related methods have been applied to WSNs, static ad hoc deployments, and indoor contexts using RSSI-derived distances [12,13]. These works demonstrate that MDS-based methods are effective at producing consistent relative maps, but they generally rely on stable distance measurements and either static or well-connected networks. Furthermore, studies [13] maintain a fixed number of active anchors throughout operation, regardless of accuracy trends, resulting in potentially unnecessary communication and computation costs that waste energy. Classical MDS-based schemes, such as MDS-MAP [24], assume near-complete distance matrices and therefore perform poorly in sparse MANETs. Distributed weighted MDS [26] relaxes the completeness requirement, offering medium suitability by working in decentralized fashion, but still pre-selects static anchors without a mechanism to adjust to mobility or energy constraints. Other variants focus on sensor networks [13]; their wake-up protocols can reduce energy consumption in fixed deployments but are not adaptable to mobile contexts.
Another variant such as Scaling by Majorizing a Complicated Function (SMACOF), optimizes stress iteratively but at a higher computational cost, making it less suitable for highly dynamic and energy-sensitive MANET scenarios [28]. Indeed, SMACOF requires multiple iterations of stress minimization; in mobile MANETs, this computational burden and the need for repeated measurements limit its practicality.
2.4. Encounter-Based Localization and Opportunistic Networks
From an energy standpoint, encounter-based localization can be advantageous since it avoids continuous measurement exchange. However, few works explicitly optimize anchor usage to minimize communication and processing energy, or integrate adaptive strategies that react to real-time accuracy requirements. Most studies either use static anchor configurations or focus solely on connectivity, without balancing accuracy against energy constraints [29]. From this review, two key gaps emerge. First, these encounter-based approaches only implicitly handle anchor selection, offering at best medium suitability for mobile or sparse MANETs; second, the lack of explicit energy awareness in anchor strategies means they do not address the critical trade-off between accuracy and power consumption.
2.5. Gap and Positioning of This Work
First, while MDS and GMDS with anchors are established techniques in WSN and indoor positioning research, prior deployments assume accurate ranging or dense connectivity conditions often absent in mobile, infrastructure-poor indoor environments—and generally overlook energy efficiency as a primary optimization goal. Second, encounter-based localization is an active area, but the combination of distance estimation based on contact duration, GMDS reconstruction, and energy-aware adaptive anchor control remains unexplored. These gaps translate to potential improvements for mobile or sparse MANETs: classical MDS variants require dense data; distributed or static-anchor MDS schemes do not adapt to node mobility; and encounter-based methods neglect the anchor-selection trade-off.
Our work addresses these gaps by proposing a GMDS-based pipeline tailored to opportunistic indoor MANETs, where infrastructure is sparse, devices are mobile, and both positioning accuracy and energy efficiency depend strongly on the number and placement of anchor nodes. The novelty lies in introducing a self-adaptive anchor mechanism that automatically increases or decreases the number of anchors based on observed localization error, thereby achieving a positive trade-off between accuracy and energy usage. This represents a shift from static anchor configurations toward an accuracy-driven, energy-aware anchor deployment strategy for opportunistic indoor localization. By explicitly targeting the mobile and sparse MANET context, our method is designed to maintain high localization accuracy while remaining energy efficient even when only intermittent contact data are available. This high suitability distinguishes our approach from prior works that implicitly assume dense connectivity or static anchors.
In summary, while prior works have established foundational techniques, they have not systematically addressed the dynamic optimization of the accuracy–energy trade-off through adaptive anchor management in MANET contexts. Table 1 summarizes this literature landscape and positions our work as a novel solution designed to fill these specific gaps.

Table 1.
Summary and comparison of key related works in localization.
3. Dynamic Anchor Optimization for Indoor Location
This section details the proposed pipeline: (i) derive pseudo-distances from encounter statistics; (ii) obtain a relative map with GMDS under missing data; and (iii) align to absolute coordinates via Procrustes using an adaptively sized anchor set. The next subsections address the workflow, system architecture, contact-based estimation, anchor adaptation, and energy model.
3.1. Overview
The operation of the system can be illustrated through a simplified example in which five mobile nodes are distributed within a m indoor area. This situation is represented by window 1 at Figure 1. Initially, two of these nodes are designated as anchors, with known absolute coordinates. In the first time window, contact data between all nodes is collected and transformed into estimated pairwise distances, from which GMDS reconstructs a relative map. Then, Procrustes analysis aligns this map to the absolute frame using the anchor coordinates. The Root Mean Square Error (RMSE) of the anchor validation error is computed, comparing their estimated and true positions. To avoid bias, the system relies on a validation-anchor strategy: at each evaluation step, a small subset of anchors is temporarily withheld from the alignment process and treated as regular nodes. The RMSE is then computed on these withheld anchors and combined with self-consistency metrics. This yields a reliable proxy for the expected error in non-anchor nodes while keeping the process feasible in real deployments.
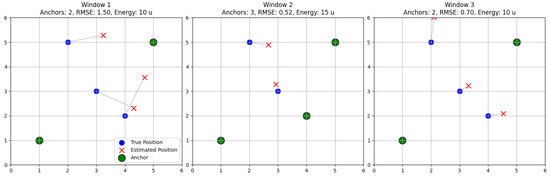
Figure 1.
Working overview of the indoor location strategy, achieving a reduction in positioning error, while keeping energy consumption reduced.
As window 2 in Figure 1 describes, if the observed error exceeds a configurable upper tolerance threshold, the system promotes an additional node to anchor status, choosing the candidate that maximizes spatial diversity and coverage. This increases the number of reference points for alignment, improving accuracy. Conversely, if the error remains below the target threshold for several consecutive windows, as window 3 in Figure 1 describes, an anchor is demoted to regular node status to reduce energy consumption. This adaptation continues over subsequent windows, balancing accuracy and resource usage. By the third window in our example, the RMSE has decreased significantly, and the number of anchors is reduced, maintaining accuracy while lowering energy consumption.
Figure 2 describes the sequential processing steps and the key decision points of the algorithm. At each time window t, the process begins by aggregating all contact events recorded by the mobile nodes. These contacts are translated into distance estimates, which are then passed to the coordinator node. This element constructs a relative spatial map of all nodes using only the inter-node distances. Because this relative map is floating with respect to the global coordinate system, a Procrustes transformation aligns it to the absolute reference frame using the current set of anchors.
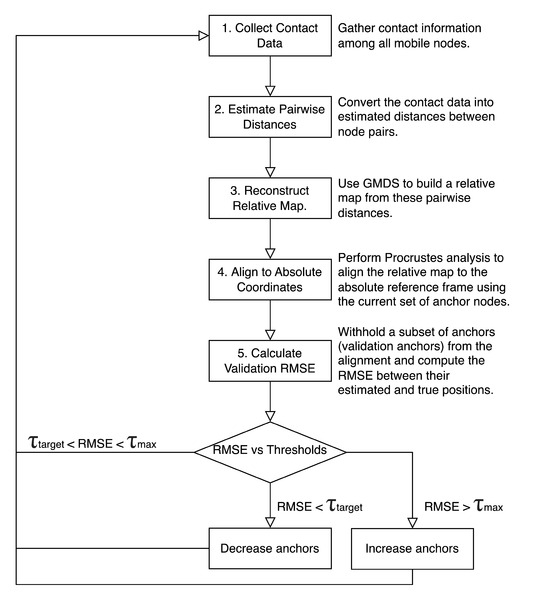
Figure 2.
Flowchart of the proposed adaptive strategy, including maximum target RMSE () and target RMSE ().
Once a set of absolute coordinates has been obtained, the algorithm computes a validation error. To avoid over-fitting to the anchors, a small subset of them is withheld from the alignment, and their estimated positions are compared with their known absolute locations. This RMSE is combined with a self-consistency metric, which measures how well the relative and aligned maps agree, to produce an overall error estimate. This error estimate triggers the adaptation phase: if the error exceeds a user-defined upper tolerance, the system promotes an additional mobile node to anchor status. Promotion is biased toward nodes whose placement increases geometric diversity, improving the conditioning of the alignment step. Conversely, if the error stays below a lower tolerance for several consecutive windows, one of the existing anchors is demoted back to a regular mobile node, reducing energy consumption. If the error falls between the two thresholds, the anchor set remains unchanged. The updated set of anchor coordinates is then used in the subsequent time window, and the cycle repeats. This workflow continuously balances localization accuracy against energy expenditure by adjusting the number of anchors based on real-time performance metrics.
Considering this overview, next section analyzes the components and communications required in the architecture to operate.
3.2. Architecture
The architecture consists of mobile nodes, a subset of which serve as anchors. Each node is equipped with short-range wireless interfaces, such as Wi-Fi or Bluetooth, to detect opportunistic contacts with nearby peers. A local contact logger records the identifier of the encountered node, the timestamp of contact initiation, and the duration of the encounter. This contact data is periodically shared with a coordinator fixed edge node to construct a global contact graph.
The coordinator node performs a distance estimation based on the contact history. Thus, pairwise distances between nodes can be estimated, producing an incomplete distance matrix. The GMDS engine then computes a relative coordinate map from this matrix. Anchors feed their known absolute positions into the module, which applies Procrustes analysis to transform the relative map into the absolute coordinate system.
The process to adapt relative to absolute positions evaluates positioning performance at the end of each time window. It determines the RMSE computed on a validation subset of anchors, combined with self-consistency indicators such as the MDS stress, temporal smoothness of position estimates, and anchor–consistency dispersion. These indicators provide a practical accuracy proxy without requiring knowledge of the true positions of regular nodes. The error metric driving adaptation is the RMSE over withheld validation anchors, never including any anchor actively used for alignment. This separation ensures that anchor activation decisions are based on an unbiased estimate of network accuracy, rather than on an inflated metric that would automatically improve when more anchors are added. Finally, a coordinator monitors the energy usage, per-window and cumulative, enforcing operational constraints and preventing the overuse of anchor mode in environments with limited energy.
The architecture assumes a coordinator node as a pragmatic, centralized point for aggregating contact logs, estimating pairwise distances, running GMDS, and orchestrating anchor selection. This choice simplifies synchronization and ensures availability despite transient partitions common in MANETs. A fully decentralized variant is conceivable (e.g., gossip or consensus over local maps), but end-to-end connectivity cannot be guaranteed, and the coordination overhead grows under mobility and churn. The centralized coordinator thus serves as a baseline for clarity and reproducibility, while distributed realizations are left as future work.
Considering these components, the proposed pipeline provides a potential strategy to perform estimations and managing the presence of anchor nodes in the scenario. Next, the specific details for the location estimation process are addressed.
3.3. Contact-Based Location Estimation
The proposed localization framework operates without any specialized ranging hardware, relying instead on the opportunistic detection of encounters between mobile devices. Each participating node continuously monitors its local wireless interfaces to detect the presence of other nodes within its communication range. A contact is formally defined as a continuous time interval during which two nodes can exchange at least one successful beacon or message, thus confirming bidirectional communication capability. For every contact, the system logs both the start and end times, enabling precise computation of the contact duration, as well as the total number of contacts observed within a sliding observation window.
From this contact history, the system infers relative proximity between nodes under the assumption that both the probability of encountering another node and the duration of such encounters are inversely correlated with physical distance. This assumption is supported by mobility models in opportunistic networks, where closer nodes have a higher likelihood of falling within mutual communication range. To capture this relationship, the pairwise distance between two nodes i and j is estimated as a decaying function of a robustly normalized contact probability :
where is a decay coefficient that encapsulates mobility and propagation effects, and is the contact probability after flooring to avoid . Let be the set of contact counts observed in window t. A robust cap is used to reduce sensitivity to outliers:
The contact probability is then
with unless otherwise stated. In practice, this process yields an incomplete distance matrix D since not all node pairs encounter each other within the same window, especially in sparse or highly mobile scenarios. Unless otherwise stated, the assessment uses for the cap quantile and .
Unlike classical MDS, which assumes a complete distance matrix, GMDS operates with missing entries by optimizing over available distances only. The method seeks the coordinates in a two-dimensional Euclidean space that minimize the stress function:
where is the set of observed distance pairs and is its cardinality. The output of GMDS is a relative map of the network, whose scale, rotation, translation, and reflection are undefined.
To resolve these ambiguities and obtain absolute coordinates, a set of anchor nodes with known positions is used. Intuitively, GMDS recovers the network’s shape but with unknown pose: shift, rotation, scale, and possibly a mirror. Procrustes then finds a single rotation (or reflection), scale, and translation that best land the anchors from the relative map onto their known absolute locations, and applies the same transform to all nodes.
Formally, Procrustes finds a similarity transform . Matrix is orthogonal and represents a rotation or a reflection. Scalar is the scale factor. Vector is the translation. Let be the set of anchors used to compute the transform. Procrustes solves
where are the relative anchor coordinates, and are the absolute coordinates. The evaluation includes both the direct and the mirrored solutions and keeps the lower-error fit. To avoid optimistic bias, anchors used in this fit are not used to report accuracy; instead, a small withheld set provides an unbiased validation RMSE that drives the adaptive controller.
After Procrustes, for each window t, the alignment step evaluates the direct and mirrored similarity transforms and selects the option with the lower anchor error. The accuracy of the absolute position estimates is then quantified using RMSE as defined below in the manuscript:
where is the true absolute coordinate of node i, and is its estimated position after transformation.
Critically, anchors used for alignment are not included in the RMSE driving adaptation. Including them would trivially reduce the error without reflecting real improvements for regular nodes. Instead, the system employs a validation-anchor strategy: at each evaluation step, a small subset of anchors is temporarily withheld from the alignment process and treated as regular nodes. The RMSE is then computed on these withheld anchors and combined with the self-consistency indicators, such as the mentioned MDS stress, positional smoothness across consecutive windows, and anchor-dispersion metrics. This ensures that the adaptation process is guided by an unbiased accuracy estimate that correlates strongly with the expected error for non-anchor nodes. As the operation of the proposed framework can be understood as a two-phase pipeline repeated over successive time windows, localization and mapping process would become the first stage. Algorithm 1 describes the process within each window, starting from raw contact logs and ending with absolute position estimates. For this, the algorithm receives several input variables, such as , which describes the decay factor, established by default to 1.2, and as the probability floor, with a value of . Respectively, these values map contact probabilities to pseudo-distances. The decay factor scales the dynamic range of distances, then a larger value of compresses distances, while a smaller expands them. In the case of , it prevents and limits extreme values when contacts are very rare.
| Algorithm 1: Localization and mapping in window t (GMDS + Procrustes + validation) |
Input: Contact logs over window t; decay factor (default ); probability floor (default ); Current anchor set with known absolute positions ; Withheld validation anchors ; Previous absolute estimate (optional); GMDS/SMACOF solver hyperparameters. Output: Absolute estimates for all nodes; Validation error on ; Self-consistency metrics ; Per-window energy .
|
For quick lookup, Table 2 summarizes all energy symbols used in the paper. Algorithms 1 and 2, figures, and captions refer to these definitions.

Table 2.
Energy symbols used throughout the paper.
Unless otherwise stated, evaluations use J/window, J/window, and J; is updated each window as described in Algorithm 2.
| Algorithm 2: Self-adaptive anchor presence (validation-driven + energy-aware) |
 |
It is worth noting that this method infers distances from encounter statistics. The distance estimates are thus inherently noisy, with error sources including heterogeneous radio ranges, mobility anisotropy, and temporal sampling effects. The use of GMDS mitigates these effects by incorporating partial observations while maintaining geometric consistency, enabling the framework to operate effectively in sparse, dynamic, and energy-constrained indoor MANET scenarios.
3.4. Self-Adaptive Anchor Presence
The number of active anchors directly affects the accuracy of the absolute position estimates. Too few anchors can cause high positioning errors, while too many increase energy consumption and operational overhead. The proposed self-adaptive mechanism dynamically adjusts the number of active anchors based on performance feedback.
The adaptation loop runs over discrete time windows. At the end of each window, the system evaluates performance using the validation anchor RMSE plus self-consistency metrics, never counting anchors used in the alignment phase. If the error remains above the upper tolerance threshold for consecutive windows, an additional anchor is activated. If the error stays below the target threshold for consecutive windows, an anchor is deactivated. A coverage gain heuristic selects nodes for promotion or demotion to maintain spatial diversity among anchors.
This separation between alignment anchors and validation anchors prevents the system from taking misleading decisions based on artificially reduced errors, ensuring that anchor activation or deactivation reflects genuine performance changes for non-anchor nodes.
Algorithm 2 details the self-adaptive anchor control mechanism, which governs how the set of active anchors evolves over time. Anchor promotion is triggered when accuracy deteriorates beyond a tolerance threshold for multiple consecutive windows, while demotion occurs when accuracy remains stably below the target error. The selection of candidate nodes for promotion or demotion is driven by a coverage-based heuristic, ensuring that spatial diversity among anchors is preserved. Energy consumption is explicitly monitored in Joules per window, with both per-window and cumulative limits enforced to prevent overuse of anchor mode. Finally, a small random subset of anchors is withheld in the next window to act as validation anchors, ensuring unbiased performance monitoring.
Algorithm 2 uses two error thresholds in meters: for the lower cap and for the upper cap. For example, potential values for these variables could be and . Then, if validation RMSE stays below 8 m for a while, the controller removes an anchor; if it stays above 12 m, it adds one. The patience counters avoid flapping, e.g., . The number of anchors is limited by (e.g., 3 and 20). Energy limits are set by the per-window anchor cost (J/window) and optional caps and ; values depend on the device and battery, such as a range of the 0.8–1.5 J/window. Another example, for unbiased accuracy checks, 20% of anchors may withhold each window (). Candidate anchors are chosen with a simple farthest-first coverage heuristic to keep them well spread. All values can be changed by the user if a scenario requires stricter accuracy or tighter energy budgets.
The fraction of nodes operating as anchors is not fixed: the controller adjusts per window based on validation RMSE and patience thresholds, subject to energy caps and bounds . To avoid over-constraining Procrustes and biasing accuracy metrics, it is recommended to cap the active-anchor fraction, e.g., of nodes.
Considering the provided details, the next subsection analyzes the computational complexity of the system.
3.5. Computational Complexity
The potential deployment of the proposed strategy requires an understanding of the scaling behavior of the method with respect to the number of nodes and the amount of observed contact information. This subsection characterizes the asymptotic time and memory costs of each architectural component in a single window.
The complexity of the proposal mainly depends on a set of contextual variables. Let N be the number of nodes, the number of active anchors in window t, the embedding dimension, and the number of observed node pairs in that window. The contact modeling step estimates contact probabilities only for the observed pairs and builds the corresponding entries of the incomplete distance matrix. This step runs in time and uses memory. Its cost is linear in the number of observations and does not depend on the full matrix.
The GMDS embedding optimizes a stress function over the observed set. Each solver iteration evaluates and updates terms that are indexed by pairs in , leading to a per iteration cost of and a total cost of over iterations. Memory usage is to store the coordinates and the sparse observation structure.
The Procrustes alignment uses only the anchor rows of the relative map. Building the cross covariance from K anchors costs time and additional memory beyond the anchor subset. The singular value decomposition of a matrix and the reflection check are constant time. Applying the similarity transform to all nodes costs time. As a result, Procrustes is negligible compared to the embedding when is moderate or large.
The coverage aware anchor selection employs a farthest first rule over the current absolute estimates. A reselection pass that considers the leverage of K anchors over N nodes costs time and additional memory beyond the coordinates. This step is only invoked when the controller proposes a change in the anchor set and does not run every iteration of the embedding. The controller itself maintains counters, accounts for energy, and samples the validation split. These operations scale with the number of anchors and therefore cost time and memory per window.
In summary, the dominant costs per window arise from the GMDS embedding and scale linearly with the number of observed pairs. All other components have linear or constant costs with respect to N and K, namely for applying the Procrustes transform, for alignment statistics and controller updates, and at most when anchor reselection is executed. This profile indicates a theoretical viability, primarily dependent of the sparsity and size of the observed contact set.
3.6. Energy Optimization
The energy consumption of anchor nodes is a critical factor in the practical deployment of the proposed system, particularly in MANETs powered by batteries, environments where device lifetime must be maximized. While the self-adaptive mechanism dynamically adjusts the number of active anchor to balance accuracy and coverage, the framework also incorporates an explicit energy optimization layer to ensure that the adaptation process does not violate resource constraints.
In our model, the energy consumption is expressed in Joules (J), the international unit for energy, defined as
This unit facilitates integration with device power models and battery specifications. Each anchor node incurs a fixed energy cost per time window, measured in Joules per window . This cost represents the additional power required to operate in anchor mode, including broadcasting its absolute coordinates at higher frequency, maintaining synchronization for positioning services and processing location requests from other nodes. The total instantaneous energy expenditure in time window t is
where is the number of active anchors in the current window, and is given in J/window.
The cumulative energy consumption over T time windows is
Considering these outputs, the proposed framework enforces two complementary constraints:
- 1.
- Per-window limit: A maximum instantaneous energy consumption (in J/window) is enforced for each window, ensuring that a sudden increase in anchor count does not exceed device or network capacity.
- 2.
- Cumulative budget: Over the operational period T, the cumulative consumption (in J) must not exceed a global energy budget . This prevents scenarios in which the adaptation mechanism gradually depletes system energy reserves.
If either limit is reached, the self-adaptive mechanism is prevented from activating additional anchors, even when RMSE metrics would suggest doing so. In such cases, the system explores alternative strategies such as the following:
- Reassigning existing anchors to maximize geometric coverage without increasing their number.
- Temporarily increasing the reflection-correction evaluation frequency to mitigate positioning error.
- Dynamically adjusting and thresholds to operate in a more energy-efficient regime.
Furthermore, by monitoring alongside the performance metrics in each window, the system provides real-time feedback on the trade-off between accuracy and energy consumption. This enables the fine-tuning of parameters such as , , and to adapt the localization strategy to specific deployment requirements, whether prioritizing extended lifetime, higher positioning accuracy, or a balance between the two.
For a practical interpretation, these numbers can be applied for an ESP32 Internet of Things (IoT) node powered by a small Li-Po battery of 3.7 V and 115 mAh, with a capacity of 1532 J. This device, acting as an anchor for 50 windows, may consumes 40 J, becoming around 2.61% of the battery, and 0.8 J/w. Thus, to avoid battery drain, the coordination to activate or deactivate anchors in the scenario becomes critical to keep the MANET operative. In summary, the integration of Joule-based energy constraints drives the proposal into resource-conscious mechanisms, suitable for sustained operation in energy-limited indoor MANET deployments.
Considering the proposed features integrated into the proposal, a proof-of-concept implementation has been developed to assess the overall performance of the proposal in terms of position estimation accuracy and energy consumption. The next section addresses these processes.
4. Evaluation
The proposed architecture is assessed in a simulation setup, comparing the performance of different positioning strategies across different simulated scenarios. To evaluate the approach, a proof-of-concept is implemented, providing the required features to simulate an indoor MANET. The next subsections address the simulation details and analyze the obtained outcomes.
4.1. Simulated Setup
The evaluation of the proposal is performed in a developed proof-of-concept simulator which includes all the relevant variables to study the indoor positioning of a MANET. Next, the details of the implementation, the configured variables for the scenarios and the benchmark algorithms are described.
4.1.1. Proof-of-Concept
The proof-of-concept is implemented as a Python 3.15.5 program (Repository available at https://github.com/Bear-the-box/adaptive-indoor-location-for-manets, accessed on 29 September 2025) that instantiates the complete pipeline and contact synthesis, including relative map recovery, absolute alignment with anchors, self-adaptation of the anchor set, and energy-aware operation. As a result, the tool provides logging and plotting utilities to reproduce the results.
The simulator advances in discrete time windows . At each window, it (i) perturbs the true node coordinates with a mobility model; (ii) generates contact evidence from those coordinates; (iii) converts that evidence into a incomplete pairwise distance matrix ; (iv) reconstructs a relative embedding via the GMDS method; (v) aligns it to the absolute frame using the current anchors via Procrustes; (vi) evaluates performance; and (vii) updates the anchor set under accuracy and energy constraints. The run-time artifacts—per-window logs, positions, and figures—are persisted to disk for posterior analysis.
The mobility model is based on updating node positions in discrete steps of duration using a random waypoint model in two dimensions. At the start of a trip, each node samples a waypoint uniformly over the deployment area and a constant speed (indoor walking range). Upon reaching the waypoint, the node draws a pause time , remains stationary for , and then samples a new waypoint and speed. At each simulator step, positions are updated by straight-line motion:
where w is the current waypoint. Walls are handled with specular reflection at boundaries. To avoid numerical artifacts, speeds below are resampled, and per-step displacement is clipped at . A small zero-mean jitter with is added to emulate local positional noise before contact synthesis. These parameters are used in all experiments.
To emulate encounter-driven operation, the implementation synthesizes contact probabilities from true inter-node distances and then inverts them back to pseudo-distances, thereby isolating the estimation stack from ground truth during the mapping step. The simulator then recovers distances derived from contacts. This choice aims to simplify the execution and focus on studying the performance of the positioning technique without additional complexities. Thus, the strong relationship between encounter frequency/duration and physical proximity in opportunistic settings produces a distance-like quantity that can feed GMDS solvers.
To avoid optimistic bias, the contact generator injects heterogeneity and noise before distances are estimated, so the pipeline is not a forward then perfectly inverted mapping. It includes (i) pair-specific range differences, so some pairs decay faster or slower; (ii) per-node radio power variability, so each device has a fixed gain or attenuation factor; (iii) window-level traffic variability, so some windows are globally more or less interactive; and (iv) random packet loss that thins successful encounters. Aiming to achieve further realism, a simple floorplan occlusion is included to reflect the presence of physical objects.
Floorplan effects are modeled with line-of-sight checks and soft attenuation. If the straight segment between nodes i and j intersects any wall segment in the 2D layout, an attenuation factor is applied, updating the encounter rate. This reduces contacts by randomly generating a value in the interval of 5–10%, obstructing pairs while preserving variability across windows.
At inference time, contacts are mapped to pseudo-distances using the robust normalization and a single decay selected by validation, which is intentionally different from the heterogeneous generator above.
Using Procrustes in the simulator raises practical issues when the active anchor set changes, driving to a drift or jitter alignment. The challenges are varied, and the simulator integrates different approaches accordingly.
- Weak anchor geometry. Nearly collinear or clustered train anchors make the alignment unstable. Then, the implementation uses coverage-aware selection with a farthest first rule to improve spatial spread.
- Too few anchors. A small increases variance in the estimated pose. Thus, the implementation enforces a minimum anchor count , preferably three anchors that are not collinear in two dimensions.
- Reflection ambiguity. With limited geometry, direct and mirrored fits can score similarly. Aiming to address this, the simulator performs an explicit reflection check and keeps the fit with the smaller anchor error.
- Inter window pose jitter. Promotions and demotions change and can cause small jumps in . As a response to this, the proposal applies temporal smoothing to the values.
For each run of the proof-of-concept, it generates (i) a csv file with window-wise K, validation RMSE, global/non-anchor RMSE, objective value, energy spent/remaining, and controller decisions; (ii) a file with the per-window validation curve ; (iii) a csv file with true and estimated coordinates (useful for plotting trajectories); (iv) per-window frames and optional GIF visualizing anchors and true→estimated displacements; and (v) a summary file aggregating means, variability, error, average K, energy totals, and guard activations. A separate aggregator script scans these stats, builds a consolidated dataset, and renders comparative charts: RMSE by method, energy per window, a Pareto plot (accuracy vs. energy), and a combined score with user-defined weights. The complete information is available at the repository of the project (https://github.com/Bear-the-box/adaptive-indoor-location-for-manets, accessed on 29 September 2025).
It is relevant to consider that the assessed proof-of-concept uses contact metadata relevant to evaluate the algorithms, such as node identifiers and contact times/durations. The prototype does not implement a privacy and security layer. Thus, any production deployment that centralizes encounter logs should add pseudonymous or rotating identifiers rather than stable device IDs; strict data minimization and short retention aligned with the windowed computation; and appropriate organizational and technical safeguards. A full privacy design is proposed to be addressed as future works.
The simulator enables a basic definition of contextual variables to build scenarios. In this case, two contexts are proposed. The next subsection details them.
4.1.2. Simulated Scenarios
The evaluation is driven by a set of contextual variables carefully chosen to capture the main factors affecting the performance of the proposed dynamic anchor selection mechanism in indoor MANET deployments:
- Node density. Defined as the number of nodes in the scenario. This variable directly impacts network connectivity, completeness of the distance matrix, and contact frequency.
- Anchor configuration. The number and spatial distribution of anchors influence the accuracy of the Procrustes alignment and the resulting absolute position estimates. Simulations considered both fixed-anchor and dynamic-anchor configurations.
- Localization update strategy. This parameter specifies an estimation based on the windows, where positions are updated once per fixed-length time interval. The window length is set to 40 s based on sensitivity tests, balancing responsiveness and computational cost.
- Energy model. Energy consumption is modeled at the per-window level, with each active anchor incurring a fixed cost in Joules (J/window). This cost accounts for beacon broadcasts, synchronization traffic, and processing overhead in anchor mode. The parameter is calibrated for a representative IoT-class device, such as ESP32, operating at 1 Hz beaconing, yielding J/window, which enables realistic battery lifetime projections.
Using these variables, two main network configurations are designed to assess scalability and robustness. The values defined for contextual variables are determined after sensibility analysis is performed to achieve relevant outcomes for the scenarios.
- Low-Density scenario. This is characterized by sparse connectivity, incomplete distance matrices, and longer inter-contact times. This scenario stresses the localization process, as fewer anchor opportunities and longer gaps between encounters increase the uncertainty in pairwise distance estimation. The context settings emulate large open spaces with few moving devices, such as warehouses, low-occupancy office floors, or industrial facilities during off-peak hours.
- High-Density scenario. This is characterized by frequent contacts and more complete distance matrices, improving the reliability of GMDS reconstruction. However, the higher number of simultaneous transmissions increases the likelihood of energy consumption. The context settings model environments such as conference halls, crowded factories, or open-plan offices during peak activity.
By systematically controlling these variables and comparing the two scenario cases, the simulation campaign evaluates the proposed framework’s ability to maintain accuracy and optimize energy usage across a wide range of realistic indoor MANET conditions. Considering these contemplated variables, Table 3 displays all the relevant contextual variables included in the simulation scenarios.

Table 3.
Simulation grid and defaults used in the simulations.
Each run spans 40 windows to capture controller dynamics over time without excessive runtime. Mobility and observation noise are toggled between low and high settings to emulate smoother versus more volatile motion and sensing. The energy model exposes easy and hard budgets by combining a per-anchor per-window cost with a cumulative cap, so methods that oversubscribe anchors are penalized. Controller parameters follow conservative defaults: a small initial anchor set, single-step changes, short patience and cooldown to react but avoid flapping, and wide bounds on the allowable number of anchors. The distance mapping uses a fixed decay to keep inference stationary across the grid, while the probability floor is defined in the core text to prevent degenerate pseudo-distances. Three adaptive cores and several fixed-K baselines are included to separate the effect of anchor adaptivity from the relative-map engine; GMDS/SMACOF baselines use a mid-range fixed K and typical solver settings. Guards are disabled by default to let the controller express its natural behavior, with a modest maximum per-step displacement recorded for diagnostics. Finally, two independent seeds are run for every grid point, and heavy visual outputs are disabled to keep batch execution tractable.
Regarding the execution environment, all testbed scenarios are executed on a MacBook Pro 14 with an Apple M1 Pro system on a chip and 16 GB of unified memory. The prototype is implemented in Python (NumPy/SciPy) with default single thread settings, without GPU acceleration. Next, the comparative set of algorithms is detailed.
4.1.3. Benchmark Algorithms
We compare four main families of algorithms, chosen to represent both classical and adaptive paradigms in contact-based localization:
- Fixed-anchor MDS (FIXK). These approaches perform classical MDS alignment to a fixed set of anchors with known absolute positions. We evaluate variants with different numbers of anchors, FIXK3, FIXK6, FIXK9, and FIXK12, and two selection schemes: S1, where anchors are preselected based on a uniform spatial distribution, and S2, where anchors are chosen using a farthest-first criterion to maximize geometric diversity. During the simulation, the anchor set remains constant across all time windows, enabling a direct assessment of how anchor quantity affect accuracy and energy usage.
- SMACOF-based MDS. This method applies the SMACOF iterative optimization framework [28] to refine the multidimensional scaling results. Unlike classical MDS, which has a closed decomposition solution, SMACOF iteratively minimizes stress, making it better suited for noisy or incomplete distance matrices, reducing the cost of higher computational complexity.
- GMDS. The original algorithm first constructs a graph from observed pairwise connectivity or contact probabilities [31]. GMDS is well established in network localization, particularly when direct Euclidean distances are unavailable or sparse, and serves as a representative of approaches guided by topologies.
- Benchmark self-adaptive strategies. The proposed adaptive approach dynamically adjusts the number of active anchors and their selection based on recent localization performance and predefined hysteresis thresholds. To isolate the benefit of adaptive anchor control from the choice of the underlying position estimator, we also implement adaptive variants using SMACOF and classical MDS in place of GMDS. This enables a multi-dimensional comparison between static and adaptive anchor management, and between different estimation cores, but keeping identical mobility and noise conditions.
The three baseline approaches’ fixed anchors, SMACOF and GMDS, are included due to their prevalence in the localization literature [28,31] and their complementary trade-offs between computational complexity, accuracy, and robustness to missing data. FIXK variants quantify the performance/energy trade-off as anchor count changes. SMACOF represents an optimization-driven alternative that can handle more irregular input data. GMDS represents a graph-theoretic approach. The adaptive methods, in turn, exploit context-aware adjustments in anchor usage and update frequency to potentially improve energy efficiency without significantly degrading accuracy, offering a more flexible alternative suited for resource-constrained MANET environments.
The applied energy model for benchmark algorithms charges consumption only to nodes operating in anchor mode. The per window cost is , where includes anchor beacons and anchor side processing; non-anchor nodes are not charged. All baselines follow the same policy. GMDS and SMACOF baselines use a fixed anchor budget for alignment in every window, so their per window energy is . Unless otherwise stated, and . FIXK variants use their stated K, and adaptive methods use selected by the controller each window.
Considering the proposed simulated setup, the next section addresses all the details about the performance results obtained in the scenarios.
4.2. Results
Next, the accuracy and energy consumption results are analyzed based on the density scenario. For this, the low-density scenario and high-density context are presented, studying the performance of the RMSE and its impact on the energy requirements based on the anchor usage.
4.2.1. Low-Density Scenario
Next, the obtained accuracy performance and energy consumption corresponding to the low-density scenario are described.
Accuracy Performance
As Figure 3 describes, in the low-density scenario, the GMDS baseline attains the lowest average RMSE, around 11–12 m, confirming that using graph distances extracted from the global contact structure is advantageous when links are sparse and many pairwise measurements are missing. The proposed adaptive[GMDS] variant sits immediately behind GMDS, reaching an average error of 12 m, with narrow Standard Error of the Mean (SEM) bars and visible overlap with GMDS, indicating that its accuracy degradation is marginal despite using a self-tuned number of anchors. By contrast, adaptive[SMACOF] concentrates around 15–16 m and adaptive[classical] degrades further, with 17–18 m of error. These results show that adaptivity in anchor count alone is not enough if the relative-map engine is less robust to missing/noisy distances.
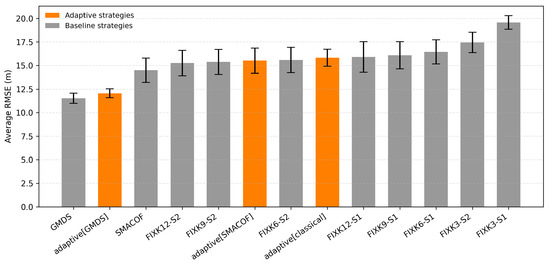
Figure 3.
Average RMSE for each positioning strategy in low-density scenario, including SEM across runs.
Fixed-K baselines show the expected monotone trend: FIXK3 performs worst, while increasing K to 6, 9, 12 reduces error but still does not reach GMDS or adaptive[GMDS]. Across K, the S2 selection is consistently a little better than S1, highlighting the benefit of a more diverse anchor placement.
Taken these outcomes together, the results suggest the following: (i) in sparse contact regimes, graph-aware distance modeling is the dominant factor for accuracy; (ii) combining that modeling with adaptive anchor control preserves GMDS-level precision while enabling anchor reduction; and (iii) methods that rely on classical stress minimization without geodesic preprocessing are more sensitive to low-density incompleteness and exhibit higher error even when anchors are plentiful.
Regarding the performance of the adaptive mechanisms of the proposal in the low-density scenario, Figure 4 details the obtained results for the different strategies applied under the adaptive scheme.
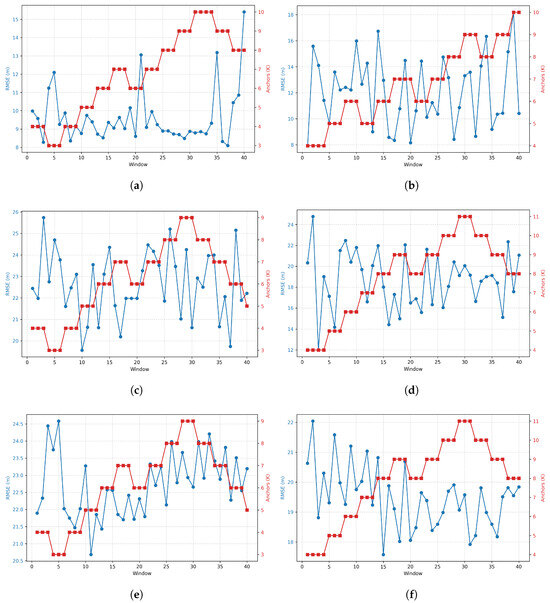
Figure 4.
Evolution of RMSE and active anchors per window in the low-density scenario. Each line corresponds to a strategy; columns correspond to S1 and S2 anchor-selection variants. The left blue y-axis is RMSE (m), while the right red y-axis is the number of active anchors and the x-axis represents the window index. The panels are: (a) adaptive[GMDS], S1; (b) adaptive[GMDS], S2; (c) adaptive[SMACOF], S1; (d) adaptive[SMACOF], S2; (e) adaptive[classical], S1; (f) adaptive[classical], S2.
In the low-density setting, the adaptive controller reacts to sparse evidence by gradually raising the anchor count when RMSE persists above the target, and it does so differently depending on the relative-map engine and the anchor-selection scheme (S1 vs. S2). In Figure 4a adaptive[GMDS] with S1, RMSE stays mostly in the 8–11 m band with a few spikes; K ramps from 3 to 10 and then plateaus, after which RMSE stabilizes. In Figure 4b adaptive[GMDS] with S2, the controller follows a similar trajectory but exhibits larger early variance and occasional peaks up to 16 m, ending at a comparable K; this suggests GMDS is robust in low density and benefits modestly more from S1’s geometry. In Figure 4c adaptive[SMACOF] with S1, RMSE is clearly higher, around 20–25 m for long stretches, despite K rising to 9; this indicates that, under sparse contacts, the SMACOF core struggles to recover a stable relative map even when anchors increase. In Figure 4d adaptive[SMACOF] with S2, RMSE improves versus S1, around 18–22 m, while K reaches 11 and later relaxes, showing that better anchor spread helps SMACOF but does not close the gap with GMDS. In Figure 4e adaptive[classical] with S1, RMSE remains high, around 21–24 m, and volatile; K steps up to 9 and then subsides without delivering a clear accuracy gain, pointing to model limits rather than anchor scarcity. In Figure 4f adaptive[classical] with S2, RMSE is lower than with S1, around 18–22 m, and K peaks higher (11) before the controller trims anchors, confirming that improved anchor geometry mitigates but does not eliminate the deficiency of the classical core under missing data. Overall, adaptive[GMDS] delivers the lowest RMSE and quickest stabilization with moderate K, S2 tends to require more anchors than S1 to reach similar errors, and when the relative-map engine is weaker (SMACOF, classical), the controller increases K but the residual error remains dominated by the embedding quality rather than anchor count.
Energy Consumption
Figure 5 displays the energy consumption average result for each strategy in the low-density scenario. In this case, FIXK3, the fixed-anchor configurations with the smallest number of anchors, achieves the lowest energy usage but at the expense of reduced flexibility and potential accuracy. The adaptive strategies stabilize around 6–7 J/window, consistently higher than FIXK3 but markedly lower than FIXK9 and FIXK12, the more demanding fixed-anchor variants. Importantly, the adaptive methods achieve this intermediate cost while dynamically adjusting anchor usage, suggesting a balance between efficiency and robustness. Meanwhile, GMDS and SMACOF baselines consume even more energy, around 8–9 J/window, without adaptation, underlining that the adaptive approach outperforms them in energy efficiency. Overall, in sparse networks where anchor availability is constrained, adaptive methods demonstrate their ability to limit energy expenditure to moderate levels while avoiding the cost escalation observed in fixed high-anchor baselines.
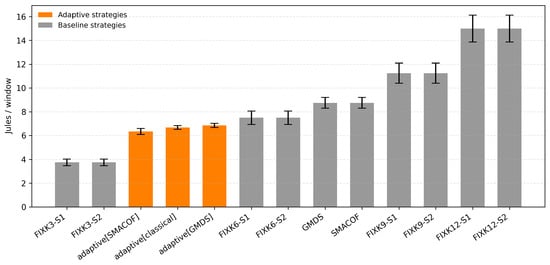
Figure 5.
Energy consumption for each positioning strategy in low-density scenario, including SEM across runs.
Considering these results, the low-density context provides relevant insights about the performance of the proposal, demonstrating a noticeable balance between performance and energy consumption. Next, the same outcomes are analyzed for the high-density scenario.
4.2.2. High-Density Scenario
Next, the obtained accuracy performance and energy consumption corresponding to the high-density scenario are described.
Accuracy Performance
In high-density scenarios, as Figure 6 displays, FIXK12 and FIXK9 configurations achieve the lowest RMSE average. Their advantage comes from having a large number of anchors, which increases the geometric constraints and reduces position uncertainty. However, this comes at the cost of significantly higher energy consumption.
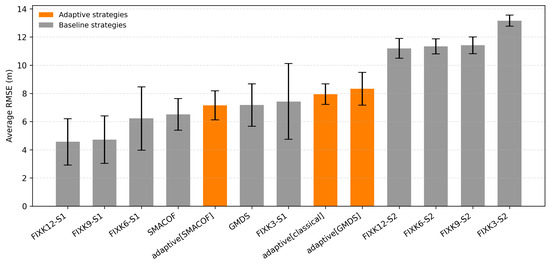
Figure 6.
Average RMSE for each positioning strategy in high-density scenario, including SEM across runs.
In the high-density case, as Figure 6 displays, the best absolute accuracy is achieved by FIXK12 and FIXK9, with average RMSEs in the range of 4.5–5.0 m and visibly low dispersion. Their advantage is unsurprising: with 9–12 anchors, the similarity transform is overconstrained, reducing scale ambiguity and tightening the geometry for all nodes. However, the provided accuracy will imply a higher energy footprint.
Among adaptive methods, adaptive[SMACOF] reaches an error around 7 m, close to the original SMACOF and GMDS fixed baselines, and clearly better than adaptive[classical] and adaptive[GMDS]. This shows that in dense contact regimes, the iterative stress majorization of SMACOF provides a robust relative map even with the self-tuned, lower anchor counts. The GMDS and FIXK3 bars exhibit the widest SEMs, indicating higher run-to-run variability when the anchor geometry is weak or when geodesic distances are sensitive to small graph changes despite many contacts.
As a result, if peak accuracy is the sole objective and energy is abundant, FIXK9–12 is best. If alternative variables, such as energy, must be conserved, it is favorable to explore the other candidates.
Regarding the performance of the adaptive mechanisms in the high-density scenario, Figure 7 displays the evolving performance and the number of required anchors for each adaptive strategy.
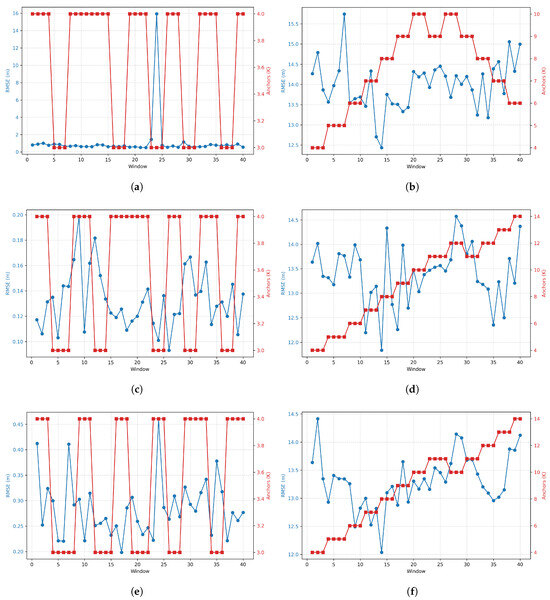
Figure 7.
Evolution of RMSE and active anchors per window in the high-density scenario. Each line corresponds to a strategy; columns correspond to S1 and S2 anchor-selection variants. The left blue y-axis is RMSE (m), while the right red y-axis is number of active anchors. x-axis represents the window index. The panels are: (a) adaptive[GMDS], S1; (b) adaptive[GMDS], S2; (c) adaptive[SMACOF], S1; (d) adaptive[SMACOF], S2; (e) adaptive[classical], S1; (f) adaptive[classical], S2.
In the high-density setting, adaptive behavior is strongly shaped by the initial anchor geometry. Figure 7a adaptive[GMDS], S1 keeps errors low throughout, with RMSE near the 1 m band and a single transient spike that is corrected in the next window; the controller maintains a very small anchor set, mostly 3 or 4, showing that well-spread anchors provide strong geometric leverage. Figure 7b adaptive[GMDS], S2 begins with poorer geometry: RMSE settles around 13–15 m and the controller ramps anchor up to about 9–10 before easing toward about 6; accuracy improves only modestly, indicating that geometry, not just K, is the limiting factor. Figure 7c adaptive[SMACOF], S1 is very stable: RMSE stays in a tight 0.1–0.2 m band with a number of anchors toggling between 3 and 4, confirming that iterative stress majorization copes well when anchors are diverse. Figure 7d adaptive[SMACOF], S2 mirrors the GMDS S2 pattern: the controller steadily increases the number of anchors to the low teens to compensate for clustered or collinear anchors, yet RMSE remains around 12–14 m; adding anchors only partially offsets poor geometry. Figure 7e adaptive[classical], S1 remains near 0.2–0.45 m with K = 3–4, showing that with good geometry even the classical core tracks reliably in dense contact regimes. Figure 7f adaptive[classical], S2 again requires many anchors (up to about 14) while RMSE drifts in the 12–14 m range. Overall, S1 versus S2 cleanly isolates the role of anchor geometry: with diverse anchors, the controller converges to a minimal number of anchors and low RMSE across all cores; with clustered or collinear anchors, it must increase K substantially and still cannot fully recover accuracy, highlighting the value of geometry-aware selection before spending more energy on additional anchors.
Energy Consumption
Figure 8 displays the average energy consumption of the different strategies in the high-density scenario. The overall energy consumption profile follows a similar trend to the low-density case but with clearer distinctions between adaptive and fixed-anchor strategies. Fixed-anchor methods with only three anchors, which is the case of FIXK3, once again achieve the lowest energy costs, averaging below 4 J per window, but they provide limited flexibility and scalability. The adaptive approaches stabilize at intermediate levels of around 6–7 J per window, striking a balance between efficiency and adaptability. Importantly, they remain consistently below the cost of more intensive baselines such as GMDS and SMACOF, around 8–9 J, and far below fixed-anchor variants with larger anchor sets, which escalate to 11–15 J. This indicates that in dense environments, where anchor availability is abundant, adaptive strategies prevent unnecessary energy expenditure by selectively activating anchors, achieving comparable efficiency to classical baselines while avoiding the steep overhead of fixed high-anchor setups.
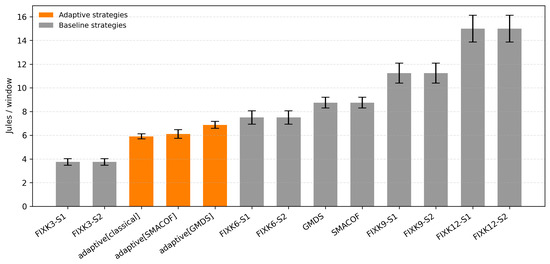
Figure 8.
Energy consumption for each positioning strategy in high-density scenario, including SEM across runs.
After analyzing the results obtained in the low and high-density scenarios, the next subsection studies the global results, normalizing scores and providing an overview of the evaluation.
4.2.3. Global Results
The global average results provide meaningful insights of the overall performance of the approaches involved in the proposal assessment. For this, three main perspectives are provided: summary of the global accuracy, analysis of the global energy consumption, and study of combined scores based on Pareto.
Runtime Results
Table 4 reports average end-to-end runtimes per simulated strategy, separating low-density and high-density cases. Each value includes contact synthesis, relative-map embedding, and Procrustes alignment, averaged across seeds. As expected, HD runs are consistently slower than LD because more nodes and contacts enlarge the observed pair set for the embedding step. SMACOF variants take longer than GMDS or classical due to iterative majorization; fixed-K baselines are faster and scale with K. All configurations remain within the 1–3 min band, supporting the near-real-time viability in our setup.

Table 4.
Average runtime per scenario in seconds. LD = low density; HD = high density.
Global Accuracy
Figure 9 displays the average RMSE for the positioning strategies. The comparative results show that accuracy performance varies significantly across methods. The lowest positioning error is achieved by classic GMDS, with an average RMSE of around 9.35 m, highlighting its strength in capturing geodesic distances despite its higher energy cost.
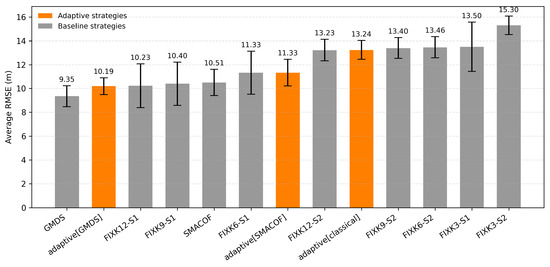
Figure 9.
Comparative of average performance in all scenarios for each positioning strategy, including SEM across runs.
The adaptive[GMDS] strategy performs closely, around 10.19 m, demonstrating that adaptivity can approximate the accuracy of GMDS while being more energy efficient as previous energy reports have displayed. Other adaptive methods show a wider range of outcomes: adaptive[SMACOF] yields moderate accuracy, around 11.33 m, while adaptive[classical] performs worse, around 13.24 m, similar to higher-anchor fixed approaches. Fixed-K methods present mixed results: FIXK12 and FIXK9 perform well, around 10–11 m, but smaller anchor configurations, such as FIXK6 or FIXK3, degrade accuracy substantially, reaching errors above 13 m. Overall, the adaptive strategies strike a favorable balance—particularly adaptive[GMDS], which combines relatively low RMSE with reduced energy demand. At the same time, fixed low-anchor setups clearly sacrifice accuracy, and large-anchor ones improve precision but at excessive energy costs.
Global Energy Consumption
Figure 10 shows a clear monotonic relationship between the anchor budget and energy: FIXK12 is the most expensive, FIXK9 sits in the middle, and FIXK6 is lower. As expected, FIXK3 is the absolute minimum, but it also delivers the weakest accuracy in for RMSE (Figure 9). The adaptive family clusters around 6–7 J/window, yielding sizable savings versus strong fixed baselines: roughly 25–35% less than GMDS/SMACOF (8.5–9) and 40–50% less than FIXK9, while avoiding the accuracy collapse seen with FIXK3. Within fixed-K, S1 vs. S2 variants have nearly identical energy (K dominates cost), so the differences we see in accuracy come from anchor geometry, not energy. Error bars are small, indicating stable consumption across seeds. Overall, adaptive GMDS/SMACOF strike the best efficiency–accuracy balance: they cut anchor transmissions substantially yet remain competitive with the most accurate non-adaptive methods.
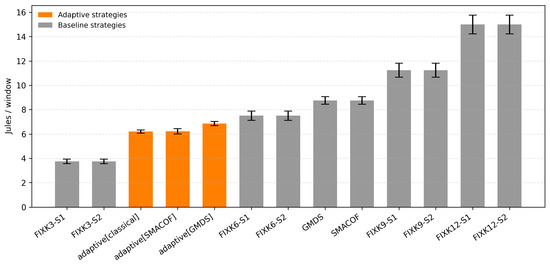
Figure 10.
Global energy consumption of each positioning strategy.
The adaptive strategies stand out as the real winners in energy efficiency while maintaining competitive accuracy. By dynamically reducing anchor usage and update frequency when network conditions allow, they significantly lower communication costs. Among them, adaptive GMDS consistently offers the best trade-off. As the global outcomes become representative, the next subsection addresses a combined score for each strategy, enabling a deeper understanding of the results.
Combined Score and Pareto Analysis
As Figure 11 displays, using equal weights for accuracy and energy (min–max normalized), adaptive[GMDS] ranks first (0.791), edging out GMDS (0.778) and adaptive[SMACOF] (0.724). The gap to GMDS is small (1.3 pp), but it is achieved with notably lower energy, which is exactly what the composite metric rewards. Pure baselines spread out below: SMACOF and FIXK6 form a middle tier; higher-anchor fixed methods, such as FIXK9 or FIXK12, fall sharply because their energy dominates the normalization range.
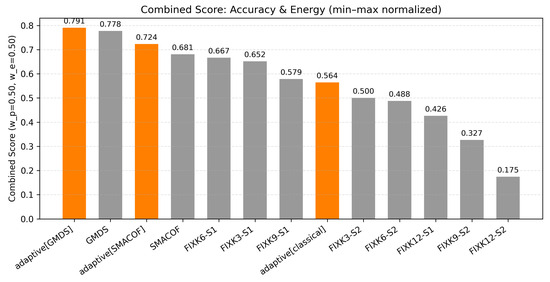
Figure 11.
Combined performance of accuracy and energy consumption for each positioning strategy.
Considering these figures, it is possible to extract two remarks: when energy matters, adaptive anchor control consistently lifts overall efficiency; and among adaptives, GMDS based gives the best balance between accuracy and energy, with adaptive[SMACOF] close behind thanks to even lower energy and only a modest accuracy penalty.
The Pareto front analysis combines average RMSE and average energy per window. As Figure 12 shows, four clusters are described.
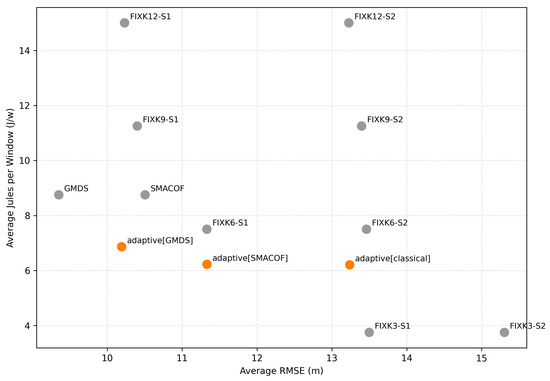
Figure 12.
Pareto front analysis relation between energy consumption and average RMSE for each positioning strategy.
- Adaptive cluster, shaped by 6–7 energy J/window: adaptive[GMDS] sits around 10.2 m, 6.9 u; and adaptive[SMACOF] near 11.4 m, 6.2 u. Both are on the Pareto front: nothing beats them simultaneously in both accuracy and energy. They give sizable energy savings versus GMDS for a modest accuracy cost.
- GMDS baseline, positioned at 9.4 m, 8.8 u. This approach obtains the best accuracy among reduced anchor baselines but at higher energy than the adaptive front. GMDS and adaptive[GMDS] mutually non-dominate each other. As a result, GMDS is more accurate, while adaptive uses less energy.
- Mid/high-anchor fixed baselines, located around 7.5–15 u: FIXK6-S1 sometimes grazes the front in the mid-energy band, but FIXK9/FIXK12 variants clearly fall off the front. These strategies only improve accuracy marginally at a large energy premium, so they are dominated by adaptive methods or GMDS.
- Ultra-low-energy corner, composed by FIXK3. This strategy sits at 3.7 u but with a high RMSE, around 13 and 15 m. It can touch the extreme low-energy end of the front, yet it is far from optimal in accuracy; any practical budget above 4 J/window is better served by an adaptive strategy.
Considering these results, the next subsection details the complete discussion about the results, providing the most relevant insights learned from the experiments.
4.3. Discussion
Across all experiments, the self-adaptive family, most notably adaptive[GMDS], offers the best balance between accuracy and energy. In the low-density scenario, classical GMDS obtains the lowest RMSE due to its global, shortest-path reconstruction over sparse contact graphs. However, adaptive[GMDS] remains very close to this optimum, showing that reducing the number of anchors with diversity aware selection does not collapse accuracy. In contrast, adaptive[SMACOF] and adaptive[classical] are more sensitive to noise and missing distances, leading to larger errors. In the high-density context, fixed high-K baselines achieve the lowest RMSE because abundant anchors over-constrain the alignment; yet adaptive[GMDS] tracks them closely while using fewer anchors on most windows. Taken together, these results indicate that anchor adaptation preserves accuracy in low-density scenarios and safely demotes anchors in high-density contexts.
Energy results mirror the anchor dynamics. The consumption per window of the three adaptive variants clusters below GMDS and far below FIXK9 or FIXK12. FIXK3 is the absolute minimum but implies the lowest accuracy in both densities. The global energy aggregates displays how adaptives are the most energy efficient among all methods that deliver competitive RMSE.
Regarding reflection, the selection of this alteration is extremely rare. Across all runs (two scenarios, 10 seeds each, 300 windows per run; 6000 windows total), the mirrored transform is chosen in only 2 windows (≈0.03%). Both flips occur in early windows with small K and weak anchor geometry (near-collinearity). After the controller increases K and the coverage-aware reselection improves spatial spread, no further flips are observed. In all mirrored cases, the train–anchor alignment error is lower than the direct fit and the validation RMSE is not worse in that window, indicating that the reflection check behaves as intended.
Considering these outcomes, if lifetime is the priority, adaptive[GMDS] is the recommended choice: it stays near the GMDS accuracy band while saving energy per window. If accuracy is the only goal and energy is abundant, GMDS or high–K fixed baselines can reduce RMSE slightly further, but the marginal gains are small relative to the energy penalty. Scheme variants (S1/S2) matter less than whether K is dynamic and diversity-aware.
In the case of the node density, if the context follows sparse low-density deployments, GMDS provides the accuracy ceiling, and adaptive[GMDS] provides a similar performance at lower energetic cost. In dense deployments, fixed high-K baselines can shave a bit more error, but adaptives reclaim most of that accuracy with dramatically better energy efficiency. As a result, adaptive GMDS ranks first in the combined score and defines the Pareto frontier in the regime that matters for battery-powered MANETs.
To sum up, Table 5 compiles the key results of the work. This table compares the global average performance of our proposed adaptive strategies against representative fixed-anchor baselines, providing a clear overview of the trade-offs between localization accuracy and energy efficiency.

Table 5.
Summary of the performance results of benchmark algorithms.
These findings demonstrate that the proposed adaptive methods allow a system to tune its resource use according to current conditions, providing an approach to the negotiation between high accuracy and long battery life. The adaptive GMDS approach delivers nearly the same accuracy as the best fixed-anchor baseline while using less energy, yielding extensions to network lifetime.
5. Conclusions and Future Work
Indoor localization in MANETs faces a persistent trade-off between accuracy and energy consumption. High-precision methods often require frequent updates and large numbers of anchors, increasing energy demands, while low-energy solutions tend to suffer from degraded accuracy. This imbalance limits the scalability and sustainability of location-based services in constrained MANET environments. To address this challenge, this work has introduced adaptive GMDS, an approach that dynamically adjusts anchor selection and update frequency according to network density and conditions, aiming to optimize energy usage while maintaining localization accuracy. Alongside GMDS, two additional adaptive strategies based on MDS and SMACOF have been proposed, achieving very low energy consumption but with higher inaccuracies. Experimental evaluation across both low- and high-density scenarios shows that adaptive GMDS consistently outperforms other strategies, including base GMDS or MDS, providing a substantial energy reduction with only a minimal loss in positioning precision.
Future research will focus on enabling the self-configuration of contextual parameters, such as density thresholds, anchor limits, anchor selection strategy and update intervals, allowing the system to autonomously fine-tune its operation to improve accuracy under varying conditions. Additionally, a proof-of-concept deployment in a real MANET will validate simulation findings against field measurements, bridging the gap between theoretical models and practical implementations. Beyond these steps, robustness will be studied under heterogeneous radios and non-stationary mobility, including mixed BLE/Wi-Fi transmit powers, time-varying crowd densities, and moving anchors; vertical ambiguity in multi-floor buildings will be addressed by extending the 2D pipeline with floor labels and lightweight 2.5D/3D alignment to mitigate cross-floor confusions; and resilience will be stress tested under temporary anchor loss, network partitions, and delayed contact uploads, reporting time-to-recovery, peak error during outages, and energy overshoot. As a result, the implementation of a new proof-of-concept in a real MANET will validate simulation findings against real-world measurements, bridging the gap between theoretical models and practical implementations.
Author Contributions
Conceptualization, M.J.-A., M.Z. and V.N.G.J.S.; methodology, M.J.-A., M.Z. and V.N.G.J.S.; software, M.J.-A., M.Z. and V.N.G.J.S.; validation, M.J.-A., M.Z. and V.N.G.J.S.; funding acquisition, V.N.G.J.S. All authors have read and agreed to the published version of the manuscript.
Funding
V.N.G.J.S. acknowledges that work is funded by FCT/MECI through national funds and, when applicable, co-funded EU funds under UID/50008: Instituto de Telecomunicações.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in https://github.com/Bear-the-box/adaptive-indoor-location-for-manets, accessed on 29 September 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Anagnostopoulos, G.G.; Barsocchi, P.; Crivello, A.; Pendão, C.; Silva, I.; Torres-Sospedra, J. ORDIP: Principle, Practice and Guidelines for Open Research Data in Indoor Positioning. Internet Things 2025, 30, 101485. [Google Scholar] [CrossRef]
- Aziz, T.; Koo, I. A Comprehensive Review of Indoor Localization Techniques and Applications in Various Sectors. Appl. Sci. 2025, 15, 1544. [Google Scholar] [CrossRef]
- Sarkar, N.I.; Ali, M.J. A Study of MANET Routing Protocols in Heterogeneous Networks: A Review and Performance Comparison. Electronics 2025, 14, 872. [Google Scholar] [CrossRef]
- Yamazaki, T.; Ohta, T. A MANET-based Building Evacuation System Considering User Characteristics. In Proceedings of the 2021 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Pervasive Intelligence and Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Virtual, 25–28 October 2021; pp. 124–129. [Google Scholar] [CrossRef]
- Tongesai, M. Enhancing MANETs for military applications: A comprehensive review of innovations, challenges, and research gaps. I-Manag. J. Wirel. Commun. Netw. 2025, 13, 46. [Google Scholar] [CrossRef]
- Wan, S.; Gu, C.; Shu, Y.; Shi, Z. Last-seen time is critical: Revisiting RSSI-based WiFi indoor localization. Signal Process. 2025, 231, 109756. [Google Scholar] [CrossRef]
- Mohsen, M.; Rizk, H.; Yamaguchi, H.; Youssef, M. TimeSense: Multiperson Device-Free Indoor Localization via RTT. IEEE Internet Things J. 2024, 11, 39593–39605. [Google Scholar] [CrossRef]
- Furfari, F.; Girolami, M.; Mavilia, F.; Barsocchi, P. Indoor localization algorithms based on Angle of Arrival with a benchmark comparison. Ad Hoc Netw. 2025, 166, 103691. [Google Scholar] [CrossRef]
- Kharmeh, S.A.; Natsheh, E.; Nasrallah, R.; Masri, M. Triangulation-Enhanced WiFi-Based Autonomous Localization and Navigation System: A Low-Cost Approach. In Proceedings of the 2024 22nd International Conference on Research and Education in Mechatronics (REM), Amman, Jordan, 24–26 September 2024; pp. 69–74. [Google Scholar] [CrossRef]
- Fathalizadeh, A.; Moghtadaiee, V.; Alishahi, M. A survey and future outlook on indoor location fingerprinting privacy preservation. Comput. Netw. 2025, 262, 111199. [Google Scholar] [CrossRef]
- Gomi, H.; Tsubouchi, K.; Teraoka, T. Indoor Trajectory Estimation with Passerby Data without GPS nor WiFi Signals. In Proceedings of the 2025 IEEE International Conference on Pervasive Computing and Communications Workshops and other Affiliated Events (PerCom Workshops), Los Alamitos, CA, USA, 17–21 March 2025; pp. 588–593. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, J.; Cao, Y. A weighted hybrid indoor positioning method based on path loss exponent estimation. Ad Hoc Netw. 2025, 166, 103684. [Google Scholar] [CrossRef]
- Souissi, R.; Sahnoun, S.; Baazaoui, M.K.; Fromm, R.; Fakhfakh, A.; Derbel, F. A Self-Localization Algorithm for Mobile Targets in Indoor Wireless Sensor Networks Using Wake-Up Media Access Control Protocol. Sensors 2024, 24, 802. [Google Scholar] [CrossRef]
- Yu, H.; She, C.; Hu, Y.; Wang, G.; Wang, R.; Vucetic, B.; Li, Y. Floor-Plan-Aided Indoor Localization: Zero-Shot Learning Framework, Data Sets, and Prototype. IEEE J. Sel. Areas Commun. 2024, 42, 2472–2486. [Google Scholar] [CrossRef]
- Li, S.; Tang, Z.; Kim, K.S.; Smith, J.S. On the Use and Construction of Wi-Fi Fingerprint Databases for Large-Scale Multi-Building and Multi-Floor Indoor Localization: A Case Study of the UJIIndoorLoc Database. Sensors 2024, 24, 3827. [Google Scholar] [CrossRef] [PubMed]
- Juston, M.F.R.; Norris, W.R. Ad Hoc Mesh Network Localization Using Ultra-Wideband for Mobile Robotics. Sensors 2024, 24, 1154. [Google Scholar] [CrossRef]
- Di Franco, C.; Marinoni, M.; Bini, E.; Buttazzo, G.C. Dynamic Multidimensional Scaling with anchors and height constraints for indoor localization of mobile nodes. Robot. Auton. Syst. 2018, 108, 28–37. [Google Scholar] [CrossRef]
- Fabris, A.; Kerusauskas Rayel, O.; Luiz Rebelatto, J.; Luiz Moritz, G.; Demo Souza, R. AoA and RSSI-Based BLE Indoor Positioning System With Kalman Filter and Data Fusion. IEEE Internet Things J. 2025, 12, 15348–15359. [Google Scholar] [CrossRef]
- Gaona Juárez, R.; García-Barrientos, A.; Acosta-Elias, J.; Stevens-Navarro, E.; Galván, C.G.; Palavicini, A.; Monroy Cruz, E. Design and Implementation of an Indoor Localization System Based on RSSI in IEEE 802.11ax. Appl. Sci. 2025, 15, 2620. [Google Scholar] [CrossRef]
- Shanthi, C.; Porselvi, R.; A, B.R.; Ganesan, S. Optimizing Indoor Localization and Tracking: An Energy-Efficient Approach Using Received Signal Strength and Mixstyle Neural Networks with Implicit Unscented Particle Filtering. Int. J. Commun. Syst. 2025, 38, e70069. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W. An improved algorithm for indoor localization fingerprint database construction. Ad Hoc Netw. 2025, 175, 103858. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Z.; Zlatanova, S.; Li, S.; Yu, B. Indoor Localization Methods for Smartphones with Multi-Source Sensors Fusion: Tasks, Challenges, Strategies, and Perspectives. Sensors 2025, 25, 1806. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X. DV-Hop Location Algorithm Based on RSSI Correction. Electronics 2023, 12, 1141. [Google Scholar] [CrossRef]
- Shang, Y.; Ruml, W. Improved MDS-based localization. In Proceedings of the IEEE INFOCOM 2004, Hong Kong, China, 7–11 March 2004; Volume 4, pp. 2640–2651. [Google Scholar] [CrossRef]
- Xia, X.; Yan, J.; Wu, C.; Meng, C.; Yan, X. ASL: An Accurate and Stable Localization algorithm for multi-hop irregular networks. J. Netw. Comput. Appl. 2025, 239, 104172. [Google Scholar] [CrossRef]
- Costa, J.A.; Patwari, N.; Hero, A.O. Distributed weighted-multidimensional scaling for node localization in sensor networks. ACM Trans. Sen. Netw. 2006, 2, 39–64. [Google Scholar] [CrossRef]
- Yan, W.; Yin, F.; Wang, J.; Leus, G.; Zoubir, A.M.; Tian, Y. Attentional Graph Neural Network Is All You Need for Robust Massive Network Localization. IEEE J. Sel. Top. Signal Process. 2025, 1–16. [Google Scholar] [CrossRef]
- Lyu, Z.; Bai, S.; Wang, X.; Li, L.; Zhang, G. Wi-Fi RTT Indoor Positioning Using Visibility Matching with NLOS Receptions. IEEE Internet Things J. 2025, 12, 18779–18790. [Google Scholar] [CrossRef]
- Shang, S.; Wang, L. Overview of WiFi fingerprinting-based indoor positioning. IET Commun. 2022, 16, 725–733. [Google Scholar] [CrossRef]
- Tao, Y.; Tan, S.; Yan, R.; Liu, N.; Wang, W.; Lü, J. CBWF+: Collaboratively Enhanced Lightweight Circular-Boundary-Based WiFi Fingerprinting. IEEE Internet Things J. 2025, 12, 650–662. [Google Scholar] [CrossRef]
- Saeed, N.; Nam, H.; Al-Naffouri, T.Y.; Alouini, M.S. A State-of-the-Art Survey on Multidimensional Scaling-Based Localization Techniques. IEEE Commun. Surv. Tutor. 2019, 21, 3565–3583. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).